 |  |  |  |  |  |
En savoir plus: Croissant de Lune |
Auteur: Alain Vienne (et le groupe IREM de Lille1)
Il est peut-être plus facile de voir les 2 cas (coplanaire et non-coplanaire)
en raisonnant sur la sphère des fixes. Précédemment,
on regardait le mouvement diurne d'un point de la sphère des fixes
(le pôle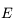 
de l'écliptique) sur la sphère locale (de pôle 
).
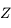Ici, nous allons faire la démarche réciproque: on regarde
le mouvement diurne de 
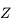sur la sphère des fixes. On utilise la
condition suivante:
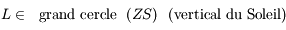
En effet, nous avons vu que c'est la condition pour voir la Lune comme une gondole (ou tout au moins, la Lune à l'horizontal).
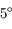au plus (en bas).
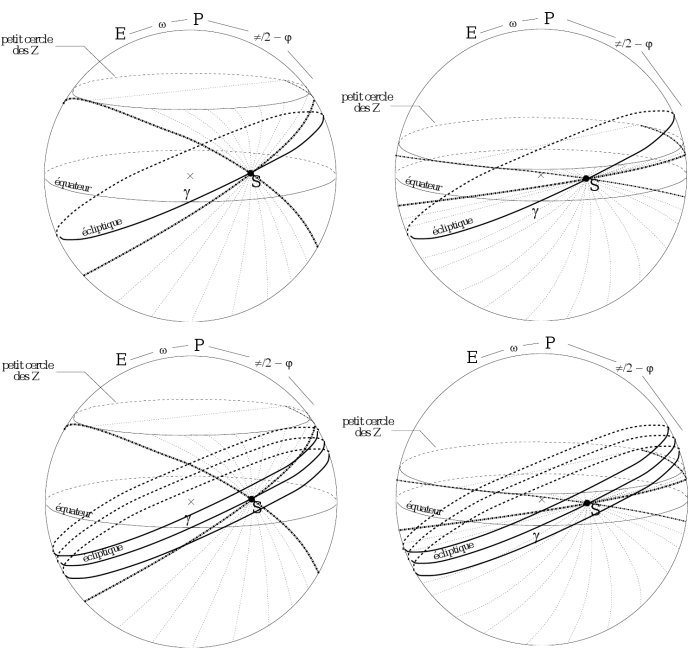
Sur une sphère des fixes où on a placé l'équateur, l'écliptique et
leur pôle, et pour une latitude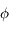 
donnée, on trace le petit
cercle correspondant aux positions prises par le zénith au cours du
mouvement diurne (petit cercle des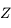 
). A chacune de
ces positions de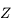 
, il correspond un seul grand cercle passant
par le Soleil: c'est le vertical du Soleil. On obtient ainsi un "faisceau"
de grands cercles dont les sommets sont le Soleil et le point diamétralement
opposé. Sur la figure, pour ne
pas encombrer celle-ci, nous en avons tracé qu'une partie puisque
qu'on les a arrétés au niveau du petit cercle des
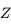. En réalité,
ces grands cercles sont bien complets de sorte que toute la calotte
sphérique se situant au dessus du petit cercle des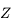 
est parcouru par ces grands cercles. Ainsi
la sphère est divisée en deux parties: celle contenant chaque vertical
du Soleil et l'autre.
La Lune doit se trouver dans la première partie (les "faisceaux" de la figure).
La frontière entre ces deux parties correspond au vertical du Soleil
qui est tangent au petit cercle des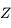 
.
Cas de la Lune sur l'écliptique: Ce cas correspond aux 2 dessins du haut de la figure. En dehors de la zone intertropicale (à gauche), l'écliptique coupe les "faisceaux" qu'en ses sommets: au Soleil et au point diamétralement opposé. Si on impose à la Lune d'être sur l'écliptique, il n'y a qu'en ces points que la condition est réalisée (éclipses). Par contre, dans la zone intertropicale, tout l'écliptique est contenu dans les "faisceaux". Ainsi la condition est réalisée deux fois par jour comme on l'a vu dans précédemment.
Cas où la Lune est de part et d'autre de l'écliptique:
L'orbite de la Lune est inclinée d'environ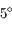 
sur l'écliptique.
Son noeud qui permettrait de positionner le grand cercle correspondant
à son orbite, a un mouvement de rétrograde de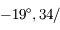 
an (période:
18,6 ans). Pour ne pas rentrer dans trop de détails superflus à la
compréhension, nous allons simplement considérer que la Lune est de
part et d'autre de l'écliptique sur une bande large de 
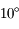. Bien-sur,
il ne faut pas oublier que la Lune parcourt en fait un grand cercle
contenu dans cette bande: la position en longitude dans cette bande
dépend de la date dans la lunaison et la position "verticale"
dans cette bande dépend de la position du noeud de l'orbite lunaire.
On remarque ainsi qu'au voisinage de la pleine Lune ou au voisinage de la nouvelle Lune, la condition de "Lune horizontale" est possible partout sur la Terre. Mais on se rend bien compte que, loin des tropiques, la zone est étroite. Elle s'agrandit au fur et à mesure que le lieu considéré s'approche du tropique.
Dans le cas d'un lieu dans la zone intertropicale, la possibilité d'une telle condition est grande. La probabilité de réalisation l'est donc aussi. Cependant cette probabilité n'est pas 1, car on voit apparaitre une petite zone de la bande lunaire qui croise la partie où il n'y a pas de vertical du Soleil (en dehors des "faisceaux"). Cette zone est petite et proche du Soleil. Ainsi même dans la zone intertropicale, il peut y avoir des jours où la Lune n'est pas vue à l'horizontal. Cela se produit pour des positions particulières de l'orbite lunaire et pour des dates proches de la pleine Lune ou de la nouvelle Lune.
 |  |
