Auteur: Stéphane Erard

 Phénomènes mutuels
Phénomènes mutuels
Difficulté : ☆☆
Temps : 45 min
Le corps céleste A a une période synodique (par rapport à la Terre) de 105 jours et passe à l'opposition à la date 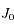 . Six jours plus tard on observe à l'opposition le corps B dont la période synodique est de 81 jours.
. Six jours plus tard on observe à l'opposition le corps B dont la période synodique est de 81 jours.
On veut déterminer la date 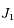 de la prochaine opposition simultanée des deux corps.
de la prochaine opposition simultanée des deux corps.
Question 1)
Trouver une condition permettant de déterminer cette date.
Solution
Question 2)
Trouver une solution particulière de cette équation.
Solution
On commence par chercher une solution particulière de l'équation plus simple 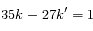 . Le couple (-10, -13) est une telle solution.
. Le couple (-10, -13) est une telle solution.
On aura donc (k,k') = 2(-10,-13) = (-20,-26), solution particulière recherchée.
Question 3)
Déterminer toutes les solutions de l'équation trouvée plus haut.
Solution
Les couples solutions (x,y) sont tels que 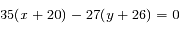 .
.
On cherche y tel que 35 divise 27(y+26), alors que 35 est premier avec 27. Le théorème de Gauss indique que 35 doit être un diviseur entier de y+26, donc qu'il existe un nombre k tel que 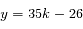
En remplaçant y dans l'équation, on trouve 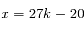 , donc la solution générale est l'ensemble des couples (27k-20,35k-26), où k est un entier.
, donc la solution générale est l'ensemble des couples (27k-20,35k-26), où k est un entier.
Question 4)
Quelle est la date de la prochaine opposition commune ?
Solution
Le plus court intervalle correspond à k = 1, soit 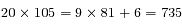 jours.
jours.
Question 5)
Application à Mars et Jupiter : une opposition de Mars a eu lieu le 24/12/2007, l'opposition suivante de Jupiter le 4/7/2008. Les périodes synodiques respectives sont de 780 et 399 jours. Quand se produira la prochaine opposition simultanée des deux planètes ?
AideSolution
L'intervalle entre les deux oppositions est de 193 jours (on calcule ce type d'intervalle en convertissant les dates en jours juliens, ce que font tous les tableurs courants).
Le même calcul que précédemment donne
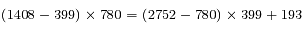 jours, soit ~ 2156 années.
On remarque aussi que ce résultat dépend de l'échelle d'échantillonnage adoptée : l'intervalle d'une journée est parfaitement arbitraire.
jours, soit ~ 2156 années.
On remarque aussi que ce résultat dépend de l'échelle d'échantillonnage adoptée : l'intervalle d'une journée est parfaitement arbitraire.


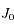 . Six jours plus tard on observe à l'opposition le corps B dont la période synodique est de 81 jours.
. Six jours plus tard on observe à l'opposition le corps B dont la période synodique est de 81 jours.
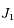 de la prochaine opposition simultanée des deux corps.
de la prochaine opposition simultanée des deux corps.