Auteur: Alexandre Pousse

 Propriété des réduites
Propriété des réduites
Difficulté : ☆
Temps : 10 min
Soient 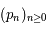 et
et 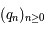 , deux suites d'entiers. Rappelons la propriété sur les réduites donnée dans le cours:
, deux suites d'entiers. Rappelons la propriété sur les réduites donnée dans le cours:
si 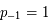 ,
, 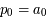 et
et 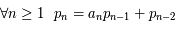 ,
,
et si 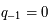 ,
, 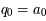 et
et 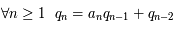 ,
,
alors ![\forall n \geq 0~~ \frac{p_n}{q_n} = [a_0;a_1;a_2;a_3;...a_n]](../pages_quotient/equations_quotient/equation93.png) .
.
Question 1)
Démontrer la propriété des réduites.
Solution
Raisonnement par récurrence. Vérifier que la propriété est vraie aux premiers rangs, puis la supposer vraie au rang n. Enfin, montrer que l'hérédité de la propriété en remarquant que ![\frac{p_{n+1}}{q_{n+1}} = [a_0;a_1;a_2;a_3;\dots;a_n;a_{n+1}]=[a_0;a_1;a_2;a_3;\dots;a_n + \frac{1}{a_{n+1}}]](../pages_quotient/equations_quotient/equation94.png) et en l'appliquant au rang n.
et en l'appliquant au rang n.
Auteur: Alexandre Pousse

 Une meilleure approximation de l'année tropique
Une meilleure approximation de l'année tropique
Difficulté : ☆
Temps : 30 min
Une année tropique correspond au temps s'écoulant entre deux équinoxes de printemps, c'est-à-dire 365.24219052 jours (année tropique moyenne à J2000). C'est donc l'année permettant "le retour des saisons" au mêmes dates et donc compensant le phénomène de précession des équinoxes.
En effet, avant la réforme du calendrier par Grégoire XIII au XVIe siècle, le calendrier était le calendrier Julien, établi par l'astronome Sosigène d'Alexandrie et comportant 365.25 jours (année bissextile tous les quatre ans). Cela impliquait un décalage d'un jour tous les 128 ans, d'où modification de la date de retour des saisons.
L'idée de cet exercice est de comprendre le calendrier utilisé aujourd'hui, puis de trouver par l'intermédiaire d'une fraction continue une valeur plus stable de l'année.
Question 1)
L'année grégorienne correspond à 366 jours les années multiples de quatre et non multiples de cent sauf les année multiples de quatre cents. Sinon, l'année vaut 365 jours.
Établir la valeur et la fraction représentant la partie décimale de l'année grégorienne.
Solution
"L'année grégorienne correspond à 366 jours les années multiples de quatre et non multiples de cent sauf les année multiples de quatre cents. Sinon, l'année vaut 365 jours."
"...Sinon, l'année vaut 365 jours.", donc par défaut 365 jours, après il faut regarder quand ajouter ou soustraire un jour.
"...366 jours les années multiples de quatre...", donc 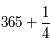 .
.
"...et non multiples de cent ...", donc 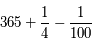 .
.
"...sauf les année multiples de quatre cents.", donc 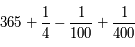 .
.
Ainsi, une année grégorienne correspond à 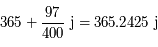
Question 2)
On définira la notion de stabilité comme l'écart la durée de l'année estimée et la durée de l'année tropique moyenne. Le réel obtenu permet de déduire le décalage du retour des équinoxes.
Évaluer la stabilité du calendrier grégorien. Au bout de combien de temps le calendrier se décale d'un jour?
Solution
Il suffit d'évaluer l'écart avec l'année tropique. Après calcul, on obtient qu'il se produit un décalage d'un jour au bout de 3231 années.
Question 3)
En utilisant la méthode d'approximation des nombres à l'aide d'une fraction continue, trouver une nouvelle définition de l'année beaucoup plus stable que l'année grégorienne. Proposer une méthode d'application pour remplacer le calendrier actuel.
Solution
Détermination de la fraction continue (par la méthode d'approximation d'un réel décrite précédemment), des réduites (par la relation de récurrence) et de la stabilité (au bout de combien de temps, y a-t-il décalage d'un jour?):
![\frac{p_0}{q_0} = [365]= 365](../pages_quotient/equations_quotient/equation99.png) donne un décalage d'un jour en 4 ans.
donne un décalage d'un jour en 4 ans.
![\frac{p_1}{q_1} = [365;4]= 365+\frac{1}{4}](../pages_quotient/equations_quotient/equation100.png) donne un décalage d'un jour en 128 ans.
donne un décalage d'un jour en 128 ans.
![\frac{p_2}{q_2} = [365;4;7]= 365+\frac{7}{29}](../pages_quotient/equations_quotient/equation101.png) donne un décalage d'un jour en 1232 ans.
donne un décalage d'un jour en 1232 ans.
![\frac{p_3}{q_3} = [365;4;7;1]= 365+\frac{8}{33}](../pages_quotient/equations_quotient/equation102.png) donne un décalage d'un jour en 4278 ans.
donne un décalage d'un jour en 4278 ans.
![\frac{p_4}{q_4} = [365;4;7;1;3]= 365+\frac{31}{128}](../pages_quotient/equations_quotient/equation103.png) donne un décalage d'un jour en 331455 ans.
donne un décalage d'un jour en 331455 ans.
Ainsi, la réduite 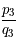 permet une meilleure approximation de l'année que l'année grégorienne mais la mise en place ne serait pas aisée pour un gain de stabilité d'un millénaire.
permet une meilleure approximation de l'année que l'année grégorienne mais la mise en place ne serait pas aisée pour un gain de stabilité d'un millénaire.
Par contre 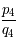 serait énormément plus interessant! Pour l'adopter, nous pouvons par exemple proposer de faire des années bissextiles les années multiples de quatre sauf les années multiples de 128 (pas évident à réaliser mais finalement peu contraignant au regard des 331455 ans de stabilité!).
serait énormément plus interessant! Pour l'adopter, nous pouvons par exemple proposer de faire des années bissextiles les années multiples de quatre sauf les années multiples de 128 (pas évident à réaliser mais finalement peu contraignant au regard des 331455 ans de stabilité!).
Auteur: Alexandre Pousse

 L'automate de Huygens
L'automate de Huygens
Difficulté : ☆
Temps : 30 min
Christian Huygens, mathématicien et astronome du XVIIe siècle, souhaitait réaliser un automate planétaire permettant de modéliser l'évolution du système solaire au cours du temps (en approximation circulaire). À cet époque, le système solaire ne comprend que 6 planètes (Mercure, Venus, Terre, Mars, Jupiter et Saturne). Rappelons qu'un automate est un système composé d'une manivelle reliée à différents rouages, chacun associé à la période de révolution d'une planète par leur nombre de dents.
Lors de la conception de cet objet, Huygens se retrouve confronté à une difficulté: le rapport de l'année terrestre et de celle de Saturne. Combien faut-il de dents sur les deux engrenages pour décrire convenablement le mouvement de la Terre et de Saturne au cours de leur révolution?
Question 1)
Dans l'approximation d'orbites circulaires, poser l'équation diophantienne du problème de l'automate.
Solution
Soient X et Y entiers naturels correspondant au nombre de dents sur chaque engrenage associé à une planète. Alors l'équation diophantienne à résoudre est 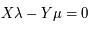 où λ est associée à la révolution de Saturne et μ de la Terre.
où λ est associée à la révolution de Saturne et μ de la Terre.
Question 2)
Sur son orbite, la Terre parcourt un angle 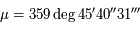 en un an. De même en un an, Saturne réalise
en un an. De même en un an, Saturne réalise 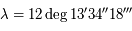 (Ce sont les valeurs de l'époque).
(Ce sont les valeurs de l'époque).
Établir la fraction rationnelle donnée par le rapport 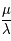 . Est-il raisonnable de réaliser deux engrenages associés à cette fraction?
. Est-il raisonnable de réaliser deux engrenages associés à cette fraction?
Solution
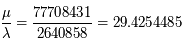 .
Ainsi il faudrait deux engrenages contenant 2640858 dents pour la Terre et 77708431 dents pour Saturne...difficilement réalisable à l'époque même avec les meilleures techniques d'horlogerie!
.
Ainsi il faudrait deux engrenages contenant 2640858 dents pour la Terre et 77708431 dents pour Saturne...difficilement réalisable à l'époque même avec les meilleures techniques d'horlogerie!
Question 3)
Maintenant, afin de supprimer ce problème technique, introduire la notion de fraction continue pour résoudre le problème par approximation diophantienne.
Solution
Question 4)
Huygens définit la notion de stabilité comme le décalage entre l'angle parcouru par Saturne sur son automate et dans la réalité après que la Terre ait réalisé 100 révolutions.
À l'aide d'un développement en fraction continue, proposer un engrenage satisfaisant d'un point de vue technique (au delà d'un millier de dents, la réalisation est difficile) et stable au sens de Huygens.
Solution
Il faut décomposer 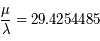 en une fraction continue tout en contrôlant la stabilité (
en une fraction continue tout en contrôlant la stabilité (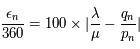 ):
):
![\frac{p_0}{q_0} = [29]= 29](../pages_quotient/equations_quotient/equation118.png) donne un décalage de 17,95° sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 17,95° sur la position de Saturne après 100 tours de la Terre.
![\frac{p_1}{q_1} = [29;2]= \frac{59}{2}](../pages_quotient/equations_quotient/equation119.png) donne un décalage de 3.09° sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 3.09° sur la position de Saturne après 100 tours de la Terre.
![\frac{p_2}{q_2} = [29;2;2]= \frac{147}{5}](../pages_quotient/equations_quotient/equation120.png) donne un décalage de 1,06° sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 1,06° sur la position de Saturne après 100 tours de la Terre.
![\frac{p_3}{q_3} = [29;2;2;1]= \frac{206}{7}](../pages_quotient/equations_quotient/equation121.png) donne un décalage de 7.79' sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 7.79' sur la position de Saturne après 100 tours de la Terre.
![\frac{p_4}{q_4} = [29;2;2;1;5]= \frac{1177}{40}](../pages_quotient/equations_quotient/equation122.png) donne un décalage de 1.12' sur la position de Saturne après 100 tours de la Terre.
donne un décalage de 1.12' sur la position de Saturne après 100 tours de la Terre.
Ainsi, en tenant compte qu'il est difficile de construire des engrenages comportant plus de 1000 dents et au regard de la stabilité obtenue après 100 révolutions de la Terre, le système le plus optimal serait d'utiliser une roue comportant 7 dents pour la Terre et 206 dents pour Saturne.
C'est ce qu'avait conclu Christian Huygens à son époque!
Auteur: Alexandre Pousse

 Le cycle de Saros
Le cycle de Saros
Difficulté : ☆
Temps : 60 min
Un cycle de Saros correspond à 223 lunaisons. C'est une période associée au retour d'une éclipse de Soleil (resp. de Lune) après une éclipse totale. Ainsi, si une éclipse a lieu à un instant t alors il est possible de prédire qu'au temps t+223 lunaisons il s'en reproduira une autre.
L'idée de cet exercice est de comprendre et de retrouver pourquoi nous avons ce nombre de 223 lunaisons pour le retour d'une éclipse.
Question 1)
Définir géométriquement la notion d'éclipse de Lune (resp. de Soleil) vu de la Terre (avec la notion de droite ou de plan par exemple).
Solution
Question 2)
Caractériser la notion d'éclipse en terme de position de la Lune sur son orbite ainsi que de son éclairement relatif à la Terre.
Solution
Le plan orbital de la Lune étant incliné relativement au plan de l'écliptique, une éclipse apparaît lorsque le satellite naturel de la Terre passe à l'intersection du plan orbital de la Terre et de celui de l'orbite lunaire. Sur l'ellipse décrite par la Lune, ce sont deux points appelés noeud ascendant et descendant.
En terme d'éclairement de la Lune relativement à la Terre, le fait d'appartenir à la droite 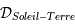 signifie soit une nouvelle-lune (Lune invisible sur Terre) pour l'éclipse de Soleil, soit une pleine-lune pour l'éclipse de Lune.
signifie soit une nouvelle-lune (Lune invisible sur Terre) pour l'éclipse de Soleil, soit une pleine-lune pour l'éclipse de Lune.
Question 3)
Introduisons deux notions pour la détermination de cycle de Saros.
Le mois draconitique, c'est le temps que met la Lune à partir du noeud ascendant pour y revenir. La durée du mois draconitique est de 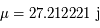 .
.
Le mois synodique ou lunaison est le temps entre deux nouvelles Lunes successives. Sa durée est d'en moyenne 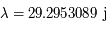 .
.
Dans l'approximation d'orbites circulaires, poser l'équation diophantienne du problème du retour d'éclipse.
Solution
En partant d'une éclipse, et donc nouvelle/pleine-lune et Lune au noeud ascendant/descendant, pour prédire une nouvelle éclipse il doit exister une équation diophantienne reliant les deux périodes. Soient X et Y entiers naturels alors l'équation diophantienne à résoudre est 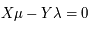 .
.
Question 4)
Introduire la notion de fraction continue pour résoudre le problème par approximation diophantienne.
Solution
Question 5)
Rappelons que le diamètre de la Lune et du Soleil vu de la Terre est de 30' d'arc.
Établir l'erreur de coincidence maximal pour que l'on ait une éclipse (on considère qu'une éclipse partielle est encore une éclipse).
Solution
Dans l'approximation des orbites circulaires, la Lune parcourt 1° en 1h48min relativement à l'axe formé par les noeuds. De même, la Lune relativement à l'axe Terre-Soleil parcourt 1° en 1h58min.
Il n'y a plus éclipse lorsque le centre de la Lune est à plus de 0.5° du passage au noeud ascendant ou à 0.5° de l'axe Terre-Soleil sur le cercle décrivant la lunaison.
Ainsi, nous pouvons considérer qu'il n'y a plus éclipse lorsque l'écart de coincidence en temps est supérieur à 54min (on regarde le minimum des deux temps de parcours pour 1° et on évalue le temps que met le centre de la Lune pour être décallé de plus de 0.5° par rapport au point donnant une éclipse totale).
Donc, pour retrouver une éclipse (totale ou partielle) à partir d'une configuration d'éclipse totale, il faut trouver deux entiers, X et Y tels que 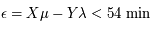 .
.
Question 6)
Développer la fraction continue jusqu'au terme adéquat (évaluation des réduites et contrôle de l'erreur de coïncidence).
Solution
Détermination de la fraction continue (par la méthode d'approximation d'un réel décrite précédemment), des réduites (par la relation de récurrence) et des erreurs de coïncidence associées (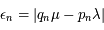 ):
):
![\frac{p_0}{q_0} = [1]= 1~~\mbox{ et } \epsilon_0 = 2\mbox{j}~7\mbox{h}38\mbox{min}](../pages_quotient/equations_quotient/equation139.png)
![\frac{p_1}{q_1} = [1;11]= \frac{12}{11}~~\mbox{ et } \epsilon_1 = 1\mbox{j}~16\mbox{h}58\mbox{min}](../pages_quotient/equations_quotient/equation140.png)
![\frac{p_2}{q_2} = [1;11;1]= \frac{13}{12}~~\mbox{ et } \epsilon_2 = 14\mbox{h}41\mbox{min}](../pages_quotient/equations_quotient/equation141.png)
![\frac{p_3}{q_3} = [1;11;1;2]= \frac{38}{35}~~\mbox{ et } \epsilon_3 = 11\mbox{h}36\mbox{min}](../pages_quotient/equations_quotient/equation142.png)
![\frac{p_4}{q_4} = [1;11;1;2;1]= \frac{51}{47}~~\mbox{ et } \epsilon_4 = 3\mbox{h}12\mbox{min}](../pages_quotient/equations_quotient/equation143.png)
![\frac{p_5}{q_5} = [1;11;1;2;1;3]= \frac{191}{176}~~\mbox{ et } \epsilon_5 = 2\mbox{h}21\mbox{min}](../pages_quotient/equations_quotient/equation144.png)
![\frac{p_6}{q_6} = [1;11;1;2;1;3;1]= \frac{242}{223}~~\mbox{ et } \epsilon_6 = 45\mbox{min}](../pages_quotient/equations_quotient/equation145.png)
Question 7)
Conclure sur la notion de cycle de Saros.
Solution
Par la question précédente, nous pouvons conclure qu'après un temps correspondant à 223 lunaisons après une éclipse totale (où 242 mois draconitiques), nous sommes dans une configuration d'éclipse approchée avec un écart de 42 minutes sur la configuration exacte mais suffisamment proche de celle-ci pour que le disque lunaire intersecte le disque solaire (éclipse de Soleil) ou que le disque lunaire entre dans le cône d'ombre de la Terre (éclipse de Lune).
Ainsi, un cycle de Saros, c'est-à-dire le temps pour prédire le retour d'une éclipse (après une éclipse totale) est bien de 223 lunaisons.
Question 8)
Vous vous rappelez peut-être de l'éclipse totale de Soleil du 11 août 1999 (éclipse totale de la Normandie à l'Alsace en France et partielle au voisinage de cette bande). Déterminer quand cette configuration va t-elle se reproduire? Va t-elle avoir lieu aux mêmes longitudes?
Solution
Tout d'abord, 223 lunaisons correspond à 6585.38 jours, c'est-à-dire un peu plus de 18 ans. Or entre le 11 août 1999 et 2017, il y a 5 années bissextiles. Donc l'éclipse se déroulera 18 ans et 10 jours après: le 21 août 2017.
Par contre, les 0.38 jours restant impliquent que la Terre aura tourné d'un quart sur son axe ce qui correspond approximativement aux longitudes de l'Amérique du Nord. Donc, malheureusement invisible en France...


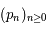 et
et 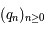 , deux suites d'entiers. Rappelons la propriété sur les réduites donnée dans le cours:
, deux suites d'entiers. Rappelons la propriété sur les réduites donnée dans le cours:
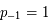 ,
, 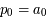 et
et 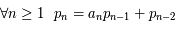 ,
,
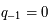 ,
, 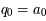 et
et 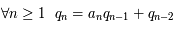 ,
,
![\forall n \geq 0~~ \frac{p_n}{q_n} = [a_0;a_1;a_2;a_3;...a_n]](../pages_quotient/equations_quotient/equation93.png) .
.
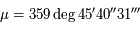 en un an. De même en un an, Saturne réalise
en un an. De même en un an, Saturne réalise 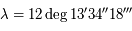 (Ce sont les valeurs de l'époque).
(Ce sont les valeurs de l'époque).
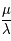 . Est-il raisonnable de réaliser deux engrenages associés à cette fraction?
. Est-il raisonnable de réaliser deux engrenages associés à cette fraction?
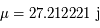 .
.
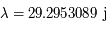 .
.