Ex: Atome de Bohr

Auteur: Stéphane Erard

Modèle de Rutherford

Difficulté : ☆ Temps : 30 min

Un des premiers modèles atomiques modernes est celui de Rutherford (1911), s'appuyant sur des expériences de diffusion de particules alpha. Ce modèle suppose que l'atome est formé d'un noyau de très petites dimensions chargé positivement, autour duquel gravitent des électrons négatifs beaucoup moins massifs sur des orbites circulaires. En raison d'une analogie évidente, on l'appelle modèle planétaire.

Question 1)

On considère un atome d'hydrogène où un électron unique orbite autour d'un noyau de charge unité. L'électron est soumis à une force électrostatique d'intensité 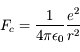$F_c = \frac{1}{4\pi\epsilon_0} \frac{e^2}{r^2}$

où e est la charge de l'électron et du noyau (opposées), r leur distance et 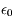$\epsilon_0$ une constante physique (permittivité du vide).

Ecrire la distance électron-noyau dans ce modèle.

Aide Solution

Question 2)

Calculer l'énergie totale (cinétique et potentielle).

Solution

Auteur: Stéphane Erard

Atome de Bohr

Difficulté : ☆ Temps : 45 min

Une difficulté avec le modèle de Rutherford est qu'il ne rend pas compte des expériences de spectroscopie de l'époque et de l'existence de raies spectrales. Par ailleurs, l'électrodynamique classique prévoit que les électrons devraient rayonner et perdre de l'énergie, ce qui les ferait tomber sur le noyau très rapidement. Niels Borh travaillait à ce problème quand il prit connaissance de la formule de Balmer qui donne la position observée des raies spectrales de l'hydrogène dans le visible :

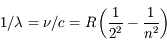
$1/ \lambda = \nu / c = R\left(\frac{1}{2^2} - \frac {1}{n^2} \right)$

où 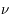$\nu$ est la fréquence associée, n est un nombre entier > 2, R une constante et c la vitesse de la lumière.

Par ailleurs il connaissait l'hypothèse d'Einstein formulée pour l'étude de l'effet photo-électrique : la lumière peut se décomposer en "quanta" (les photons) dont l'énergie est liée à la fréquence 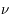$\nu$ du rayonnement : $E = h \nu$ .

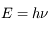En rapprochant ces faits, Bohr formula l'hypothèse que l'atome ne peut prendre que certains états d'énergie donnés dans son modèle atomique (1913).

Question 1)

Calculer les longueurs d'onde des raies visibles et dessiner le spectre de l'hydrogène à l'aide de la formule ci-dessus. On prendra les raies de Balmer n = 3 à 6 qui sont dans le domaine visible, et 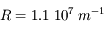$R = 1.1\;10^7\; m^{-1}$ (constante de Rydberg).

Solution

Série de Balmer
Niveau de départ	Niveau d'arrivée	Nom de la raie	Longueur d'onde (nm)
3	2	$H_{\alpha}$	656
4	2	$H_{\beta}$	486
5	2	$H_{\gamma}$	434
6	2	$H_{\delta}$	410

Question 2)

Ecrire les variations d'énergie de l'atome d'hydrogène liées à l'émission d'une raie de la série de Balmer.

Solution

Question 3)

En déduire les valeurs possibles du rayon de l'électron et du moment cinétique 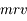mrv .

Solution

Question 4)

Comment interpréter ce résultat ?

Solution

remarque

Les autres séries de raies de l'hydrogène correspondent à des transitions vers les couches n ≠ 2. On peut représenter les niveaux énergétiques de l'hydrogène de la façon suivante :

Diagramme énergétique de l'hydrogène

Crédit : Astrophysique sur Mesure / FSU

La première raie de Balmer 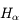$H_{\alpha}$ est particulièrement importante en Astronomie car elle permet de détecter l'hydrogène atomique dans le milieu interstellaire.