Détermination de zéro par dichotomie
C'est une méthode simple à comprendre et efficace car fonctionnant toujours, mais avec le désavantage de ne pas converger rapidement vers la solution.
Elle repose sur le théorème de la valeur intermédiaire :
Si nous prenons un intervalle [a,b] tel que
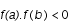
, alors nous savons que la fonction f s'annule dans l'intervalle (ici f représente l'une des 3 fonctions dont nous cherchons le zéro), nous pouvons donc couper l'intervalle en deux partie égale : [a,c] et [c,b]. Il suffit alors, comme sur le schéma ci-dessous,de comparer
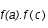
et
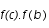
pour savoir si le zéro de la fonction est dans l'intervalle [a,c] ou [c,b].
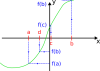
Ainsi nous n'obtenons pas la valeur exacte de l'abscisse du zéro de la fonction mais un encadrement. Et à chaque fois que nous appliquons la dichotomie, cet intervalle diminue de moitié. Dans ce programme, nous utilisons la dichotomie pour encadrer le zéro des fonction au dixième de la distance entre les deux corps pesants.

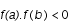 , alors nous savons que la fonction f s'annule dans l'intervalle (ici f représente l'une des 3 fonctions dont nous cherchons le zéro), nous pouvons donc couper l'intervalle en deux partie égale : [a,c] et [c,b]. Il suffit alors, comme sur le schéma ci-dessous,de comparer
, alors nous savons que la fonction f s'annule dans l'intervalle (ici f représente l'une des 3 fonctions dont nous cherchons le zéro), nous pouvons donc couper l'intervalle en deux partie égale : [a,c] et [c,b]. Il suffit alors, comme sur le schéma ci-dessous,de comparer 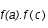 et
et 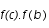 pour savoir si le zéro de la fonction est dans l'intervalle [a,c] ou [c,b].
pour savoir si le zéro de la fonction est dans l'intervalle [a,c] ou [c,b].