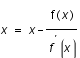Détermination de zéro par méthode de Newton-Raphson
Une fois l'encadrement au dixième donné par dichotomie, nous utilisons la méthode de Newton Raphson pour déterminer une valeur approchée à
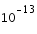
près.
Pour cela, nous utilisons la connaissance de la fonction et de sa dérivée. Le principe est celui exposé dans le schéma. Donc, pour un point donné, nous calculons l'ordonnée et la valeur de la dérivée. Ceci nous permet de déterminer une nouvelle valeur d'abscisse plus proche du zéro de la fonction par la formule :
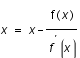
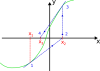
L'intérêt de la méthode de Newton Raphson est qu'elle est quadratique, i.e. que le nombre de chiffres significatifs double à chaque itération. En revanche, si la fonction présente un extremum local, il y a risque que jamais la méthode ne converge, car alors, la valeur de la dérivée est nulle et le nouveau point n'est pas plus proche du zéro mais à l'infini.
C'est pour cela que nous commençons par utiliser la dichotomie pour être suffisamment proche du zéro, sans problèmes de convergence, puis nous changeons d'algorithme de manière à être plus rapide une fois les éventuels problèmes de convergence éliminés.

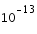 près.
près.