L'analyse des spectres interstellaires requiert l'introduction d'un certain nombre de notions théoriques de transfert de rayonnement. Cette théorie consiste en une description macroscopique de la propagation du rayonnement et de son interaction avec la matière qui compose le milieu traversé. Dans cette description le rayonnement est supposé se propager, dans le vide ou dans un milieu homogène, rectilignement (les lignes de propagation sont appelées rayons) si l'échelle du système considéré est très supérieure à la longueur d'onde du rayonnement.
 Intensité spécifique
Intensité spécifique
On considère en un point de l'espace un faisceau de rayonnement contenu dans un angle solide 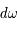 , dans un intervalle de fréquence de
, dans un intervalle de fréquence de 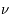 à
à 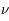 +
+ 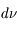 et traversant une surface
et traversant une surface 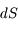 perpendiculaire à sa direction de propagation. L'énergie de ce rayonnement qui passe à travers la surface pendant le temps
perpendiculaire à sa direction de propagation. L'énergie de ce rayonnement qui passe à travers la surface pendant le temps 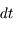 est :
est :
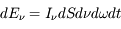 .
Le coefficient de proportionnalité
.
Le coefficient de proportionnalité 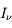 dans cette expression est appelé intensité spécifique et représente donc l'énergie par unité de surface, par unité de fréquence, par unité d'angle solide et par unité de temps, qui traverse une surface perpendiculaire au faisceau de rayonnement. L'intensité spécifique s'exprime en erg cm-2 Hz-1 sr-1 s-1 dans le système CGS.
Si la direction du rayonnement, centrée sur l'angle solide
dans cette expression est appelé intensité spécifique et représente donc l'énergie par unité de surface, par unité de fréquence, par unité d'angle solide et par unité de temps, qui traverse une surface perpendiculaire au faisceau de rayonnement. L'intensité spécifique s'exprime en erg cm-2 Hz-1 sr-1 s-1 dans le système CGS.
Si la direction du rayonnement, centrée sur l'angle solide 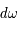 , fait un angle
, fait un angle 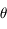 avec la normale à
avec la normale à 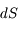 (voir la figure), la surface efficace perpendiculaire au faisceau vaut
(voir la figure), la surface efficace perpendiculaire au faisceau vaut 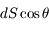 et l'énergie s'écrit alors :
et l'énergie s'écrit alors : 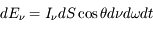 .
.
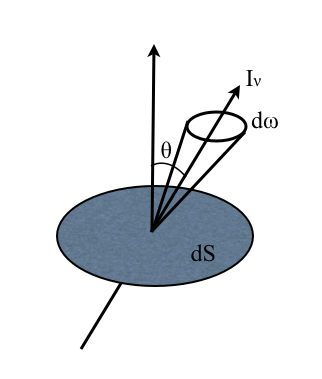
Crédit :
Cecilia Pinto
L'intensité spécifique est fonction du point de l'espace considéré, de la direction du rayonnement, de la fréquence et du temps. Elle peut être exprimée en termes de longueur d'onde plutôt que de fréquence avec l'égalité : 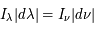 . Puisque
. Puisque 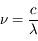 , on en déduit que
, on en déduit que 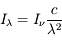 avec
avec 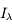 en erg cm-2
en erg cm-2 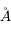 -1 sr-1 s-1. L'intensité spécifique est une quantité fondamentale dont dérivent les autres grandeurs physiques qui caractérisent le rayonnement, comme la densité d'énergie monochromatique
-1 sr-1 s-1. L'intensité spécifique est une quantité fondamentale dont dérivent les autres grandeurs physiques qui caractérisent le rayonnement, comme la densité d'énergie monochromatique 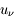 par unité de volume et par unité d'intervalle de fréquence,
par unité de volume et par unité d'intervalle de fréquence, 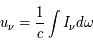 , ou le flux net
, ou le flux net 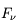 , c'est-à-dire le flux d'énergie par unité de surface, de fréquence et de temps,
, c'est-à-dire le flux d'énergie par unité de surface, de fréquence et de temps, 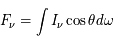 .
.
La conservation de l'énergie implique que l'intensité spécifique du rayonnement reste constante le long d'un rayon uniquement si la propagation se produit dans l'espace vide. Autrement dit, l'intensité spécifique est indépendante de la distance entre la source de rayonnement et l'observateur en l'absence de gains ou pertes d'énergie le long de la ligne de visée. Lorsqu'un rayonnement traverse un milieu, l'interaction avec la matière qui le compose ajoute ou soustrait de l'énergie du faisceau. Cette modification de l'intensité spécifique se réalise par des processus d'émission, d'absorption et de diffusion.
L'équation de transfert de rayonnement décrit la variation de l'intensité spécifique le long de la direction de propagation d'un faisceau de rayonnement traversant un milieu qui absorbe et émet. En se limitant au cas stationnaire (intensité spécifique indépendante du temps) et en négligeant la diffusion du rayonnement, cette équation se réduit à une équation différentielle ordinaire qui peut être résolue à chaque fréquence donnée, les coefficients d'absorption et d'émission étant connus. Lorsque les effets de diffusion sont inclus, l'équation devient une équation intégro-différentielle, car l'émission entraîne une intégrale de l'intensité spécifique sur l'angle solide de diffusion (voir la page Interaction rayonnement-matière), et il faut employer des méthodes numériques pour sa résolution.
Equation de transfert et profondeur optique
Dans le cas stationnaire et en absence de diffusion, l'équation de transfert est obtenue par le bilan d'énergie absorbée et émise dans le passage d'un faisceau de rayonnement à travers un volume élémentaire d'épaisseur 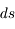 et surface
et surface 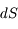 = 1 perpendiculaire à la direction de propagation
= 1 perpendiculaire à la direction de propagation 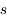 . En utilisant les définitions des coefficients d'absorption et d'émission données à la page Interaction rayonnement-matière on obtient :
. En utilisant les définitions des coefficients d'absorption et d'émission données à la page Interaction rayonnement-matière on obtient :
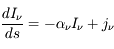 .
.
Considérons d'abord le cas limite où le milieu émet, mais n'absorbe pas le rayonnement. Dans ce cas 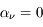 et l'équation de transfert devient :
et l'équation de transfert devient : 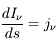 qui admet la solution
qui admet la solution 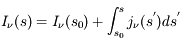 . Cela signifie que l'augmentation de l'intensité spécifique entre la position initiale
. Cela signifie que l'augmentation de l'intensité spécifique entre la position initiale 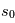 et le point final
et le point final 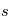 est égale au coefficient d'émission intégré le long de cette "ligne de visée" à travers la couche de matière.
est égale au coefficient d'émission intégré le long de cette "ligne de visée" à travers la couche de matière.
Dans le cas inverse où le milieu absorbe, mais n'émet pas de rayonnement (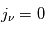 ) on obtient :
) on obtient : 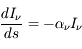 , dont la solution est
, dont la solution est 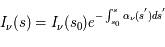 . L'intensité spécifique au point final
. L'intensité spécifique au point final 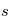 est égale à l'intensité spécifique au point initial
est égale à l'intensité spécifique au point initial 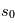 , atténuée par un facteur exponentiel dont l'argument est l'intégrale du coefficient d'absorption le long de la ligne de visée entre
, atténuée par un facteur exponentiel dont l'argument est l'intégrale du coefficient d'absorption le long de la ligne de visée entre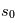 et
et 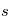 . Cette intégrale est un nombre sans dimension appelé la profondeur optique du milieu:
. Cette intégrale est un nombre sans dimension appelé la profondeur optique du milieu:
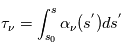 .
.
La solution de l'équation de transfert dans un milieu purement absorbant s'écrit alors 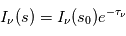 . On voit ainsi que la profondeur optique détermine la fraction de l'intensité incidente qui peut s'échapper du milieu. Afin de mieux comprendre le concept de profondeur optique, on introduit le libre parcours moyen du rayonnement qui représente la distance moyenne qu'un photon parcourt à travers un milieu sans être absorbé. Le coefficient
. On voit ainsi que la profondeur optique détermine la fraction de l'intensité incidente qui peut s'échapper du milieu. Afin de mieux comprendre le concept de profondeur optique, on introduit le libre parcours moyen du rayonnement qui représente la distance moyenne qu'un photon parcourt à travers un milieu sans être absorbé. Le coefficient 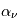 est l'inverse de ce libre parcours moyen, pour un photon de fréquence
est l'inverse de ce libre parcours moyen, pour un photon de fréquence 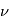 . La profondeur optique
. La profondeur optique 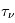 est donc égale au nombre total de libres parcours moyens traversés entre
est donc égale au nombre total de libres parcours moyens traversés entre 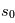 et
et 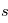 . Si la distance à travers le nuage est égale au libre parcours moyen (
. Si la distance à travers le nuage est égale au libre parcours moyen (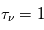 ), l'intensité subit une atténuation d'un facteur e-1 =0.368, ie. en moyenne seulement 36.8% des photons incidents sortiront du nuage. Si la distance parcourue équivaut à deux fois le libre parcours moyen (
), l'intensité subit une atténuation d'un facteur e-1 =0.368, ie. en moyenne seulement 36.8% des photons incidents sortiront du nuage. Si la distance parcourue équivaut à deux fois le libre parcours moyen (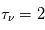 ), seulement 13.5% (e-2 =0.135) des photons incidents survivront en traversant le nuage. Pour cette raison, un milieu caractérisé par une profondeur optique
), seulement 13.5% (e-2 =0.135) des photons incidents survivront en traversant le nuage. Pour cette raison, un milieu caractérisé par une profondeur optique 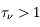 est dit optiquement épais ou opaque, alors qu'un milieu avec
est dit optiquement épais ou opaque, alors qu'un milieu avec 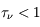 est dit optiquement mince ou transparent.
est dit optiquement mince ou transparent.
L'équation de transfert décrit la variation macroscopique de l'intensité spécifique du rayonnement lorsqu'il traverse de la matière. De leur coté, les coefficients d'absorption et d'émission qui apparaissent dans cette équation contiennent l'information concernant les processus microscopiques qui interviennent. En étudiant l'interaction entre le rayonnement et un système (atome ou molécule) avec des niveaux d'énergie quantifiés, Einstein a identifié 3 processus d'émission et d'absorption de photons, caractérisés chacun par un coefficient. Il est donc possible d'exprimer l'équation de transfert en fonction de ces coefficients et d'en dériver des solutions en fonction des propriétés microscopiques locales de l'atome considéré.
 Définition des coefficients d'Einstein
Définition des coefficients d'Einstein
Considérons pour simplifier un milieu formé d'atomes (ou de molécules) identiques avec seulement deux niveaux d'énergie : le niveau fondamental l et le niveau excité u, séparés par une énergie 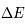 . Nous nous intéressons aux transitions radiatives entres ces deux états. Comme nous verrons en détail dans la suite du cours ces transitions ne se produisent pas uniquement à la fréquence
. Nous nous intéressons aux transitions radiatives entres ces deux états. Comme nous verrons en détail dans la suite du cours ces transitions ne se produisent pas uniquement à la fréquence 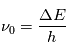 mais également aux fréquences voisines de
mais également aux fréquences voisines de 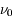 . Par conséquent les raies spectrales associées à ces transitions sont caractérisées par un profil de raie
. Par conséquent les raies spectrales associées à ces transitions sont caractérisées par un profil de raie 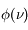 , piqué à la fréquence
, piqué à la fréquence 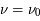 , qui décrit l'efficacité des fréquences voisines de
, qui décrit l'efficacité des fréquences voisines de 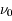 à induire ces transitions. L'agitation thermique du gaz (mouvement brownien) produit par exemple un élargissement du profil par effet Doppler, car un atome en mouvement peut absorber un photon de fréquence légèrement différente de
à induire ces transitions. L'agitation thermique du gaz (mouvement brownien) produit par exemple un élargissement du profil par effet Doppler, car un atome en mouvement peut absorber un photon de fréquence légèrement différente de 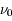 . La largeur du profil est alors de l'ordre de
. La largeur du profil est alors de l'ordre de 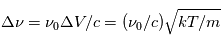 . Dans la suite on fera l'hypothèse que la forme de la raie est la même en absorption et en émission. Les 3 processus de transitions radiatives quantifiés par Einstein sont les suivants :
. Dans la suite on fera l'hypothèse que la forme de la raie est la même en absorption et en émission. Les 3 processus de transitions radiatives quantifiés par Einstein sont les suivants :
- L'émission spontanée qui est la désexcitation spontanée du niveau u vers le niveau l par l'émission d'un photon d'énergie
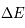 . Cette transition se produit même en l'absence d'un champ de rayonnement. Elle est caractérisée par le coefficient d'Einstein
. Cette transition se produit même en l'absence d'un champ de rayonnement. Elle est caractérisée par le coefficient d'Einstein 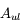 , qui représente une probabilité de transition par unité de temps et est exprimé en s-1. Ce coefficient ne dépend que des termes de couplages électro-magnétique entre les 2 niveaux quantiques u et l.
, qui représente une probabilité de transition par unité de temps et est exprimé en s-1. Ce coefficient ne dépend que des termes de couplages électro-magnétique entre les 2 niveaux quantiques u et l. - L'absorption stimulée (ou excitation radiative) qui est l'absorption d'un photon d'énergie
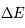 , faisant passer les atomes du niveaux l au niveau u. Elle est caractérisée par une probabilité de transition par unité de temps
, faisant passer les atomes du niveaux l au niveau u. Elle est caractérisée par une probabilité de transition par unité de temps 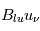 , où
, où 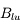 est le coefficient d'absorption d'Einstein et
est le coefficient d'absorption d'Einstein et 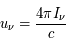 est la densité d'énergie monochromatique à la fréquence
est la densité d'énergie monochromatique à la fréquence 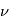 pour un champ de rayonnement isotrope.
pour un champ de rayonnement isotrope. - L'émission stimulée qui est le processus inverse de l'absorption stimulée : Lors de cette transition, l'atome absorbe un photon d'énergie
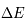 et passe de l'état u à l'état l en emettant un deuxième photon identique à celui qu'il a absorbé. Ce processus est caractérisé par une probabilité par unité de temps
et passe de l'état u à l'état l en emettant un deuxième photon identique à celui qu'il a absorbé. Ce processus est caractérisé par une probabilité par unité de temps 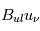 .
.
Les 3 coefficients d'Einstein décrivant les probabilités de ces 3 processus sont reliés par les relations d'Einstein :
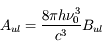 et
et
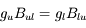 .
.
Il est important de noter que ces relations ne dépendent ni de la température du gaz, ni du profil de la raie. Elles représentent des relations de bilan détaillé, c'est-à-dire des relations entre un processus microscopique quantique et son processus inverse, dans ce cas l'absorption et l'émission de rayonnement. La connaissance d'un seul des coefficients d'Einstein (à partir de calculs quantiques) permet ainsi de déterminer les 2 autres. Notons aussi que ces coefficients donnent la probabilité de transition par atome dans le niveau de départ (u ou l) considéré. Le bilan net de ces 3 types de transitions va donc dépendre des densités de populations moyennes respectives dans les niveaux u et l.
L'équation de transfert en termes de coefficients d'Einstein
Considérons un rayonnement à la fréquence 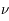 (contenue dans le profil de la raie) qui arrive sur une tranche du milieu avec une intensité spécifique
(contenue dans le profil de la raie) qui arrive sur une tranche du milieu avec une intensité spécifique 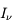 par unité de surface, de fréquence, et d'angle solide. Le long de la distance
par unité de surface, de fréquence, et d'angle solide. Le long de la distance 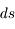 dans sa direction de propagation, l'intensité sera augmentée à la fois par l'émission spontanée et par l'émission stimulée des atomes dans l'état u ; simultanément elle sera diminuée par l'absorption de photons par les atomes dans l'état l. Considérons d'abord le cas de l'émission spontanée : le nombre total d'atomes dans l'état u rencontré par unité de surface est
dans sa direction de propagation, l'intensité sera augmentée à la fois par l'émission spontanée et par l'émission stimulée des atomes dans l'état u ; simultanément elle sera diminuée par l'absorption de photons par les atomes dans l'état l. Considérons d'abord le cas de l'émission spontanée : le nombre total d'atomes dans l'état u rencontré par unité de surface est 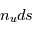 . L'augmentation d'intensité à la fréquence
. L'augmentation d'intensité à la fréquence 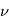 causée par ce processus est obtenue en multipliant
causée par ce processus est obtenue en multipliant 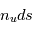 par le coefficient d'Einstein correspondant
par le coefficient d'Einstein correspondant 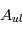 divisé par
divisé par 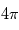 (car chaque photon est supposé émis ou absorbé de façon isotrope et nous regardons la variation par unité d'angle solide), par le profil de la raie
(car chaque photon est supposé émis ou absorbé de façon isotrope et nous regardons la variation par unité d'angle solide), par le profil de la raie 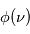 , et enfin par l'énergie de chaque photon (
, et enfin par l'énergie de chaque photon (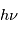 ) ; en appliquant le même raisonnement à l'émission et absorption stimulées, le bilan de ces transition radiatives donne l'équation de transfert :
) ; en appliquant le même raisonnement à l'émission et absorption stimulées, le bilan de ces transition radiatives donne l'équation de transfert :
![\frac{dI_\nu}{ds} = \frac{h\nu }{4\pi} \phi(\nu) [n_u A_{ul} +(n_u B_{ul} - n_l B_{lu})\frac{4\pi I_\nu}{c}]](../pages_transfert-rayon/equations_transfert-rayon/equation110.png) .
.
En comparant avec l'expression générale de l'équation de transfert 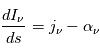 , présentée dans la section précédente on obtient en fonction des coefficients d'Einstein :
, présentée dans la section précédente on obtient en fonction des coefficients d'Einstein :
le coefficient d'émissivité 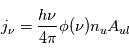
le coefficient d'absorption 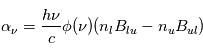
et la fonction source, 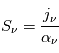
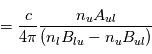 .
.
On remarque que la fonction source 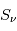 ne dépend pas de
ne dépend pas de 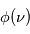 , mais uniquement des coefficients d'Einstein et des populations des niveaux impliqués. Plus précisément elle ne dépend que du rapport entre ces populations . En effet, en utilisant les relations entre coefficients d'Einstein données ci-dessus, on obtient :
, mais uniquement des coefficients d'Einstein et des populations des niveaux impliqués. Plus précisément elle ne dépend que du rapport entre ces populations . En effet, en utilisant les relations entre coefficients d'Einstein données ci-dessus, on obtient :
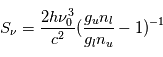 , où
, où 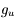 et
et 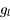 sont les poids statistiques (dégénérescences) de chaque niveau.
sont les poids statistiques (dégénérescences) de chaque niveau.
En utilisant les relations d'Einstein on voit aussi que le coefficient d'absorption peut se réécrire sous la forme :
![\alpha_\nu=\frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-\frac{n_ug_l}{n_lg_u}]](../pages_transfert-rayon/equations_transfert-rayon/equation121.png) .
.
Si l'on dénote par 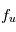 et
et 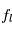 les fractions
les fractions 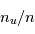 et
et 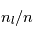 d'atomes qui sont dans les niveaux u et l, on remarque qu'
d'atomes qui sont dans les niveaux u et l, on remarque qu'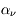 est proportionnel à la densité volumique totale des atomes,
est proportionnel à la densité volumique totale des atomes, 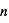 , et à une fonction qui ne dépend que de
, et à une fonction qui ne dépend que de 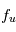 et
et 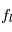 , c'est-à-dire à la répartition statistique des atomes entre leurs différents niveaux d'énergie. Il en découle que la profondeur optique, obtenue en intégrant cette quantité le long de la ligne de visée, sera proportionnelle à
, c'est-à-dire à la répartition statistique des atomes entre leurs différents niveaux d'énergie. Il en découle que la profondeur optique, obtenue en intégrant cette quantité le long de la ligne de visée, sera proportionnelle à 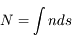 que l'on appelle la densité de colonne des atomes (en unité d'atomes par cm-2), c'est-à-dire le nombre d'atomes dans un cylindre de section unité le long de la ligne de visée. C'est par ce biais que l'observation des raies spectrales pourra nous donner accès à la masse de gaz émetteur --- à condition que l'on puisse connaître (ou estimer) les fractions
que l'on appelle la densité de colonne des atomes (en unité d'atomes par cm-2), c'est-à-dire le nombre d'atomes dans un cylindre de section unité le long de la ligne de visée. C'est par ce biais que l'observation des raies spectrales pourra nous donner accès à la masse de gaz émetteur --- à condition que l'on puisse connaître (ou estimer) les fractions 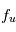 et
et 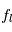 d'atomes peuplant les niveaux u et l, ou en d'autres termes les "conditions d'excitation" de la transition.
d'atomes peuplant les niveaux u et l, ou en d'autres termes les "conditions d'excitation" de la transition.
Puisque les coefficients d'absorption et d'émission dépendent des populations des niveaux, la résolution de l'équation de transfert de rayonnement requiert la connaissance de l'état d'excitation de l'atome (ou de la molécule). De façon générale, ces conditions d'excitation dépendent à la fois de la température, de la densité, et du champ de rayonnement dans lequel baigne le gaz. Nous introduisons ici les quantités importantes (densité critique, équilibre thermodynamique local, et température d'excitation) qui permettent de caractériser ces conditions d'excitation et de comprendre les observations spectrales du milieu interstellaire.
Densité critique et Equilibre thermodynamique local
En régime stationnaire, la fraction d'atomes (ou "population") dans chaque niveau est fixée par l'équilibre statistique entre les taux de transitions qui peuplent ce niveau et celles qui le dépeuplent. Ces transitions sont produites non seulement par les 3 processus radiatifs d'absorption et émission discutés plus haut, étudiés par Einstein, mais aussi par des processus collisionnels d'excitation et désexcitation, lors de collisions inélastiques de l'atome considéré avec les particules les plus abondantes et rapides du milieu (H2, He, H, et les électrons si les gaz est significativement ionisé). Pour chaque transition, on peut calculer une densité critique au-dessus de laquelle les transitions collisionnelles deviennent plus importantes que les transitions radiatives. Pour les systèmes à deux niveaux, et avec un seul collisionneur dominant, elle s'écrit simplement :
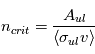
où 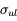 est la section efficace de désexcitation collisionnelle, qui dépend en général de la vitesse
est la section efficace de désexcitation collisionnelle, qui dépend en général de la vitesse 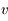 du collisionneur. Les crochets signifient qu'on prend la moyenne sur toute la distribution statistique des vitesses
du collisionneur. Les crochets signifient qu'on prend la moyenne sur toute la distribution statistique des vitesses 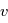 (distribution Boltzmanienne) ce qui donne une valeur dépendant de la température du gaz.
(distribution Boltzmanienne) ce qui donne une valeur dépendant de la température du gaz.
Lorsque la densité des collisionneurs 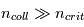 , les transitions radiatives sont négligeables devant les transitions collisionnelles et on atteint l'équilibre thermodynamique local (ou ETL),
où les populations relatives des niveaux des atomes (ou molécules) ne dépendent ni de
, les transitions radiatives sont négligeables devant les transitions collisionnelles et on atteint l'équilibre thermodynamique local (ou ETL),
où les populations relatives des niveaux des atomes (ou molécules) ne dépendent ni de 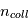 ni du champ de rayonnement et obéissent simplement à la loi de Boltzmann :
ni du champ de rayonnement et obéissent simplement à la loi de Boltzmann :
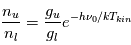
ici 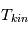 est la température cinétique des collisionneurs, qui caractérise la distribution de vitesse des particules,
est la température cinétique des collisionneurs, qui caractérise la distribution de vitesse des particules, 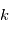 la constante de Boltzmann,
la constante de Boltzmann, 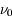 est la fréquence de la transition entre les états u et l,
est la fréquence de la transition entre les états u et l, 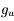 et
et 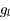 sont les poids statistiques. Plus le coefficient d'Einstein est fort, et plus la densité critique nécessaire pour atteindre l'ETL sera élevée. Cette densité critique est très variable selon les espèces et les transitions considérées : elle est très faible pour la raie hyperfine de l'hydrogène atomique (voir ci-dessous), de l'ordre de 1000 cm-3 pour les premières raies rotationnelles de CO, mais atteint 108 cm-3 pour H2O.
sont les poids statistiques. Plus le coefficient d'Einstein est fort, et plus la densité critique nécessaire pour atteindre l'ETL sera élevée. Cette densité critique est très variable selon les espèces et les transitions considérées : elle est très faible pour la raie hyperfine de l'hydrogène atomique (voir ci-dessous), de l'ordre de 1000 cm-3 pour les premières raies rotationnelles de CO, mais atteint 108 cm-3 pour H2O.
Température d'excitation de la transition
Par analogie avec la loi de Boltzmann, on peut toujours définir une température d'excitation de la transition 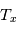 , telle que
, telle que
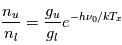 .
.
A l'équilibre thermodynamique local (ETL), on a 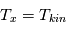 . Dans le cas contraire,
. Dans le cas contraire, 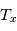 dépend aussi du rapport
dépend aussi du rapport 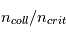 et de l'intensité du champ de rayonnement local, qui peuvent varier fortement d'un point à l'autre. Elle peut être inférieure à
et de l'intensité du champ de rayonnement local, qui peuvent varier fortement d'un point à l'autre. Elle peut être inférieure à 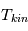 (cas le plus courant dans le MIS) ou bien supérieure si le pompage radiatif est important (par exemple à proximité d'une source de rayonnement intense), voire négative en présence d'un effet maser (inversion de population). En outre, il peut y avoir des températures d'excitation différentes pour différentes transitions d'un même atome.
(cas le plus courant dans le MIS) ou bien supérieure si le pompage radiatif est important (par exemple à proximité d'une source de rayonnement intense), voire négative en présence d'un effet maser (inversion de population). En outre, il peut y avoir des températures d'excitation différentes pour différentes transitions d'un même atome.
En insérant cette définition de la température d'excitation dans la définition de la fonction source dérivée dans la page Coefficients d'Einstein, on peut exprimer la fonction source comme une fonction de Planck :
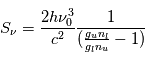
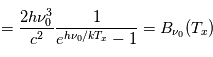 .
.
Notons aussi que le coefficient d'absorption peut s'écrire :
![\alpha_\nu=\frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-\frac{n_ug_l}{n_lg_u}]](../pages_transfert-rayon/equations_transfert-rayon/equation153.png)
![= \frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-e^{-h\nu_0/kT_x}]](../pages_transfert-rayon/equations_transfert-rayon/equation154.png) .
.
Si la température d'excitation est uniforme le long de ligne de visée, la solution formelle de l'équation du transfert radiatif devient :
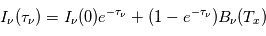 .
.
Notons qu'aux fréquences situées en dehors du profil spectral de la raie, on aura 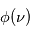 = 0, donc
= 0, donc 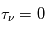 , et
, et 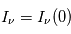 . Ceci définit le niveau du "continuum" que l'on mesure autour de la raie spectrale. Dans ce qui suit nous allons examiner sous quelles conditions la raie apparaîtra en émission ou en absorption par rapport à ce niveau de continu de référence.
. Ceci définit le niveau du "continuum" que l'on mesure autour de la raie spectrale. Dans ce qui suit nous allons examiner sous quelles conditions la raie apparaîtra en émission ou en absorption par rapport à ce niveau de continu de référence.
Limites optiquement épaisse et optiquement mince
Dans un milieu optiquement épais (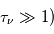 , on obtient
, on obtient 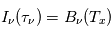 : le rayonnement d'un nuage optiquement épais s'apparente au rayonnement d'un corps noir à la température d'excitation
: le rayonnement d'un nuage optiquement épais s'apparente au rayonnement d'un corps noir à la température d'excitation 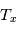 de la transition considérée. Si de plus on est à l'ETL, alors
de la transition considérée. Si de plus on est à l'ETL, alors 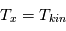 et on peut déduire la température cinétique du gaz à partir de
et on peut déduire la température cinétique du gaz à partir de 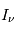 . Cette technique s'applique par exemple à la raie rotationnelle fondamentale de CO à une longueur d'onde de 2.6mm ; elle donne des valeurs typiques de température de 10-20 K dans les nuages moléculaires. Par contre, on voit que dans le cas optiquement épais l'intensité ne dépend plus de
. Cette technique s'applique par exemple à la raie rotationnelle fondamentale de CO à une longueur d'onde de 2.6mm ; elle donne des valeurs typiques de température de 10-20 K dans les nuages moléculaires. Par contre, on voit que dans le cas optiquement épais l'intensité ne dépend plus de  , c'est-à-dire de la quantité de matière traversée ; on dit que la raie est "saturée". Il n'est donc pas possible de déduire la masse de gaz.
, c'est-à-dire de la quantité de matière traversée ; on dit que la raie est "saturée". Il n'est donc pas possible de déduire la masse de gaz.
Pour un milieu optiquement mince (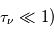 , on obtient
, on obtient ![I_\nu(\tau_\nu) - I_\nu(0) = \tau_\nu [B_\nu(T_x) - B_\nu(T_{bg})]](../pages_transfert-rayon/equations_transfert-rayon/equation173.png) : l'excès d'intensité au-dessus du continu est proportionnel à l'opacité, dont nous avons vu qu'est elle-même proportionnelle à la densité colonne
: l'excès d'intensité au-dessus du continu est proportionnel à l'opacité, dont nous avons vu qu'est elle-même proportionnelle à la densité colonne 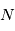 de l'atome considéré, et à une fonction de
de l'atome considéré, et à une fonction de 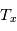 (qui fixe les populations relatives des niveaux). Avec une estimation indépendante de
(qui fixe les populations relatives des niveaux). Avec une estimation indépendante de 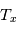 (par ex.
(par ex. 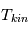 si la raie est à l'ETL), il est donc possible de déduire de ces observations la valeur de
si la raie est à l'ETL), il est donc possible de déduire de ces observations la valeur de 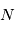 , et ensuite de la masse de gaz si la taille de la région d'émission et l'abondance de l'atome ou molécule sont connues. Cette technique est utilisée par exemple pour mesurer les masses des nuages moléculaires, grâce à des isotopes peu abondants comme 13CO et C18O qui sont (généralement) optiquement minces.
, et ensuite de la masse de gaz si la taille de la région d'émission et l'abondance de l'atome ou molécule sont connues. Cette technique est utilisée par exemple pour mesurer les masses des nuages moléculaires, grâce à des isotopes peu abondants comme 13CO et C18O qui sont (généralement) optiquement minces.
Enfin, une façon d'obtenir à la fois la température et la densité colonne de gaz est la combinaison d'observations en absorption et en émission. Nous en verrons un exemple détaillé plus loin avec la raie hyperfine de HI à 21 cm.
Les notions de transfert de rayonnement apprises au cours de ce chapitre nous donnent tous les éléments pour mieux comprendre les observations de la raie à 21 cm de HI que nous avons vu être le traceur principal de la composante de gaz atomique neutre du milieu interstellaire (voir la page Détection du gaz neutre atomique : raies spectrales).
Mesure en émission: approximation optiquement mince
Nous allons maintenant calculer l'opacité de la raie à 21 cm en utilisant l'expression du coefficient d'absorption en fonction de la température d'excitation, obtenue dans la page Conditions d'excitation de la transition.
![\alpha_\nu = \frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-e^{-h\nu_0/kT_x}]](../pages_transfert-rayon/equations_transfert-rayon/equation201.png) .
.
Pour cette transition, on a 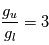 . De plus, à la basse fréquence de cette raie, 1420 MHz, nous sommes toujours dans le domaine
. De plus, à la basse fréquence de cette raie, 1420 MHz, nous sommes toujours dans le domaine 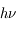 <<
<<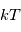 (approximation de Rayleigh-Jeans). Le facteur de Boltzmann
(approximation de Rayleigh-Jeans). Le facteur de Boltzmann 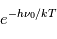 est donc proche de 1 et le rapport entre les populations des 2 sous-niveaux hyperfins à l'ETL vaut
est donc proche de 1 et le rapport entre les populations des 2 sous-niveaux hyperfins à l'ETL vaut 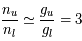 . Le gaz étant beaucoup trop froid pour peupler le premier niveau électronique excité
. Le gaz étant beaucoup trop froid pour peupler le premier niveau électronique excité 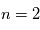 de l'hydrogène, l'essentiel des atomes se trouvent dans l'un de ces deux sous-niveaux hyperfins du niveau fondamental. La densité totale de HI est donc reliée à
de l'hydrogène, l'essentiel des atomes se trouvent dans l'un de ces deux sous-niveaux hyperfins du niveau fondamental. La densité totale de HI est donc reliée à 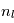 par :
par :
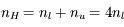 .
.
Enfin, dans le régime Rayleigh-Jeans, le facteur ![[1- e^{-h\nu_0/kT_s}] \simeq h\nu_0 / kT_s](../pages_transfert-rayon/equations_transfert-rayon/equation210.png) au premier ordre. En insérant ces expressions dans l'équation de
au premier ordre. En insérant ces expressions dans l'équation de 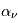 on en déduit :
on en déduit :
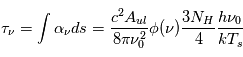 ,
,
où 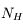 est la densité de colonne de l'hydrogène atomique neutre. On a fait ici l'hypothèse d'un milieu homogène, de sorte que
est la densité de colonne de l'hydrogène atomique neutre. On a fait ici l'hypothèse d'un milieu homogène, de sorte que 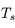 et
et 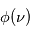 ne dépendent pas de la position
ne dépendent pas de la position 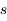 le long de la ligne de visée. On note ainsi que la profondeur optique de la raie à 21 cm est inversement proportionnelle à la température de spin,
le long de la ligne de visée. On note ainsi que la profondeur optique de la raie à 21 cm est inversement proportionnelle à la température de spin,
En supposant le rayonnement de fond négligeable et la raie optiquement mince, la température de brillance vaut : 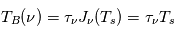 (approximation de Rayleigh-Jeans). Puisque
(approximation de Rayleigh-Jeans). Puisque 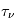 est inversement proportionnel à la température de spin, on voit que
est inversement proportionnel à la température de spin, on voit que 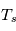 se simplifie dans cette expression et que l'intensité de la raie ne dépend plus de la température mais uniquement de la densité de colonne totale d'hydrogène,
se simplifie dans cette expression et que l'intensité de la raie ne dépend plus de la température mais uniquement de la densité de colonne totale d'hydrogène, 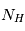 , dont on obtient ainsi une détermination directe. Cette approche est souvent appliquée même dans des cas où l'approximation de raie optiquement mince ne peut pas être vérifiée, et il faut garder à l'esprit que les estimations de la densité de colonne ainsi obtenues sont alors des limites inférieures.
, dont on obtient ainsi une détermination directe. Cette approche est souvent appliquée même dans des cas où l'approximation de raie optiquement mince ne peut pas être vérifiée, et il faut garder à l'esprit que les estimations de la densité de colonne ainsi obtenues sont alors des limites inférieures.
Mesure en absorption et émission: masse et température
Considérons l'absorption de la raie à 21 cm par une source de continuum radio variant lentement avec la fréquence dans un nuage de HI uniforme et écrivons la solution de l'équation de transfert en fonction de la température de brillance du continuum 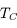 et de la température cinétique du nuage de HI interposé
et de la température cinétique du nuage de HI interposé 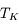 , telle que :
, telle que : 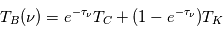 .
.
Les observations en absorption sont effectuées avec des interféromètres à haute résolution angulaire qui sont insensibles à l'émission étendue du nuage. Le deuxième terme dans l'équation pour la température de brillance est donc nul, et la solution devient 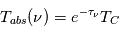 . Le rapport entre la température de brillance dans la raie d'absorption et la température de brillance dans le continu hors de la raie (où
. Le rapport entre la température de brillance dans la raie d'absorption et la température de brillance dans le continu hors de la raie (où 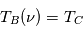 ) permet d'obtenir la valeur de
) permet d'obtenir la valeur de 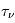 . Mais comme la profondeur optique est proportionnelle à
. Mais comme la profondeur optique est proportionnelle à 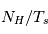 (voir section précédente), il n'est pas possible de dériver la densité de colonne
(voir section précédente), il n'est pas possible de dériver la densité de colonne 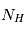 à partir de ces mesures en absorption seules. Il faut une information supplémentaire sur la température du gaz.
à partir de ces mesures en absorption seules. Il faut une information supplémentaire sur la température du gaz.
La technique généralement adoptée est la combinaison de ces résultats avec des observations en émission effectuées à l'aide d'un radiotélescope à plus basse résolution angulaire pointé sur des régions immédiatement adjacentes, où l'intensité moyenne du fond est négligeable. Cela donne la quantité : 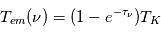 .
.
En combinant ces observations en absorption et en émission on voit qu'on peut déterminer à la fois la température cinétique 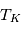 et la profondeur optique
et la profondeur optique 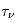 (qu'on suppose identiques entre les 2 régions observées), et d'en déduire ainsi la densité de colonne
(qu'on suppose identiques entre les 2 régions observées), et d'en déduire ainsi la densité de colonne 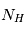 du nuage. Cette méthode est pratiquement la seule qui permet d'obtenir directement la température des nuages interstellaires atomiques.
du nuage. Cette méthode est pratiquement la seule qui permet d'obtenir directement la température des nuages interstellaires atomiques.
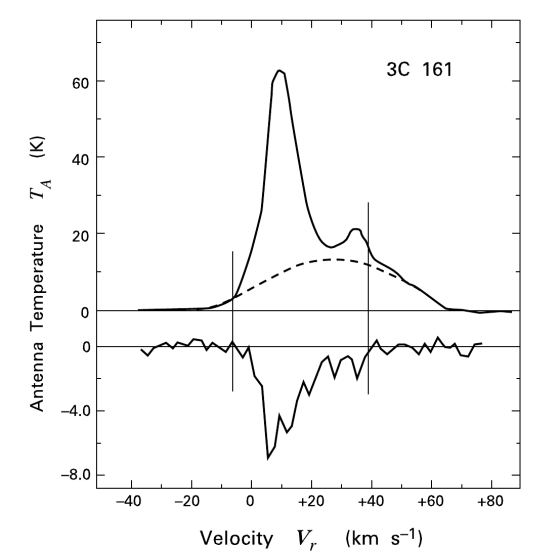
Ces observations sont compliquées en présence d'un mélange des composantes tièdes et froides le long de la ligne de visée, qui sont difficiles à séparer. On montre ci-dessous le spectre d'un nuage de HI interposé entre l'observateur et le quasar 3C 161. En ordonnée est présentée la température d'antenne 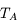 , généralement utilisée par les radioastronomes comme mesure de l'énergie reçue par une antenne radio. Il s'agit de la température du corps noir qui entourerait totalement l'antenne pour donner le signal observé. La puissance captée par l'antenne est alors
, généralement utilisée par les radioastronomes comme mesure de l'énergie reçue par une antenne radio. Il s'agit de la température du corps noir qui entourerait totalement l'antenne pour donner le signal observé. La puissance captée par l'antenne est alors 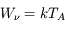 . Si l'antenne était parfaite, une région étendue de brillance uniforme
. Si l'antenne était parfaite, une région étendue de brillance uniforme 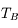 donnerait
donnerait 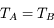 (en général il faut introduire un facteur de rendement). La quantité en abscisse de la figure est la vitesse radiale donnée par la formule de l'effet Doppler
(en général il faut introduire un facteur de rendement). La quantité en abscisse de la figure est la vitesse radiale donnée par la formule de l'effet Doppler 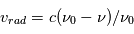 , utilisée d'habitude par les radioastronomes plutôt que la fréquence. La courbe en émission est associée au signal des régions immédiatement adjacentes. En soustrayant cette émission du signal obtenu avec l'antenne pointée sur le quasar on obtient la courbe en absorption. Enfin, la ligne en pointillé est due à une composante tiède pour laquelle l'absorption est plus faible.
, utilisée d'habitude par les radioastronomes plutôt que la fréquence. La courbe en émission est associée au signal des régions immédiatement adjacentes. En soustrayant cette émission du signal obtenu avec l'antenne pointée sur le quasar on obtient la courbe en absorption. Enfin, la ligne en pointillé est due à une composante tiède pour laquelle l'absorption est plus faible.
Observations de la raie à 21 cm devant le quasar 3C 161
Crédit :
Stahler & Palla, "The Formation of Stars"
On observe des raies spectrales en émission ou en absorption lors des transitions entre deux niveaux discrets dans un atome ou une molécule. Ces niveaux ne sont pas infiniment fins, de sorte que la raie est élargie. Afin de prendre en compte cet élargissement, nous avons introduit (voir la page Coefficients d'Einstein) un profil de raie 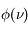 , normalisé et centré sur
, normalisé et centré sur 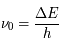 , avec
, avec 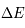 >0 l'écart en énergie entre les niveaux. Dans cette page nous présenterons les différents processus qui causent l'élargissement et analyserons les caractéristiques des profils de raie associés à chacun de ces processus. Nous ne considérons pas les effets associés à la présence de champs électromagnétiques externes (par exemple l'effet Zeeman).
>0 l'écart en énergie entre les niveaux. Dans cette page nous présenterons les différents processus qui causent l'élargissement et analyserons les caractéristiques des profils de raie associés à chacun de ces processus. Nous ne considérons pas les effets associés à la présence de champs électromagnétiques externes (par exemple l'effet Zeeman).
Largeur naturelle et collisionnelle : profil de raie Lorentzien
La largeur naturelle d'une raie spectrale est la largeur minimale que la raie, en émission ou en absorption, puisse présenter. Elle est reliée à l'inégalité de Heisenberg. Soit une transition entre les niveaux u et l d'un atome. Les relations d'incertitude nous donnent : 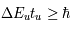 , où
, où 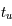 représente la durée de vie du niveau u, telle que
représente la durée de vie du niveau u, telle que 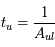 . La largeur de raie naturelle en énergie
. La largeur de raie naturelle en énergie 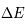 correspond au cas de l'égalité. Elle est proportionnelle au coefficient d'Einstein d'émission spontanée en absence de rayonnement (en présence de rayonnement il faudra considérer ainsi la désexcitation stimulée qui contribue à réduire la durée de vie du niveau u et donc à augmenter la largeur de raie). Du fait de l'élargissement des niveaux il faut prendre en compte toutes les transitions possibles avec une énergie
correspond au cas de l'égalité. Elle est proportionnelle au coefficient d'Einstein d'émission spontanée en absence de rayonnement (en présence de rayonnement il faudra considérer ainsi la désexcitation stimulée qui contribue à réduire la durée de vie du niveau u et donc à augmenter la largeur de raie). Du fait de l'élargissement des niveaux il faut prendre en compte toutes les transitions possibles avec une énergie 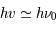 . On définit généralement une largeur naturelle de la raie en fréquence
. On définit généralement une largeur naturelle de la raie en fréquence 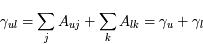 , où les indices
, où les indices 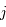 et
et 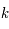 correspondent à des états d'énergie inférieure respectivement à l'énergie du niveau supérieur et à l'énergie du niveau inférieur et les deux sommes donnent la largeur du niveau supérieur et du niveau inférieur. Par exemple, on observera une raie faible mais large si le niveau inférieur est fortement élargi.
correspondent à des états d'énergie inférieure respectivement à l'énergie du niveau supérieur et à l'énergie du niveau inférieur et les deux sommes donnent la largeur du niveau supérieur et du niveau inférieur. Par exemple, on observera une raie faible mais large si le niveau inférieur est fortement élargi.
Une autre cause d'élargissement de raie est représentée par les collisions qui perturbent l'atome pendant le processus d'émission. Les collisions modifient soudainement la phase du rayonnement émis par l'atome. Les sauts de phase se produisent à une fréquence moyenne 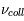 (chaque atome subit en moyenne
(chaque atome subit en moyenne 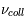 collisions par unité de temps) et contribuent à l'élargissement de la raie en fréquence qu'on écrit :
collisions par unité de temps) et contribuent à l'élargissement de la raie en fréquence qu'on écrit : 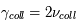 . Il faut remarquer que la fréquence des collisions augmente avec la densité du milieu. On s'attend donc à observer des élargissements collisionnels plus importants dans des environnement denses, comme les atmosphères planétaires et stellaires. Dans les nuages d'hydrogène atomique et les nuages moléculaires les effets collisionnels sont dominés par d'autres sources d'élargissement que nous allons voir dans la suite du cours (effet Doppler, turbulence). Puisque à la fois l'élargissement naturel et l'élargissement associé aux collisions sont caractérisés par des profils de la même forme, on peut définir une constante
. Il faut remarquer que la fréquence des collisions augmente avec la densité du milieu. On s'attend donc à observer des élargissements collisionnels plus importants dans des environnement denses, comme les atmosphères planétaires et stellaires. Dans les nuages d'hydrogène atomique et les nuages moléculaires les effets collisionnels sont dominés par d'autres sources d'élargissement que nous allons voir dans la suite du cours (effet Doppler, turbulence). Puisque à la fois l'élargissement naturel et l'élargissement associé aux collisions sont caractérisés par des profils de la même forme, on peut définir une constante 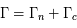 qui contient une contribution naturelle
qui contient une contribution naturelle 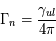 et une contribution collisionnelle
et une contribution collisionnelle 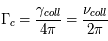 et décrire le profil de la raie tel que :
et décrire le profil de la raie tel que :
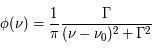 .
.
Il s'agit d'une fonction lorentzienne caractérisée par son aire, calculée comme l'intégrale sur la fréquence et égal à 1, sa valeur maximale atteinte à 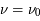 , qui vaut
, qui vaut 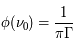 et sa largeur totale à mi-hauteur en unité de fréquence
et sa largeur totale à mi-hauteur en unité de fréquence 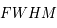 (de l'anglais Full Width at Half Maximum). Cette largeur est déterminée en remplaçant la valeur de la fonction à mi-hauteur (
(de l'anglais Full Width at Half Maximum). Cette largeur est déterminée en remplaçant la valeur de la fonction à mi-hauteur (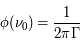 ) dans l'équation qui décrit
) dans l'équation qui décrit 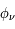 , dont on obtient
, dont on obtient 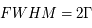 . Un profil Lorentzien centré (
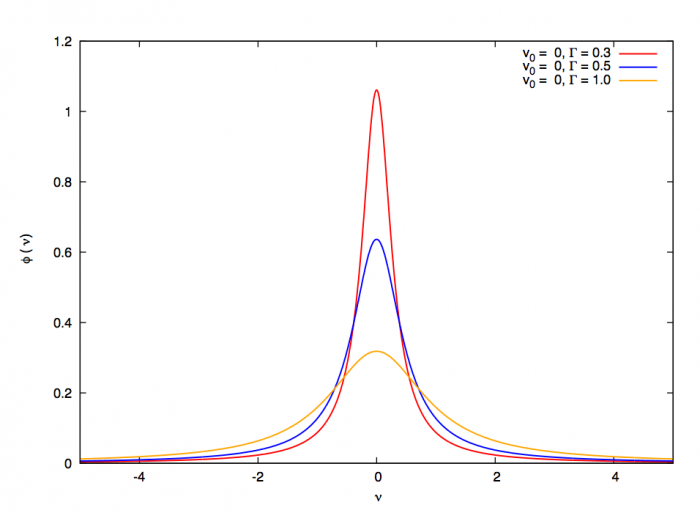
. Un profil Lorentzien centré (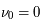 ) est montré sur la figure pour différentes valeurs de la constante
) est montré sur la figure pour différentes valeurs de la constante 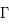 .
.
Profil de Lorentz
Crédit :
Cecilia Pinto
Agitation thermique : profil Doppler
Jusqu'à présent, nous avons considéré que les atomes et les molécules étaient à repos. Dans cette page nous allons analyser l'effet d'élargissement de raie par les mouvements des particules. Du fait de l'effet Doppler, les photons émis à une fréquence 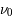 dans le référentiel d'un atome en mouvement seront détectés à une fréquence
dans le référentiel d'un atome en mouvement seront détectés à une fréquence 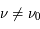 par l'observateur. Le décalage en fréquence d'un atome qui possède une vitesse relative le long de la ligne de visée
par l'observateur. Le décalage en fréquence d'un atome qui possède une vitesse relative le long de la ligne de visée 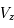 , pour des vitesses non relativistes, vaut :
, pour des vitesses non relativistes, vaut : 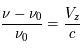 .
.
Puisque chaque atome subit son propre décalage Doppler, l'effet net est un élargissement de la raie, tandis que son intensité totale ne change pas. Les atomes et les molécules d'un gaz effectuent des mouvement aléatoires dépendant de la température. La théorie cinétique des gaz prévoit que cette agitation thermique induit une distribution maxwellienne de vitesse. Le nombre d'atomes à la température 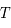 dont la projection de la vitesse sur l'axe de visée
dont la projection de la vitesse sur l'axe de visée 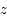 est comprise entre
est comprise entre 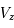 et
et 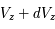 est donc proportionnel à la fonction
est donc proportionnel à la fonction 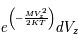 , où M est la masse d'un atome. En utilisant la formule pour le décalage Doppler on déduit
, où M est la masse d'un atome. En utilisant la formule pour le décalage Doppler on déduit 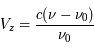 ,
, 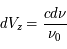 et on peut exprimer la distribution des atomes en fonction de la fréquence. Par conséquent, l'intensité de l'émission dans l'intervalle de fréquence de
et on peut exprimer la distribution des atomes en fonction de la fréquence. Par conséquent, l'intensité de l'émission dans l'intervalle de fréquence de 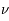 à
à 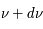 est proportionnelle à
est proportionnelle à 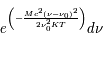 . Si l'effet Doppler est la source dominant d'élargissement de la raie, son profil est la somme des contributions de chaque atome, ce qui donne un profil de forme gaussienne :
. Si l'effet Doppler est la source dominant d'élargissement de la raie, son profil est la somme des contributions de chaque atome, ce qui donne un profil de forme gaussienne :
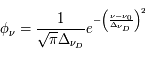 .
.
La quantité 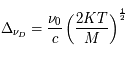 , appelée largeur Doppler de la raie, est reliée à la largeur à mi-hauteur de la gaussienne par
, appelée largeur Doppler de la raie, est reliée à la largeur à mi-hauteur de la gaussienne par 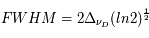 . L'aire du profil, obtenue intégrant sur la fréquence, vaut 1 et sa valeur maximale, atteinte à
. L'aire du profil, obtenue intégrant sur la fréquence, vaut 1 et sa valeur maximale, atteinte à 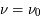 , est
, est 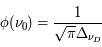 . Dans le milieu interstellaire, l'élargissement associé à l'effet Doppler est généralement plus important que la largeur naturelle et l'élargissement dû aux collisions. Un exemple est représenté par la raie à 21 cm de l'hydrogène atomique, l'élargissement lorentzien étant extrêmement faible puisque la durée de vie du niveau supérieur n'est limitée que par les collisions, rares dans le milieu interstellaire diffus.
. Dans le milieu interstellaire, l'élargissement associé à l'effet Doppler est généralement plus important que la largeur naturelle et l'élargissement dû aux collisions. Un exemple est représenté par la raie à 21 cm de l'hydrogène atomique, l'élargissement lorentzien étant extrêmement faible puisque la durée de vie du niveau supérieur n'est limitée que par les collisions, rares dans le milieu interstellaire diffus.
D'autres mouvements peuvent se superposer à la distribution de vitesse due à l'excitation thermique. S'il s'agit d'un mouvement d'ensemble, le centre de la raie est globalement déplacé par effet Doppler. Si, par contre, il s'agit d'une distribution de vitesse supplémentaire, la raie subit un élargissement gaussien. Par exemple, en présence de mouvements aléatoires de turbulence au sein du milieu, la largeur Doppler devient, par composition de profils gaussiens : 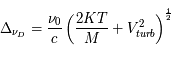 , où
, où 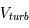 est la vitesse caractéristique de la turbulence. Dans les nuages interstellaires, la vitesse turbulente est de l'ordre de quelques kilomètres par seconde. Puisque la température des nuages n'est pas élevée, l'effet Doppler est dominé par la turbulence. Des mouvements turbulents plus importants ont été observés dans la nébuleuse d'Orion (voir le TP Spectre en émission).
est la vitesse caractéristique de la turbulence. Dans les nuages interstellaires, la vitesse turbulente est de l'ordre de quelques kilomètres par seconde. Puisque la température des nuages n'est pas élevée, l'effet Doppler est dominé par la turbulence. Des mouvements turbulents plus importants ont été observés dans la nébuleuse d'Orion (voir le TP Spectre en émission).
Convolution de profils : profil de Voigt
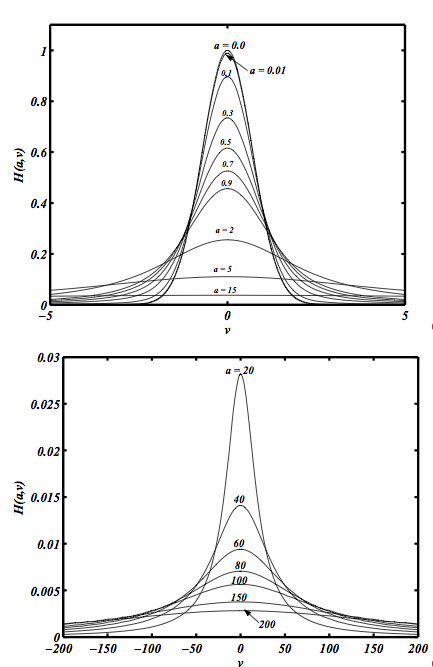
En général, le profil d'une raie résulte de la composition des profils induits par tous les différents effets décrits précédemment : élargissement naturel, collisions, effet Doppler thermique et turbulent. On obtient un profil qui dérive de la convolution d'une courbe Lorentzienne et d'une courbe gaussienne appelé profil de Voigt. Ce profil est exprimé en termes d'une fonction mathématiquement connue, la fonction de Voigt 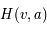 , dont les valeurs sont données dans la littérature :
, dont les valeurs sont données dans la littérature : 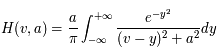 . Cette forme est obtenue par un changement de variable dans les fonctions lorentzienne et gaussienne tel que :
. Cette forme est obtenue par un changement de variable dans les fonctions lorentzienne et gaussienne tel que : 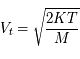 ,
, 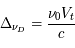 ,
, 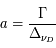 ,
, 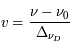 et donne le profil de raie normalisé :
et donne le profil de raie normalisé :
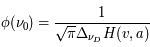 .
.
La fonction de Voigt est montrée sur la figure pour différentes valeurs du paramètre 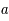 qui quantifie l'importance relative des différents processus qui contribuent à l'élargissement de raie. On remarque que dans le cas limite d'élargissement naturel et collisionnel négligeable (a=0) la fonction a une forme gaussienne, tandis que c'est une lorentzienne pour un élargissement Doppler négligeable (voir par exemple la courbe a=20). En général la fonction présente une allure gaussienne au coeur (
qui quantifie l'importance relative des différents processus qui contribuent à l'élargissement de raie. On remarque que dans le cas limite d'élargissement naturel et collisionnel négligeable (a=0) la fonction a une forme gaussienne, tandis que c'est une lorentzienne pour un élargissement Doppler négligeable (voir par exemple la courbe a=20). En général la fonction présente une allure gaussienne au coeur (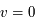 ) et lorentzienne dans les ailes.
) et lorentzienne dans les ailes.
Fonction de Voigt
Crédit :
M.R. Zaghloul, MNRAS, 375,1043,2007
Dans le premier chapitre du cours (Détection du gaz neutre atomique : raies spectrales) nous avons mentionné que les raies d'absorption interstellaires observées dans le visible et l'ultraviolet fournissent des informations précieuses sur les conditions physiques au sein du milieu interstellaire. Nous allons analyser en détail ce sujet en montrant comment on peut en déduire la densité de colonne des éléments observés.
Courbe de croissance
On peut exprimer la profondeur optique de la raie en terme de la fonction de Voigt 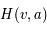 , qui contient l'information sur le profil de la raie dans le cas général où la largeur naturelle, les effets collisionnels et l'effet Doppler sont pris en compte, et un paramètre
, qui contient l'information sur le profil de la raie dans le cas général où la largeur naturelle, les effets collisionnels et l'effet Doppler sont pris en compte, et un paramètre 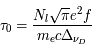 qui représente la profondeur optique au centre de la raie et dépend de la densité de colonne, de la largeur Doppler de la raie et des caractéristiques de la transition atomique par la quantité
qui représente la profondeur optique au centre de la raie et dépend de la densité de colonne, de la largeur Doppler de la raie et des caractéristiques de la transition atomique par la quantité 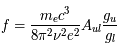 . Il s'agit d'un coefficient sans dimension souvent utilisé pour exprimer la probabilité d'émission spontanée qu'on appelle force de l'oscillateur. Il est possible de trouver dans la littérature des tables de
. Il s'agit d'un coefficient sans dimension souvent utilisé pour exprimer la probabilité d'émission spontanée qu'on appelle force de l'oscillateur. Il est possible de trouver dans la littérature des tables de 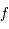 pour chaque raie. Nous pouvons donc écrire
pour chaque raie. Nous pouvons donc écrire 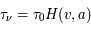 .
.
On identifie trois régimes concernant le profil de raie dépendant de la valeur du paramètre 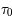 et donc du nombre d'atomes absorbants le long de la ligne de visée.
et donc du nombre d'atomes absorbants le long de la ligne de visée.
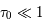 : la raie est optiquement mince. On en déduit que
: la raie est optiquement mince. On en déduit que 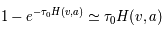 et le calcul de la largeur équivalente se réduit à :
et le calcul de la largeur équivalente se réduit à : 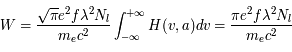 car l'intégrale de la fonction de Voigt vaut
car l'intégrale de la fonction de Voigt vaut 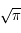 . Il s'agit en effet de raies faibles où la partie centrale domine le profil. On a vu que dans cette région la fonction de Voigt a une allure gaussienne. Le coeur dû à l'effet Doppler domine. Pour les raies optiquement minces la largeur équivalente est proportionnelle à la densité de colonne et on parle de régime linéaire. Dans ce régime les mesures de la largeur équivalente permettent une détermination précise de la densité de colonne, les paramètres atomiques étant connus.
. Il s'agit en effet de raies faibles où la partie centrale domine le profil. On a vu que dans cette région la fonction de Voigt a une allure gaussienne. Le coeur dû à l'effet Doppler domine. Pour les raies optiquement minces la largeur équivalente est proportionnelle à la densité de colonne et on parle de régime linéaire. Dans ce régime les mesures de la largeur équivalente permettent une détermination précise de la densité de colonne, les paramètres atomiques étant connus. 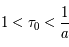 : lorsque le nombre d'atomes absorbants augmente, le centre de la raie devient de plus en plus optiquement épais. La contribution des ailes du profil reste toutefois négligeable. L'absorption principale est toujours due à l'effet Doppler, mais il y a une saturation de la raie qui prend une forme rectangulaire au centre. En s'éloignant du centre une absorption partielle persiste et la largeur équivalente croît lentement en fonction de la densité de colonne. On peut montrer que dans ce domaine
: lorsque le nombre d'atomes absorbants augmente, le centre de la raie devient de plus en plus optiquement épais. La contribution des ailes du profil reste toutefois négligeable. L'absorption principale est toujours due à l'effet Doppler, mais il y a une saturation de la raie qui prend une forme rectangulaire au centre. En s'éloignant du centre une absorption partielle persiste et la largeur équivalente croît lentement en fonction de la densité de colonne. On peut montrer que dans ce domaine 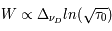 . Malheureusement des nombreuses raies d'absorption interstellaire se trouvent dans ce régime où la largeur équivalente est très peu sensible à la densité de colonne, ce qui en rend difficile l'estimation. De plus les mesures sont compliquées par la dépendance de la largeur Doppler.
. Malheureusement des nombreuses raies d'absorption interstellaire se trouvent dans ce régime où la largeur équivalente est très peu sensible à la densité de colonne, ce qui en rend difficile l'estimation. De plus les mesures sont compliquées par la dépendance de la largeur Doppler.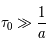 : la raie est saturée jusqu'aux ailes lorentziennes et la largeur équivalente varie proportionnellement à la racine de la densité de colonne et de la largeur naturelle (
: la raie est saturée jusqu'aux ailes lorentziennes et la largeur équivalente varie proportionnellement à la racine de la densité de colonne et de la largeur naturelle (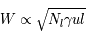 ).
).
Pour chaque raie spectrale il est donc possible de construire une courbe de croissance théorique où l'on porte 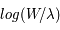 en fonction de
en fonction de 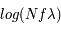 . Elle est composée d'une partie linéaire, d'une portion plate dont la position sur l'axe vertical dépend de la valeur de la largeur Doppler et d'une région dont la pente est fonction de la largeur naturelle (et éventuellement de la densité du gaz s'il existe une contribution des collisions à l'élargissement). Pour construire cette courbe il faut donc connaître
. Elle est composée d'une partie linéaire, d'une portion plate dont la position sur l'axe vertical dépend de la valeur de la largeur Doppler et d'une région dont la pente est fonction de la largeur naturelle (et éventuellement de la densité du gaz s'il existe une contribution des collisions à l'élargissement). Pour construire cette courbe il faut donc connaître 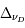 et
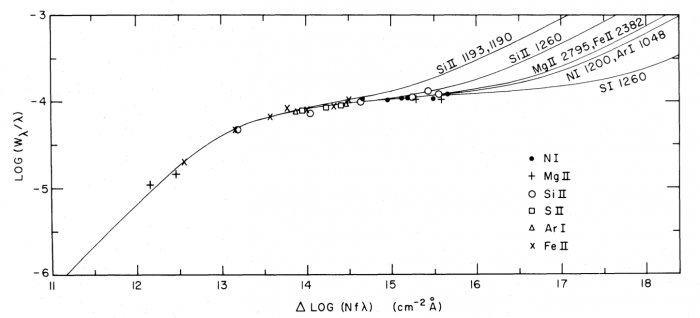
et 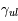 . Dans ce cas, on peut placer la raie sur la courbe, en déterminant la largeur équivalente et en déduire la densité de colonne. Dans la figure on montre les courbes de croissance obtenues d'observations de l'étoile ζ Ophiuchi. Les valeurs mesurées, pour différents éléments à différentes longueurs d'onde provenant du même nuage, sont superposées à une courbe de croissance théorique obtenue avec une distribution fixée des vitesses, ce qui donne ainsi des renseignements sur la dispersion de vitesse ou les mouvement aléatoires d'ensemble au sein du nuage.
. Dans ce cas, on peut placer la raie sur la courbe, en déterminant la largeur équivalente et en déduire la densité de colonne. Dans la figure on montre les courbes de croissance obtenues d'observations de l'étoile ζ Ophiuchi. Les valeurs mesurées, pour différents éléments à différentes longueurs d'onde provenant du même nuage, sont superposées à une courbe de croissance théorique obtenue avec une distribution fixée des vitesses, ce qui donne ainsi des renseignements sur la dispersion de vitesse ou les mouvement aléatoires d'ensemble au sein du nuage.
Courbe de croissance
Crédit :
D. Morton, Apj, 197, 85, 1975
Au cours du premier chapitre nous avons souligné l'importance des poussières pour le bilan énergétique (émission thermique et chauffage photoélectrique) et la chimie (déplétion des éléments) du milieu interstellaire. Pendant les travaux pratiques nous avons également constaté l'absorption de la lumière stellaire en comparant des images à différentes longueurs d'onde. Dans cette page nous allons détailler ce processus grâce aux notions de transfert de rayonnement acquises. Il faut remarquer que, différemment de l'absorption des atomes et des molécules que nous avons vu se produire dans des raies spectrales étroites, l'absorption par les poussières a lieu dans le continu, et dans quelques bandes larges produites par les modes de vibration ou pliage des molécules du matériau solide (silicates, glaces, PAHs...).
Extinction et rougissement interstellaires
La diminution de la luminosité d'une étoile vue à travers un nuage de poussières est due à deux phénomènes physiques : l'absorption des photons par le matériau du grain, et la diffusion des photons dans d'autres directions que la direction incidente. La somme de ces 2 processus est appelée extinction. Cette quantité dépend de la composition des poussières, de leur forme, de la distribution de leurs tailles et de la longueur d'onde. En particulier, la diffusion étant sélective en longueur d'onde, la lumière diffusée est plus bleue que celle de l'étoile, tandis que la lumière transmise à travers un nuage de poussières est plus rouge. La lumière diffusée forme des objets étendus, appelés nébuleuses par réflexion, qui réfléchissent la lumière de l'étoile illuminatrice et sont habituellement bleues. En expliquant les méthodes de mesure du champ magnétique (voir la page Source d'énergie : champ magnétique ) nous avons également mentionné que la lumière diffusée ou transmise est partiellement polarisée.
L'extinction d'un nuage de poussières à une longueur d'onde 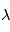 est décrite par la quantité
est décrite par la quantité 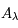 (mesurée en magnitude), définie comme la différence entre la magnitude observée
(mesurée en magnitude), définie comme la différence entre la magnitude observée 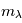 d'une étoile dont la lumière a traversé le nuage de poussières (de profondeur optique
d'une étoile dont la lumière a traversé le nuage de poussières (de profondeur optique 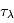 ) et celle qu'on observerait en l'absence d'extinction,
) et celle qu'on observerait en l'absence d'extinction, 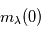 . Comme l'émission des poussières est en général négligeable à la longueur d'onde considérée, le flux spécifique
. Comme l'émission des poussières est en général négligeable à la longueur d'onde considérée, le flux spécifique 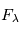 est atténué par un facteur
est atténué par un facteur 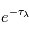 . Avec la relation entre magnitude et flux, on obtient :
. Avec la relation entre magnitude et flux, on obtient : ![A_\lambda(mag)=m_\lambda - m_\lambda(0) = -2.5log_{10}\left[\frac{F_\lambda(\tau_\lambda)}{F_\lambda(0)}\right]=-2.5log_{10}[e^{-\tau_\lambda}]=1.086\tau_\lambda](../pages_transfert-rayon/equations_transfert-rayon/equation328.png) . On voit que la valeur de
. On voit que la valeur de 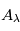 en magnitude est essentiellement égale à l'opacité des poussières à cette longueur d'onde ; elle est donc proportionnelle à la densité colonne de poussières sur la ligne de visée.
en magnitude est essentiellement égale à l'opacité des poussières à cette longueur d'onde ; elle est donc proportionnelle à la densité colonne de poussières sur la ligne de visée.
Courbe d'extinction
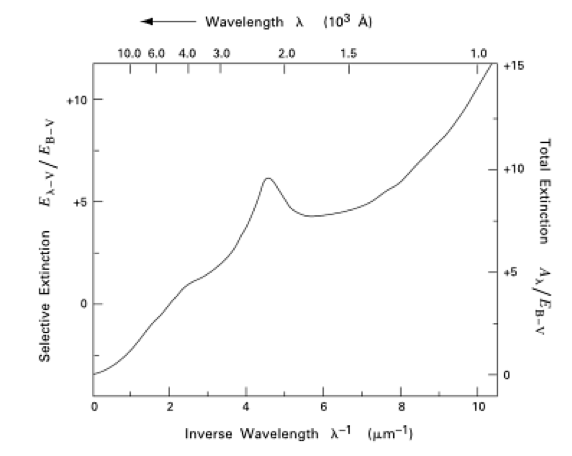
Crédit :
Stahler & Palla, "The Formation of Stars"
 Intensité spécifique
Intensité spécifique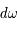 , dans un intervalle de fréquence de
, dans un intervalle de fréquence de 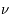 à
à 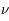 +
+ 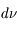 et traversant une surface
et traversant une surface 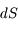 perpendiculaire à sa direction de propagation. L'énergie de ce rayonnement qui passe à travers la surface pendant le temps
perpendiculaire à sa direction de propagation. L'énergie de ce rayonnement qui passe à travers la surface pendant le temps 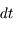 est :
est :
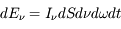 .
Le coefficient de proportionnalité
.
Le coefficient de proportionnalité 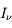 dans cette expression est appelé intensité spécifique et représente donc l'énergie par unité de surface, par unité de fréquence, par unité d'angle solide et par unité de temps, qui traverse une surface perpendiculaire au faisceau de rayonnement. L'intensité spécifique s'exprime en erg cm-2 Hz-1 sr-1 s-1 dans le système CGS.
Si la direction du rayonnement, centrée sur l'angle solide
dans cette expression est appelé intensité spécifique et représente donc l'énergie par unité de surface, par unité de fréquence, par unité d'angle solide et par unité de temps, qui traverse une surface perpendiculaire au faisceau de rayonnement. L'intensité spécifique s'exprime en erg cm-2 Hz-1 sr-1 s-1 dans le système CGS.
Si la direction du rayonnement, centrée sur l'angle solide 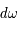 , fait un angle
, fait un angle 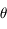 avec la normale à
avec la normale à 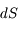 (voir la figure), la surface efficace perpendiculaire au faisceau vaut
(voir la figure), la surface efficace perpendiculaire au faisceau vaut 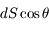 et l'énergie s'écrit alors :
et l'énergie s'écrit alors : 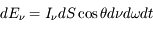 .
.

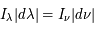 . Puisque
. Puisque 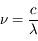 , on en déduit que
, on en déduit que 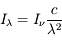 avec
avec 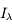 en erg cm-2
en erg cm-2 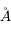 -1 sr-1 s-1. L'intensité spécifique est une quantité fondamentale dont dérivent les autres grandeurs physiques qui caractérisent le rayonnement, comme la densité d'énergie monochromatique
-1 sr-1 s-1. L'intensité spécifique est une quantité fondamentale dont dérivent les autres grandeurs physiques qui caractérisent le rayonnement, comme la densité d'énergie monochromatique 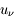 par unité de volume et par unité d'intervalle de fréquence,
par unité de volume et par unité d'intervalle de fréquence, 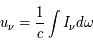 , ou le flux net
, ou le flux net 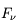 , c'est-à-dire le flux d'énergie par unité de surface, de fréquence et de temps,
, c'est-à-dire le flux d'énergie par unité de surface, de fréquence et de temps, 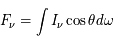 .
.
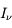 traverse une épaisseur
traverse une épaisseur 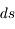 de matière, il subit une atténuation
de matière, il subit une atténuation 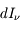 proportionnelle à
proportionnelle à 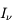 telle que :
telle que :
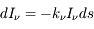 . La quantité
. La quantité 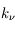 est appelée coefficient d'extinction et inclut à la fois les processus d'absorption et de diffusion. On peut donc l'exprimer comme la somme d'un coefficient d'absorption
est appelée coefficient d'extinction et inclut à la fois les processus d'absorption et de diffusion. On peut donc l'exprimer comme la somme d'un coefficient d'absorption 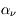 et d'un coefficient de diffusion
et d'un coefficient de diffusion 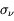 :
: 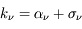 . L'absorption résulte de divers processus physiques intervenant dans le milieu qui impliquent des changements des degrés de liberté internes d'un atome ou d'une molécule. Des exemples de ces processus sont :
. L'absorption résulte de divers processus physiques intervenant dans le milieu qui impliquent des changements des degrés de liberté internes d'un atome ou d'une molécule. Des exemples de ces processus sont :
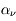 dépend de l'état thermodynamique de la matière traversée (pression, température, abondances chimiques) en un point donné du milieu. Le faisceau peut perdre de l'énergie également à cause du processus de diffusion, qui change à la fois la direction et l'énergie des photons. Cette énergie, contrairement au processus d'absorption, n'est pas transformée en énergie cinétique du milieu. Les variations locales d'énergie associées au processus de diffusion dépendent donc principalement du champ de rayonnement et faiblement des propriétés thermodynamiques locales du milieu.
dépend de l'état thermodynamique de la matière traversée (pression, température, abondances chimiques) en un point donné du milieu. Le faisceau peut perdre de l'énergie également à cause du processus de diffusion, qui change à la fois la direction et l'énergie des photons. Cette énergie, contrairement au processus d'absorption, n'est pas transformée en énergie cinétique du milieu. Les variations locales d'énergie associées au processus de diffusion dépendent donc principalement du champ de rayonnement et faiblement des propriétés thermodynamiques locales du milieu.
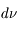 à
à 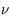 +
+ 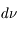 :
: 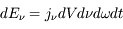 . Il s'exprime en erg cm-3 Hz-1 sr-1 s-1. En parcourant une distance
. Il s'exprime en erg cm-3 Hz-1 sr-1 s-1. En parcourant une distance 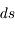 , un faisceau de rayonnement de section efficace
, un faisceau de rayonnement de section efficace 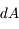 traverse un volume
traverse un volume 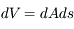 . On en déduit que l'intensité ajoutée au faisceau par l'émission est
. On en déduit que l'intensité ajoutée au faisceau par l'émission est 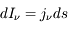 . L'émission résulte de la combinaison des processus physiques inverses à ceux qui provoquent l'absorption. Ces processus sont :
. L'émission résulte de la combinaison des processus physiques inverses à ceux qui provoquent l'absorption. Ces processus sont :
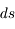 et surface
et surface 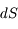 = 1 perpendiculaire à la direction de propagation
= 1 perpendiculaire à la direction de propagation 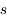 . En utilisant les définitions des coefficients d'absorption et d'émission données à la page
. En utilisant les définitions des coefficients d'absorption et d'émission données à la page 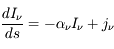 .
.
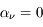 et l'équation de transfert devient :
et l'équation de transfert devient : 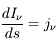 qui admet la solution
qui admet la solution 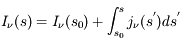 . Cela signifie que l'augmentation de l'intensité spécifique entre la position initiale
. Cela signifie que l'augmentation de l'intensité spécifique entre la position initiale 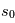 et le point final
et le point final 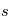 est égale au coefficient d'émission intégré le long de cette "ligne de visée" à travers la couche de matière.
est égale au coefficient d'émission intégré le long de cette "ligne de visée" à travers la couche de matière.
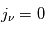 ) on obtient :
) on obtient : 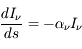 , dont la solution est
, dont la solution est 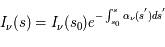 . L'intensité spécifique au point final
. L'intensité spécifique au point final 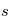 est égale à l'intensité spécifique au point initial
est égale à l'intensité spécifique au point initial 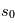 , atténuée par un facteur exponentiel dont l'argument est l'intégrale du coefficient d'absorption le long de la ligne de visée entre
, atténuée par un facteur exponentiel dont l'argument est l'intégrale du coefficient d'absorption le long de la ligne de visée entre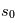 et
et 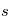 . Cette intégrale est un nombre sans dimension appelé la profondeur optique du milieu:
. Cette intégrale est un nombre sans dimension appelé la profondeur optique du milieu:
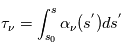 .
.
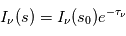 . On voit ainsi que la profondeur optique détermine la fraction de l'intensité incidente qui peut s'échapper du milieu. Afin de mieux comprendre le concept de profondeur optique, on introduit le libre parcours moyen du rayonnement qui représente la distance moyenne qu'un photon parcourt à travers un milieu sans être absorbé. Le coefficient
. On voit ainsi que la profondeur optique détermine la fraction de l'intensité incidente qui peut s'échapper du milieu. Afin de mieux comprendre le concept de profondeur optique, on introduit le libre parcours moyen du rayonnement qui représente la distance moyenne qu'un photon parcourt à travers un milieu sans être absorbé. Le coefficient 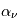 est l'inverse de ce libre parcours moyen, pour un photon de fréquence
est l'inverse de ce libre parcours moyen, pour un photon de fréquence 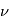 . La profondeur optique
. La profondeur optique 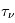 est donc égale au nombre total de libres parcours moyens traversés entre
est donc égale au nombre total de libres parcours moyens traversés entre 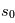 et
et 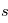 . Si la distance à travers le nuage est égale au libre parcours moyen (
. Si la distance à travers le nuage est égale au libre parcours moyen (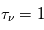 ), l'intensité subit une atténuation d'un facteur e-1 =0.368, ie. en moyenne seulement 36.8% des photons incidents sortiront du nuage. Si la distance parcourue équivaut à deux fois le libre parcours moyen (
), l'intensité subit une atténuation d'un facteur e-1 =0.368, ie. en moyenne seulement 36.8% des photons incidents sortiront du nuage. Si la distance parcourue équivaut à deux fois le libre parcours moyen (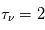 ), seulement 13.5% (e-2 =0.135) des photons incidents survivront en traversant le nuage. Pour cette raison, un milieu caractérisé par une profondeur optique
), seulement 13.5% (e-2 =0.135) des photons incidents survivront en traversant le nuage. Pour cette raison, un milieu caractérisé par une profondeur optique 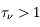 est dit optiquement épais ou opaque, alors qu'un milieu avec
est dit optiquement épais ou opaque, alors qu'un milieu avec 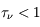 est dit optiquement mince ou transparent.
est dit optiquement mince ou transparent.
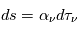 et en définissant la quantité
et en définissant la quantité 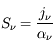 (appelée fonction source) ; l'équation prend la forme :
(appelée fonction source) ; l'équation prend la forme :
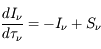 .
.
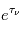 et posé
et posé 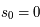 ) on obtient la solution formelle :
) on obtient la solution formelle :
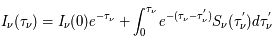 .
.
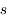 . Le second terme décrit l'émission dérivant de toutes les couches
. Le second terme décrit l'émission dérivant de toutes les couches 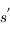 (car
(car 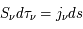 ) dont la contribution est atténuée par la profondeur optique
) dont la contribution est atténuée par la profondeur optique 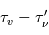 entre le point d'émission
entre le point d'émission 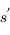 et le points
et le points 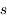 où l'on calcule l'intensité.
où l'on calcule l'intensité.
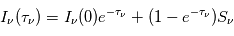 .
.
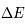 . Nous nous intéressons aux transitions radiatives entres ces deux états. Comme nous verrons en détail dans la suite du cours ces transitions ne se produisent pas uniquement à la fréquence
. Nous nous intéressons aux transitions radiatives entres ces deux états. Comme nous verrons en détail dans la suite du cours ces transitions ne se produisent pas uniquement à la fréquence 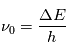 mais également aux fréquences voisines de
mais également aux fréquences voisines de 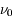 . Par conséquent les raies spectrales associées à ces transitions sont caractérisées par un profil de raie
. Par conséquent les raies spectrales associées à ces transitions sont caractérisées par un profil de raie 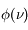 , piqué à la fréquence
, piqué à la fréquence 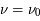 , qui décrit l'efficacité des fréquences voisines de
, qui décrit l'efficacité des fréquences voisines de 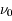 à induire ces transitions. L'agitation thermique du gaz (mouvement brownien) produit par exemple un élargissement du profil par effet Doppler, car un atome en mouvement peut absorber un photon de fréquence légèrement différente de
à induire ces transitions. L'agitation thermique du gaz (mouvement brownien) produit par exemple un élargissement du profil par effet Doppler, car un atome en mouvement peut absorber un photon de fréquence légèrement différente de 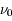 . La largeur du profil est alors de l'ordre de
. La largeur du profil est alors de l'ordre de 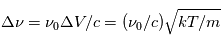 . Dans la suite on fera l'hypothèse que la forme de la raie est la même en absorption et en émission. Les 3 processus de transitions radiatives quantifiés par Einstein sont les suivants :
. Dans la suite on fera l'hypothèse que la forme de la raie est la même en absorption et en émission. Les 3 processus de transitions radiatives quantifiés par Einstein sont les suivants :
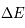 . Cette transition se produit même en l'absence d'un champ de rayonnement. Elle est caractérisée par le coefficient d'Einstein
. Cette transition se produit même en l'absence d'un champ de rayonnement. Elle est caractérisée par le coefficient d'Einstein 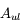 , qui représente une probabilité de transition par unité de temps et est exprimé en s-1. Ce coefficient ne dépend que des termes de couplages électro-magnétique entre les 2 niveaux quantiques u et l.
, qui représente une probabilité de transition par unité de temps et est exprimé en s-1. Ce coefficient ne dépend que des termes de couplages électro-magnétique entre les 2 niveaux quantiques u et l. 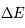 , faisant passer les atomes du niveaux l au niveau u. Elle est caractérisée par une probabilité de transition par unité de temps
, faisant passer les atomes du niveaux l au niveau u. Elle est caractérisée par une probabilité de transition par unité de temps 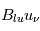 , où
, où 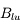 est le coefficient d'absorption d'Einstein et
est le coefficient d'absorption d'Einstein et 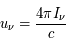 est la densité d'énergie monochromatique à la fréquence
est la densité d'énergie monochromatique à la fréquence 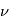 pour un champ de rayonnement isotrope.
pour un champ de rayonnement isotrope. 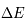 et passe de l'état u à l'état l en emettant un deuxième photon identique à celui qu'il a absorbé. Ce processus est caractérisé par une probabilité par unité de temps
et passe de l'état u à l'état l en emettant un deuxième photon identique à celui qu'il a absorbé. Ce processus est caractérisé par une probabilité par unité de temps 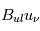 .
. 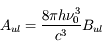 et
et
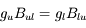 .
.
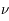 (contenue dans le profil de la raie) qui arrive sur une tranche du milieu avec une intensité spécifique
(contenue dans le profil de la raie) qui arrive sur une tranche du milieu avec une intensité spécifique 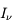 par unité de surface, de fréquence, et d'angle solide. Le long de la distance
par unité de surface, de fréquence, et d'angle solide. Le long de la distance 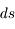 dans sa direction de propagation, l'intensité sera augmentée à la fois par l'émission spontanée et par l'émission stimulée des atomes dans l'état u ; simultanément elle sera diminuée par l'absorption de photons par les atomes dans l'état l. Considérons d'abord le cas de l'émission spontanée : le nombre total d'atomes dans l'état u rencontré par unité de surface est
dans sa direction de propagation, l'intensité sera augmentée à la fois par l'émission spontanée et par l'émission stimulée des atomes dans l'état u ; simultanément elle sera diminuée par l'absorption de photons par les atomes dans l'état l. Considérons d'abord le cas de l'émission spontanée : le nombre total d'atomes dans l'état u rencontré par unité de surface est 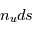 . L'augmentation d'intensité à la fréquence
. L'augmentation d'intensité à la fréquence 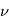 causée par ce processus est obtenue en multipliant
causée par ce processus est obtenue en multipliant 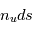 par le coefficient d'Einstein correspondant
par le coefficient d'Einstein correspondant 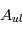 divisé par
divisé par 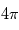 (car chaque photon est supposé émis ou absorbé de façon isotrope et nous regardons la variation par unité d'angle solide), par le profil de la raie
(car chaque photon est supposé émis ou absorbé de façon isotrope et nous regardons la variation par unité d'angle solide), par le profil de la raie 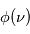 , et enfin par l'énergie de chaque photon (
, et enfin par l'énergie de chaque photon (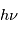 ) ; en appliquant le même raisonnement à l'émission et absorption stimulées, le bilan de ces transition radiatives donne l'équation de transfert :
) ; en appliquant le même raisonnement à l'émission et absorption stimulées, le bilan de ces transition radiatives donne l'équation de transfert :
![\frac{dI_\nu}{ds} = \frac{h\nu }{4\pi} \phi(\nu) [n_u A_{ul} +(n_u B_{ul} - n_l B_{lu})\frac{4\pi I_\nu}{c}]](../pages_transfert-rayon/equations_transfert-rayon/equation110.png) .
.
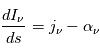 , présentée dans la section
, présentée dans la section 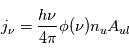
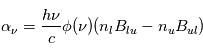
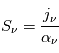
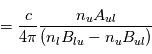 .
.
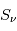 ne dépend pas de
ne dépend pas de 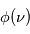 , mais uniquement des coefficients d'Einstein et des populations des niveaux impliqués. Plus précisément elle ne dépend que du rapport entre ces populations . En effet, en utilisant les relations entre coefficients d'Einstein données ci-dessus, on obtient :
, mais uniquement des coefficients d'Einstein et des populations des niveaux impliqués. Plus précisément elle ne dépend que du rapport entre ces populations . En effet, en utilisant les relations entre coefficients d'Einstein données ci-dessus, on obtient :
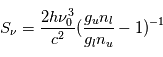 , où
, où 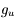 et
et 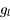 sont les poids statistiques (dégénérescences) de chaque niveau.
sont les poids statistiques (dégénérescences) de chaque niveau.
![\alpha_\nu=\frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-\frac{n_ug_l}{n_lg_u}]](../pages_transfert-rayon/equations_transfert-rayon/equation121.png) .
.
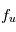 et
et 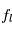 les fractions
les fractions 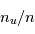 et
et 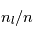 d'atomes qui sont dans les niveaux u et l, on remarque qu'
d'atomes qui sont dans les niveaux u et l, on remarque qu'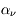 est proportionnel à la densité volumique totale des atomes,
est proportionnel à la densité volumique totale des atomes, 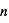 , et à une fonction qui ne dépend que de
, et à une fonction qui ne dépend que de 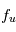 et
et 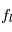 , c'est-à-dire à la répartition statistique des atomes entre leurs différents niveaux d'énergie. Il en découle que la profondeur optique, obtenue en intégrant cette quantité le long de la ligne de visée, sera proportionnelle à
, c'est-à-dire à la répartition statistique des atomes entre leurs différents niveaux d'énergie. Il en découle que la profondeur optique, obtenue en intégrant cette quantité le long de la ligne de visée, sera proportionnelle à 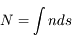 que l'on appelle la densité de colonne des atomes (en unité d'atomes par cm-2), c'est-à-dire le nombre d'atomes dans un cylindre de section unité le long de la ligne de visée. C'est par ce biais que l'observation des raies spectrales pourra nous donner accès à la masse de gaz émetteur --- à condition que l'on puisse connaître (ou estimer) les fractions
que l'on appelle la densité de colonne des atomes (en unité d'atomes par cm-2), c'est-à-dire le nombre d'atomes dans un cylindre de section unité le long de la ligne de visée. C'est par ce biais que l'observation des raies spectrales pourra nous donner accès à la masse de gaz émetteur --- à condition que l'on puisse connaître (ou estimer) les fractions 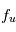 et
et 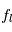 d'atomes peuplant les niveaux u et l, ou en d'autres termes les "conditions d'excitation" de la transition.
d'atomes peuplant les niveaux u et l, ou en d'autres termes les "conditions d'excitation" de la transition.
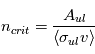
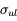 est la section efficace de désexcitation collisionnelle, qui dépend en général de la vitesse
est la section efficace de désexcitation collisionnelle, qui dépend en général de la vitesse 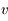 du collisionneur. Les crochets signifient qu'on prend la moyenne sur toute la distribution statistique des vitesses
du collisionneur. Les crochets signifient qu'on prend la moyenne sur toute la distribution statistique des vitesses 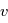 (distribution Boltzmanienne) ce qui donne une valeur dépendant de la température du gaz.
(distribution Boltzmanienne) ce qui donne une valeur dépendant de la température du gaz.
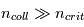 , les transitions radiatives sont négligeables devant les transitions collisionnelles et on atteint l'équilibre thermodynamique local (ou ETL),
où les populations relatives des niveaux des atomes (ou molécules) ne dépendent ni de
, les transitions radiatives sont négligeables devant les transitions collisionnelles et on atteint l'équilibre thermodynamique local (ou ETL),
où les populations relatives des niveaux des atomes (ou molécules) ne dépendent ni de 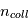 ni du champ de rayonnement et obéissent simplement à la loi de Boltzmann :
ni du champ de rayonnement et obéissent simplement à la loi de Boltzmann :
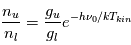
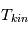 est la température cinétique des collisionneurs, qui caractérise la distribution de vitesse des particules,
est la température cinétique des collisionneurs, qui caractérise la distribution de vitesse des particules, 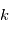 la constante de Boltzmann,
la constante de Boltzmann, 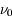 est la fréquence de la transition entre les états u et l,
est la fréquence de la transition entre les états u et l, 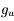 et
et 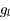 sont les poids statistiques. Plus le coefficient d'Einstein est fort, et plus la densité critique nécessaire pour atteindre l'ETL sera élevée. Cette densité critique est très variable selon les espèces et les transitions considérées : elle est très faible pour la raie hyperfine de l'hydrogène atomique (voir ci-dessous), de l'ordre de 1000 cm-3 pour les premières raies rotationnelles de CO, mais atteint 108 cm-3 pour H2O.
sont les poids statistiques. Plus le coefficient d'Einstein est fort, et plus la densité critique nécessaire pour atteindre l'ETL sera élevée. Cette densité critique est très variable selon les espèces et les transitions considérées : elle est très faible pour la raie hyperfine de l'hydrogène atomique (voir ci-dessous), de l'ordre de 1000 cm-3 pour les premières raies rotationnelles de CO, mais atteint 108 cm-3 pour H2O.
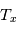 , telle que
, telle que
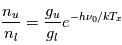 .
.
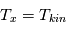 . Dans le cas contraire,
. Dans le cas contraire, 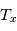 dépend aussi du rapport
dépend aussi du rapport 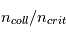 et de l'intensité du champ de rayonnement local, qui peuvent varier fortement d'un point à l'autre. Elle peut être inférieure à
et de l'intensité du champ de rayonnement local, qui peuvent varier fortement d'un point à l'autre. Elle peut être inférieure à 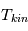 (cas le plus courant dans le MIS) ou bien supérieure si le pompage radiatif est important (par exemple à proximité d'une source de rayonnement intense), voire négative en présence d'un effet maser (inversion de population). En outre, il peut y avoir des températures d'excitation différentes pour différentes transitions d'un même atome.
(cas le plus courant dans le MIS) ou bien supérieure si le pompage radiatif est important (par exemple à proximité d'une source de rayonnement intense), voire négative en présence d'un effet maser (inversion de population). En outre, il peut y avoir des températures d'excitation différentes pour différentes transitions d'un même atome.
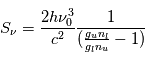
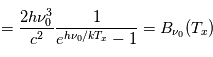 .
.
![\alpha_\nu=\frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-\frac{n_ug_l}{n_lg_u}]](../pages_transfert-rayon/equations_transfert-rayon/equation153.png)
![= \frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-e^{-h\nu_0/kT_x}]](../pages_transfert-rayon/equations_transfert-rayon/equation154.png) .
.
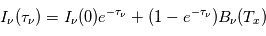 .
.
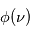 = 0, donc
= 0, donc 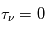 , et
, et 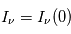 . Ceci définit le niveau du "continuum" que l'on mesure autour de la raie spectrale. Dans ce qui suit nous allons examiner sous quelles conditions la raie apparaîtra en émission ou en absorption par rapport à ce niveau de continu de référence.
. Ceci définit le niveau du "continuum" que l'on mesure autour de la raie spectrale. Dans ce qui suit nous allons examiner sous quelles conditions la raie apparaîtra en émission ou en absorption par rapport à ce niveau de continu de référence.
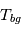 , telle que l'intensité du continu en dehors de la raie s'écrive
, telle que l'intensité du continu en dehors de la raie s'écrive
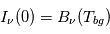 . La solution formelle de l'équation du transfert radiatif devient
. La solution formelle de l'équation du transfert radiatif devient
![I_\nu(\tau_\nu) - I_\nu(0) = (1 - e^{-\tau_\nu} )[B_\nu(T_x) - B_\nu(T_{bg})]](../pages_transfert-rayon/equations_transfert-rayon/equation161.png) .
.
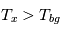 alors le terme de droite est positif et la raie spectrale apparaîtra en émission, avec une intensité supérieure au niveau du continu
alors le terme de droite est positif et la raie spectrale apparaîtra en émission, avec une intensité supérieure au niveau du continu 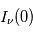 ;
alors que si
;
alors que si 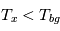 la raie apparaîtra en absorption, avec une intensité qui descend sous le niveau du continu. Enfin dans le cas particulier où
la raie apparaîtra en absorption, avec une intensité qui descend sous le niveau du continu. Enfin dans le cas particulier où 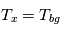 , la raie spectrale se confondra avec le continu et ne sera plus observable en tant que telle. Cette situation ne se rencontre que très rarement dans le MIS.
, la raie spectrale se confondra avec le continu et ne sera plus observable en tant que telle. Cette situation ne se rencontre que très rarement dans le MIS.
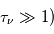 , on obtient
, on obtient 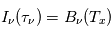 : le rayonnement d'un nuage optiquement épais s'apparente au rayonnement d'un corps noir à la température d'excitation
: le rayonnement d'un nuage optiquement épais s'apparente au rayonnement d'un corps noir à la température d'excitation 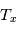 de la transition considérée. Si de plus on est à l'ETL, alors
de la transition considérée. Si de plus on est à l'ETL, alors 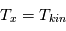 et on peut déduire la température cinétique du gaz à partir de
et on peut déduire la température cinétique du gaz à partir de 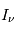 . Cette technique s'applique par exemple à la raie rotationnelle fondamentale de CO à une longueur d'onde de 2.6mm ; elle donne des valeurs typiques de température de 10-20 K dans les nuages moléculaires. Par contre, on voit que dans le cas optiquement épais l'intensité ne dépend plus de
. Cette technique s'applique par exemple à la raie rotationnelle fondamentale de CO à une longueur d'onde de 2.6mm ; elle donne des valeurs typiques de température de 10-20 K dans les nuages moléculaires. Par contre, on voit que dans le cas optiquement épais l'intensité ne dépend plus de  , c'est-à-dire de la quantité de matière traversée ; on dit que la raie est "saturée". Il n'est donc pas possible de déduire la masse de gaz.
, c'est-à-dire de la quantité de matière traversée ; on dit que la raie est "saturée". Il n'est donc pas possible de déduire la masse de gaz.
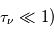 , on obtient
, on obtient ![I_\nu(\tau_\nu) - I_\nu(0) = \tau_\nu [B_\nu(T_x) - B_\nu(T_{bg})]](../pages_transfert-rayon/equations_transfert-rayon/equation173.png) : l'excès d'intensité au-dessus du continu est proportionnel à l'opacité, dont nous avons vu qu'est elle-même proportionnelle à la densité colonne
: l'excès d'intensité au-dessus du continu est proportionnel à l'opacité, dont nous avons vu qu'est elle-même proportionnelle à la densité colonne 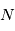 de l'atome considéré, et à une fonction de
de l'atome considéré, et à une fonction de 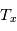 (qui fixe les populations relatives des niveaux). Avec une estimation indépendante de
(qui fixe les populations relatives des niveaux). Avec une estimation indépendante de 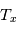 (par ex.
(par ex. 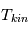 si la raie est à l'ETL), il est donc possible de déduire de ces observations la valeur de
si la raie est à l'ETL), il est donc possible de déduire de ces observations la valeur de 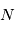 , et ensuite de la masse de gaz si la taille de la région d'émission et l'abondance de l'atome ou molécule sont connues. Cette technique est utilisée par exemple pour mesurer les masses des nuages moléculaires, grâce à des isotopes peu abondants comme 13CO et C18O qui sont (généralement) optiquement minces.
, et ensuite de la masse de gaz si la taille de la région d'émission et l'abondance de l'atome ou molécule sont connues. Cette technique est utilisée par exemple pour mesurer les masses des nuages moléculaires, grâce à des isotopes peu abondants comme 13CO et C18O qui sont (généralement) optiquement minces.
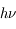 <<
<< 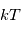 si bien que
si bien que 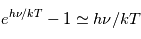 et la fonction de Planck s'écrit :
et la fonction de Planck s'écrit :
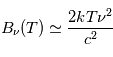 .
.
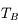 définie par :
définie par :
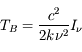 ,
,
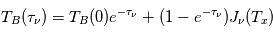 où on a défini la fonction
où on a défini la fonction
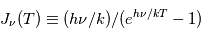 qui tend vers
qui tend vers 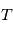 dans la limite de Rayleigh-Jeans.
dans la limite de Rayleigh-Jeans.
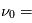 1420 MHz) correspond à une transition hyperfine du niveau fondamental de l'hydrogène atomique, où le photon est émis lorsque le spin de l'électron passe d'un état parallèle (
1420 MHz) correspond à une transition hyperfine du niveau fondamental de l'hydrogène atomique, où le photon est émis lorsque le spin de l'électron passe d'un état parallèle (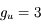 ) à un état antiparallèle (
) à un état antiparallèle (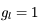 ) au spin du proton. La transition possède un coefficient d'Einstein très faible
) au spin du proton. La transition possède un coefficient d'Einstein très faible 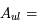 2.85 x 10-15 s-1 (raie "interdite") mais la très grande quantité d'hydrogène le long de la ligne de visée dans la Galaxie la rend cependant parfaitement visible. Du fait de cette très faible valeur d'
2.85 x 10-15 s-1 (raie "interdite") mais la très grande quantité d'hydrogène le long de la ligne de visée dans la Galaxie la rend cependant parfaitement visible. Du fait de cette très faible valeur d'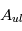 , la densité critique est elle aussi très faible :
, la densité critique est elle aussi très faible : 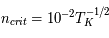 cm-3,
cm-3, 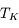 étant la température cinétique du gaz. Dans le milieu atomique neutre du MIS, les températures cinétiques typiques sont de l'ordre de 50-5000 K pour des densités de 30 à 0.1 cm-3 ; On a donc
étant la température cinétique du gaz. Dans le milieu atomique neutre du MIS, les températures cinétiques typiques sont de l'ordre de 50-5000 K pour des densités de 30 à 0.1 cm-3 ; On a donc 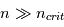 et les niveaux sont à l'équilibre thermodynamique local (ETL), c'est-à-dire
et les niveaux sont à l'équilibre thermodynamique local (ETL), c'est-à-dire 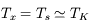 (pour cette raie, la température d'excitation
(pour cette raie, la température d'excitation 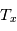 est appelée "température de spin"
est appelée "température de spin" 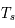 ).
).
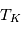 du nuage), la raie à 21 cm peut être observée à la fois en émission et en absorption. La détection est en émission lorsque le nuage est observé sur le fond cosmologique plus froid à 2,7 K, ce qui est la situation la plus courante. La détection est en absorption lorsque le nuage s'interpose sur la la ligne de visée d'une source puissante de rayonnement continu radio synchrotron (quasar lointain) où
du nuage), la raie à 21 cm peut être observée à la fois en émission et en absorption. La détection est en émission lorsque le nuage est observé sur le fond cosmologique plus froid à 2,7 K, ce qui est la situation la plus courante. La détection est en absorption lorsque le nuage s'interpose sur la la ligne de visée d'une source puissante de rayonnement continu radio synchrotron (quasar lointain) où 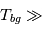 5000 K. Les nuages absorbent alors les photons possédant la bonne énergie pour exciter les électrons du premier niveau hyperfin de l'hydrogène. Ce type d'observation en absorption nécessite un interféromètre pour que le signal vers la source continuum (ponctuelle) ne soit pas complètement "dilué" dans l'émission étendue provenant des lignes de visée adjacentes.
5000 K. Les nuages absorbent alors les photons possédant la bonne énergie pour exciter les électrons du premier niveau hyperfin de l'hydrogène. Ce type d'observation en absorption nécessite un interféromètre pour que le signal vers la source continuum (ponctuelle) ne soit pas complètement "dilué" dans l'émission étendue provenant des lignes de visée adjacentes.
![\alpha_\nu = \frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-e^{-h\nu_0/kT_x}]](../pages_transfert-rayon/equations_transfert-rayon/equation201.png) .
.
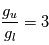 . De plus, à la basse fréquence de cette raie, 1420 MHz, nous sommes toujours dans le domaine
. De plus, à la basse fréquence de cette raie, 1420 MHz, nous sommes toujours dans le domaine 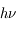 <<
<<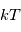 (approximation de Rayleigh-Jeans). Le facteur de Boltzmann
(approximation de Rayleigh-Jeans). Le facteur de Boltzmann 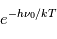 est donc proche de 1 et le rapport entre les populations des 2 sous-niveaux hyperfins à l'ETL vaut
est donc proche de 1 et le rapport entre les populations des 2 sous-niveaux hyperfins à l'ETL vaut 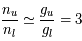 . Le gaz étant beaucoup trop froid pour peupler le premier niveau électronique excité
. Le gaz étant beaucoup trop froid pour peupler le premier niveau électronique excité 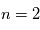 de l'hydrogène, l'essentiel des atomes se trouvent dans l'un de ces deux sous-niveaux hyperfins du niveau fondamental. La densité totale de HI est donc reliée à
de l'hydrogène, l'essentiel des atomes se trouvent dans l'un de ces deux sous-niveaux hyperfins du niveau fondamental. La densité totale de HI est donc reliée à 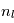 par :
par :
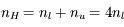 .
.
![[1- e^{-h\nu_0/kT_s}] \simeq h\nu_0 / kT_s](../pages_transfert-rayon/equations_transfert-rayon/equation210.png) au premier ordre. En insérant ces expressions dans l'équation de
au premier ordre. En insérant ces expressions dans l'équation de 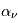 on en déduit :
on en déduit :
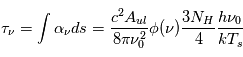 ,
,
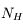 est la densité de colonne de l'hydrogène atomique neutre. On a fait ici l'hypothèse d'un milieu homogène, de sorte que
est la densité de colonne de l'hydrogène atomique neutre. On a fait ici l'hypothèse d'un milieu homogène, de sorte que 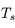 et
et 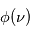 ne dépendent pas de la position
ne dépendent pas de la position 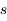 le long de la ligne de visée. On note ainsi que la profondeur optique de la raie à 21 cm est inversement proportionnelle à la température de spin,
le long de la ligne de visée. On note ainsi que la profondeur optique de la raie à 21 cm est inversement proportionnelle à la température de spin,
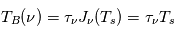 (approximation de Rayleigh-Jeans). Puisque
(approximation de Rayleigh-Jeans). Puisque 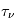 est inversement proportionnel à la température de spin, on voit que
est inversement proportionnel à la température de spin, on voit que 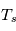 se simplifie dans cette expression et que l'intensité de la raie ne dépend plus de la température mais uniquement de la densité de colonne totale d'hydrogène,
se simplifie dans cette expression et que l'intensité de la raie ne dépend plus de la température mais uniquement de la densité de colonne totale d'hydrogène, 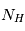 , dont on obtient ainsi une détermination directe. Cette approche est souvent appliquée même dans des cas où l'approximation de raie optiquement mince ne peut pas être vérifiée, et il faut garder à l'esprit que les estimations de la densité de colonne ainsi obtenues sont alors des limites inférieures.
, dont on obtient ainsi une détermination directe. Cette approche est souvent appliquée même dans des cas où l'approximation de raie optiquement mince ne peut pas être vérifiée, et il faut garder à l'esprit que les estimations de la densité de colonne ainsi obtenues sont alors des limites inférieures.
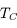 et de la température cinétique du nuage de HI interposé
et de la température cinétique du nuage de HI interposé 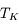 , telle que :
, telle que : 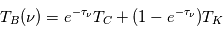 .
.
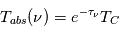 . Le rapport entre la température de brillance dans la raie d'absorption et la température de brillance dans le continu hors de la raie (où
. Le rapport entre la température de brillance dans la raie d'absorption et la température de brillance dans le continu hors de la raie (où 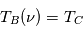 ) permet d'obtenir la valeur de
) permet d'obtenir la valeur de 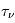 . Mais comme la profondeur optique est proportionnelle à
. Mais comme la profondeur optique est proportionnelle à 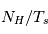 (voir section précédente), il n'est pas possible de dériver la densité de colonne
(voir section précédente), il n'est pas possible de dériver la densité de colonne 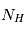 à partir de ces mesures en absorption seules. Il faut une information supplémentaire sur la température du gaz.
à partir de ces mesures en absorption seules. Il faut une information supplémentaire sur la température du gaz.
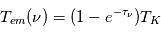 .
.
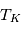 et la profondeur optique
et la profondeur optique 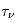 (qu'on suppose identiques entre les 2 régions observées), et d'en déduire ainsi la densité de colonne
(qu'on suppose identiques entre les 2 régions observées), et d'en déduire ainsi la densité de colonne 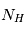 du nuage. Cette méthode est pratiquement la seule qui permet d'obtenir directement la température des nuages interstellaires atomiques.
du nuage. Cette méthode est pratiquement la seule qui permet d'obtenir directement la température des nuages interstellaires atomiques.
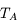 , généralement utilisée par les radioastronomes comme mesure de l'énergie reçue par une antenne radio. Il s'agit de la température du corps noir qui entourerait totalement l'antenne pour donner le signal observé. La puissance captée par l'antenne est alors
, généralement utilisée par les radioastronomes comme mesure de l'énergie reçue par une antenne radio. Il s'agit de la température du corps noir qui entourerait totalement l'antenne pour donner le signal observé. La puissance captée par l'antenne est alors 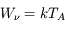 . Si l'antenne était parfaite, une région étendue de brillance uniforme
. Si l'antenne était parfaite, une région étendue de brillance uniforme 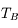 donnerait
donnerait 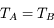 (en général il faut introduire un facteur de rendement). La quantité en abscisse de la figure est la vitesse radiale donnée par la formule de l'effet Doppler
(en général il faut introduire un facteur de rendement). La quantité en abscisse de la figure est la vitesse radiale donnée par la formule de l'effet Doppler 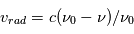 , utilisée d'habitude par les radioastronomes plutôt que la fréquence. La courbe en émission est associée au signal des régions immédiatement adjacentes. En soustrayant cette émission du signal obtenu avec l'antenne pointée sur le quasar on obtient la courbe en absorption. Enfin, la ligne en pointillé est due à une composante tiède pour laquelle l'absorption est plus faible.
, utilisée d'habitude par les radioastronomes plutôt que la fréquence. La courbe en émission est associée au signal des régions immédiatement adjacentes. En soustrayant cette émission du signal obtenu avec l'antenne pointée sur le quasar on obtient la courbe en absorption. Enfin, la ligne en pointillé est due à une composante tiède pour laquelle l'absorption est plus faible.

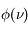 , normalisé et centré sur
, normalisé et centré sur 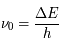 , avec
, avec 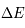 >0 l'écart en énergie entre les niveaux. Dans cette page nous présenterons les différents processus qui causent l'élargissement et analyserons les caractéristiques des profils de raie associés à chacun de ces processus. Nous ne considérons pas les effets associés à la présence de champs électromagnétiques externes (par exemple l'effet Zeeman).
>0 l'écart en énergie entre les niveaux. Dans cette page nous présenterons les différents processus qui causent l'élargissement et analyserons les caractéristiques des profils de raie associés à chacun de ces processus. Nous ne considérons pas les effets associés à la présence de champs électromagnétiques externes (par exemple l'effet Zeeman).
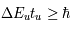 , où
, où 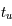 représente la durée de vie du niveau u, telle que
représente la durée de vie du niveau u, telle que 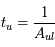 . La largeur de raie naturelle en énergie
. La largeur de raie naturelle en énergie 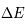 correspond au cas de l'égalité. Elle est proportionnelle au coefficient d'Einstein d'émission spontanée en absence de rayonnement (en présence de rayonnement il faudra considérer ainsi la désexcitation stimulée qui contribue à réduire la durée de vie du niveau u et donc à augmenter la largeur de raie). Du fait de l'élargissement des niveaux il faut prendre en compte toutes les transitions possibles avec une énergie
correspond au cas de l'égalité. Elle est proportionnelle au coefficient d'Einstein d'émission spontanée en absence de rayonnement (en présence de rayonnement il faudra considérer ainsi la désexcitation stimulée qui contribue à réduire la durée de vie du niveau u et donc à augmenter la largeur de raie). Du fait de l'élargissement des niveaux il faut prendre en compte toutes les transitions possibles avec une énergie 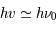 . On définit généralement une largeur naturelle de la raie en fréquence
. On définit généralement une largeur naturelle de la raie en fréquence 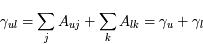 , où les indices
, où les indices 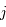 et
et 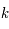 correspondent à des états d'énergie inférieure respectivement à l'énergie du niveau supérieur et à l'énergie du niveau inférieur et les deux sommes donnent la largeur du niveau supérieur et du niveau inférieur. Par exemple, on observera une raie faible mais large si le niveau inférieur est fortement élargi.
correspondent à des états d'énergie inférieure respectivement à l'énergie du niveau supérieur et à l'énergie du niveau inférieur et les deux sommes donnent la largeur du niveau supérieur et du niveau inférieur. Par exemple, on observera une raie faible mais large si le niveau inférieur est fortement élargi.
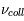 (chaque atome subit en moyenne
(chaque atome subit en moyenne 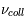 collisions par unité de temps) et contribuent à l'élargissement de la raie en fréquence qu'on écrit :
collisions par unité de temps) et contribuent à l'élargissement de la raie en fréquence qu'on écrit : 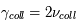 . Il faut remarquer que la fréquence des collisions augmente avec la densité du milieu. On s'attend donc à observer des élargissements collisionnels plus importants dans des environnement denses, comme les atmosphères planétaires et stellaires. Dans les nuages d'hydrogène atomique et les nuages moléculaires les effets collisionnels sont dominés par d'autres sources d'élargissement que nous allons voir dans la suite du cours (effet Doppler, turbulence). Puisque à la fois l'élargissement naturel et l'élargissement associé aux collisions sont caractérisés par des profils de la même forme, on peut définir une constante
. Il faut remarquer que la fréquence des collisions augmente avec la densité du milieu. On s'attend donc à observer des élargissements collisionnels plus importants dans des environnement denses, comme les atmosphères planétaires et stellaires. Dans les nuages d'hydrogène atomique et les nuages moléculaires les effets collisionnels sont dominés par d'autres sources d'élargissement que nous allons voir dans la suite du cours (effet Doppler, turbulence). Puisque à la fois l'élargissement naturel et l'élargissement associé aux collisions sont caractérisés par des profils de la même forme, on peut définir une constante 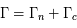 qui contient une contribution naturelle
qui contient une contribution naturelle 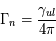 et une contribution collisionnelle
et une contribution collisionnelle 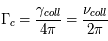 et décrire le profil de la raie tel que :
et décrire le profil de la raie tel que :
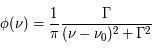 .
.
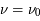 , qui vaut
, qui vaut 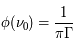 et sa largeur totale à mi-hauteur en unité de fréquence
et sa largeur totale à mi-hauteur en unité de fréquence 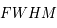 (de l'anglais Full Width at Half Maximum). Cette largeur est déterminée en remplaçant la valeur de la fonction à mi-hauteur (
(de l'anglais Full Width at Half Maximum). Cette largeur est déterminée en remplaçant la valeur de la fonction à mi-hauteur (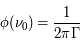 ) dans l'équation qui décrit
) dans l'équation qui décrit 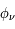 , dont on obtient
, dont on obtient 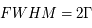 . Un profil Lorentzien centré (
. Un profil Lorentzien centré (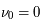 ) est montré sur la figure pour différentes valeurs de la constante
) est montré sur la figure pour différentes valeurs de la constante 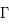 .
.

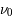 dans le référentiel d'un atome en mouvement seront détectés à une fréquence
dans le référentiel d'un atome en mouvement seront détectés à une fréquence 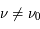 par l'observateur. Le décalage en fréquence d'un atome qui possède une vitesse relative le long de la ligne de visée
par l'observateur. Le décalage en fréquence d'un atome qui possède une vitesse relative le long de la ligne de visée 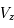 , pour des vitesses non relativistes, vaut :
, pour des vitesses non relativistes, vaut : 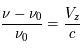 .
.
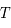 dont la projection de la vitesse sur l'axe de visée
dont la projection de la vitesse sur l'axe de visée 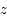 est comprise entre
est comprise entre 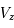 et
et 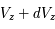 est donc proportionnel à la fonction
est donc proportionnel à la fonction 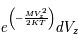 , où M est la masse d'un atome. En utilisant la formule pour le décalage Doppler on déduit
, où M est la masse d'un atome. En utilisant la formule pour le décalage Doppler on déduit 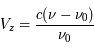 ,
, 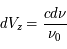 et on peut exprimer la distribution des atomes en fonction de la fréquence. Par conséquent, l'intensité de l'émission dans l'intervalle de fréquence de
et on peut exprimer la distribution des atomes en fonction de la fréquence. Par conséquent, l'intensité de l'émission dans l'intervalle de fréquence de 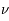 à
à 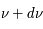 est proportionnelle à
est proportionnelle à 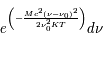 . Si l'effet Doppler est la source dominant d'élargissement de la raie, son profil est la somme des contributions de chaque atome, ce qui donne un profil de forme gaussienne :
. Si l'effet Doppler est la source dominant d'élargissement de la raie, son profil est la somme des contributions de chaque atome, ce qui donne un profil de forme gaussienne :
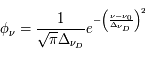 .
.
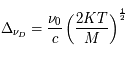 , appelée largeur Doppler de la raie, est reliée à la largeur à mi-hauteur de la gaussienne par
, appelée largeur Doppler de la raie, est reliée à la largeur à mi-hauteur de la gaussienne par 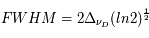 . L'aire du profil, obtenue intégrant sur la fréquence, vaut 1 et sa valeur maximale, atteinte à
. L'aire du profil, obtenue intégrant sur la fréquence, vaut 1 et sa valeur maximale, atteinte à 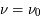 , est
, est 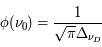 . Dans le milieu interstellaire, l'élargissement associé à l'effet Doppler est généralement plus important que la largeur naturelle et l'élargissement dû aux collisions. Un exemple est représenté par la raie à 21 cm de l'hydrogène atomique, l'élargissement lorentzien étant extrêmement faible puisque la durée de vie du niveau supérieur n'est limitée que par les collisions, rares dans le milieu interstellaire diffus.
. Dans le milieu interstellaire, l'élargissement associé à l'effet Doppler est généralement plus important que la largeur naturelle et l'élargissement dû aux collisions. Un exemple est représenté par la raie à 21 cm de l'hydrogène atomique, l'élargissement lorentzien étant extrêmement faible puisque la durée de vie du niveau supérieur n'est limitée que par les collisions, rares dans le milieu interstellaire diffus.
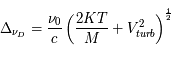 , où
, où 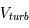 est la vitesse caractéristique de la turbulence. Dans les nuages interstellaires, la vitesse turbulente est de l'ordre de quelques kilomètres par seconde. Puisque la température des nuages n'est pas élevée, l'effet Doppler est dominé par la turbulence. Des mouvements turbulents plus importants ont été observés dans la nébuleuse d'Orion (voir le TP
est la vitesse caractéristique de la turbulence. Dans les nuages interstellaires, la vitesse turbulente est de l'ordre de quelques kilomètres par seconde. Puisque la température des nuages n'est pas élevée, l'effet Doppler est dominé par la turbulence. Des mouvements turbulents plus importants ont été observés dans la nébuleuse d'Orion (voir le TP 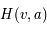 , dont les valeurs sont données dans la littérature :
, dont les valeurs sont données dans la littérature : 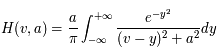 . Cette forme est obtenue par un changement de variable dans les fonctions lorentzienne et gaussienne tel que :
. Cette forme est obtenue par un changement de variable dans les fonctions lorentzienne et gaussienne tel que : 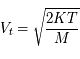 ,
, 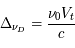 ,
, 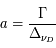 ,
, 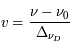 et donne le profil de raie normalisé :
et donne le profil de raie normalisé :
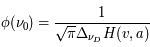 .
.
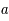 qui quantifie l'importance relative des différents processus qui contribuent à l'élargissement de raie. On remarque que dans le cas limite d'élargissement naturel et collisionnel négligeable (a=0) la fonction a une forme gaussienne, tandis que c'est une lorentzienne pour un élargissement Doppler négligeable (voir par exemple la courbe a=20). En général la fonction présente une allure gaussienne au coeur (
qui quantifie l'importance relative des différents processus qui contribuent à l'élargissement de raie. On remarque que dans le cas limite d'élargissement naturel et collisionnel négligeable (a=0) la fonction a une forme gaussienne, tandis que c'est une lorentzienne pour un élargissement Doppler négligeable (voir par exemple la courbe a=20). En général la fonction présente une allure gaussienne au coeur (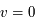 ) et lorentzienne dans les ailes.
) et lorentzienne dans les ailes.

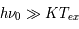 . Le niveau supérieur de la transition a une énergie très élevée et il est donc très peu peuplé, ce qui nous autorise à négliger l'émission spontanée et induite à partir du niveau supérieur. Sous ces hypothèses, la solution de l'équation de transfert et la profondeur optique se réduisent à
. Le niveau supérieur de la transition a une énergie très élevée et il est donc très peu peuplé, ce qui nous autorise à négliger l'émission spontanée et induite à partir du niveau supérieur. Sous ces hypothèses, la solution de l'équation de transfert et la profondeur optique se réduisent à 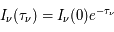 et
et 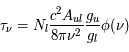 (voir les pages
(voir les pages 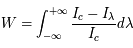 , où
, où 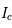 est l'intensité du continuum stellaire du spectre considéré et
est l'intensité du continuum stellaire du spectre considéré et 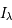 l'intensité de la raie à la longueur d'onde
l'intensité de la raie à la longueur d'onde 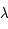 . On l'appelle largeur équivalente car cette quantité est équivalente à la largeur d'une raie absorbante rectangulaire allant du continu jusqu'à 0 et ayant la même aire que la raie observée. En remplaçant l'expression pour l'intensité de raie dans le cas de pure absorption et en posant
. On l'appelle largeur équivalente car cette quantité est équivalente à la largeur d'une raie absorbante rectangulaire allant du continu jusqu'à 0 et ayant la même aire que la raie observée. En remplaçant l'expression pour l'intensité de raie dans le cas de pure absorption et en posant 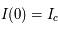 on obtient que
on obtient que 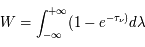 .
.
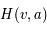 , qui contient l'information sur le profil de la raie dans le cas général où la largeur naturelle, les effets collisionnels et l'effet Doppler sont pris en compte, et un paramètre
, qui contient l'information sur le profil de la raie dans le cas général où la largeur naturelle, les effets collisionnels et l'effet Doppler sont pris en compte, et un paramètre 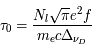 qui représente la profondeur optique au centre de la raie et dépend de la densité de colonne, de la largeur Doppler de la raie et des caractéristiques de la transition atomique par la quantité
qui représente la profondeur optique au centre de la raie et dépend de la densité de colonne, de la largeur Doppler de la raie et des caractéristiques de la transition atomique par la quantité 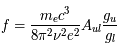 . Il s'agit d'un coefficient sans dimension souvent utilisé pour exprimer la probabilité d'émission spontanée qu'on appelle force de l'oscillateur. Il est possible de trouver dans la littérature des tables de
. Il s'agit d'un coefficient sans dimension souvent utilisé pour exprimer la probabilité d'émission spontanée qu'on appelle force de l'oscillateur. Il est possible de trouver dans la littérature des tables de 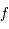 pour chaque raie. Nous pouvons donc écrire
pour chaque raie. Nous pouvons donc écrire 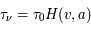 .
.
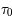 et donc du nombre d'atomes absorbants le long de la ligne de visée.
et donc du nombre d'atomes absorbants le long de la ligne de visée.
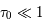 : la raie est optiquement mince. On en déduit que
: la raie est optiquement mince. On en déduit que 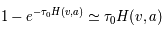 et le calcul de la largeur équivalente se réduit à :
et le calcul de la largeur équivalente se réduit à : 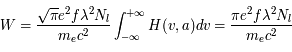 car l'intégrale de la fonction de Voigt vaut
car l'intégrale de la fonction de Voigt vaut 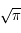 . Il s'agit en effet de raies faibles où la partie centrale domine le profil. On a vu que dans cette région la fonction de Voigt a une allure gaussienne. Le coeur dû à l'effet Doppler domine. Pour les raies optiquement minces la largeur équivalente est proportionnelle à la densité de colonne et on parle de régime linéaire. Dans ce régime les mesures de la largeur équivalente permettent une détermination précise de la densité de colonne, les paramètres atomiques étant connus.
. Il s'agit en effet de raies faibles où la partie centrale domine le profil. On a vu que dans cette région la fonction de Voigt a une allure gaussienne. Le coeur dû à l'effet Doppler domine. Pour les raies optiquement minces la largeur équivalente est proportionnelle à la densité de colonne et on parle de régime linéaire. Dans ce régime les mesures de la largeur équivalente permettent une détermination précise de la densité de colonne, les paramètres atomiques étant connus. 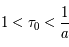 : lorsque le nombre d'atomes absorbants augmente, le centre de la raie devient de plus en plus optiquement épais. La contribution des ailes du profil reste toutefois négligeable. L'absorption principale est toujours due à l'effet Doppler, mais il y a une saturation de la raie qui prend une forme rectangulaire au centre. En s'éloignant du centre une absorption partielle persiste et la largeur équivalente croît lentement en fonction de la densité de colonne. On peut montrer que dans ce domaine
: lorsque le nombre d'atomes absorbants augmente, le centre de la raie devient de plus en plus optiquement épais. La contribution des ailes du profil reste toutefois négligeable. L'absorption principale est toujours due à l'effet Doppler, mais il y a une saturation de la raie qui prend une forme rectangulaire au centre. En s'éloignant du centre une absorption partielle persiste et la largeur équivalente croît lentement en fonction de la densité de colonne. On peut montrer que dans ce domaine 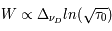 . Malheureusement des nombreuses raies d'absorption interstellaire se trouvent dans ce régime où la largeur équivalente est très peu sensible à la densité de colonne, ce qui en rend difficile l'estimation. De plus les mesures sont compliquées par la dépendance de la largeur Doppler.
. Malheureusement des nombreuses raies d'absorption interstellaire se trouvent dans ce régime où la largeur équivalente est très peu sensible à la densité de colonne, ce qui en rend difficile l'estimation. De plus les mesures sont compliquées par la dépendance de la largeur Doppler.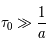 : la raie est saturée jusqu'aux ailes lorentziennes et la largeur équivalente varie proportionnellement à la racine de la densité de colonne et de la largeur naturelle (
: la raie est saturée jusqu'aux ailes lorentziennes et la largeur équivalente varie proportionnellement à la racine de la densité de colonne et de la largeur naturelle (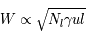 ).
).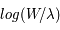 en fonction de
en fonction de 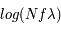 . Elle est composée d'une partie linéaire, d'une portion plate dont la position sur l'axe vertical dépend de la valeur de la largeur Doppler et d'une région dont la pente est fonction de la largeur naturelle (et éventuellement de la densité du gaz s'il existe une contribution des collisions à l'élargissement). Pour construire cette courbe il faut donc connaître
. Elle est composée d'une partie linéaire, d'une portion plate dont la position sur l'axe vertical dépend de la valeur de la largeur Doppler et d'une région dont la pente est fonction de la largeur naturelle (et éventuellement de la densité du gaz s'il existe une contribution des collisions à l'élargissement). Pour construire cette courbe il faut donc connaître 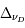 et
et 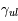 . Dans ce cas, on peut placer la raie sur la courbe, en déterminant la largeur équivalente et en déduire la densité de colonne. Dans la figure on montre les courbes de croissance obtenues d'observations de l'étoile
. Dans ce cas, on peut placer la raie sur la courbe, en déterminant la largeur équivalente et en déduire la densité de colonne. Dans la figure on montre les courbes de croissance obtenues d'observations de l'étoile 
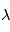 est décrite par la quantité
est décrite par la quantité 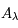 (mesurée en magnitude), définie comme la différence entre la magnitude observée
(mesurée en magnitude), définie comme la différence entre la magnitude observée 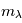 d'une étoile dont la lumière a traversé le nuage de poussières (de profondeur optique
d'une étoile dont la lumière a traversé le nuage de poussières (de profondeur optique 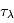 ) et celle qu'on observerait en l'absence d'extinction,
) et celle qu'on observerait en l'absence d'extinction, 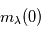 . Comme l'émission des poussières est en général négligeable à la longueur d'onde considérée, le flux spécifique
. Comme l'émission des poussières est en général négligeable à la longueur d'onde considérée, le flux spécifique 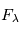 est atténué par un facteur
est atténué par un facteur 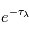 . Avec la relation entre magnitude et flux, on obtient :
. Avec la relation entre magnitude et flux, on obtient : ![A_\lambda(mag)=m_\lambda - m_\lambda(0) = -2.5log_{10}\left[\frac{F_\lambda(\tau_\lambda)}{F_\lambda(0)}\right]=-2.5log_{10}[e^{-\tau_\lambda}]=1.086\tau_\lambda](../pages_transfert-rayon/equations_transfert-rayon/equation328.png) . On voit que la valeur de
. On voit que la valeur de 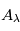 en magnitude est essentiellement égale à l'opacité des poussières à cette longueur d'onde ; elle est donc proportionnelle à la densité colonne de poussières sur la ligne de visée.
en magnitude est essentiellement égale à l'opacité des poussières à cette longueur d'onde ; elle est donc proportionnelle à la densité colonne de poussières sur la ligne de visée.
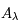 est portée en fonction de l'inverse de la longueur d'onde. Elle est obtenue en comparant à différentes longueurs d'onde la distribution spectrale d'énergie de deux étoiles supposées identiques, puisque de même type spectral et classe de luminosité, l'une de deux étoiles est fortement affectée par l'extinction et donc par la présence d'une grande quantité de poussières le long de la ligne de visée, l'autre se trouve en l'absence d'extinction. Afin d'obtenir un résultat indépendant de la quantité totale de poussières sur la ligne de visée, il est d'usage de normaliser la courbe ainsi obtenue à la différence d'extinction dans les bandes spectrales B (bleue, centrée à 4400
est portée en fonction de l'inverse de la longueur d'onde. Elle est obtenue en comparant à différentes longueurs d'onde la distribution spectrale d'énergie de deux étoiles supposées identiques, puisque de même type spectral et classe de luminosité, l'une de deux étoiles est fortement affectée par l'extinction et donc par la présence d'une grande quantité de poussières le long de la ligne de visée, l'autre se trouve en l'absence d'extinction. Afin d'obtenir un résultat indépendant de la quantité totale de poussières sur la ligne de visée, il est d'usage de normaliser la courbe ainsi obtenue à la différence d'extinction dans les bandes spectrales B (bleue, centrée à 4400 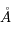 ) et V (visible, centrée à 5500
) et V (visible, centrée à 5500 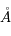 ) dite excès de couleur,
) dite excès de couleur, 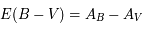 . La courbe d'extinction totaleest alors donnée par
. La courbe d'extinction totaleest alors donnée par 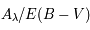 en fonction de
en fonction de 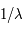 en
en 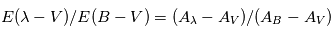 . Un exemple de courbe interstellaire moyenne de l'infrarouge proche à l'ultraviolet est montrée sur la figure ci-dessous. Dans cette courbe on peut distinguer trois régimes selon le domaine de longueur d'onde considéré : une croissance de l'extinction approximativement linéaire en
. Un exemple de courbe interstellaire moyenne de l'infrarouge proche à l'ultraviolet est montrée sur la figure ci-dessous. Dans cette courbe on peut distinguer trois régimes selon le domaine de longueur d'onde considéré : une croissance de l'extinction approximativement linéaire en 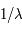 dans la partie proche infrarouge et visible, un pic ultraviolet centré à 2175
dans la partie proche infrarouge et visible, un pic ultraviolet centré à 2175 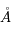 associé à des particules carbonées, une forte augmentation dans l'ultraviolet lointain. La lumière reçue sera donc soumise à un rougissement à cause de la présence d'une extinction plus forte de la lumière bleue que de la lumière rouge.
associé à des particules carbonées, une forte augmentation dans l'ultraviolet lointain. La lumière reçue sera donc soumise à un rougissement à cause de la présence d'une extinction plus forte de la lumière bleue que de la lumière rouge.
