Coefficients d'Einstein |
L'équation de transfert décrit la variation macroscopique de l'intensité spécifique du rayonnement lorsqu'il traverse de la matière. De leur coté, les coefficients d'absorption et d'émission qui apparaissent dans cette équation contiennent l'information concernant les processus microscopiques qui interviennent. En étudiant l'interaction entre le rayonnement et un système (atome ou molécule) avec des niveaux d'énergie quantifiés, Einstein a identifié 3 processus d'émission et d'absorption de photons, caractérisés chacun par un coefficient. Il est donc possible d'exprimer l'équation de transfert en fonction de ces coefficients et d'en dériver des solutions en fonction des propriétés microscopiques locales de l'atome considéré.
Considérons pour simplifier un milieu formé d'atomes (ou de molécules) identiques avec seulement deux niveaux d'énergie : le niveau fondamental l et le niveau excité u, séparés par une énergie 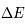 . Nous nous intéressons aux transitions radiatives entres ces deux états. Comme nous verrons en détail dans la suite du cours ces transitions ne se produisent pas uniquement à la fréquence
. Nous nous intéressons aux transitions radiatives entres ces deux états. Comme nous verrons en détail dans la suite du cours ces transitions ne se produisent pas uniquement à la fréquence 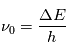 mais également aux fréquences voisines de
mais également aux fréquences voisines de 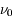 . Par conséquent les raies spectrales associées à ces transitions sont caractérisées par un profil de raie
. Par conséquent les raies spectrales associées à ces transitions sont caractérisées par un profil de raie 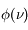 , piqué à la fréquence
, piqué à la fréquence 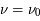 , qui décrit l'efficacité des fréquences voisines de
, qui décrit l'efficacité des fréquences voisines de 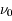 à induire ces transitions. L'agitation thermique du gaz (mouvement brownien) produit par exemple un élargissement du profil par effet Doppler, car un atome en mouvement peut absorber un photon de fréquence légèrement différente de
à induire ces transitions. L'agitation thermique du gaz (mouvement brownien) produit par exemple un élargissement du profil par effet Doppler, car un atome en mouvement peut absorber un photon de fréquence légèrement différente de 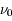 . La largeur du profil est alors de l'ordre de
. La largeur du profil est alors de l'ordre de 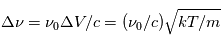 . Dans la suite on fera l'hypothèse que la forme de la raie est la même en absorption et en émission. Les 3 processus de transitions radiatives quantifiés par Einstein sont les suivants :
. Dans la suite on fera l'hypothèse que la forme de la raie est la même en absorption et en émission. Les 3 processus de transitions radiatives quantifiés par Einstein sont les suivants :
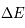 . Cette transition se produit même en l'absence d'un champ de rayonnement. Elle est caractérisée par le coefficient d'Einstein
. Cette transition se produit même en l'absence d'un champ de rayonnement. Elle est caractérisée par le coefficient d'Einstein 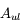 , qui représente une probabilité de transition par unité de temps et est exprimé en s-1. Ce coefficient ne dépend que des termes de couplages électro-magnétique entre les 2 niveaux quantiques u et l.
, qui représente une probabilité de transition par unité de temps et est exprimé en s-1. Ce coefficient ne dépend que des termes de couplages électro-magnétique entre les 2 niveaux quantiques u et l. 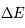 , faisant passer les atomes du niveaux l au niveau u. Elle est caractérisée par une probabilité de transition par unité de temps
, faisant passer les atomes du niveaux l au niveau u. Elle est caractérisée par une probabilité de transition par unité de temps 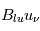 , où
, où 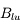 est le coefficient d'absorption d'Einstein et
est le coefficient d'absorption d'Einstein et 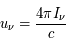 est la densité d'énergie monochromatique à la fréquence
est la densité d'énergie monochromatique à la fréquence 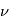 pour un champ de rayonnement isotrope.
pour un champ de rayonnement isotrope. 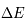 et passe de l'état u à l'état l en emettant un deuxième photon identique à celui qu'il a absorbé. Ce processus est caractérisé par une probabilité par unité de temps
et passe de l'état u à l'état l en emettant un deuxième photon identique à celui qu'il a absorbé. Ce processus est caractérisé par une probabilité par unité de temps 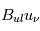 .
. Les 3 coefficients d'Einstein décrivant les probabilités de ces 3 processus sont reliés par les relations d'Einstein :
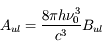 et
et
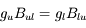 .
.
Il est important de noter que ces relations ne dépendent ni de la température du gaz, ni du profil de la raie. Elles représentent des relations de bilan détaillé, c'est-à-dire des relations entre un processus microscopique quantique et son processus inverse, dans ce cas l'absorption et l'émission de rayonnement. La connaissance d'un seul des coefficients d'Einstein (à partir de calculs quantiques) permet ainsi de déterminer les 2 autres. Notons aussi que ces coefficients donnent la probabilité de transition par atome dans le niveau de départ (u ou l) considéré. Le bilan net de ces 3 types de transitions va donc dépendre des densités de populations moyennes respectives dans les niveaux u et l.
Considérons un rayonnement à la fréquence 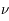 (contenue dans le profil de la raie) qui arrive sur une tranche du milieu avec une intensité spécifique
(contenue dans le profil de la raie) qui arrive sur une tranche du milieu avec une intensité spécifique 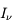 par unité de surface, de fréquence, et d'angle solide. Le long de la distance
par unité de surface, de fréquence, et d'angle solide. Le long de la distance 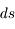 dans sa direction de propagation, l'intensité sera augmentée à la fois par l'émission spontanée et par l'émission stimulée des atomes dans l'état u ; simultanément elle sera diminuée par l'absorption de photons par les atomes dans l'état l. Considérons d'abord le cas de l'émission spontanée : le nombre total d'atomes dans l'état u rencontré par unité de surface est
dans sa direction de propagation, l'intensité sera augmentée à la fois par l'émission spontanée et par l'émission stimulée des atomes dans l'état u ; simultanément elle sera diminuée par l'absorption de photons par les atomes dans l'état l. Considérons d'abord le cas de l'émission spontanée : le nombre total d'atomes dans l'état u rencontré par unité de surface est 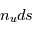 . L'augmentation d'intensité à la fréquence
. L'augmentation d'intensité à la fréquence 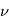 causée par ce processus est obtenue en multipliant
causée par ce processus est obtenue en multipliant 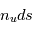 par le coefficient d'Einstein correspondant
par le coefficient d'Einstein correspondant 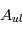 divisé par
divisé par 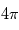 (car chaque photon est supposé émis ou absorbé de façon isotrope et nous regardons la variation par unité d'angle solide), par le profil de la raie
(car chaque photon est supposé émis ou absorbé de façon isotrope et nous regardons la variation par unité d'angle solide), par le profil de la raie 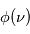 , et enfin par l'énergie de chaque photon (
, et enfin par l'énergie de chaque photon (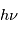 ) ; en appliquant le même raisonnement à l'émission et absorption stimulées, le bilan de ces transition radiatives donne l'équation de transfert :
) ; en appliquant le même raisonnement à l'émission et absorption stimulées, le bilan de ces transition radiatives donne l'équation de transfert :
![\frac{dI_\nu}{ds} = \frac{h\nu }{4\pi} \phi(\nu) [n_u A_{ul} +(n_u B_{ul} - n_l B_{lu})\frac{4\pi I_\nu}{c}]](../pages_transfert-rayon/equations_transfert-rayon/equation110.png) .
.
En comparant avec l'expression générale de l'équation de transfert 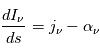 , présentée dans la section précédente on obtient en fonction des coefficients d'Einstein :
, présentée dans la section précédente on obtient en fonction des coefficients d'Einstein :
le coefficient d'émissivité 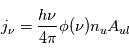
le coefficient d'absorption 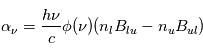
et la fonction source, 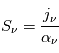
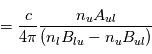 .
.
On remarque que la fonction source 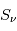 ne dépend pas de
ne dépend pas de 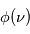 , mais uniquement des coefficients d'Einstein et des populations des niveaux impliqués. Plus précisément elle ne dépend que du rapport entre ces populations . En effet, en utilisant les relations entre coefficients d'Einstein données ci-dessus, on obtient :
, mais uniquement des coefficients d'Einstein et des populations des niveaux impliqués. Plus précisément elle ne dépend que du rapport entre ces populations . En effet, en utilisant les relations entre coefficients d'Einstein données ci-dessus, on obtient :
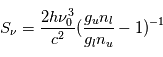 , où
, où 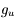 et
et 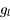 sont les poids statistiques (dégénérescences) de chaque niveau.
sont les poids statistiques (dégénérescences) de chaque niveau.
En utilisant les relations d'Einstein on voit aussi que le coefficient d'absorption peut se réécrire sous la forme :
![\alpha_\nu=\frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-\frac{n_ug_l}{n_lg_u}]](../pages_transfert-rayon/equations_transfert-rayon/equation121.png) .
.
Si l'on dénote par 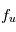 et
et 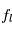 les fractions
les fractions 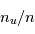 et
et 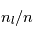 d'atomes qui sont dans les niveaux u et l, on remarque qu'
d'atomes qui sont dans les niveaux u et l, on remarque qu'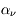 est proportionnel à la densité volumique totale des atomes,
est proportionnel à la densité volumique totale des atomes, 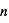 , et à une fonction qui ne dépend que de
, et à une fonction qui ne dépend que de 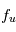 et
et 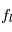 , c'est-à-dire à la répartition statistique des atomes entre leurs différents niveaux d'énergie. Il en découle que la profondeur optique, obtenue en intégrant cette quantité le long de la ligne de visée, sera proportionnelle à
, c'est-à-dire à la répartition statistique des atomes entre leurs différents niveaux d'énergie. Il en découle que la profondeur optique, obtenue en intégrant cette quantité le long de la ligne de visée, sera proportionnelle à 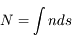 que l'on appelle la densité de colonne des atomes (en unité d'atomes par cm-2), c'est-à-dire le nombre d'atomes dans un cylindre de section unité le long de la ligne de visée. C'est par ce biais que l'observation des raies spectrales pourra nous donner accès à la masse de gaz émetteur --- à condition que l'on puisse connaître (ou estimer) les fractions
que l'on appelle la densité de colonne des atomes (en unité d'atomes par cm-2), c'est-à-dire le nombre d'atomes dans un cylindre de section unité le long de la ligne de visée. C'est par ce biais que l'observation des raies spectrales pourra nous donner accès à la masse de gaz émetteur --- à condition que l'on puisse connaître (ou estimer) les fractions 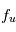 et
et 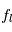 d'atomes peuplant les niveaux u et l, ou en d'autres termes les "conditions d'excitation" de la transition.
d'atomes peuplant les niveaux u et l, ou en d'autres termes les "conditions d'excitation" de la transition.