Raies en absorption

Auteur: Cecilia Pinto & Sylvie Cabrit

Dans le premier chapitre du cours (Détection du gaz neutre atomique : raies spectrales) nous avons mentionné que les raies d'absorption interstellaires observées dans le visible et l'ultraviolet fournissent des informations précieuses sur les conditions physiques au sein du milieu interstellaire. Nous allons analyser en détail ce sujet en montrant comment on peut en déduire la densité de colonne des éléments observés.

Largeur équivalente

Considérons un milieu purement absorbant situé devant une source de rayonnement continu. Cette hypothèse est raisonnable pour les raies d'absorption dans le visible et l'ultraviolet pour lesquelles 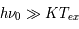$h\nu_0\gg KT_{ex}$ . Le niveau supérieur de la transition a une énergie très élevée et il est donc très peu peuplé, ce qui nous autorise à négliger l'émission spontanée et induite à partir du niveau supérieur. 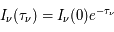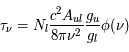Sous ces hypothèses, la solution de l'équation de transfert et la profondeur optique se réduisent à $I_\nu(\tau_\nu) = I_\nu(0)e^{-\tau_\nu}$ et $\tau_\nu=N_l\frac {c^2 A_{ul}} {8\pi \nu^2 }\frac{g_u}{g_l}\phi(\nu)$ (voir les pages L'équation de transfert de rayonnement, Coefficients d'Einstein et L'état thermodynamique du gaz). Idéalement, la mesure du profil de la raie dépendant de la fréquence permet de déterminer la profondeur optique. Concrètement, la résolution spectrale limitée et le rapport entre le signal désiré de l'objet et le bruit de fond (rapport signal sur bruit) rendent plus pratique l'utilisation d'une quantité observable intégrée qu'on appelle largeur équivalente. 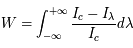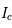Elle est, par définition : $W=\int_{-\infty}^{+\infty}\frac{I_c-I_\lambda}{I_c}d\lambda$ , où I_c est l'intensité du continuum stellaire du spectre considéré et 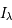$I_\lambda$ l'intensité de la raie à la longueur d'onde 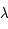$\lambda$ . On l'appelle largeur équivalente car cette quantité est équivalente à la largeur d'une raie absorbante rectangulaire allant du continu jusqu'à 0 et ayant la même aire que la raie observée. 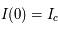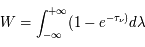En remplaçant l'expression pour l'intensité de raie dans le cas de pure absorption et en posant I(0)=I_c on obtient que $W=\int_{-\infty}^{+\infty}(1-e^{-\tau_\nu)}d\lambda$ .

Courbe de croissance

On peut exprimer la profondeur optique de la raie en terme de la fonction de Voigt 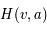H(v,a) , qui contient l'information sur le profil de la raie dans le cas général où la largeur naturelle, les effets collisionnels et l'effet Doppler sont pris en compte, et un paramètre 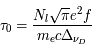$\tau_0=\frac{N_l\sqrt{\pi}e^2f}{m_ec\Delta_{\nu_D}}$ qui représente la profondeur optique au centre de la raie et dépend de la densité de colonne, de la largeur Doppler de la raie et des caractéristiques de la transition atomique par la quantité 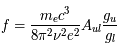$f=\frac{m_ec^3}{8\pi^2 \nu^2e^2}A_{ul}\frac{g_u}{g_l}$ . Il s'agit d'un coefficient sans dimension souvent utilisé pour exprimer la probabilité d'émission spontanée qu'on appelle force de l'oscillateur. Il est possible de trouver dans la littérature des tables de 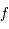pour chaque raie. 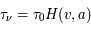Nous pouvons donc écrire $\tau_\nu=\tau_{0}H(v,a)$ .

On identifie trois régimes concernant le profil de raie dépendant de la valeur du paramètre 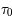$\tau_{0}$ et donc du nombre d'atomes absorbants le long de la ligne de visée.

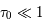$\tau_{0}\ll 1$ : la raie est optiquement mince. On en déduit que 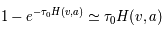$1-e^{-\tau_0H(v,a)}\simeq\tau_0H(v,a)$ et le calcul de la largeur équivalente se réduit à : 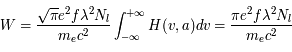$W=\frac{\sqrt{\pi}e^2f\lambda^2N_l}{m_ec^2}\int_{-\infty}^{+\infty}H(v,a)dv=\frac{\pi e^2f\lambda^2N_l}{m_ec^2}$ car l'intégrale de la fonction de Voigt vaut 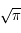$\sqrt{\pi}$ . Il s'agit en effet de raies faibles où la partie centrale domine le profil. On a vu que dans cette région la fonction de Voigt a une allure gaussienne. Le coeur dû à l'effet Doppler domine. Pour les raies optiquement minces la largeur équivalente est proportionnelle à la densité de colonne et on parle de régime linéaire. Dans ce régime les mesures de la largeur équivalente permettent une détermination précise de la densité de colonne, les paramètres atomiques étant connus.
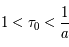$1<\tau_{0}<\frac{1}{a}$ : lorsque le nombre d'atomes absorbants augmente, le centre de la raie devient de plus en plus optiquement épais. La contribution des ailes du profil reste toutefois négligeable. L'absorption principale est toujours due à l'effet Doppler, mais il y a une saturation de la raie qui prend une forme rectangulaire au centre. En s'éloignant du centre une absorption partielle persiste et la largeur équivalente croît lentement en fonction de la densité de colonne. On peut montrer que dans ce domaine 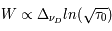$W\propto\Delta_{\nu_D}ln({\sqrt{\tau_0}})$ . Malheureusement des nombreuses raies d'absorption interstellaire se trouvent dans ce régime où la largeur équivalente est très peu sensible à la densité de colonne, ce qui en rend difficile l'estimation. De plus les mesures sont compliquées par la dépendance de la largeur Doppler.
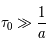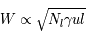$\tau_{0}\gg\frac{1}{a}$ : la raie est saturée jusqu'aux ailes lorentziennes et la largeur équivalente varie proportionnellement à la racine de la densité de colonne et de la largeur naturelle ( $W\propto{\sqrt{N_l\gamma{ul}}}$ ).

Pour chaque raie spectrale il est donc possible de construire une courbe de croissance théorique où l'on porte 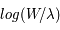$log(W/\lambda)$ en fonction de 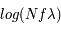$log(Nf\lambda)$ . Elle est composée d'une partie linéaire, d'une portion plate dont la position sur l'axe vertical dépend de la valeur de la largeur Doppler et d'une région dont la pente est fonction de la largeur naturelle (et éventuellement de la densité du gaz s'il existe une contribution des collisions à l'élargissement). 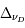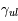Pour construire cette courbe il faut donc connaître $\Delta_{\nu_D}$ et $\gamma_{ul}$ . Dans ce cas, on peut placer la raie sur la courbe, en déterminant la largeur équivalente et en déduire la densité de colonne. Dans la figure on montre les courbes de croissance obtenues d'observations de l'étoile ζ Ophiuchi. Les valeurs mesurées, pour différents éléments à différentes longueurs d'onde provenant du même nuage, sont superposées à une courbe de croissance théorique obtenue avec une distribution fixée des vitesses, ce qui donne ainsi des renseignements sur la dispersion de vitesse ou les mouvement aléatoires d'ensemble au sein du nuage.

Courbe de croissance

Crédit : D. Morton, Apj, 197, 85, 1975