Notions de transfert de rayonnement

Auteur: Cecilia Pinto & Sylvie Cabrit

L'analyse des spectres interstellaires requiert l'introduction d'un certain nombre de notions théoriques de transfert de rayonnement. Cette théorie consiste en une description macroscopique de la propagation du rayonnement et de son interaction avec la matière qui compose le milieu traversé. Dans cette description le rayonnement est supposé se propager, dans le vide ou dans un milieu homogène, rectilignement (les lignes de propagation sont appelées rayons) si l'échelle du système considéré est très supérieure à la longueur d'onde du rayonnement.

Intensité spécifique

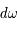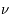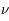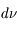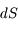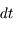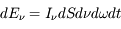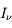On considère en un point de l'espace un faisceau de rayonnement contenu dans un angle solide $d\omega$ , dans un intervalle de fréquence de $\nu$ à $\nu$ + $d\nu$ et traversant une surface perpendiculaire à sa direction de propagation. L'énergie de ce rayonnement qui passe à travers la surface pendant le temps est : $dE_\nu=I_\nu dS d\nu d\omega dt$ . Le coefficient de proportionnalité $I_\nu$ dans cette expression est appelé intensité spécifique et représente donc l'énergie par unité de surface, par unité de fréquence, par unité d'angle solide et par unité de temps, qui traverse une surface perpendiculaire au faisceau de rayonnement. L'intensité spécifique s'exprime en erg cm^-2 Hz^-1 sr^-1 s^-1dans le système CGS. 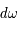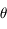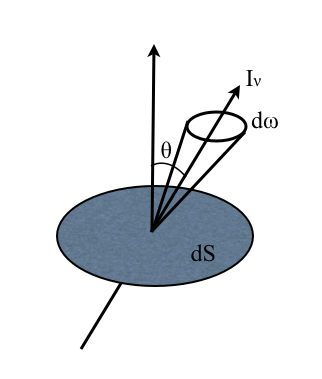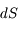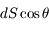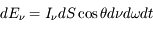Si la direction du rayonnement, centrée sur l'angle solide $d\omega$ , fait un angle $\theta$ avec la normale à (voir la figure), la surface efficace perpendiculaire au faisceau vaut $dS\cos\theta$ et l'énergie s'écrit alors : $dE_\nu=I_\nu dS\cos\theta d\nu d\omega dt$ .

Crédit : Cecilia Pinto

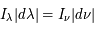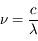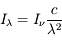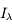L'intensité spécifique est fonction du point de l'espace considéré, de la direction du rayonnement, de la fréquence et du temps. Elle peut être exprimée en termes de longueur d'onde plutôt que de fréquence avec l'égalité : $I_\lambda |d\lambda| = I_\nu |d\nu|$ . Puisque $\nu = \frac{c}{\lambda}$ , on en déduit que $I_\lambda=I_\nu \frac{c}{\lambda^2}$ avec $I_\lambda$ en erg cm^-2 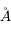$\AA$ ^-1 sr^-1 s^-1. 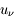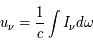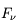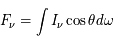L'intensité spécifique est une quantité fondamentale dont dérivent les autres grandeurs physiques qui caractérisent le rayonnement, comme la densité d'énergie monochromatique $u_\nu$ par unité de volume et par unité d'intervalle de fréquence, $u_\nu = \frac{1}{c}\int I_\nu d\omega$ , ou le flux net $F_\nu$ , c'est-à-dire le flux d'énergie par unité de surface, de fréquence et de temps, $F_\nu = \int I_\nu \cos \theta d\omega$ .