Profils de raie pour les atomes et les molécules en l'absence de mouvements d'ensemble

Auteur: Cecilia Pinto & Sylvie Cabrit

On observe des raies spectrales en émission ou en absorption lors des transitions entre deux niveaux discrets dans un atome ou une molécule. Ces niveaux ne sont pas infiniment fins, de sorte que la raie est élargie. Afin de prendre en compte cet élargissement, nous avons introduit (voir la page Coefficients d'Einstein) un profil de raie 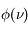$\phi(\nu)$ , normalisé et centré sur 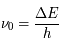$\nu_0=\frac{\Delta E}{h}$ , avec 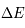$\Delta E$ >0 l'écart en énergie entre les niveaux. Dans cette page nous présenterons les différents processus qui causent l'élargissement et analyserons les caractéristiques des profils de raie associés à chacun de ces processus. Nous ne considérons pas les effets associés à la présence de champs électromagnétiques externes (par exemple l'effet Zeeman).

Largeur naturelle et collisionnelle : profil de raie Lorentzien

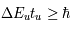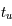La largeur naturelle d'une raie spectrale est la largeur minimale que la raie, en émission ou en absorption, puisse présenter. Elle est reliée à l'inégalité de Heisenberg. Soit une transition entre les niveaux u et l d'un atome. Les relations d'incertitude nous donnent : $\Delta E_u t_u\geq \hbar$ , où t_u représente la durée de vie du niveau u, telle que 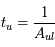$t_u=\frac{1}{A_{ul}}$ . La largeur de raie naturelle en énergie 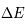$\Delta E$ correspond au cas de l'égalité. Elle est proportionnelle au coefficient d'Einstein d'émission spontanée en absence de rayonnement (en présence de rayonnement il faudra considérer ainsi la désexcitation stimulée qui contribue à réduire la durée de vie du niveau u et donc à augmenter la largeur de raie). Du fait de l'élargissement des niveaux il faut prendre en compte toutes les transitions possibles avec une énergie 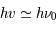$hv\simeq h\nu_0$ . On définit généralement une largeur naturelle de la raie en fréquence 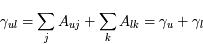$\gamma_{ul}=\sum_j A_{uj}+\sum_k A_{lk}=\gamma_u+\gamma_l$ , où les indices 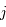et 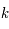correspondent à des états d'énergie inférieure respectivement à l'énergie du niveau supérieur et à l'énergie du niveau inférieur et les deux sommes donnent la largeur du niveau supérieur et du niveau inférieur. Par exemple, on observera une raie faible mais large si le niveau inférieur est fortement élargi.

Une autre cause d'élargissement de raie est représentée par les collisions qui perturbent l'atome pendant le processus d'émission. Les collisions modifient soudainement la phase du rayonnement émis par l'atome. Les sauts de phase se produisent à une fréquence moyenne 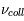$\nu_{coll}$ (chaque atome subit en moyenne 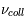$\nu_{coll}$ collisions par unité de temps) et contribuent à l'élargissement de la raie en fréquence qu'on écrit : 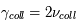$\gamma_{coll}=2\nu_{coll}$ . Il faut remarquer que la fréquence des collisions augmente avec la densité du milieu. On s'attend donc à observer des élargissements collisionnels plus importants dans des environnement denses, comme les atmosphères planétaires et stellaires. Dans les nuages d'hydrogène atomique et les nuages moléculaires les effets collisionnels sont dominés par d'autres sources d'élargissement que nous allons voir dans la suite du cours (effet Doppler, turbulence). Puisque à la fois l'élargissement naturel et l'élargissement associé aux collisions sont caractérisés par des profils de la même forme, on peut définir une constante 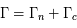$\Gamma=\Gamma_n+\Gamma_c$ qui contient une contribution naturelle 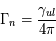$\Gamma_n=\frac{\gamma_{ul}}{4\pi}$ et une contribution collisionnelle 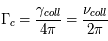$\Gamma_c=\frac{\gamma_{coll}}{4\pi}=\frac{\nu_{coll}}{2\pi}$ et décrire le profil de la raie tel que :

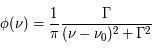$\phi(\nu)=\frac{1}{\pi}\frac{\Gamma}{(\nu-\nu_0)^2+\Gamma^2}$ .

Il s'agit d'une fonction lorentzienne caractérisée par son aire, calculée comme l'intégrale sur la fréquence et égal à 1, sa valeur maximale atteinte à 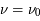$\nu=\nu_0$ , qui vaut 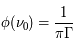$\phi(\nu_0)=\frac{1}{\pi \Gamma}$ et sa largeur totale à mi-hauteur en unité de fréquence 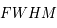FWHM (de l'anglais Full Width at Half Maximum). Cette largeur est déterminée en remplaçant la valeur de la fonction à mi-hauteur ( 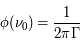$\phi(\nu_0)=\frac{1}{2 \pi \Gamma}$ ) dans l'équation qui décrit 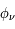$\phi_\nu$ , dont on obtient 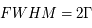$FWHM=2\Gamma$ . Un profil Lorentzien centré ( $\nu_0=0$ ) est montré sur la figure pour différentes valeurs de la constante $\Gamma$ .

Profil de Lorentz

Crédit : Cecilia Pinto