Interaction rayonnement-matière

Auteur: Cecilia Pinto & Sylvie Cabrit

La conservation de l'énergie implique que l'intensité spécifique du rayonnement reste constante le long d'un rayon uniquement si la propagation se produit dans l'espace vide. Autrement dit, l'intensité spécifique est indépendante de la distance entre la source de rayonnement et l'observateur en l'absence de gains ou pertes d'énergie le long de la ligne de visée. Lorsqu'un rayonnement traverse un milieu, l'interaction avec la matière qui le compose ajoute ou soustrait de l'énergie du faisceau. Cette modification de l'intensité spécifique se réalise par des processus d'émission, d'absorption et de diffusion.

Coefficient d'extinction

Lorsqu'un faisceau d'intensité spécifique 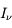$I_\nu$ traverse une épaisseur 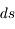de matière, il subit une atténuation 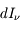$dI_\nu$ proportionnelle à 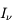$I_\nu$ telle que : 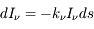$dI_\nu = -k_\nu I_\nu ds$ . La quantité 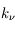$k_\nu$ est appelée coefficient d'extinction et inclut à la fois les processus d'absorption et de diffusion. On peut donc l'exprimer comme la somme d'un coefficient d'absorption 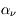$\alpha_\nu$ et d'un coefficient de diffusion 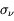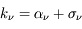$\sigma_\nu$ : $k_\nu=\alpha_\nu+\sigma_\nu$ . L'absorption résulte de divers processus physiques intervenant dans le milieu qui impliquent des changements des degrés de liberté internes d'un atome ou d'une molécule. Des exemples de ces processus sont :

la photo-ionisation (ou absorption lié-libre) où l'excès d'énergie lors de l'absorption d'un photon est transformé en énergie cinétique de l'électron qui se thermalise par collisions avec les autres électrons du milieu ;
l'absorption libre-libre, qui entraîne un changement de l'énergie cinétique d'un électron libre lorsque il absorbe un photon ;
la photo-excitation (ou absorption lié-lié) qui correspond à la transition entre deux états liés induite de l'absorption d'un photon par un atome.

Il faut remarquer que le coefficient d'absorption 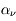$\alpha_\nu$ dépend de l'état thermodynamique de la matière traversée (pression, température, abondances chimiques) en un point donné du milieu. Le faisceau peut perdre de l'énergie également à cause du processus de diffusion, qui change à la fois la direction et l'énergie des photons. Cette énergie, contrairement au processus d'absorption, n'est pas transformée en énergie cinétique du milieu. Les variations locales d'énergie associées au processus de diffusion dépendent donc principalement du champ de rayonnement et faiblement des propriétés thermodynamiques locales du milieu.

Coefficient d'émission

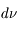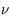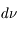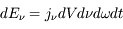Le coefficient d'émission monochromatique est défini comme l'énergie émise par unité de temps, par unité d'angle solide, par unité de volume et dans un intervalle de fréquence de $d\nu$ à $\nu$ + $d\nu$ : $dE_\nu=j_\nu dV d\nu d\omega dt$ . Il s'exprime en erg cm^-3 Hz^-1 sr^-1 s^-1. En parcourant une distance 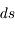, un faisceau de rayonnement de section efficace 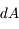traverse un volume 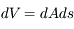dV=dAds . On en déduit que l'intensité ajoutée au faisceau par l'émission est 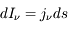$dI_\nu = j_\nu ds$ . L'émission résulte de la combinaison des processus physiques inverses à ceux qui provoquent l'absorption. Ces processus sont :

la recombinaison radiative et l'émission libre-libre décrites en détail à la page Détection du gaz ionisé ;
la photo désexcitation (ou désexcitation collisionnelle) qui engendre l'émission d'un photon par collision lors du passage d'un électron dans un état lié à un autre état lié.

Les photons diffusés peuvent également contribuer à l'émission. Dans ce cas le coefficient d'émission dépend de la distribution angulaire du rayonnement diffusé. Cette dépendance est exprimée sous forme d'une intégrale sur l'angle solide de diffusion, ce qui complique considérablement les calculs. La diffusion ne sera pas prise en compte dans la suite du cours.