Conditions d'excitation et intensité émergente |
Puisque les coefficients d'absorption et d'émission dépendent des populations des niveaux, la résolution de l'équation de transfert de rayonnement requiert la connaissance de l'état d'excitation de l'atome (ou de la molécule). De façon générale, ces conditions d'excitation dépendent à la fois de la température, de la densité, et du champ de rayonnement dans lequel baigne le gaz. Nous introduisons ici les quantités importantes (densité critique, équilibre thermodynamique local, et température d'excitation) qui permettent de caractériser ces conditions d'excitation et de comprendre les observations spectrales du milieu interstellaire.
En régime stationnaire, la fraction d'atomes (ou "population") dans chaque niveau est fixée par l'équilibre statistique entre les taux de transitions qui peuplent ce niveau et celles qui le dépeuplent. Ces transitions sont produites non seulement par les 3 processus radiatifs d'absorption et émission discutés plus haut, étudiés par Einstein, mais aussi par des processus collisionnels d'excitation et désexcitation, lors de collisions inélastiques de l'atome considéré avec les particules les plus abondantes et rapides du milieu (H2, He, H, et les électrons si les gaz est significativement ionisé). Pour chaque transition, on peut calculer une densité critique au-dessus de laquelle les transitions collisionnelles deviennent plus importantes que les transitions radiatives. Pour les systèmes à deux niveaux, et avec un seul collisionneur dominant, elle s'écrit simplement :
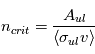
où 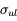 est la section efficace de désexcitation collisionnelle, qui dépend en général de la vitesse
est la section efficace de désexcitation collisionnelle, qui dépend en général de la vitesse 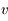 du collisionneur. Les crochets signifient qu'on prend la moyenne sur toute la distribution statistique des vitesses
du collisionneur. Les crochets signifient qu'on prend la moyenne sur toute la distribution statistique des vitesses 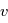 (distribution Boltzmanienne) ce qui donne une valeur dépendant de la température du gaz.
(distribution Boltzmanienne) ce qui donne une valeur dépendant de la température du gaz.
Lorsque la densité des collisionneurs 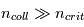 , les transitions radiatives sont négligeables devant les transitions collisionnelles et on atteint l'équilibre thermodynamique local (ou ETL),
où les populations relatives des niveaux des atomes (ou molécules) ne dépendent ni de
, les transitions radiatives sont négligeables devant les transitions collisionnelles et on atteint l'équilibre thermodynamique local (ou ETL),
où les populations relatives des niveaux des atomes (ou molécules) ne dépendent ni de 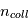 ni du champ de rayonnement et obéissent simplement à la loi de Boltzmann :
ni du champ de rayonnement et obéissent simplement à la loi de Boltzmann :
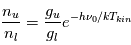
ici 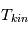 est la température cinétique des collisionneurs, qui caractérise la distribution de vitesse des particules,
est la température cinétique des collisionneurs, qui caractérise la distribution de vitesse des particules, 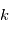 la constante de Boltzmann,
la constante de Boltzmann, 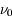 est la fréquence de la transition entre les états u et l,
est la fréquence de la transition entre les états u et l, 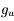 et
et 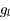 sont les poids statistiques. Plus le coefficient d'Einstein est fort, et plus la densité critique nécessaire pour atteindre l'ETL sera élevée. Cette densité critique est très variable selon les espèces et les transitions considérées : elle est très faible pour la raie hyperfine de l'hydrogène atomique (voir ci-dessous), de l'ordre de 1000 cm-3 pour les premières raies rotationnelles de CO, mais atteint 108 cm-3 pour H2O.
sont les poids statistiques. Plus le coefficient d'Einstein est fort, et plus la densité critique nécessaire pour atteindre l'ETL sera élevée. Cette densité critique est très variable selon les espèces et les transitions considérées : elle est très faible pour la raie hyperfine de l'hydrogène atomique (voir ci-dessous), de l'ordre de 1000 cm-3 pour les premières raies rotationnelles de CO, mais atteint 108 cm-3 pour H2O.
Par analogie avec la loi de Boltzmann, on peut toujours définir une température d'excitation de la transition 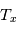 , telle que
, telle que
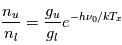 .
.
A l'équilibre thermodynamique local (ETL), on a 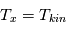 . Dans le cas contraire,
. Dans le cas contraire, 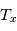 dépend aussi du rapport
dépend aussi du rapport 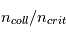 et de l'intensité du champ de rayonnement local, qui peuvent varier fortement d'un point à l'autre. Elle peut être inférieure à
et de l'intensité du champ de rayonnement local, qui peuvent varier fortement d'un point à l'autre. Elle peut être inférieure à 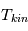 (cas le plus courant dans le MIS) ou bien supérieure si le pompage radiatif est important (par exemple à proximité d'une source de rayonnement intense), voire négative en présence d'un effet maser (inversion de population). En outre, il peut y avoir des températures d'excitation différentes pour différentes transitions d'un même atome.
(cas le plus courant dans le MIS) ou bien supérieure si le pompage radiatif est important (par exemple à proximité d'une source de rayonnement intense), voire négative en présence d'un effet maser (inversion de population). En outre, il peut y avoir des températures d'excitation différentes pour différentes transitions d'un même atome.
En insérant cette définition de la température d'excitation dans la définition de la fonction source dérivée dans la page Coefficients d'Einstein, on peut exprimer la fonction source comme une fonction de Planck :
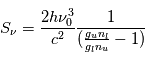
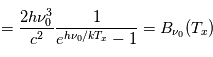 .
.
Notons aussi que le coefficient d'absorption peut s'écrire :
![\alpha_\nu=\frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-\frac{n_ug_l}{n_lg_u}]](../pages_transfert-rayon/equations_transfert-rayon/equation153.png)
![= \frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-e^{-h\nu_0/kT_x}]](../pages_transfert-rayon/equations_transfert-rayon/equation154.png) .
.
Si la température d'excitation est uniforme le long de ligne de visée, la solution formelle de l'équation du transfert radiatif devient :
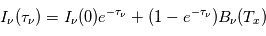 .
.
Notons qu'aux fréquences situées en dehors du profil spectral de la raie, on aura 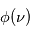 = 0, donc
= 0, donc 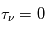 , et
, et 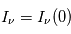 . Ceci définit le niveau du "continuum" que l'on mesure autour de la raie spectrale. Dans ce qui suit nous allons examiner sous quelles conditions la raie apparaîtra en émission ou en absorption par rapport à ce niveau de continu de référence.
. Ceci définit le niveau du "continuum" que l'on mesure autour de la raie spectrale. Dans ce qui suit nous allons examiner sous quelles conditions la raie apparaîtra en émission ou en absorption par rapport à ce niveau de continu de référence.
Définissons maintenant une "température effective de fond", 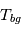 , telle que l'intensité du continu en dehors de la raie s'écrive
, telle que l'intensité du continu en dehors de la raie s'écrive
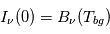 . La solution formelle de l'équation du transfert radiatif devient
. La solution formelle de l'équation du transfert radiatif devient
![I_\nu(\tau_\nu) - I_\nu(0) = (1 - e^{-\tau_\nu} )[B_\nu(T_x) - B_\nu(T_{bg})]](../pages_transfert-rayon/equations_transfert-rayon/equation161.png) .
.
On voit que si 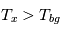 alors le terme de droite est positif et la raie spectrale apparaîtra en émission, avec une intensité supérieure au niveau du continu
alors le terme de droite est positif et la raie spectrale apparaîtra en émission, avec une intensité supérieure au niveau du continu 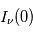 ;
alors que si
;
alors que si 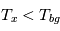 la raie apparaîtra en absorption, avec une intensité qui descend sous le niveau du continu. Enfin dans le cas particulier où
la raie apparaîtra en absorption, avec une intensité qui descend sous le niveau du continu. Enfin dans le cas particulier où 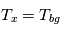 , la raie spectrale se confondra avec le continu et ne sera plus observable en tant que telle. Cette situation ne se rencontre que très rarement dans le MIS.
, la raie spectrale se confondra avec le continu et ne sera plus observable en tant que telle. Cette situation ne se rencontre que très rarement dans le MIS.
Dans un milieu optiquement épais (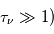 , on obtient
, on obtient 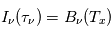 : le rayonnement d'un nuage optiquement épais s'apparente au rayonnement d'un corps noir à la température d'excitation
: le rayonnement d'un nuage optiquement épais s'apparente au rayonnement d'un corps noir à la température d'excitation 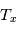 de la transition considérée. Si de plus on est à l'ETL, alors
de la transition considérée. Si de plus on est à l'ETL, alors 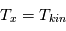 et on peut déduire la température cinétique du gaz à partir de
et on peut déduire la température cinétique du gaz à partir de 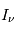 . Cette technique s'applique par exemple à la raie rotationnelle fondamentale de CO à une longueur d'onde de 2.6mm ; elle donne des valeurs typiques de température de 10-20 K dans les nuages moléculaires. Par contre, on voit que dans le cas optiquement épais l'intensité ne dépend plus de
. Cette technique s'applique par exemple à la raie rotationnelle fondamentale de CO à une longueur d'onde de 2.6mm ; elle donne des valeurs typiques de température de 10-20 K dans les nuages moléculaires. Par contre, on voit que dans le cas optiquement épais l'intensité ne dépend plus de  , c'est-à-dire de la quantité de matière traversée ; on dit que la raie est "saturée". Il n'est donc pas possible de déduire la masse de gaz.
, c'est-à-dire de la quantité de matière traversée ; on dit que la raie est "saturée". Il n'est donc pas possible de déduire la masse de gaz.
Pour un milieu optiquement mince (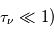 , on obtient
, on obtient ![I_\nu(\tau_\nu) - I_\nu(0) = \tau_\nu [B_\nu(T_x) - B_\nu(T_{bg})]](../pages_transfert-rayon/equations_transfert-rayon/equation173.png) : l'excès d'intensité au-dessus du continu est proportionnel à l'opacité, dont nous avons vu qu'est elle-même proportionnelle à la densité colonne
: l'excès d'intensité au-dessus du continu est proportionnel à l'opacité, dont nous avons vu qu'est elle-même proportionnelle à la densité colonne 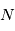 de l'atome considéré, et à une fonction de
de l'atome considéré, et à une fonction de 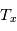 (qui fixe les populations relatives des niveaux). Avec une estimation indépendante de
(qui fixe les populations relatives des niveaux). Avec une estimation indépendante de 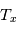 (par ex.
(par ex. 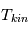 si la raie est à l'ETL), il est donc possible de déduire de ces observations la valeur de
si la raie est à l'ETL), il est donc possible de déduire de ces observations la valeur de 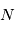 , et ensuite de la masse de gaz si la taille de la région d'émission et l'abondance de l'atome ou molécule sont connues. Cette technique est utilisée par exemple pour mesurer les masses des nuages moléculaires, grâce à des isotopes peu abondants comme 13CO et C18O qui sont (généralement) optiquement minces.
, et ensuite de la masse de gaz si la taille de la région d'émission et l'abondance de l'atome ou molécule sont connues. Cette technique est utilisée par exemple pour mesurer les masses des nuages moléculaires, grâce à des isotopes peu abondants comme 13CO et C18O qui sont (généralement) optiquement minces.
Enfin, une façon d'obtenir à la fois la température et la densité colonne de gaz est la combinaison d'observations en absorption et en émission. Nous en verrons un exemple détaillé plus loin avec la raie hyperfine de HI à 21 cm.
Aux fréquences radio, on a en général 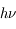 <<
<< 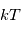 si bien que
si bien que 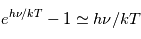 et la fonction de Planck s'écrit :
et la fonction de Planck s'écrit :
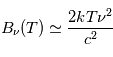 .
.
Il s'agit de l'approximation de Rayleigh-Jeans pour le spectre de corps noir. Par extension de cette expression, les radioastronomes ont l'habitude d'exprimer l'intensité spécifique en termes de température de brillance 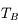 définie par :
définie par :
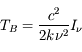 ,
,
et ce même en dehors du domaine de validité de l'approximation de Rayleigh-Jeans. L'équation de transfert s'écrit alors : 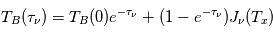 où on a défini la fonction
où on a défini la fonction
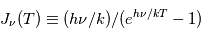 qui tend vers
qui tend vers 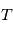 dans la limite de Rayleigh-Jeans.
dans la limite de Rayleigh-Jeans.