L'équation de transfert de rayonnement

Auteur: Cecilia Pinto & Sylvie Cabrit

L'équation de transfert de rayonnement décrit la variation de l'intensité spécifique le long de la direction de propagation d'un faisceau de rayonnement traversant un milieu qui absorbe et émet. En se limitant au cas stationnaire (intensité spécifique indépendante du temps) et en négligeant la diffusion du rayonnement, cette équation se réduit à une équation différentielle ordinaire qui peut être résolue à chaque fréquence donnée, les coefficients d'absorption et d'émission étant connus. Lorsque les effets de diffusion sont inclus, l'équation devient une équation intégro-différentielle, car l'émission entraîne une intégrale de l'intensité spécifique sur l'angle solide de diffusion (voir la page Interaction rayonnement-matière), et il faut employer des méthodes numériques pour sa résolution.

Equation de transfert et profondeur optique

Dans le cas stationnaire et en absence de diffusion, l'équation de transfert est obtenue par le bilan d'énergie absorbée et émise dans le passage d'un faisceau de rayonnement à travers un volume élémentaire d'épaisseur 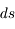et surface 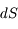= 1 perpendiculaire à la direction de propagation 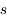. En utilisant les définitions des coefficients d'absorption et d'émission données à la page Interaction rayonnement-matière on obtient :

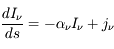$\frac{dI_\nu}{ds} = -\alpha_\nu I_\nu+ j_\nu$ .

Considérons d'abord le cas limite où le milieu émet, mais n'absorbe pas le rayonnement. Dans ce cas 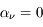$\alpha_\nu=0$ et l'équation de transfert devient : 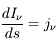$\frac{dI_\nu}{ds} = j_\nu$ qui admet la solution 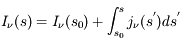$I_\nu(s) = I_\nu(s_0) + \int_{s_0}^sj_\nu(s^{'} )ds^'$ . Cela signifie que l'augmentation de l'intensité spécifique entre la position initiale 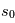s_0 et le point final 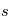est égale au coefficient d'émission intégré le long de cette "ligne de visée" à travers la couche de matière.

Dans le cas inverse où le milieu absorbe, mais n'émet pas de rayonnement (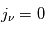 $j_\nu=0$ ) on obtient : 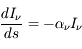$\frac{dI_\nu}{ds} = -\alpha_\nu I_\nu$ , dont la solution est 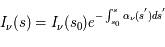$I_\nu(s) = I_\nu(s_0) e^{- \int_{s_0}^s\alpha_\nu(s^{'} )ds^{'}}$ . L'intensité spécifique au point final 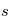est égale à l'intensité spécifique au point initial 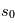s_0 , atténuée par un facteur exponentiel dont l'argument est l'intégrale du coefficient d'absorption le long de la ligne de visée entre 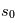s_0 et 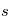. Cette intégrale est un nombre sans dimension appelé la profondeur optique du milieu:

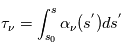$\tau_\nu=\int_{s_0}^s\alpha_\nu(s^{'} )ds^'$ .

La solution de l'équation de transfert dans un milieu purement absorbant s'écrit alors 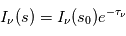$I_\nu(s) = I_\nu(s_0) e^{- \tau_\nu}$ . On voit ainsi que la profondeur optique détermine la fraction de l'intensité incidente qui peut s'échapper du milieu. Afin de mieux comprendre le concept de profondeur optique, on introduit le libre parcours moyen du rayonnement qui représente la distance moyenne qu'un photon parcourt à travers un milieu sans être absorbé. Le coefficient 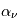$\alpha_\nu$ est l'inverse de ce libre parcours moyen, pour un photon de fréquence $\nu$ . 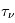La profondeur optique $\tau_\nu$ est donc égale au nombre total de libres parcours moyens traversés entre 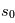s_0 et 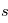. Si la distance à travers le nuage est égale au libre parcours moyen ( 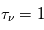$\tau_\nu = 1$ ), l'intensité subit une atténuation d'un facteur e^-1 =0.368, ie. en moyenne seulement 36.8% des photons incidents sortiront du nuage. Si la distance parcourue équivaut à deux fois le libre parcours moyen ( 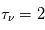$\tau_\nu = 2$ ), seulement 13.5% (e^-2 =0.135) des photons incidents survivront en traversant le nuage. Pour cette raison, un milieu caractérisé par une profondeur optique 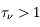$\tau_\nu>1$ est dit optiquement épais ou opaque, alors qu'un milieu avec 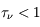$\tau_\nu<1$ est dit optiquement mince ou transparent.

Solution formelle de l'équation de transfert

La solution formelle de l'équation de transfert dans le cas général où à la fois absorption et émission sont présentes est obtenue en effectuant le changement de variable 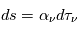$ds = \alpha_\nu d\tau_\nu$ et en définissant la quantité 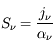$S_\nu=\frac{j_\nu}{\alpha_\nu}$ (appelée fonction source) ; l'équation prend la forme :

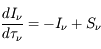$\frac{dI_\nu}{d\tau_\nu} = -I_\nu+ S_\nu$ .

En intégrant cette équation (après avoir multiplié tous les termes par 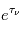$e^{\tau_\nu}$ et posé 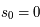s_0=0 ) on obtient la solution formelle :

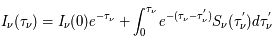$I_\nu(\tau_\nu) = I_\nu(0)e^{-\tau_\nu} + \int_{0}^{\tau_\nu}e^{-(\tau_\nu-\tau_\nu^{'} )}S_\nu (\tau_\nu^{'} )d\tau_\nu^'$ .

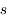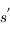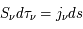L'interprétation physique de cette formule est claire. Le premier terme représente l'intensité de rayonnement initiale atténuée par l'absorption qui intervient sur le parcours de 0 à . Le second terme décrit l'émission dérivant de toutes les couches $s^{'}$ (car $S_\nu d\tau_\nu=j_\nu ds$ ) dont la contribution est atténuée par la profondeur optique 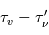$\tau_v-\tau_\nu'$ entre le point d'émission 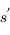$s^{'}$ et le points 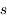où l'on calcule l'intensité.

Dans le cas particulier d'un milieu homogène où la fonction source est uniforme, la solution formelle ci-dessus s'intègre analytiquement pour donner une formule qui sera très utilisée dans la suite de ce cours :

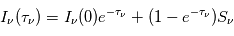$I_\nu(\tau_\nu) = I_\nu(0)e^{-\tau_\nu} + (1 - e^{-\tau_\nu} )S_\nu$ .