
|
Difficulté : ☆☆ Temps : 60 min
On s'intéresse au bilan radiatif d'une planète en orbite circulaire de rayon 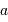 autour de son étoile.
On suppose l'espace interplanétaire vide, ce qui entraîne la conservation du flux stellaire intégrée sur toute surface entourant l'étoile. La rotation propre de la planète est suffisamment rapide pour que l'on puisse
considérer sa température
autour de son étoile.
On suppose l'espace interplanétaire vide, ce qui entraîne la conservation du flux stellaire intégrée sur toute surface entourant l'étoile. La rotation propre de la planète est suffisamment rapide pour que l'on puisse
considérer sa température 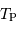 comme uniforme sur toute la surface. On néglige toute autre source
d'énergie que stellaire.
comme uniforme sur toute la surface. On néglige toute autre source
d'énergie que stellaire.
La planète réfléchit une fraction 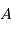 du rayonnement solaire, et en
absorbe une fraction
du rayonnement solaire, et en
absorbe une fraction 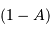 , où
, où 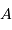 est l'albédo.
On peut, en première approximation à basse résolution spectrale,
considérer ce spectre comme la superposition du spectre de 2 corps noirs, dont
on cherche à déterminer les températures.
On note
est l'albédo.
On peut, en première approximation à basse résolution spectrale,
considérer ce spectre comme la superposition du spectre de 2 corps noirs, dont
on cherche à déterminer les températures.
On note 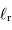 la composante énergétique directement
réfléchie, et
la composante énergétique directement
réfléchie, et 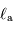 la composante absorbée puis rerayonnée.
la composante absorbée puis rerayonnée.
Montrer que la puissance interceptée par la planète vaut :
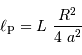
où 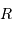 représente le rayon planétaire.
représente le rayon planétaire.
Calculer le rapport 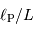 dans le cas de Jupiter et de la Terre.
dans le cas de Jupiter et de la Terre.
| Objet | 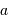 (UA) (UA) | 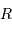 (km) (km) |
| Jupiter | 5.2 | 71000 |
| Terre | 1 | 6400 |
Pour mémoire 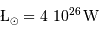 .
.
La planète étant à l'équilibre thermodynamique,
exprimer 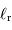 et
et 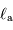 en fonction de la luminosité totale
en fonction de la luminosité totale
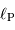 et de l'albédo
et de l'albédo 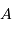 .
.
Quelle est la température 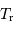 associée au rayonnement réfléchi
associée au rayonnement réfléchi 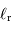 , assimilé à un rayonnement de corps noir ?
, assimilé à un rayonnement de corps noir ?
Montrer que la température associée à la composante
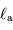 , voisine de la température d'équilibre de la planète, est alors:
, voisine de la température d'équilibre de la planète, est alors:
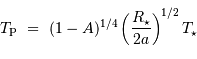
Faire l'application numérique pour une exoplanète avec une
albédo
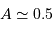 et un demi-grand axe
et un demi-grand axe
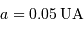 . Pour l'étoile, on prendra :
. Pour l'étoile, on prendra : 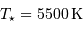 et
et 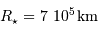 .
.