
|
Difficulté : ☆☆☆ Temps : 45 min
La limite de Roche d'une planète est la distance à partir de laquelle la force de marée sur un satellite est plus importante que les forces de cohésion du satellite. La force du raisonnement de Roche, que nous allons reprendre ici, repose sur l'hypothèse simplificatrice suivante : bien que le satellite naturel soit généralement de forme patatoïdale, on l'imagine constitué de deux sphères (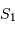 et
et 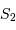 ) de rayons
) de rayons 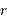 , maintenues ensemble par interaction gravitationnelle. On notera cette force de cohésion
, maintenues ensemble par interaction gravitationnelle. On notera cette force de cohésion 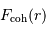 .
.

Nous supposons donc qu'un satellite de masse 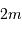 peut être assimilé à deux sphères de masse
peut être assimilé à deux sphères de masse 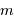 et de rayon
et de rayon 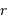 .
Ce satellite orbite autour d'une planète de masse
.
Ce satellite orbite autour d'une planète de masse 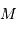 (
(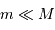 ), et de rayon
), et de rayon 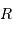 . La distance entre les centres de masse de la planète et du satellite est notée
. La distance entre les centres de masse de la planète et du satellite est notée 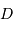 , avec
, avec 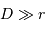 .
.
| Objet | Masse (kg) | Rayon (m) | Masse volumique (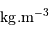 ) ) |
| Soleil | 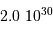 | 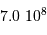 | 1400 |
| la Terre | 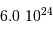 | 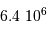 | 5450 |
| Lune | 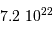 | 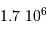 | 3500 |
| Saturne | 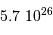 | 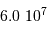 | 630 |
| Comète | 200 | ||
| Satellites de Saturne | Distance (km) | Rayon (km) | Masse (kg) |
| Mimas | 186 000 | 196 | 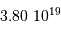 |
| Encelade | 238 000 | 260 | 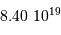 |
| Téthys | 295 000 | 530 | 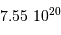 |
| Dioné | 377 000 | 560 | 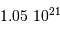 |
| Les anneaux de Saturne | Rayon Interne (km) | Rayon Externe (km) | Largeur (km) |
| Anneau D | 60 000 | 72 600 | 12600 |
| Division Guerin | 72 600 | 73 800 | 1200 |
| Anneau C | 73 800 | 91 800 | 18000 |
| Division Maxwell | 91 800 | 92 300 | 500 |
| Anneau B | 92 300 | 115 800 | 23500 |
| Division Cassini | 115 800 | 120 600 | 4800 |
Montrer que la 3ème loi de Kepler appliquée au satellite peut s'écrire :
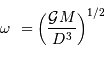
avec 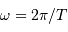 la pulsation du mouvement.
la pulsation du mouvement.
Énoncer les forces d'interaction gravitationnelle 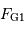 et
et 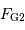 exercées par l'astre massif sur
exercées par l'astre massif sur 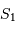 et
et 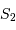 .
.
L'étude du mouvement dans le référentiel tournant introduit une accélération d'entraînement. La déterminer, et exprimer le terme d'inertie qui va s'ajouter dans l'écriture de l'équilibre des forces exprimé dans le référentiel tournant. Pour simplifier les calculs, on confond le barycentre du système planète-satellite avec le barycentre de la planète.
On note 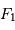 et
et 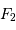 les contributions totales (gravitationnelle et inertielle) sur
les contributions totales (gravitationnelle et inertielle) sur 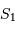 et
et 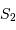 .
Comment appelle-t-on la force
.
Comment appelle-t-on la force 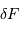 , définie comme étant la différence de
, définie comme étant la différence de 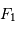 et
et 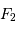 ? La calculer.
? La calculer.
Calculer la force de cohésion 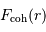 entre
entre 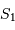 et
et 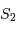 . Estimer d'abord son origine.
. Estimer d'abord son origine.
Déterminer la limite de Roche 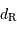 , distance à laquelle les termes de cohésion et marée s'équilibrent. L'exprimer en fonction de
, distance à laquelle les termes de cohésion et marée s'équilibrent. L'exprimer en fonction de 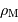 et de
et de 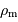 , les masses volumiques respectives de la planète et du satellite.
, les masses volumiques respectives de la planète et du satellite.
Calculer la limite de Roche pour le cas du système Terre-Lune. Comparer la limite de Roche de la Terre à la distance Terre-Lune.
Solution [1 points]
Même question pour Saturne et son satellite Mimas, on suppose que le satellite en formation dans ses anneaux a une masse volumique identique à celle de Saturne. Calculer la limite de Roche dans ce cas. La comparer aux rayons des anneaux et aux rayons des satellites de Saturne.
Solution [2 points]
Même question pour Soleil visité par une comète à son périhélie. Comparer au périhélie de la comète de Halley 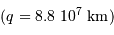 (on supposera que l'expression de l'accélération d'entraînement trouvée dans le cas d'une orbite circulaire garde ici un ordre de grandeur convenable, même si elle ne peut plus s'appliquer a priori).
(on supposera que l'expression de l'accélération d'entraînement trouvée dans le cas d'une orbite circulaire garde ici un ordre de grandeur convenable, même si elle ne peut plus s'appliquer a priori).
Solution [1 points]