La découverte d'exoplanètes, planètes orbitant autour d'une étoile autre que le Soleil, a constitué l'un des principaux événements astronomiques de la fin du XXe siècle. Cette section aborde la quête des exoplanètes sous deux angles : les propriétés de ces exoplanètes, et les techniques instrumentales utilisées pour les détecter et les étudier.
Courbe de vitesse radiale de 51 Peg A
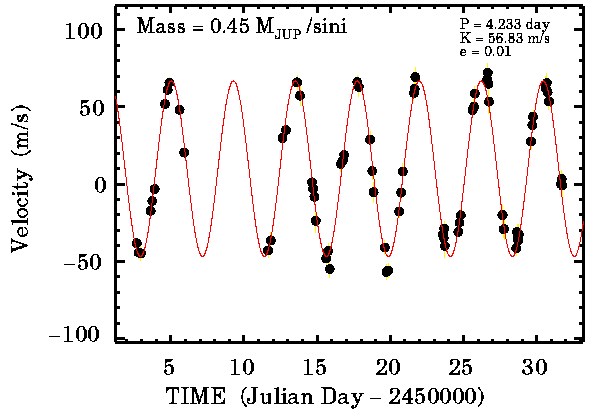
Mesure de vitesse radiale de l'étoile 51Peg, première exoplanète découverte autour d'une étoile de type solaire, en 1995, à l'Observatoire de Haute Provence par les astrophysiciens suisses Michel Mayor et Didier Queloz.
Crédit :
Butler & Marcy
 Objectifs
Objectifs
Ces pages présentent une grande découverte des années 90, les planètes
extrasolaires, et décrivent :
- les principales caractéristiques de ces objets ;
- les différentes techniques mises au point afin de détecter la
présence de planète(s) autour d'étoiles de type solaire, proche de la
Terre.
Ces méthodes sont basées sur l'observation des
perturbations produites sur le mouvement de l'étoile par ses compagnons planétaires, ou sur la baisse du flux stellaire occulté par un compagnon. C'est à partir de ces perturbations que l'on est capable d'obtenir certaines des caractéristiques de la planète.
Les premières tentatives
Les tentatives de détection de compagnons planétaires ont été nombreuses... dès le début du XXe siècle, par astrométrie, et non moins nombreuses furent les tentatives infructueuses. Une planète est par essence très peu massive par rapport à son étoile, et excessivement moins lumineuse...
Diverses détections ont été annoncées en 1988 puis démenties. Certaines ont été confirmées depuis (autour de 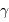 Ceph,
Ceph, 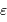 Eri)... En 1989, Latham et ses collègues identifièrent un compagnon d'environ dix fois la masse de Jupiter, autour de HD 114762. Mais ces auteurs évoquèrent alors la détection d'une naine brune et non d'une planète.
Eri)... En 1989, Latham et ses collègues identifièrent un compagnon d'environ dix fois la masse de Jupiter, autour de HD 114762. Mais ces auteurs évoquèrent alors la détection d'une naine brune et non d'une planète.
En 1992, trois planètes furent détectées sans ambiguïté par Wolszczan & Frail, autour du pulsar PSR 1257+12. Mais l'environnement d'un pulsar ne laisse guère espérer que des planètes brûlées par l'évolution de leur étoile.
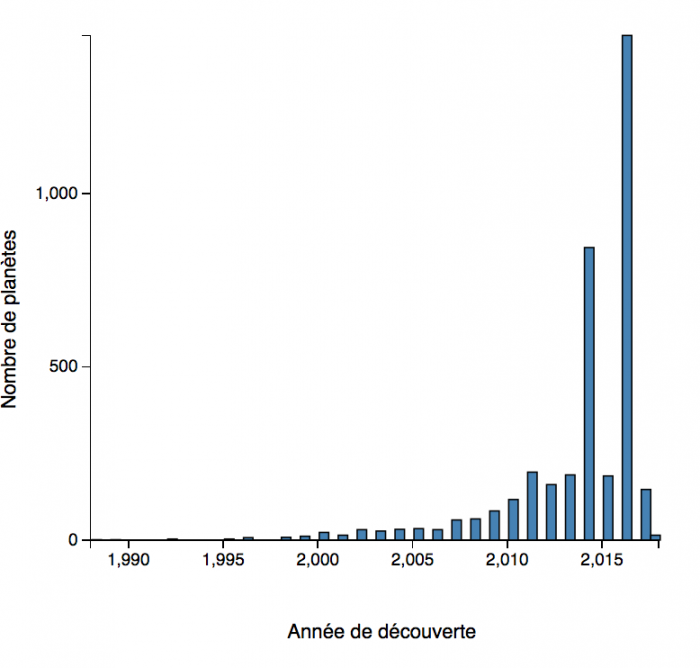
Evolution du nombre d'exoplanètes détectées par année.
Autour de 51 Peg
En 1995, on retient la découverte de la première planète extrasolaire autour d'une étoile semblable à notre Soleil, par Michel Mayor et Didier Queloz, de
l'Observatoire de Genève. Elle fut détectée à l'Observatoire de
Haute-Provence, et immédiatement confirmée par Geoff Marcy et Paul
Butler, des Universités de San Francisco et Berkeley, qui eux l'avaient
observée à l'Observatoire Lick en Californie.
Ces mesures ont vraiment lancé l'un des grands sujets de
l'astrophysique actuelle : la quête des exoplanètes. Depuis, plusieurs milliers de
planètes ont été recensées. Ce nombre est en constante
augmentation, les projets de recherche se multipliant, si bien que tenir un décompte précis est impossible.
La découverte de ces planètes apporte aux astrophysiciens des données permettant de mieux comprendre
la formation des systèmes planétaires, avec d'autres exemples que notre
système solaire.
Que voit-on ?
Plusieurs dizaines de planètes ont été vues directement, mais la plupart des découvertes sont basées sur des détections indirectes, soit la détection de l'influence gravitationnelle de la planète sur l'étoile soit la baisse de luminosité de l'étoile due au passage de la planète sur sa ligne de visée.
Méthodes de détection
A ce jour (2018), cinq méthodes ont permis de découvrir ou redécouvrir l'essentiel des exoplanètes :
- Vitesse radiale de l'étoile hôte perturbée par la planète
- Transit de la planète devant son étoile
- Transit secondaire de la planète derrière son étoile
- Variation de l'instant de transit
- Effet de microlentille
- Chronométrage (autour d'un pulsar)
- Imagerie
Les méthodes de
vitesse radiale et
transit, les plus productives, sont décrites plus loin, ainsi que la méthode par astrométrie.
Un sujet à la mode
Les exoplanètes sont un sujet à la mode, pour les raisons que l'on devine aisément. Désolé si ces pages n'annoncent pas en temps réel les dernières découvertes !
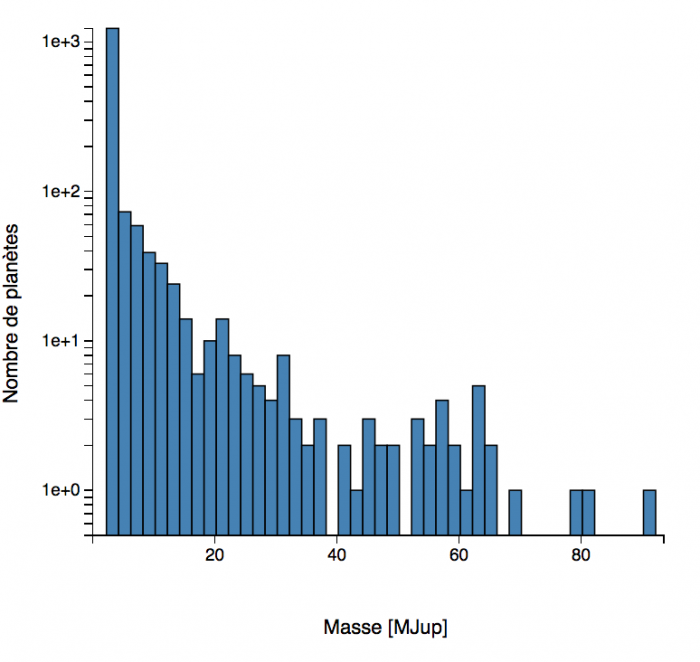
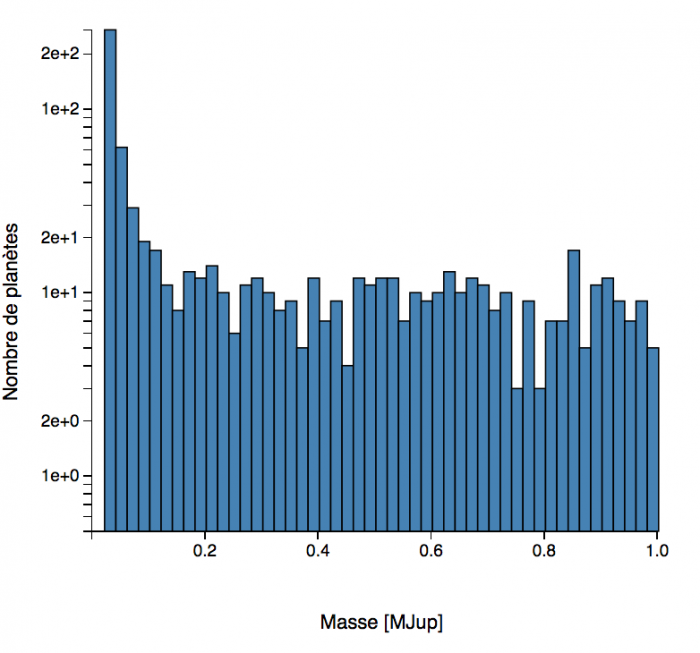
Décompte des masses des exoplanètes, ou plus exactement des
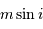
, l'inclinaison

n'étant pas une
observable (septembre 2018).
Deux échelles de masse permettent de distinguer les
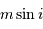
plus petits que la masse de Jupiter, et la distribution totale jusqu'à 15 masses de Jupiter.
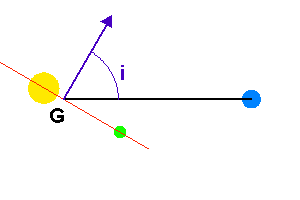
Définition de l'angle entre la normale au plan orbital et l'axe de visée. Avec les paramètres usuels, le barycentre G du système est à l'intérieur de l'étoile.
Crédit :
ASM
Masse
L'histogramme
des masses montre que la très grande majorité des planètes découvertes sont des planètes géantes.
Cela n'est pas dû au caractère unique de la présence de planètes
telluriques dans notre système solaire, mais au fait que les méthodes de
détection favorisent les fortes masses planétaires.
La limite à 13 fois la masse de Jupiter est une limite physique : au-delà,
l'objet commence à brûler son deutérium, c'est alors une naine brune.
Stricto sensu, les masses ici considérées sont affectées d'un facteur de
projection inconnu, égal au sinus de l'angle entre la normale au plan orbital et l'axe de visée. On parle non de masse 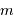 , mais de
, mais de 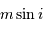 .
.
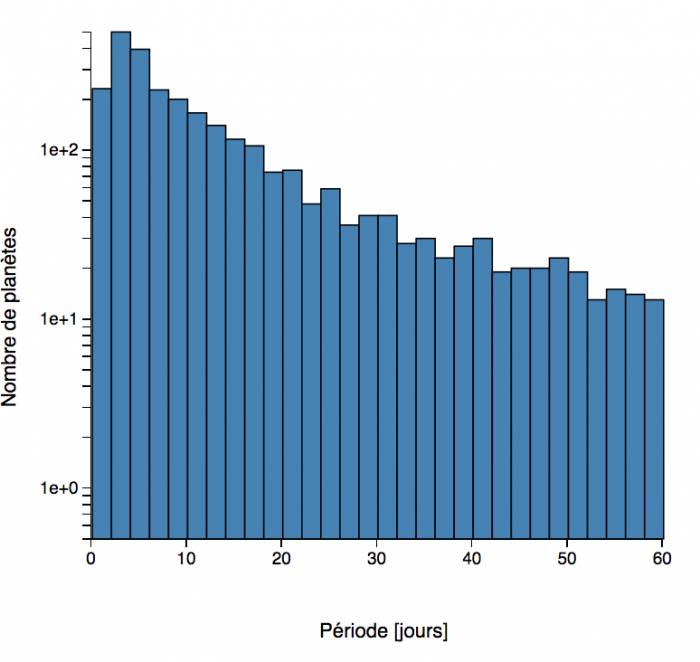
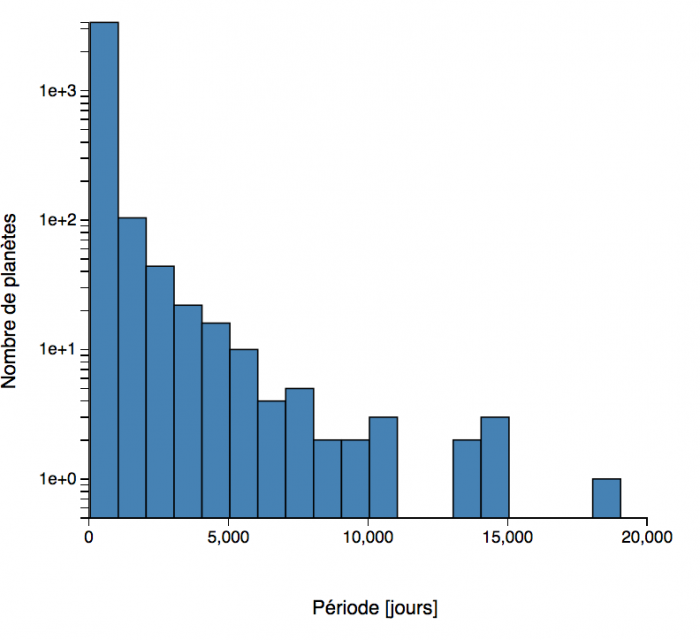
Histogrammes des périodes orbitales des exoplanètes. Zoom sur les périodes courtes (en échelle linéaire), et aperçu général (avec le décompte en échelle logarithmique) (septembre 2018).
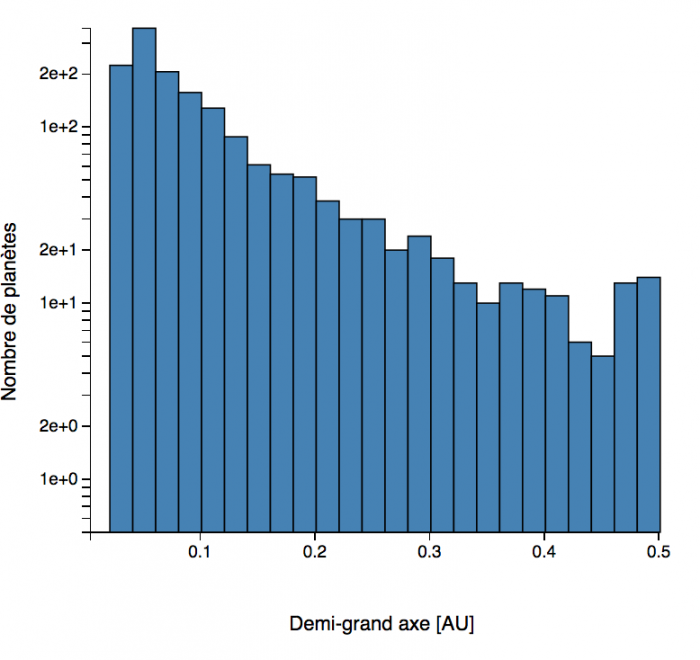
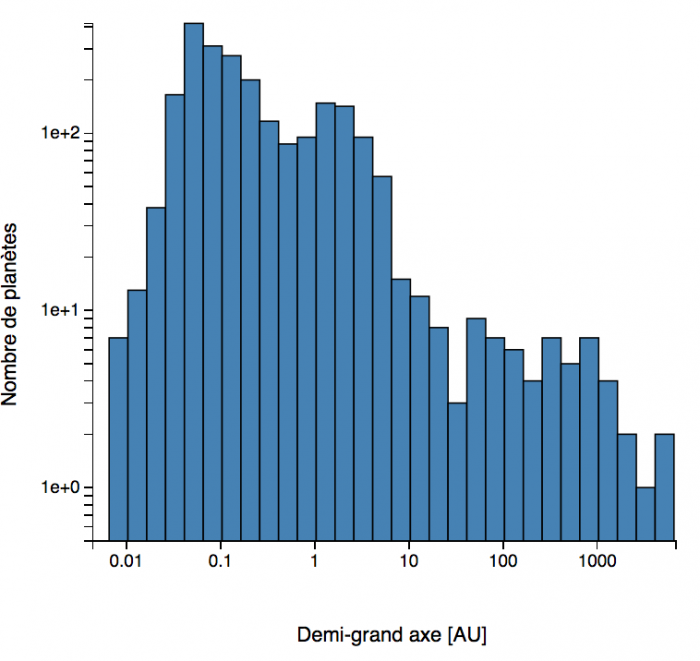
Histogrammes des demi-grands axes de l'orbite des exoplanètes. Zoom sur les demi-grands axes inférieurs à 1 UA, et aperçu général.(septembre 2018)
Demi-grand axe et période de l'orbite
L'histogramme
des demi-grands axes montre qu'ont préférentiellement été découvertes des
planètes orbitant très près de leur étoile, bien plus près que Mercure
dans le cas du système solaire. Là encore, ce sont les méthodes de détection et la 3ème loi de Kepler qui favorisent cette situation. Une nouvelle classe d'objets a été mise en évidence : les planètes géantes chaudes.
L'histogramme
des périodes orbitales aboutit à la même analyse.
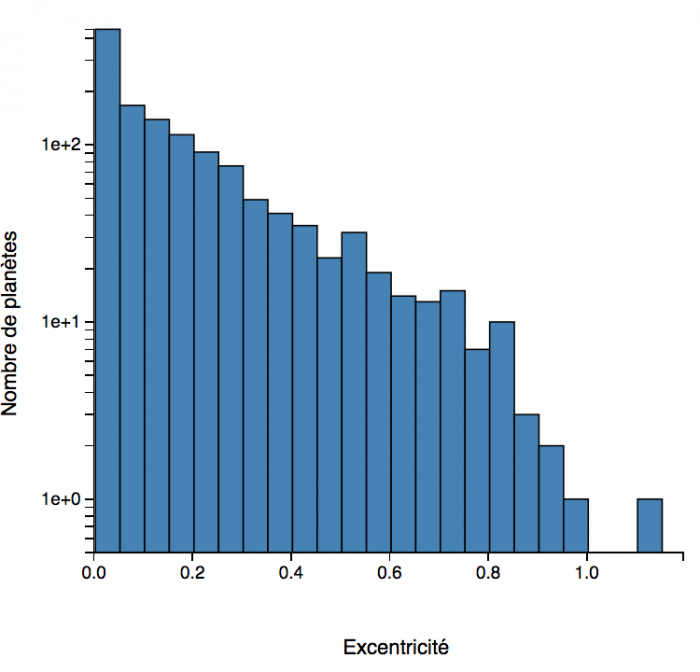
Histogramme des excentricités des exoplanètes. (septembre 2018)
Excentricité de l'orbite
L'histogramme
des excentricités orbitales dévoile une très grande variabilité de ce
paramètre. Contrairement au cas du système solaire, où les planètes
présentent des excentricités quasi nulles, les exoplanètes peuvent
suivre des orbites très excentrées. Et contrairement aux effets précédents, ceci est un phénomène réel et non un biais observationnel, qui dénote une grande variété dans la formation et l'évolution des systèmes planétaires.
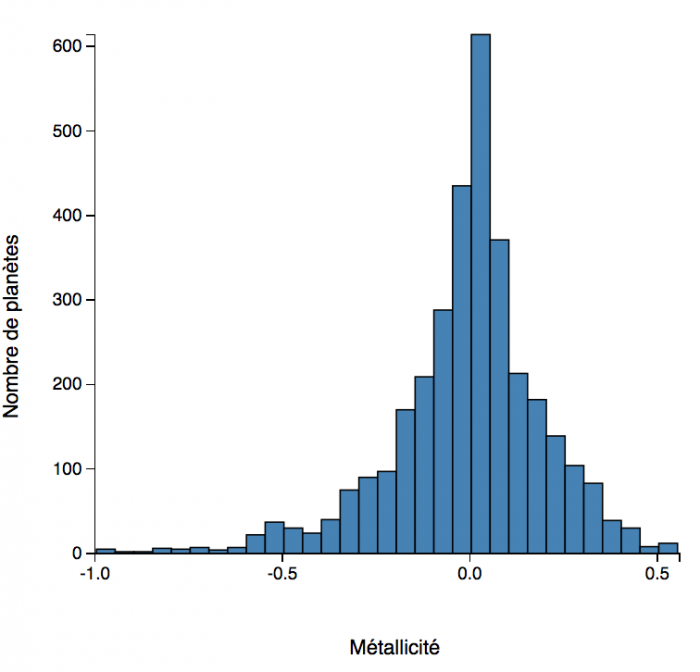
Histogramme de la métallicité des étoiles à exoplanètes. La métallicité est donnée en échelle logarithmique relative ; elle compare l'abondance de l'élément Fe dans l'étoile par rapport à celle dans le Soleil (0 = valeur solaire). (septembre 2018)
Métallicité de l'étoile hôte
L'histogramme
de la métallicité de l'étoile hôte montre qu'une metallicité solaire favorise la présence d'une planète autour d'une étoile.
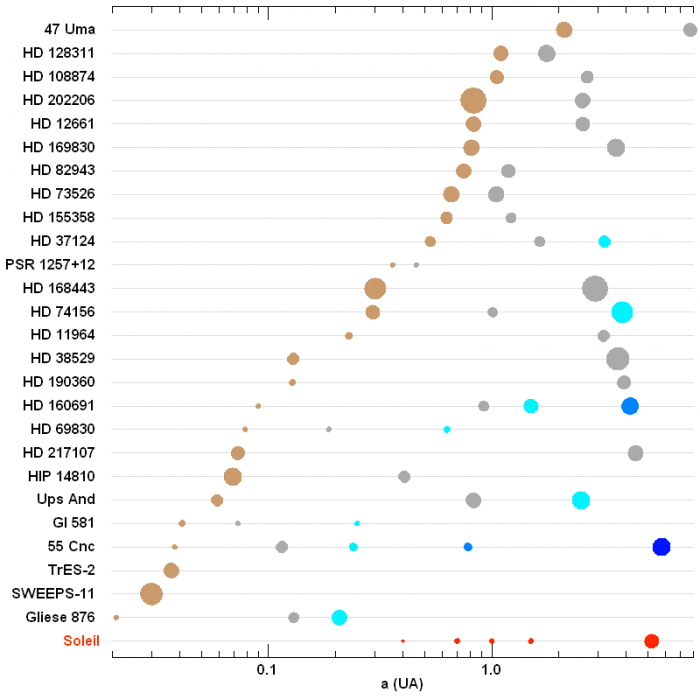
Quelques systèmes exoplanétaires. La couleur code le rang de la planète.
La plupart de ces systèmes sont plus tassés et plus massifs que le système solaire.
Crédit :
ASM
Systèmes planétaires
À ce jour, un grand nombre de systèmes planétaires ont été identifiés, présentant des caractéristiques différentes de notre système solaire. Les planètes les moins massives sont détectées par les perturbations qu'elles exercent sur les plus massives.
Méthode des vitesses radiales
Considérons un système binaire constitué d'une étoile et d'une planète.
Chacun des objets décrit une orbite elliptique dont le foyer est le
centre de masse du système.
Effet Doppler dû à l'oscillation de l'étoile
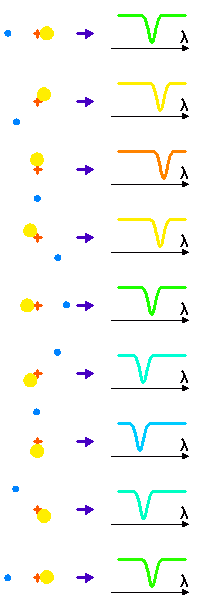
Dans son mouvement, l'étoile tantôt se rapproche, tantôt s'éloigne de l'observateur.
Une raie spectrale est alternativement décalée vers le bleu ou vers le
rouge, selon la vitesse relative entre l'étoile et l'observateur (direction indiquée par une flèche violette).
Crédit :
ASM
Les raies spectrales stellaires qui nous parviennent (à travers un
spectromètre) sont en conséquence tantôt décalées vers le bleu (longueur d'onde plus courte), tantôt vers le rouge (longueur d'onde plus grande), par effet Doppler.
L'orbite de la planète et l'axe de visée

L'angle

est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
Crédit :
ASM
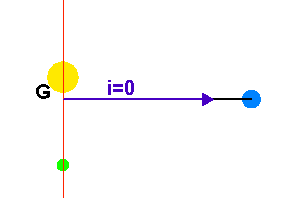
Cas particulier où l'angle

est nul. Pas de mouvement détectable.
Crédit :
ASM
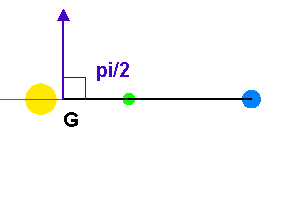
Cas particulier où l'angle

vaut
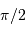
.
Crédit :
ASM
Courbe de vitesse radiale de 51 Peg A

Mesure de vitesse radiale de l'étoile 51Peg.
Crédit :
Butler & Marcy
Vitesse radiale
Animation des mouvements orbitaux planétaires et stellaires, et signature spectrale due à la vitesse radiale de l'étoile.
Effet Doppler dû au mouvement de l'étoile
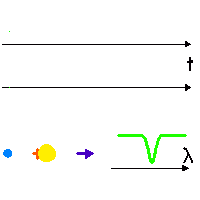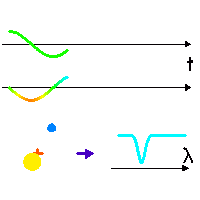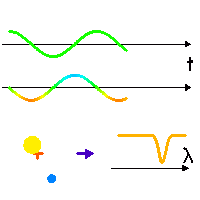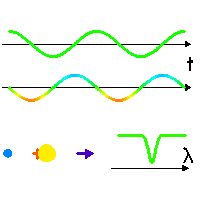
Dans son mouvement (séquence animée), l'étoile en rotation autour du barycentre (croix rouge, fixe) tantôt se rapproche, tantôt s'éloigne (courbe verte) de l'observateur (direction indiquée par la flèche bleu foncé), avec une vitesse donnée par la courbe du milieu (couleur modifiée selon une convention de type
effet Doppler .
Une raie spectrale (courbe du bas) est alternativement décalée vers le bleu ou vers le rouge, selon la vitesse relative entre l'étoile et l'observateur.
Crédit :
ASM

L'angle

est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
Crédit :
ASM
 QCM
QCM
 Le paramètre m sin i
Le paramètre m sin i
Difficulté : ☆☆
Temps : 20 min
On s'intéresse à la distribution du facteur multiplicatif 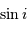 qui intervient dans la détermination de la masse
qui intervient dans la détermination de la masse 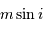 .
.
Question 1)
Rappeler la définition de l'angle 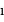 .
.
Question 2)
Statistiquement, trouve-t-on plus de systèmes avec 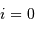 ou bien
ou bien
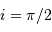 ?
?
Faire un schéma. A quelle condition sur le plan orbital a-t-on
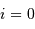 ou
ou 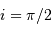 ?
?
Y'a-t-il autant de plans avec 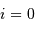 ou
ou 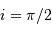 ?
?
Question 3)
Montrer, en faisant un schéma, que la probabilité de voir un
système sous une inclinaison  est proportionnelle à
est proportionnelle à 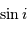 .
.
Question 4)
Calculer la valeur moyenne de 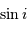 .
.
La définition d'une valeur moyenne conduit à :
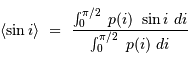
avec 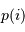 la loi de probabilité associée.
la loi de probabilité associée.
 La vélocimétrie Doppler
La vélocimétrie Doppler
Difficulté : ☆☆
Temps : 45 min
Cette technique permet la détection de planètes, via la perturbation en vitesse (vitesse réflexe) qu'elles induisent sur leur étoile.
On observe un système constitué d'une planète de masse 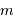 , en orbite circulaire autour d'une étoile de masse
, en orbite circulaire autour d'une étoile de masse 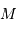 . La composante de vitesse de l'étoile
. La composante de vitesse de l'étoile 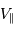 , parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse
, parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse 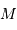 de l'étoile est supposée connue.
de l'étoile est supposée connue.
Schéma du système
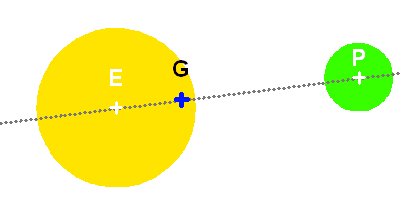
On note respectivement
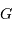
,
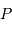
et
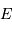
les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
Crédit :
ASM
Question 1)
Définir la position du barycentre du système étoile-planète.
Montrer que, dans le référentiel barycentrique, les vitesses 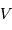 de l'étoile et
de l'étoile et 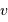 de la planète satisfont à la relation :
de la planète satisfont à la relation :
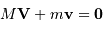
Définir la position du barycentre.
Le barycentre 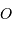 du système obéit à:
du système obéit à:
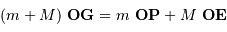
Différencier cette relation pour obtenir l'information en vitesse.
Question 4)
Quelle information inédite apporte cette relation?
Reformulation de la question :
quelle grandeur non directement observable peut finalement être ainsi mesurée ?
Question 5)
Substituer à l'observable 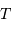 la variable
la variable 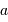 , et montrer que l'on aboutit à l'égalité suivante entre les variables
, et montrer que l'on aboutit à l'égalité suivante entre les variables 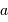 et
et 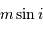 :
:
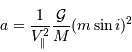
Commencer par réécrire la 3ème loi de Kepler.
Série temporelle
La mesure de ce décalage spectral est traduite en une vitesse. Ce décalage, apparaissant comme un phénomène périodique
et d'amplitude bien inférieure à ce que l'on attendrait d'une perturbation due à un compagnon stellaire, s'interprète comme la signature d'une perturbation due à la présence de la planète autour de l'étoile.
Vitesse radiale de l'étoile en fonction du temps

Le décalage Doppler du spectre est mesuré puis traduit en vitesse
radiale
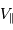
. On obtient une série temporelle de vitesse radiale, qui
semble présenter des variations répétitives.
Crédit :
Butler &Marcy
Sur une période
Vitesse radiale rapportée sur une période
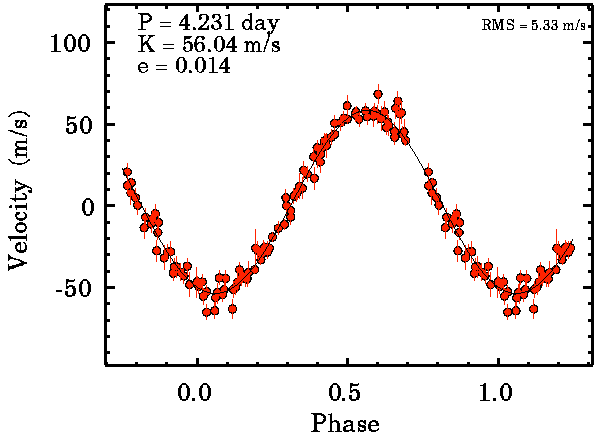
Une longue série temporelle, plus longue qu'une période,
donne accès à la période de
rotation du système, ici visualisée par repliement : la variable temporelle est la phase, et non plus la date d'observation.
Crédit :
Butler & Marcy
Lorsque l'orbite de la planète est quasi-circulaire, le graphe de la
vitesse a la forme d'une sinusoïde. L'excentricité de l'orbite a pour effet de déformer cette sinusoïde.
Graphe de vitesse de HD 108147
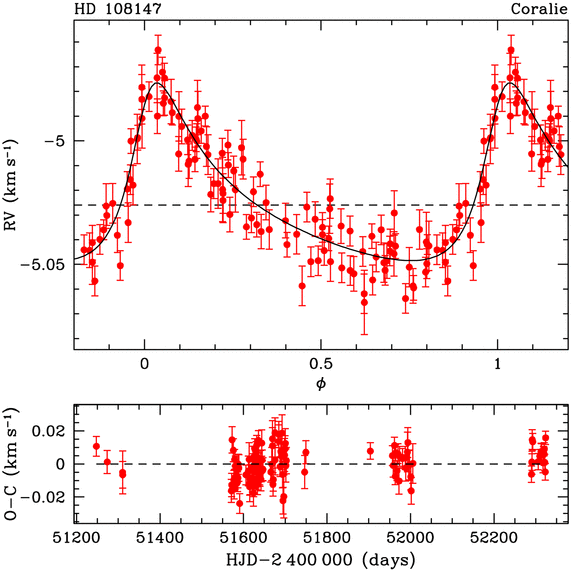
L'excentricité de l'orbite, voisine de 0.5, et la géométrie de l'observation conduisent à une telle courbe de vitesse radiale. Le schéma du dessous représente les résidus entre les valeur observées et la courbe de vitesse modélisée.
Crédit :
Observatoire de Genève
Système multiple
Lorsque l'étoile réagit à plusieurs compagnons planétaires, la complexité de la courbe de vitesse radiale s'accroît.
Dans certain cas, comme pour le système observé autour de HD 82943, on observe une résonance, avec pour ce système des périodes orbitales planétaires dans un rapport 1:2.
Graphe de vitesse de HD 168443
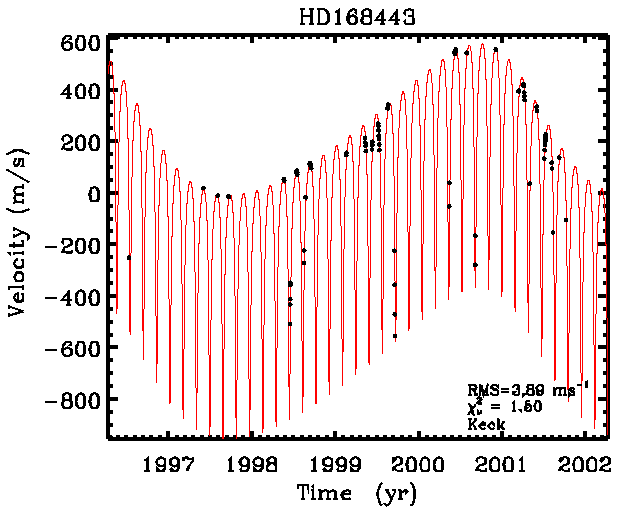
La courbe de vitesse radiale de l'étoile
HD 168443présente 2 composantes, dues à 2 compagnons planétaires. Les orbites des deux planètes détectées autour de HD 168443 ont des périodes d'ordres de grandeur bien distincts et une excentricité élevée (0.53 et 0.23)
Crédit :
Butler & Marcy
Graphe de vitesse de HD 82943
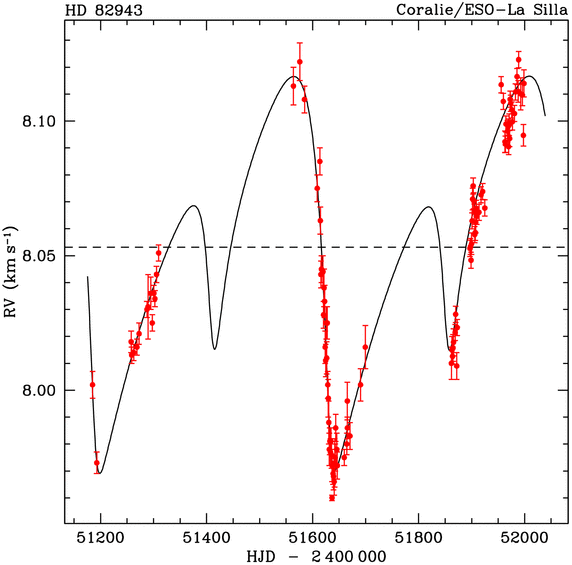
Les 2 périodes (respectivement 222 et 444 j) sont multiples l'une de l'autre, dans un rapport 2.
Crédit :
Observatoire de Genève
Diagramme a-m sin i
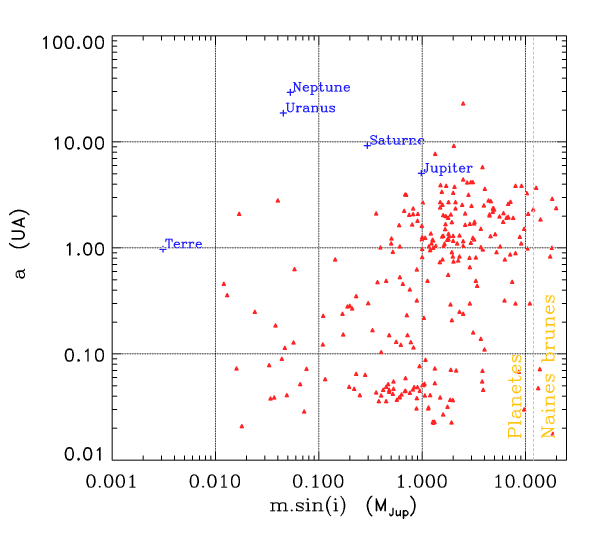
Diagramme msini-a des exoplanètes et des planètes du système solaire. Au delà de 13 fois la masse de Jupiter, on considère qu'il ne s'agit plus de planètes, mais de
naines brunes.
Crédit :
ASM
Systèmes pouvant être détectés par cette méthode
La méthode des vitesses radiales ne permet d'obtenir qu'une limite
inférieure de la masse des planètes, 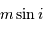 , car l'angle sous lequel
le système est observé,
, car l'angle sous lequel
le système est observé,  , reste en général inconnu. Cela a bien sûr
été un obstacle à l'interprétation du premier cas qui annonçait la
découverte d'une d'exoplanète. Cependant, une centaine d'objets avec
une masse
, reste en général inconnu. Cela a bien sûr
été un obstacle à l'interprétation du premier cas qui annonçait la
découverte d'une d'exoplanète. Cependant, une centaine d'objets avec
une masse 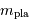 les rangeant dans la catégorie des planètes ont
été détectés, et, statistiquement, la masse réelle de la plupart
d'entre eux est bien une masse planétaire.
Cette méthode est biaisée, car elle favorise la détection des planètes
massives et relativement proches de leur étoile. En effet :
les rangeant dans la catégorie des planètes ont
été détectés, et, statistiquement, la masse réelle de la plupart
d'entre eux est bien une masse planétaire.
Cette méthode est biaisée, car elle favorise la détection des planètes
massives et relativement proches de leur étoile. En effet :
- Plus la planète est massive, plus l'étoile est perturbée, car
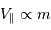 .
. - Plus la planète est proche, plus la période est courte et
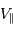 important, car
important, car 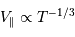 .
.
Il est commode de réécrire 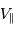 sous la forme :
sous la forme :
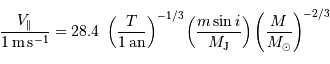
où 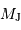 et
et 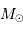 sont, respectivement, les masses de Jupiter et du Soleil.
sont, respectivement, les masses de Jupiter et du Soleil.
On rappelle, qu'avec les mêmes unités :
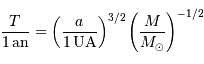
où 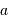 est exprimé en unité astronomique.
est exprimé en unité astronomique.
Limite de détection par la méthode des vitesses radiales
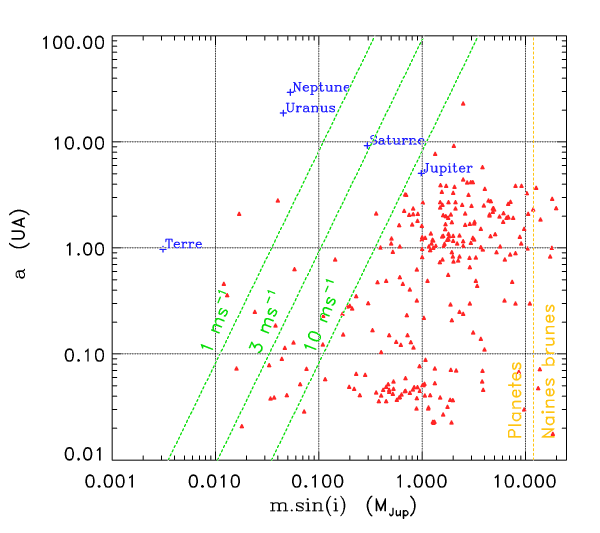
Cette méthode permet de détecter des variations de vitesse de
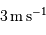
. Il faut également observer les étoiles longtemps pour avoir accès aux plus longues périodes. Les exoplanètes les moins massives n'ont pas été détectées par mesure Doppler, mais par la méthode des
transits.
Crédit :
ASM
Limite de détection
La limite de détection des instruments utilisés actuellement est de l'ordre de 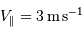 . Cela ne signifie qu'une planète similaire à la Terre autour d'une étoile de type solaire induisant une modulation de vitesse
. Cela ne signifie qu'une planète similaire à la Terre autour d'une étoile de type solaire induisant une modulation de vitesse 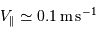 reste largement indétectable.
reste largement indétectable.
Néanmoins, il ne suffit pas que la vitesse réflexe de l'étoile soit supérieure à cette limite pour détecter une planète. En effet, une planète de masse égale à la masse de Jupiter va induire un effet Doppler de cet ordre pour une distance étoile-planète de 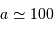 UA. Cependant, la période de révolution d'une telle planète est de 1000 ans, et il est donc exclu de l'observer ! Notons que la même planète située à la distance de Jupiter
UA. Cependant, la période de révolution d'une telle planète est de 1000 ans, et il est donc exclu de l'observer ! Notons que la même planète située à la distance de Jupiter 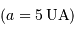 entraîne
entraîne 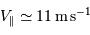 , ce qui est largement observable.
, ce qui est largement observable.
Les mesures de vitesses radiales pour la recherche de planètes extrasolaires sont menées systématiquement depuis 1995. Ceci limite la détection aux planètes de période orbitale inférieure à 15 ans en 2010, 30 ans en 2025...
Jusqu'à ce jour, la plupart des planètes extrasolaires détectées l'ont été par cette méthode.
Un exercice traite de cette limite de détection.
 Limite de détection
Limite de détection
Difficulté : ☆☆☆
Temps : 45 min
Un exercice précédent a montré que la vitesse réflexe de l'étoile dépend de la masse et de l'orbite de la planète via la relation :
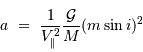
Un graphe (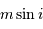 - rayon orbital
- rayon orbital 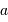 ) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse
) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse 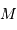 de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.
de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.
Diagramme m sin i - a
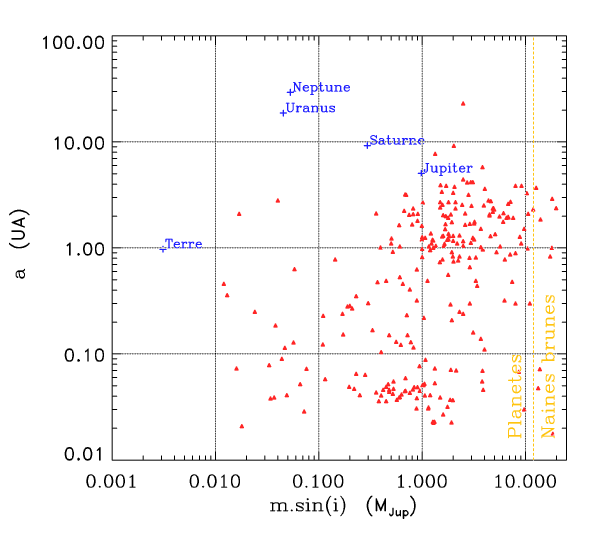
Crédit :
ASM
Données numériques
| objet | masse (kg) |
|---|
| Soleil | 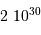 |
| Jupiter | 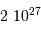 |
| la Terre | 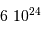 |
| 1 UA | 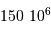 km km |
Question 1)
Les mesures en 2000 atteignaient une précision en vitesse de l'ordre de
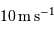 . En déduire la relation numérique entre les variables
. En déduire la relation numérique entre les variables 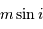 et
et 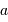 correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et
correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et 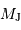 .
.
[3 points]
Faire le calcul en SI, puis passer aux unités demandées.
Question 2)
Reporter la relation trouvée sur le diagramme masse-distance, avec comme unités la masse de Jupiter pour 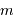 , et l'unité astronomique pour
, et l'unité astronomique pour 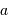 .
Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de
.
Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de 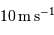 ) ?
) ?
[3 points]
Les axes du diagramme sont en échelle logarithmique décimale. Il faut prendre le logarithme de l'équation précédente pour tracer des droites sur le diagramme. En échelle log-log, l'origine du repère est en (a=1, et msin i=1).
Question 3)
Même question, si l'on parvient à détecter des amplitudes en vitesse de 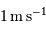 .
.
[1 points]
Question 4)
Montrer que Saturne, de période orbitale sidérale de l'ordre de 30 ans, ne pourrait tout de même pas être détecté avant l'année 2025.
[1 points]
Les observations ont vraiment débuté en 1995.
Question 5)
Montrer que cette technique d'observation comporte un biais, car elle favorise la détection de planète ayant des paramètres orbitaux particuliers.
[1 points]
Détection par transit
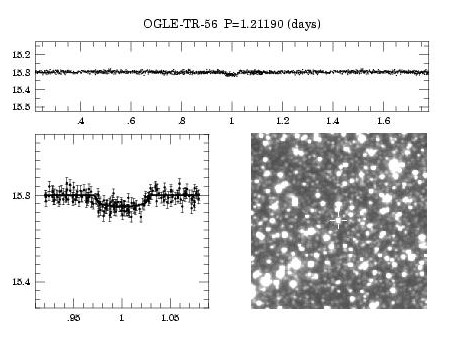
Occultation détectée par la campagne d'observation OGLE (Optical Gravitational Lensing Experiment ; Warsaw Telescope (1.3 m) installé à l'Observatoire de Las Campanas au Chili). L'aperçu de la courbe de lumière, et le zoom autour du transit montre combien la signature de ce dernier est ténue. Le champ stellaire localise la cible, de faible magnitude (V = 16).
Le temps est donné en unité de la période orbitale.
Crédit :
OGLE
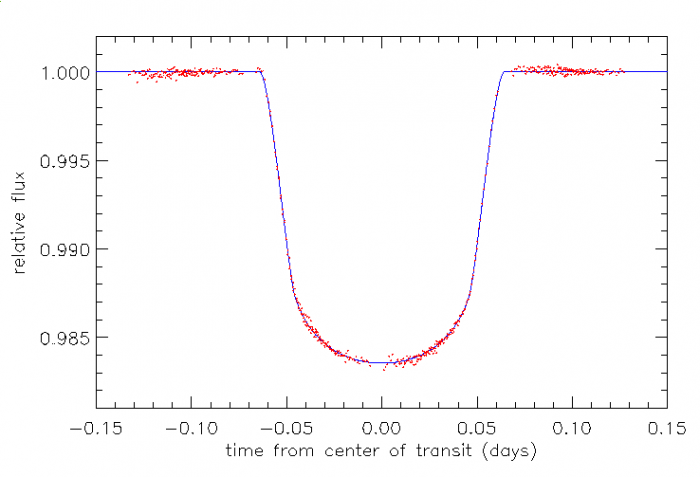
Occultation de
HD209458 par sa planète, vue par le télescope spatial Hubble. Le profil d'assombrissement du centre au bord de l'étoile occasionne la concavité du fond du transit.
Crédit :
HST
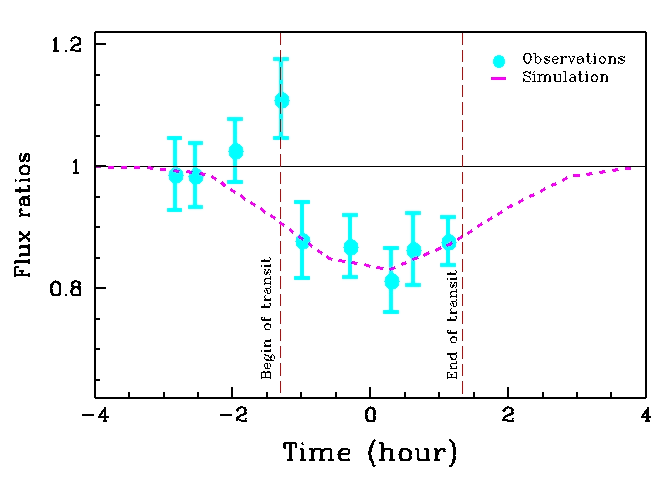
Occultation de HD209458 par sa planète, vue dans le filtre étroit de la raie Lyman alpha de l'hydrogène. L'augmentation du flux est due à la composante planétaire, et dénote vraisemblablement une atmosphère planétaire étendue.
Crédit :
HST
Transit
Le passage répété d'une planète devant son étoile provoque une diminution périodique de la luminosité de l'étoile. La forme de la figure de transit dépend du diamètre relatif de la
planète par rapport à celui de l'étoile, de l'inclinaison du système
par rapport à la ligne de visée, de l'épaisseur et de la composition de
l'éventuelle atmosphère de la planète.
Mesures orbitales
On retire des observations : la période orbitale, le demi-grand axe, et surtout l'inclinaison de l'orbite (voisine de 90°). Cette dernière n'est pas mesurable par la méthode des vitesses radiales.
L'atmosphère planétaire
Potentiellement, la comparaison des mesures spectroscopiques de l'étoile avant et pendant le transit peut donner accès à la composition de l'atmosphère planétaire.
Le transit de l'étoile HD 209458 a conduit à la détection d'une atmosphère planétaire étendue, qui explique l'allure de la courbe d'occultation dans la raie Lyman alpha de l'hydrogène.
Transit d'une planète devant son étoile

Crédit :
ASM
Méthode de détection d'éléments chimiques dans une atmosphère
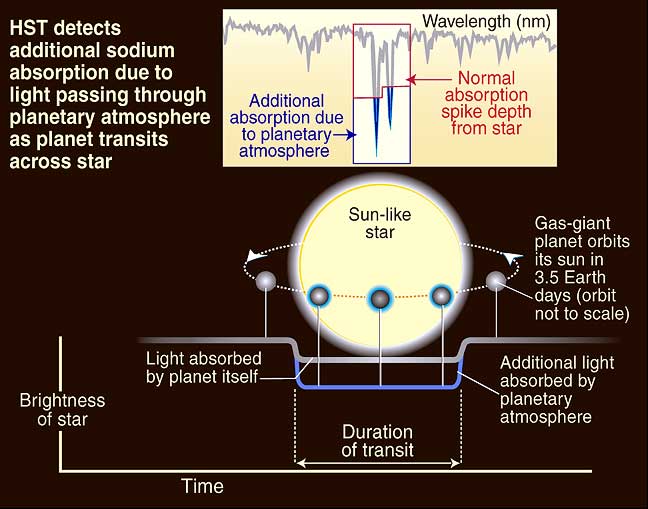
Crédit :
HST
Baisse de flux
Le passage récurrent d'une planète devant son étoile parente provoque une diminution périodique du flux reçu de l'étoile si le système est observé sous un angle adéquat, i.e. si la planète traverse la ligne de visée de l'observateur.
La diminution relative du flux émis par l'étoile dans la direction de l'observateur lors du transit de la planète est :
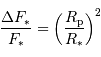
où 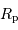 est le rayon de la planète et
est le rayon de la planète et 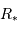 celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en exercice).
celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en exercice).
Ordres de grandeurs
Les systèmes les plus facilement détectables, avec une planète de type Jupiter chaud, ont un rayon de l'ordre de 10 à 20% du rayon stellaire d'une étoile froide de la séquence principale. Ils induisent des baisses de flux de l'ordre de quelques pourcents.
La variation relative de flux pour un système de type Soleil-Jupiter est de 1%, et de 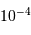 pour un système tel que Soleil-Terre.
pour un système tel que Soleil-Terre.
Sondage atmosphérique
Une information essentielle pourra également être apportée par cette méthode : la présence ou non d'une atmosphère autour de la planète, reliée à la pente de l'extinction du flux, progressive en présence d'une atmosphère. Cette détection est extrêmement importante, car on peut connaître la composition de cette atmosphère en comparant les mesures spectroscopiques de l'étoile avant et pendant le transit.
Il est en principe possible de rechercher des signes d'activités exobiologiques en détectant des composants gazeux dont l'abondance est un indice de la présence d'organismes vivants... mais hors de portée des moyens actuels.
Occultations
Animation reliant la courbe de lumière à l'évolution temporelle de la géométrie du système. L'inclinaison du plan orbital planétaire est un paramètre crucial.
La signature photométrique diffère selon que l'inclinaison est
très proche ou
voisine de 90 degrés, ou
trop éloignée.

Transit planétaire, avec une inclinaison proche de 90 degrés. La signature photométrique reste ténue. Le rapport des luminosités stellaire et planétaire est tel que l'occultation de la planète par l'étoile reste n'est pas observable.
Crédit :
ASM

Transit planétaire. L'inclinaison, voisine de 90 deg, ne conduit qu'à une occultation partielle, et donc une très faible signature photométrique.
Crédit :
ASM

Pas de transit planétaire, l'inclinaison différant trop de 90 deg. Aucune occultation, et donc aucune signature photométrique.
Crédit :
ASM
 Transit de HD 209458
Transit de HD 209458
Difficulté : ☆
Temps : 20 min
HD 209458 est une des nombreuses étoiles hébergeant une exoplanète. On cherche à caractériser le transit de cette dernière. Les notations sont les mêmes que celles des pages précédentes.
Question 1)
Retrouver l'expression de la diminution relative de luminosité 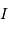 :
:
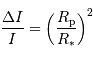
On suppose le flux (équivalent à une luminosité, ou puissance, surfacique) stellaire 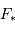 uniforme :
uniforme :
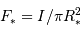 .
.
Estimer la différence de luminosité avec et sans éclipse, fonction de la
surface stellaire visible, variable, et du flux surfacique, fixe.
Question 3)
Calculer la masse volumique 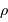 de l'exoplanète, sachant que sa masse
de l'exoplanète, sachant que sa masse 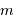 vaut
vaut 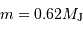 . Quelle remarque vous inspire ce résultat ?
. Quelle remarque vous inspire ce résultat ?

Fraction d'un champ stellaire observée par le satellite CoRoT. Au total, plusieurs milliers de cibles sont suivies simultanément.
Crédit :
CoRoT/CNES
Détecter et identifier un transit nécessite une grande précision photométrique, telle que l'apporte CoRoT, la première mission dédiée à ce thème de recherche.
Crédit :
CoRoT/CNES
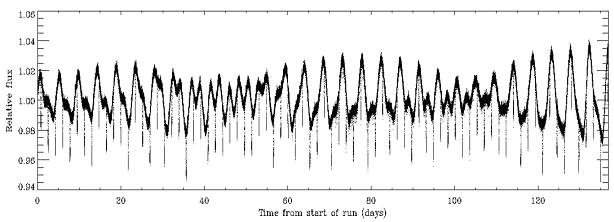
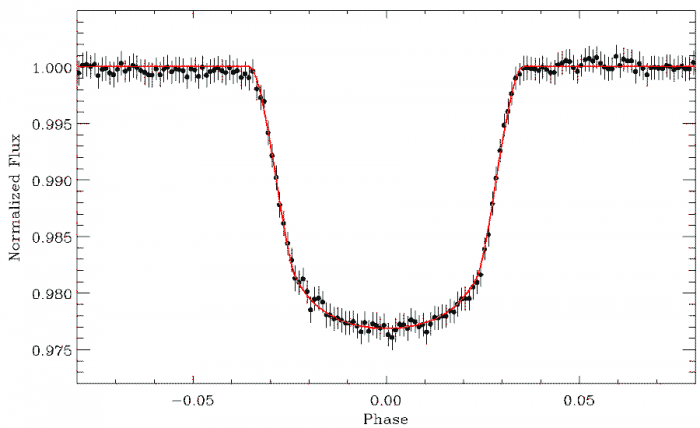
Les transits, ici événements très fins de profondeur relative 4%, se superposent à un flux stellaire éminemment variable.
Crédit :
CoRoT/CNES
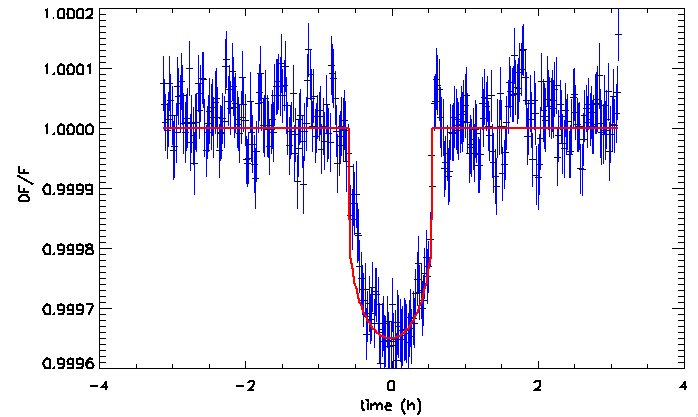
Transit profond de seulement 0.4% observé par CoRoT (planète CoRoT-Exo-7b, de rayon égal à 1.8 fois celui de la Terre).
Crédit :
CoRoT/CNES
Observer beaucoup d'étoiles
La probabilité de détection d'une planète étant faible, un programme de détection par transits doit nécessairement suivre simultanément un
grand nombre de cibles, ce que permet la photométrie.
Observer longtemps
Un transit seul n'apporte pas d'information, et peut être confondu avec un événement non planétaire. Les séquences d'observation de CoRoT durent 5 mois, et la répétition de trois événements est attendue.
Observer précisément
Distinguer un transit planétaire des multiples autres sources possibles de
variation du flux stellaire n'est pas toujours simple.
Les planètes les moins massives détectées, par transit et donc sans l'ambiguïté du facteur de projection 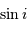 , ont été observées par le satellite CoRoT puis Kepler.
, ont été observées par le satellite CoRoT puis Kepler.
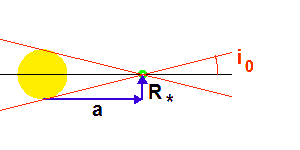
Le rayon planétaire étant négligé devant le rayon stellaire, l'angle séparant le plan orbital de l'axe de visée doit être inférieur à une valeur limite pour qu'il y ait occultation.
Crédit :
ASM
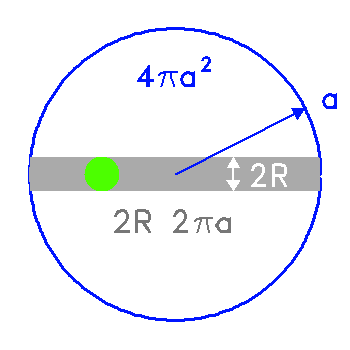
La probabilité de transit
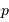
est obtenue par le rapport de l'aire balayée par la planète à l'aire de la sphère de rayon égal au demi-grand axe planétaire :
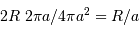
.
Crédit :
ASM
Précision photométrique
Le deuxième facteur limitant est photométrique. En effet, depuis le sol il est difficile d'obtenir une précision photométrique meilleure que 1 % (c'est-à-dire 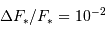 ) en raison de l'agitation atmosphérique. Les observations depuis l'espace, en revanche, permettent d'atteindre une précision aussi bonne que
) en raison de l'agitation atmosphérique. Les observations depuis l'espace, en revanche, permettent d'atteindre une précision aussi bonne que 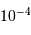 , et donc de détecter des planètes de type tellurique.
, et donc de détecter des planètes de type tellurique.
Limite de détection par la méthode des transits
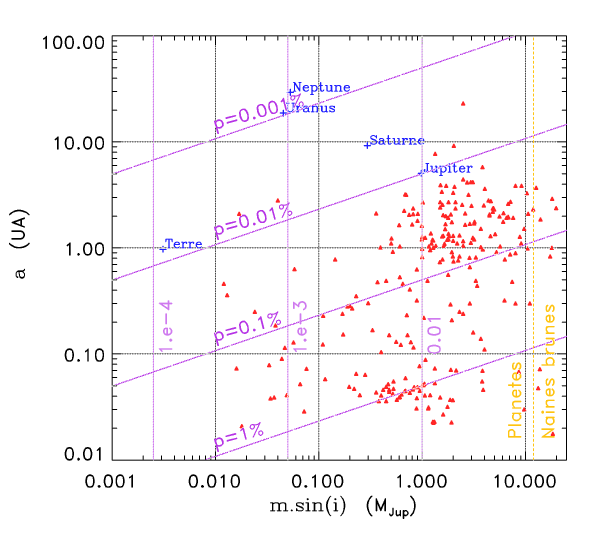
La détection des planètes les moins massives nécessite une
excellente précision photométrique. La probabilité de détection
décroît fortement avec l'évolution du demi-grand axe.
Crédit :
ASM
Observation de transits
Il s'ensuit que, pour être efficace, les projets de détection
d'exoplanètes par transit doivent observer un très grand nombre de
cibles, avec la meilleure précision
photométrique possible. De plus, pour éviter tout effet
stroboscopique, il faut observer continûment. L'espace est l'endroit idéal pour ceci, comme l’ont démontré les mission CoRoT et Kepler.
Confirmation des observations
Plusieurs artefacts observationnels peuvent imiter la signature
d'un transit planétaire. Les plus courants sont l'observation d'un
système stellaire double, ou d'une binaire à éclipses présente
dans le champ d'observation de l'étoile principale. Dans ces deux
cas, la baisse de flux peut être faible et confondue avec celle
d'une hypothétique planète. Une vérification a posteriori s'impose
pour déterminer les éventuels faux positifs, menée le plus souvent
en vélocimétrie Doppler, et parfois par imagerie en optique adaptative.
 Limitation de la méthode du transit
Limitation de la méthode du transit
Difficulté : ☆☆
Temps : 30 min
Avant les missions spatiales CoRoT et Kepler, peu de transits avaient été observés ; leur nombre a ensuite explosé. L'exercice se propose de déterminer la probabilité 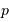 d'un tel événement, fonction du rayon de l'étoile
d'un tel événement, fonction du rayon de l'étoile 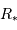 et du rayon orbital de la planète
et du rayon orbital de la planète 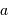 , et d'établir
, et d'établir
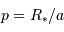 .
.

Crédit :
ASM
Question 1)
L'angle  de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum
de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum 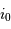 pour lequel une éclipse peut être observée, en fonction de
pour lequel une éclipse peut être observée, en fonction de 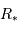 et
et 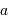 , en supposant le rayon planétaire négligeable.
, en supposant le rayon planétaire négligeable.
Faire un schéma, basé sur la figure de l'énoncé.
Question 2)
En vous aidant des propriétés de symétrie du système, déterminer de quelle(s) variable(s) dépend 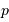 .
.
Question 3)
La probabilité 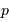 de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet
de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet 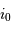 .
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet
.
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet 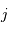 .
.
Définition de la mesure d'un angle solide (unité stéradian):
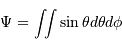
avec 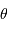 et
et 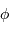 les angles d'Euler.
les angles d'Euler.
Dans le cas étudié, il y a symétrie de révolution autour de l'axe de
révolution du système.
Question 4)
Exprimer 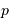 en fonction de
en fonction de 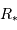 et
et 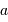 .
.
La probabilité 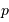 mesure la non-appartenance au cône précédemment
défini.
mesure la non-appartenance au cône précédemment
défini.
Question 5)
Application numérique pour le cas l'exoplanète 51 Peg.
Données : 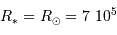 km, et
km, et 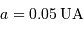 .
.
Astrométrie
Il est possible de détecter le mouvement de l'étoile perpendiculairement à la ligne de visée, c'est-à-dire sur
la sphère céleste, et d'en déduire les caractéristiques de
la planète et de son orbite.
Déplacement astrométrique du Soleil dû à Jupiter
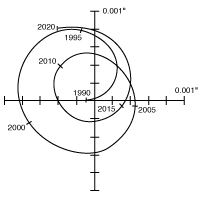
Déplacement du Soleil sous l'effet des mouvements planétaires (Jupiter et Saturne principalement), vu à une distance de 10 pc.
L'amplitude de ce déplacement est de 500 microsecondes d'arc (
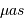
). Le déplacement dû à la Terre présenterait une amplitude de
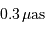
à la même distance.
Crédit :
NASA
 Objectifs
Objectifs
L'astrométrie s'intéresse à la position des astres sur la sphère céleste. Cette technique peut être sensible à la modulation de la position d'une étoile légèrement perturbée par la présence d'une planète.
Astrométrie
Il est possible de détecter le mouvement de l'étoile
perpendiculairement à la ligne de visée, c'est-à-dire sur
la sphère céleste, et d'en déduire les caractéristiques de la
planète et de son orbite.
On se limite au cas d'une orbite
circulaire, mais bien sûr cette méthode s'applique aussi à la détection
de planètes sur des orbites elliptiques. Le mouvement de l'étoile
projeté sur le plan du ciel, c'est-à-dire sur le plan perpendiculaire à
la ligne de visée, est une ellipse de demi-grand axe 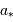 . Comme
la distance
. Comme
la distance 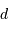 à l'étoile est grande devant
à l'étoile est grande devant 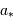 , la déviation
angulaire correspondante est
, la déviation
angulaire correspondante est 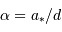 , ou encore :
, ou encore :
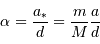
avec 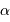 exprimé
seconde d'arc,
exprimé
seconde d'arc, 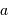 le
rayon de l'orbite de la planète (en UA) et
le
rayon de l'orbite de la planète (en UA) et 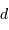 la distance
Soleil-étoile. La masse
la distance
Soleil-étoile. La masse 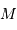 de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire
de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire 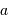 de la périodicité du
mouvement, et donc la masse de la planète
de la périodicité du
mouvement, et donc la masse de la planète 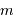 de la mesure de
de la mesure de 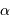 .
.
En pratique, la variation de la position d'un astre sur la sphère céleste n'est pas mesurée de façon absolue, mais différentiellement par rapport à un objet du champ, angulairement proche mais très lointain en distance, dont la position reste fixe.

Diagramme masse-distance, montrant les performances de la détection astrométrique, fonction de la précision de mesure (respectivement 10, 1 et 0.05 milliseconde d'arc). Les triangles rouges marquent les exoplanètes déjà détectées.
Crédit :
ASM
Systèmes pouvant être détectés par cette méthode
Les mesures faites à l'heure actuelle depuis le sol ont une précision d'une milliseconde d'arc (mas), et devraient atteindre 10 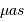 dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des zones habitables (i.e.
dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des zones habitables (i.e. 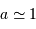 UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
 Petite révision sur la formation d'image
Petite révision sur la formation d'image
Difficulté : ☆
Temps : 30 min
Un astronome extraterrestre regarde notre système solaire à une distance de 10 AL de notre Soleil. On souhaite dimensionner le télescope dont il aurait besoin pour distinguer Jupiter autour du Soleil.
On suppose le pouvoir de résolution de l'appareil limité par la seule diffraction : la tache de diffraction vaut angulairement 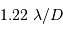 radian, où
radian, où 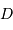 est le diamètre du télescope.
est le diamètre du télescope.
Pour la suite, on prendra 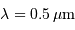 .
.
Question 1)
Déterminer la distance angulaire maximale 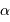 entre le soleil et Jupiter
entre le soleil et Jupiter 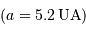 .
.
Rappel : 1 AL = 63 000 UA.
Question 2)
Déterminer 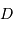 , le diamètre minimum du collecteur nécessaire.
, le diamètre minimum du collecteur nécessaire.
Un objet est résolu spatialement si sa taille angulaire est supérieure à la taille de la tache de diffraction.
Question 3)
Cela est-il suffisant?
S'intéresser au rapport des flux respectifs du Soleil et de Jupiter.
 Astrométrie
Astrométrie
Difficulté : ☆☆
Temps : 40 min
Le mouvement apparent d'une étoile voisine du soleil, corrigé de la parallaxe annuelle, est a priori rectiligne uniforme en l'absence de perturbation. On cherche à quantifier l'influence d'un compagnon planétaire.
On observe un système binaire composé d'une étoile de masse 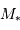 et d'une planète de masse
et d'une planète de masse 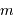 ( avec
( avec 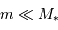 ) de rayon orbital
) de rayon orbital 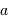 .
.
Question 1)
Justifier le caractère rectiligne et uniforme du mouvement stellaire, en l'absence de compagnon.
Un mouvement rectiligne uniforme est un mouvement non perturbé par quoi
que ce soit.
Question 2)
Exprimer l'amplitude de la perturbation angulaire maximale 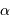 de la position de l'étoile, située à une distance
de la position de l'étoile, située à une distance 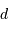 du Soleil.
du Soleil.
Question 3)
Retrouver l'expression :
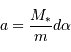
Définir le centre de masse.
Etablir 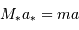
Question 4)
A quelle distance 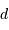 se situe l'étoile si sa parallaxe annuelle vaut 0.1" ?
se situe l'étoile si sa parallaxe annuelle vaut 0.1" ?
Le parsec est défini comme étant la distance d'une étoile ayant une parallaxe de 1".
Question 5)
Quelles planètes du système solaire, supposé vu à 10 pc, pourrait-on détecter, si l'on est capable de mesurer des variations de position à 0.01" ou 0.001" près ?
Compléter le diagramme ci-joint, positionnant les objets en fonction de leur masse 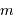 et de leur demi-grand axe
et de leur demi-grand axe 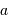 , en définissant la frontière qui marque la limite de détectabilité
(rappel
, en définissant la frontière qui marque la limite de détectabilité
(rappel 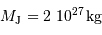 ).
).
Diagramme a-msin i

Crédit :
ASM
Traduire la relation établie précédemment entre 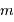 et
et 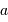 , et l'exprimer dans le système d'unités (UA, masse de Jupiter).
, et l'exprimer dans le système d'unités (UA, masse de Jupiter).
Question 6)
A terme, on imagine être capable de mesurer des écarts de position 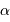 avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme
avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme 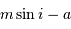 , pour un système à 10 pc et
, pour un système à 10 pc et 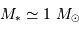 .
.
C'est la même chose que précédemment. Seule l'application numérique change.
Question 7)
Quelles planètes du système solaire deviennent ainsi détectables ?
Si les graphes ont été dressés, la réponse n'est plus qu'une question de domaine.

GQ Lupi A et son compagnon froid b.
Crédit :
ESO
Une exoplanète attrapée au vol
Alors que les méthodes de détection par transit et vélocimétrie Doppler donnent de plus en plus de résultats, plusieurs objets ont été détectés en imagerie directe. Cette population comprend des planètes flottantes ou des naines brunes sans qu'il soit facile/possible de faire la différence.
Un des premier objets décourts est GQ Lupi b qui orbite autour de l'étoile QG Lupi A. A une distance d'environ 100 UA, 270 fois moins brillant que GQ Lupi A, GQ Lupi b a une masse entre une et 30 fois la masse du Jupiter. Ni les observations, ni leur modélisation ne permettent de conclure à l'heure actuelle sur la nature exacte de cet objet.
Observables
L'examen des différentes méthodes de détection montre qu'elles ne donnent pas accès aux mêmes observables, et qu'elles ne subissent pas les mêmes biais observationnels. Ces différentes méthodes (et il y en a d'autres) sont donc complémentaires : le sujet astrophysique est d'ailleurs suffisamment important pour motiver de nombreux projets observationnels, au sol ou spatiaux.
Performance de détection
La méthode des vitesses radiales favorise la détection des planètes massives et proches de l'étoile, alors que l'astrométrie favorise les planètes massives et de grands rayons orbitaux. Là encore, les méthodes apparaissent complémentaires.
Planètes détectables
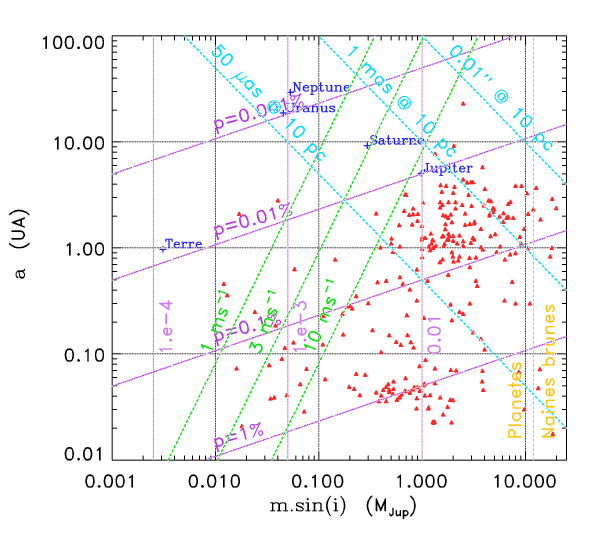
Les triangles rouges marquent les exoplanètes déjà détectées. Les limites en violet concernent la détection par transit, en vert par mesure Doppler, en bleu par astrométrie.
Crédit :
ASM
Détections
L'existence de spectromètres performants et stables a favorisé jusqu'à ce jour la détection par vitesse radiale. L'accroissement
du nombre de projets de recherche par transit fait augmenter le nombre de telles détections.
Nombre d'exoplanètes détectées par les différentes méthodes (octobre 2018)
| Méthode | Planètes | Systèmes planétaires |
|---|
| Vitesse radiale | 771 | 574 |
| Transit | 2847 | 2127 |
| Microlentille | 82 | 79 |
| Imagerie | 100 | 82 |
| Chronométrage | 29 | 23 |
 Discours de la méthode
Discours de la méthode
Difficulté : ☆
Temps : 30 min
Question 1)
Distinguer les différentes techniques en fonction de leurs biais respectifs portant sur 1) la masse de la planète 2) son demi-grand axe 3) l'inclinaison orbitale.
[3 points]
Question 2)
Quelle technique est à votre avis la plus facilement spatialisable ?
[1 points]
L'étude des exoplanètes, champ de l'astrophysique en pleine effervescence, appartient de plain-pied à ces domaines scientifiques qui éveillent en chacun un intérêt qui n'est pas que purement scientifique.
De nombreux grands projets sont développés pour mieux détecter ou, plus difficile, voir directement les exoplanètes (ce qui demande alors d'éteindre la lumière stellaire avec une excellente efficacité, et motive des projets instrumentaux alliant interférométrie et coronographie).
Deux grands projets spatiaux ont apporté une moisson importante d'observations par transits. Le suivi au sol des candidats exoplanétaires doit se poursuivre avec des observations au sol pour vérifier qu'il s'agit bien de planètes vues en transit et non d'autres objets.
Différents observatoires ont mené des campagnes intensives de recherche d'exoplanètes par vitesse radiale :
- Spectromètre HARPS au 3.6-m de l'ESO au Chili,
- Spectomètre équivalent télescope Keck,
- HARPS nord, clone de l'instrument HARPS sud.
Lister tous les projets en cours et oeuvrant prochainement est une tâche ardue tant la discipline progresse rapidement. On note :
- Projet SPHERE pour imager avec un grand contraste de l'environnement stellaire,
- Mission spatiale TESS de la NASA pour la recherche d'exoterres,
- Caractérisation des atmosphères exoplanétaires avec la mission JWST de la NASA,
- Mission spatiale PLATO de l'ESA pour la caractérisation des systèmes étoiles-planètes
- ...
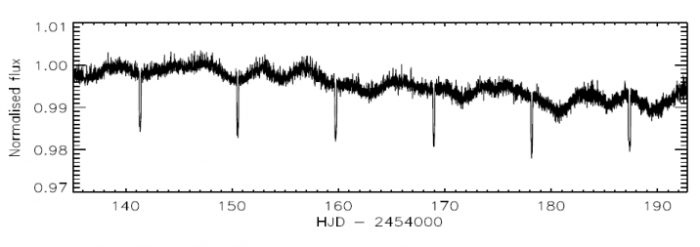
Courbe de transit d'une exoplanète détectée par la mission CoRoT.
Crédit :
CNES
Une technique prometteuse pour l'observation directe d'une planète est l'interférométrie annulante, où l'étoile est éteinte par interférométrie (ou là) destructive, quand la planète apparaît en revanche en opposition de phase.
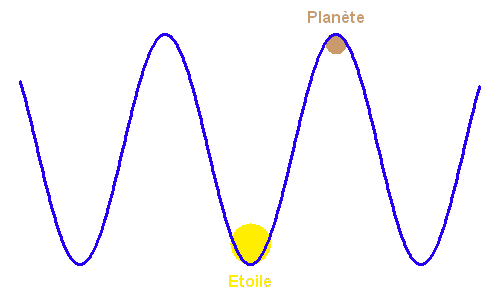
Le flux de l'étoile, positionnée sur une frange d'interférence destructive, apparaît éteint par rapport à celui de la planète.
Crédit :
ASM
- Question 1
Aide :
Revoir le cours !
Solution :
C'est l'angle entre la normale au plan orbital et l'axe de visée.
- Question 2
Aide :
Faire un schéma. A quelle condition sur le plan orbital a-t-on
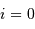 ou
ou 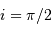 ?
?
Aide :
Y'a-t-il autant de plans avec 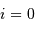 ou
ou 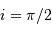 ?
?
Solution :
Il y a un seul plan perpendiculaire à la ligne de visée (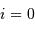 ),
mais une infinité qui la contiennent (
),
mais une infinité qui la contiennent (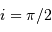 ).
).
- Question 3
Aide :
Il faut estimer toutes les directions  , et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture
, et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture  et
et 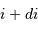 .
.
Solution :
La probabilité est mesurée par l'ouverture du cône de demi-angle
au sommet  . Son angle solide est
. Son angle solide est 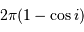 . Le rayon
d'ouverture du cône, proportionnel à
. Le rayon
d'ouverture du cône, proportionnel à 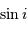 , permet d'estimer
comment la probabilité cherchée varie avec
, permet d'estimer
comment la probabilité cherchée varie avec  .
.
La différentielle de l'angle solide aboutit au même résultat.
On retrouve intuitivement que le cas 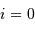 est peu probable.
est peu probable.
- Question 4
Aide :
La définition d'une valeur moyenne conduit à :
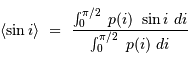
avec 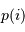 la loi de probabilité associée.
la loi de probabilité associée.
Solution :
Avec 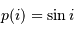 la loi de probabilité, la définition de la valeur moyenne de la variable
la loi de probabilité, la définition de la valeur moyenne de la variable 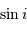 conduit à :
conduit à :
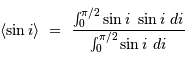
Le numérateur vaut 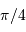 , car il est égal à la moyenne sur le même intervalle, de largeur
, car il est égal à la moyenne sur le même intervalle, de largeur 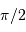 , de
, de 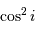 , et que la somme des carrés des sinus et cosinus vaut 1.
, et que la somme des carrés des sinus et cosinus vaut 1.
Le dénominateur vaut 1.
La valeur moyenne est donc :
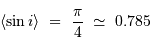
- Question 1
Aide :
Définir la position du barycentre.
Aide :
Le barycentre 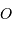 du système obéit à:
du système obéit à:
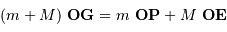
Différencier cette relation pour obtenir l'information en vitesse.
Solution :
Par définition du barycentre, 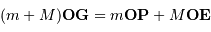 , avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
, avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
Dans le référentiel du centre de masse :
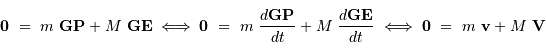
- Question 2
Aide :
Commencer par faire le schéma, pour estimer 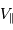 dans les cas
dans les cas  nul ou angle droit.
nul ou angle droit.
Solution :
La relation entre 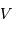 , le module de
, le module de 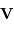 et
et 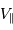 s'écrit :
s'écrit :
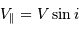
- Question 3
Solution :
La troisième loi de Kepler appliquée à la planète s'écrit :
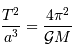
Par ailleurs, la définition du périmètre de l'orbite donne le demi-grand axe en fonction de la période et de la vitesse :
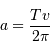
On en déduit :
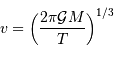
Et on en tire :
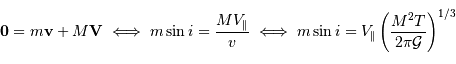
- Question 4
Aide :
Reformulation de la question :
quelle grandeur non directement observable peut finalement être ainsi mesurée ?
Solution :
A partir des observables, 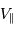 et
et 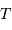 , et de la masse stellaire
, et de la masse stellaire 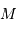 déduite des modèles stellaires, on a accès, au facteur
déduite des modèles stellaires, on a accès, au facteur 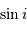 près,
à la masse de la planète... inaccessible par ailleurs.
près,
à la masse de la planète... inaccessible par ailleurs.
- Question 5
Aide :
Commencer par réécrire la 3ème loi de Kepler.
Solution :
La 3ème loi de Kepler... toujours elle, permet d'écrire :
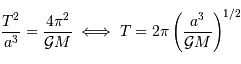
![\Rightarrow m\sin i = V _{\mathrm{\parallel}}\left[{M^{2}\over 2\pi{\cal G}}2\pi\left({a^{3}\over {\cal G}M}\right)^{1/2}\right]^{1/3} = V _{\mathrm{\parallel}}\left({Ma\over {\cal G}}\right)^{1/2}](../pages_exoplanete/equations_vitesse-radiale-extrasolaire/equation105.png)
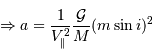
- Question 1
Aide :
Faire un schéma, basé sur la figure de l'énoncé.
Solution :
Le triangle étoile-diamètre planétaire permet d'écrire, le rayon de la planète étant supposé très petit :
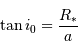
- Question 2
Solution :
Le problème est à symétrie de révolution. La position de la ligne de visée autour de l'étoile ne joue aucun rôle, la seule variable pertinente est l'angle  .
.
- Question 3
Aide :
Définition de la mesure d'un angle solide (unité stéradian):
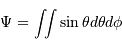
avec 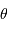 et
et 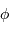 les angles d'Euler.
les angles d'Euler.
Dans le cas étudié, il y a symétrie de révolution autour de l'axe de
révolution du système.
Solution :
Mesure de l'angle solide d'un hémisphère :
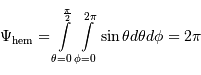
Mesure de l'angle solide d'un cône de demi-angle au sommet 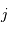 :
:
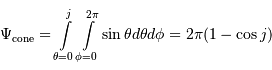
- Question 4
Aide :
La probabilité 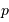 mesure la non-appartenance au cône précédemment
défini.
mesure la non-appartenance au cône précédemment
défini.
Solution :
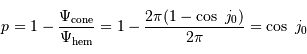
Les angles 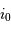 et
et 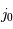 sont complémentaires :
sont complémentaires : 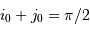 . On en tire :
. On en tire :
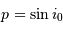
Comme de plus le rayon stellaire est petit devant le rayon de la trajectoire de l'exoplanète, l'angle 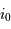 est petit, et l'on peut le confondre avec son sinus ou sa tangente.
est petit, et l'on peut le confondre avec son sinus ou sa tangente.
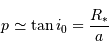
- Question 5
Solution :
Application numérique directe :
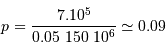
- Question 1
Aide :
Un mouvement rectiligne uniforme est un mouvement non perturbé par quoi
que ce soit.
Solution :
L'étoile observée est isolée, et donc elle obéit au principe de Galilée.
- Question 2
Aide :
Faire un schéma.
Solution :
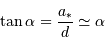
avec 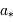 étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
- Question 3
Aide :
Définir le centre de masse.
Aide :
Etablir 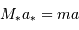
Solution :
D'après la définition du barycentre 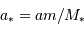 . Alors :
. Alors :
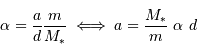
- Question 4
Aide :
Le parsec est défini comme étant la distance d'une étoile ayant une parallaxe de 1".
Solution :
Une étoile ayant une parallaxe de 0.1" est, par définition, à 10 pc.
- Question 5
Aide :
Traduire la relation établie précédemment entre 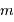 et
et 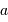 , et l'exprimer dans le système d'unités (UA, masse de Jupiter).
, et l'exprimer dans le système d'unités (UA, masse de Jupiter).
Aide :
Le produit 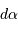 , avec
, avec 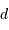 en pc et
en pc et 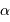 en seconde d'arc, donne directement une distance en UA.
en seconde d'arc, donne directement une distance en UA.
Solution :
On traite l'équation :
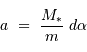
en tenant en compte que le produit 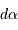 , avec
, avec 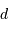 en pc et
en pc et 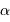 en " donne une distance en UA directement, par définition. En prenant
en " donne une distance en UA directement, par définition. En prenant 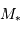 directement en masse jovienne (
directement en masse jovienne (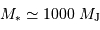 ), on obtient dans le système d'unités (UA,
), on obtient dans le système d'unités (UA, 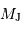 ), pour
), pour 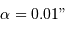 :
:
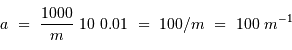
En échelle logarithmique, cette équation définit une droite de pente -1 ; elle passe par le point 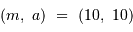 .
.
Pour une précision de 1 mas (1 millième de seconde d'arc), la courbe obtenue est définie par :
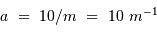
Parallèle à la précédente, elle contient le point
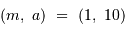 .
.
Comme le montre le diagramme ci-joint, aucune planète du système solaire n'est ainsi détectable à ce niveau de précision astrométrique.
Diagramme a-msin i
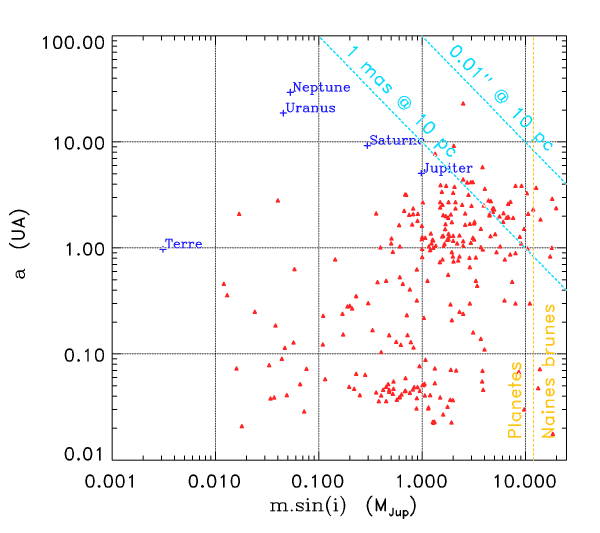
Crédit :
ASM
- Question 6
Aide :
C'est la même chose que précédemment. Seule l'application numérique change.
Solution :
Par rapport au cas précédent, le gain en précision d'un facteur 20 déplace la
limite vers les faibles masses, passant p.ex. par le point
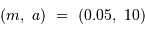 .
.
Planètes détectables
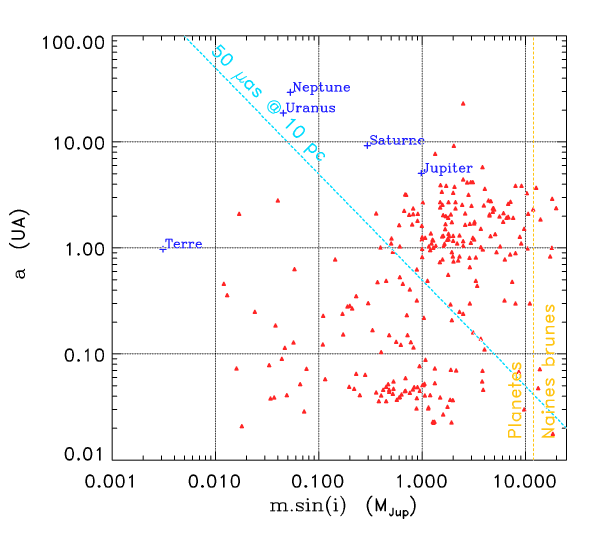
Crédit :
ASM
- Question 7
Aide :
Si les graphes ont été dressés, la réponse n'est plus qu'une question de domaine.
Solution :
Planètes détectables : Jupiter, Saturne, Uranus et Neptune. Seules les planètes géantes sont donc détectables, pas la Terre !
Planètes détectables
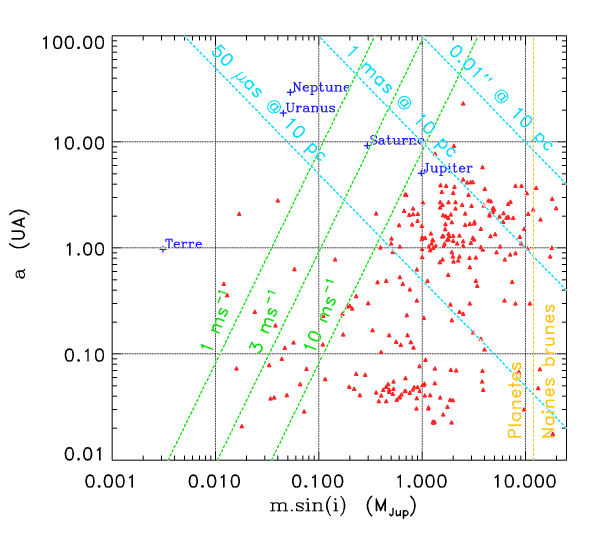
Crédit :
ASM

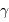 Ceph,
Ceph, 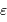 Eri)... En 1989, Latham et ses collègues identifièrent un compagnon d'environ dix fois la masse de Jupiter, autour de HD 114762. Mais ces auteurs évoquèrent alors la détection d'une
Eri)... En 1989, Latham et ses collègues identifièrent un compagnon d'environ dix fois la masse de Jupiter, autour de HD 114762. Mais ces auteurs évoquèrent alors la détection d'une 


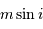 , l'inclinaison
, l'inclinaison  n'étant pas une
n'étant pas une 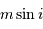 plus petits que la masse de Jupiter, et la distribution totale jusqu'à 15 masses de Jupiter.
plus petits que la masse de Jupiter, et la distribution totale jusqu'à 15 masses de Jupiter.

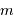 , mais de
, mais de 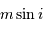 .
.








 est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.

 est nul. Pas de mouvement détectable.
est nul. Pas de mouvement détectable.

 vaut
vaut 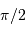 .
.
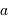 .
.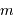 la masse de la planète, et
la masse de la planète, et 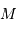 celle de l'étoile.
celle de l'étoile.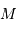 . Mais une variable reste inconnue :
. Mais une variable reste inconnue : 
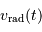 .
Ce type d'observation spectrométrique fournit deux
.
Ce type d'observation spectrométrique fournit deux 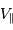 , parallèle à l'axe de visée (car
, parallèle à l'axe de visée (car 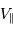 ).
).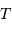 de rotation du système.
de rotation du système.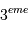 loi de Kepler appliquée au couple planète-étoile relie le rayon de l'orbite à la période de rotation :
loi de Kepler appliquée au couple planète-étoile relie le rayon de l'orbite à la période de rotation :
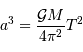
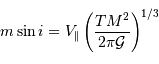
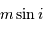 est la masse de la planète
est la masse de la planète 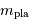 affectée du facteur
géométrique
affectée du facteur
géométrique 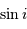 , inconnu.
Le calcul complet est proposé en
, inconnu.
Le calcul complet est proposé en  dépend de l'ouverture du cône de demi-angle au sommet
dépend de l'ouverture du cône de demi-angle au sommet  : elle vaut
: elle vaut 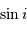 .
La probabilité de voir un système
.
La probabilité de voir un système 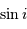 vaut
vaut 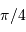 ;
ce calcul est proposé en
;
ce calcul est proposé en 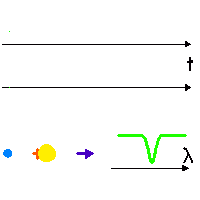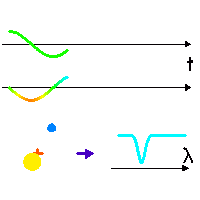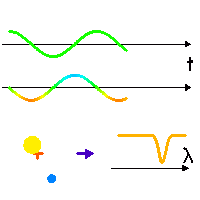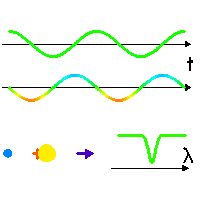
 est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
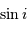 qui intervient dans la détermination de la masse
qui intervient dans la détermination de la masse 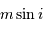 .
.
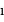 .
.
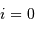 ou bien
ou bien
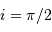 ?
?
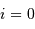 ou
ou 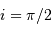 ?
?
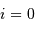 ou
ou 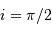 ?
?
 est proportionnelle à
est proportionnelle à 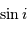 .
.
 , et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture
, et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture  et
et 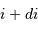 .
.
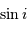 .
.
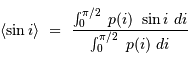
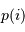 la loi de probabilité associée.
la loi de probabilité associée.
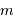 , en orbite circulaire autour d'une étoile de masse
, en orbite circulaire autour d'une étoile de masse 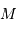 . La composante de vitesse de l'étoile
. La composante de vitesse de l'étoile 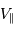 , parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse
, parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse 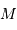 de l'étoile est supposée connue.
de l'étoile est supposée connue.

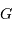 ,
, 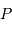 et
et 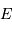 les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
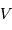 de l'étoile et
de l'étoile et 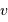 de la planète satisfont à la relation :
de la planète satisfont à la relation :
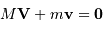
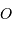 du système obéit à:
du système obéit à:
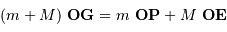
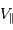 au module
au module 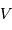 de la vitesse de l'étoile et à l'angle
de la vitesse de l'étoile et à l'angle  entre l'axe de visée et la normale au plan de rotation du système. Faire un schéma.
entre l'axe de visée et la normale au plan de rotation du système. Faire un schéma.
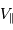 dans les cas
dans les cas  nul ou angle droit.
nul ou angle droit.
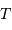 et
et 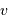 , puis montrer que la masse de la planète s'exprime en fonction des
, puis montrer que la masse de la planète s'exprime en fonction des 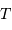 et
et 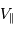 par :
par :
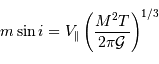
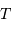 la variable
la variable 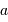 , et montrer que l'on aboutit à l'égalité suivante entre les variables
, et montrer que l'on aboutit à l'égalité suivante entre les variables 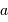 et
et 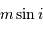 :
:
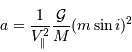
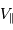 . On obtient une série temporelle de vitesse radiale, qui
semble présenter des variations répétitives.
. On obtient une série temporelle de vitesse radiale, qui
semble présenter des variations répétitives.





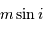 , car l'angle sous lequel
le système est observé,
, car l'angle sous lequel
le système est observé,  , reste en général inconnu. Cela a bien sûr
été un obstacle à l'interprétation du premier cas qui annonçait la
découverte d'une d'exoplanète. Cependant, une centaine d'objets avec
une masse
, reste en général inconnu. Cela a bien sûr
été un obstacle à l'interprétation du premier cas qui annonçait la
découverte d'une d'exoplanète. Cependant, une centaine d'objets avec
une masse 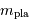 les rangeant dans la catégorie des planètes ont
été détectés, et, statistiquement, la masse réelle de la plupart
d'entre eux est bien une masse planétaire.
Cette méthode est biaisée, car elle favorise la détection des planètes
massives et relativement proches de leur étoile. En effet :
les rangeant dans la catégorie des planètes ont
été détectés, et, statistiquement, la masse réelle de la plupart
d'entre eux est bien une masse planétaire.
Cette méthode est biaisée, car elle favorise la détection des planètes
massives et relativement proches de leur étoile. En effet :
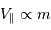 .
.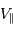 important, car
important, car 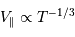 .
.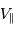 sous la forme :
sous la forme :
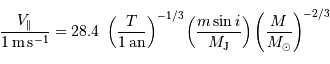
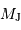 et
et 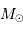 sont, respectivement, les masses de Jupiter et du Soleil.
sont, respectivement, les masses de Jupiter et du Soleil.
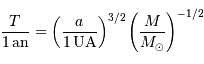
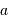 est exprimé en unité astronomique.
est exprimé en unité astronomique.

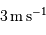 . Il faut également observer les étoiles longtemps pour avoir accès aux plus longues périodes. Les exoplanètes les moins massives n'ont pas été détectées par mesure Doppler, mais par la méthode des
. Il faut également observer les étoiles longtemps pour avoir accès aux plus longues périodes. Les exoplanètes les moins massives n'ont pas été détectées par mesure Doppler, mais par la méthode des 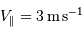 . Cela ne signifie qu'une planète similaire à la Terre autour d'une étoile de type solaire induisant une modulation de vitesse
. Cela ne signifie qu'une planète similaire à la Terre autour d'une étoile de type solaire induisant une modulation de vitesse 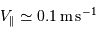 reste largement indétectable.
reste largement indétectable.
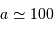 UA. Cependant, la période de révolution d'une telle planète est de 1000 ans, et il est donc exclu de l'observer ! Notons que la même planète située à la distance de Jupiter
UA. Cependant, la période de révolution d'une telle planète est de 1000 ans, et il est donc exclu de l'observer ! Notons que la même planète située à la distance de Jupiter 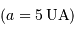 entraîne
entraîne 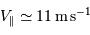 , ce qui est largement observable.
, ce qui est largement observable.
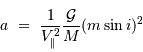
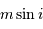 - rayon orbital
- rayon orbital 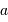 ) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse
) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse 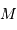 de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.
de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.

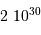
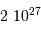
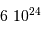
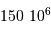 km
km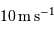 . En déduire la relation numérique entre les variables
. En déduire la relation numérique entre les variables 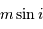 et
et 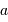 correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et
correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et 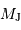 .
.
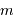 , et l'unité astronomique pour
, et l'unité astronomique pour 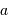 .
Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de
.
Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de 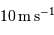 ) ?
) ?
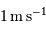 .
.





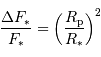
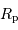 est le rayon de la planète et
est le rayon de la planète et 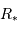 celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en
celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en 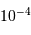 pour un système tel que Soleil-Terre.
pour un système tel que Soleil-Terre.
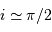 . La masse
. La masse 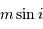 est donc dans ce cas égale à la masse réelle
est donc dans ce cas égale à la masse réelle 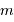 . Le transit permet également de déterminer le rayon de la planète, le rayon de l'étoile étant estimé par une autre méthode.
. Le transit permet également de déterminer le rayon de la planète, le rayon de l'étoile étant estimé par une autre méthode.


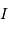 :
:
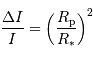
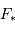 uniforme :
uniforme :
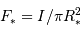 .
.
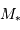
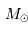
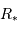
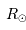
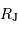
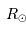

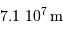
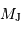
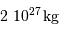
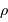 de l'exoplanète, sachant que sa masse
de l'exoplanète, sachant que sa masse 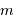 vaut
vaut 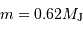 . Quelle remarque vous inspire ce résultat ?
. Quelle remarque vous inspire ce résultat ?




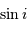 , ont été observées par le satellite
, ont été observées par le satellite 

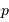 est obtenue par le rapport de l'aire balayée par la planète à l'aire de la sphère de rayon égal au demi-grand axe planétaire :
est obtenue par le rapport de l'aire balayée par la planète à l'aire de la sphère de rayon égal au demi-grand axe planétaire : 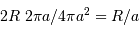 .
.
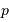 d'un tel événement vaut
d'un tel événement vaut 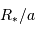 ,
, 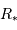 étant le rayon stellaire, et
étant le rayon stellaire, et 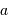 le demi-grand axe de l'orbite planétaire. Ce résultat est démontré par un calcul complet en
le demi-grand axe de l'orbite planétaire. Ce résultat est démontré par un calcul complet en 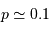 pour
pour 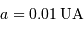 , c'est-à-dire pour les planètes détectées à ce jour qui sont sur les orbites les plus serrées. Cette probabilité décroît avec l'augmentation du demi-grand axe.
, c'est-à-dire pour les planètes détectées à ce jour qui sont sur les orbites les plus serrées. Cette probabilité décroît avec l'augmentation du demi-grand axe.
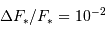 ) en raison de l'
) en raison de l'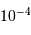 , et donc de détecter des planètes de type
, et donc de détecter des planètes de type 
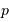 d'un tel événement, fonction du rayon de l'étoile
d'un tel événement, fonction du rayon de l'étoile 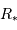 et du rayon orbital de la planète
et du rayon orbital de la planète 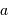 , et d'établir
, et d'établir 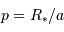 .
. de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum
de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum 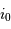 pour lequel une éclipse peut être observée, en fonction de
pour lequel une éclipse peut être observée, en fonction de 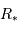 et
et 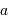 , en supposant le rayon planétaire négligeable.
, en supposant le rayon planétaire négligeable.
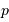 .
.
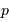 de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet
de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet 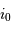 .
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet
.
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet 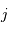 .
.
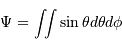
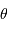 et
et 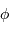 les angles d'Euler.
les angles d'Euler.
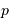 en fonction de
en fonction de 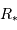 et
et 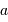 .
.
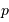 mesure la non-appartenance au cône précédemment
défini.
mesure la non-appartenance au cône précédemment
défini.
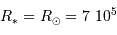 km, et
km, et 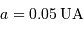 .
.

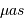 ). Le déplacement dû à la Terre présenterait une amplitude de
). Le déplacement dû à la Terre présenterait une amplitude de 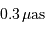 à la même distance.
à la même distance.
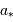 . Comme
la distance
. Comme
la distance 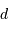 à l'étoile est grande devant
à l'étoile est grande devant 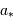 , la déviation
angulaire correspondante est
, la déviation
angulaire correspondante est 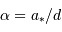 , ou encore :
, ou encore :
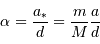
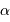 exprimé
seconde d'arc,
exprimé
seconde d'arc, 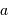 le
rayon de l'orbite de la planète (en UA) et
le
rayon de l'orbite de la planète (en UA) et 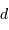 la distance
Soleil-étoile. La masse
la distance
Soleil-étoile. La masse 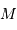 de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire
de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire 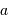 de la périodicité du
mouvement, et donc la masse de la planète
de la périodicité du
mouvement, et donc la masse de la planète 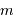 de la mesure de
de la mesure de 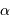 .
.

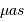 dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des
dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des 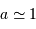 UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
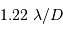 radian, où
radian, où 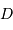 est le diamètre du télescope.
est le diamètre du télescope.
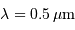 .
.
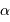 entre le soleil et Jupiter
entre le soleil et Jupiter 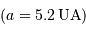 .
.
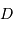 , le diamètre minimum du collecteur nécessaire.
, le diamètre minimum du collecteur nécessaire.
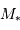 et d'une planète de masse
et d'une planète de masse 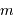 ( avec
( avec 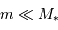 ) de rayon orbital
) de rayon orbital 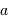 .
.
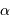 de la position de l'étoile, située à une distance
de la position de l'étoile, située à une distance 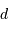 du Soleil.
du Soleil.
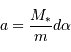
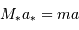
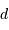 se situe l'étoile si sa
se situe l'étoile si sa 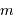 et de leur demi-grand axe
et de leur demi-grand axe 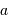 , en définissant la frontière qui marque la limite de détectabilité
(rappel
, en définissant la frontière qui marque la limite de détectabilité
(rappel 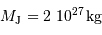 ).
).
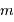 et
et 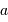 , et l'exprimer dans le système d'unités (UA, masse de Jupiter).
, et l'exprimer dans le système d'unités (UA, masse de Jupiter).
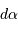 , avec
, avec 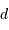 en pc et
en pc et 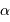 en seconde d'arc, donne directement une distance en UA.
en seconde d'arc, donne directement une distance en UA.
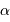 avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme
avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme 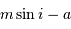 , pour un système à 10 pc et
, pour un système à 10 pc et 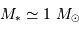 .
.




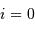 ),
mais une infinité qui la contiennent (
),
mais une infinité qui la contiennent (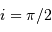 ).
).
 . Son angle solide est
. Son angle solide est 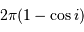 . Le rayon
d'ouverture du cône, proportionnel à
. Le rayon
d'ouverture du cône, proportionnel à 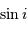 , permet d'estimer
comment la probabilité cherchée varie avec
, permet d'estimer
comment la probabilité cherchée varie avec  .
.
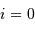 est peu probable.
est peu probable.
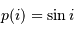 la loi de probabilité, la définition de la valeur moyenne de la variable
la loi de probabilité, la définition de la valeur moyenne de la variable 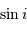 conduit à :
conduit à :
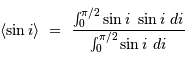
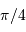 , car il est égal à la moyenne sur le même intervalle, de largeur
, car il est égal à la moyenne sur le même intervalle, de largeur 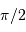 , de
, de 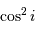 , et que la somme des carrés des sinus et cosinus vaut 1.
, et que la somme des carrés des sinus et cosinus vaut 1.
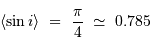
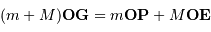 , avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
, avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
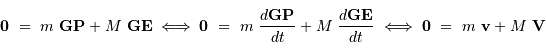
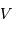 , le module de
, le module de 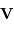 et
et 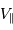 s'écrit :
s'écrit :
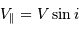
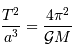
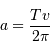
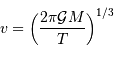
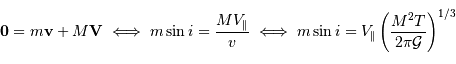
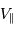 et
et 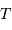 , et de la masse stellaire
, et de la masse stellaire 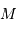 déduite des modèles stellaires, on a accès, au facteur
déduite des modèles stellaires, on a accès, au facteur 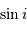 près,
à la masse de la planète... inaccessible par ailleurs.
près,
à la masse de la planète... inaccessible par ailleurs.
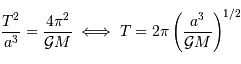
![\Rightarrow m\sin i = V _{\mathrm{\parallel}}\left[{M^{2}\over 2\pi{\cal G}}2\pi\left({a^{3}\over {\cal G}M}\right)^{1/2}\right]^{1/3} = V _{\mathrm{\parallel}}\left({Ma\over {\cal G}}\right)^{1/2}](../pages_exoplanete/equations_vitesse-radiale-extrasolaire/equation105.png)
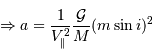
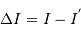 avec
avec 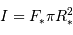 , et
, et 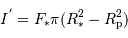 . Donc :
. Donc :
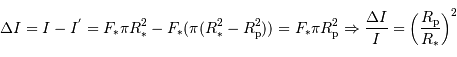
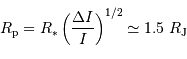
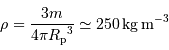
 ). C'est une géante gazeuse. Et si l'on trouvait un océan suffisamment grand, la planète y flotterait ...
). C'est une géante gazeuse. Et si l'on trouvait un océan suffisamment grand, la planète y flotterait ...
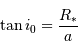
 .
.
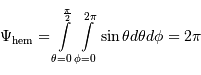
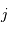 :
:
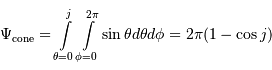
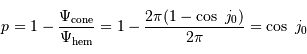
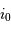 et
et 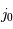 sont complémentaires :
sont complémentaires : 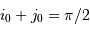 . On en tire :
. On en tire :
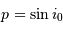
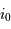 est petit, et l'on peut le confondre avec son sinus ou sa tangente.
est petit, et l'on peut le confondre avec son sinus ou sa tangente.
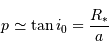
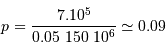
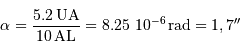
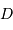 du collecteur est atteint lorsque la tache de diffraction est égale la distance angulaire maximum
du collecteur est atteint lorsque la tache de diffraction est égale la distance angulaire maximum 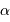 entre le soleil et Jupiter :
entre le soleil et Jupiter :
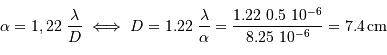
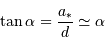
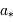 étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
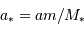 . Alors :
. Alors :
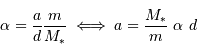
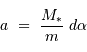
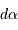 , avec
, avec 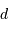 en pc et
en pc et 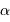 en " donne une distance en UA directement, par définition. En prenant
en " donne une distance en UA directement, par définition. En prenant 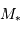 directement en masse jovienne (
directement en masse jovienne (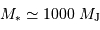 ), on obtient dans le système d'unités (UA,
), on obtient dans le système d'unités (UA, 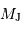 ), pour
), pour 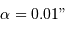 :
:
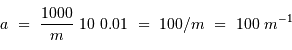
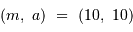 .
.
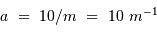
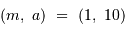 .
.

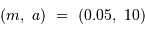 .
.

