
|
Difficulté : ☆☆ Temps : 1.5 heure
Le but de l'exercice est d'interpréter les observations radio de la planète Mercure, menées au radio-télescope d'Arecibo en 1965 (Dyce et al. 1965, Astronomical Journal 72, 351-359). Il s'agissait alors de mesurer la période de rotation propre de Mercure, et de déterminer si elle était égale ou non à la période de rotation orbitale.
| demi-grand axe | 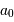 | 0.39 UA |
| révolution sidérale | 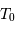 | 88 j |
| rayon | 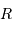 | 2420 km |
| diamètre du radiotél. | 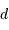 | 305 m |
| fréquence émise | 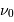 | 430 MHz |
Propagation :
L'écho d'un signal radio émis par le télescope d'Arecibo et
réfléchi par Mercure est réceptionné 616.125 s après son
émission. En déduire la distance Terre-Mercure 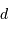 lors de l'observation,
et représenter la position relative de ces 2 planètes et du Soleil. Les observations effectuées pourraient-elles être menées en lumière visible ?
lors de l'observation,
et représenter la position relative de ces 2 planètes et du Soleil. Les observations effectuées pourraient-elles être menées en lumière visible ?
Le champ de vitesse :
On repère un point 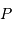 de la surface
visible de Mercure par ses coordonnées cartésiennes dans le repère
de la surface
visible de Mercure par ses coordonnées cartésiennes dans le repère
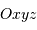 , où
, où 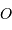 est le barycentre de la planète,
est le barycentre de la planète,
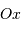 pointe vers la Terre et
pointe vers la Terre et 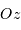 est parallèle à l'axe de rotation de la
planète. On note
est parallèle à l'axe de rotation de la
planète. On note 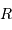 le rayon de la planète Mercure,
le rayon de la planète Mercure, 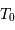 sa période de révolution sidérale, et
sa période de révolution sidérale, et 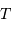 sa période de rotation propre.
sa période de rotation propre.
Donner les coordonnées du point sub-terrestre [i.e. le point de Mercure qui voit la Terre au zénith].
Montrer que la composante radiale (colinéaire à l'axe Terre-Mercure)
de la vitesse d'entraînement de rotation
ne dépend que de l'une des composantes de la position de 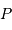 .
.
L'analyse temps-fréquence de l'écho radar :
Quelles régions de la surface contribuent au début (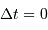 ) et à la fin (
) et à la fin (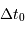 ) du signal d'écho.
Déterminer la durée totale théorique
) du signal d'écho.
Déterminer la durée totale théorique 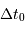 de l'écho ?
Représenter l'allure des lignes d'iso-retard
de l'écho ?
Représenter l'allure des lignes d'iso-retard 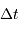 sur la carte
de Mercure [
sur la carte
de Mercure [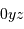 ].
].
On note 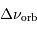 le décalage Doppler du signal
réfléchi au point subterrestre.
Quelles régions contribuent
à l'élargissement Doppler extrêmal
le décalage Doppler du signal
réfléchi au point subterrestre.
Quelles régions contribuent
à l'élargissement Doppler extrêmal
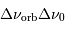 du signal ?
Représenter sur la carte de Mercure
l'allure des lignes d'iso-fréquence
du signal ?
Représenter sur la carte de Mercure
l'allure des lignes d'iso-fréquence 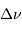 (à
(à 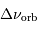 près).
près).
Calculer, pour un point de Mercure de coordonnées
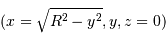 , le retard
, le retard 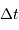 de l'écho et son décalage
spectral
de l'écho et son décalage
spectral 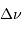 . Montrer que l'on a :
. Montrer que l'on a :
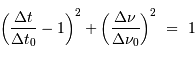
L'écho :
Le document ci-joint (Dyce et al. 1965)
montre l'étalement en fréquence de l'écho en
fonction du retard à la réception.
Comparer le retard maximal théorique à celui enregistré, et interpréter
le désaccord. En déduire, que la relation entre 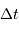 et
et 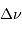 se réduit, pour les mesures effectuées, à
se réduit, pour les mesures effectuées, à 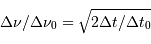 Comment interpréter les variations temporelles d'intensité du signal ?
Comment interpréter les variations temporelles d'intensité du signal ?
Estimer 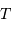 , la période de rotation propre de Mercure.
, la période de rotation propre de Mercure.
On pose 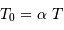 . Quelle signification donner à
. Quelle signification donner à 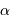 ?
De quelle fraction simple
?
De quelle fraction simple 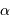 est-il proche ? Est-ce un hasard ?
est-il proche ? Est-ce un hasard ?
Pourquoi les données présentant un plus fort retard ne sont-elles pas facilement exploitables ?
La puissance de l'écho : Quelle fraction du signal Mercure intercepte-t-il ? [on se contentera d'un ordre de grandeur grossier, en supposant que le flux radar est homogène dans un champ d'angle solide égal au lobe principal de diffraction ; un calcul précis est hors de portée de la modélisation proposé].
Estimer, à l'aide d'un modèle simple, le nombre de photons incidents nécessaires pour réceptionner 1 photon en retour après réflexion au point subterrestre.
Une puissance d'émission de 2 MW vous étonne-t-elle ?
[l'impulsion radar incidente est très brève : 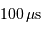 ; on se contentera également d'un ordre de grandeur grossier]
; on se contentera également d'un ordre de grandeur grossier]