Ex: Système de Laplace-Lagrange

Auteurs: Alain Vienne, Marc Fouchard

Auteur: Alain Vienne

Exercice

Difficulté : ☆ Temps : 1h30

Question 1)

La partie linéaire des équations séculaires relatives à 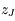z_J (Jupiter) et à 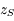z_S (Saturne) peut s'écrire:

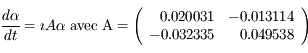
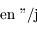
$\frac{d\alpha}{dt} = \imath A \alpha \ \rm{avec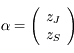} \ A = \left( \begin{array}{rr}0.020031 & -0.013114\\-0.032335 & 0.049538\end{array} \right)$ $\rm{en\ } $''/j$$

avec $\alpha = \left( \begin{array}{c} z_J \\ z_S \end{array} \right)$

Montrer que 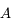est diagonalisable et donner ses valeurs propres (appelées ici, "fréquences propres").

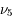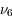Remarque: on notera les valeurs propres $\nu_5$ et $\nu_6$ . Ces indices 5 et 6 font référence respectivement à la cinquième et à la sixième ligne de la matrice obtenue par Le Verrier lorsque celui-ci considérait les 8 planètes.

Solution

Question 2)

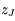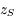Intégrer le système différentiel en recherchant pour z_J et z_S une solution sous la forme de termes périodiques. On montrera que les valeurs propres de la matrice 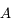sont les fréquences de ces termes périodiques.

Aide Solution

Question 3)

Donner les périodes de ces termes périodiques en années.

Solution

Question 4)

Sachant qu'à 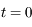t=0 , on a les valeurs:

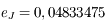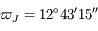
e_J = 0,04833475 et $\varpi_J = 12^{\circ} 43' 15''$

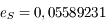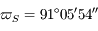
e_S = 0,05589231 et $\varpi_S = 91^{\circ} 05' 54''$

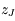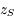calculer les constantes d'intégration de la solution, puis les amplitudes des termes à très longues périodes des solutions de z_J et z_S (on ne demande pas les phases)

Solution

Question 5)

En déduire les valeurs extrêmes que peuvent atteindre les excentricités de Jupiter et de Saturne.

Solution

Remarque

Le fait que le système de Laplace-Lagrange conduit à des valeurs bornées de l'excentricité est illustré par la figure suivante. C'est la variable 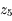z_5 qui est représentée.

Solution de la variable en excentricité de Jupiter ( z_J

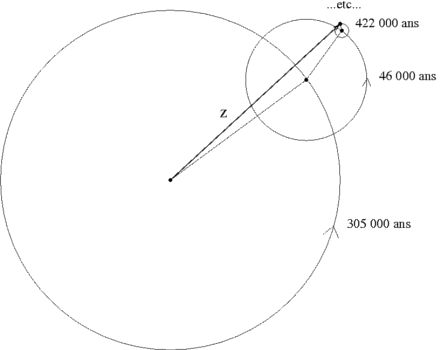
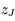) issue d'un système séculaire complet (non linéarisé et avec les 8 planètes).

Crédit : Astrophysique sur Mesure / Vienne

Cette solution diffère de la notre car elle est issue d'un système séculaire complet, c'est à dire non linéarisé et avec les 8 planètes.