Auteur: Marc Fouchard

 Etoiles doubles
Etoiles doubles
Difficulté : ☆
Temps : 20 mn
Question 1)
Quelle est l'équation générale d'une conique dans le plan.
Solution
L'équation d'une conique correspond à un polynôme en 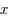 et
et 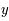 de degré deux, c'est-à-dire :
de degré deux, c'est-à-dire :
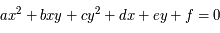 ,
,
où 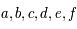 sont des constantes réelles.
sont des constantes réelles.
Question 2)
Pour une ellipse, on a la contrainte supplémentaire que 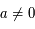 (entre autre). En déduire une équation de l'ellipse contenant cinq paramètres.
(entre autre). En déduire une équation de l'ellipse contenant cinq paramètres.
Solution
Il suffit de diviser l'équation précédente par 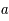 . On obtient :
. On obtient :
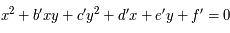 .
.
Question 3)
On a donc cinq paramètres indépendants à déterminer. Combien, au moins, nous faut-il d'observation pour pouvoir déterminer les paramètres ?
Solution
Il faut au moins 5 observations permettant d'écrire cinq équations.
Question 4)
Soit 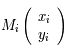 ,
, 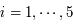 , ces 5 observations. Ecrire sous forme matricielle le système à résoudre.
, ces 5 observations. Ecrire sous forme matricielle le système à résoudre.
Solution
On a 5 équations de la forme :
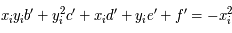 .
.
Qui s'écrivent sous forme matricielle :
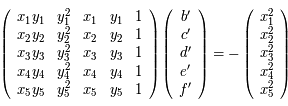 .
.
Question 5)
Donner une astuce pour se ramener à la résolution d'un système à trois inconnues que l'on déterminera.
AideSolution
Il faut pour cela choisir un repère orthormé dans lequel les coordonnées de 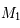 et
et 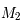 sont les plus simples possibles.
sont les plus simples possibles.
Comme on est libre sur le système de coordonnées, on peut choisir 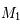 à l'origine et
à l'origine et 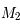 qui nous définie l'axe des abscisses ainsi que la norme. Ainsi on a
qui nous définie l'axe des abscisses ainsi que la norme. Ainsi on a 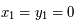 , et
, et 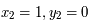 .
.
Le système devient :
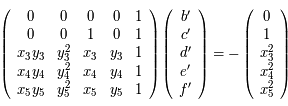 .
.
Qu'on peut écrire :
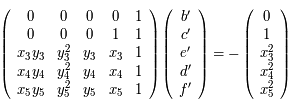 .
.
Ainsi  et
et 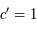 .
.
Le système à résoudre est donc :
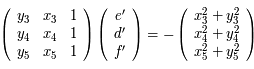 .
.


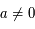 (entre autre). En déduire une équation de l'ellipse contenant cinq paramètres.
(entre autre). En déduire une équation de l'ellipse contenant cinq paramètres.
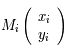 ,
, 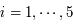 , ces 5 observations. Ecrire sous forme matricielle le système à résoudre.
, ces 5 observations. Ecrire sous forme matricielle le système à résoudre.