 |  |  |  |  |  |
Système de Laplace-Lagrange |
Alain Vienne
Les mouvements de Jupiter et de Saturne sont très proches d'un mouvement képlérien. En effet, chacune de ces planètes est principalement attirée par le Soleil mais très peu par l'autre planète (la masse du Soleil est 1047 fois celle de Jupiter et 3498 fois celle de Saturne; ces 2 planètes étant les plus massives du système solaire). Leurs éléments d'orbite, notamment le demi-grand axe, l'excentricité (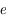
) et la direction du péricentre (
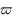), sont quasi constants. Plus précisément, soit ils varient peu (oscillations rapides de faible amplitude), soit ils varient lentement ("variations séculaires"). On dit que l'influence de Jupiter sur le mouvement de Saturne est une perturbation (et vice versa) du mouvement képlérien. L'objet de la mécanique céleste dans le cas de systèmes perturbés, est de modéliser ces variations.
Laplace (1749-1827) avait déjà montré que les demi-grands axes des planètes n'avaient pas de variations séculaires (plus précisément: à un certain degré d'approximation, les demi-grands axes des planètes n'ont que des petites variations périodiques). Ce qui était, à l'époque, un argument fort en faveur de la stabilité du système solaire.
Il fallait quand même s'assurer que les excentricités n'atteignent pas de valeurs trop grandes. En effet, de grandes excentricités conduisent vite à des collisions! L'objet de cette application est de voir que les variations d'excentricités sont bornées.
On simplifie notablement le calcul et la compréhension en utilisant la variable complexe suivante:
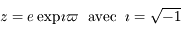
Par exemple, on verra dans l'exercice suivant que l'"execntricité complexe"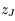 
asssociée à Jupiter a le mouvement suivant:
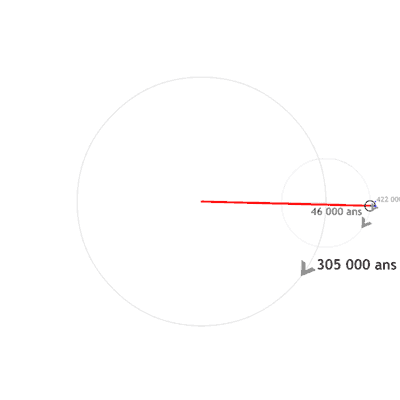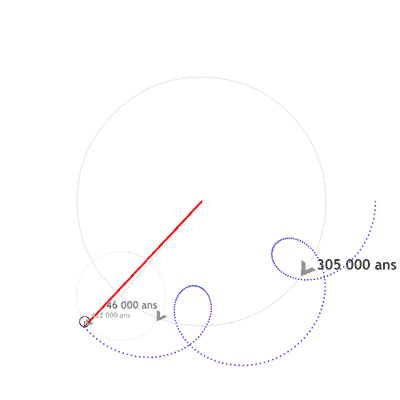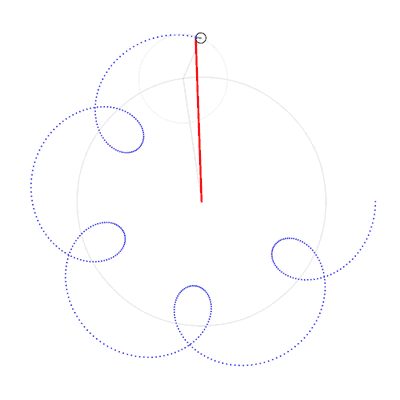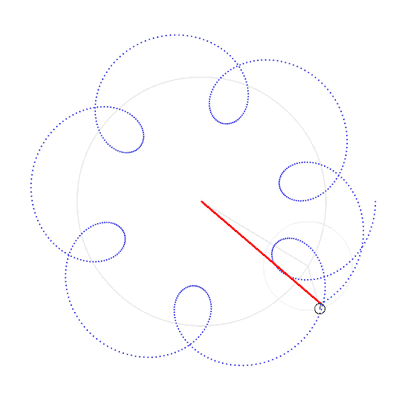
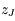) qui montre que l'exentricité de Jupiter est bornée.
 |  |
