Les outils mathématiques en astronomie
- Introduction
- Importance des approximations
- L'orbite de la planète Mars
- Ex: L'orbite de la planète Mars
- Précession du périastre
- Ex: Précession du périastre
- Dimensions et unités
- Dimensions et unités physiques
- Equation aux dimensions
- En savoir plus: Analyse dimensionnelle
- Ex: analyse dimensionnelle
- Obtention pragmatique de développements
- Séries du problème des 2-corps
- Ex : Séries du problème des 2-corps
- Séries du problème des 2-corps (Lagrange)
- Ex : Séries du problème des 2-corps (Lagrange)
- Description épicyclique du mouvement keplerien
- Ex: Description épicyclique du mouvement keplerien
- Sphère d'influence
- Ex: Sphère d'influence
Introduction
On trouvera dans cette section quelques rappels essentiels de Physique:
- Notion de grandeur physique, équation aux dimensions
- Approximations numériques
- Utilisation de développements limités
On pourra reconstruire et caractériser l'orbite de la planète de la planète Mars, en utilisant les données d'observation historiques de Tycho Brahé, ou s'intéresser au phénomène de précession du périastre.
Ces deux applications permettent de se familiariser avec l'importance des approximations en astronomie ou en physique en général.
A l'aide de développements, on pourra s'intéresser à la description épicyclique du mouvement keplerien ou à la notion de sphère d'influence.
Importance des approximations
Auteur: S. Renner
L'orbite de la planète Mars
Auteur: S. Renner
Date de création: 17 février 2009
L'objectif de cet exercice est d'établir les caractéristiques de l'orbite de la planète Mars, en utilisant les données d'observation de Tycho Brahé, celles-là mêmes qui furent utilisées par Kepler.
On suppose que les mouvements des planètes s'effectuent dans le même plan, qui est celui de l'écliptique. La position des planètes est alors repérée par une coordonnée, la longitude écliptique. On choisit pour origine des longitudes la direction du point vernal (noté 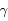 ).
La tableau ci-dessous rassemble les données concernant 5 couples d'observations de Mars, effectuées par Tycho Brahé. On y indique la longitude écliptique géocentrique du Soleil, notée
).
La tableau ci-dessous rassemble les données concernant 5 couples d'observations de Mars, effectuées par Tycho Brahé. On y indique la longitude écliptique géocentrique du Soleil, notée 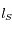 (c'est-à-dire l'angle, mesurée depuis la Terre, entre la direction du Soleil et celle du point vernal), et la longitude écliptique géocentrique de Mars, notée
(c'est-à-dire l'angle, mesurée depuis la Terre, entre la direction du Soleil et celle du point vernal), et la longitude écliptique géocentrique de Mars, notée 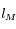 (angle vu de la Terre entre la direction de Mars et celle du point vernal).
(angle vu de la Terre entre la direction de Mars et celle du point vernal).
|
DATE
|
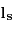
|
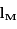
|
| 1a |
17/02/1585 |
339°23' |
135°12' |
| 1b |
05/01/1587 |
295°21' |
182°08' |
| 2a |
19/09/1591 |
185°47' |
284°18' |
| 2b |
06/08/1593 |
143°26' |
346°56' |
| 3a |
07/12/1593 |
265°53' |
3°04' |
| 3b |
25/10/1595 |
221°42' |
49°42' |
| 4a |
28/03/1587 |
16°50' |
168°12' |
| 4b |
12/02/1589 |
333°42' |
218°48' |
| 5a |
10/03/1585 |
359°41' |
131°48' |
| 5b |
26/01/1587 |
316°06' |
184°42' |
Ex: L'orbite de la planète Mars
Auteur: S. Renner
 Orbite de Mars
Orbite de Mars
Difficulté : ☆
Temps : 2h30
Question 1)
L'observation de Mars en opposition a fourni la période qui sépare ces oppositions, ou période synodique notée 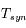 . Cette période est égale à 780 jours.
. Cette période est égale à 780 jours.
En déduire la valeur de la période sidérale de mars, que l'on notera 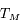 .
.
Question 2)
Calculer la durée qui sépare les 2 dates successives de chaque couple d'observations. Quelle conclusion peut-on en tirer?
Question 3)
Trouver la relation entre la longitude écliptique héliocentrique de la Terre 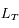 (angle entre la direction de la Terre et celle du point vernal mesurée depuis le Soleil) et la longitude géocentrique du Soleil
(angle entre la direction de la Terre et celle du point vernal mesurée depuis le Soleil) et la longitude géocentrique du Soleil 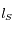 . Calculer
. Calculer 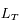 pour chacune des dates du tableau.
pour chacune des dates du tableau.
Question 4)
Représenter sur une feuille de papier millimétré l'orbite de la Terre par un cercle de centre 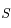 (Soleil) et de rayon égal à 5 cm. Choisir la direction du point vernal selon une des lignes du papier.
(Soleil) et de rayon égal à 5 cm. Choisir la direction du point vernal selon une des lignes du papier.
Pour chacun des 5 couples d'observations, construire:
- la première position Ti de la Terre sur son orbite et la direction Tix de Mars telle qu'on l'observe depuis la Terre
- la seconde position T'i de la Terre sur son orbite et la direction T'ix' de Mars
Montrer que le point Mi représentant Mars est à l'intersection des deux demi-droites Tix et T'ix'.
On déterminera ainsi les 5 positions de M1, M2, M3, M4 et M5 de Mars.
Question 5)
Vérifier que ces 5 points ne sont pas sur un cercle centré sur le Soleil.
Dans ce qui suit, on admet que l'orbite de Mars est une ellipse de faible excentricité, dont la forme ne diffère pas significativement de celle d'un cercle, mais dont le centre n'est pas le Soleil.
Pour déterminer le rayon de ce cercle, on partira d'une première approximation qui est la moyenne des 5 rayons SMi. On tracera le cercle ayant ce rayon sur une feuille de papier calque et on cherchera, par tâtonnement, à le faire passer au mieux parmi les 5 points Mi. Si le rayon du cercle est trop petit, la majorité des points se trouveront toujours à l'extérieur du cercle; inversement, s'il est trop grand, la majorité des points se trouveront toujours à l'intérieur. On modifiera donc le rayon de ce cercle, millimètre par millimètre, pour qu'il passe au mieux parmi les 5 points. Soit alors 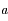 la valeur du rayon de ce cercle.
la valeur du rayon de ce cercle.
Autre possibilité: connaissant la période sidérale de Mars, calculer son demi-grand axe en UA (unité astronomique, égale à la distance moyenne Terre-Soleil, soit 149 597 871 km). Tracer le cercle correspondant à cette orbite et estimer une erreur en mm sur les positions de Mars.
Question 7)
Sachant que l'excentricité de la Terre est 0.016, l'approximation de l'orbite de la Terre par un cercle centré sur le Soleil est-elle justifiée?
Question 8)
Quelle est la distance minimale de Mars à la Terre lors d'une opposition? A quelle date de l'année ces oppositions favorables se produisent-elles? Quelle est la distance maximale de Mars à la Terre lors d'une opposition? A quelle date de l'année ces oppositions défavorables se produisent-elles?
Question 9)
Afin de vérifier la loi des aires, mesurer l'aire balayée par le rayon-vecteur Soleil-Mars entre le 6 août et le 7 décembre 1593 et celle balayée entre le 26 janvier et le 28 mars 1587. En déduire la valeur moyenne de l'aire balayée par jour dans chacun des deux cas. On pourra, pour cela, compter les carreaux du papier.
Précession du périastre
Auteur: S. Renner
Date de création: 06 janvier 2011
L'objectif de cet exercice est de quantifier la précession du périastre d'un satellite en orbite autour d'un corps central légèrement aplati aux pôles.
Il est conseillé de s'intéresser au préalable à la résolution du problème à 2 corps.
Ex: Précession du périastre
Dimensions et unités
Auteur: Stéphane Erard
Dimensions et unités physiques
Les formules mathématiques utilisées en Astronomie définissent des relations entre grandeurs physiques. Ces grandeurs ont une dimension physique, et sont mesurées dans une certaine unité.
La dimension est inhérente à une grandeur physique, sa valeur est fonction de l'unité utilisée. On distingue sept types de grandeurs physiques, ou dimensions, indépendantes. Toute quantité physique peut s'exprimer comme combinaison de ces grandeurs de base.
Le système officiel en vigueur est le SI (Système International d'unités) ou MKSA, qui définit les unités de mesure des sept grandeurs indépendantes (voir par exemple la définition de la seconde). Différents systèmes d'unités ont été utilisés au cours de l'histoire, et d'autres systèmes sont en usage dans des domaines particuliers. En Astronomie, on utilise couramment des unités en rapport avec les phénomènes étudiés, par exemple l'unité astronomique, l'année-lumière, le parsec, ou le décalage vers le rouge pour les distances.
Table 1
|
Grandeur de base
|
Dimension
|
Unité S. I.
|
Symbole S. I.
|
| Longueur |
L |
mètre |
m |
| Masse |
M |
kilogramme |
kg |
| Temps |
T |
seconde |
s |
| Intensité de courant |
I |
Ampère |
A |
| Température |
Θ
|
Kelvin |
K |
| Quantité de matière |
N |
mole |
mol |
| Intensité lumineuse |
J |
candela |
cd |
Deux autres grandeurs sont utilisées en complément de celles-ci. Elles sont dépourvues de dimension physique (elles peuvent être comprises comme des rapports de longueurs ou de surfaces), mais peuvent s'exprimer dans différentes échelles. En pratique, on préfère l'échelle qui n'introduit pas de coefficient dans les fonctions trigonométriques (en radians, par opposition aux degrés pour les angles plats).
Table 2
|
Grandeur dérivée
|
Dimension
|
Unité S. I.
|
Symbole S. I.
|
| Angle plan |
1 |
radian |
rad |
| Angle solide |
1 |
stéradian |
sr |
Ecrire une équation aux dimensions consiste à remplacer dans une formule les grandeurs par leurs dimensions et à négliger les coefficients de proportionnalité.
 Exemple
Exemple
La définition de la vitesse donne la dimension physique de cette grandeur :
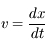
L'équation aux dimensions est :
![[V] = LT^{-1}](../pages_dim-unites/equations_dim-unites/equation2.png)
et la vitesse se mesure en m/s dans le Système International.
Equation aux dimensions
On peut toujours multiplier ou diviser des grandeurs quelconques entre elles, mais on ne peut additionner que des grandeurs physiques de même dimension — l'inverse reviendrait littéralement à additionner les torchons et les serviettes.
Les équations ou formules doivent donc être homogènes : chaque membre (et chaque terme) d'une équation doit avoir la même dimension physique. La vérification de l'homogénéité d'une formule ou d'un résultat de calcul doit être un réflexe en physique : c'est un moyen efficace pour éliminer les erreurs de calcul, et éviter les non-sens.
 Exemple
Exemple
Le principe fondamental de la dynamique donne la dimension physique de la force :
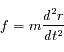
L'équation aux dimensions est :
![[F]= MLT^{-2}](../pages_dim-unites/equations_dim-unites/equation4.png)
et l'unité SI de la force est le 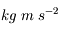 (couramment appelée Newton).
(couramment appelée Newton).
Les constantes qui apparaissent dans les lois physiques ont également une dimension. On peut dériver celle-ci en posant l'équation aux dimensions. La valeur numérique dépend encore une fois du système d'unités utilisé.
 Exemple
Exemple
L'attraction universelle (loi de Newton) s'écrit :
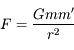
où G est la constante de gravitation. La dimension de G est donc
![[G]= [F]L^2M^{-2}=L^3T^{-2}M^{-1}](../pages_dim-unites/equations_dim-unites/equation7.png)
La valeur numérique doit se mesurer expérimentalement, et dépend du système d'unités adopté.
Les fonctions mathématiques n'acceptent que des arguments sans dimension, ou dédimensionalisés. En pratique, ce sont des nombres purs ou des rapports de quantités de même grandeur.
 Exemple
Exemple
L'équation de Boltzmann donne la population d'un niveau d'énergie atomique ou moléculaire en fonction de la température :
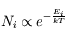
La quantité kT est donc homogène à une énergie.
On peut en déduire la dimension physique de la constante de Boltzmann k :
-
La dimension d'une énergie est donnée par exemple par 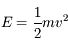
On a donc 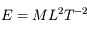 (l'unité SI est le
(l'unité SI est le 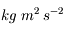 , couramment appelée Joule)
, couramment appelée Joule)
-
La dimension de la constante de Boltzmann est donc ![[k] = ML^2T^{-2}K^{-1}](../pages_dim-unites/equations_dim-unites/equation12.png) . La valeur de k est donnée en J/K en SI.
. La valeur de k est donnée en J/K en SI.
Les équations aux dimensions permettent également de dériver les ordres de grandeur de phénomènes physiques, éventuellement en utilisant des modèles dérivés d'hypothèses simples.
 Exemple
Exemple
L'équation barométrique dérive d'un modèle basique d'atmosphère isotherme. Elle donne la pression P en fonction de l'altitude z sous ces hypothèses très simplifiées :
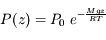
où 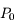 est la pression au sol, M la masse molaire moyenne, R la constante des gaz parfaits, g l'accélération de la pesanteur, et T la température (supposée constante) de l'atmosphère.
est la pression au sol, M la masse molaire moyenne, R la constante des gaz parfaits, g l'accélération de la pesanteur, et T la température (supposée constante) de l'atmosphère.
La quantité h = RT/Mg est donc homogène à une distance — c'est l'altitude à laquelle la pression est réduite d'un facteur 2,7 dans ce modèle. Elle est appelée échelle de hauteur, et donne une estimation de l'épaisseur de la basse atmosphère des planètes.
On peut l'évaluer dans la troposphère terrestre :
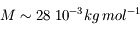 (masse molaire de l'azote, principal constituant)
(masse molaire de l'azote, principal constituant)
T ~ 280 K (température au sol)
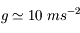
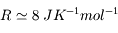
Ce qui donne pour l'échelle de hauteur h ~ 8 km.
De façon similaire, chaque grandeur possède une dimension tensorielle : scalaire, vecteur, ou tenseur d'ordre supérieur. La dimension tensorielle se préserve de la même façon que la dimension physique (chaque terme d'une équation doit avoir la même dimension tensorielle).
 Exemple
Exemple
Le principe fondamental de la dynamique peut s'écrire de manière vectorielle, et donne la direction de la force :
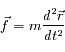
On peut aussi l'écrire de manière scalaire en utilisant les normes :
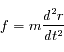
Les tenseurs d'ordre 2 sont utilisés pour décrire des quantités qui en chaque endroit dépendent aussi de la direction. Des exemples de tenseurs d'ordre 2 sont donnés par le tenseur métrique de la relativité générale, ou par les tenseurs de contrainte et de déformation en mécanique des milieux continus.
En savoir plus: Analyse dimensionnelle
L'analyse des dimensions d'un problème complexe permet de prédire la forme d'une loi physique, dans le cas fréquent où elle s'exprime comme produit des grandeurs qui interviennent.
Théorème de Vaschy-Buckingham
Si une loi physique s'écrit comme une relation entre n grandeurs indépendantes ayant k dimensions physiques indépendantes :
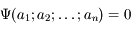
on peut l'exprimer comme une relation entre (n-k) nombres sans dimensions :
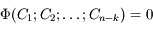
ceux-ci étant des produits de puissances des grandeurs de départ : 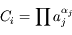
En particulier, si (n-k) = 2 on peut toujours écrire 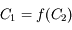
Ex: analyse dimensionnelle
 Ex: analyse dimensionnelle
Ex: analyse dimensionnelle
Difficulté : ☆
Temps : 20 min
Question 1)
On étudie les oscillations d'un pendule à l'aide d'une simple analyse dimensionnelle. Enumérer les paramètres physiques qui interviennent dans ce problème.
Question 2)
Combien de grandeurs et de dimensions indépendantes interviennent dans le problème ? Combien de nombres sans dimension peut-on construire avec celles-ci ?
Question 3)
Dériver ces nombres sans dimension.
Question 4)
Ecrire une relation décrivant le problème. Commenter.
Obtention pragmatique de développements
Auteurs: Alain Vienne, S. Renner
Séries du problème des 2-corps
Auteur: Alain Vienne
Souvent, lorsque l'on considère le problème des 2 corps et quand l'excentricité  de l'orbite est petite, on a besoin de l'approximation suivante:
de l'orbite est petite, on a besoin de l'approximation suivante:
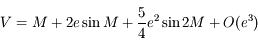
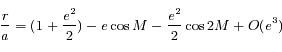
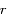 et
et 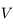 sont les coordonnées polaires du corps,
sont les coordonnées polaires du corps, 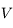 étant compté à partir du péricentre (anomalie vraie).
étant compté à partir du péricentre (anomalie vraie). 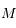 est le temps ou plus précisément c'est l'anomalie moyenne
est le temps ou plus précisément c'est l'anomalie moyenne 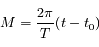 avec
avec 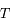 la période,
la période, 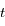 le temps et
le temps et 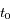 l'instant de passage au péricentre.
l'instant de passage au péricentre. 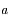 et
et  sont respectivement le demi-grand axe et l'excentricité de l'orbite.
sont respectivement le demi-grand axe et l'excentricité de l'orbite.
Dans l'exercice qui est proposé ci-après, on utilisera en plus des anomalies moyennes et vraies, l'anomalie excentrique.
L'animation qui est donnée ici visualise leur évolution dans le cas d'une excentricité de 0,7.
Evolution des 3 anomalies (respectivement vraie, excentrique et moyenne)
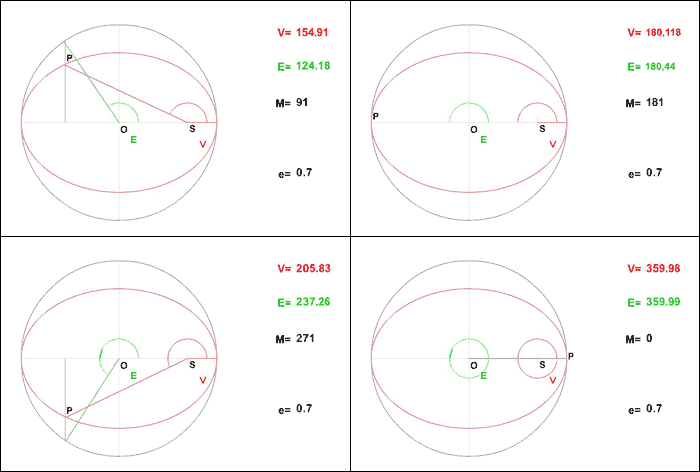
Si l'existence des développements ci-dessus est admise, l'astronome s'autrorise alors une démarche pragmatique pour les obtenir. Sa démarche n'a pas la rigueur du mathématicien. Dans le cas présenté ici, elle n'a pas non plus une grande efficacité si on souhaite "pousser" le développement plus loin en ordre.Elle a le seul avantage de pouvoir "se tirer d'affaire" dans le cas qui le préoccupe.
Dans l'exercice qui est proposé, on utilisera au besoin le développement de Taylor, l'intégration d'un développement, la substitution de développements.
Ex : Séries du problème des 2-corps
Auteur: Alain Vienne
 Séries du problème des 2-corps
Séries du problème des 2-corps
Difficulté : ☆☆
Temps : 1h
 Introduction
Introduction
Quand on intègre le problème des 2-corps, la loi des aires permet d'écrire:
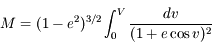
Question 1)
On utilisant cette relation et en négligeant les termes d'ordre supérieur ou égal à 3 en excentricité, montrer que l'on a:
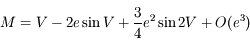
Développer d'abord 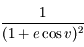 et intégrer le développement obtenu. Mutiplier enfin par celui de
et intégrer le développement obtenu. Mutiplier enfin par celui de 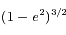 . Dans ces calculs, on prend soin de se limiter à l'ordre 2.
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
Question 3)
A partir du développement obtenu à la première question, déduire celui qui donne 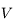 en fonction de
en fonction de 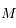 (limité à l'ordre 2 en
(limité à l'ordre 2 en  ).
).
Faire d'abord l'ordre 0 puis l'ordre 1 et enfin l'ordre 2.
A l'ordre 0: 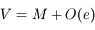
A l'ordre 1, il suffit d'avoir 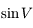 à l'ordre 0 (obtenu précédemment).
à l'ordre 0 (obtenu précédemment).
A l'ordre 2, il suffit d'avoir 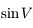 à l'ordre 1 et
à l'ordre 1 et 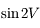 à l'ordre 0 (obtenus précédemment).
à l'ordre 0 (obtenus précédemment).
L'ordre 1 pour 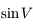 est obtenu de la manière suivante:
est obtenu de la manière suivante: 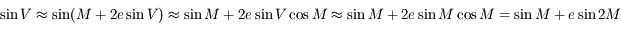 . Attention à la discussion sur l'ordre à chaque étape du calcul.
. Attention à la discussion sur l'ordre à chaque étape du calcul.
 Remarque
Remarque
Dans cette dernière question, le calcul est fait "en crabe", il faut donc veiller à la discussion sur l'ordre en excentricité. Plus généralement, tous ces calculs supposent l'existence des développements recherchés. Cette supposition et l'unicité ont permis d'éviter de se soucier des conditions d'application des théorèmes utilisés.
Séries du problème des 2-corps (Lagrange)
Auteur: S. Renner
Date de création: 10 avril 2013
Dans le problème des 2 corps, lorsque l'excentricité 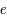 de l'orbite est petite, on peut écrire :
de l'orbite est petite, on peut écrire :
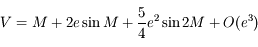 ,
,
où 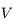 est l'angle entre la direction du péricentre et la position du corps sur son orbite (anomalie vraie),
est l'angle entre la direction du péricentre et la position du corps sur son orbite (anomalie vraie), 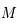 est le temps ou plus précisément l'anomalie moyenne
est le temps ou plus précisément l'anomalie moyenne 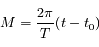 , avec
, avec 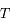 la période,
la période, 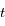 le temps et
le temps et 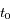 l'instant de passage au péricentre.
l'instant de passage au péricentre.
L'animation donnée ci-après montre l'évolution des anomalies vraie et moyenne (et excentrique) dans le cas d'une excentricité 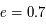 .
.
Evolution des 3 anomalies (respectivement vraie, excentrique et moyenne)

Dans l'exercice proposé, on établit le développement ci-dessus à l'aide du théorème d'inversion de Lagrange.
Ex : Séries du problème des 2-corps (Lagrange)
Auteur: S. Renner
 Séries du problème des 2-corps (Lagrange)
Séries du problème des 2-corps (Lagrange)
Difficulté : ☆☆
Temps : 1h
Question 1)
On utilisant cette relation et en négligeant les termes d'ordre supérieur ou égal à 3 en excentricité, montrer que l'on a:
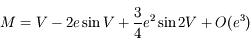
Développer d'abord 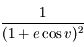 et intégrer le développement obtenu. Mutiplier enfin par celui de
et intégrer le développement obtenu. Mutiplier enfin par celui de 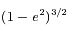 . Dans ces calculs, on prend soin de se limiter à l'ordre 2.
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
Description épicyclique du mouvement keplerien
Auteur: S. Renner
Date de création: 3 février 2010
Souvent en dynamique du système solaire, l'excentricité est très faible, et il est donc utile de considérer des approximations au premier ordre en excentricité, en particulier pour des systèmes vus dans des repères tournants. Cette approche est par exemple intéressante pour décrire la dynamique des anneaux planétaires, ou les effets de l'aplatissement d'une planète sur les orbites de satellites.
On propose ici un exercice qui porte sur la description du mouvement keplerien par des épicycles : le mouvement elliptique d'une particule P autour d'un foyer F est vu dans un repère centré sur un point G (le centre guide) en orbite circulaire uniforme autour de F (de rayon a égal au demi-grand axe de la particule, et de vitesse angulaire égale au moyen mouvement 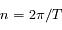 , où
, où 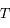 est la période orbitale de P).
est la période orbitale de P).
L'exercice est largement inspiré du livre Solar System Dynamics (C.D. Murray & S.F. Dermott, 1999).
Ex: Description épicyclique du mouvement keplerien
Auteur: S. Renner
 Description épicyclique du mouvement keplerien
Description épicyclique du mouvement keplerien
Difficulté : ☆☆
Temps : 2h
Question 2)
A partir de la loi des aires, montrer que: 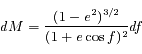 .
.
Question 3)
Ainsi en intégrant on obtient: 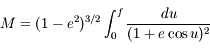 . Montrer à l'aide de cette relation que
. Montrer à l'aide de cette relation que 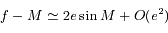 .
.
Sphère d'influence
Auteur: S. Renner et A. Vienne
Date de création: 3 mars 2010
Nous allons définir la notion de sphère d'influence en s'intéressant au problème à trois corps Soleil + Jupiter + satellite, de masses respectives 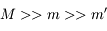 (qui constitue ce que l'on appelle un problème de Kepler perturbé).
(qui constitue ce que l'on appelle un problème de Kepler perturbé).
Ex: Sphère d'influence
Auteurs: S. Renner, A. Vienne
 Sphère d'influence
Sphère d'influence
Difficulté : ☆☆
Temps : 3h
Question 1)
Ecrire les équations du mouvement héliocentrique de 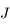 (c'est-à-dire de
(c'est-à-dire de 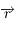 ).
).
Question 2)
Quelle est la nature du mouvement de 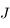 si la quantité
si la quantité 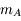 est négligeable?
est négligeable?
Question 4)
Montrer que l'équation du mouvement jovicentique de 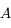 (c'est-à-dire de
(c'est-à-dire de 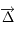 ) est
) est 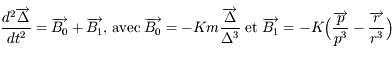 .
.
Question 5)
Dans la suite, on cherche à étudier la surface 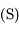 définie par
définie par 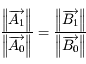 . On va voir notamment qu'elle a presque la forme d'une sphère,
appelée sphère d'influence de Jupiter. Justifier cette appellation en expliquant ce qui se passe pour le mouvement de
. On va voir notamment qu'elle a presque la forme d'une sphère,
appelée sphère d'influence de Jupiter. Justifier cette appellation en expliquant ce qui se passe pour le mouvement de 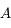 lorsque celui-ci est respectivement très à
l'intérieur ou très à l'extérieur de cette sphère.
lorsque celui-ci est respectivement très à
l'intérieur ou très à l'extérieur de cette sphère.
Question 6)
On pose 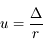 et
et 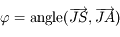 . Montrer que l'on a
. Montrer que l'on a 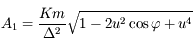 .
.
Question 7)
Montrer que l'on a 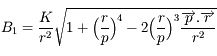 .
.
Question 9)
En déduire que l'équation de la surface 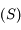 peut s'écrire
peut s'écrire 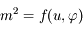 , et donner l'expression de
, et donner l'expression de 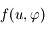 .
.
Question 11)
Calculer le rayon de la sphère d'influence de Jupiter sachant que 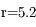 UA.
UA.
Réponses aux exercices
pages_approxim/exo-orb-mars.html
Exercice
'Orbite de Mars'
-
Question 1
Solution :
On peut écrire que la différence entre l'angle balayé en une période synodique par la Terre d'une part et Mars d'autre part vaut 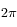 , c'est-à-dire:
, c'est-à-dire: 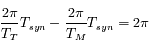 .
.
On en déduit 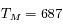 jours
jours
-
Question 2
Solution :
On note que les années 1585, 1587, 1591, 1593 et 1595 ne sont pas bissextiles. Il y a exactement 687 jours entre deux dates successives. Mars se trouve donc au même endroit de son orbite pour chaque couple d'observations.
-
Question 3
Solution :
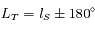 (modulo 360°).
(modulo 360°).
|
DATE
|
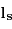
|
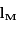
|
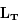
|
| 1a |
17/02/1585 |
339°23' |
135°12' |
159°23' |
| 1b |
05/01/1587 |
295°21' |
182°08' |
115°21' |
| 2a |
19/09/1591 |
185°47' |
284°18' |
5°47' |
| 2b |
06/08/1593 |
143°26' |
346°56' |
323°26' |
| 3a |
07/12/1593 |
265°53' |
3°04' |
85°53' |
| 3b |
25/10/1595 |
221°42' |
49°42' |
41°42' |
| 4a |
28/03/1587 |
16°50' |
168°12' |
196°50' |
| 4b |
12/02/1589 |
333°42' |
218°48' |
153°42' |
| 5a |
10/03/1585 |
359°41' |
131°48' |
179°41' |
| 5b |
26/01/1587 |
316°06' |
184°42' |
136°06' |
-
Question 4
-
Question 5
Solution :
Le rayon du cercle est égal à 76 mm. L'erreur maximale sur les positions est d'environ 1 mm.
D'après la troisième loi de Kepler avec 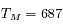 jours et
jours et 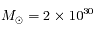 kg, on trouve
kg, on trouve 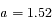 UA. Or 1 UA = 50 mm, donc le rayon du cercle est 76 mm.
UA. Or 1 UA = 50 mm, donc le rayon du cercle est 76 mm.
-
Question 6
Solution :
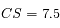 mm. Comme 1 UA = 50 mm, on en déduit que
mm. Comme 1 UA = 50 mm, on en déduit que 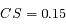 UA.
UA.
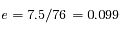 (à comparer à la valeur exacte: 0.093)
(à comparer à la valeur exacte: 0.093)
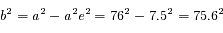 d'où
d'où 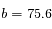 mm
mm 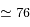 mm.
mm.
-
Question 7
Solution :
Distance centre-foyer de l'ellipse: 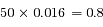 mm. Donc l'approximation est correcte étant donnée la précision du tracé.
mm. Donc l'approximation est correcte étant donnée la précision du tracé.
-
Question 8
Solution :
La distance minimale en opposition est 19 mm soit 0.38 UA (au mois d'août).
La distance maximale en opposition est 33 mm soit 0.66 UA (au mois de janvier).
-
Question 9
Solution :
Entre le 6 août et le 7 décembre, l'aire balayée est égale à 130 carreaux. Il s'est écoulé 123 jours, et l'aire balayée par jour est de 1.06 carreaux par jour.
Entre le 26 janvier et le 28 mars, l'aire balayée est égale à 60 carreaux. Il s'est écoulé 61 jours, et l'aire balayée est de 1.098 carreaux par jour.
pages_approxim/exo-precession-peri-approxim.html
Exercice
'Précession du périastre'
pages_dim-unites/dim4.html
Exercice
'Ex: analyse dimensionnelle'
-
Question 1
Solution :
Les paramètres physiques qui interviennent sont : la masse oscillante m, la longueur l du pendule, la période d'oscillation p, l'angle initial 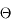 et la pesanteur g (on néglige au premier ordre les autres paramètres tels que le frottement ou la masse du fil, qui décrivent des écarts au problème idéal).
et la pesanteur g (on néglige au premier ordre les autres paramètres tels que le frottement ou la masse du fil, qui décrivent des écarts au problème idéal).
-
Question 2
Solution :
Au total, on a 5 grandeurs et 3 dimensions physiques indépendantes (longueur, temps et masse). La relation cherchée peut donc s'écrire comme une relation entre deux nombres sans dimension construits avec ces 5 grandeurs.
-
Question 3
Solution :
Le premier nombre est évidemment l'angle initial 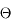 , sans dimension.
, sans dimension.
Le second nombre est de la forme 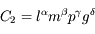
L'équation aux dimensions est
![[1] = L^{\alpha+\delta}M^{\beta}T^{\gamma-2\delta}](../pages_dim-unites/equations_dim-unites/equation27.png) , donc
, donc 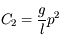 est sans dimension.
est sans dimension.
-
Question 4
Solution :
Le relation cherchée est de la forme 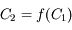 , soit
, soit 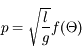
Le calcul à partir de l'équation du mouvement donne 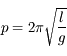 , et l'expérience confirme que la période ne dépend pas de l'angle initial si celui-ci est petit. On a montré sans le moindre effort la forme générale de la période (à une constante près) et le fait qu'elle ne dépend pas de la masse du pendule.
, et l'expérience confirme que la période ne dépend pas de l'angle initial si celui-ci est petit. On a montré sans le moindre effort la forme générale de la période (à une constante près) et le fait qu'elle ne dépend pas de la masse du pendule.
pages_develop-appli/exo-series-2corps.html
Exercice
' Séries du problème des 2-corps'
pages_develop-appli/exo-series-2corps-lagrange.html
Exercice
' Séries du problème des 2-corps (Lagrange)'
-
Question 1
Aide :
Développer d'abord 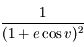 et intégrer le développement obtenu. Mutiplier enfin par celui de
et intégrer le développement obtenu. Mutiplier enfin par celui de 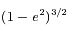 . Dans ces calculs, on prend soin de se limiter à l'ordre 2.
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
-
Question 2
Solution :
D'après la question précédente, on a donc : 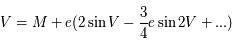 .
.
Le théorème d'inversion de Lagrange permet d'écrire : ![V = M + \Sigma_{j=1}^\infty \frac{e^j}{j!} \frac{d^{j-1}}{dM^{j-1}} \Big{[} 2 \sin M - \frac{3}{4} e \sin 2M + ... \Big{]}^j](../pages_develop-appli/equations_develop-appli/equation56.png) .
.
On obtient ainsi 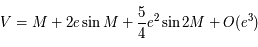 en développant la formule ci-dessus au second ordre.
en développant la formule ci-dessus au second ordre.
pages_develop-appli/exo-epicycle-kepler.html
Exercice
'Description épicyclique du mouvement keplerien'
pages_develop-appli/exo-sphere-influence.html
Exercice
'Sphère d'influence'
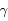 ).
La tableau ci-dessous rassemble les données concernant 5 couples d'observations de Mars, effectuées par Tycho Brahé. On y indique la longitude écliptique géocentrique du Soleil, notée
).
La tableau ci-dessous rassemble les données concernant 5 couples d'observations de Mars, effectuées par Tycho Brahé. On y indique la longitude écliptique géocentrique du Soleil, notée 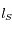 (c'est-à-dire l'angle, mesurée depuis la Terre, entre la direction du Soleil et celle du point vernal), et la longitude écliptique géocentrique de Mars, notée
(c'est-à-dire l'angle, mesurée depuis la Terre, entre la direction du Soleil et celle du point vernal), et la longitude écliptique géocentrique de Mars, notée 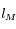 (angle vu de la Terre entre la direction de Mars et celle du point vernal).
(angle vu de la Terre entre la direction de Mars et celle du point vernal).
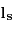
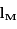
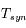 . Cette période est égale à 780 jours.
. Cette période est égale à 780 jours.
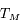 .
.
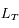 (angle entre la direction de la Terre et celle du point vernal mesurée depuis le Soleil) et la longitude géocentrique du Soleil
(angle entre la direction de la Terre et celle du point vernal mesurée depuis le Soleil) et la longitude géocentrique du Soleil 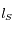 . Calculer
. Calculer 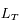 pour chacune des dates du tableau.
pour chacune des dates du tableau.
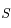 (Soleil) et de rayon égal à 5 cm. Choisir la direction du point vernal selon une des lignes du papier.
(Soleil) et de rayon égal à 5 cm. Choisir la direction du point vernal selon une des lignes du papier.
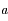 la valeur du rayon de ce cercle.
la valeur du rayon de ce cercle.
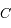 du cercle ainsi déterminé au point
du cercle ainsi déterminé au point 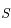 (Soleil). En déduire l'excentricité de l'orbite
(Soleil). En déduire l'excentricité de l'orbite 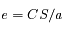 .
.
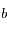 de l'ellipse, et discuter la validité de l'approximation faite ici, qui a conduit à assimiler l'ellipse à un cercle de rayon
de l'ellipse, et discuter la validité de l'approximation faite ici, qui a conduit à assimiler l'ellipse à un cercle de rayon 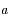 .
.
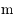 par rapport à un corps central de masse
par rapport à un corps central de masse 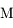 et de rayon
et de rayon 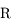 . On note
. On note 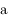 le demi-grand axe du satellite,
le demi-grand axe du satellite, 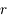 sa distance au corps central, et
sa distance au corps central, et 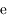 son excentricité supposée faible (
son excentricité supposée faible (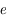 <<1).
<<1).
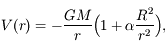 où
où 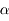 est une constante <<1 qui caractérise l'applatissement. On peut montrer qu'alors l'équation du mouvement du satellite s'écrit:
est une constante <<1 qui caractérise l'applatissement. On peut montrer qu'alors l'équation du mouvement du satellite s'écrit:
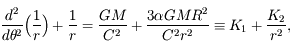 où
où 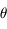 est la position angulaire du satellite sur sa trajectoire (
est la position angulaire du satellite sur sa trajectoire (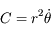 le moment cinétique.
le moment cinétique.
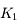 et
et 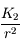 , et en déduire que la trajectoire du satellite est peu modifiée sous l'effet de l'applatissement du corps central, par rapport au problème à 2 corps classique.
, et en déduire que la trajectoire du satellite est peu modifiée sous l'effet de l'applatissement du corps central, par rapport au problème à 2 corps classique.
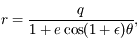 avec
avec 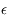 <<1, et exprimer
<<1, et exprimer 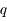 et
et 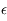 en fonction de
en fonction de 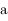 ,
, 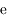 ,
, 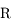 et
et 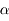 .
.
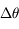 du périastre de la trajectoire, c'est-à-dire l'angle dont les axes de l'ellipse ont tourné après une révolution du satellite.
du périastre de la trajectoire, c'est-à-dire l'angle dont les axes de l'ellipse ont tourné après une révolution du satellite.
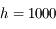 km autour de la Terre (
km autour de la Terre (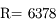 km,
km, 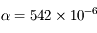 ).
).
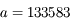 km et période orbitale
km et période orbitale 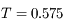 jours) autour de Saturne (
jours) autour de Saturne (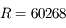 km,
km, 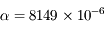 ).
).
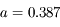 UA
UA 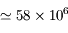 km,
km, 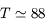 jours) autour du Soleil (
jours) autour du Soleil (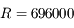 km,
km, 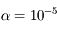 ). La précession observée du périhélie de Mercure s'élève en fait à
). La précession observée du périhélie de Mercure s'élève en fait à 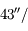 siècle. Commenter.
siècle. Commenter.
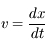
![[V] = LT^{-1}](../pages_dim-unites/equations_dim-unites/equation2.png)
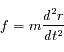
![[F]= MLT^{-2}](../pages_dim-unites/equations_dim-unites/equation4.png)
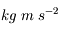 (couramment appelée Newton).
(couramment appelée Newton).
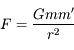
![[G]= [F]L^2M^{-2}=L^3T^{-2}M^{-1}](../pages_dim-unites/equations_dim-unites/equation7.png)
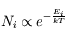
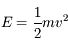
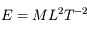 (l'unité SI est le
(l'unité SI est le 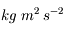 , couramment appelée Joule)
, couramment appelée Joule)
![[k] = ML^2T^{-2}K^{-1}](../pages_dim-unites/equations_dim-unites/equation12.png) . La valeur de k est donnée en J/K en SI.
. La valeur de k est donnée en J/K en SI.
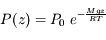
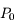 est la pression au sol, M la masse molaire moyenne, R la constante des gaz parfaits, g l'accélération de la pesanteur, et T la température (supposée constante) de l'atmosphère.
est la pression au sol, M la masse molaire moyenne, R la constante des gaz parfaits, g l'accélération de la pesanteur, et T la température (supposée constante) de l'atmosphère.
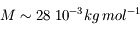 (masse molaire de l'azote, principal constituant)
(masse molaire de l'azote, principal constituant)
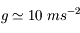
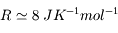
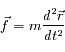
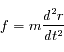
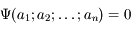
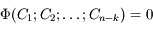
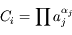
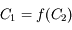
 de l'orbite est petite, on a besoin de l'approximation suivante:
de l'orbite est petite, on a besoin de l'approximation suivante:
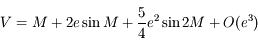
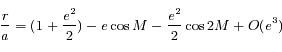
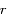 et
et 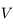 sont les coordonnées polaires du corps,
sont les coordonnées polaires du corps, 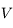 étant compté à partir du péricentre (
étant compté à partir du péricentre (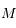 est le temps ou plus précisément c'est l'anomalie moyenne
est le temps ou plus précisément c'est l'anomalie moyenne 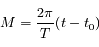 avec
avec 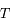 la période,
la période, 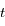 le temps et
le temps et 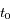 l'instant de passage au péricentre.
l'instant de passage au péricentre. 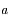 et
et  sont respectivement le demi-grand axe et l'excentricité de l'orbite.
sont respectivement le demi-grand axe et l'excentricité de l'orbite.

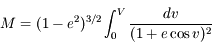
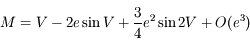
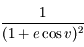 et intégrer le développement obtenu. Mutiplier enfin par celui de
et intégrer le développement obtenu. Mutiplier enfin par celui de 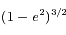 . Dans ces calculs, on prend soin de se limiter à l'ordre 2.
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
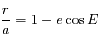 et
et 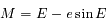 (
(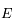 est l'
est l' en puissance de
en puissance de  et en fonction de
et en fonction de 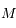 (limité à l'ordre 2)
(limité à l'ordre 2)
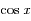 en
en 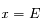 au voisinage de
au voisinage de 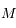 , c'est-à-dire, écrire:
, c'est-à-dire, écrire: 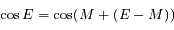 .
.
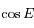 n'est utile que jusque l'ordre 1 !
n'est utile que jusque l'ordre 1 !
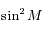 .
.
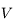 en fonction de
en fonction de 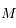 (limité à l'ordre 2 en
(limité à l'ordre 2 en  ).
).
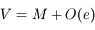
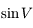 à l'ordre 0 (obtenu précédemment).
à l'ordre 0 (obtenu précédemment).
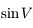 à l'ordre 1 et
à l'ordre 1 et 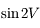 à l'ordre 0 (obtenus précédemment).
à l'ordre 0 (obtenus précédemment).
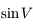 est obtenu de la manière suivante:
est obtenu de la manière suivante: 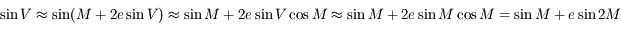 . Attention à la discussion sur l'ordre à chaque étape du calcul.
. Attention à la discussion sur l'ordre à chaque étape du calcul.
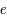 de l'orbite est petite, on peut écrire :
de l'orbite est petite, on peut écrire :
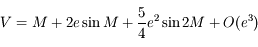 ,
,
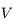 est l'angle entre la direction du péricentre et la position du corps sur son orbite (
est l'angle entre la direction du péricentre et la position du corps sur son orbite (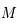 est le temps ou plus précisément l'anomalie moyenne
est le temps ou plus précisément l'anomalie moyenne 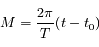 , avec
, avec 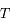 la période,
la période, 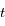 le temps et
le temps et 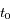 l'instant de passage au péricentre.
l'instant de passage au péricentre.
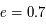 .
.
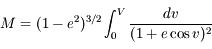
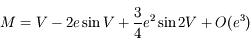
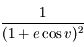 et intégrer le développement obtenu. Mutiplier enfin par celui de
et intégrer le développement obtenu. Mutiplier enfin par celui de 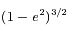 . Dans ces calculs, on prend soin de se limiter à l'ordre 2.
. Dans ces calculs, on prend soin de se limiter à l'ordre 2.
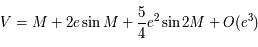 .
.
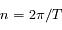 , où
, où 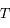 est la période orbitale de P).
est la période orbitale de P).
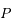 sur une ellipse de foyer
sur une ellipse de foyer 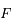 et de demi-grand axe
et de demi-grand axe 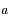 . On note
. On note 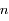 le moyen mouvement de la particule, et
le moyen mouvement de la particule, et 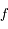 son
son 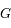 un point fictif tournant autour du foyer
un point fictif tournant autour du foyer 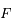 sur une orbite circulaire de rayon
sur une orbite circulaire de rayon 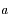 égal au demi-grand axe de
égal au demi-grand axe de 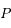 , avec une vitesse angulaire égale au moyen mouvement
, avec une vitesse angulaire égale au moyen mouvement 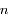 de la particule. On note
de la particule. On note 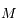 l'angle entre la ligne
l'angle entre la ligne 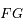 et la direction du péricentre de la particule (c'est donc l'
et la direction du péricentre de la particule (c'est donc l'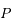 et on a
et on a 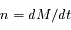 ).
).
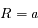 avec la Terre au foyer
avec la Terre au foyer 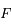 , et uniforme par rapport à
, et uniforme par rapport à 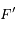 (appelé l'équant). Le modèle de Ptolémée était donc du premier ordre en excentricité, et le triomphe de Kepler fut d'élaborer une théorie à l'ordre 2.
(appelé l'équant). Le modèle de Ptolémée était donc du premier ordre en excentricité, et le triomphe de Kepler fut d'élaborer une théorie à l'ordre 2.
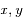 de
de 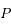 dans le repère orthonormé (
dans le repère orthonormé (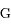 ,
,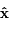 ,
,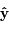 ) tel que
) tel que 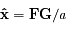 .
.
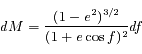 .
.
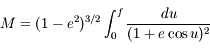 . Montrer à l'aide de cette relation que
. Montrer à l'aide de cette relation que 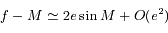 .
.
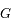 , la particule
, la particule 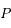 suit une orbite elliptique de demi-grand axe
suit une orbite elliptique de demi-grand axe 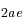 et de demi-petit axe
et de demi-petit axe 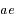 . Dans quel sens s'effectue ce mouvement et avec quelle période?
. Dans quel sens s'effectue ce mouvement et avec quelle période?
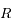 la distance entre
la distance entre 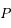 et le centre
et le centre 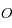 de l'ellipse. Montrer que
de l'ellipse. Montrer que 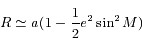 .
.
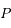 est alors un cercle centré sur
est alors un cercle centré sur 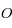 , et que l'angle
, et que l'angle 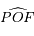 est confondu avec l'anomalie excentrique
est confondu avec l'anomalie excentrique 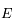 .
.
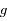 l'angle
l'angle 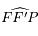 , où
, où 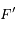 est le second foyer (vide) de l'ellipse. Ecrire
est le second foyer (vide) de l'ellipse. Ecrire 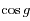 et en déduire que
et en déduire que 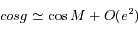 . On rappelle que
. On rappelle que 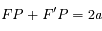 , et on utilisera le développement:
, et on utilisera le développement: 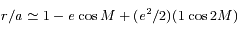 (voir cet
(voir cet 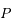 , vu du foyer
, vu du foyer 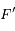 , est uniforme avec une vitesse angulaire égale au moyen mouvement
, est uniforme avec une vitesse angulaire égale au moyen mouvement 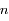 . Que peut-on dire des droites
. Que peut-on dire des droites 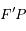 et
et 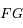 ?
?
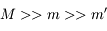 (qui constitue ce que l'on appelle un problème de Kepler perturbé).
(qui constitue ce que l'on appelle un problème de Kepler perturbé).
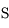 de masse
de masse 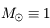 , de Jupiter
, de Jupiter 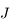 de masse
de masse 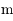 petite devant 1 (
petite devant 1 (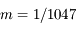 ) et d'un troisième corps
) et d'un troisième corps 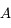 de masse
de masse 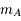 petite devant
petite devant 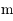 (par exemple un astéroïde ou une sonde spatiale). On note
(par exemple un astéroïde ou une sonde spatiale). On note 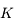 la constante de gravitation universelle,
la constante de gravitation universelle, 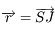 ,
, 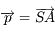 , et
, et 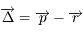 .
.
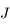 (c'est-à-dire de
(c'est-à-dire de 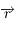 ).
).
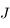 si la quantité
si la quantité 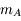 est négligeable?
est négligeable?
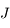 est circulaire (c'est-à-dire que
est circulaire (c'est-à-dire que 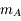 est négligeable et que
est négligeable et que 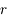 est constant). Montrer que l'équation du mouvement héliocentrique de
est constant). Montrer que l'équation du mouvement héliocentrique de 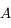 (c'est-à-dire de
(c'est-à-dire de 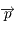 ) est
) est 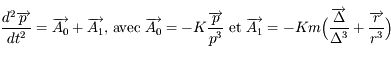 .
.
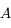 (c'est-à-dire de
(c'est-à-dire de 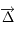 ) est
) est 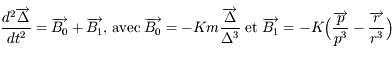 .
.
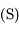 définie par
définie par 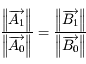 . On va voir notamment qu'elle a presque la forme d'une sphère,
appelée sphère d'influence de Jupiter. Justifier cette appellation en expliquant ce qui se passe pour le mouvement de
. On va voir notamment qu'elle a presque la forme d'une sphère,
appelée sphère d'influence de Jupiter. Justifier cette appellation en expliquant ce qui se passe pour le mouvement de 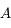 lorsque celui-ci est respectivement très à
l'intérieur ou très à l'extérieur de cette sphère.
lorsque celui-ci est respectivement très à
l'intérieur ou très à l'extérieur de cette sphère.
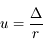 et
et 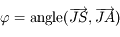 . Montrer que l'on a
. Montrer que l'on a 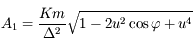 .
.
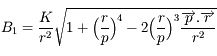 .
.
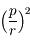 et
et 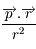 en fonction de
en fonction de 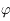 et
et 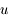 , montrer que
, montrer que 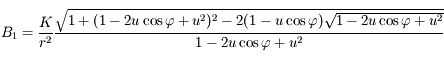 .
.
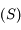 peut s'écrire
peut s'écrire 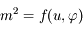 , et donner l'expression de
, et donner l'expression de 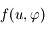 .
.
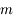 est petit devant 1, on peut considérer que, sur la surface
est petit devant 1, on peut considérer que, sur la surface 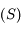 ,
, 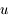 est également petit. Montrer que le développement de
est également petit. Montrer que le développement de 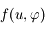 suivant les puissances de
suivant les puissances de 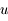 , limité à son terme de plus bas degré vaut
, limité à son terme de plus bas degré vaut 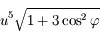 . Justifier alors le mot sphère dans l'expression sphère d'influence qui désigne la surface
. Justifier alors le mot sphère dans l'expression sphère d'influence qui désigne la surface 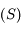 .
.
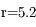 UA.
UA.
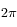 , c'est-à-dire:
, c'est-à-dire: 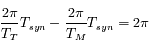 .
.
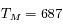 jours
jours
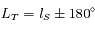 (modulo 360°).
(modulo 360°).
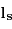
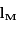
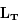
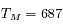 jours et
jours et 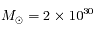 kg, on trouve
kg, on trouve 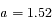 UA. Or 1 UA = 50 mm, donc le rayon du cercle est 76 mm.
UA. Or 1 UA = 50 mm, donc le rayon du cercle est 76 mm.
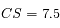 mm. Comme 1 UA = 50 mm, on en déduit que
mm. Comme 1 UA = 50 mm, on en déduit que 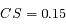 UA.
UA.
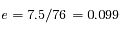 (à comparer à la valeur exacte: 0.093)
(à comparer à la valeur exacte: 0.093)
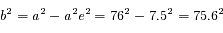 d'où
d'où 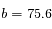 mm
mm 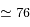 mm.
mm.
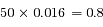 mm. Donc l'approximation est correcte étant donnée la précision du tracé.
mm. Donc l'approximation est correcte étant donnée la précision du tracé.
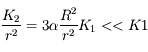 car
car 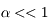 ,
, 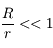
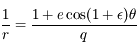
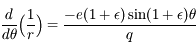
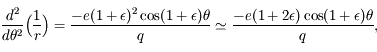 car
car 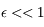 .
.
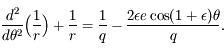
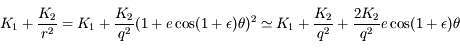 , car
, car 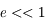 .
.
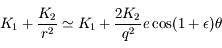 , car
, car 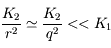 .
.
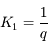 et
et 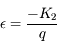 .
.
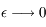 ,
, 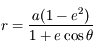 (solution du problème keplerien) donc
(solution du problème keplerien) donc 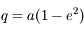 .
.
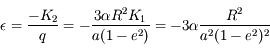 donc
donc 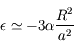 .
.
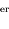 passage au périastre
passage au périastre 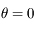 , au 2
, au 2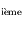 passage
passage  .
.
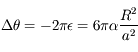 .
.
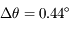
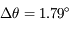
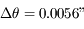 , i.e
, i.e 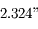 /siècle (période orbitale de Mercure = 88 jours). En fait la précession réelle est de
/siècle (période orbitale de Mercure = 88 jours). En fait la précession réelle est de 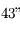 /siècle et s'explique par la relativité générale. Dans cette théorie,
/siècle et s'explique par la relativité générale. Dans cette théorie, 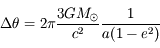 , où
, où 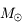 désigne la masse du Soleil.
désigne la masse du Soleil.
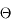 et la pesanteur g (on néglige au premier ordre les autres paramètres tels que le frottement ou la masse du fil, qui décrivent des écarts au problème idéal).
et la pesanteur g (on néglige au premier ordre les autres paramètres tels que le frottement ou la masse du fil, qui décrivent des écarts au problème idéal).
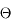 , sans dimension.
, sans dimension.
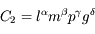
![[1] = L^{\alpha+\delta}M^{\beta}T^{\gamma-2\delta}](../pages_dim-unites/equations_dim-unites/equation27.png) , donc
, donc 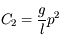 est sans dimension.
est sans dimension.
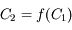 , soit
, soit 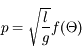
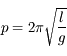 , et l'expérience confirme que la période ne dépend pas de l'angle initial si celui-ci est petit. On a montré sans le moindre effort la forme générale de la période (à une constante près) et le fait qu'elle ne dépend pas de la masse du pendule.
, et l'expérience confirme que la période ne dépend pas de l'angle initial si celui-ci est petit. On a montré sans le moindre effort la forme générale de la période (à une constante près) et le fait qu'elle ne dépend pas de la masse du pendule.
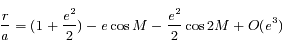
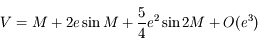
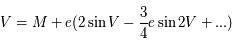 .
.
![V = M + \Sigma_{j=1}^\infty \frac{e^j}{j!} \frac{d^{j-1}}{dM^{j-1}} \Big{[} 2 \sin M - \frac{3}{4} e \sin 2M + ... \Big{]}^j](../pages_develop-appli/equations_develop-appli/equation56.png) .
.
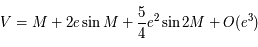 en développant la formule ci-dessus au second ordre.
en développant la formule ci-dessus au second ordre.
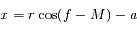 ,
, 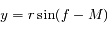
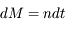
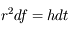 , avec
, avec 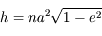 .
.
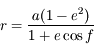 .
.
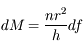 .
.
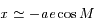 ,
, 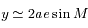 et
et 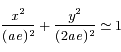 .
.
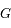 est en orbite circulaire autour de
est en orbite circulaire autour de 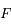 ,
, 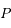 est en orbite autour de
est en orbite autour de 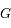 dans le sens opposé. La période est la même
dans le sens opposé. La période est la même 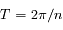 .
.
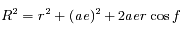 donc
donc 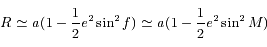 .
.
 , la trajectoire de
, la trajectoire de 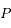 est ainsi un cercle de centre
est ainsi un cercle de centre 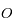 et l'angle
et l'angle 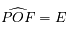
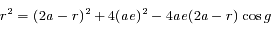
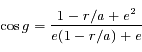 .
.
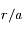 ,
, 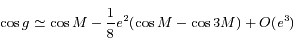 .
.
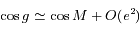 et
et 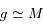 à l'ordre
à l'ordre  .
.
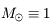 :
: 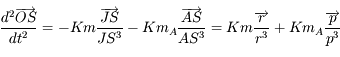 .
.
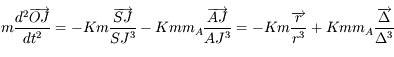 et
et 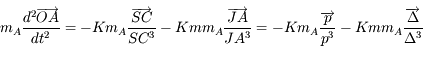 .
.
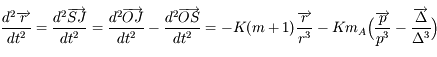 .
.
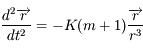 . C'est le problème de Kepler et le mouvement de
. C'est le problème de Kepler et le mouvement de 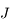 est une conique de foyer
est une conique de foyer 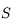 parcourue selon la loi des aires.
parcourue selon la loi des aires.
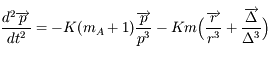 et
et 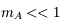 donc
donc 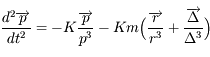
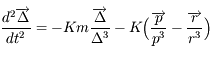 .
.
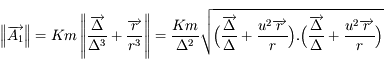
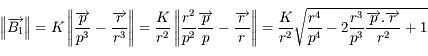
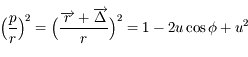 et
et 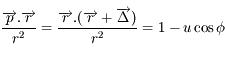 .
.
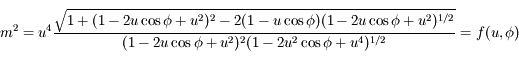
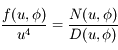 . On remarque que
. On remarque que 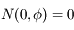 et
et 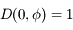 . Donc en développant
. Donc en développant 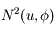 jusqu'au terme
jusqu'au terme 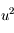 , on obtient
, on obtient 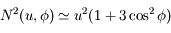 .
.
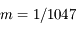 ,
, 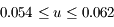 ,
, 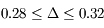 UA.
UA.