

Ex : carte du ciel |
Difficulté : ☆ Temps : 2h
L'exercice se fait en deux étapes, la première consiste à construire le profile de l'horizon, et la deuxième à placer sur cet horizon le fond d'étoiles fixes contenant la trajectoire apparente annuelle du Soleil.
On se place en un lieu de latitude 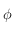 . Dessiner sur une sphère céleste avec l'équateur céleste comme plan de référence, le pôle céleste nord, l'horizon céleste, et les points cardinaux Sud, Ouest, Nord et Est. On notera aussi
. Dessiner sur une sphère céleste avec l'équateur céleste comme plan de référence, le pôle céleste nord, l'horizon céleste, et les points cardinaux Sud, Ouest, Nord et Est. On notera aussi 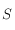 le point d'intersection du méridien passant par les pôles célestes nord et sud et par le zénith avec l'équateur céleste. On notera
le point d'intersection du méridien passant par les pôles célestes nord et sud et par le zénith avec l'équateur céleste. On notera 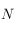 le point opposé à
le point opposé à 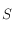 sur l'équateur céleste.
sur l'équateur céleste.

On mettra en évidence les angles suivants sur la figure: la déclinaison 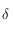 d'un point
d'un point 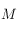 de l'horizon céleste, la latitude, la colatitude
de l'horizon céleste, la latitude, la colatitude 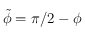 , et l'angle
, et l'angle 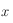 entre la direction ouest et le méridien équatorial passant par
entre la direction ouest et le méridien équatorial passant par 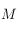 ,et compté positivement vers
,et compté positivement vers 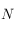 .
.
En utilisant la formule suivante, valable dans un triangle sphérique (voir le dessin ci-dessous),
déterminer la déclinaison 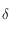 de
de 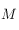 en fonction de
en fonction de 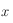 et
et 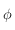 .
.
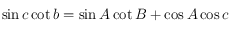 .
.
Au lieu de l'angle 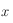 , on souhaite utiliser un angle associé au Soleil, appelé heure solaire vraie et noté
, on souhaite utiliser un angle associé au Soleil, appelé heure solaire vraie et noté 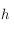 . Cet angle est mesuré sur l'équateur céleste, à partir de la direction
. Cet angle est mesuré sur l'équateur céleste, à partir de la direction 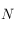 , et compté positivement vers l'Est.
Ainsi, l'Est,
, et compté positivement vers l'Est.
Ainsi, l'Est, 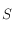 et l'Ouest correspondent respectivement à
et l'Ouest correspondent respectivement à 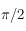 ,
, 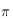 et
et 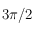 . Ecrire
. Ecrire 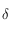 en fonction de
en fonction de 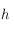 .
.
Etudier la fonction 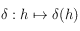 . On déterminera en particulier la valeur de
. On déterminera en particulier la valeur de 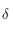 et de sa dérivée pour
et de sa dérivée pour 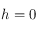 et
et 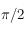 .
.
On souhaite maintenant déterminer l'équation de la trajectoire apparente annuelle du Soleil (qui est dans un plan appelé éclitpique) dans un repère où on a l'ascension droite en abscisse et la déclinaison en ordonnées.
La normale au plan de l'écliptique dirigée vers l'hémisphère nord a une direction constante par rapport à la direction du pôle céleste nord 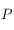 . L'angle entre ces deux directions est appelé obliquité est vaut
. L'angle entre ces deux directions est appelé obliquité est vaut 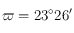 . Vu du pôle céleste nord, le Soleil décrit sa trajectoire dans le sens trigonométrique, c'est-à-dire que son ascension droite augmente au cours du temps.
. Vu du pôle céleste nord, le Soleil décrit sa trajectoire dans le sens trigonométrique, c'est-à-dire que son ascension droite augmente au cours du temps.
Faire un dessin de la sphère des fixes mettant en évidence l'équateur céleste, le grand cercle de l'écliptique et les coordonnées équatoriales du Soleil.
En déduire 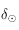 en fonction de
en fonction de 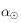 et de l'obliquité
et de l'obliquité 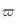 .
.
Etudier la fonction 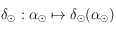 . On déterminera en particulier la valeur de
. On déterminera en particulier la valeur de 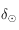 et de sa dérivée pour
et de sa dérivée pour 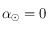 et
et 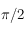 .
.
Déterminer les coordonnées du Soleil, aux équinoxes et aux solstices.
Il s'agit maintenant de positionner les deux graphes l'un par rapport à l'autre. C'est le Soleil qui fait le lien entre les deux. Il faut d'abord placer le Soleil en fonction de la date du jours. Une fois celui-ci positionné, il est facile de placer le graphe de l'horizon pour une heure solaire vraie donnée, puisque l'abscisse du Soleil sur cette carte correspond à l'heure solaire vraie. Ainsi lorsque le temps s'écoule le graphe de l'horizon va glisser sur le graphe des étoiles fixes et de l'écliptique (ou l'inverse suivant comment on choisi la transparence).
Il faut faire attention au fait que pour le graphe comportant l'horizon céleste, l'axe des abcisses est orienté de la droite vers la gauche, alors que pour la carte des étoiles fixes avec l'écliptique, l'axe des abscisses est orienté de la gauche vers la droite. Les deux axes vont de 0 à 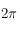 (en astronomie cependant on préfère noter les longitudes entre 0h et 24h).
(en astronomie cependant on préfère noter les longitudes entre 0h et 24h).
Déterminer l'ascension droite du Soleil en fonction de la date du jours (ceci permet finalement de résoudre complètement l'animation présentée dans l'introduction à cet exercice).
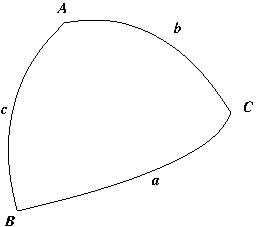
On utilisera la relation suivante valable dans un triangle sphérique de sommet 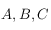 et de côté
et de côté 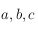 (
(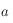 étant le côté opposé au sommet
étant le côté opposé au sommet 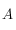 , etc.) où
, etc.) où  (voir la figure ci-dessous) :
(voir la figure ci-dessous) :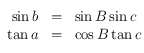 .
.