

Ex : astrolabe |
Difficulté : ☆☆ Temps : 2h
L'astrolabe est basée sur la projection stéréographique d'une sphère sur un plan. On considère ici la projection de pôle céleste sud 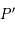 . Un point
. Un point 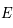 de la sphère aura pour image, le point
de la sphère aura pour image, le point 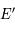 intersection de la droite
intersection de la droite 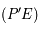 avec le plan
avec le plan 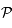 passant par le centre de la sphère
passant par le centre de la sphère 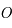 et perpendiculaire à la droite
et perpendiculaire à la droite 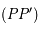 reliant les pôles. La figure suivante illustre cette projection.
reliant les pôles. La figure suivante illustre cette projection.
Quelle est l'image du pôle 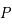 ? Quelles sont les points invariants par cette projection ?
? Quelles sont les points invariants par cette projection ?
On définie un repère sur le plan 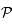 , centré en
, centré en 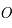 , l'axe des abscisses est dirigé vers l'origine des angles horaires sur l'équateur céleste et l'axe des ordonnées fait un angle de
, l'axe des abscisses est dirigé vers l'origine des angles horaires sur l'équateur céleste et l'axe des ordonnées fait un angle de 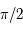 dans le sens trigonométrique vu du pôle céleste Sud. On utilisera alors un système de coordonnées polaires
dans le sens trigonométrique vu du pôle céleste Sud. On utilisera alors un système de coordonnées polaires 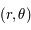 pour placer un point sur
pour placer un point sur 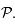
Soit 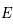 un point de
un point de 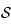 , de coordonnées
, de coordonnées 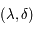 où
où 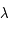 est l'angle horaire et
est l'angle horaire et 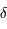 la déclinaison. Montrer que les coordonnées polaires de son image
la déclinaison. Montrer que les coordonnées polaires de son image 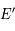 sont
sont 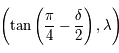 .
.
Montrer que la projection d'un cercle 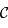 passant par le pôle céleste Sud
passant par le pôle céleste Sud 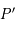 est une droite.
est une droite.
Soit 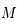 et
et 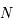 deux points de
deux points de 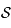 . Soit
. Soit 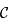 le cercle de
le cercle de 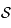 passant par ces points. On suppose que
passant par ces points. On suppose que 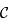 n'est pas un grand cercle. Il existe donc un cône de sommet
n'est pas un grand cercle. Il existe donc un cône de sommet 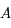 tangent à
tangent à 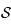 en
en 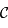 . Soit
. Soit 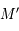 l'image de
l'image de 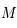 par projection sur
par projection sur 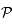 . La droite
. La droite 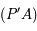 coupe le plan
coupe le plan 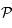 en
en 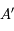 . Enfin, on appelle
. Enfin, on appelle  , le plan tangent à
, le plan tangent à 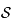 en
en 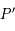 . La droite
. La droite 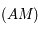 , coupe le plan
, coupe le plan  en
en 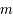 , et la droite
, et la droite 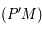 coupe le plan parallèle à
coupe le plan parallèle à  passant par
passant par 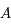 en
en 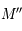 . La figure ci-dessous montre la construction.
. La figure ci-dessous montre la construction.
Montrer que 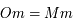 . En déduire que
. En déduire que 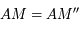 puis que
puis que 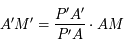 . En déduire que l'image de
. En déduire que l'image de 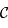 est un cercle.
est un cercle.
On suppose maintenant que le cercle 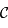 est un grand cercle.
Les tangentes en tout point de
est un grand cercle.
Les tangentes en tout point de 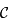 sont maintenant parallèles.
sont maintenant parallèles. 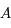 n'est plus défini, mais on peut encore construire le plan
n'est plus défini, mais on peut encore construire le plan  et le point
et le point 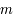 . On appelle
. On appelle 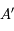 le point où la parallèle à
le point où la parallèle à 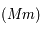 passant par
passant par 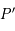 coupe la plan
coupe la plan 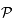 et
et 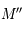 , le point où la droite
, le point où la droite 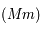 coupe le plan
coupe le plan 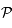 . Voir la figure ci-dessous.
. Voir la figure ci-dessous.
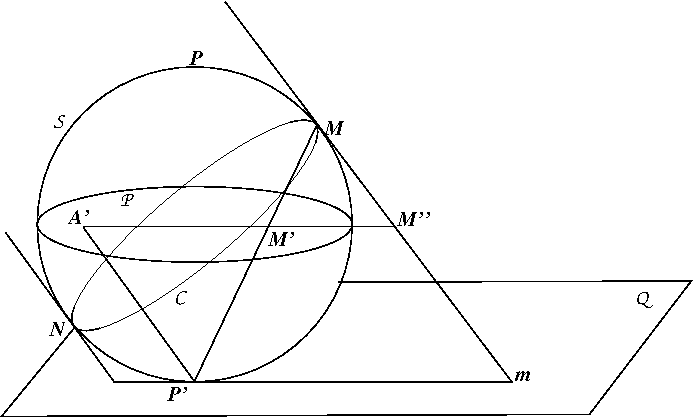
Montrer que 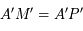 . En déduire de nouveau que l'image de
. En déduire de nouveau que l'image de 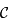 est un cercle.
est un cercle.
On définit un cercle 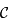 de
de 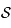 par son centre
par son centre 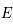 et son rayon
et son rayon 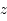 qui correspond en fait à l'angle sous lequel est vu le rayon depuis le centre
qui correspond en fait à l'angle sous lequel est vu le rayon depuis le centre 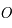 de la sphère
de la sphère 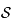 . On suppose que
. On suppose que ![z\in]0,\pi/2]](../pages_trigo/equations_trigo/equation162.png) . La figure ci-dessous illustre la situation.
. La figure ci-dessous illustre la situation.
On considère le grand cercle passant par 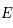 , ayant pour coordonnées horaires
, ayant pour coordonnées horaires 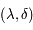 , et
, et 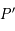 , coupant
, coupant 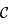 en
en 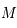 et
et 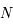 . Déterminer les coordonnées horaires de
. Déterminer les coordonnées horaires de 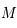 et
et 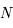 .
.
Montrer que les images 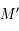 et
et 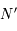 de
de 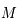 et
et 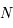 sont diamétralement opposées.
sont diamétralement opposées.
Ceci permet donc de construire facilement la projection du cercle, puisque connaissant 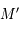 et
et 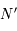 on peut déterminer le rayon et le centre du cercle projeté.
on peut déterminer le rayon et le centre du cercle projeté.
Ces propriétés permettent de construire facilement des cercles de latitude constante par rapport à l'équateur, comme les tropiques.
On connaît les coordonnées du Zénith (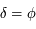 et
et 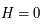 ). Ainsi, il est facile de tracer la projection de l'horizon puisqu'il correspond à un cercle de
). Ainsi, il est facile de tracer la projection de l'horizon puisqu'il correspond à un cercle de 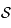 de centre
de centre 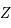 et de rayon
et de rayon 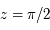 . De même différents cercles de hauteur constante
. De même différents cercles de hauteur constante 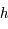 par rapport à l'horizon peuvent être obtenus en changeant la valeur de
par rapport à l'horizon peuvent être obtenus en changeant la valeur de 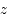 (on prend
(on prend 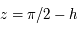 ).
).
Les projections des méridiens par rapport à l'équateur sont aussi faciles à tracer puisqu'ils correspondent à des demi-grands cercles passant par le pôle céleste sud 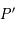 . Les projections correspondent donc à des demi-droites. On doit juste faire attention au fait qu'en astronomie le méridien d'origine par rapport à l'équateur correspond à celui qui contient le point vernal. Or, l'angle horaire du point vernal, appelé temps sidéral et noté
. Les projections correspondent donc à des demi-droites. On doit juste faire attention au fait qu'en astronomie le méridien d'origine par rapport à l'équateur correspond à celui qui contient le point vernal. Or, l'angle horaire du point vernal, appelé temps sidéral et noté 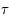 , varie dans le temps. Ainsi les projections des méridiens équatoriaux vont tourner en même temps que
, varie dans le temps. Ainsi les projections des méridiens équatoriaux vont tourner en même temps que 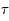 .
.
On souhaite maintenant tracer la direction des points cardinaux Sud, Sud-Ouest, Ouest, Nord-Ouest, Nord, Nord-Est, Est, Sud-Est. Ces directions sont par définition sur l'horizon céleste, et leur azimut (voir la partie sphère céleste dans le préambule) respectives sont 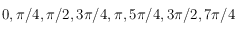 . On doit donc seulement calculer les coordonnées horaires de ces points pour pouvoir déterminer leur projection. Calculer donc les coordonnées horaires d'un point
. On doit donc seulement calculer les coordonnées horaires de ces points pour pouvoir déterminer leur projection. Calculer donc les coordonnées horaires d'un point 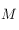 de l'horizon céleste d'azimut
de l'horizon céleste d'azimut 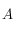 en un lieu de latitude
en un lieu de latitude 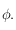
On veut maintenant construire la projection des méridiens par rapport à l'horizon céleste. Soit donc le méridien d'azimut 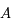 et le méridien d'azimut
et le méridien d'azimut 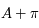 . Justifier que ces deux méridiens forment un grand cercle
. Justifier que ces deux méridiens forment un grand cercle 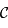 de
de 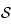 , dont on déterminera le centre sur
, dont on déterminera le centre sur 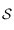 et le rayon. Ceci permet de construire facilement la projection des méridiens d'après ce qu'on a vu précédemment.
et le rayon. Ceci permet de construire facilement la projection des méridiens d'après ce qu'on a vu précédemment.
La trajectoire apparente du Soleil vue depuis la Terre est dans un plan appelé écliptique. L'inclinaison entre le plan de l'écliptique et le plan de l'équateur est constante et est appelée obliquité, notée 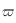 . Les variations de l'obliquité sont tellement faibles qu'on peut la supposer constante ici. La droite d'intersection entre ces deux plans passe par le point vernal et le centre de la sphère céleste
. Les variations de l'obliquité sont tellement faibles qu'on peut la supposer constante ici. La droite d'intersection entre ces deux plans passe par le point vernal et le centre de la sphère céleste 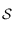 .
En s'aidant d'un dessin, déterminer les coordonnées équatoriales, puis les coordonnées horaires du pôle de l'écliptique
.
En s'aidant d'un dessin, déterminer les coordonnées équatoriales, puis les coordonnées horaires du pôle de l'écliptique 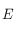 ayant une déclinaison positive.
ayant une déclinaison positive.
En déduire la méthode pour construire la projection de l'écliptique.
On suppose que le mouvement apparent du Soleil sur l'écliptique se fait de manière uniforme . Sachant que le 22 Mars de chaque année, le Soleil se trouve au point vernal, et que le mouvement se fait à ascension droite croissante au cours de l'année, déterminer les coordonnées équatoriales du Soleil, en fonction de la date du jours. En déduire ses coordonnées horaires.
On utilisera la relation suivante valable dans un triangle sphérique de sommet 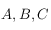 et de côté
et de côté 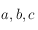 (
(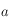 étant le côté opposé au sommet
étant le côté opposé au sommet 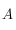 , etc.) où
, etc.) où 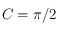 (voir la figure ci-dessous) :
(voir la figure ci-dessous) :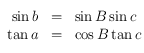 .
.