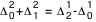En savoir plus: l'interpolation des éphémérides

En savoir plus

Une éphéméride est une table qui fournit, pour des dates particuières en principe équidistantes, les valeurs d'une ou de plusieurs fonctions qui décrivent l'évolution des positions des astres concernés, ou d'autres grandeurs relatives à ces astres. On appelle interpolation la technique de calcul qui permet d'évaluer les valeurs de ces fonctions pour des dates intermédiaires autres que celles qui figurent dans l'éphéméride.

Le cas le plus simple est celui où la fonction considérée varie assez lentement, ou est donnée avec assez peu de précision pour qu'aucun calcul ne soit nécessaire. On se contente alors d'une interpolation à vue (par exemple, magnitude de la planète Jupiter : aucun calcul n'est nécessaire, quand on examine l'éphéméride du chapitre 5, pour estimer que sa valeur est -1,8 le 2 juillet 2002).

Plus souvent, on devra employer l'interpolation linéaire et procéder comme suit. Soit :

t, l'instant pour lequel on veut calculer le fonction f ;

t₁, l'instant immédiatement inférieur ou égal à t et figurant dans l'éphéméride, la valeur correspondante de f étant f₁ ;

t₂, l'instant immédiatement supérieur à t et figurant dans l'éphéméride, la valeur correspondante de f étant f₂.

Alors, on calculera f par la formule :

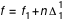
où

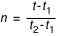et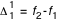

s'appellent respectivement facteur d'interpolation et différence première.

Dans certains cas, l'interpolation linéaire fournit un résultat trop imprécis. Pour s'en rendre compte, on forme le tableau suivant :

où t₀, t₁, t₂, t₃, etc sont des instants figurant dans l'éphéméride, et f₀, f₁, f₂, f₃, etc les valeurs correspondantes de la fonction f données par cette éphéméride. Les quantités :

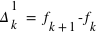
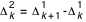{k=0,1,2,...}

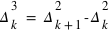
s'appellent respectivement différences premières, différences secondes, différences troisièmes, etc. L'interpolation linéaire est suffisante si les différences secondes sont inférieures à 4 unités du dernier ordre envisagé. Sinon (et à condition que les différences troisièmes n'excèdent pas 62 unités du dernier ordre envisagé, ce qui sera toujours le cas dans cet ouvrage), on emploie la formule de Bessel :

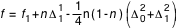
où n est le même facteur d'interpolation que plus haut, et, compte tenu des expressions ci-dessus :