
En savoir plus: approximation de Tchébychev (2) |
Soit t une date julienne appartenant à l'intervalle de temps t0, t0 + DT et y une coordonnée d'un astre. On calcule 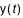 par la formule :
par la formule :
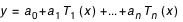
Où
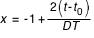
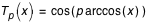 ;
; 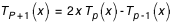 Avec :
Avec : 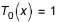 ;
; 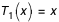
Les éphémérides de l'année sont publiées corps par corps. Pour chaque corps, on compte un certain nombre de variables qui pour des intervalles de temps donnés, sont représentées par des tableaux donnant les coefficients de leurs développements en polynômes de Tchebychev ou sous forme de fonctions mixtes.
En haut de chaque page, on trouve :
En bas de chaque page, on trouve les unités utilisées.
Les coefficients d'un tableau sont publiés en colonne. Pour chaque tableau, on précise :
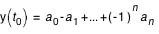
La valeur de contrôle permet de vérifier que les coefficients ont été correctement entrés en mémoire sur une calculette ou un calculateur. De plus, l'ensemble des valeurs de contrôle des tableaux d'une même variable donne une idée de l'évolution de cette variable au cours de l'année.
Pour calculer la valeur d'une coordonnée d'un astre pour une date t exprimée en UTC, on commence par :
Le calcul se poursuit de la manière suivante :