 |  |  |  |  |  |
Mécanique céleste, Temps et Calendriers Les éphéméridesEn savoir plus: approximation de Tchébychev (3) exemple de calcul |
En savoir plusExemple 1. Calculer le rayon vecteur héliocentrique de Mars le 5 Novembre 2003 à 16h 51m 42s UTC.
On effectue d'abord une correction pour se ramener à l'argument des éphémérides. Pour 2003, la valeur de TT - UTC n'est pas encore connue, mais on peut la prendre égale à 65 s. La date t est donc le 5 novembre 2003 à 16h 52m 47s argument des éphémérides.
On utilise les coefficients de la page B36 valables du 0 juillet 0h au 33 décembre 0h. Le calendrier des pages B148 et B149 donne les numéros JDA des jours de l'année correspondant au 0 juillet (JDA = 181) et au 5 novembre (JDA = 309). On a :
DT = 186 ;
t - t0 = 309 - 181 + 16h 52m 47s = 128.703 321 759 jours
On en déduit par la formule (2) :
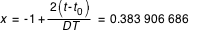
On peut calculer les polynômes de Tchebychev par l'un des deux algorithmes suivants :
Les polynômes de Tchebychev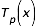 
sont calculés par la relation (3) :
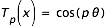où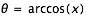 
On a : θ = 67°.424 117 27. On en déduit :
T1(x)= cos (θ) = x = 0.383 906 686
T2(x)= cos 2(θ) = -0.705 231 314
T4(x)= cos 4(θ) = -0.005 297 589
T6(x)= cos 6(θ) = 0.712 703 365
T8(x)= cos 8(θ) = -0.999 943 871
Les polynômes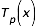 
sont calculés par la relation de récurrence (4) :
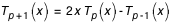
avec : 
; 
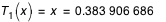
On en déduit :
,
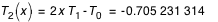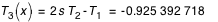, etc
Les polynômes de Tchebychev étant déterminés, le rayon vecteur R de Mars se déduit de la formule (1) :
,
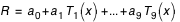Où les coefficients de a0, a1, ..., a9 sont ceux du tableau de la page B36 valables du 0 juillet 0h au 33 décembre 0h. On a donc :
R = 1.415 514 22 + 0.035 889 20 T1 + ... + 0.000 000 04 T9,
Soit finalement :
R = 1.412 255 01 ua.
 |  |