Les 3 lois énoncées par Johannes Kepler il y a 4 siècles ont apporté une alternative au paradigme alors en vigueur, les épicycles de Ptolémée, pour décrire le mouvement des planètes.
Elles ont substitué à une version idéalisée du monde des lois physiques basées sur une idée fertile, l'héliocentrisme, développée par Nicolas Copernic, et un concept novateur, la primauté de l'observation (Tycho Brahe).
Un rappel du formalisme mathématique et physique des
trajectoires rencontrées dans le problème à 2-corps est donné en fin de sous-chapitre.
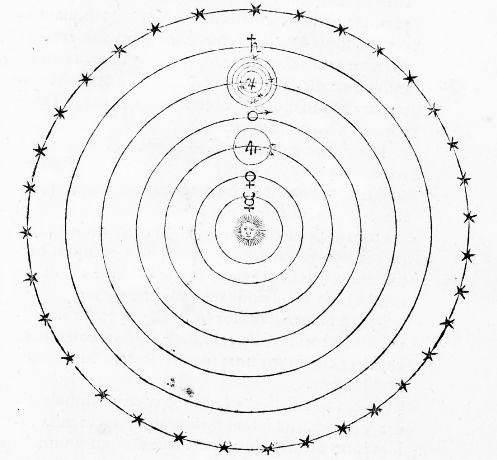
Dans le système de Copernic, le Soleil occupe la place centrale précédemment dévolue à la Terre.
Crédit :
Bibliothèque de l'Observatoire de Paris
Avant Copernic : le système de Ptolémée
Ptolémée (100-170) au deuxième siècle après J.-C., mettait la Terre au centre du système solaire (et donc au centre de l'Univers, à cette époque), et reproduisait le mouvement des planètes par une succession de mouvements circulaires emboîtés. Il contribua à faire admettre pendant plus de quatorze siècles l'idée que la Terre est immobile au centre de l'Univers.
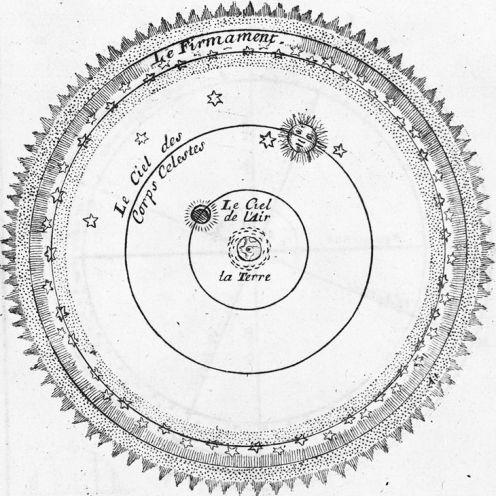
La Terre au centre. Une évidence après tout...
Crédit :
Bibliothèque de l'Observatoire de Paris
Les travaux astronomiques de Ptolémée sont regroupés dans un ouvrage majeur, la grande syntaxe mathématique, plus connu sous le nom arabe de l'Almageste. L'Almageste reprend dans ses grandes lignes la vision aristotélicienne du monde physique, avec les mêmes dogmes et principes : dichotomie Terre/Univers, immobilité de la Terre, etc.
Ptolémée rejeta le modèle des sphères emboîtées et perfectionna grandement les modèles grecs en introduisant la notion de point équant, un point fictif symétrique de la Terre par rapport au centre excentrique de l'orbite d'une planète. Le système résultant est extrêmement complexe, mais d'une précision mathématique remarquable (le modèle de Ptolémée permet ainsi de prédire des éclipses de Soleil). La perfection de ce modèle fera qu'il ne sera globalement pas remis en cause avant le XVIème siècle.
Le système de Copernic
Copernic (1473-1543), frappé par la complexité du système de Ptolémée, va bâtir une nouvelle représentation du monde, dans laquelle le Soleil est fixe au centre du système solaire.
Cette révolution de pensée ne s'imposera qu'après les observations de Galilée.
Dans le système de Copernic, le Soleil remplace la Terre comme centre du monde.

Le Soleil au centre du monde, à la place de la Terre.
Crédit :
Bibliothèque de l'Observatoire de Paris
Nicolas Copernic a publié son ouvrage De Revolutionibus orbium caelestium l'année de sa mort. Tous les mouvements planétaires sont centrés sur le Soleil, et la Terre n'est ni immobile, ni au centre du monde.
Elle est en effet animée de 2 mouvements : l'un sur elle-même en 24 h (qui remplace le mouvement de la sphère des fixes des Grecs anciens) et l'autre autour du Soleil en un an, faisant de la Terre une planète comme les autres.
Contrairement à ce que l'on croit parfois, Copernic ne va pas démontrer l'héliocentrisme, car il faudra attendre plus de 150 ans pour avoir une preuve du mouvement de la Terre. L'argument de Copernic est que son modèle est plus simple, plus logique et plus "harmonieux" que celui de Ptolémée (même si dans le détail le fonctionnement mathématique du système copernicien est assez complexe).
Le De Revolutionibus, malgré son côté fondamentalement révolutionnaire, fut reçu avec relativement d'indifférence par les savants de l'époque. Les travaux de Copernic connurent dans un premier temps la célébrité grâce aux éphémérides des planètes qui en furent déduites.
Repère chronologiques
Divers éléments d'histoire sont proposés au fil des pages, tel que le présente le tableau suivant.
- Ptolémée : géocentrisme et combinaisons de mouvements circulaires
- Copernic : un pas vers l'héliocentrisme
- Tycho Brahe : des observations de qualité inédite
- Kepler : des lois performantes
- Galilée : le principe fondamental de la dynamique
- Newton : la gravitation universelle
Un grand observateur
Tycho Brahe à Uraniborg

Tycho Brahe observant dans son observatoire d'Uraniborg. Pas d'instrument optique, mais des instruments de visée précise, tel le quart de cercle.
Crédit :
Bibliothèque de l'Observatoire de Paris
L'observatoire d'Uraniborg

L'observatoire d'Uraniborg.
Crédit :
Bibliothèque de l'Observatoire de Paris
Tycho Brahe a introduit une composante essentielle dans l'histoire de l'astronomie : des observations de qualité hors pair, menées pourtant sans l'aide d'aucun instrument optique.
Dans sa démarche, Tycho Brahe fut grandement aidé par le roi du Danemark, qui subventionna largement l'observatoire d'Uraniborg.
La vie de Kepler
Jean Kepler est né en Allemagne en 1571. Elève brillant, il devient
professeur de mathématiques en 1594 ; il a pour
maître en astronomie l'astronome Michel Maestlin, qui l'initie au système de Copernic.
En dessinant une figure au tableau noir en
juillet 1595, Kepler eut la révélation d'une idée à laquelle il
attacha une importance considérable : pourquoi le système
solaire comporte-t-il six planètes, et quel lien existe entre les
dimensions de leurs orbes ? Euclide ayant montré qu'il existait cinq polyèdres réguliers, chacun inscriptible dans une sphère et
circonscriptible à une autre sphère de même centre, les cinq
intervalles qui existent entre les six planètes ne peuvent pas, aux
yeux de Kepler, être le fruit du hasard : le Créateur a agi en
géomètre et l'homme est en mesure de découvrir le plan et la
perfection du monde créé.
Kepler publia ses théories en 1596, ce qui lui valu une certaine
notoriété, notamment celle d'être appelé auprès du plus grand
astronome-observateur de l'époque, Tycho Brahe. Lorsque Kepler arrive à Prague en février 1600, il se voit confier par Tycho Brahe l'étude de l'orbite de Mars. Cette planète présentait depuis l'Antiquité des anomalies dans son mouvement, alors impossibles à expliquer.
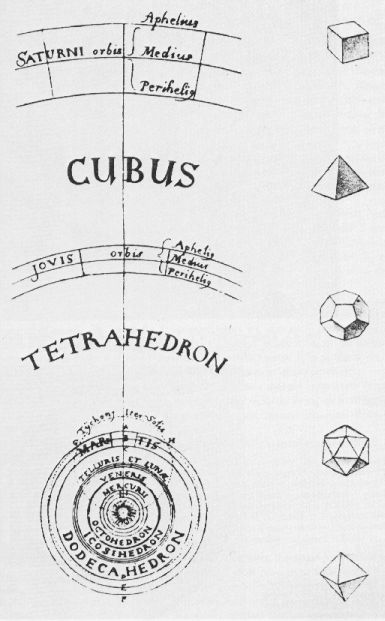
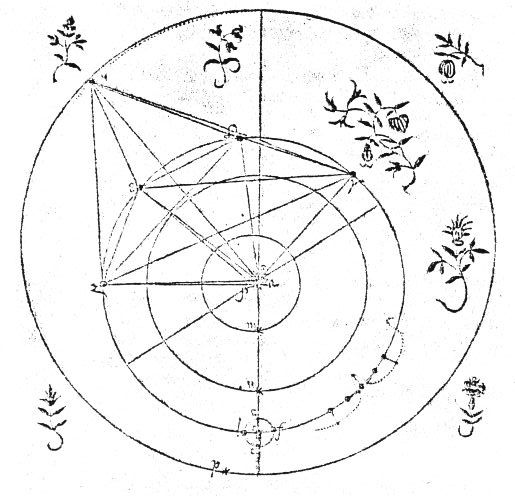
Pour Tycho Brahe, les orbites des planètes du système solaire se situent au niveau des sphères circonscrites
dans les solides platoniciens (polyèdres convexes réguliers, dont les faces sont des polygones convexes réguliers : le tétraèdre, le cube, l'octaèdre, l'icosaèdre et le dodécaèdre réguliers).
Crédit :
Bibliothèque de l'Observatoire de Paris
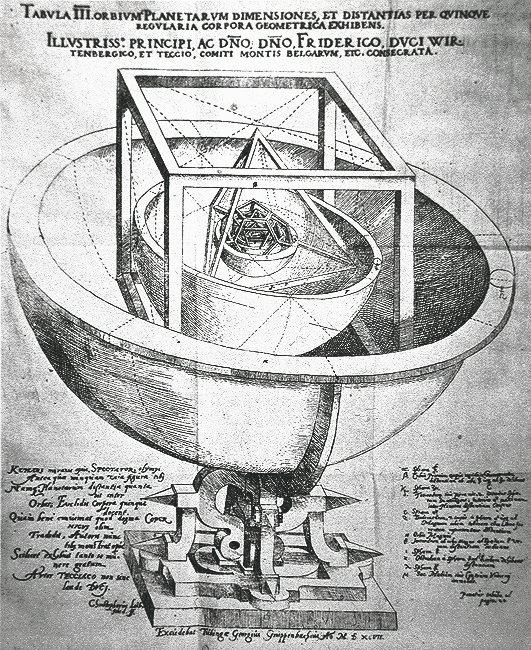
La succession de sphères et de solides emboîtés a permis à Kepler
l'élaboration d'une
cosmogonie originale... mais moins performante que ses 3 futures lois !
Crédit :
Bibliothèque de l'Observatoire de Paris
La primauté aux données observationnelles
A partir des observations accumulées par Tycho Brahe, Kepler se rend
compte qu'il faut rejeter la théorie des mouvements
circulaires uniformes. Pour résoudre le problème de l'orbite de Mars,
Kepler choisit quatre positions de la planète et, après de laborieux
calculs entachés d'erreurs qui, par chance, se compensent, parvient à
obtenir une orbite circulaire où le Soleil occupe le point équant. Ce
point équant, inventé au IIe siècle de notre ère par l'astronome
Ptolémée, est un point symétrique du Soleil par rapport au centre de
l'orbite. Pourtant, si d'autres positions de Mars s'insèrent
parfaitement dans la nouvelle orbite ainsi définie, deux observations
s'écartent de près de 8' de la position théorique : cette différence est supérieure à la précision des mesures. Au lieu de les
rejeter, Kepler renonce à son hypothèse : l'orbite ne peut pas être un
cercle.
Avant de se replonger dans la quête du mouvement de Mars,
Kepler décide de revoir dans le détail le mouvement de la Terre autour
du Soleil. En effet, pour passer d'une position géocentrique à une
position héliocentrique de Mars, il est nécessaire de traiter
correctement le mouvement orbital de la Terre : si celui-ci est
entaché d'erreurs, elles se répercuteront sur le mouvement de
Mars.
Le rôle central du Soleil
La vision géocentrique est nécessaire - c'est ce que l'on voit - mais pas suffisante : elle ne permet pas une approche totalement raisonnée.
Mettre le soleil au centre, comme l'a fait Copernic, permet non seulement de simplifier la forme de l'orbite, mais de plus a conduit Kepler à mesurer précisément la trajectoire de Mars.
En effet, si l'on observe Mars à des dates différentes, mais espacées d'un multiple de la période de révolution sidérale de Mars, alors la position de Mars par rapport au Soleil et aux étoiles est fixe. Il n'en est rien pour la Terre, qui en une durée non reliée à sa propre période de révolution a parcouru une portion de son orbite.
Cette situation permet d'observer Mars dans la même position par rapport au Soleil et aux étoiles, mais sous un angle différent. On peut alors mesurer la distance à Mars par triangulation.
Mesure de l'orbite de Mars
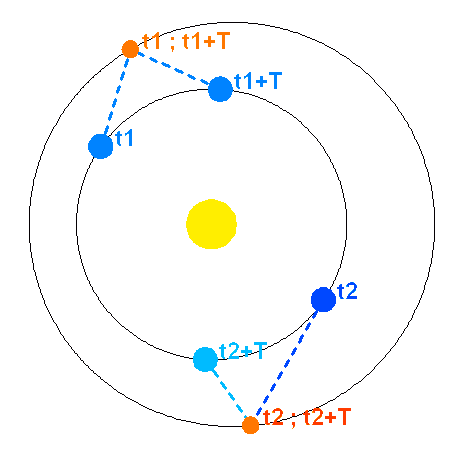
Faire tourner Mars autour du Soleil permet de reconstruire totalement son orbite.
Crédit :
ASM
La quête du mouvement de Mars, où comment rendre compte d'observations
Kepler imagine une méthode pour obtenir l'excentricité de l'orbite de
Mars à partir de trois observations de Mars faites à 687 jours
d'intervalle (période de révolution sidérale de Mars). Il sait en
outre que plus les planètes sont proches du Soleil, plus elles se
déplacent vite, tandis que plus elles s'en éloignent, plus leur
mouvement ralentit. Kepler en déduit que l'action du Soleil doit
varier en fonction de la distance de la planète au Soleil ; il la suppose
inversement proportionnelle à la distance. Première erreur.
Kepler cherche ensuite à calculer la durée que met la Terre pour passer d'une
position à une autre. Il décompose pour cela une portion de l'orbite
en petits segments et s'aperçoit que la durée passée par la Terre sur
de petits arcs est approximativement proportionnelle à la distance de
ces arcs au Soleil. Il assimile donc une surface à une somme de
lignes. Deuxième erreur.
Mais il transforme ces deux déductions en une loi correcte, la loi
des aires : le rayon
vecteur qui joint une planète au Soleil balaie des
aires égales en des intervalles de temps égaux. Historiquement,
Kepler découvrit donc en premier la loi que nous appelons la deuxième loi.
L'orbite martienne
L'observation de Mars à quatre dates différentes, mais correspondant toutes à une même position sidérale de la planète. Mars occupe alors la même position par rapport aux étoiles, les dates étant séparées par des intervalles de temps multiples de la période sidérale de révolution. Ceci a permis à Kepler la reconstruction de l'orbite de Mars.
Crédit :
Bibliothèque de l'Observatoire de Paris
Kepler reprend alors son étude de l'orbite de Mars. En calculant avec
son hypothèse des aires un grand nombre de positions, il obtient un
ovale, qu'il assimile à une
ellipse. Il constate alors que les positions de Mars sont
correctement représentées. La trajectoire elliptique, appelée
aujourd'hui la première loi, est découverte : les planètes décrivent
autour du Soleil des ellipses dont ce dernier occupe l'un des
foyers. Kepler publie ses découvertes en 1609 dans un ouvrage
difficile, l'Astronomia nova ("l'Astronomie nouvelle").
L'abandon d'une théorie inadaptée
Si la chance a favorisé Kepler dans ses recherches (forte excentricité
de l'orbite de Mars, erreurs de principe qui se compensent), on doit
reconnaître en lui un travailleur acharné et inspiré. On lui doit surtout l'abandon du mouvement circulaire
uniforme -- principe remontant à l'Antiquité auquel Tycho Brahe
accordait encore une valeur absolue -- et un souci constant de
vérifier que les hypothèses s'accordent avec les observations (ce qui
n'était pas le cas de Copernic), en quoi il mêle intimement faits et
théories, deux composantes fondamentales de la démarche scientifique.
Toujours attaché à trouver des harmonies dans les orbites planétaires,
Kepler essaye d'associer les intervalles musicaux aux diamètres des orbites planétaires. Cette idée qui nous semble aujourd'hui un peu étrange le conduit à la troisième loi en 1618 : les cubes des
demi-grands axes sont proportionnels aux carrés des périodes de révolution. La troisième loi de Kepler contribuera à stimuler les découvertes ultérieures de Newton sur la gravitation universelle et le
mouvement des deux corps.
Reconstruire l'orbite de Mars
Kepler a reconstruit l'orbite de Mars en analysant son orbite sous une double approche : le mouvement de Mars autour du Soleil est à considérer dans un référentiel héliocentrique ; l'observation de ce mouvement est réalisée depuis la Terre, et apporte un point de vue différent à chaque période sidérale de Mars.
L'appliquette ci-jointe explicite ce point de vue :
Reconstruire l'orbite de Mars 
La 1ère loi de Kepler
La première loi de Kepler énonce que la trajectoire des planètes est plane. C'est ce que dévoile la trace d'une orbite planétaire, lors d'une révolution sidérale.
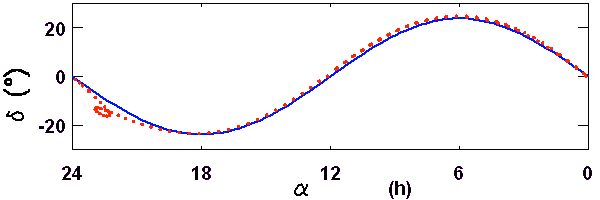
Trace de l'orbite de Mars au cours d'une année sidérale (points rouge). L'allure de la courbe correspond à l'un des éléments introduits par la 1ère loi de Kepler : l'orbite des planètes est plane. La trace bleue représente ce que l'on observerait si les plans orbitaux de la Terre et de Mars coïncidaient, ce qui n'est pas exactement le cas.
Crédit :
ASM
 Prérequis
Prérequis
Référentiels - Notion sur les coniques
Enoncé des lois de Kepler
Les 3 lois de Kepler expriment les conclusions que Kepler a tirées des
observations de Tycho Brahe.
Leur caractère empirique -- elles décrivent le mouvement d'une planète
autour du soleil, mais ne l'expliquent pas -- n'obère en rien leur portée.
Elles ont permis la formalisation par Newton de la loi de gravitation universelle.
 Définition
Définition
- 1ère loi :
Les planètes parcourent des orbites planes, elliptiques.
Le Soleil occupe l'un des foyers de l'ellipse.
- 2ème loi :
En des durées égales, une planète balaye des aires égales.
- 3ème loi :
Le rapport du carré de la période de rotation au cube du demi-grand axe
est identique pour toutes les planètes du système solaire.
La 2ème loi de Kepler
La 2ème loi de Kepler, ou loi des aires, illustrée dans plusieurs cas.
Les différentes "aires balayées" par le rayon vecteur en des durées
égales sont égales. Le secteur angulaire correspondant est donc bien
plus grand au voisinage du périhélie que de l'aphélie, et cet effet est
d'autant plus marqué que l'excentricité de la trajectoire est proche de
1.
La 2e loi de Kepler, dite loi des aires

Illustration de la 2ème loi de Kepler : cas de Mars. L'excentricité de 0.09 suffit pour
s'écarter sensiblement d'une rotation à vitesse angulaire uniforme.
Crédit :
ASM
La 2e loi de Kepler, dite loi des aires

Illustration de la 2ème loi de Kepler : orbite de transfert (entre une orbite basse,
accessible avec un lanceur tel Ariane, et
une orbite géostationnaire).
Crédit :
ASM
La 2e loi de Kepler, dite loi des aires

Illustration de la 2ème loi de Kepler : comète de Halley. La comète passe bien plus de
temps au voisinage de l'
aphélie qu'à celui du
périhélie.
Crédit :
ASM
La 2ème loi de Kepler permet la détermination de l'équation horaire du
mouvement le long de la trajectoire de l'objet.
Les positions des objets (comète de Halley, satellite sur orbite de transfert géostationnaire)
sont ici représentées à des dates équiréparties le long d'une période
orbitale. Le mouvement est d'autant moins uniforme que l'excentricité de l'orbite
est proche de 1 ; la vitesse orbitale est plus rapide au périastre qu'à
l'apoastre.
La 2e loi de Kepler, loi horaire

L'intervalle de temps est constant d'une position à l'autre. Le
mouvement est rapide au
périgée, lent à l'
apogée.
Crédit :
ASM
La 2e loi de Kepler, loi horaire

L'intervalle de temps est constant d'une position à l'autre. Le
mouvement est rapide au périhélie, lent à l'aphélie.
Crédit :
ASM
La 3e loi de Kepler

Cette simulation suppose les 4 planètes internes du système solaire en phase à un instant donné. Cette hypothèse est irréaliste, mais elle permet de montrer les avancées angulaires de Vénus, de la Terre et de Mars, Mercure ayant accompli une révolution entière.
Crédit :
ASM
La 3ème loi de Kepler
La 3ème loi de Kepler entraîne une période d'autant plus rapide que la planète est proche de l'étoile. L'animation ci-jointe, supposant de manière uniquement illustrative qu'à une date donnée les planètes telluriques pourraient être en phase, montre leur avancée respective au bout d'une durée égale à la période de révolution de Mercure.

La loi de Kepler dans le système solaire
Vérifier à l'aide de l'appliquette la 3ème loi de Kepler pour les planètes du système solaire.
- Sélectionner la première case de la dernière colonne.
- Afficher : =c1^2/b1^3
- Pourquoi, dans le système d'unité proposé (distance en UA, période en années), le résultat est-il quasiment égal à 1 ?
On remarque que la validité est moins bonne pour les planètes au-delà de Jupiter, qui ressentent en fait un champ de force moyen de masse totale la masse du Soleil complétée par celle de Jupiter.
 QCM
QCM
 Les lois de Kepler par J. Kepler
Les lois de Kepler par J. Kepler
Difficulté : ☆☆
Temps : 20 min
Cet exercice vous propose une lecture commentée de
l'histoire de
l'obtention des lois de Kepler.
Il se réfère au texte présentant les
aspects historiques de l'oeuvre de J. Kepler.
Question 1)
Pourquoi 6 planètes seulement sont-elles citées ? Les identifier.
Lesquelles étaient connues en l'an 1600 ?
Question 2)
Que signifie "traduire correctement le mouvement orbital de la Terre"
à l'époque de Kepler?
Introduire la notion de référentiel.
Question 3)
Que représentent 8' (8 minutes d'angle) dans le ciel ? Traduire cette
distance angulaire en : fraction du diamètre lunaire, diamètre martien
maximal, longueur rapportée sur l'orbite martienne, durée de parcours sur
l'orbite martienne. On donne :
- diamètre martien : 6800 km
- demi-grand axe de l'orbite martienne : 1.5 UA
- révolution sidérale : 687 j
Le diamètre lunaire couvre environ 1/2 degré.
 Le cadre des lois de Kepler
Le cadre des lois de Kepler
Difficulté : ☆☆
Temps : 20 min
Question 1)
Préciser les conditions dans lesquelles les lois de Kepler s'appliquent.
[1 points]
Question 2)
Que représente et signifie le terme "constante", dans l'équation
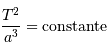
qui traduit la 3ème loi de Kepler.
[1 points]
Question 3)
A quelle(s) condition(s) pourrait-on appliquer les lois de Kepler à une
étoile au sein d'un amas stellaire ?
[1 points]
Quel point de vue adopter ?
Comme le montrent les observations de Kepler, le mouvement de Mars, vu de la Terre et décrit dans un référentiel géocentrique, n'est pas des plus simples à comprendre. Ce qui ne va pas ? Le référentiel !
Mouvement de Mars vu de la Terre
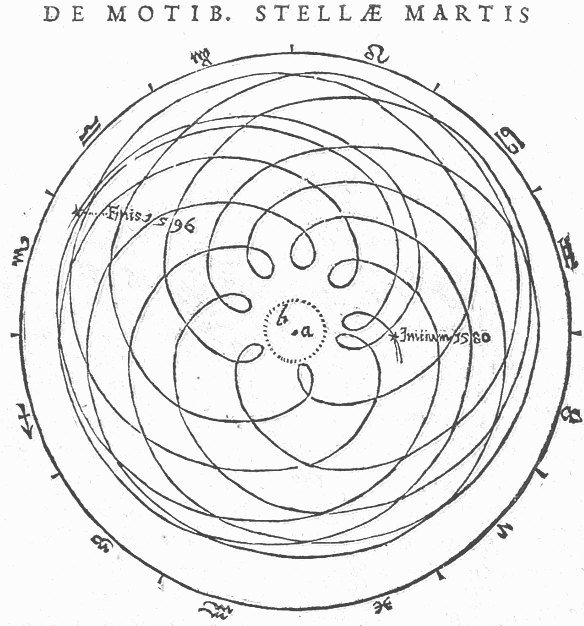
L'orbite de Mars vue dans le référentiel géocentrique. Schémas de Kepler de 1580 à 1596. La Terre est au centre, le soleil orbite sur le cercle en pointillés. Au cours de l'année martienne, la distance Terre-Mars peut varier dans des proportions de 1 à 6.
Crédit :
Bibliothèque de l'Observatoire de Paris
Mouvement de Mars vu de la Terre et du Soleil

L'orbite de Mars au voisinage de
l'
opposition planétaire, vue de la Terre ou dans le référentiel héliocentrique
Crédit :
ASM
Vue de la Terre, l'orbite apparente de Mars dessine une boucle.
Cette vision géocentrique complique la perception du phénomène. Vue du Soleil, à la conjonction planétaire, la Terre se contente de doubler Mars.
Problème : comment avoir, lorsque l'on est observateur terrestre, autre chose qu'une vision géocentrique ?
Point de vue héliocentrique
Les astronomes Copernic et Kepler ont résolu ce problème, en
conceptualisant ces mouvements, Copernic, en mettant le soleil au centre
du système solaire, Kepler en décrivant les mouvements planétaires par
ses 3 lois.
 Objectifs
Objectifs
La page "Des lois de Newton aux lois de
Kepler" montre comment l'on dérive aujourd'hui les lois de Kepler des lois de la gravitation et du formalisme de mécanique classique. Mais historiquement, les 3 lois de Kepler sont antérieures au formalisme newtonien, comme le plus souvent le fait observationnel précède la formalisation théorique. Il est important de voir comment les lois de Kepler portent en elles les germes de la loi de gravitation.
Ce qu'induit la première loi
La 1ère loi de Kepler donne
un rôle particulier
au soleil, qui peut être doublement interprété.
Du point de vue dynamique, le rôle central du soleil est clairement énoncé. Si
aujourd'hui la prépondérance du soleil au sein du système solaire
est un fait avéré et reconnu, il
n'en était rien au XVIIe siècle. Le Soleil est centre de force, et ce
d'autant plus que toute masse dans le système solaire est négligeable
devant la masse du soleil.
En terme de référentiel d'étude, la 1ère loi
introduit clairement le référentiel héliocentrique, qui est le "bon"
référentiel d'étude, car bien mieux galiléen que le référentiel
géocentrique. La première loi identifie donc clairement un centre de force supposé
immobile, ainsi que le bon référentiel associé.
Définition des coordonnées et vecteurs unitaires polaires
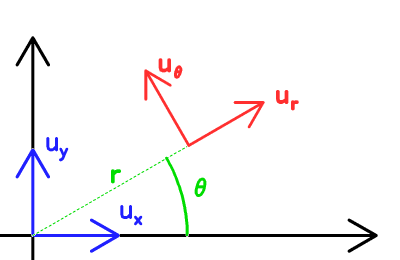
La base polaire plane est bien adaptée au problème képlérien : la 1ère
loi de Kepler énonce en effet que la trajectoire s'inscrit dans un plan,
et la 2ème loi que la force est centrale.
Crédit :
ASM
Ce qu'induit la deuxième loi
La 2ème loi de Kepler énonce la loi des aires,
càd la conservation du moment cinétique du système. Ceci est spécifique
des forces centrales. Des 1ère et 2ème lois ressort donc
l'idée que le soleil est centre de force. Cette force peut s'écrire
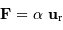 ,
le vecteur
,
le vecteur  étant un vecteur
unitaire radial défini par
rapport au centre de force.
étant un vecteur
unitaire radial défini par
rapport au centre de force.
Ce qu'induit la troisième loi
Le lien entre la période et le
demi-grand axe donné
par la 3ème loi de Kepler est spécifique à une
dépendance particulière du module de la force vis à vis de la variable
radiale. Cette loi n'apparaît que pour une force variant en 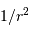 .
.
L'ensemble des lois de Kepler conduit finalement à une force s'écrivant de
la forme :
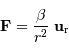
Les lois de Kepler n'en disent pas plus sur ce paramètre 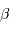 .
Ce sont les lois de la gravitation, dues à Isaac Newton, qui permettent d'expliciter sa forme.
.
Ce sont les lois de la gravitation, dues à Isaac Newton, qui permettent d'expliciter sa forme.
Des lois de Kepler à une force centrale variant comme l'inverse du carré de la distance
 Démonstration
Démonstration
En coordonnées polaires planes, définies dans le plan de l'orbite par rapport au foyer décrit par la 1ère loi de Kepler, on exprime les rayon vecteur, vitesse et accélération de l'objet par :
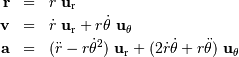
La composante orthoradiale de l'accélération s'identifie, à une constante près, à la dérivée temporelle du moment cinétique (perpendiculaire au plan de la trajectoire) :
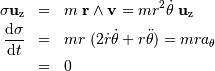
La nullité de la composante orthoradiale de l'accélération est bien la
signature d'une force centrale.
La démonstration de la 3ème loi de Kepler,
dans le cas d'un mouvement circulaire, dérive du jeu d'écriture suivant,
avec 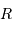 le rayon de l'orbite,
le rayon de l'orbite, 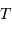 la période et
la période et 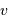 la vitesse de l'objet :
la vitesse de l'objet :
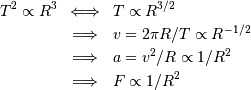
 Objectifs
Objectifs
Si, historiquement, les lois de Newton ont été
dérivées des lois de
Kepler, on retrouve aujourd'hui les lois de Kepler comme
application des lois de Newton.
Hypothèses
L'examen des masses des principaux objets du système solaire dévoile un
poids lourd, le soleil, entouré d'un cortèges de petits objets, les
planètes. Ceci définit le cadre des approximations usuellement faites
pour décrire le mouvement d'une planète : on la considère de masse
négligeable par rapport à la masse du soleil, et l'on néglige les
interactions interplanétaires.
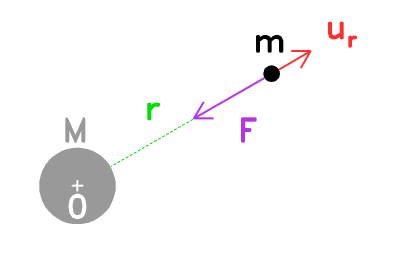
Force gravitationnelle.
Crédit :
ASM
 Le vecteur excentricité
Le vecteur excentricité
Difficulté : ☆☆☆
Temps : 40 min
Une façon très performante de faire de la physique consiste à associer à
une loi physique un invariant.
Pour une particule dans un champ de force gravitationnel, le champ de force étant à circulation conservative (voir la
signification de ces termes dans le cours de physique), l'énergie
mécanique se conserve ; la force étant centrale, le moment cinétique se conserve.
Le but de cet exercice est de montrer
quel invariant est associé au fait que le module de la force
gravitationnel varie comme l'inverse du carré de la distance. Il permet
par ailleurs de retrouver l'équation de la trajectoire elliptique d'un
satellite dans un champ de force central, moyennant un peu de
gymnastique calculatoire.
On considère un satellite, de masse 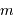 , dans le champ de force central d'un corps de
masse
, dans le champ de force central d'un corps de
masse 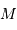 . On repère sa
position par le vecteur radial
. On repère sa
position par le vecteur radial 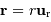 . On note
. On note 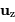 le vecteur
orthonormé normal au plan de la trajectoire, et portant le moment
cinétique du satellite, tel que le trièdre
le vecteur
orthonormé normal au plan de la trajectoire, et portant le moment
cinétique du satellite, tel que le trièdre 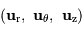 forme
un trièdre orthonomé direct.
forme
un trièdre orthonomé direct.
Question 2)
On construit le produit vectoriel 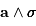 . Donner son expression
en fonction du vecteur
. Donner son expression
en fonction du vecteur 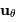 .
.
Dans la base directe 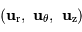 :
:
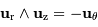
Question 3)
Intégrer l'équation précédemment obtenue pour 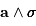 .
.
Dans le premier terme, 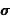 est constant.
est constant.
Par définition, 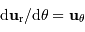 , et donc
, et donc
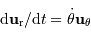
Question 4)
On multiplie scalairement l'équation précédemment obtenue
par le vecteur position 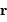 .
Montrer que ceci permet de retrouver l'équation de la trajectoire
.
Montrer que ceci permet de retrouver l'équation de la trajectoire
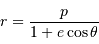
en choisissant pour origine de la variable angulaire 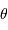 la
direction et le sens du vecteur
excentricité
la
direction et le sens du vecteur
excentricité 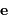
On rappelle la relation concernant le produit mixte :
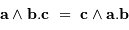
Question 5)
Faire un schéma, représentant le vecteur excentricité 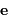 et la
trajectoire.
et la
trajectoire.
Systèmes doubles
L'astéroide Eugénie et son satellite
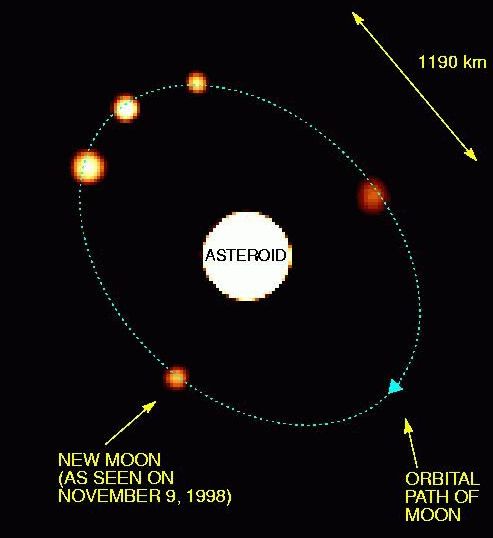
Superposition d'images obtenues
par optique adaptative au télescope
CFH (Merline, 1998). La détermination des paramètres
orbitaux du satellite -- période de rotation et demi-grand axe -- permet
de mesurer la masse de l'astéroïde
(
exercice).
La période est 4.7 jours, le demi-grand axe 1190 km.
Crédit :
CFHT
Le mouvement d'Eugénie

Le satellite de l'astéroïde Eugénie, observé en optique adaptative :
film obtenu avec 5 poses à 5 dates différentes
Crédit :
CFHT
Sirius A et B
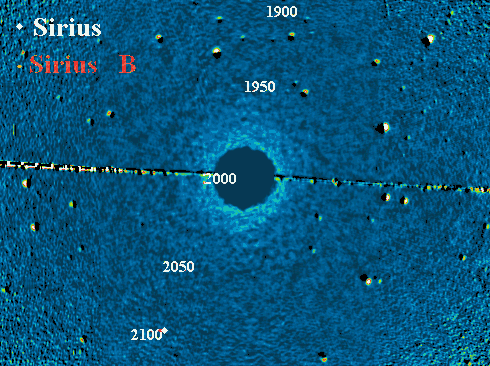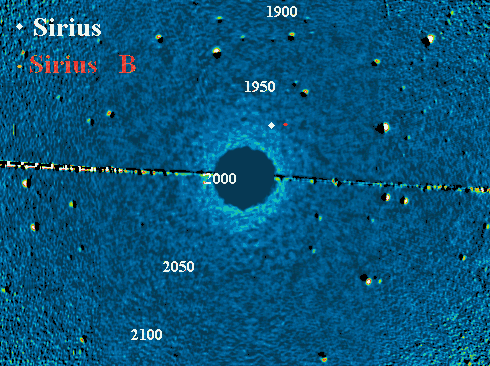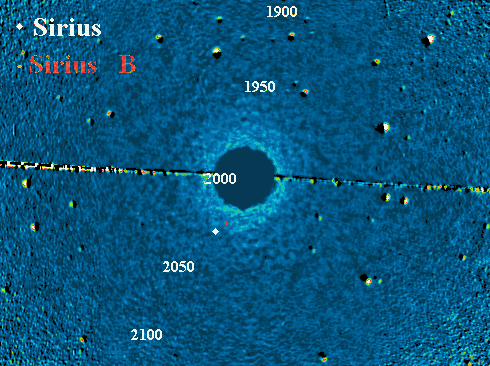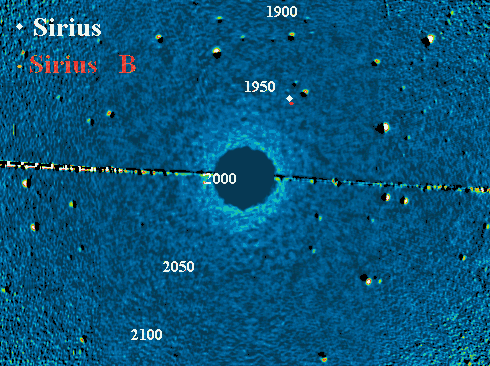
Animation des orbites de Sirius A et B (respectivement les points blanc et
rouge), sur fond d'étoiles fixes. Au mouvement apparent du système se superpose
la rotation du système.
Crédit :
Observatoire du Pic du Midi
L'observation des systèmes doubles est cruciale en astronomie, car elle donne accès à la mesure de la masse du système. On en voit deux exemples, à des échelles différentes :
 Objectifs
Objectifs
La 3ème loi de Kepler porte en elle, comme toute loi physique, une
potentialité énorme : généraliser le particulier, pour mieux comprendre
comment fonctionne l'univers.
Il se trouve que sur ce point de vue, elle fonctionne extraordinairement
bien. Elle permet de "peser" tout objet de l'Univers, à la seule
condition qu'un objet moins massif tourne autour de lui.
Déterminer la masse du centre de force
Peser est à prendre ici non dans son sens physique (mesurer le poids),
mais dans son sens de la vie courante : mesurer la masse.
La mécanique newtonienne permet de préciser la constante intervenant
dans la 3ème loi de Kepler appliquée à un système ressemblant au système
solaire : un ou des objets peu massifs tournant dans le potentiel
central d'un corps plus massif.
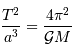
Cette loi implique 3 paramètres physiques : la période 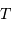 de révolution
et le demi-grand axe de l'orbite, et la masse
de révolution
et le demi-grand axe de l'orbite, et la masse 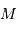 du corps central.
du corps central.
La mesure de 2 parmi ces 3 paramètres permet d'en déduire le 3ème : ceci
est mis à profit pour déterminer la masse 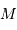 du centre de force à
partir des paramètres orbitaux
du centre de force à
partir des paramètres orbitaux 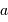 et
et 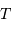 . Ces 2 termes sont en effet
observables, alors que la masse ne l'est pas.
. Ces 2 termes sont en effet
observables, alors que la masse ne l'est pas.
La mesure de la période 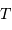 nécessite de repérer le mouvement le long de
la trajectoire.
nécessite de repérer le mouvement le long de
la trajectoire.
La mesure du demi-grand axe de l'orbite découle de la mesure de sa
taille angulaire, et nécessite de connaître la distance du système.
On voit une fois encore l'importance de la mesure des distances en
astronomie.
La 3ème loi de Kepler appliquée au système solaire
| Planète | 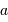 | 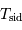 |  | 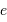 | 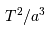 |
| UA | an | deg | | 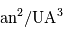 |
| Mercure | 0.3871 | 0.2408 | 7.0 | 0.206 | 0.9996 |
| Vénus | 0.7233 | 0.6152 | 3.4 | 0.007 | 1.0002 |
| Terre | 1.0000 | 1.0000 | -- | 0.017 | 1 |
| Mars | 1.5237 | 1.8808 | 1.8 | 0.093 | 1.0000 |
| Jupiter | 5.2026 | 11.862 | 1.3 | 0.048 | 0.9992 |
| Saturne | 9.5547 | 29.457 | 2.5 | 0.056 | 0.9948 |
| Uranus | 19.218 | 84.020 | 0.8 | 0.046 | 0.9946 |
| Neptune | 30.109 | 164.77 | 1.8 | 0.009 | 0.9946 |
Indépendamment de l'inclinaison  sur l'écliptique et de l'excentricité
sur l'écliptique et de l'excentricité
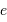 de l'orbite de chacune des 8 planètes, la relation
de l'orbite de chacune des 8 planètes, la relation 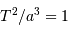 est vérifiée, avec
est vérifiée, avec 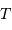 la période de révolution sidérale.
Les désaccords proviennent des écarts aux hypothèses de Kepler.
Remarque : dans le système solaire, les masses des planètes et de la
plupart de leurs satellites sont connues avec une précision relative de
l'ordre de
la période de révolution sidérale.
Les désaccords proviennent des écarts aux hypothèses de Kepler.
Remarque : dans le système solaire, les masses des planètes et de la
plupart de leurs satellites sont connues avec une précision relative de
l'ordre de 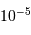 . Il s'agit de la précision à laquelle est mesurée
la constante gravitationnelle
. Il s'agit de la précision à laquelle est mesurée
la constante gravitationnelle 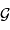 . Le produit
. Le produit 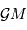 est souvent
déterminé avec une précision bien meilleure.
est souvent
déterminé avec une précision bien meilleure.
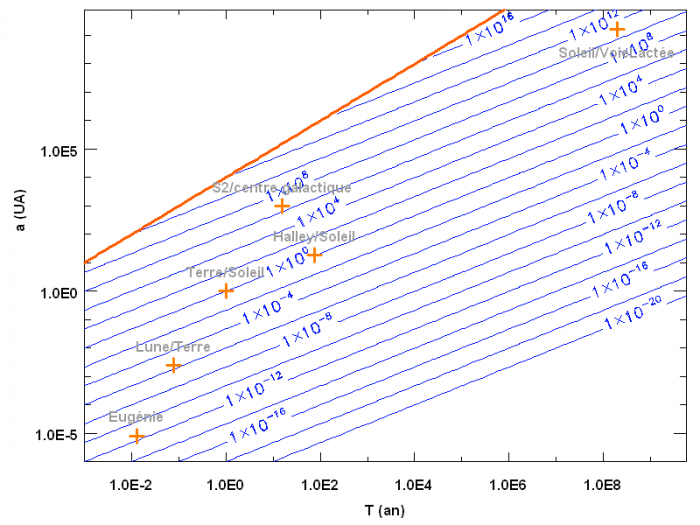
Lignes isomasses de la masse (en unité de masse solaire) du centre force dérivée de la mesure des paramètres orbitaux de différents systèmes. La limite en rouge est relativiste : la vitesse orbitale ne peut pas dépasser la vitesse de la lumière. Les différents systèmes représentés illustrent la diversité de la gamme d'application des lois de la gravitation.
Crédit :
ASM
Différents systèmes d'unités
Lorsque l'on choisit le système d'unités où les temps se comptent en année, les distances en unité astronomique, et les masses en masse solaire, la 3ème loi de Kepler se réécrit, pour le système solaire.
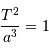
Sans mener aucun calcul, il suffit pour s'en convaince d'examiner le cas de l'orbite terrestre, pour lequel  = 1 UA,
= 1 UA,  = 1 an, qui valide le cas de tout autre planète.
= 1 an, qui valide le cas de tout autre planète.
Pour un autre système caractérisé par un centre de force de masse 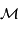 ,
la 3ème loi devient, toujours dans le système d'unités (UA, an,
,
la 3ème loi devient, toujours dans le système d'unités (UA, an,
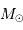 ) :
) :
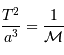
Une application de cette loi sur différents exemples illustre comment une loi physique peut étendre sa validité sur une très large gamme de valeurs.
 Peser un astéroide
Peser un astéroide
Difficulté : ☆
Temps : 15 min
Une équipe dirigée par W. Merline a observé en 1998 l'astéroïde
(45)Eugénie avec l'optique adaptative du télescope CFH. Les
observations
ont mis en évidence la présence d'un petit satellite.
Paramètres orbitaux
| Période | 4.7 j |
| Demi-grand axe | 1190 km |
| Diamètre de Eugénie | 215 km |
| Diamètre du satellite | 13 km |
Question 1)
Déterminer la masse de (45)Eugénie
Il s'agit d'une application de la 3ème loi de Kepler. On rappelle 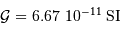
Question 2)
En déduire la masse volumique moyenne de Eugénie. Estimer sa
composition.
On suppose une forme sphérique de rayon 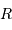 , de volume
, de volume 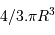
Question 3)
Peut-on estimer la masse du petit satellite ?
Une hypothèse sur la masse volumique du petit satellite est nécessaire.
 Peser la Voie Lactée
Peser la Voie Lactée
Difficulté : ☆☆
Temps : 20 min
Notre galaxie, la Voie Lactée, a la forme d'une galette d'environ 30000 pc de diamètre et 2000 pc d'épaisseur. La région centrale est
formée d'un bulbe d'allure sphérique de 2 700 pc de rayon, qui
contient l'essentiel de la masse galactique.
Le Soleil orbite à 8000 pc du centre galactique.
D'après les mesures Doppler effectuées sur la raie à 21 cm de l'hydrogène,
l'orbite du Soleil est approximativement circulaire, et la vitesse
orbitale du Soleil est d'environ  .
.
Question 1)
Déterminer la période 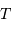 du mouvement du soleil autour du centre
galactique. L'exprimer en années.
du mouvement du soleil autour du centre
galactique. L'exprimer en années.
Commencer par déterminer le rayon 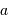 de la trajectoire du soleil autour du centre galactique, avec
de la trajectoire du soleil autour du centre galactique, avec
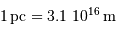 .
.
Question 2)
Estimer la masse du bulbe galactique,
en unité de masse solaire 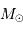 .
.
Mener le calcul en unités UA, an et 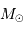 , avec
, avec
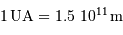 .
.
 La 3ème loi de Kepler pour une orbite circulaire
La 3ème loi de Kepler pour une orbite circulaire
Difficulté : ☆
Temps : 20 min
Question 1)
Retrouver l'expression de la 3ème loi
de Kepler d'après le cas particulier d'une orbite circulaire, lorsque
l'on suppose que les masses des 2 objets vérifient 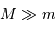 .
.
[1 points]
Définir convenablement un système, et faire un bilan de force
Exprimer l'accélération radiale en fonction de la vitesse 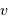 et du rayon de
courbure
et du rayon de
courbure 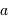 de la trajectoire.
de la trajectoire.
Relier la vitesse orbitale au rayon 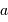 et à la période orbitale
et à la période orbitale 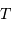 .
.
 Comète de Halley
Comète de Halley
Difficulté : ☆
Temps : 20 min
Question 1)
La comète de Halley a une période sidérale de 76 années. En déduire le
demi-grand axe de son orbite.
[1 points]
Traiter le calcul directement en UA et années
En UA et années; 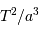 = 1 dans le système solaire
= 1 dans le système solaire
Question 2)
L'excentricité de son orbite vaut 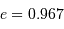 , Déterminer son aphélie
, Déterminer son aphélie 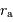 , son
périhélie
, son
périhélie 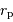 . Situer ces distances par rapport aux autres planètes.
. Situer ces distances par rapport aux autres planètes.
[1 points]
Le lien entre demi-grand axe, excentricité, périhélie et aphélie s'exprime
par :
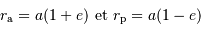
- Question 1
Aide :
Lesquelles étaient connues en l'an 1600 ?
Solution :
De Mercure à Saturne, on compte 6 planètes, Terre incluse. Kepler,
suivant l'option de Copernic, compte la Terre comme planète : c'est une
forte opinion héliocentrique.
- Question 2
Aide :
Introduire la notion de référentiel.
Solution :
Il s'agit de choisir le référentiel héliocentrique comme référentiel
d'étude, afin de pouvoir proprement corriger tout mouvement du mouvement
relatif de la Terre autour du Soleil.
- Question 3
Aide :
Le diamètre lunaire couvre environ 1/2 degré.
Solution :
L'erreur de 8', rapportée au diamètre de la Lune de l'ordre de 30', en
représente un petit quart.
Le diamètre angulaire maximal de Mars est donné par le rapport de son
diamètre linéaire à la distance minimale Terre-Mars, de l'ordre de
0.5 UA (parfois moins, en raison de l'excentricité de l'orbite
martienne) :
Le diamètre angulaire, donné par le rapport du diamètre linéaire à la
distance considérée, vaut :
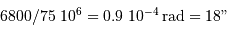 .
.
Il est à comparer à 8' = 480" ;
8' représentent 26.5 diamètres angulaires martiens.
La distance linéaire sur l'orbite est donc de 26.5 diamètres linéaires
martiens, soit 180 000 km.
La fraction de l'orbite correspondante s'élève à 8' / 360.60' = 1/2700.
Elle est parcourue en 687 j/2700 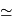 0.25 j, soit 6 heures.
0.25 j, soit 6 heures.
- Question 1
Aide :
Revenir aux définitions. Revoir l'expression du moment cinétique.
Solution :
Le vecteur accélération s'identifie au champ gravitationnel :
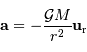
Le vecteur moment cinétique s'écrit par définition :
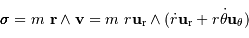
Et donc :
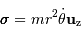
car 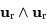 est nul, et
est nul, et 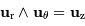
- Question 2
Aide :
Dans la base directe 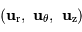 :
:
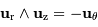
Solution :
Le produit vectoriel donne sans piège :
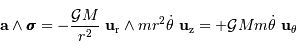
- Question 3
Aide :
Dans le premier terme, 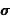 est constant.
est constant.
Aide :
Par définition, 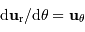 , et donc
, et donc
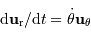
Solution :
L'intégration du produit vectoriel est immédiate,
le moment cinétique 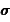 étant un vecteur constant :
étant un vecteur constant :
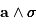 s'intègre en
s'intègre en 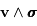 .
.
Intégration du 2e membre :
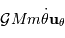 s'intègre en
s'intègre en
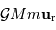 .
.
Et il ne faut pas oublier la constante d'intégration, vectorielle, ici dénommée
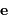 :
:
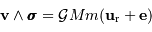
Le vecteur 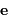 est perpendiculaire au vecteur moment cinétique, donc dans le plan de la trajectoire.
est perpendiculaire au vecteur moment cinétique, donc dans le plan de la trajectoire.
- Question 4
Aide :
On rappelle la relation concernant le produit mixte :
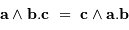
Solution :
En permutant les termes du produit mixte :
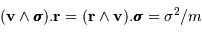 .
.
Par ailleurs :
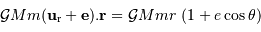 .
.
On en tire la relation demandée, avec le paramètre 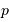 égal à
égal à
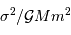 .
.
- Question 5
Solution :
Schémas pour des excentricités de 0.4 et 0.7. On peut par exemple appuyer le vecteur excentricité sur le bipoint OF, le point O étant le centre de l'ellipse, et F le foyer correspondant au centre de force.
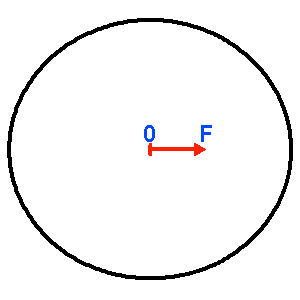
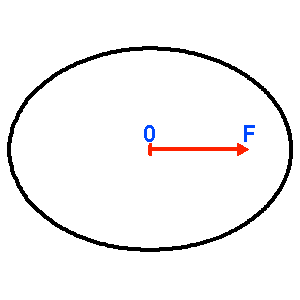
Vecteur excentricité
Crédit :
ASM
- Question 1
Aide :
Il s'agit d'une application de la 3ème loi de Kepler. On rappelle 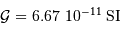
Solution :
Le calcul en unités SI avec les données:
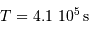 ,
, 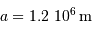 , et la constante gravitationnelle
, et la constante gravitationnelle 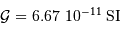 ,
,
aboutit par application de la 3e loi de Kepler à :
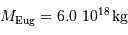
- Question 2
Aide :
On suppose une forme sphérique de rayon  , de volume
, de volume 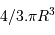
Solution :
La masse volumique s'écrit : 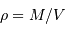 ,
,
avec le volume
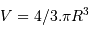 , on trouve :
, on trouve :
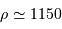 kg.m
kg.m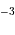 .
.
L'astéroïde (45)Eugénie semble peu dense, avec vraisemblablement un empilement lacunaire de roches.
- Question 3
Aide :
Une hypothèse sur la masse volumique du petit satellite est nécessaire.
Solution :
C'est impossible par la 3ème loi de Kepler. Une estimation, supposant
une masse volumique moyenne identique à celle de Eugénie, conduit à une
masse dans le rapport du cube des rayons :
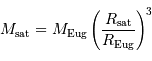
D'où : 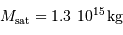 .
On peut vérifier, a posteriori et dans le cadre de l'hypothèse posée, que cette masse est très petite devant la masse du satellite principale, et que donc la 3ème loi de Kepler s'applique bien pour déterminer la masse d'Eugénie (cf. question 1).
.
On peut vérifier, a posteriori et dans le cadre de l'hypothèse posée, que cette masse est très petite devant la masse du satellite principale, et que donc la 3ème loi de Kepler s'applique bien pour déterminer la masse d'Eugénie (cf. question 1).










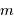 très inférieure à la masse
très inférieure à la masse 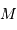 du potentiel central, et n'étant pas perturbé par
d'autres satellites de
du potentiel central, et n'étant pas perturbé par
d'autres satellites de 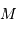 , présente alors les propriétés suivantes :
, présente alors les propriétés suivantes :
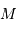 est plane, elliptique, avec
est plane, elliptique, avec 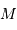 à l'un des
foyers.
à l'un des
foyers.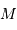 .
.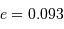
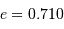
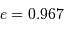






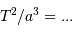
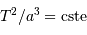 . Et cette constante dépend en fait
. Et cette constante dépend en fait
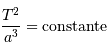



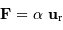 ,
le vecteur
,
le vecteur 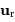 étant un
étant un 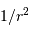 .
.
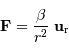
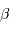 .
Ce sont les
.
Ce sont les 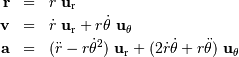
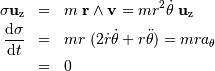
 le rayon de l'orbite,
le rayon de l'orbite,  la période et
la période et 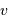 la vitesse de l'objet :
la vitesse de l'objet :
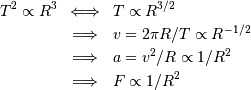

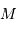 et la planète de masse
et la planète de masse 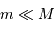 . Le référentiel d'étude
est héliocentrique, de centre
. Le référentiel d'étude
est héliocentrique, de centre 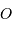 . On y repère la planète
. On y repère la planète 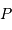 par le
rayon vecteur
par le
rayon vecteur 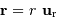 .
La planète subit de la part du soleil une force
.
La planète subit de la part du soleil une force 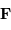 , exprimée par :
, exprimée par :
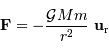
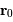 et
et 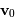 les
position et vitesse de la planète à un instant donné, et
les
position et vitesse de la planète à un instant donné, et  le plan
défini par ces 2 vecteurs, la relation annonce que l'accélération
le plan
défini par ces 2 vecteurs, la relation annonce que l'accélération 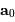 , colinéaire à
, colinéaire à 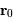 , est également dans ce plan. Aucun terme
d'accélération ne conduisant hors de ce plan, toute la trajectoire s'y
inscrit nécessairement.
, est également dans ce plan. Aucun terme
d'accélération ne conduisant hors de ce plan, toute la trajectoire s'y
inscrit nécessairement.
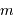 , dans le champ de force central d'un corps de
masse
, dans le champ de force central d'un corps de
masse 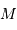 . On repère sa
position par le vecteur radial
. On repère sa
position par le vecteur radial 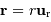 . On note
. On note 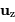 le vecteur
orthonormé normal au plan de la trajectoire, et portant le moment
cinétique du satellite, tel que le trièdre
le vecteur
orthonormé normal au plan de la trajectoire, et portant le moment
cinétique du satellite, tel que le trièdre 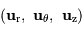 forme
un trièdre orthonomé direct.
forme
un trièdre orthonomé direct.
 et moment cinétique
et moment cinétique 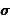 dans la
base (
dans la
base (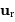 ,
, 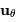 ,
, 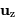 ).
).
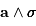 . Donner son expression
en fonction du vecteur
. Donner son expression
en fonction du vecteur 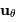 .
.
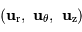 :
:
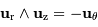
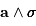 .
.
 est constant.
est constant.
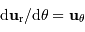 , et donc
, et donc
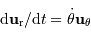
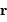 .
Montrer que ceci permet de retrouver l'équation de la trajectoire
.
Montrer que ceci permet de retrouver l'équation de la trajectoire
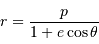
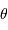 la
direction et le sens du vecteur
excentricité
la
direction et le sens du vecteur
excentricité 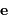
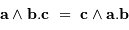
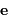 et la
trajectoire.
et la
trajectoire.



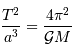
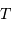 de révolution
et le demi-grand axe de l'orbite, et la masse
de révolution
et le demi-grand axe de l'orbite, et la masse 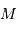 du corps central.
du corps central.
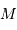 du centre de force à
partir des paramètres orbitaux
du centre de force à
partir des paramètres orbitaux 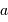 et
et 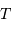 . Ces 2 termes sont en effet
observables, alors que la masse ne l'est pas.
. Ces 2 termes sont en effet
observables, alors que la masse ne l'est pas.
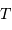 nécessite de repérer le mouvement le long de
la trajectoire.
nécessite de repérer le mouvement le long de
la trajectoire.
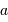
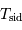

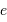
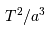
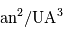
 sur l'
sur l' de l'orbite de chacune des 8 planètes, la relation
de l'orbite de chacune des 8 planètes, la relation 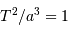 est vérifiée, avec
est vérifiée, avec 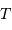 la période de révolution sidérale.
Les désaccords proviennent des écarts aux hypothèses de Kepler.
Remarque : dans le système solaire, les masses des planètes et de la
plupart de leurs satellites sont connues avec une précision relative de
l'ordre de
la période de révolution sidérale.
Les désaccords proviennent des écarts aux hypothèses de Kepler.
Remarque : dans le système solaire, les masses des planètes et de la
plupart de leurs satellites sont connues avec une précision relative de
l'ordre de 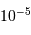 . Il s'agit de la précision à laquelle est mesurée
la constante gravitationnelle
. Il s'agit de la précision à laquelle est mesurée
la constante gravitationnelle 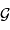 . Le produit
. Le produit 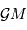 est souvent
déterminé avec une précision bien meilleure.
est souvent
déterminé avec une précision bien meilleure.

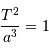
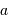 = 1 UA,
= 1 UA, 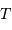 = 1 an, qui valide le cas de tout autre planète.
= 1 an, qui valide le cas de tout autre planète.
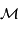 ,
la 3ème loi devient, toujours dans le système d'unités (UA, an,
,
la 3ème loi devient, toujours dans le système d'unités (UA, an,
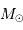 ) :
) :
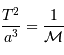
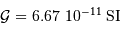
 , de volume
, de volume 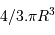
 .
.
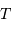 du mouvement du soleil autour du centre
galactique. L'exprimer en années.
du mouvement du soleil autour du centre
galactique. L'exprimer en années.
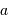 de la trajectoire du soleil autour du centre galactique, avec
de la trajectoire du soleil autour du centre galactique, avec
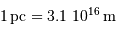 .
.
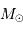 .
.
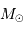 , avec
, avec
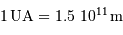 .
.
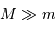 .
.
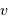 et du rayon de
courbure
et du rayon de
courbure 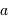 de la trajectoire.
de la trajectoire.
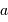 et à la période orbitale
et à la période orbitale 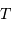 .
.
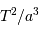 = 1 dans le système solaire
= 1 dans le système solaire
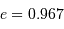 , Déterminer son
, Déterminer son 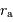 , son
, son
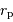 . Situer ces distances par rapport aux autres planètes.
. Situer ces distances par rapport aux autres planètes.
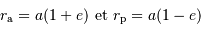
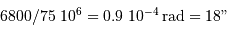 .
.
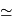 0.25 j, soit 6 heures.
0.25 j, soit 6 heures.
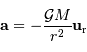
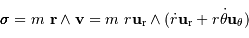
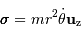
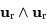 est nul, et
est nul, et 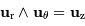
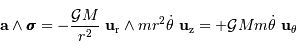
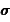 étant un vecteur constant :
étant un vecteur constant :
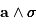 s'intègre en
s'intègre en 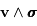 .
.
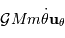 s'intègre en
s'intègre en
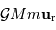 .
.
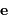 :
:
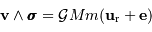
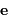 est perpendiculaire au vecteur moment cinétique, donc dans le plan de la trajectoire.
est perpendiculaire au vecteur moment cinétique, donc dans le plan de la trajectoire.
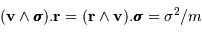 .
.
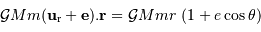 .
.
 égal à
égal à
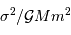 .
.


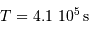 ,
, 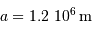 , et la constante gravitationnelle
, et la constante gravitationnelle 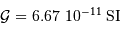 ,
,
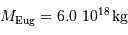
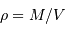 ,
,
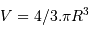 , on trouve :
, on trouve :
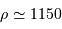 kg.m
kg.m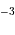 .
.
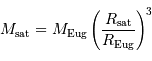
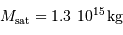 .
On peut vérifier, a posteriori et dans le cadre de l'hypothèse posée, que cette masse est très petite devant la masse du satellite principale, et que donc la 3ème loi de Kepler s'applique bien pour déterminer la masse d'Eugénie (cf. question 1).
.
On peut vérifier, a posteriori et dans le cadre de l'hypothèse posée, que cette masse est très petite devant la masse du satellite principale, et que donc la 3ème loi de Kepler s'applique bien pour déterminer la masse d'Eugénie (cf. question 1).
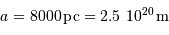 La détermination de la période résulte alors de la simple cinématique :
La détermination de la période résulte alors de la simple cinématique :
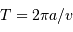 , soit
, soit 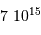 s : de
l'ordre de 230 millions d'années.
s : de
l'ordre de 230 millions d'années.
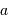 en UA donne :
en UA donne : 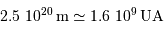 .
.
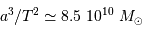 .
.