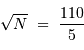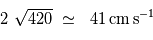Chaîne de mesure
- Introduction
- Collecter le signal
- Introduction
- Miroirs et collecteurs
- Foyers
- Observer
- Apprendre
- Simuler
- S'évaluer
- Qualité optique du collecteur
- Les très grands télescopes du futur
- Observer
- Apprendre
- S'exercer
- Mettre en forme le signal
- Introduction
- Principes
- Astrométrie
- Observer
- Apprendre
- Simuler
- S'évaluer
- Photométrie
- Imagerie
- Imagerie multispectrale
- Observer
- Apprendre
- S'exercer
- S'évaluer
- Spectrométrie à haute résolution
- Observer
- Apprendre
- Simuler
- S'exercer
- Spectro-imagerie
- Observer
- Apprendre
- Simuler
- S'exercer
- Interférométrie
- Observer
- Apprendre
- Simuler
- S'exercer
- Observatoire virtuel
- Conclusion
- Détecter le signal
- Introduction
- Propriétés générales
- Phénomène physique de détection
- Détection quantique
- Détection : dynamique
- Réponse spectrale
- Réponse temporelle
- Observer
- Apprendre
- S'exercer
- Géométrie des détecteurs
- Observer
- Apprendre
- S'exercer
- Bruits de détection
- Observer
- Apprendre
- S'exercer
- Rendement de la chaîne de détection
- Observer
- Apprendre
- S'exercer
- S'évaluer
- Conclusion
- Analyser le signal
- Introduction
- Bruit et signal
- Probabilités, réalisations, estimations
- Rapport signal à bruit
- Observer
- Apprendre
- Simuler
- S'exercer
- Le bruit gaussien
- Observer
- Apprendre
- Simuler
- S'exercer
- Le bruit poissonnien
- Le bruit de photons
- Observer
- Apprendre
- S'exercer
- S'évaluer
- Bruit instrumental
- Le critère de Shannon
- Observer
- Apprendre
- S'exercer
- S'évaluer
- Traiter le signal
- Introduction
- Filtrage
- Sommation d'image
- Analyse par transformée de Fourier : formalisme
- Apprendre
- Simuler
- S'exercer
- Analyse par transformée de Fourier : signal
- Observer
- Apprendre
- Simuler
- S'exercer
- Analyse par transformée de Fourier : bruit
- Observer
- Apprendre
- Simuler
- S'exercer
Introduction
On peut diviser la chaîne de mesure en plusieurs étapes. Parfois, il peut être difficile de distinguer aisément leur rôle : d'une part, elles sont intimement liées dans la qualité de l'observation ; d'autre part, leur intégration dans une outil d'observation efficace peut les solidariser intimement. L'ambition de ce chapitre : mettre un peu d'ordre dans cette complexité.
- Collecter : Choisir un entonnoir à photons aux propriétés voulues, souvent le plus grand possible, et transformer le front d'onde initial en un front d'onde plus concentré.
- Mettre en forme : Travailler les photons pour les compter, les classer par couleur et/ou les repérer spatialement.
- Détecter : Convertir le signal lumineux en signal électrique, sans perdre aucune des propriétés gagnées par l'instrument.
- Analyser : Traduire en mesures physiquement pertinentes les observables.
- Traiter : Commencer (modestement) à traiter les mesures.
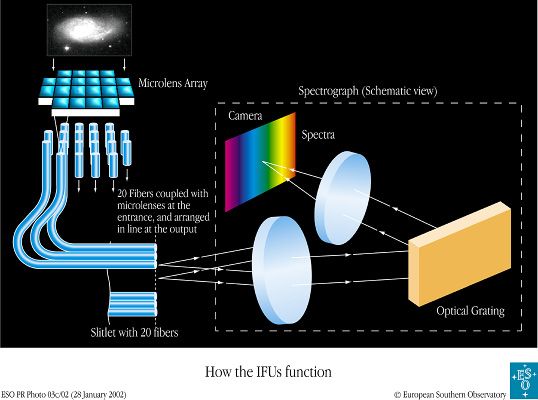
Schéma optique d'un spectromètre intégral de champ.
Crédit :
ESO
Collecter le signal
Auteur: B. Mosser
Introduction
Collecter le signal, c'est assurer que les photons arrivent nombreux et en bon ordre aux différents foyers d'un télescope. Qualités optique et mécanique se conjuguent pour accomplir cette tâche.

Miroir de 8.2 m poli par la société SAGEM/REOSC, pour le télescope VLT de l'ESO.
Crédit :
REOSC
Miroirs et collecteurs
Observer
Miroirs
Le miroir primaire est le ... premier miroir vu par les photons. Il présente généralement un profil parabolique. Le deuxième, s'il y en a un, est appelé ... secondaire.

Miroir de 8.2 m poli par la société SAGEM/REOSC, pour le télescope VLT de l'ESO.
Crédit :
REOSC
Miroirs segmentés
Les 2 télescopes Keck,
plus grands collecteurs dans le visible depuis le début des années 1990, ont des miroirs segmentés (càd en plusieurs morceaux), et illuminent les foyers Cassegrain
et Nasmyth. Ce dernier, après passage du faisceau sur l'axe en altitude, est découplé du télescope.
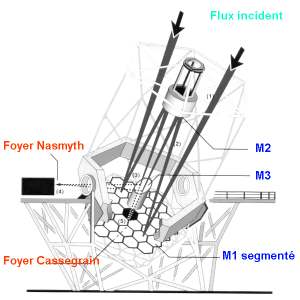
Miroir segmenté, foyers Cassegrain et Nasmyth d'un des 2 télescopes Keck.
Crédit :
Keck
Domaines visible, UV et IR
Une configuration classique est la combinaison de 2 miroirs, l'un parabolique, l'autre hyperbolique convexe, dans la configuration Cassegrain.
Les miroirs ne sont plus nécessairement monoblocs ; c'est le cas du télescope optique le plus grand en service actuellement, le télescope Keck.
Domaine radio
Dans le domaine radio, il est nécessaire d'avoir une antenne de grande taille :
- Pour collecter un grand nombre de photons, car l'énergie
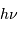 par photon est très faible dans le domaine radio.
par photon est très faible dans le domaine radio. - Afin d'améliorer la fonction de transfert, très étalée par la diffraction à grande longueur d'onde
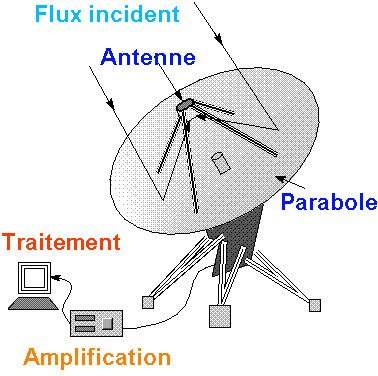
Les éléments de collecte du signal d'un radiotélescope.
Crédit :
ASM
Domaine X
Le domaine des courtes longueurs d'onde présente de nombreuses particularités. Entre autres :
- Seules les observations dans l'espace sont possibles, l'atmosphère étant opaque aux rayonnements X et
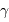 .
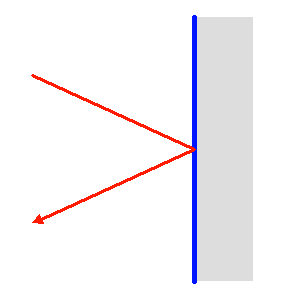
. - Il est difficile de focaliser efficacement un rayonnement très énergétique. Pour y parvenir, les miroirs des collecteurs X travaillent en incidence rasante.
- L'imagerie X nécessite un grand nombre de surfaces collectrices.

Télescope XMM de l'agence spatiale européenne, lancé fin 1999 pour une mission de 6 ans.
Crédit :
ESA

Télescope X : principe. Pour assurer un bon coefficient de réflexion dans ce domaine de longueur d'onde, les miroirs sont attaqués en incidence rasante.
Crédit :
ESA

Paraboloïdes chargés de recueillir le flux X en incidence quasi rasante ; 58 paires de paraboloïdes et hyperboloïdes associés assurent les possibilités d'imagerie du collecteur du satellite XMM.
Crédit :
ESA
Apprendre
 Prérequis
Prérequis
Optique géométrique. Formation d'image au foyer primaire d'un télescope.
 Objectifs
Objectifs
Quelques notions sur les collecteurs de photons en astronomie.
Voir à l'infini
Le signal d'un objet très lointain, non résolu spatialement, est une onde plane. Observer cette onde plane, c'est la focaliser en un point. Une surface mathématique sait faire cette opération : le paraboloïde de révolution
(révolution d'une parabole autour de son axe).
La parabole
Mathématiquement, la parabole conjugue l'infini à un point ; optiquement, elle permet de transformer une onde plane en onde sphérique.
Ceci n'est rigoureusement vrai que pour un rayon parallèle à l'axe optique. L'aberration de sphéricité apparaît pour les rayons inclinés sur l'axe.
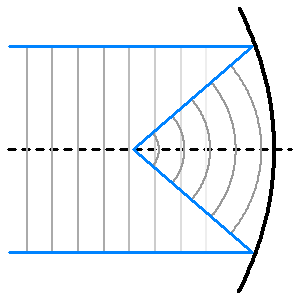
La parabole conjugue l'infini à un point, le foyer. Elle transforme une onde plane en onde sphérique.
Crédit :
ASM

Aberration de sphéricité pour tout objet paraxial, avec un collecteur parabolique.
Crédit :
ASM
Propriétés
Les lois de l'optique permettent de caractériser les qualités de la collecte.
Foyers
Observer
Foyer, doux foyer
Les collecteurs de photons s'appuient sur de multiples configurations optiques.
On note principalement :
- Le foyer primaire, devant le collecteur, occulte une partie du faisceau.
- Le foyer Cassegrain se situe juste derrière le miroir primaire du télescope. Ce dernier est percé.
- Le foyer Nasmyth, pour les montures azimutales ; comme pour le foyer Cassegrain,
- Le foyer coudé est renvoyé, par un jeu de miroir, en une position qui ne bouge plus avec le télescope, largement déportée.
- Le transport par fibre optique permet d'emporter le flux loin du collecteur.

Caméra grand champ (gros cylindre noir) au foyer primaire du télescope CFH.
Crédit :
CFHT

Instrumentation au foyer Cassegrain du télescope CFH. Le télescope est en station. L'instrument est dans une cuve à vide, sous le logement du miroir primaire.
Crédit :
CFHT

Instrument VIMOS sur l'un des 2 foyers Nasmyth d'un des télescopes du VLT, le long de l'axe en élévation.
Crédit :
VLT
Apprendre
 Objectifs
Objectifs
Aperçu des diverses configurations optiques pour un télescope.
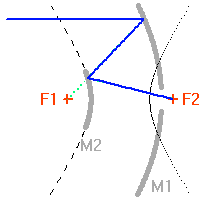
Collecte du faisceau au foyer Cassegrain. La parabole conjugue l'infini avec son foyer
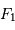
, transformant une onde plane en onde sphérique. L'hyperbole échange les 2 foyers
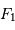
et
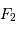
: l'onde sphérique converge alors en
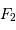
.
Crédit :
ASM
Combinaisons optiques
Plusieurs configurations optiques permettent de réaliser pratiquement la convergence d'une onde plane en un foyer. Selon l'usage, astronomie amateur ou professionnelle, elles diffèrent, par leur performances et leurs coûts.
- Un télescope de Newton associe un miroir primaire parabolique à un secondaire plan incliné à 45deg par rapport à l'axe optique. Pour des télescopes de petite taille (10 cm, soit le télescope du débutant), le miroir parabolique peut être approximé par un forme sphérique, beaucoup moins coûteuse à polir.
- A un primaire parabolique, percé, le télescope Cassegrain associe un secondaire convexe hyperbolique. Le foyer Cassegrain est situé juste derrière le miroir primaire. Epargné par l'aberration de sphéricité, le miroir parabolique présente un défaut de coma qui limite le champ utile.
- Une variante est le télescope de Schmidt-Cassegrain, où une lame de forme complexe (et coûteuse) en entrée du collecteur permet l'utilisation d'un primaire sphérique.
- Une autre variante est le Maksutov-Cassegrain, avec primaire et secondaire sphériques, respectivement concave et convexe, et une petite lentille de correction.
- Le télescope Ritchey-Chrétien, un télescope de type Cassegrain particulier, est la combinaison aujourd'hui la plus utilisée pour les observatoires fonctionnant dans le visible et le proche infrarouge. Primaire et secondaire sont hyperboliques, ce qui assure une absence d'aberrations de coma et de sphéricité.
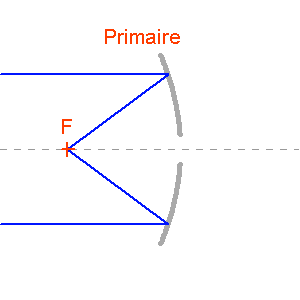
Foyer primaire.
Crédit :
ASM
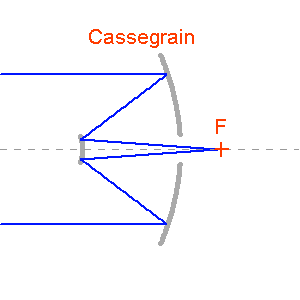
Foyer Cassegrain : le miroir secondaire occulte une partie du faisceau. Le miroir primaire doit être évidé.
Crédit :
ASM
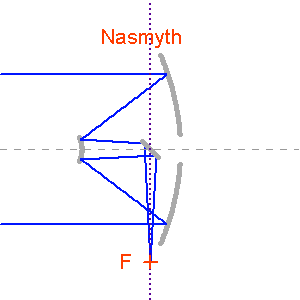
Foyer Nasmyth : le miroir tertiaire renvoie le faisceau sur l'axe de hauteur de la monture.
Crédit :
ASM
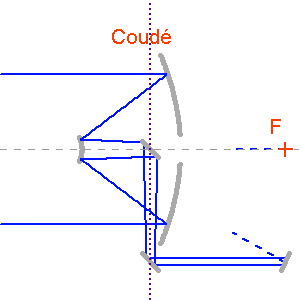
Foyer coude : un train de miroirs assure le découplage entre la position du foyer Coudé et le pointage du télescope.
Crédit :
ASM
Foyers
Un télescope professionnel, usuellement de type Cassegrain ou Ritchey-Chrétien, présentera plusieurs combinaison de foyers.
- Le foyer primaire est interne au tube du télescope de type Cassegrain. S'il est idéal pour les observations grand champ (surtout dans la configuration de Schmidt-Cassegrain), l'instrumentation ne peut y être ni volumineuse ni massive.
- Le foyer Cassegrain, situé derrière le miroir primaire, aboutit à une configuration de plus longue focale. Comme il est également lié au télescope, l'instrumentation est limitée en encombrement.
- Le foyer Nasmyth, pour une monture azimutale, se situe sur la plate-forme mobile en azimut, sur l'axe de hauteur. Il est donc partiellement découplé du télescope et peut accueillir une instrumentation plus volumineuse.
- Le foyer coudé est renvoyé, par un jeu de miroir, en une position qui ne bouge plus avec le télescope, quelque soit la direction de pointage.
Simuler
Collecte du faisceau au foyer Cassegrain. La parabole conjugue l'infini avec son foyer
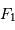
, transformant une onde plane en onde sphérique. L'hyperbole échange les 2 foyers
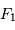
et
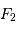
: l'onde sphérique converge alors en
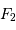
.
Crédit :
ASM
Convergence au foyer Cassegrain
La transformation d'une onde plane en onde sphérique, puis de l'onde sphérique en une autre onde sphérique convergeant au foyer du télescope, est une application directe des propriétés des coniques.
VLT 
Chemins optiques et foyers
Pour un télescope en monture azimutale, telles les 4 unités du VLT, plusieurs trains optiques permettent d'illuminer les différents foyers : Cassegrain, Nasmyth, coudé.
Un observatoire aujourd'hui
L'appliquette ci-dessous décompose différents éléments d'une des
unités du VLT.

S'évaluer
 Focale équivalente
Focale équivalente
Difficulté : ☆
Temps : 15 min
La figure ci-jointe, proposée en appliquette, montre un montage de type Cassegrain. Le diamètre du miroir primaire vaut 128 cm.

Question 1)
Positionner graphiquement la lentille équivalente du télescope, et déterminer ensuite sa focale équivalente.
[2 points]
Question 2)
Calculer le nombre d'ouverture du télescope.
[1 points]
Qualité optique du collecteur
Observer
Forme idéale
La forme des miroirs doit s'approcher au mieux de la forme idéale (parabolique, hyperbolique, plane...). A grande comme à petite échelle, aucun défaut ne doit excéder une limite, dont la valeur dépend des performances souhaitées.
Qualité du miroir
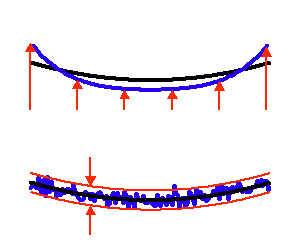
Mise en évidence, fortement exagérée, des défauts de forme d'un miroir parabolique à grande ou à petite échelle.
Crédit :
ASM
Miroir primaire du VLT

Miroir de 8.2 m poli par la société REOSC pour le VLT. L'échelle est donnée par les ingénieurs figurant sur le cliché.
Crédit :
REOSC
Optique active
Plutôt que de confier la forme idéale du collecteur à une position statique et rigide, l'optique active préfère inclure une chaîne de correction
commandant la forme idéale du miroir au moyen d'actuateurs positionnant idéalement chaque sous-élément du miroir.
Cette technique est employée p.ex. pour les miroirs de 8.2 m du VLT. Si leur forme idéale devait découler de leur seule rigidité, ces miroirs auraient une épaisseur supérieure à 2 m : solution inadaptée. Les miroirs sont minces (18 cm) ; leur faible épaisseur leur assure une certaine souplesse, et quelle que soit leur position, des actuateurs les repositionnent pour une forme idéale.
Miroir primaire du VLT
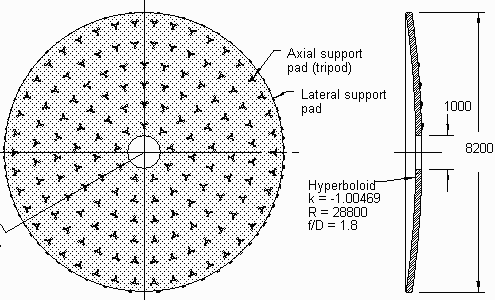
Optique active : miroir mince et actuateurs. Remarquer que la forme du miroir est hyperbolique : les télescopes du VLT sont de type
Ritchey-Chrétien.
Crédit :
ESO
Miroir du VLT : résidus

En mode actif, les actuateurs assurent un profil idéal. Les écarts à la forme idéale (ici hyperbolique), mesurés par le senseur du front d'onde, ont un écart-type de 43 nm, soit environ 10 fois moins qu'une longueur d'onde dans le visible.
Crédit :
ESO
Domaine radio
Dans le domaine radio, caractérisé par des longueurs d'onde relativement grandes, un grillage peut suffire à constituer un bon miroir. Il est vu par l'onde tel une surface pleine, et sa forme rapportée à la longueur d'onde considérée est suffisamment précise.
Miroir du radiotélescope de Nançay

Le collecteur du radiotélescope de Nançay inclut un miroir sphérique. Aux longueurs d'ondes étudiées (typiquement décimétriques), la surface collectrice grillagée présente les mêmes propriétés de réflexion qu'une surface pleine plane.
Crédit :
Observatoire de Paris
Apprendre
 Objectifs
Objectifs
L'étude technologique des qualités optiques des éléments des collecteurs astronomiques s'appuie sur de multiples domaines non ici explorés. On s'intéresse essentiellement à la forme géométrique idéale des collecteurs, en laissant de côté : les aberrations, les propriétés thermomécaniques des miroirs et de leurs supports, les propriétés de réflexion des surfaces ; la transmission dans les verres des lentilles...
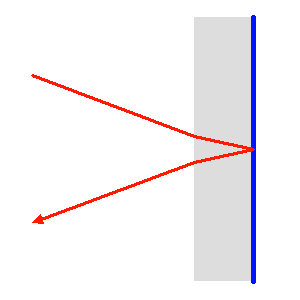
Miroir de "salle de bain". La plaque de verre protège la couche métallique réfléchissante (en bleu).
Crédit :
ASM
Miroir optique. Le substrat de verre supporte le fin dépôt métallique réfléchissant. Sa forme, sa taille et son poli sont essentiels, conférant au miroir ses qualités optiques.
Crédit :
ASM
Miroirs
Un miroir optique diffère d'un miroir usuel.
Un miroir usuel est constitué d'une plaque de verre protégeant une feuille métallique réfléchissante. Le faisceau optique traverse par 2 fois cette vitre, avant et après la réflexion métallique.
Un miroir astronomique est constitué d'un support vitreux, précisément taillé, recouvert d'une très fine couche métallique réfléchissante (aluminium, argent ou or principalement, selon le domaine de longueurs d'onde utilisé), éventuellement protégée d'une mince couche d'oxyde. Le faisceau optique ne traverse pas le verre.
Le substrat en verre est typiquement du zérodur, verre se caractérisant par un très faible coefficient de dilatation thermique.
Qualité
La qualité des optiques de toute la chaîne de détection est essentielle. Elle se traduit par la fonction d'étalement du point, qui rend compte de l'image d'un objet ponctuel à l'infini.
Cette qualité, pour un miroir, se résume souvent à un paramètre : à grande ou à petit échelle, le miroir ne doit pas s'écarter de sa forme idéale de plus d'une fraction de longueur d'onde (typiquement de 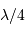 pour un dioptre usuel à
pour un dioptre usuel à 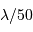 pour une optique d'interféromètre).
pour une optique d'interféromètre).
Optique active
On appelle optique active un système restituant la forme idéale des surfaces collectrices non de façon statique, avec des miroirs très rigides, mais dynamique, avec des miroirs minces positionnés par des actuateurs. L'optique active corrige les déformations lentes d'origine thermique et mécanique.
Optique adaptative
L'optique adaptative corrige en temps réel les défauts du front d'onde induits par la turbulence. Voir les pages dédiées à l'optique adaptative.
Les très grands télescopes du futur
Observer
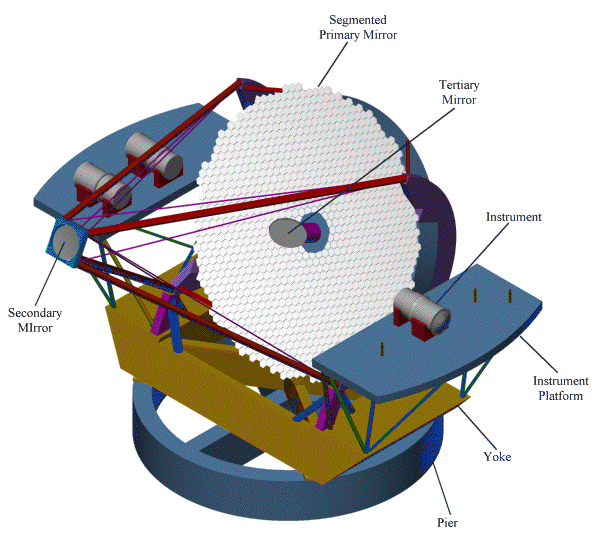
Projet du grand télescope CELT (California extremely large telescope). L'échelle est donnée par les personnes sur la plateforme. Ce projet présente les caractéristiques des grands télescopes du futur : monture azimutale, diamètre collecteur segmenté de l'ordre de 30 m, instrumentation aux foyers Nasmyth.
Crédit :
CELT
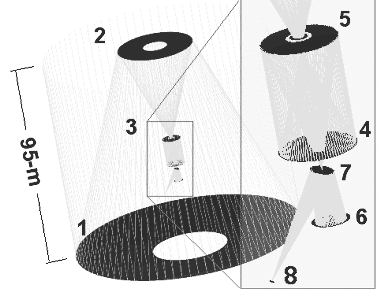
Projet du grand télescope OWL de l'ESO (overwhelmingly large telescope ; overwhelming = de façon écrasante), abandonné en 2006. Le miroir primaire (1), de diamètre 100 m, est segmenté et sphérique. Le miroir secondaire (2) est plan. Le système des miroirs 4 et 5 assure la correction de la sphéricité du miroir primaire, ainsi que l'optique adaptative ; ces miroirs ont un diamètre de 8.2 m, càd autant que les miroirs primaires du VLT de l'ESO.
Crédit :
ESO
Vers les très grandes surfaces collectrices
Les diamètres collecteurs ont régulièrement augmenté au cours du temps, pour collecter
plus, et plus précisément, de photons. Divers projets de télescopes optiques de miroir primaire de 30 à 50 m sont dans les cartons. Des structures de telles dimensions existent déjà, mais dans le domaine radio, avec des longueurs d'onde centimétriques et non submicrométriques.
Le projet CELT illustre les caractéristiques des futurs projets. Le projet OWL de l'ESO, préparant la classe des télescopes de 100 m, n'a pas abouti, car il supposait un trop radical changement d'échelle. Il a été remplacé par un projet de télescope de 39 mètres de diamètre, l'Extremely Large Telescope (ELT) de l'Observatoire Européen Austral, dont la première lumière est prévue en 2024.
Apprendre
 Objectifs
Objectifs
Dévoiler les grandes lignes des projets de grands observatoires.
Pourquoi une grande surface collectrice
Certains besoins scientifiques (pas tous) nécessitent la collecte de flux de plus en plus faible, et donc des collecteurs encore plus grands que ceux de la classe 10 m entrés en action dans les années 1990.
Quelques principes
Les télescope de cette classe 10 m ont montré des changements importants par rapport à leurs prédécesseurs, induits simplement par leur taille.
- Monture azimutale et non plus équatoriale, cette dernière devenant impossible à mettre en oeuvre.
- Nombre d'ouverture plus petit, afin de réduire la focale du collecteur.
- Instrumentation sur une plateforme Nasmyth, le foyer Cassegrain ne pouvant plus accueillir une instrumentation trop lourde ou volumineuse.
Ces principes sont conservés pour les projets de télescope de la
classe 30 m, avec en plus la généralisation des miroirs segmentés.
Difficultés pratiques
Si le principe des très grands télescopes est mûr, leur réalisation pratique pose de nombreux problèmes. Par exemple :
- Par conservation de l'étendue de
faisceau, la taille de leur instrumentation focale croît
à la mesure de la taille du collecteur.
- Une optique adaptative performante est nécessaire pour bénéficier pleinement du gain en diamètre. La complexité de l'OA croît plus rapidement que la surface du télescope.
- Le coût d'un observatoire varie environ comme la puissance quatrième du
diamètre du collecteur.
Hypertélescope
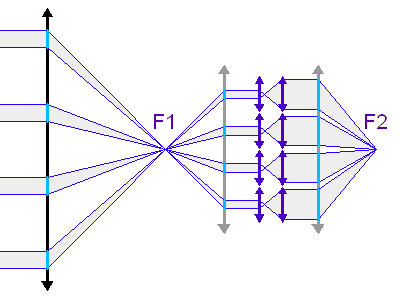
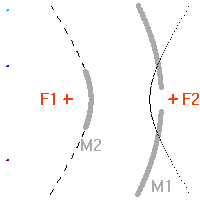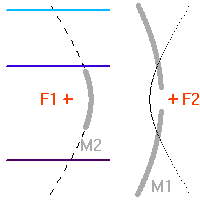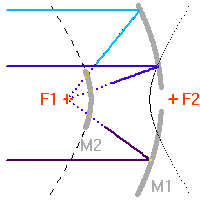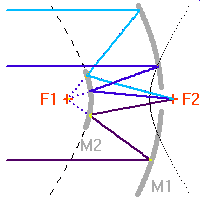
Schéma de principe d'un hypertélescope. Une surface collectrice, ici modélisée par une lentille équivalente, est partiellement reconstituée par divers segments non jointifs pour une focalisation d'un faisceau parallèle au foyer commun F1. Ce foyer est réimagé en F2, chaque voie étant individuellement élargie par un système afocal grossissant : ceci conduit à la densification de la pupille. La taille du système optique entre F1 et F2 a été agrandie pour la clarté du schéma.
Crédit :
ASM
Hypertélescope
Une solution alternative aux très grands télescopes pourrait consister à réaliser une surface collectrice avec plusieurs pupilles reconstituant une seule surface collectrice, mais non entièrement
pavée ; un système optique apporte la densification de pupilles, et conduit au principe de l'hypertélescope. La réalisation pratique d'un hypertélescope n'est pas prévue dans un futur proche, un certain nombre de points durs techniques subsistant encore.
S'exercer
 Hypertélescope
Hypertélescope
Difficulté : ☆☆☆
Temps : 60 min
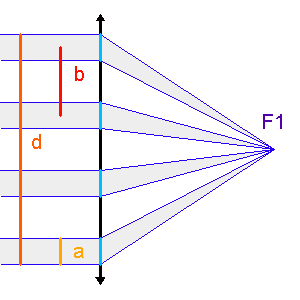
Télescope de Fizeau. Une surface collectrice, ici modélisée par une lentille équivalente, est partiellement reconstituée par divers éléments non jointifs partageant un même foyer F1.
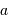
mesure le diamètre d'une sous-pupille,
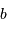
l'écartement entre 2 sous-pupilles et
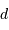
le diamètre total.
Crédit :
ASM
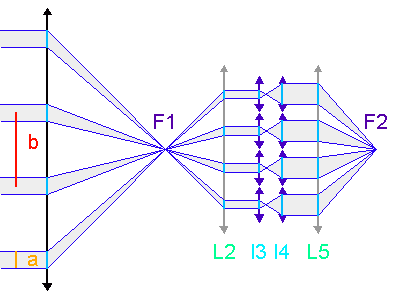
Schéma de principe d'un hypertélescope. Les morceaux de paraboles
collectrices ont été remplacées par leur équivalent lentille.
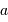
mesure le diamètre d'une sous-pupille ;
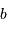
leur écartement.
Crédit :
ASM
La première figure donne le schéma
de principe d'un hypertélescope. L'équivalent du miroir primaire
est constitué de sous-pupilles, reconstituant de façon incomplète
une surface collectrice correspondant à une immense parabole.
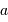 mesure le diamètre d'une sous-pupille ;
mesure le diamètre d'une sous-pupille ; 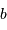 leur écartement.
leur écartement.
La deuxième figure présente le montage du densificateur de pupille. Les lentilles L2 et L5 sont supposées identiques, si bien que le grossissement du système constitué de ces lentilles vaut -1 ; le grossissement angulaire du système afocal constitué des lentilles l3 et l4 est noté 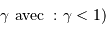 .
.
Cet exercice est à résoudre sans gros calcul ! Pour simplifier l'approche, on travaille sur une seule dimension, comme le montre la figure (sans chercher à reconstituer la surface collectrice).
Question 1)
On s'intéresse juste à l'optique en amont de F1. Quels paramètres
dimensionnent la taille angulaire de la tache image en F1 d'une
sous-pupille, de l'ensemble des sous-pupilles ? Mener l'analogie avec un réseau d'interférence composé de fentes de largeur 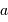 séparées d'une distance
séparées d'une distance 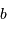 , s'étalant sur une longueur totale
, s'étalant sur une longueur totale 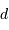 .
.
Réfléchir au rôle de la diffraction par une sous-pupille,
à celui des interférences entres sous-pupilles.
Mener l'analogie avec un réseau.
Question 2)
Déterminer l'action du système (l3, l4), en comparant les
situations en F1 et F2.
Pour une comparaison aisée, imaginer que L2 et L5 ont les mêmes diamètre et focale que L1.
Question 3)
Quel est l'intérêt du système ? Que se passe-t-il lorsque 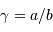 ?
?
Mener un raisonnement géométrique s'appuyant sur la figure.
S'intéresser à la localisation de l'énergie dans les pics d'interférence.
Question 4)
Qu'a-t-on gagné, qu'a-t-on perdu avec cette opération ?
S'intéresser à la tache de diffraction.
S'intéresser au champ accessible, dimensionné par une tache de diffraction élémentaire
Que devient la tache de diffraction d'une sous-pupille ?
Mettre en forme le signal
Auteur: Benoît Mosser
Introduction
L'information recherchée dans un signal s'exprime de diverses façons.
Cette section présente les grands principes en oeuvre
et les techniques instrumentales associées, pour traiter au mieux les photons selon :
- Leur direction d'origine
- Leur quantité.
- Leur couleur.
- Et toute combinaison de ces 3 propriétés, sans oublier éventuellement leurs variations temporelles.
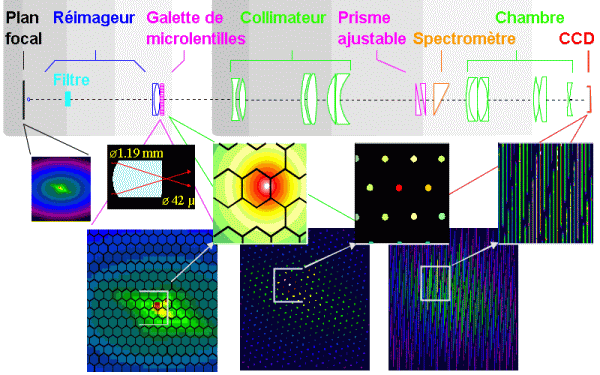
Principe de la spectrométrie intégrale de champ.
Crédit :
CFHT
Principes
Observer
L'information portée par les photons peut être traitée de diverses façons, ainsi que le montrent les illustrations suivantes.
L'amas des Hyades
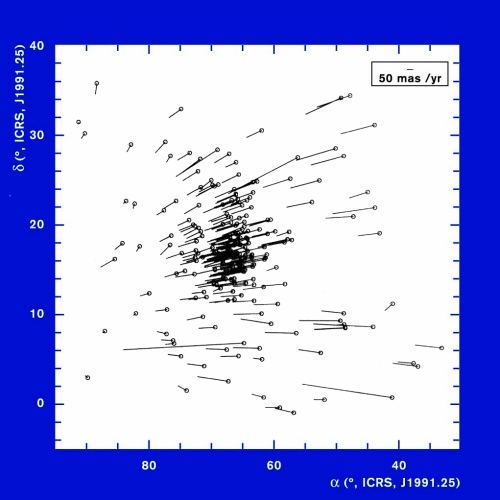
Le mouvement propre des étoiles de l'amas des Hyades a pu être reconstruit par le satellite Hipparcos.
Crédit :
ESA
Cartographie grand champ

Le ciel profond vu par le télescope spatial. Remarquer la corrélation entre la couleur et la luminosité des objets.
Crédit :
HST
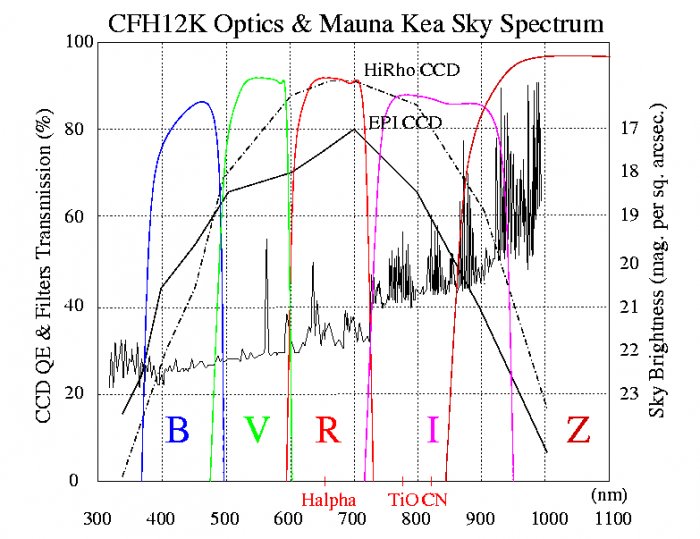
Système de filtres BVRI normalisés permettant de mesurer précisément les
magnitudesassociées.
Crédit :
CFHT

Assemblage de filtres pour des mesures dans le système BVRI
Crédit :
ESO/Cyril Cavadore
- Astrométrie : Mesure de position et mouvement. Le satellite Hipparcos a relevé la position, à la milliseconde d'arc près, de 120 000 étoiles (jusqu'à la magnitude 12).
- Imagerie : Cartographie, pour une étude morphologique, statistique, sans ou à très faible résolution spectrale, ou bien dans des filtres très précis.
- Photométrie : Mesure de flux lumineux dans un système de bandes spectrales
- Spectrométrie : Identification des photons selon leur couleur.
Ex. : observation du spectre IR de Procyon.
- Spectroimagerie : Les photons sont traités pour recueillir simultanément les informations spatiale et spectrale qu'ils véhiculent.
Spectro 2-D
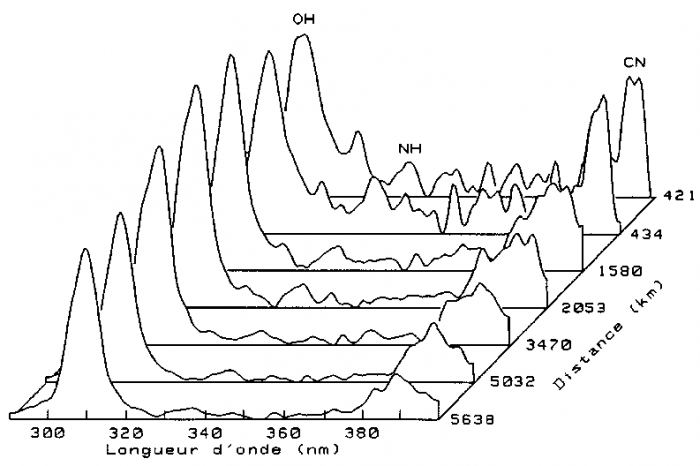
Chaque point de la fente source est dispersée, dans une direction perpendiculaire à celle de la fente. Une dimension du CCD traduit la variable spatiale, l'autre la variable spectrale.
Crédit :
ESO
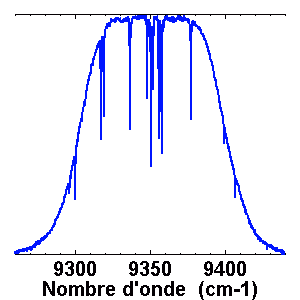
Procyon, aux alentours de
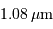
. Ce domaine spectral est sélectionné par un filtre étroit. Noter l'unité spectrale, inverse de la longueur d'onde.
Crédit :
CFHT/ASM
Apprendre
 Objectifs
Objectifs
Distinguer différents principes instrumentaux.
Différents principes
- Astrométrie : Repérages de positions, pour la mesure de distance et de mouvement. La mesure des parallaxes des étoiles du proche voisinage solaire est une étape indispensable pour la détermination des distances interstellaires, et le point de départ obligé d'un juste arpentage de l'Univers.
- Imagerie :
L'imagerie, ce n'est pas que de belles images d'intérêt cosmico-esthétique, mais le support de diverses activités : relevés statistiques, morphologie, activité... Aujourd'hui se développe l'imagerie grand champ, à base de
mosaïques de CCD.
- Photométrie : Mesure de flux lumineux, dans des bandes spectrales bien définies (p.ex. le système BVRI utilisé dans le visible et le proche infrarouge).
Les mesures photométriques nécessitent d'excellentes conditions atmosphériques. Les différents éléments de la chaîne d'acquisition (transparence atmosphérique, efficacité de l'instrumentation et du détecteur) interdisent toute mesure absolue directe. Un étalonnage sur une source connue est nécessaire : source céleste bien référencée, ou source d'étalonnage interne à l'instrument.
- Bolométrie : Mesure de flux lumineux,
l'énergie des photons incidents (essentiellement les domaines X et IR)
étant convertie en agitation thermique dans le détecteur, dont la résistance électrique varie avec la température. Les bolomètres n'ont intrinsèquement aucune sélectivité spectrale.
- Spectrométrie :
Différents types de spectromètres sont utilisés
en astronomie : spectromètre à résonance,
spectromètre interférentiel
(spectromètre par transformée
de Fourier, Fabry-Pérot, spectromètre à réseau), spectromètre hétérodyne.
Selon différents
critères (largeur spectrale admissible, résolution spectrale) l'une ou l'autre des
techniques s'impose.
- Spectroimagerie : La spectroimagerie permet l'obtention de l'information spectrale pour toute une région spatiale. Selon les techniques (spectrométrie
multi-objets, spectro intégrale de champ), cette région est un ensemble
de différentes cibles ponctuelles, un objet étendu...
Quels principes, pour quelle mesure ?
La liste qui précède est austère. Les pages qui suivent illustrent comment ces techniques sont mises en pratique, et dans quel but.
Astrométrie
Observer

Le champ stellaire analysé, autour de l'étoile HD 49933 (abondamment observée par une mission spatiale du CNES).
Crédit :
CDS
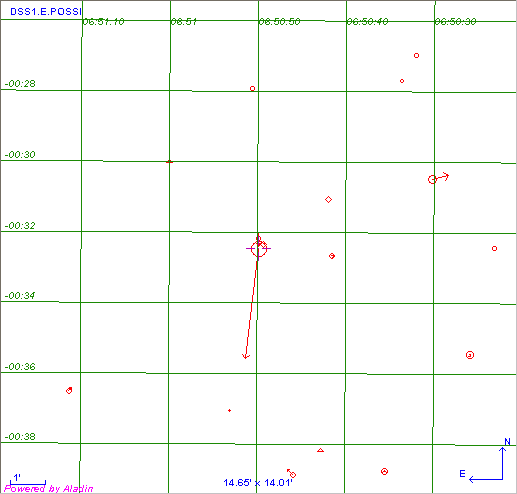
La carte des étoiles précédemment répertoriées, avec de plus leur mouvement propre.
Crédit :
CDS
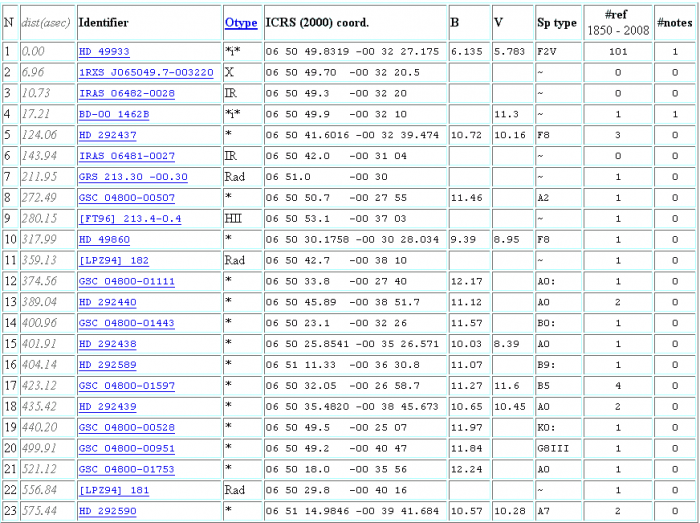
Le catalogue des étoiles précédemment répertoriées.
Crédit :
CDS
Un exemple : environnement d'une étoile
Les données astrométriques permettent une foultitude de choses, comme par exemple de précisément caractériser un champ autour d'un objet. Les figures ci-jointes décrivent de diverses manières l' environnement d'une étoile,
une carte, ou par
les coordonnées.
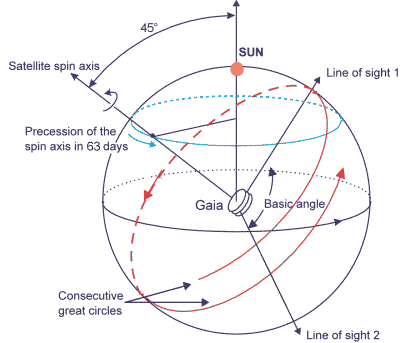
Le satellite Gaia, au point de
Lagrange L2, est animé d'un mouvement de rotation régulier, avec un axe (spin axis) orienté à 45 deg par rapport à la direction du Soleil. Il observe simultanément 2 régions du ciel (line of sight 1 et 2). Le mouvement de rotation induit le balayage de 2 grands cercles. La précession du mouvement de rotation induit l'évolution de ces grands cercles, pour observer tout le ciel.
Crédit :
ESA

Le montage de Gaia repose sur une structure octogonale très stable, pour la définition de l'angle entre les 2 lignes de visée astrométriques. Une 3ème ligne de visée est utilisée pour des mesures spectrométriques. La collecte du signal sur chaque ligne de visée implique 3 miroirs : les miroirs primaire et tertiaire se situent dans un même plan, et font face au miroir secondaire et au détecteur. Vu le nombre gigantesque de cibles à mesurer, le plan focal est composé d'une mosaïque de plusieurs dizaines de CCD. Le mode de lecture des CCD est original : les lignes du CCD sont positionnées exactement parallèlement au déplacement apparent de l'image suite à la rotation propre du satellite, et la pose et le transfert des charges d'un pixel à l'autre suivent le déplacement de l'image stellaire le long de la ligne du CCD.
Crédit :
EADS/Astrium
Le projet Gaia
Le principe de mesure de Gaia repose sur le balayage du ciel simultanément le long de deux lignes de visée. Le scénario de pointage met en oeuvre la rotation propre et la précession du satellite. Le montage optique s'appuie sur une structure stable.
Apprendre
 Définition
Définition
L'astrométrie a pour but de mesurer la position des astres, leur parallaxe et donc leur distance, leur mouvement propre. Elle opère un travail indispensable de repérage et d'arpentage.
Comment ?
L'agence spatiale européenne a exploité le satellite Hipparcos durant les années 1990, et lancé la mission Gaia fin 2013. Ces 2 missions ont pour but principal l'arpentage de l'Univers, obtenu par une très grande précision astrométrique.
Hipparcos comme Gaia sont des missions spatiales. L'écran de l'atmosphère terrestre est évité, la déviation d'un rayon lumineux au travers des couches atmosphériques étant bien trop importante par rapport à la précision recherchée, de l'ordre de la milliseconde d'arc.
La précision des missions Hipparcos et Gaia s'appuie sur le principe de l'observation simultanée de 2 champs stellaires, dans 2 directions faisant entre elles un angle fixé et stable (106.5 deg).
Comme un compas sert à repérer des distances (linéaires ou angulaires), de proche en proche les positions relatives des objets sont fixées les unes par rapport aux autres.
Gaia doit mesurer la précision d'un milliard d'objets dans la galaxies (soit 1% de son contenu stellaire), avec une précision de quelques millionièmes secondes d'arc pour les cibles les plus brillantes.
Performances attendues avec Gaia, pour une étoile de type G2
| magnitude | 10 | 15 | 20 |
| parallaxe (mas) | 0.007 | 0.027 | 0.3 |
Simuler
Positions et mouvements
La
simulation ci-dessous permet de lire les positions et mouvements repérés par le satellite européen Hipparcos dans l'amas ouvert des Hyades. Noter que la précision des positions effectivement repérées par Hipparcos est infiniment meilleure que celle restituée par l'appliquette.

S'évaluer
 Précision astrométrique et inégalité de Heisenberg
Précision astrométrique et inégalité de Heisenberg
Difficulté : ☆☆☆
Temps : 45 min
Cet exercice se propose de montrer que la précision astrométrique
d'un satellite tel Hipparcos ou Gaia peut être estimée par
l'application des inégalités de Heisenberg. On s'intéresse pour
ceci à la propagation d'un photon, issu d'un objet ponctuel à
l'infini, dont la trajectoire intercepte le miroir primaire de
détection (!). On munit l'espace d'un repère orthonormé 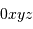 telle que le plan
telle que le plan 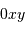 corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à
corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à 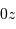 . On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
. On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
Question 1)
On s'intéresse à l'interception du photon selon la direction 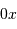 .
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe
.
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe 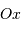 est inconnue, et que donc elle est
affublée d'une incertitude de position
est inconnue, et que donc elle est
affublée d'une incertitude de position 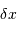 .
.
[2 points]
Réfléchir (!) à la formation d'image. Considérer une lentille
équivalente pour se simplifier la vie.
Question 2)
On rappelle qu'un échantillonnage par valeur entière correspond à
un bruit de numérisation de 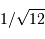 . En déduire
l'incertitude de mesure de la composant selon
. En déduire
l'incertitude de mesure de la composant selon 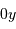 de la quantité
de mouvement du photon.
de la quantité
de mouvement du photon.
[1 points]
L'échantillonnage en position se fait ici par pas de largeur 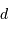 .
.
Question 3)
Par inégalité de Heisenberg, les incertitudes de position et
quantité de mouvement doivent vérifier :
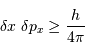
avec la quantité de mouvement totale 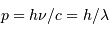 .
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
.
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
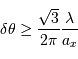
[3 points]
Déterminer d'abord 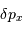 .
.
Déterminer 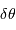 en fonction de
en fonction de 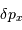 .
.
Question 4)
Faire l'application numérique pour Gaia, observant à la longueur
d'onde moyenne de 600 nm, avec 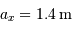 . Cela est-il
compatible avec les performances annoncées, de l'ordre de
. Cela est-il
compatible avec les performances annoncées, de l'ordre de 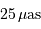 à la magnitude
à la magnitude 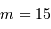 ? Pourquoi ?
? Pourquoi ?
[1 points]
Question 5)
La question précédente dimensionne l'incertitude pour 1 photon. On
montre plus loin dans le cours que pour 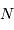 photons effectivement
détectés, l'incertitude est divisée par
photons effectivement
détectés, l'incertitude est divisée par 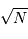 . Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
. Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
[1 points]
Photométrie
Observer
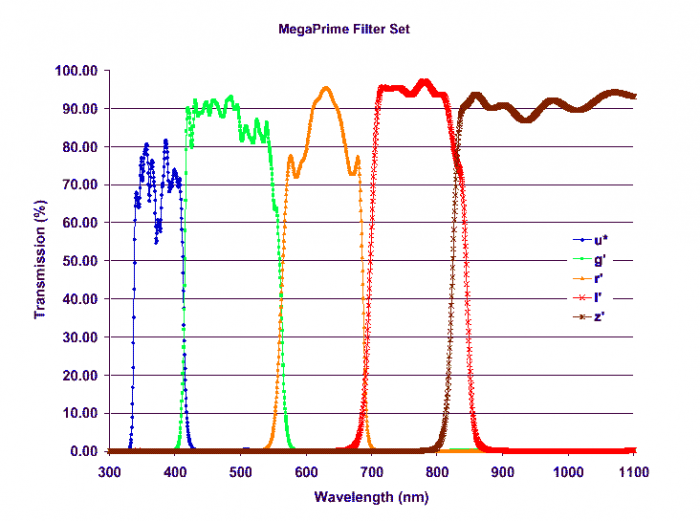
Le système de filtres de la caméra MEGACAM du télescope CFH
Crédit :
CFHT
Mesure de flux dans un système de filtres
Toute mesure photométrique doit s'appuyer sur un système de filtres précis, calibrés par rapport aux filtres des autres systèmes utilisés. Le projet MEGACAM au
télescope CFH
utilise le système ci-joint, couvrant du très proche UV au proche IR.
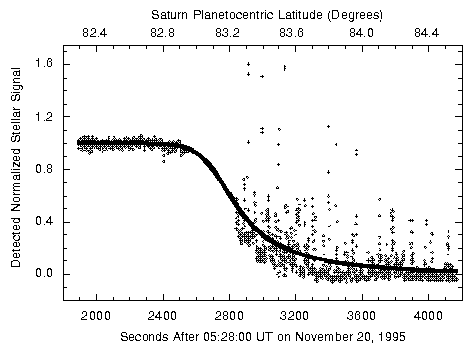
Courbe d'occultation : éclipse de l'étoile GSC5249-01240 par Saturne.
Crédit :
NASA/IRTF
Mesure de variations de flux
Les occultations, qui réunissent sur un même axe un objet du système solaire et une étoile, comme une éclipse réunit la Lune et le Soleil, ne sont pas que de simples événements fortuits : leur observation est riche en enseignement (métrologie, sondage atmosphérique...).
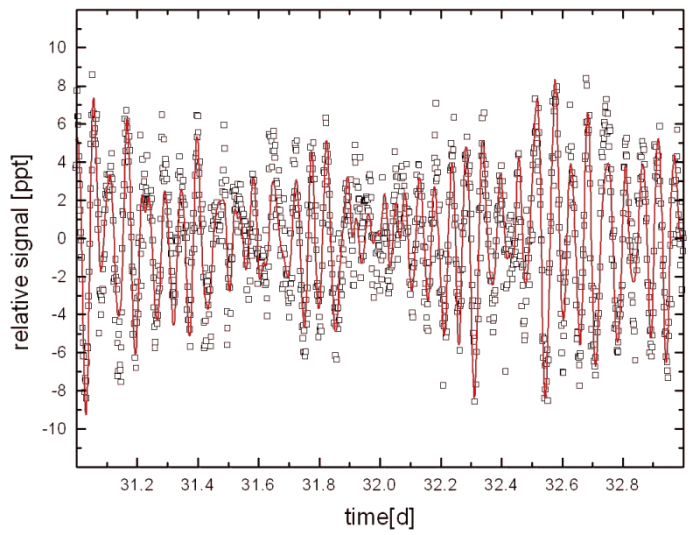
Échantillon de la série temporelle de la variabilité d'une étoile observée par le micro-satellite canadien MOST. L'échelle des ordonnées représente les variations relatives comptée en pourmille. La courbe rouge donne une estimation des variations observées : elle s'interprète comme les battements entre différents modes de pulsation stellaire.
Crédit :
MOST
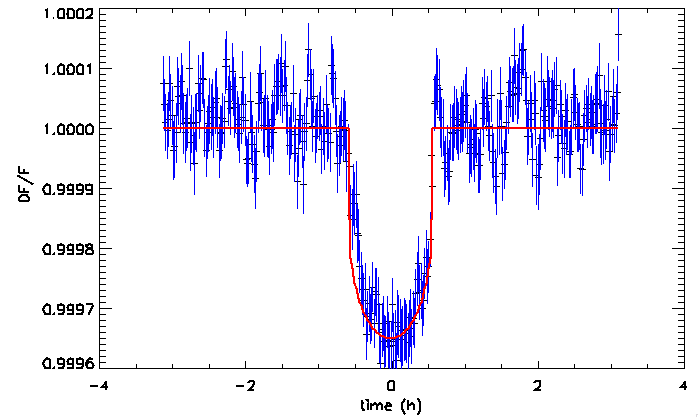
Transit de la planète CoRoT-exo-7b, détectée par le satellite CoRoT.
Crédit :
CoRoT/CNES
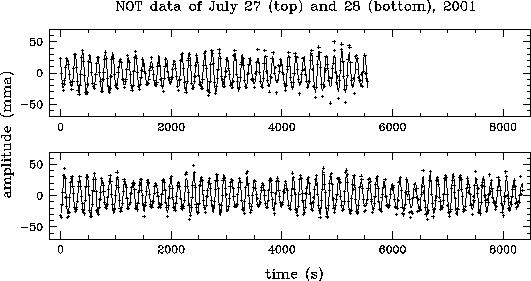
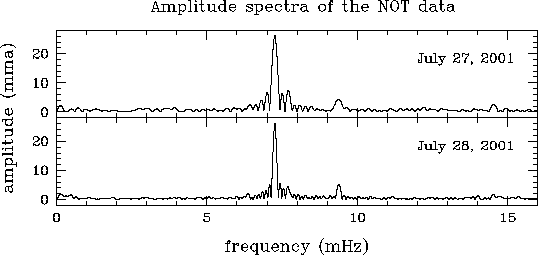
Courbe de variabilité d'une naine blanche. Les oscillation stellaires modulent le signal. Le rapport signal à bruit est suffisant pour mettre en évidence directement les oscillations. Plusieurs (9 en fait) observatoires ont été mis à contribution pour éviter au mieux - aléa météorologique mis à part - les interruptions diurnes sur les 25 jours & nuits d'observation.
Crédit :
WET
Crédit :
WET
Microvariabilité
Les mesures photométriques recherchent souvent des variabilités, dont l'étude ouvre de multiples champs d'investigation. Plusieurs satellites passent actuellement leur temps à mesurer des flux stellaires avec une précision de plus en plus grande. Le satellite CoRoT a ainsi découvert une très petite planète.
La microvariabilité d'une naine blanche (PG1159) est étudiée pour l'analyse de ses oscillations : la série temporelle enregistrée sur 8 nuits aboutit au spectre de Fourier.
Apprendre
 Définition
Définition
Photométrie : étude de la magnitude d'un astre dans un système de bandes spectrales.
Pourquoi la photométrie ?
Connaître précisément le nombre de photons de couleur donnée qui arrivent en un intervalle de temps donné permet de remonter à des considérations énergétiques.
Le problème est très souvent complexe, car il nécessite de tenir compte précisément de la transparence atmosphérique, de la fonction de transfert du collecteur et de l'instrument, de la réponse spectrale du détecteur...
Comment ?
Les effets mentionnés ci-dessus illustrent la complexité, voire l'impossibilité, d'une mesure photométrique absolue. Les mesures effectuées sont des mesures relatives, où la luminosité de l'objet, intégrée ou spectrale, est comparée à une référence.
Cette référence peut être une cible stellaire (telle l'étoile Véga p.ex, qui définit la magnitude apparente visuelle 0). Les mesures bolométriques, dans l'IR ou le submillimétrique, comparent le flux étudié à celui d'un corps noir calibré.
Variation photométrique
L'étude de la variabilité et de la
microvariabilité
est très fructueuse, pour observer des phénomènes à haute
fréquence, associés à des variations intrinsèquement rapides ou
bien dues à des phénomènes transitoires.
Simuler

Techniques
Mesurer un flux nécessite de la méthode, et cette dernière dépend du signal étudié. On peut pratiquer :
- La photométrie d'ouverture consiste à considérer tout le flux dans une ouverture donnée. La part de bruit dans cette ouverture sera incluse, peut être indûment, dans l'énergie du signal.
- La photométrie à seuil consiste à considérer comme signal tout ce qui dépasse un niveau de référence. Le choix du seuil est crucial : trop bas, il va considérer comme composante du signal ce qui n'est que du bruit ; trop haut, il ampute le signal.
- La photométrie par ajustement modélise la fonction d'étalement du point attendue, pour aller au plus juste de la mesure. Elle est plus précise que les autres méthodes, mais pas nécessairement simple à mettre en oeuvre. Elle peut être impossible à réaliser à bord d'un satellite, en l'absence de la puissance de calcul nécessaire.
Imagerie
Observer

Nuage moléculaire sculpté par le rayonnement ultraviolet ionisant de jeune étoiles en formation. Les doigts de matière qui résistent à l'érosion UV sont dans l'ombre portée par des régions plus denses. Ces dernières sont les plus violemment illuminées, et apparaissent les plus brillantes.
Crédit :
HST
Résolution spatiale, structures et détails
Imager permet de tracer la distribution de matière qui rayonne, qui absorbe... Une image en fausse couleur résulte de la superposition de 3 images prises dans 3 filtres différents.

Autrefois, avant l'introduction de la photographie à usage astronomique, à la fin du XIXe siècle, imager signifiait dessiner !
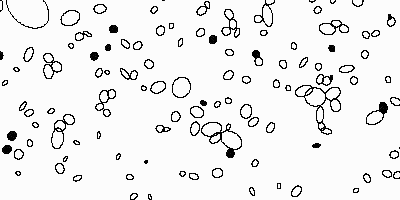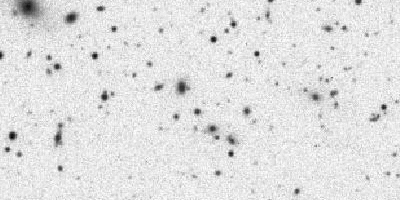
Champ stellaire, et identification des étoiles (points noirs) et des galaxies, via un logiciel de reconnaissance automatique de forme.
Crédit :
IAP
Identification
L'imagerie permet d'identifier les objets, pour les classer, pour faire le lien entre diverses observations à diverses longueurs d'onde... Un problème courant est de distinguer les sources stellaires des sources galactiques.

Déplacement d'un objet de Kuiper au cours d'une nuit. C'est justement son mouvement propre qui permet d'identifier un tel objet, de magnitude typique supérieure à 20.
Crédit :
CFHT

Rotation propre de l'astéroïde Eros, observée par la sonde NEAR.
Crédit :
NEAR/Nasa
Mouvements
L'imagerie, répétée sur un même champ, permet la découverte des petits corps du système solaire, en mouvement apparent sur fond d'étoiles fixes. C'est p.ex. ainsi qu'ont été découverts les objets de Kuiper, éléments du système solaire situés au-delà des planètes géantes, en deçà des comètes, et s'en distinguant par des orbites relativement proche de l'écliptique et d'excentricité modérée.

Rotation de Jupiter. Suivi des impacts des fragments de la comète SL9 sur Jupiter, en juillet 1994.
Crédit :
ESO
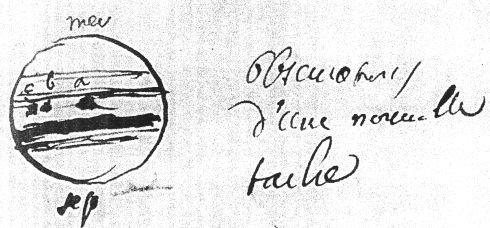
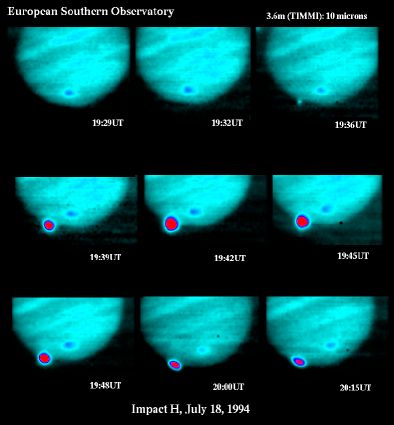
Observation d'une nouvelle tache sur Jupiter, par Cassini, en mars 1684. Et chute, observée en direct, d'un fragment cométaire sur Jupiter 3 siècles plus tard (juillet 1994, observation dans l'IR thermique à l'ESO) ; un fragment précédent a provoqué la tache à la même latitude que l'impact.
Crédit :
Bibliothèque de l'Observatoire de Paris / ESO
Événements
L'imagerie permet aussi de repérer des événements particuliers, comme p.ex. l'apparition de taches sur Jupiter.
Apprendre
 Objectifs
Objectifs
Tentative, désespérée, de classification des divers et nombreux champs d'application de l'imagerie en astrophysique
 Définition 😁
Définition 😁
Imagerie : fournir des images dans des systèmes de filtres standards, ou au-moins précisément référencés.
Pourquoi l'imagerie ?
L'imagerie fournit des images. Pour obtenir une image, il faut au préalable avoir reçu 10 bons points. On peut échanger 10 images contre un petit livre.
Les images en astrophysique apportent l'information spatiale, qui permet le traçage et l'identification de la matière lumineuse. Cette information dépend essentiellement de la longueur d'onde d'observation.
La résolution spatiale, couplée avec une faible résolution spectrale, donne par exemple accès à des informations de température ; avec une forte résolution spectrale : traçage fin d'un élément, mesures Doppler...
Comment ?
Obtenir une image est relativement trivial dans certains cas, pas du tout dans d'autres.
Ceci peut être dû à la mise en forme du signal.
Dans les domaines X et surtout 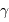 , la capacité d'imagerie des détecteurs est très limitée, et il est souvent difficile de bien localiser une source même intense. Du côté des très grandes longueurs d'onde, la tache d'Airy due à la diffraction peut atteindre une extension angulaire très grande ce qui limite la résolution spatiale.
, la capacité d'imagerie des détecteurs est très limitée, et il est souvent difficile de bien localiser une source même intense. Du côté des très grandes longueurs d'onde, la tache d'Airy due à la diffraction peut atteindre une extension angulaire très grande ce qui limite la résolution spatiale.
La capacité d'imagerie dépend aussi de la technologie des détecteurs. Si en lumière visible les mosaïques CCD atteignent 2k x 4k, les performances sont bien plus limitées dans les longueurs d'onde infrarouges. En submillimétrique et radio, les détecteurs étant monopixels, les images sont construites par juxtaposition d'images élémentaires.
Systèmes de filtres
L'imagerie est le plus souvent menée dans des systèmes de filtres si possible référencées, afin de pouvoir mener des comparaisons entre diverses observations. Ces filtres couvrent continûment le spectre, en bande large.
Imagerie multispectrale
Observer
Spectrohéliogrammes

Le disque solaire, dans diverses bandes spectrales : raie Halpha à 656.3 nm ; et raie K du calcium à 393.4 nm (K3 dans le minimum de la raie ; K1v dans l'aile de la raie côté violet). La morphologie des structures dépend intimement de la longueur d'onde d'observation.
Crédit :
Observatoire de Paris

Le disque jovien est quasiment éteint à la longueur d'onde
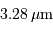
, alors que Io apparaît bien plus brillant à cette longueur d'onde.
Crédit :
ESO

Titan observé en optique adaptative dans différentes domaines de longueur d'onde du proche infrarouge. Lorsque le domaine spectral est sensible à un élément dans la stratosphère, le
limbe apparaît plus brillant.
Crédit :
ESO
Objets brillants
L'imagerie multispectrale, gourmande en photons, est menée sur des objets brillants, comme typiquement les objets du système solaire.
Selon la longueur d'onde d'observation, les disques solaire, jovien ou de Titan présentent différents aspects. Les domaines spectraux sont ici adaptés au phénomène étudié.

L'intérêt de l'imagerie multi-spectrale est de permettre une modélisation précise de l'objet observé. Par application de code de transfert de rayonnement, cette modélisation permet typiquement de contraindre la température et la composition de l'objet. Le diaporama ci-contre illustre une application sur la calotte martienne sud, observée par l'instrument OMEGA à bord de la sonde Mars Express.
La Voie Lactée

Images reconstruites de la Voie Lactée en différentes bandes spectrales.
Crédit :
NASA
La Voie Lactée
Selon la longueur d'onde d'observation, la Voie Lactée se présente sous différents aspects : chaque longueur d'onde apporte des informations complémentaires sur sa structure.
- Continu radio à 408 MHz : l'émission provient spécialement de la diffusion des électrons libres (émis lors des supernovae) dans le plasma interstellaire chaud, ou alors d'électrons accélérés dans des régions avec un fort champ magnétique. La boucle dans l'hémisphère galactique nord signale le plasma chaud résiduel d'une supernova ayant explosé relativement proche du Soleil il y a quelques milliers d'années.
- Hydrogène atomique à 21 cm (transition hyperfine de l'hydrogène atomique) : signature de milieu interstellaire froid, cette raie signale la présence de nombreux ensembles de gaz et de poussières.
- Continu radio à 2.5 GHz : signe la présence du gaz chaud et ionisé dans les régions de formation stellaire.
- Hydrogène moléculaire : mesuré indirectement, via la transition J=1-0 du monoxyde de carbone. Cette raie donne la carte des nuages d'hydrogène froids et denses.
- Infrarouge lointain : l'émission provient principalement des nuages du milieu interstellaire réchauffés par les étoiles nouvellement formées des régions de genèse stellaire.
- Infrarouge thermique (12, 60 et 100 micromètres) : l'émission provient également des nuages du milieu interstellaire réchauffés, mais signale plus particulièrement la présence de molécules complexes.
- Proche infrarouge (1.5, 2.2 et 3.5 micromètres) : la majeure partie de l'émission provient des étoiles de type spectral K, froides et peu massives. L'absorption par la matière interstellaire est faible dans ces domaines de longueur d'onde.
- Visible (600 nm): la lumière stellaire visible est fortement absorbée par les nuages du milieu interstellaire. L'efficacité du processus d'absorption limite la portée de cette carte aux plus proches régions de l'environnement solaire.
Les régions les plus obscurcies en lumière visible correspondent aux régions les plus brillantes en infrarouge.
- X (0.25, 0.75 et 1.5 keV) : l'émission de ces rayons X de faible énergie est principalement issu des nuages chauds ; elle est absorbée par la matière interstellaire, dont la concentration est d'autant plus forte que les régions apparaissent sombres.
- Rayonnement gamma : les photons au delà de 100 MeV sont issus de la collision entre les rayons cosmiques produits par les pulsars de la Voie Lactée et la matière interstellaire.
Apprendre
Imagerie spectrale
L'imagerie spectrale, comme son nom l'indique, fournit des images enregistrées dans un domaine spectral bien précis, défini par un filtre adapté aux propriétés de l'objet. Cela permet de tracer la distribution de matière contribuant à une signature spectrale donnée.
Cette technique est coûteuse en photons, et l'utilisation de filtres étroits nécessite une source brillante (dans le cas du soleil, ce genre de problème ne se pose bien sûr pas).
Clair obscur
L'imagerie multispectrale combine les avantages de l'imagerie et de la spectrométrie. Comme le nombre de photons est divisé et spatialement et spectralement, la source se doit d'être lumineuse pour des observations avec un rapport signal à bruit suffisant.
S'exercer
S'évaluer
 La Voie Lactée en couleurs
La Voie Lactée en couleurs
Difficulté : ☆☆
Temps : 20 min
Exercice de synthèse, basé sur les images multi-spectrales de la Voie Lactée, en 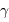 , X, visible, proche, moyen et lointain infrarouge, raie de
, X, visible, proche, moyen et lointain infrarouge, raie de 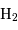 , H atomique, et radio.
, H atomique, et radio.
Question 1)
Dans quel système de coordonnées ces cartes sont-elles représentées ?
[1 points]
Question 2)
Quels domaines spectraux sont dominés par, respectivement, des sources ponctuelles intenses, une émission de type corps noir, l'absorption par des molécules ou des poussières, la réémission de ces derniers ?
[3 points]
Spectrométrie à haute résolution
Observer
Spectre du Soleil à haute résolution
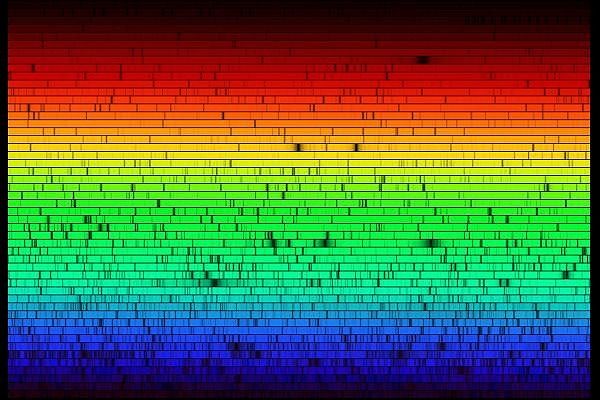
Le spectre solaire à haute résolution spectrale, observée avec un spectromètre à dispersion croisée. Les différents ordres d'interférence du spectromètre à haute dispersion ont été désenchevêtrés par la dispersion croisée.
Crédit :
NOAO
Dispersion croisée
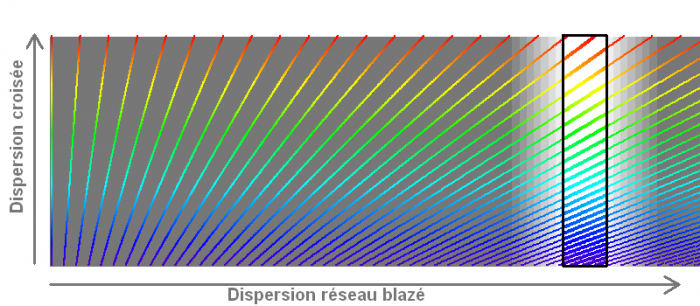
Schéma de principe :
une double dispersion permet l'enregistrement du spectre entier sur une caméra CCD. Un
réseau blazé disperse la lumière à haute résolution ; une dispersion à plus basse résolution, réalisée à l'aide d'un prisme, permet de distinguer les ordres entre eux. Le détecteur enregistre le signal dans les ordres élevés : chacun porte l'information spectrale, à haute résolution, dans un domaine de couleur différent. L'ensemble des ordres ainsi collectés permet de reconstituer le
spectre entier. Le réseau est blazé de façon à optimiser le rendement énergétique instrumental.
Crédit :
ASM
Réseau blazé
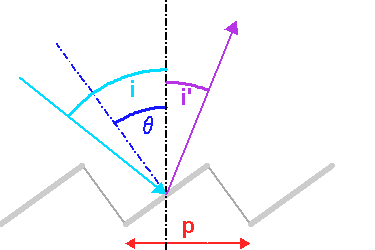
Profil d'un réseau blazé. Le profil en crête permet de réfléchir l'énergie dans un ordre d'interférence non nul.
Crédit :
ASM
Du bon usage des progrès technologiques
Les spectromètres pour la haute résolution spectrale ne datent pas d'hier. Mais l'avènement des caméras CCD, qui permettent d'enregistrer un signal sur 2 dimensions, a renouvelé le principe instrumental de la spectrométrie à haute résolution,
en ajoutant à la dispersion principale
une dispersion croisée, qui permet l'enregistrement simultané de tout le domaine spectral sur une caméra CCD.
Un spectromètre à réseau disperse la lumière dans ses ordres élevés, et les différents ordres sont séparés par une dispersion croisée obtenue à plus basse résolution. L'avantage d'une telle instrumentation est d'aboutir à un enregistrement simultané de tout le spectre, comme p.ex. ce spectre solaire.
Le spectromètre HARPS

Le spectromètre HARPS (High Accuracy Radial velocity Planet Searcher) est dédié à la recherche d'exoplanètes, par la méthode de mesure des vitesses radiales.
Crédit :
ESO/HARPS
Spectre obtenu par HARPS

Image d'un
spectre-échelle à haute résolution spectrale obtenu avec une caméra CCD. Le spectre de l'étoile apparaît ici sous l'aspect de bandes sombres.
L'étalonnage en longueur d'onde est apporté par les raies en émission d'une lampe spectrale (Thorium Argon), dont le spectre est intercalé avec celui de l'étoile, et enregistré simultanément.
Crédit :
ESO/HARPS
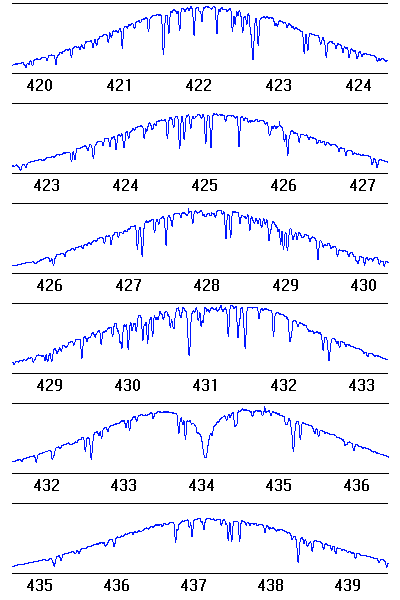
Spectre blazé obtenu avec le spectromètre Harps : la diffraction par chaque trait du réseau est responsable du profil d'étalement du flux.
Crédit :
ESO/HARPS
Le spectromètre HARPS
Le spectromètre HARPS dédié à la recherche d'exoplanètes est à l'heure actuelle le meilleur instrument de sa catégorie. Il atteint la résolution 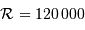 , en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une image ; l'image, traitée, conduit au spectre.
, en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une image ; l'image, traitée, conduit au spectre.
Apprendre
 Définition
Définition
Spectrométrie : étude des spectres.
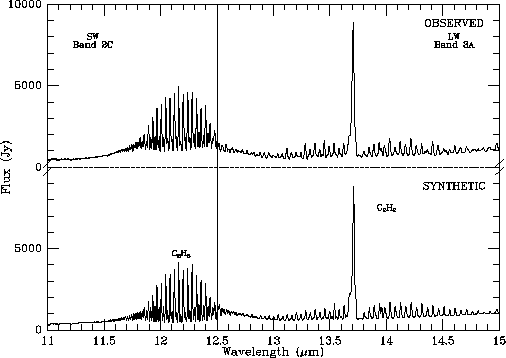
Spectre IR thermique de Saturne observé par le satellite ISO de l'Agence Spatiale Européenne, et interprétation des raies dues aux hydrocarbures présents dans la troposphère.
Crédit :
ESA
Pourquoi la spectrométrie à haute résolution ?
Bien distinguer l'identité spectrale des photons permet de remonter à la nature des éléments construisant le rayonnement, par absorption ou par émission.
La spectrométrie à haute résolution permet aussi, via l'analyse Doppler, des mesures très précises de vitesses radiales, comme p.ex. celles qui ont conduit à la découverte des planètes extrasolaires.
Simuler
Le principe
Le principe du spectromètre HARPS (ESO/Observatoire de Genève) est expliqué ci-joint.
Principe du spectromètre HARPS 
S'exercer
 Le spectromètre HARPS
Le spectromètre HARPS
Difficulté : ☆☆☆
Temps : 45 min
Le spectromètre HARPS, mis en service au printemps 2003 à La Silla, l'un des sites chiliens de l'ESO, a pour but la recherche des exoplanètes. On se propose ici de retrouver quelques-unes des qualités qui lui permettent d'atteindre les objectifs scientifiques fixés.
Question 1)
Le spectromètre est installé derrière le télescope de 3.6 m de l'ESO. Sa pièce principale, le réseau, présente une hauteur 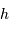 de 20 cm. Déterminer le grossissement
de 20 cm. Déterminer le grossissement 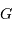 du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
Rappel du montage afocal
Faisceau de sortie du montage afocal
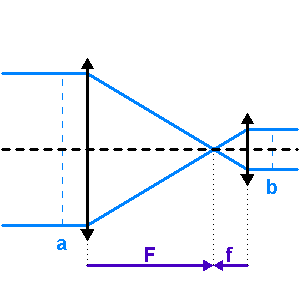
Crédit :
ASM
Question 2)
Montrer qu'une déviation 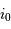 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 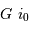 de l'angle dispersé.
de l'angle dispersé.
Relier la déviation de 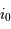 à celle de
à celle de 
Question 3)
Rappeler l'expression donnant les variations 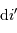 de l'angle de dispersion
de l'angle de dispersion 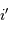 en fonction des variations de longueur d'onde
en fonction des variations de longueur d'onde 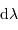 , du pas
, du pas 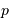 du réseau, et selon l'ordre d'interférence
du réseau, et selon l'ordre d'interférence 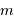 .
.
Le réseau envoie la lumière préférentiellement dans la direction 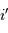 obéissant à :
obéissant à :
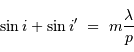
Différencier l'expression précédente.
Question 4)
On cherche à déterminer le champ objet maximal, qui permette
d'atteindre un pouvoir de résolution 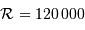 . Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
. Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
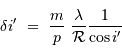
et conclure. On fera l'application numérique avec les données :
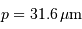 ,
, 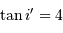 et un ordre d'interférence
et un ordre d'interférence 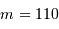 à
à 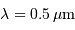 :
:
Question 5)
Justifier a posteriori l'hypothèse de non-divergence du faisceau. On pourra considérer un faisceau optique de longueur 8 m dans l'instrument.
Estimer la divergence en fonction de la longueur 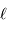 proposée et de l'angle
proposée et de l'angle 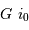 .
.
Spectro-imagerie
Observer
Plusieurs techniques permettent de réaliser la spectro-imagerie, càd une information spectrales pour plusieurs objets, plusieurs points du champ ou bien tout un champ.
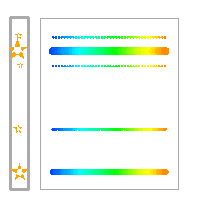
La fente sélectionne les objets du champ. La mosaïque CCD enregistre un spectre de chaque objet du champ.
Crédit :
ASM
Spectrométrie à longue fente
La fente du spectromètre sélectionne les objets du champ. La dispersion, perpendiculaire à la fente, apporte un spectre pour chacun de ses objets .
Découpe d'image
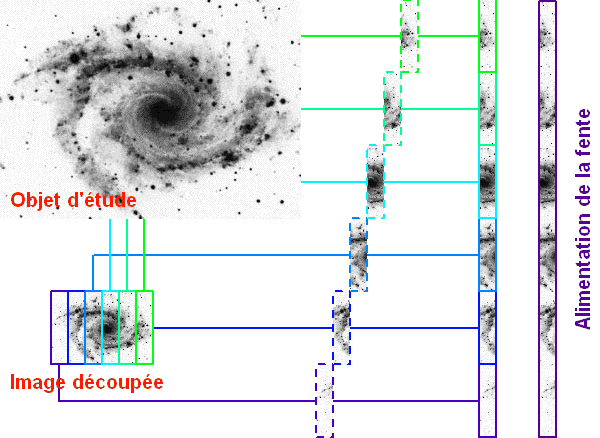
Le découpeur d'image permet, à partir d'une source étendue, d'illuminer la fente du spectromètre. Le champ entier est préservé, à un réarrangement près. Le découpeur correspond simplement à une collage de prismes, avec l'équivalent de 2 prismes croisés par tranche découpée. L'étape intermédiaire (avec les tiretés) a été représentée uniquement à des fins didactiques.
Crédit :
ASM
Découpage d'image
L'image est optiquement découpée en tranches, afin de couvrir la fente d'entrée du spectro. L'analyse des images monochromatiques de la fente d'entrée permettra de reconstituer chacune des régions initiales.
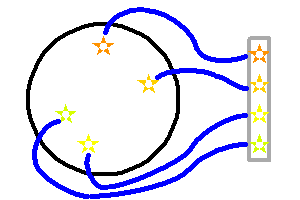
Sélection des objets par le faisceau de fibres, et alimentation de la fente d'entrée.
Crédit :
ASM

Une image intermédiaire est formée au niveau du système ici visualisé. Les têtes de fibre, chacune positionnable à l'extrémité d'un bras mobile, peuvent aller chercher le flux de tout point du champ.
L'instrument doit également fonctionner en imageur, pour repérer très précisément au préalable les positions des objets sélectionnés.
Crédit :
ESO

Les 7 cibles sélectionnés sont 7 galaxies d'un amas : les décalages des spectres donnent la dispersion des vitesses des différentes galaxies.
Crédit :
ESO
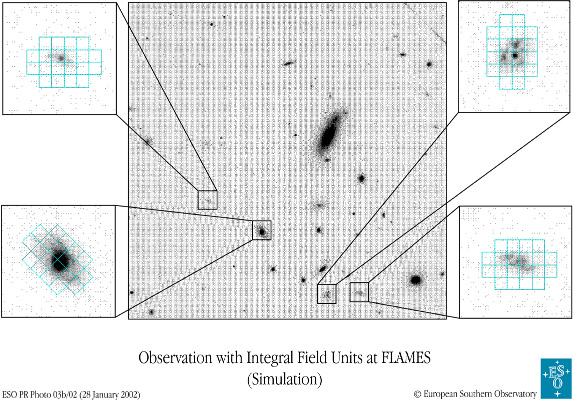
Spectroscopie multi-objet avec l'instrument FLAMES au VLT.
Crédit :
ESO
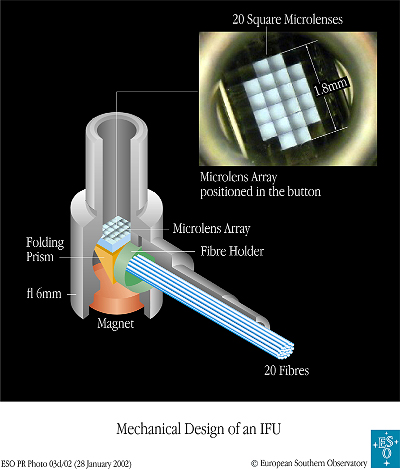
Concept optique pour la spectroscopie multi-objets : les 20 microlentilles irriguent 20 fibres optiques.
Crédit :
ESO
Apprendre
 Définition
Définition
Spectro-imagerie : spectrométrie sur un champ non limité à un seul point source.
Spectrométrie à fente longue
La spectrométrie à fente longue a pour objet l'enregistrement simultané de spectres à basse résolution pour les différentes sources sélectionnées par la fente.
Le flux issu de chaque sous-région de la fente est dispersé. La dispersion étant perpendiculaire à la fente, l'image bidimensionnelle finale résulte du produit de 2 dimensions : l'une est spectrale, l'autre est spatiale.
Spectrométrie multi-objets
La spectrométrie multi-objets réalise l'enregistrement simultané de spectres à basse résolution pour plusieurs régions d'une image.
Les flux de ces régions sont collectés via des fibres, qui organisent une anamorphose de l'image. En entrée, les sources sont réparties indifféremment dans le champ ; en sortie, leurs images par les fibres, sources pour le spectromètre, sont alignées le long de la fente.
Le flux issu de chaque fibre est dispersé. Comme pour la spectrométrie à fente longue, l'image bidimensionnelle finale résulte du produit de 2 dimensions : l'une spectrale, l'autre spatiale. Mais la correspondance entre les pixels et le champ est à considérer selon l'anamorphose effectuée.
Par rapport à la spectrométrie à longue fente, la souplesse des fibres permet de sélectionner plus pertinemment les sources.
Spectrométrie intégrale de champ
La spectrométrie intégrale de champ propose l'enregistrement simultané de spectres à basse résolution de tout un champ objet.
L'objet est découpé en un certain nombre de régions, chacune étant alors considérée comme une source ponctuelle, ensuite dispersée.
L'espace entre les images de chacune de ces sources ponctuelles est suffisant pour permettre d'enregistrer, pour chacune, un spectre à basse résolution.
Simuler
Spectrométrie multi-objets
La fente du spectromètre UVES de l'ESO, fonctionnant en spectrométrie multi-objets, est illuminée par 8 fibres. Sept d'entre elles visent 7 cibles, la 8ème est réservée à la référence spectrale (une lampe à vapeur spectrale, dont on voit les raies en émission).
Spectrométrie multi-objets 
Spectrométrie intégrale de champ 
Spectrométrie intégrale de champ
La résolution spatiale est dégradée, pour permettre l'enregistrement de spectre sur une grille de régions du champ.
Le réseau de microlentilles découpe le faisceau, et crée autant d'images ponctuelles qu'il y a de microlentilles. Ces images ponctuelles sont ensuite autant de sources pour un spectrographe.
On récupère en sortie un spectre de résolution moyenne pour chaque région de l'objet découpée par la microlentille
(cf instrument CFHT/Observatoire de Lyon).
S'exercer
 Spectrométrie intégrale de champ : résolutions spatiale et spectrale
Spectrométrie intégrale de champ : résolutions spatiale et spectrale
Difficulté : ☆☆
Temps : 20 min
Cet exercice a pour but d'estimer l'ordre de grandeur des performances d'un spectromètre intégral de champ, qui donne des images sur un CCD de 2k  2k (2000 fois 2000 pixels).
On note
2k (2000 fois 2000 pixels).
On note 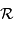 le pouvoir de résolution spectrale visé,
le pouvoir de résolution spectrale visé, 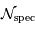 le nombre d'éléments spectraux correspondant,
le nombre d'éléments spectraux correspondant, 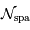 le nombre d'informations spatiales souhaité.
le nombre d'informations spatiales souhaité.
Question 1)
Montrer que, si l'intervalle spectral est large, alors en ordre de grandeur
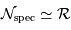 . On se place par la suite dans le cadre de cette hypothèse.
. On se place par la suite dans le cadre de cette hypothèse.
Pour fixer les ordres de grandeur, on peut traduire large intervalle spectral comme 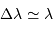 .
.
Les définitions de 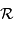 et
et 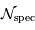 sont :
sont :
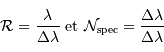
Question 2)
Montrer que le produit 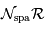 est nécessairement borné.
est nécessairement borné.
Réfléchir à la signification du mot pixel. Combien d'informations spatiales élémentaires un CCD de 2k 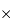 2k peut-il traiter?
2k peut-il traiter?
Question 3)
On considère pour la suite qu'entre le codage, l'étalonnage, la séparation des spectres..., une information élémentaire nécessite 20 pixels.
On souhaite une résolution spectrale de 200. En déduire le nombre d'informations spatiales maximal.
Montrer que, vu les hypothèses :
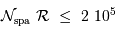
Interférométrie
Observer
Antenne millimétrique


Réseau des 6 antennes millimétriques de l'observatoire du Pic de Bure de l'
IRAM. L'extension maximale de l'interféromètre atteint 408 m sur la branche Est-Ouest, et 232 m en Nord-Sud.
Crédit :
IRAM
VLA

Réseau d'antenne VLA (Very Large Array) du NRAO (National Radio Astronomy Observatory), travaillant aux longueurs d'onde de 1.2, 2, 6 et 21 cm. 27 antennes sont disposées sur 3 branches en Y, s'étendant sur 19
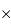
21 km
Crédit :
NRAO
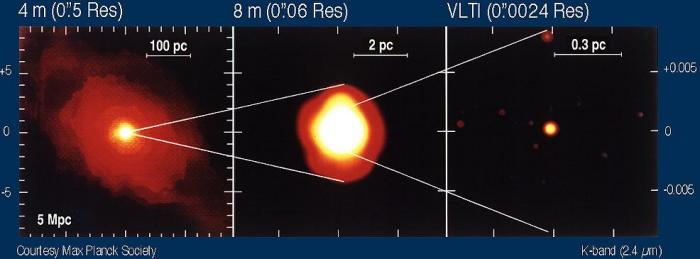
Séquence illustrant le gain en résolution spatiale entre une image non corrigée par optique adaptative, corrigée, ou enregistrée en mode interférométrique.
Crédit :
ESO/Max Planck Society

Les 4 télescopes du VLT. La configuration VLTI, interférométrique, s'obtient en recombinant les faisceaux via les galeries enterrées qui apparaissent sur la photo.
Crédit :
ESO
Ligne à retard du VLTI

Le faisceau issu du collecteur le plus proche de la source doit être rallongé, pour interférer avec l'autre faisceau à différence de marche quasi-nulle. Cela nécessite des lignes à retard de grande longueur (extension maximale de 60 m, pour un retard double après un aller-retour), dans le tunnel interférométrique.
Crédit :
ESO
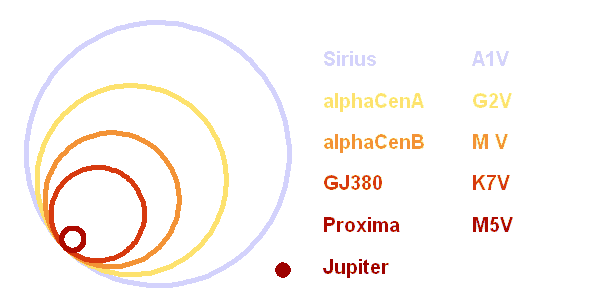
Schéma à l'échelle du rayon de différentes étoiles naines de la séquence principale. Rayons mesurés avec le VLTI.
Crédit :
ASM
Le VLTI
On nomme VLTI la configuration interférométrique des télescopes du VLT. La longueur de cohérence pour une source astronomique étant limitée, l'obtention de franges d'interférence nécessite des lignes à retard pour mélanger les faisceaux des différents collecteurs.
Une des premières opérations du VLTI a consisté en la mesure de diamètres stellaires d'étoiles de la séquence principale. La mesure de ces diamètres angulaires est impossible sans la haute résolution apportée par l'interférométrie.
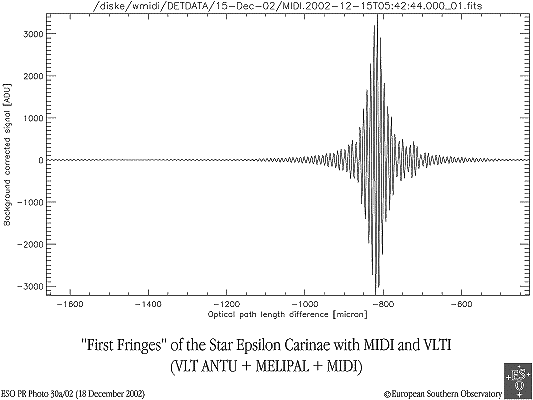
Enregistrement de franges d'interférence. La cohérence spatiale est limitée par la taille angulaire de la source.
Crédit :
ESO
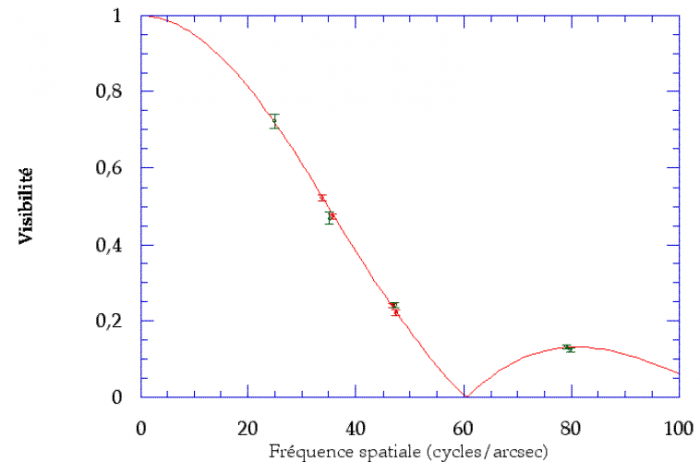
La mesure du diamètre angulaire de l'étoile
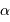
du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.
Crédit :
ESO
Apprendre
 Objectifs
Objectifs
Augmenter la résolution angulaire, ultimement limitée par la diffraction d'un collecteur, en faisant interférer les faisceaux de plusieurs collecteurs.
 Prérequis
Prérequis
Diffraction, interférence ; la notion de cohérence spatiale est nécessaire pour justifier les techniques d'interférométrie.
Recombinaison
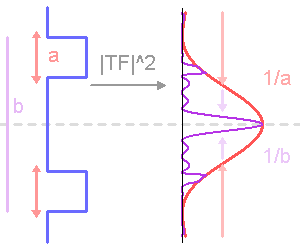
La tache de diffraction d'un seul télescope de diamètre collecteur
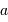
est en
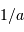
; la tache image résultant de l'interférence sur la base
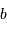
est en
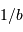
.
Crédit :
ASM
Configuration de Fizeau
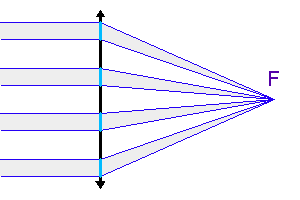
Interféromètre dans la configuration de Fizeau. Les différentes surfaces collectrices sont des sous-parties d'une unique surface. Les faisceau convergent en phase au foyer commun.
Crédit :
ASM
Configuration de Michelson
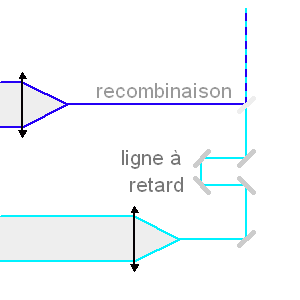
Interféromètre dans la configuration de Michelson. Une ligne à retard doit assurer le cophasage des faisceaux recombinés.
Crédit :
ASM
Le principe
Les faisceaux issus de 2 collecteurs pointant le même objet sont recombinés, de manière cohérente, pour interférer.
Exemple de valeur numérique : dans le proche infrarouge, pour une base de 100 m :
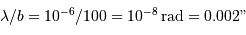 .
.
Exemple de recombinaison : interféromètre de type Michelson, ou bien Fizeau. Dans ce dernier cas, les surfaces collectrices sont des éléments disjoints d'une surface collectrice unique.
Vers la haute résolution angulaire
L'interférométrie s'est développée dans un premier temps dans le domaine radio. Dans ce domaine de fréquence, la détection cohérente permet une recombinaison du signal plus aisément qu'aux fréquences optiques. La phase du signal étant enregistrée, cette recombinaison n'a même pas à être nécessairement menée en temps réel.
L'interférométrie dans le domaine des grandes longueurs d'onde apparaît par ailleurs le plus souvent indispensable, la taille de la tache de diffraction dans ce domaine conduisant, malgré les grands diamètres collecteurs, à une résolution angulaire médiocre.
L'interférométrie est aujourd'hui développée jusque dans le domaine visible : en l'absence de pupille de grande taille, c'est la seule technique donnant accès à la haute résolution angulaire.
Technique d'observation
On s'intéresse aux interférences construites entre paires de collecteurs. Le problème se ramène à une situation de type trous d'Young, avec l'analogie entre les trous d'Young et les collecteurs.
La longueur de cohérence du faisceau stellaire est limitée. Réaliser des interférences ne se limite pas à une sommation des intensités lumineuses : observer des franges d'interférence nécessite d'égaler les chemins optiques des 2 voies à quelques longueurs d'onde près avant leur recombinaison.
Des lignes à retard optiques permettent de réaliser ceci.
De la même façon que le paramètre pertinent pour visualiser les franges d'interférences issus des trous d'Young est l'écart angulaire 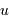 par rapport à l'image géométrique, il est utile de faire la correspondance entre la projection des lignes de bases de l'interféromètre, projetées sur le plan d'onde. Une configuration donnée, à une date donnée, va conduire à la mesure de la visibilité des franges d'interférences pour un vecteur angulaire donné
par rapport à l'image géométrique, il est utile de faire la correspondance entre la projection des lignes de bases de l'interféromètre, projetées sur le plan d'onde. Une configuration donnée, à une date donnée, va conduire à la mesure de la visibilité des franges d'interférences pour un vecteur angulaire donné 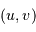 .
.
La courbe de visibilité dépend de la taille angulaire de la source, dès lors que celle-ci est résolue par l'interféromètre. Plus la source sera étendue, plus les franges d'interférence apparaîtront brouillées dès lors que l'on s'éloigne angulairement de la direction de l'optique géométrique.
Simuler
Base
La ligne de base correspond à la projection sur le plan du ciel, donc orthogonale à la ligne de visée, de la position des télescopes.
Du fait de la rotation de la Terre, elle varie au cours de l'observation.
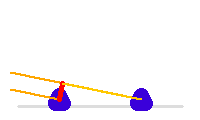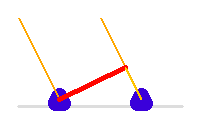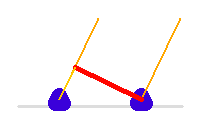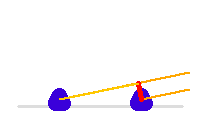
La ligne de base, en rouge, varie en cours de la nuit. Le trajet supplémentaire de la lumière sur l'un des voies est à compenser par une ligne à retard.
Crédit :
ASM
Synthèse d'ouverture
Les animations ci-jointes montrent comment évoluent, au cours d'une séquence d'observation, les lignes de base d'un site avec 3 télescopes interférant, avec les fréquences spatiales sur le plan du ciel.
Si l'objet ne varie pas rapidement dans le temps, il est possible de prendre le temps de nombreuses configurations interférométriques, au besoin avec des changements de positions des télescopes (lorsque cela est possible), pour reconstituer suffisamment de fréquences spatiales et imager en détail l'objet.
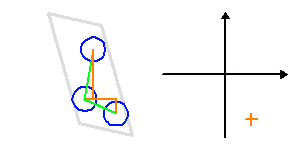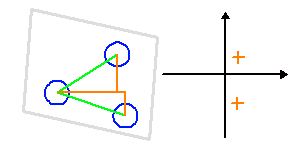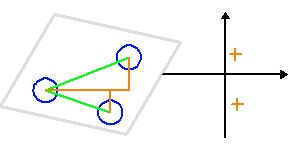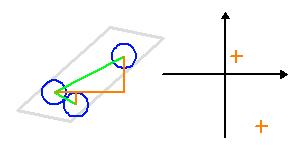
Au cours d'une nuit d'observation, une source donnée voit le plan de 3 télescopes d'un interféromètre sous un angle variable. A 3, ils construisent 2 lignes de base indépendantes, et donnent accès à 2 fréquences spatiales différentes (croix orange).
Crédit :
ASM
S'exercer
 QCM
QCM
 L'interféromètre du plateau de Bure
L'interféromètre du plateau de Bure
Difficulté : ☆
Temps : 10 min
Les antennes de l'IRAM du plateau de Bure ont un diamètre de 15 m.
Question 1)
Déterminer la tache d'Airy, pour une observation menée à 230 GHz.
Une fréquence de 230 GHz correspond à une longueur d'onde de 1.3 mm.
Question 2)
Que devient cette résolution pour une observation interférométrique avec une ligne de base de 400 m ?
Déterminer le gain en éléments de résolution sur un objet.
Observatoire virtuel
Observer
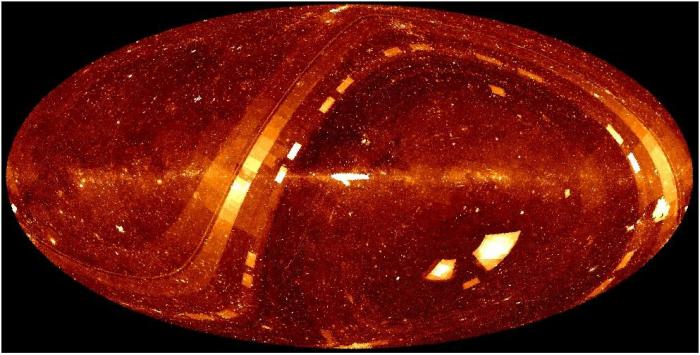
Carte du ciel en coordonnées galactiques, avec représentation de la densité des régions les plus étudiées et accessible dans le catalogue Vizir tenu par le Centre de Données Stellaires de l'Observatoire de Strasbourg.
Crédit :
CDS
Catalogues
Les différents programmes d'observations des différents télescopes ont conduit à l'accumulation de très nombreuses données, compilées dans de non moins nombreux catalogues. Aujourd'hui, soit ces catalogues sont devenus obsolètes, soit ils sont accessibles en ligne pour être accessibles, pour profiter à la plus large communauté, pour être intercroisés avec d'autres observations...

C'est par comparaison avec une image d'archive que peut être mis en évidence un événement tel une supernova.
Crédit :
ESO
Exemple d'intérêt : archive
Un intérêt majeur d'un observatoire virtuel consiste à fournir des archives, p.ex. pour détecter un phénomène nouveau, tel l'apparition d'une supernova.
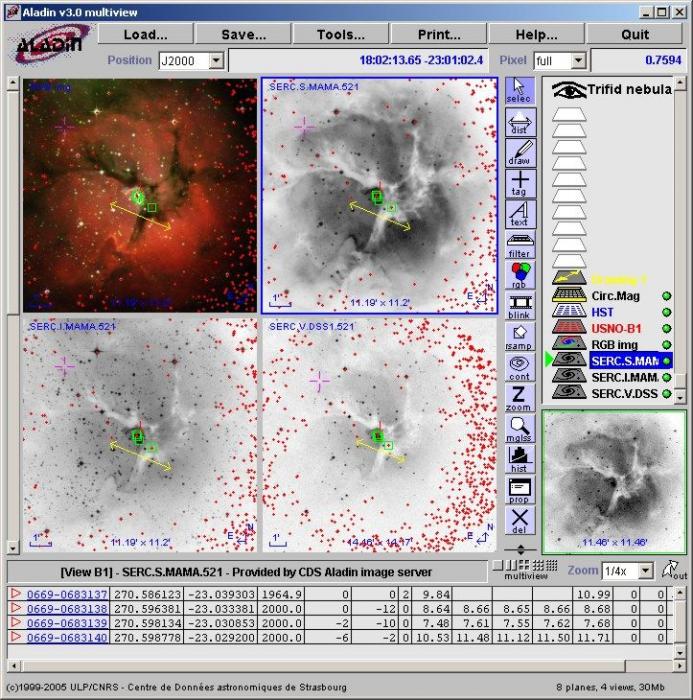
Aperçu d'un outil permettant de comparer des clichés dûment catalogués d'un même objet à différentes longueurs d'onde.
Crédit :
CDS
Exemple d'intérêt : analyse multispectrale
Approche
multispectrale de M20 proposée par le Centre de Données Stellaires de l'Observatoire de Strasbourg. Les outils permettent de retrouver des informations, les comparer...
Apprendre
 Définition
Définition
Un observatoire virtuel correspond à un centre de données, donnant accès à des observations passées classées, archivées, ainsi que des outils spécifiquement développés pour travailler ces observations.
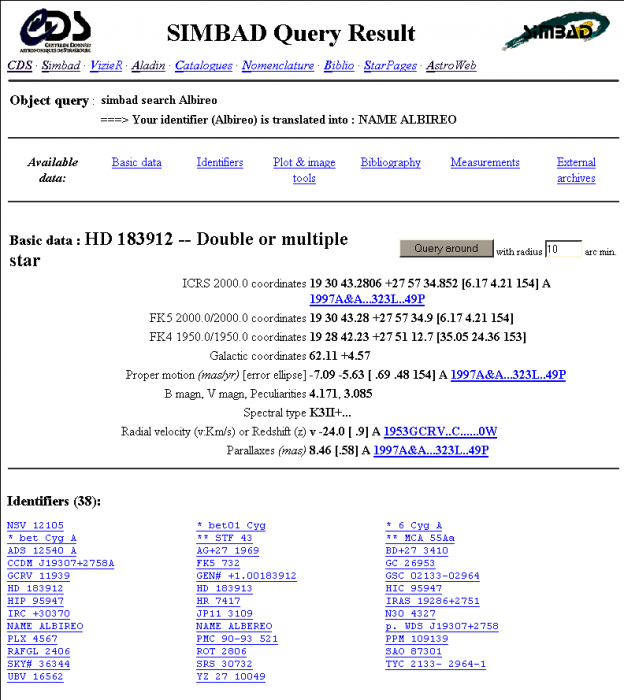
Une page, parmi tant d'autres, de la base de donnée SIMBAD. Renseignements sur une cible donnée : coordonnées, articles de référence, et liens vers ses multiples dénominations, différant les unes des autres selon le catalogue d'observation.
Crédit :
CDS
Base de données
Les évolutions technologies ne permettent pas seulement d'avoir des instruments plus performants, pilotés par des interfaces efficaces. Elles ouvrent aussi la possibilité de mettre à la disposition de la communauté des chercheurs les observations menées par les différents programmes.
Les bases de données
classent et organisent dans des formats facilement portables les résultats obtenus par les grands observatoires, leurs programmes majeurs d'atlas et d'observation de régions précises, les missions spatiales...
Vers les observatoires virtuels
Un observatoire virtuel, c'est une base de données suffisamment bien achalandée, organisée et agencée pour permettre non de réaliser une observation, mais d'accéder à des observations passées susceptibles de fournir les renseignements cherchés.
Un observatoire virtuel doit ainsi permettre :
- de comparer des observations concernant un même objet,
- de comparer des observations obtenues à des dates différentes,
- de croiser des observations obtenues à des longueurs d'onde différentes...
Pour en savoir plus, voir p.ex. le site du Centre de Données astronomiques de Strasbourg (CDS).
Conclusion
Cette section a exposé les principales mises en forme du signal astronomique. Chacune correspond à une instrumentation spécifique.
Une bonne part de la recherche astrophysique concerne le développement d'instruments encore plus puissants, efficaces, sensibles, précis, stables... sachant qu'il est impossible de tout faire simultanément.

Instrument AMBER, spectromètre du VLTI observant dans le proche infrarouge avec un pouvoir de résolution pouvant monter jusqu'à 10 000.
Crédit :
ESO
Détecter le signal
Auteur: B. Mosser
Introduction
Plus de dix ordres de grandeurs séparent les énergies des photons
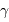 à radio auxquels s'intéressent les astrophysiciens. Les techniques de détection, tout comme les
détecteurs, sont évidemment bien différentes selon le domaine spectral.
à radio auxquels s'intéressent les astrophysiciens. Les techniques de détection, tout comme les
détecteurs, sont évidemment bien différentes selon le domaine spectral.
Cette section présente des caractéristiques générales, et explore préférentiellement le domaine spectral visible ainsi que les domaines proches du visibles où les détecteurs présentent des propriétés semblables.
Une section est spécialement dédiée aux détecteurs CCD et aux observations avec une caméra CCD. Une autre s'intéresse aux observations dans l'infrarouge thermique.
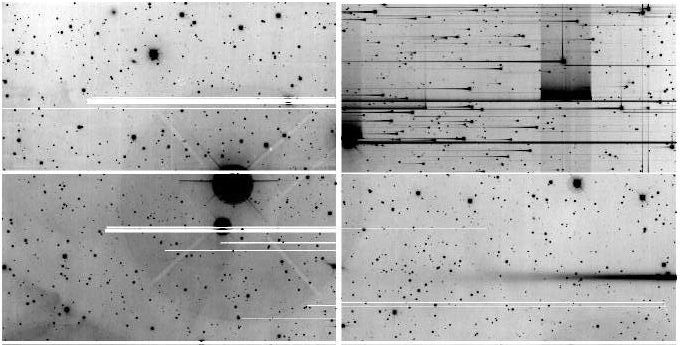
Fragment d'image, brute, obtenue par la caméra CFH12k du télescope
CFH
Crédit :
CFHT
Propriétés générales
Observer
Réponse spectrale
La réponse spectrale d'un détecteur indique son rendement en fonction de la longueur d'onde. Sans l'instrumentation appropriée, un détecteur ne fournit pas d'information sur la couleur précise d'un photon détecté.
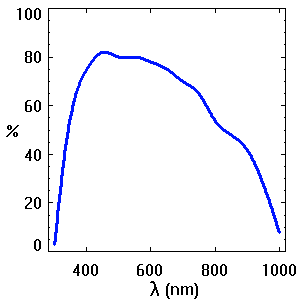
Réponse spectrale d'un CCD éclairé par l'arrière. Un tel détecteur ne voit ni les photons UV ni les photons IR. Il n'est pas non plus capable de distinguer un photon rouge d'un photon bleu s'il n'est pas précédé de l'instrumentation appropriée (filtre ou spectrographe).
Crédit :
ASM
Pixels
La taille et le nombre des pixels est un paramètre important. Une photodiode est monopixel ; les mosaïque CCD pour l'astronomie peuvent compter jusqu'à 2k  4k pixels, les plus grands CCD actuels (2003) atteignant la taille 8k
4k pixels, les plus grands CCD actuels (2003) atteignant la taille 8k  8k pixels.
8k pixels.

La résolution atteinte sur cet objet du voisinage de NGC3486, observé en bande B et I dans des conditions de
seeing de 0.7", met clairement en évidence la pixélisation de la caméra grand champ.
Crédit :
CFHT
Saturation
Exemple de détecteur saturé, en raison d'une trop grande dynamique entre les signaux à enregistrer. La saturation conduit à élargir démesurément la tache image, car les trop nombreux photo-électrons ont débordé du puits de potentiel où ils auraient dû être stockés.

Système binaire Gliese 229. La composante Gb299A est totalement saturée, pour mettre en évidence le compagnon Gl229B, de masse substellaire, qui est une
naine brune.
Crédit :
HST
Apprendre
Propriétés d'un détecteur
On peut synthétiser les propriétés d'un détecteur selon différentes caractéristiques, chacune associée à une dimension physique particulière.
Les principales caractéristiques sont traitées avec plus de détail dans des pages dédiées.
Simuler
Caractéristiques
Exemple de caractéristiques d'un détecteur : mosaïque de la caméra CFH12k du télescope CFH.

Phénomène physique de détection
Apprendre
Détecteurs
On peut distinguer 3 grands type de détection :
- Détection quantique :
Un photon incident, absorbé, conduit à l'apparition d'un porteur de charges.
- Détection cohérente : Les récepteurs d'amplitude sont
sensibles à l'amplitude et à la phase du signal électromagnétique.
Le collecteur est dans ce cas souvent appelé antenne. La détection
cohérente nécessite, dans les plus hautes fréquences auxquelles
elle peut être menée, le mélange du signal scientifique et d'un
signal de référence. La création d'un signal de référence stable,
cohérent, n'est technologiquement réalisable qu'aux basses
fréquences, en pratique pour les signaux de fréquence
inférieure à 1500 GHz (longueur d'onde de 200 micromètres).
- Détection thermique : Un bolomètre absorbe l'énergie du
rayonnement incident et la dégrade en agitation thermique.
L'élévation thermique qui en résulte est mesurée par la variation
d'une grandeur physique reliée à la température.
S'exercer
 Principe de la détection hétérodyne
Principe de la détection hétérodyne
Difficulté : ☆
Temps : 15 min
La détection hétérodyne compare le signal scientifique à un signal de référence délivré par un oscillateur local à haute fréquence. On note 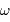 la pulsation du signal scientifique, et
la pulsation du signal scientifique, et  celle de la référence, cette dernière étant voisine de
celle de la référence, cette dernière étant voisine de 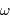 .
.
Question 1)
Un mélangeur fournit le signal produit des signaux observé et de référence.
Montrer que ce signal est composé de 2 fréquences bien distinctes.
On rappelle :
![\cos a \cos b = {1\over 2} \Bigl[ \cos (a+b) + \cos (a-b) \Bigr]](../pages_detecter/equations_detection-physique/equation7.png)
Question 2)
On applique au signal un filtre passe-bas, pour éliminer les hautes fréquences.
Montrer l'intérêt du mélange des signaux.
Que reste-t-il du signal précédent après élimination des hautes fréquences ?
Détection quantique
Apprendre
 Objectifs
Objectifs
Illustrer comment l'interaction matière-rayonnement permet de
transférer l'information utile d'un photon à un photo-électron.
Photo-électron
L'absorption d'un photon permet à un électron du détecteur de
changer d'état. Cette création d'un photo-électron par absorption
d'un photon caractérise les détecteurs quantiques.
Du signal lumineux au signal enregistrable
La conversion photon + électron  photo-électron s'appuie sur différents effets.
photo-électron s'appuie sur différents effets.
| Effet | Description | Récepteur |
| Effet photochimique | Changement d'état chimique | Plaques photo, plus guère employées aujourd'hui. Les photo-électrons activés par le rayonnement réduisent les ions Ag+ en argent métallique. |
| Effet photoélectrique | Extraction d'un électron d'un métal vers le vide | Phototube, photomultiplicateur |
| Effet photoconducteur | Au sein d'un semi-conducteur, l'absorption d'un photon permet à un électron de franchir le gap de la bande de valence vers la bande de conduction | Photodiode |
| Effet photovoltaïque | Effet photoconducteur dans une jonction PN.
Un photon crée une paire
électron-trou, qui se traduit pas une différence de potentiel
aux bornes de la jonction ;
IR lointain  radio radio
| |
S'exercer
Détection : dynamique
Observer
Linéarité
On demande à une mesure physique de fournir une mesure en liaison avec l'observable voulue. Une propriété importante est la linéarité : si elle n'est pas assurée, la relation entre le signal mesuré et le signal observé est complexe.
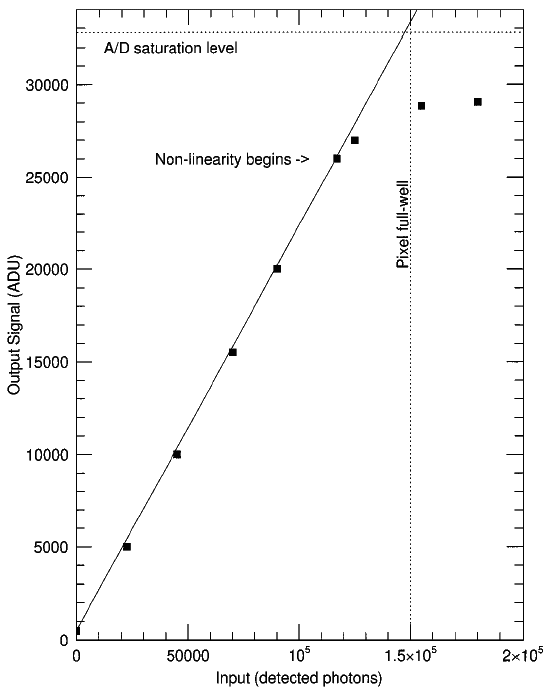
Courbe de linéarité typique d'une caméra CCD. Ici, la linéarité est assurée d'environ 500 à 25000 ADU (unités de signal numérisé), puis le détecteur sature.
Crédit :
CFHT
Seuil et saturation
L'effet de seuil peut introduire un décalage sur une faible mesure. Le niveau de signal doit être suffisant pour sortir du bruit propre du détecteur. A faible niveau, la définition du signal nul (offset) peut également affecter le signal. La saturation affecte les fortes valeurs de signal.
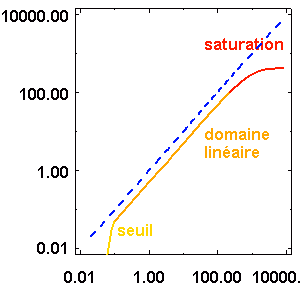
L'excitation est en abscisse, la réponse en ordonnée (échelle log-log). La ligne tiretée en bleu donne une réponse idéale, identique à l'excitation, sans seuil ni saturation, de rendement unité. En deçà du seuil, la réponse d'un détecteur réel est mauvaise ; au-delà d'une certaine valeur, le détecteur sature.
Noter que le rendement n'est pas 1.
Crédit :
ASM
Apprendre
 Objectifs
Objectifs
Un bon détecteur est linéaire sur une grande dynamique, et propose un seuil de sensibilité bas.
Seuil de sensibilité
Un récepteur sera d'autant plus sensible que... son seuil de sensibilité est bas. Ceci nécessite le plus souvent son refroidissement, afin de diminuer le bruit d'agitation thermique.
Linéarité
La linéarité assure une réponse proportionnelle au signal incident.
C'est une propriété importante pour convertir une observable en mesure. Si le détecteur est linéaire, il est possible par un simple facteur d'échelle de convertir le signal électrique enregistré en signal photométrique.
Saturation
La saturation limite le flux maximum observable. Un niveau de saturation élevé assure une grande dynamique.
Réponse spectrale
Observer
Réponse spectrale d'un CCD
La réponse spectrale d'un CCD dépend du matériau semi-conducteur utilisé et des caractéristiques géométriques du sandwich de détection.
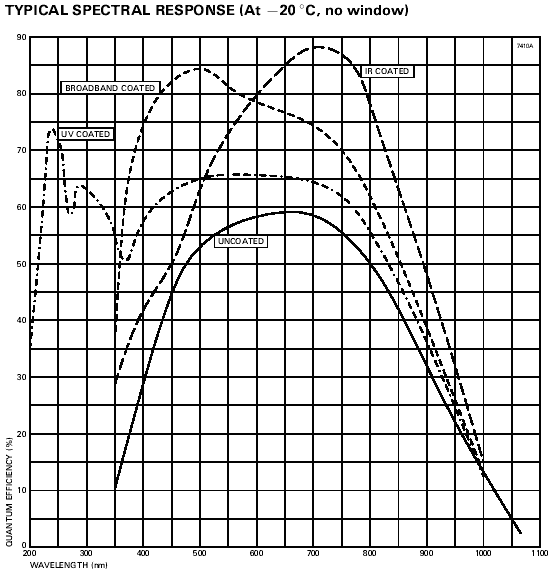
Réponse spectrale d'un CCD, selon le traitement de surface (=coating), optimisé vers l'IR, l'UV, ou bien plus une plus grande bande spectrale visible. CCD30-11 de Marconi Applied Technologies
Crédit :
Marconi
Réponse spectrale d'un bolomètre pour la radioastronomie
Un bolomètre ne discrimine pas les longueurs d'onde... mais cela ne signifie pas qu'il est également sensible à toutes les longueurs d'onde. Le signal délivré est en fait intégré selon une fenêtre spectrale donnée.
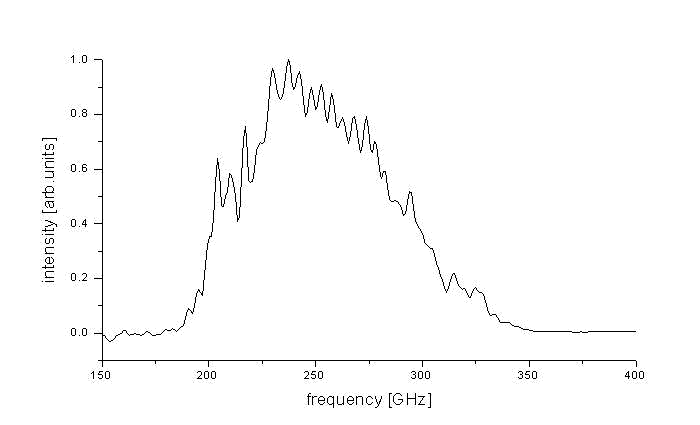
Courbe de réponse spectrale de l'instrument Mambo de l'
IRAM (Max Planck Millimetre Bolometer).
Crédit :
IRAM
Apprendre
Sensibilité spectrale
Un détecteur n'est sensible que dans une gamme spectrale donnée. Il n'a en général aucune sélectivité spectrale intrinsèque, sauf s'il est muni de filtre adéquat.
Résolution spectrale
De ce qui précède, on déduit que la résolution spectrale dépend essentiellement des filtres ou de l'instrumentation associés au détecteur.
Réponse temporelle
Observer

Fréquence de lecture d'une caméra CCD. Plus elle est rapide, plus le bruit de lecture augmente.
Crédit :
ANDOR technologies
Réponse temporelle
La rapidité de lecture d'un CCD dépend de la fréquence d'horloge de l'électronique et du nombre de pixel. Le fait de n'avoir qu'un nombre de registre de lecture limité (1 à 4 typiquement) ralentit considérablement la réponse temporelle d'un détecteur composé de millions de pixels.

Obturateur géant (1 m) de la caméra Megacam du CFHT.
Crédit :
CEA/CFHT
Obturateur
Un obturateur mécanique est souvent nécessaire pour stopper l'arrivée des photons durant le temps de lecture de la caméra. Dans certains cas, cet élément peut limiter la cadence d'observation.
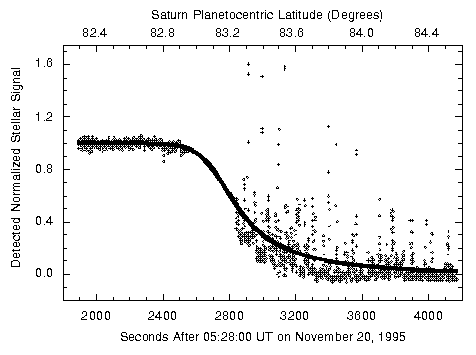
La réponse temporelle devient un paramètre important pour l'observation d'un phénomène rapidement variable. Ici : occultation d'une étoile brillante par
Saturne.
Crédit :
NASA/IRTF
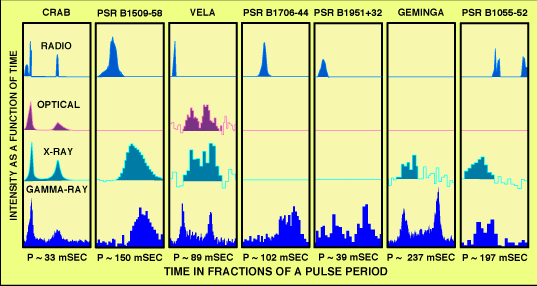

Variations temporelles d'un signal émis par un pulsar. Echantillonner un signal très rapide est souvent orthogonal aux capacités d'imagerie : le détecteur le plus rapide sera mono-pixel.
Crédit :
NASA/CGRO (Compton Gamma Ray Observatory)
De la nécessité d'observer avec une bonne cadence
L'observation astronomique se caractérise souvent par des poses très longues, nécessaires pour l'obtention d'un signal intrinsèquement très faible. Mais il est aussi utile de pouvoir compter sur des détecteurs rapides.
La réponse temporelle prend son importance pour l'observation d'un phénomène périodique rapide, comme p.ex. le clignotement d'un pulsar, ou pour un phénomène transitoire, tel une occultation stellaire.
Apprendre
Temps de réponse, temps de lecture
Un détecteur a un temps de réponse, propre ou dépendant de l'électronique de contrôle et de lecture, qui n'est pas infiniment bref.
Par exemple, un bolomètre, qui convertit l'énergie des photons en échauffement, ne peut pas réponde instantanément. De même que la lecture d'une matrice CCD de plusieurs millions de pixels ne peut pas être instantanée, mais prendra jusqu'à une minute.
Il s'ensuit que le signal d'un détecteur est échantillonné dans le temps.
Filtrage
De ce qui précède, on en déduit qu'un détecteur fonctionne comme un filtre passe-bas : les hautes fréquences temporelles sont filtrées.
Pose longue ou échantillonnage rapide
Certains phénomènes astronomiques présentent de rapides variations temporelles, soit parce qu'intrinsèquement variables, soit parce que correspondant à un phénomène transitoire. L'observation de tels phénomènes demande un temps de réponse rapide, et donc une stratégie de détection appropriée.
S'exercer
 Temps de réponse
Temps de réponse
Difficulté : ☆
Temps : 10 min
Une observation astérosismique avec le spectromètre HARPS nécessite
la lecture d'une caméra de 2k×4k. Par ailleurs, l'échantillonnage du signal temporel nécessite l'acquisition d'une image par minute.
Question 1)
Déterminer le temps de pose en fonction de la magnitude, sachant que le détecteur sature à partir de 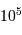 photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
Rappel : magnitude et luminosité varient dans le rapport :
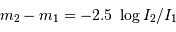
Question 2)
Le temps de lecture de la caméra est de 20 s. Pour quelle magnitude minimale l'observation reste-t-elle pertinente, avec au-moins la moitié du temps passée sur la source et non à lire la caméra ?
Question 3)
L'observation demande un échantillonnage plus rapide que 3 minutes. Montrer qu'une cible peu brillante ne sera pas observée dans de bonnes conditions. Estimer la limite en magnitude dans le cas où l'on accepte de remplir les pixels à 1/10 de la valeur optimale.
La pose sur l'objet est nécessairement limitée à 160 s.
Géométrie des détecteurs
Observer
Format
Les CCD actuels pour l'astronomie ont des tailles limitées à 2k 4k.
Pour augmenter la capacité de détection, on pave le plan focal de plusieurs détecteurs, comme par exemple pour la caméra MEGACAM du télescope CFH mise en service à l'été 2003.
4k.
Pour augmenter la capacité de détection, on pave le plan focal de plusieurs détecteurs, comme par exemple pour la caméra MEGACAM du télescope CFH mise en service à l'été 2003.

Les 40 CCD de la caméra MEGACAM du télescope
CFH.
Crédit :
CFHT
Apprendre
Pixel
 Définition
Définition
Un pixel, pour picture element, est un élément d'image. Par
extension, un pixel d'une caméra CCD correspond à l'entité
physique qui aboutit à un élément d'image.
Le nombre de pixels court de 1 à plusieurs millions ; on note couramment
1 kpx = 1000 px.
Format
Les caméras actuelles ont typiquement des formats de 256  256 px (dans l'infrarouge thermique) à 2k
256 px (dans l'infrarouge thermique) à 2k  4k pixels (dans le visible).
4k pixels (dans le visible).
Le format est la seule caractéristique où la détection par plaque photographique fut plus performante. Les détecteurs de type CCD comptent un nombre de pixels bien inférieur à celui atteint par les plus grandes plaques photos.
S'exercer
 Projet MEGACAM du télescope CFH
Projet MEGACAM du télescope CFH
Difficulté : ☆
Temps : 10 min

Champ plat des 40 CCD de la caméra MEGACAM du
CFH
Crédit :
CFHT
La caméra MEGACAM du télescope CFH, mise en service à l'été 2003, comprend
40 mosaïques CCD, de 2k  4.5k pixels. L'information d'un pixel est codé sur 16 bits. Le temps de lecture d'une image totale est de 30 secondes.
4.5k pixels. L'information d'un pixel est codé sur 16 bits. Le temps de lecture d'une image totale est de 30 secondes.
Question 1)
Les 36 CCD centraux, couvrent une surface carrée de 0.94 degré par 0.94 degré. Déterminer le champ de vue d'un pixel.
Déterminer le nombre total de pixels pour 36 CCD.
Question 2)
Déterminer la capacité de stockage nécessaire pour 1 champ observé en 3 couleurs.
1 pixel codé sur 16 bits nécessite 2 octets pour le stockage.
Question 3)
Une nuit moyenne aboutit à une dizaine de champs, chacun pris dans 3 filtres.
A raison de 100 nuits d'observation par an, déterminer le volume de données au bout de 5 années de fonctionnement.
Bruits de détection
Observer
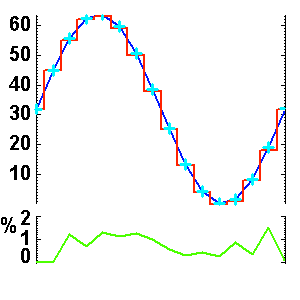
Signal analogique et numérisé sur 8 bits (64 valeurs possibles). La différence entre les valeurs réelles et codées introduit un
bruit de numérisation.
Crédit :
ASM
Bruit de numérisation
Le simple fait de numériser un signal analogique, càd de le coder sur une échelle de valeurs discrétisée (typiquement, sur 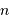 bits, ce qui permet de coder
bits, ce qui permet de coder 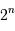 valeurs), peut rajouter du bruit au signal.
valeurs), peut rajouter du bruit au signal.
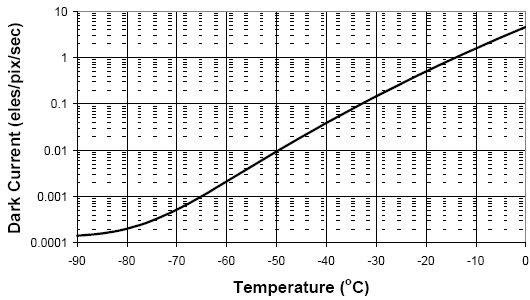
Le signal d'obscurité est un bruit d'origine thermique. Données pour une caméra CCD, en fontions de la température. A -15 deg, 1 électron thermique est généré par pixel par seconde ; à -65 deg, il faut attendre 1000 s pour qu'un moyenne un électron thermique apparaisse par pixel.
Crédit :
ANDOR
Bruit d'origine thermique
La température du détecteur conditionne le signal d'obscurité d'un détecteur. Suite à l'agitation thermique, des porteurs de charge apparaissent aléatoirement, d'autant plus que la température est élevée.
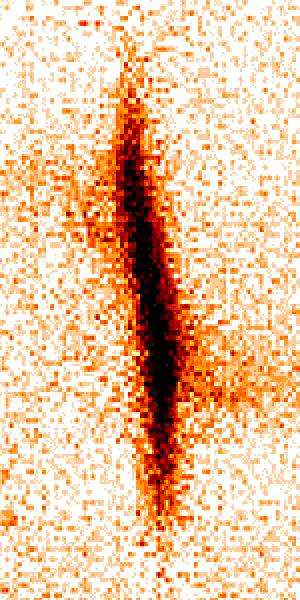
Bruit de fond
Crédit :
ESO
Apprendre
Signaux parasites et bruits
Au signal scientifique se superposent des signaux parasites et des bruits.
Un bruit sera caractérisé par son caractère aléatoire, et les propriétés statistiques correspondantes.
Un signal parasite possède, comme son nom l'indique, les propriétés d'un signal et non celles d'un bruit.
Bruit quantique
La nature du rayonnement, quantique par excellence, montre le hiatus à décrire une intensité lumineuse par une quantité analogique, alors que les porteurs de ce rayonnement sont quantifiés.
On montre que la
statistique d'arrivée des photons est poissonnienne.
Lorsque l'on attend 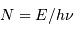 photons, la valeur moyenne
observée est
photons, la valeur moyenne
observée est 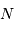 et la fluctuation
et la fluctuation 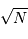 autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
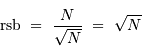
En électronique, on parle de bruit de grenaille, et de bruit de
photons en optique.
Bruit de fond
Le bruit de fond représente le bruit de photons de la lumière parasite qui se superpose au signal scientifique. Comme le bruit quantique, il est lié aux sources (ici parasites) et non au détecteur. Dans l'infrarouge, il est dominé par l'environnement chaud que voit le détecteur.
Bruit thermique
Le bruit thermique provient de l'agitation thermique des porteurs de charge du détecteur. Il est à moyenne nulle, son écart-type augmente avec la température.
Ce bruit, comme les suivants, dépend du détecteur et de la chaîne de détection.
Bruit de lecture
Le processus de lecture contribue au bruit de lecture, par exemple dans un CCD lorsque les photo-électrons sont transférés le long d'une colonne vers un registre de lecture.
On quantifie le bruit de lecture par son écart-type en nombre de photoélectrons par pixel. Une valeur typique de 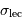 est de l'ordre de quelques photo-électrons par pixel
est de l'ordre de quelques photo-électrons par pixel
Bruit d'amplification
L'électronique d'amplification introduit un gain 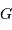 , dont la valeur n'est pas fixe mais sujette à différents bruits.
, dont la valeur n'est pas fixe mais sujette à différents bruits.
S'exercer
 Numérisation
Numérisation
Difficulté : ☆
Temps : 15 min
On souhaite numériser le signal photométrique d'un détecteur dédié à une étude de la microvariabilité. Ce signal est composé d'un fort continu, de diverses modulations et bruit, et du signal scientifique. Les amplitudes respectives sont données dans le tableau ci-dessous.
| continu | 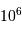 |
| variations | 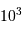 |
| microvariabilité | 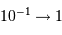 |
Question 1)
Sans traitement préalable, sur combien de bits faut-il coder le signal afin de ne pas introduire de bruit lors de cette opération (si besoin, voir les pages sur
l'échantillonnage d'un signal) ?
L'échantillonnage du signal requiert de coder le niveau de signal à la moitié de la plus petite variation.
Déterminer l'amplitude relative du signal entre le niveau de codage et la valeur maximale
Question 2)
Même question, après filtrage permettant de séparer les composantes continue et lentement variable d'une part, et la microvariabilité se distinguant du fond variable de l'autre.
Même démarche que précédemment.
Rendement de la chaîne de détection
Observer
Diverses contributions au rendement
Lorsque l'on décompte toutes les pertes de transmission des différents éléments d'une chaîne instrumentale, on s'aperçoit que le rendement final n'est pas nécessairement bon. Pour 100 photons collectables au sommet de l'atmosphère, la plupart des instruments ne travailleront finalement qu'avec une poignée de photoélectrons.
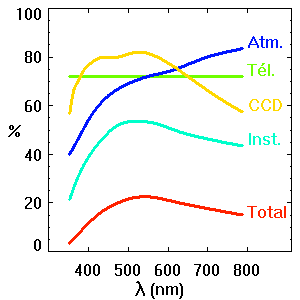
Transmissions des différentes contributions d'une chaîne instrumentale : l'atmosphère (au niveau de la mer, pour une observation au zénith), du télescope, de l'instrument, du détecteur CCD, et finalement transmission totale.
Crédit :
ASM
Choix d'un site
On peut considérer comme partie intégrante du rendement celui de la couverture temporelle durant laquelle la météo est favorable. L'image satellite illustre le fait que le Chili offre de bien meilleurs sites d'observations que l'Argentine, avec un ciel parfaitement dégagé.

Image satellite de l'Amérique du Sud, dans la fenêtre à 10 micromètres, sensible à la couverture nuageuse. Les courants froids du Pacifique Sud sont responsables du faible taux moyen d'humidité au Chili. Les bons sites comme dans la Cordillère des Andes au Chili offrent plus de 300 nuits claires par an.
Crédit :
GEOS
Apprendre
Rendement de la chaîne de détection
Lorsque les photons sont rares, pour des sources faiblement lumineuses, il faut viser l'efficacité lors de chacune des étapes participant à la chaîne de mesure, et ce bien avant le détecteur.
- Atmosphère :
La transmission atmosphérique dépend de la longueur d'onde et de la quantité d'atmosphère traversée (sauf pour une observation spatiale).
- Collecteur :
L'efficacité de la collection dépend du pouvoir de réflexion des miroirs. En fonction de la longueur d'onde et du traitement de surface adapté (aluminure, argenture, dorure...), le facteur de réflexion d'un miroir vaut typiquement entre 80 et 99%.
- Instruments :
Un instrument efficace n'égare pas ses photons. Mais chaque dioptre, traversées vitreuses (lentilles...), chaque passage par fibre optique... épluche les photons par réflexion, transmission, absorption.
- Détecteur :
Le rendement du détecteur est la dernière étape limitant le rendement global de la chaine de détection.
Transmissions
Valeurs typiques de transmission de différentes composantes d'une chaîne de mesure
| atmosphère | 60 à 80%, dépend de la masse d'air (mesure la quantité d'atmosphère traversée, càd 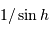 , avec , avec 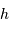 la hauteur sur l'horizon de l'objet visé) la hauteur sur l'horizon de l'objet visé) |
| miroir | jusqu'à 99%, en fonction du traitement réfléchissant de surface |
| fibre | de l'ordre de 80% |
| dioptre | une réflexion verre-air a un coefficient de transmission typiquement de 96%. Un traitement antireflet permet d'accroître ce coefficient jusque vers 99% |
S'exercer
S'évaluer
 De l'intérêt d'un traitement de surface
De l'intérêt d'un traitement de surface
Difficulté : ☆
Temps : 5 min
Question 1)
Un instrument comprend en tout 10 lentilles. Sans traitement antireflet, chaque dioptre a une transmission de 96%.
Déterminer la transmission globale.
[2 points]
Question 2)
Un traitement antireflet permet de porter le coefficient de transmission à 99%. Que devient la transmission globale ?
[1 points]
Question 3)
Conclure.
[1 points]
 Transmission atmosphérique
Transmission atmosphérique
Difficulté : ☆
Temps : 15 min
Les données de l'appliquette ci-jointe montrent l'évolution de la transmission atmosphérique avec la longueur dans le domaine visible, pour 2 altitudes d'observation : au niveau de la mer et au sommet du Mauna Kea (Hawaï, 4200 m d'altitude).

Question 1)
Tracer, pour les 2 altitudes d'observation, les transmissions en fonction de la longueur d'onde, et commenter l'allure des courbes.
[2 points]
Question 2)
La relation de l'extinction avec la masse d'air de l'objet visé 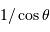 , l'angle
, l'angle 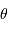 mesurant la distance angulaire entre le zénith et la direction de visée, est de la forme :
mesurant la distance angulaire entre le zénith et la direction de visée, est de la forme :
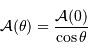
Commenter et justifier cette relation.
[1 points]
Faire un schéma montrant les couches d'atmosphère traversées avant la détection.
Question 3)
Montrer, en calculant l'extinction au CFH, que la courbe d'extinction est compatible avec la diffusion Rayleigh, qui varie comme l'inverse de la puissance quatrième de la longueur d'onde
[1 points]
Dans l'appliquette :
- sélectionner la 1ère case de la colonne 1-T (D1) et réaliser :
=100-C1
- sélectionner la 1ère case de la colonne (lambda^-4) (E1) et réaliser :
=(1000/A1)^4
Conclusion
Pour en savoir plus sur les thématiques de cette section ; voir
p.ex. le livre Méthodes physiques de l'observation, de
Pierre Léna, CNRS éditions.
Crédit :
ASM
Analyser le signal
Auteur: B. Mosser
Introduction
L'instrumentation astrophysique conduit souvent à des observations à la pointe de ce qui est faisable. Les signaux, obtenus après des heures d'observations chèrement acquises, doivent exprimer toute leur substantifique moelle. Une étape très importante est donc l'analyse du signal.
Cette section expose diverses pistes pour :
- Comprendre l'allure d'un signal.
- Extraire le signal du bruit.
- Analyser le signal.
Quelques-unes des sources de bruit physique sont répertoriées à la page
bruits de détection.
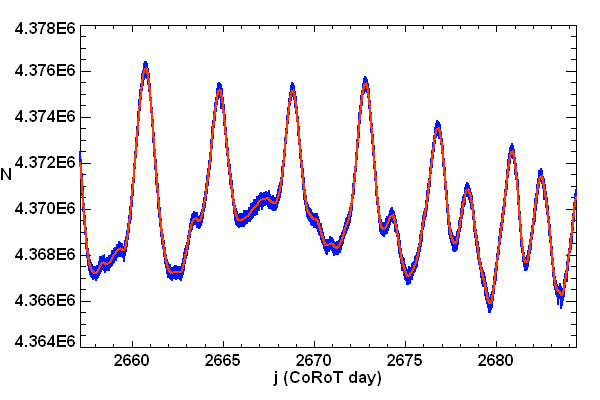
Exemple de filtrage. Série temporelle du flux de l'étoile HD 175726 observée par le photomètre à bord du satellite CoRoT, exprimé en nombre de photons, et série filtrée des hautes fréquences.
Crédit :
CNES/ASM
Bruit et signal
Observer
Détection et rapport signal à bruit
La détection d'un phénomène, comme par exemple une raie spectrale, nécessite de pouvoir distinguer le signal par rapport à ce qui n'est pas du signal, appelé bruit s'il présente un caractère aléatoire. On exprime ceci par un rapport, le rapport signal à bruit, d'autant plus important que le signal est fort par rapport au bruit.
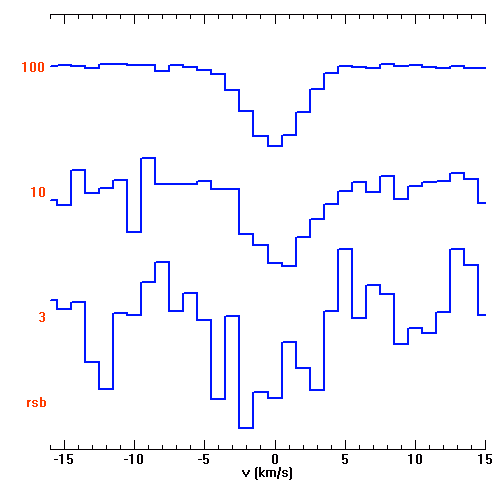
Allure d'une raie en absorption, observée à différents rapports signal à bruit.
La détection commence à être possible avec un rapport signal à bruit supérieur à 5. L'échelle spectrale est donnée en vitesse (km/s), centrée sur la raie.
Crédit :
ASM
Biais
Il ne faut pas confondre un signal parasite, ou biais observationnel, avec un bruit. Le biais qui affecte le signal possède des propriétés qui le distinguent tout à fait d'un bruit.
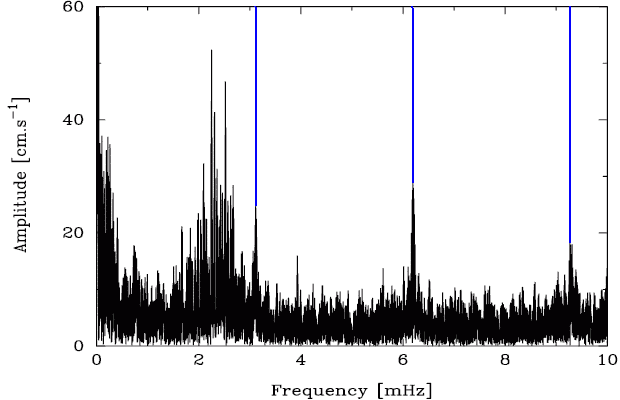
Exemple de biais. Un défaut dans le système de pointage du télescope est mis en évidence sur une cible atypique (alpha du Centaure, extrêmement brillant). Il s'ensuit une signature spectrale parasite à 3.1 mHz et à ses harmoniques.
Crédit :
ESO
Un biais très commun est un offset, càd un décalage du signal dû au fait que le niveau zéro du signal physique et le niveau zéro de sa traduction en signal électrique ne coïncident pas.
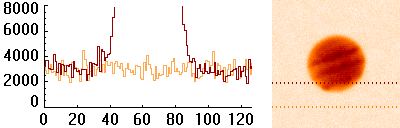
Exemple d'offset, sur une image simulée de Jupiter dans l'infrarouge thermique.
Les courbes orange et rouge sont des coupes de l'image ; elles représentent le flux (unité arbitraire) en fonction du numéro de pixel. Le fond de ciel, qui devrait être à zéro, ne l'est pas.
Crédit :
ASM
Bruits et signaux
L'astronomie regorge d'exemple de bruits devenus des signaux célèbres à partir du moment où leurs caractéristiques ont été identifiées.
- Le bruit remarqué par les radioastronomes dans toutes les directions d'observations, a été identifié par Penzias et Wilson en 1965 comme étant le rayonnement à 3 K du fond cosmologique
- Le bruit des observations de la photosphère solaire dans les années 1970 s'est révélé un signal acoustique très régulier, signature des modes d'oscillation du soleil. Aujourd'hui, plus de 10 millions de modes d'oscillations ont été identifiés, si bien que l'on connaît très précisément l'intérieur du Soleil.
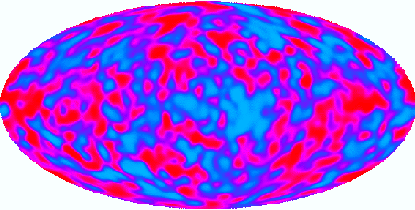
La carte du rayonnement du fond cosmologique, observée par le satellite Cobe, représentée en
coordonnées galactiques. Les couleurs codent les fluctuations par rapport à la température moyenne 2.728 K
Crédit :
NASA
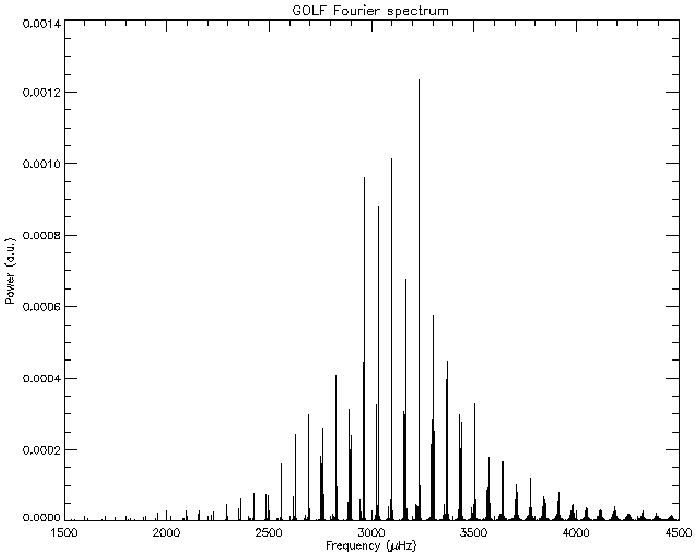
Spectre des modes d'oscillations du Soleil, avec des périodes voisines de 5 minutes. Observation de l'instrument Golf à bord de Soho.
Crédit :
SOHO
Apprendre
 Objectifs
Objectifs
Distinguer signaux et bruits.
Qualitativement
Le bruit de la circulation qui vous empêche d'entendre ce que dit votre ami(e) dans la rue, c'est du bruit... et ce que vous dit votre ami(e) a priori du signal. Mais une voiture qui accélère, est-ce vraiment un bruit, ou un signal parasite ?
Par analogie, la lumière du ciel diurne qui empêche de voir les étoiles de jour est-elle un bruit, un signal parasite ?
Signal, bruit
Tout observation va comporter, en plus du signal, des perturbations à ce signal.
Ces dernières résultent principalement de deux causes, intrinsèques et extrinsèques :
- Intrinsèquement, la nature même de la physique du signal implique l'existence de fluctuations (voir p.ex. comment l'arrivée des photons construit le bruit de Poisson).
- Par ailleurs, les conditions d'observation superposent au signal diverses autres contributions : signaux parasites, biais ou bruits.
Exemple de biais : le niveau de biais d'une image numérique prise avec une caméra CCD peut provenir du signal généré par la tension d'alimentation appliquée au détecteur.
Les propriétés d'un bruit
 Définition
Définition
Un bruit est un phénomène aléatoire.
On découvre par la suite deux types de bruit plus spécialement importants, obéissant à des statistiques poissonniennes ou gaussiennes.
Exemples
La distinction entre bruit et signal parasite est parfois complexe.
On peut prendre l'exemple du courant d'obscurité d'un détecteur, qui se superpose au flux observé.
Sa valeur moyenne est parfaitement quantifiable (tant de photoélectrons par pixel et par seconde), ce qui montre qu'il s'agit là d'un signal, parasite certes mais avec les propriétés d'un signal.
La vraie composante de bruit concerne les fluctuations de ce courant d'obscurité.
Simuler
Identification d'un offset
A l'aide de l'appliquette, estimer l'offset affectant cette image de Jupiter dans l'infrarouge thermique.

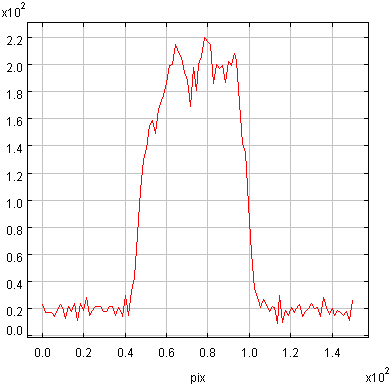
Une coupe montre un niveau d'offset aux alentours de 18 à 20, pour un signal planétaire 10 fois plus important.
Crédit :
ASM
Solution
Probabilités, réalisations, estimations
Observer
Réalisations
Une loi de probabilité est déterministe. Mais ses réalisations sont ... aléatoires. C'est seulement avec un nombre élevé de réalisations que l'ensemble de ces réalisations retrace fidèlement la loi de probabilité. Si le nombre de réalisations est petit, on n'observe rien d'identifiable.
Loi uniforme, tirage d'un dé.
Crédit :
ASM
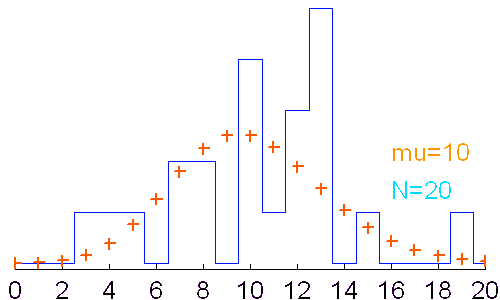
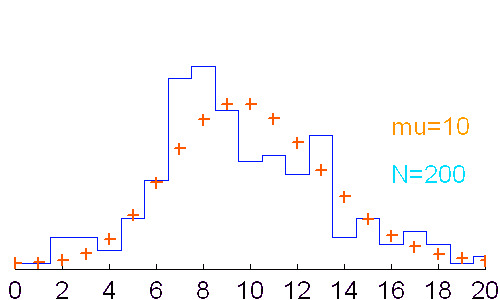
Réalisations d'un phénomène aléatoire obéissant à la loi de Poisson (moyenne = 10). Avec un nombre N de tirages peu élevé, la distribution des valeurs (courbe en bleu) ne ressemble que de très loin à la fonction de probabilité attendue (croix en rouge).
Crédit :
ASM
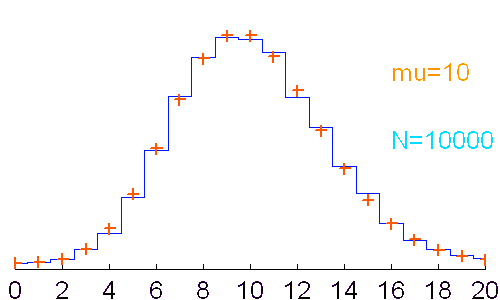
Réalisations d'un phénomène aléatoire obéissant à la loi de Poisson. Avec un nombre de tirages élevé, la distribution des valeurs trace convenablement la fonction de probabilité.
Crédit :
ASM
Estimations
Estimation de la moyenne et de l'écart type d'une loi. La moyenne peut être estimée de diverses façons, et la meilleure façon d'estimer une moyenne dépend de la loi de probabilité.
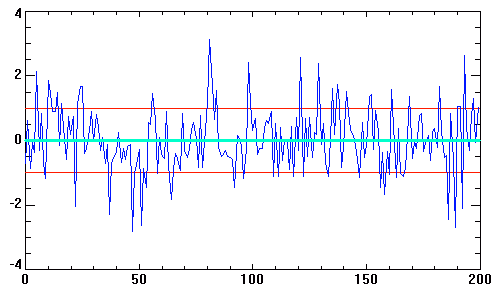
Moyenne (trait bleu ciel) et écart-type (droites de part et d'autre de la moyenne) pour un bruit blanc.
Crédit :
ASM
Apprendre
 Prérequis
Prérequis
Notions élémentaires de statistiques
 Objectifs
Objectifs
La définition d'un bruit repose sur ses propriétés statistiques. Cette page rappelle des notions simples de statistiques, en distinguant les lois de probabilité, leurs réalisations, et l'estimation de paramètres statistiques.
Loi de probabilité
La loi de probabilité d'une variable aléatoire 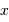 va être donnée par
va être donnée par 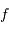 sa densité de probabilité, ou bien
sa densité de probabilité, ou bien 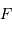 sa fonction de répartition
sa fonction de répartition 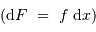 .
.
Parmi les moments centrés associés,
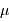 la moyenne et
la moyenne et 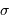 l'écart-type sont respectivement définis par :
l'écart-type sont respectivement définis par :
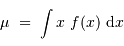
et :
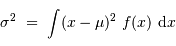
(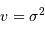 est la variance).
est la variance).
Une loi statistique possède des propriétés particulières, qui caractérisent tel ou tel phénomène : une loi poissonnienne (discrète) rend compte de l'arrivée d'événements indépendants, une loi gaussienne est souvent issue de l'addition d'un grand nombre de phénomènes indépendants...
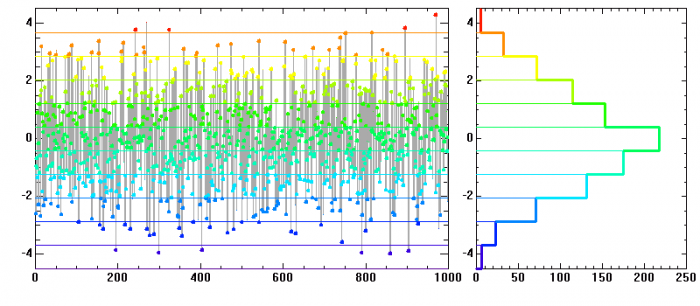
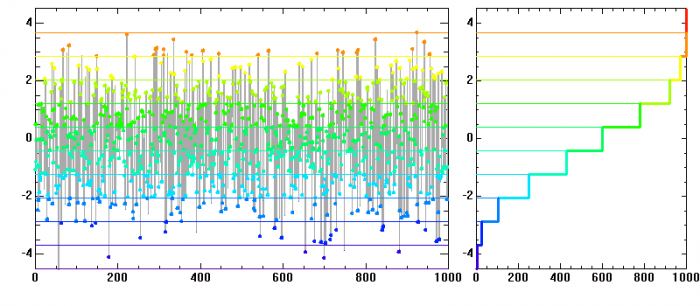
Réalisation d'une loi normale. L'histogramme se rapproche de la loi de probabilité.
Crédit :
ASM
Réalisations
La réalisation d'une loi de probabilité est aléatoire : un tirage de dés, réalisé 6 fois, ne conduira pas nécessaire à l'obtention une fois et une seule de chaque chiffre de 1 à 6. Plus le nombre de réalisations est grand, meilleur est l'accord entre l'observation de ces réalisations et la loi de probabilité.
Simuler
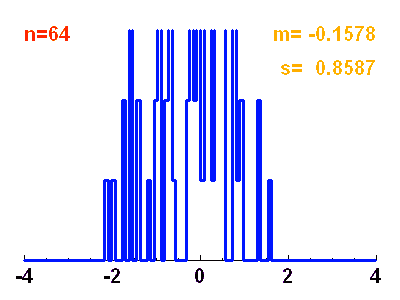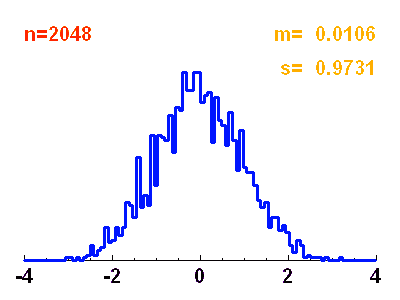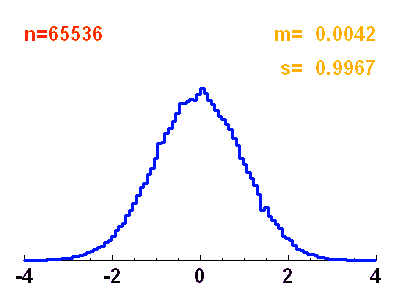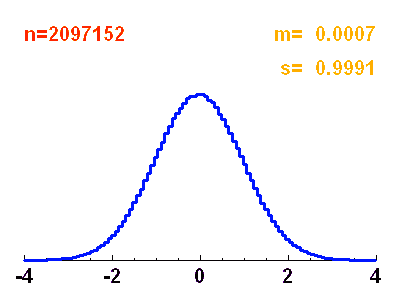
Histogramme d'une distribution de
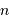
points obéissant à une loi normale de moyenne nulle et écart-type unité. Ce n'est qu'avec un très grand nombre de points que les réalisations représentent précisément la courbe théorique gaussienne.
Crédit :
ASM
Loi statistique et réalisation
L'animation ci-joint montre comment est réalisée en pratique une distribution normale. Ce n'est qu'avec un très grand nombre de tirages que l'histogramme des réalisations ressemble vraiment à la distribution statistique.


Mesure de bruits
Les appliquettes ci-jointes dévoilent des signaux temporels bruités, affectés ou non d'une lente dérive. On se propose d'en mesurer le bruit et le
rapport signal à bruit.
Se servir des appliquettes pour :
- Déterminer la moyenne du signal.
- Le cas échéant, corriger de la dérive.
- Mesurer l'écart-type, en appliquant sa définition et la fonction ajustement.
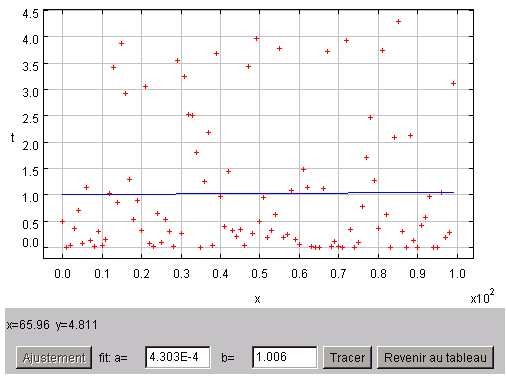
Avec l'appliquette, on calcule
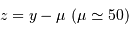
et puis
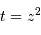
. L'ajustement donne un écart-type de 1.
Crédit :
ASM
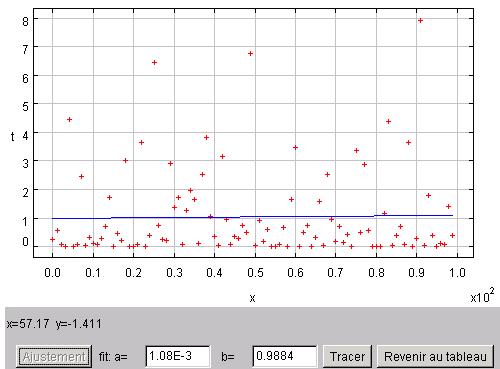
On remarque que la distribution des valeurs de
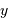
n'est pas uniforme autour d'une valeur moyenne, mais suis une relation linéaire. Il est nécessaire de soustraire la pente. On estime cette dernière avec l'appliquette, et on calcule alors la valeur centrée sur 0
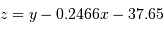
et puis
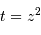
. L'ajustement donne un écart-type de 1.04.
Crédit :
ASM
Rapport signal à bruit
Observer
Rapport signal à bruit
Le rapport signal à bruit conditionne toute observation. S'il est faible, on ne voit que du ... bruit.

Allure d'une raie en absorption, observée à différents rapports signal à bruit.
L'identification de la raies peut être possible avec un rapport signal à bruit supérieur à 3.
Crédit :
ASM
Détection et rapport signal à bruit
La détection d'un phénomène, comme par exemple une raie spectrale, nécessite un rapport signal à bruit typiquement supérieur à 3.
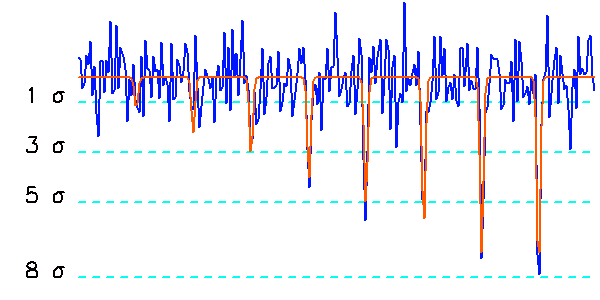
Simulation d'une portion de spectre en absorption, à rapport signal de bruit de 5 et 10.
Un motif avec un rapport signal à bruit supérieur à 3 peut très bien être du bruit, et ne peut donc être identifié à quelque signal que ce soit.
Si le bruit est strictement gaussien, on admet qu'une détection est certaine dès lors qu'elle sort de plus de 5 fois du niveau de bruit.
Crédit :
ASM
Apprendre
 Prérequis
Prérequis
Notions de probabilités et statistiques
Définition
On définit le rapport signal à bruit d'un signal comme le rapport des énergies du signal et du bruit. L'énergie du signal est représentée par sa valeur moyenne 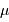 , et celle du bruit par l'écart-type
, et celle du bruit par l'écart-type 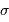 . Le rapport signal à bruit est donc :
. Le rapport signal à bruit est donc :
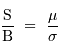
Si le signal est affecté d'un biais systématique 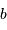 , il faut en tenir compte dans l'estimation de ce rapport, et retirer au préalable sa contribution :
, il faut en tenir compte dans l'estimation de ce rapport, et retirer au préalable sa contribution :
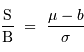
La composante de biais peut être p.ex., pour un signal évoluant dans le temps, un signal parasite apparaissant à plus basse fréquence.
Addition des bruits
Si les différents bruits contribuant à un signal sont indépendants les uns des autres, leurs
écarts-types s'ajoutent quadratiquement pour construire l'écart-type total :
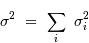
Il s'ensuit le rapport signal à bruit :
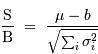
Simuler
Détection et rapport signal à bruit
Identifier un spectre est d'autant plus aisé que le rapport signal à bruit est bon. En pratique, une raie a priori inconnue devient détectable pour un rapport signal à bruit supérieur à 5.
Spectre stellaire bruité
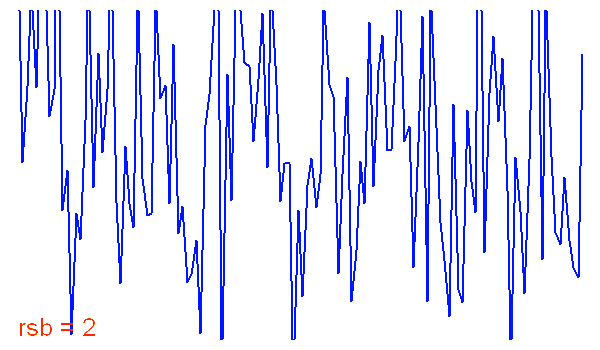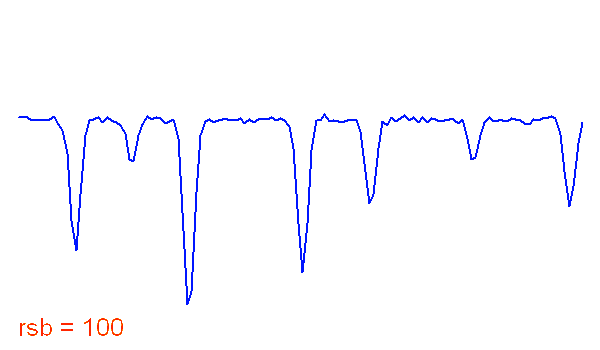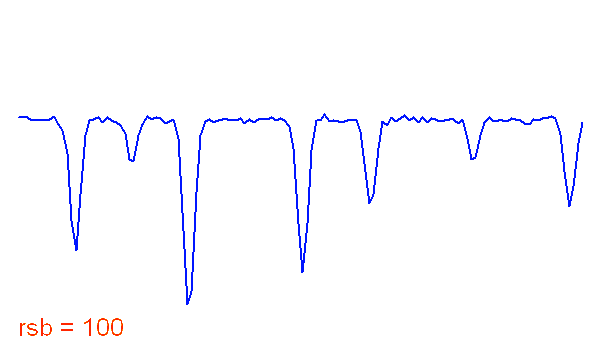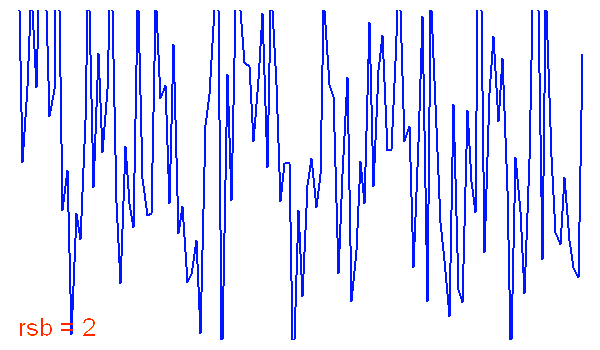
Allure d'une portion de spectre stellaire, en fonction du rapport signal à bruit.
Crédit :
ASM
Evolution temporelle du rapport signal à bruit
Si le bruit est dominé par le bruit de photons, le rapport signal à bruit augmente avec la durée d'observation, comme le montre cette
simulation.
Observation bruitée

La galaxie M31, imagée à différents niveaux de bruit.
Crédit :
ASM
S'exercer
 Bruit dominant
Bruit dominant
Difficulté : ☆☆
Temps : 30 min
On recueille le signal d'une cible stellaire. Le rapport signal à bruit s'écrit :
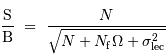
avec 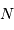 le nombre de photoélectrons reçus,
le nombre de photoélectrons reçus, 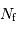 relié à un signal de fond,
relié à un signal de fond, 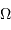 la taille angulaire de la cible, et
la taille angulaire de la cible, et 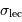 le bruit de lecture
le bruit de lecture
Question 1)
Identifier précisément les différents termes de bruit contribuant au rapport signal à bruit, en précisant leur écart-type.
Au numérateur, on a tout simplement le signal, au dénominateur les bruits.
Il reste à identifier le terme 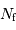 et à interpréter la somme du dénominateur.
et à interpréter la somme du dénominateur.
Question 2)
Simplifier l'expression du rapport signal à bruit pour le cas d'un objet très brillant, puis pour un objet très peu lumineux. Identifier l'exposant qui caractérise la dépendance en 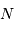 du rapport signal à bruit.
du rapport signal à bruit.
Déterminer l'importance relative des différents bruits.
Question 3)
Déterminer comment le rapport signal à bruit varie avec le diamètre 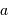 du collecteur ou le temps de pose
du collecteur ou le temps de pose 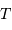 .
.
Comment le nombre de photoélectrons collectés varie-t-il avec le diamètre du collecteur ou le temps de pose ?
Le bruit gaussien
Observer
Conséquence du théorème de la limite centrale
La superposition de plusieurs variables aléatoires indépendantes les unes des autres conduit à une loi normale. C'est l'une des conséquences du théorème de la limite centrale. L'animation ci-jointe en montre un exemple.
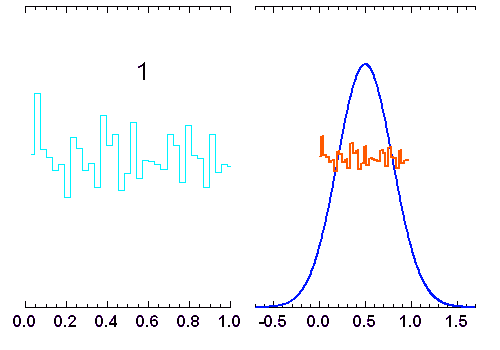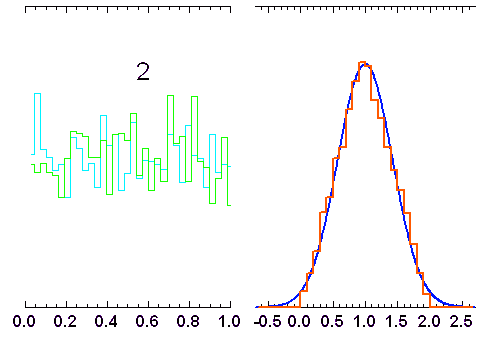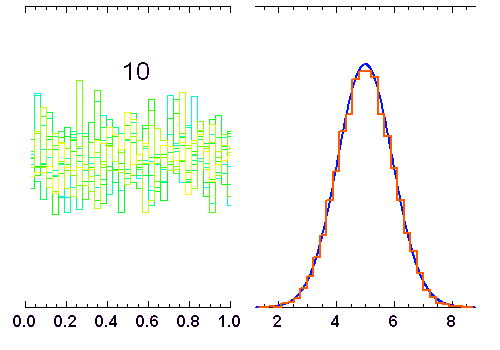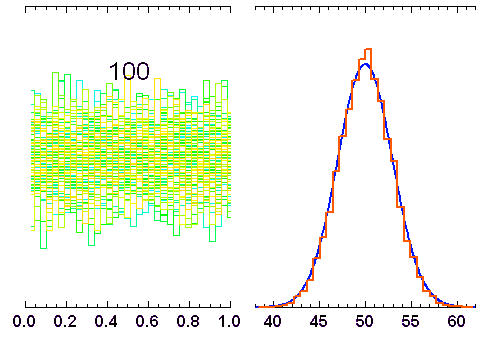
Addition de
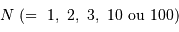
variables indépendantes, obéissant à une loi de distribution uniforme (entre 0 et 1). Lorsque
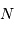
augmente, la distribution tend vers une loi gaussienne de moyenne
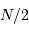
et écart type
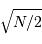
(courbe rouge). Pour
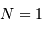
, la distribution reste bien sûr uniforme,
pour
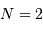
elle garde une allure triangulaire.
Crédit :
ASM
Distribution gaussienne
Exemples de distributions gaussiennes.
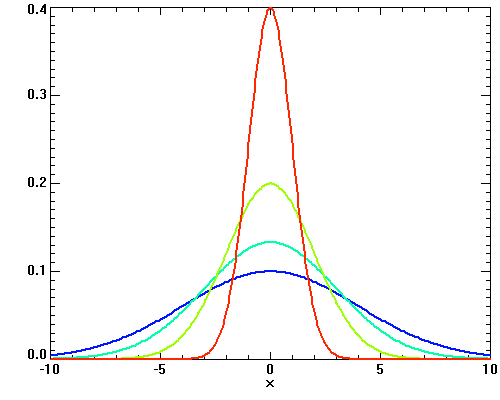
Distributions de Gauss. Moyennes toutes nulles et écarts-types de 1 à 4.
Crédit :
ASM
Bruit gaussien
Si un bruit est gaussien, la probabilité qu'il s'écarte de plus ou moins 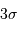 de la valeur moyenne est très faible. Cette propriété est mise à profit pour identifier le signal du bruit, mais ne marche que si le bruit est vraiment gaussien.
de la valeur moyenne est très faible. Cette propriété est mise à profit pour identifier le signal du bruit, mais ne marche que si le bruit est vraiment gaussien.
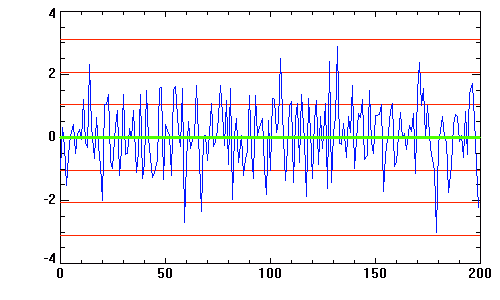
Bruit gaussien de moyenne nulle et d'écart-type 1. Peu de valeurs s'écartent de plus que
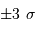
de la moyenne.
Crédit :
ASM
Apprendre
 Prérequis
Prérequis
Loi de probabilité ; éléments de statistique
Définition
Le théorème de la limite central implique qu'un bruit résultant de l'action indépendante de différents facteurs physiquesobéit à la loi de probabilité, dite loi normale :
![f(x) \ = \ {1\over \sqrt{2\pi}\sigma}\ \exp \left[ -{(x-\mu)^2\over 2 \sigma^2} \right]](../pages_analyser/equations_bruit-gaussien/equation9.png)
avec 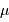 la moyenne et
la moyenne et 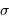 l'écart-type. Un tel bruit est dit gaussien.
l'écart-type. Un tel bruit est dit gaussien.
Détection d'un signal ?
De ce qui précède, peut-on dire qu'un événement qui s'écarte de plus de 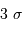 de la moyenne est sûrement dû à un signal et non à un bruit, et l'identifier comme tel ?
de la moyenne est sûrement dû à un signal et non à un bruit, et l'identifier comme tel ?
On considère une détection sûre lorsqu'elle dépasse un seuil de 4 ou 5 fois l'écart-type. Mais, la difficulté réside souvent dans le fait que la nature d'un bruit n'est pas exactement gaussienne, ou que des signaux parasites non identifiés compliquent l'interprétation d'un signal.
Analyse en fréquence d'un bruit gaussien
L'analyse fréquentielle d'un bruit gaussien ne montre aucune composante privilégiée. Pour cette raison, on parle d'un bruit blanc.
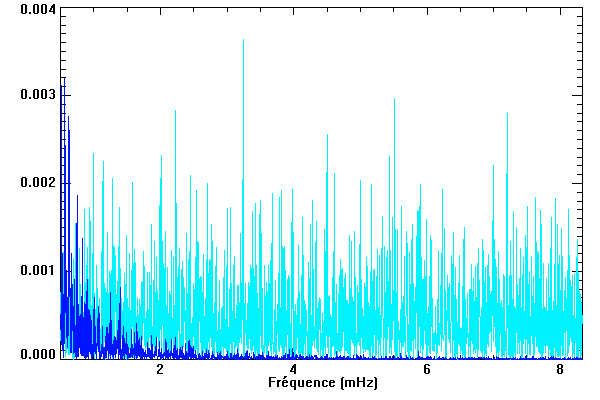
Les spectres de puissance de différents types de bruits : bruit instrumental en bleu foncé, bruit gaussienn en bleu clair. Le spectre du bruit gaussien ne présente pas de fréquence privilégiée, contrairement au bruit instrumental.
Crédit :
ASM
Simuler

Marche au hasard à partir d'un point fixe. Le cercle mesure l'évolution moyenne, qui varie comme la racine carrée du nombre de pas effectués.
La couleur code l'évolution temporelle.
Crédit :
ASM
Marche au hasard
L'ivrogne et son lampadaire sont des acolytes précieux du physicien statisticien. L'ivrogne est supposé partir du lampadaire et accomplir un certain nombre de pas par unité de temps, mais dans n'importe quelle direction.
Au bout de 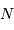 pas, il se sera éloigné du lampadaire d'une distance moyenne de
pas, il se sera éloigné du lampadaire d'une distance moyenne de 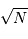 .
.

Identification d'un niveau de bruit
A l'aide de l'appliquette, estimer le niveau de bruit affectant cette image de Jupiter dans l'infrarouge thermique. L'exprimer en fonction du niveau maximal du signal (conseil : faire une coupe non sur la planète mais sur le fond de ciel).
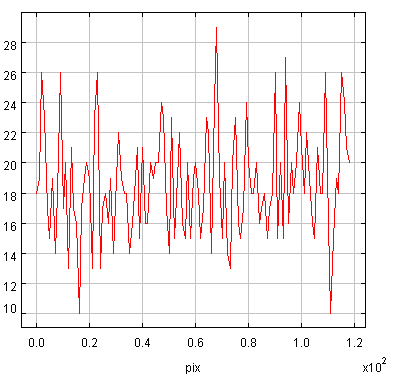
Une coupe sur le ciel seul montre un niveau d'offset aux alentours de 18 à 20, et un niveau de bruit entre 10 et 26. En supposant que le bruit est gaussien, on voit ses variations essentiellement à
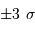
. On en déduit un niveau de bruit de l'ordre de 16/6=2.7. Le signal moyen étant d'environ 200, le rapport signal à bruit est voisin de 75.
Crédit :
ASM
Solution
S'exercer
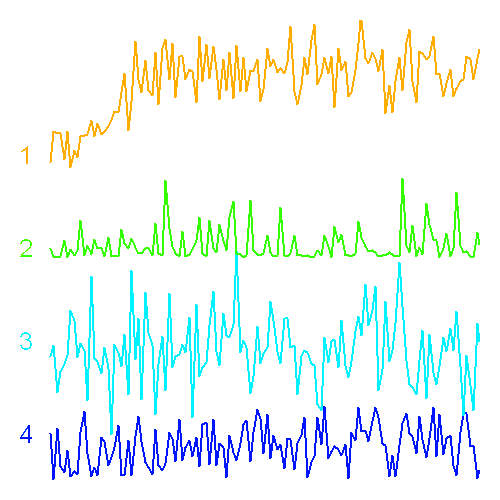
Quatre signaux : bruits gaussiens ou non ?
Crédit :
ASM
Le bruit poissonnien
Observer
Statistique de Poisson
Lorsqu'une moyenne de 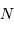 quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de
quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de 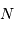 . La distribution des valeurs dépend du nombre N :
10,
100,
1000.
Plus
. La distribution des valeurs dépend du nombre N :
10,
100,
1000.
Plus 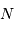 est grand, plus la distribution apparaît piquée en valeur relative, quand bien même elle est plus étalée en valeur absolue.
est grand, plus la distribution apparaît piquée en valeur relative, quand bien même elle est plus étalée en valeur absolue.
Distribution de Poisson
Série de valeurs et histogramme, dans le cas N = 10
Crédit :
ASM
Distribution de Poisson
Série de valeurs et histogramme, dans le cas N = 100
Crédit :
ASM
Distribution de Poisson
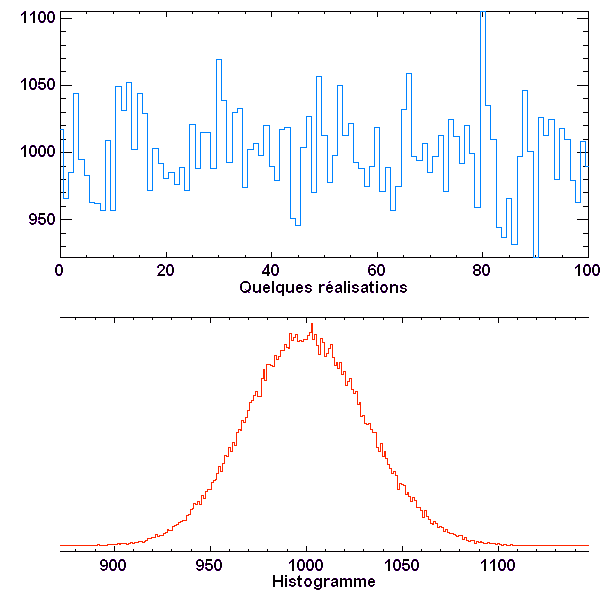
Série de valeurs et histogramme, dans le cas N = 1000
Crédit :
ASM
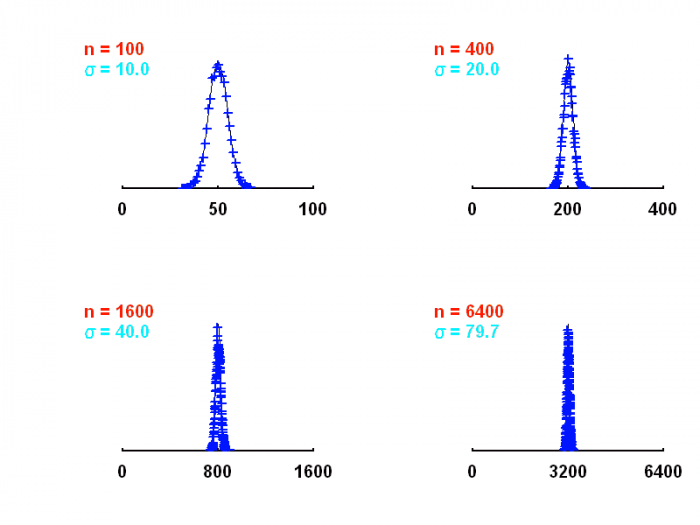
Statistiques poissonniennes. La dispersion relative décroît avec le nombre de quanta attendus.
Crédit :
ASM
Apprendre
 Objectifs
Objectifs
La statistique de Poisson concerne un phénomène régulier quantifié.
La détection d'un rayonnement électromagnétique en est un exemple concret, l'arrivée d'énergie étant quantifiée en photons.
Plus le nombre de photons attendus est grand, mieux on pourra préciser la valeur moyenne observée.
Un exemple concret... et discret
La statistique de Poisson va être abordée via un cas concret. L'analyse de l'arrivée de photons d'une signal lumineux de moyenne constante.
Un rayonnement monochromatique de fréquence 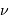 de luminosité
de luminosité 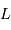 , observé pendant une durée
, observé pendant une durée 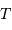 , apporte une énergie
, apporte une énergie 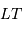 . Ce rayonnement est véhiculé par un nombre moyen de photons
. Ce rayonnement est véhiculé par un nombre moyen de photons 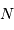 obéissant à :
obéissant à :
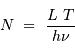
La discrétisation du flux en quanta d'énergie implique que le nombre de photons arrivant par intervalle de temps fluctue autour de cette valeur moyenne.
Extrapolation aux grandes valeurs
Pour les grandes valeurs de 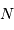 , on peut montrer que cette loi se confond très rapidement avec la gaussienne :
, on peut montrer que cette loi se confond très rapidement avec la gaussienne :
![p(n) \ \propto \ \exp \left[ - {(n-N)^2 \over 2 N}\right]](../pages_analyser/equations_bruit-poisson/equation32.png)
On en conclut alors, en se basant sur la statistique gaussienne, que pour une valeur moyenne 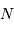 , l'écart-type vaut
, l'écart-type vaut 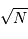 .
.
Il en résulte un point important : lorsque 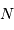 croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
Simuler
Distribution de Poisson
A l'aide de l'appliquette : tracer une distribution de Poisson, et identifier les variations majeures lorsque la moyenne 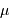 varie.
varie.

Le bruit de photons
Observer
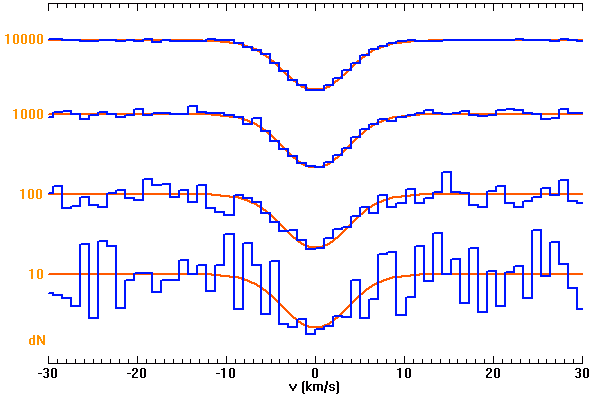
Simulation de la détection d'une raie, en fonction du nombre de photoélectrons dN détectés par intervalle spectral, en supposant la détection limitée par le seul bruit de photons. L'échelle spectrale est donnée en vitesse.
Crédit :
ASM
Bruit de photons et photodétection
Une bonne détection, par exemple l'identification d'une raie spectrale, nécessite l'enregistrement d'un nombre suffisant de photoélectrons, afin que la statistique d'arrivée des photons, de type poissonnien, n'empêche pas la détection.
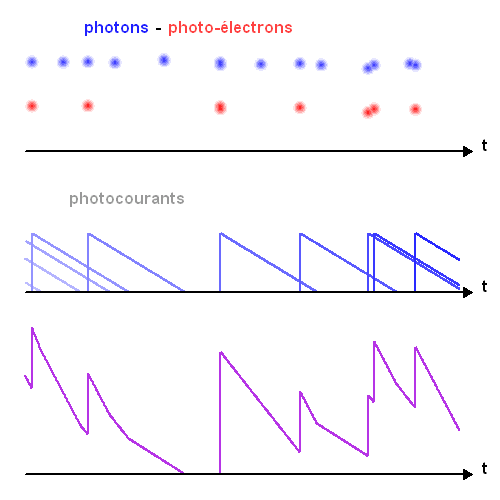
Distribution en fonction du temps de
l'arrivée de photons, des photoélectrons créés et du photocourant résultant. Les photons (points bleus) n'arrivent pas à intervalles de temps réguliers. Seuls un certain nombre d'entre eux donnent naissance à des photoélectrons (points rouges). Le photocourant total (bleu) résulte de la somme des contributions individuelles (couleur variable).
Crédit :
ASM
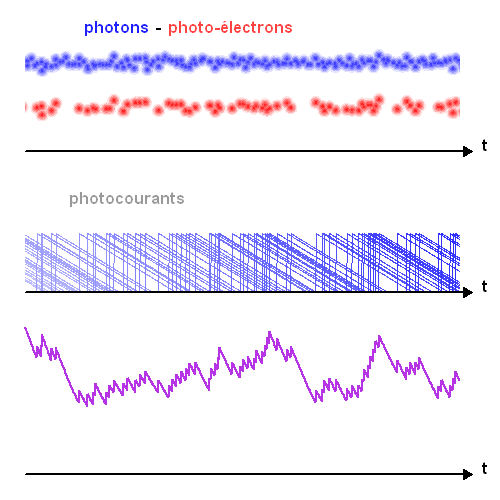
Distribution en fonction du temps de
l'arrivée de photons, des photoélectrons créés et du photocourant résultant. Les photons (points bleus) n'arrivent pas à intervalles de temps réguliers. Seuls un certain nombre d'entre eux donnent naissance à des photoélectrons (points rouges). Le photocourant total (bleu) résulte de la somme des contributions individuelles (couleur variable).
Crédit :
ASM
Photons et photoélectrons
Le bruit de photons est en fait un bruit... de photoélectrons.
L'arrivée dispersée des photons, conjuguée à la conversion aléatoire d'un photon en photoélectron, construisent la statistique de création de photoélectrons, qui dépend bien sûr du nombre de photons.
Apprendre
 Prérequis
Prérequis
Statistique de Poisson : le bruit de photons obéit à la statistique de Poisson.
 Objectifs
Objectifs
Evaluer le bruit et le rapport signal à bruit du bruit de photons.
Statistique de Poisson
La statistique d'arrivée des photons est poissonnienne, vu que les photons sont par définition des quanta d'énergie.
Lorsque l'on attend 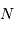 photons par intervalle de temps, la valeur moyenne observée est ...
photons par intervalle de temps, la valeur moyenne observée est ... 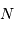 et sa fluctuation autour de cette valeur moyenne vaut
et sa fluctuation autour de cette valeur moyenne vaut 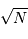 .
.
Il s'ensuit un rapport signal à bruit déterminé par le flux de photons égal à :
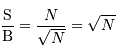
Ce rapport signal à bruit croît avec la racine carrée du nombre de photons collectés.
Photoélectrons
Les photons que l'on observe sont le plus souvent traduits par le détecteurs en photoélectrons, qui suivent la même statistique que les photons, à un facteur de rendement près inférieur à l'unité.
Avec 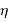 le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
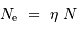
Le bruit de photoélectrons et le rapport signal à bruit résultant valent en pratique 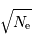 .
.
S'exercer
 Le projet COROT
Le projet COROT
Difficulté : ☆
Temps : 20 min
Question 1)
En supposant que le rendement de la chaîne de détection vaut l'unité, combien de photons doivent être enregistrés pour que le bruit de photons permette une détection à 1 ppm
Avec 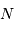 photons, le rapport signal à bruit du bruit de photons vaut
photons, le rapport signal à bruit du bruit de photons vaut 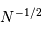 .
.
Question 2)
Le rendement de la chaîne de détection est de 25% seulement. Par quel facteur doit on corriger le nombre de photons à collecter.
Avec 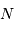 photons, on obtient seulement
photons, on obtient seulement 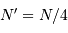 photoélectrons.
photoélectrons.
Question 3)
Le nombre de photons requis est collecté en 5 jours. En déduire le nombre de photons accumulés en une pose élémentaire de 1 minute, et la performance atteinte sur une pose élémentaire.
1 jour = 86400 s = 1440 min
S'évaluer
 Au photon près
Au photon près
Difficulté : ☆
Temps : 20 min
La figure ci-jointe représente la courbe de lumière de l'étoile HD 49933, l'une des cibles principales du satellite CoRoT. Le signal stellaire est composé de multiples signaux (activité, oscillations...) et bien sûr du bruit de photons. On admet que celui-ci domine à haute fréquence.
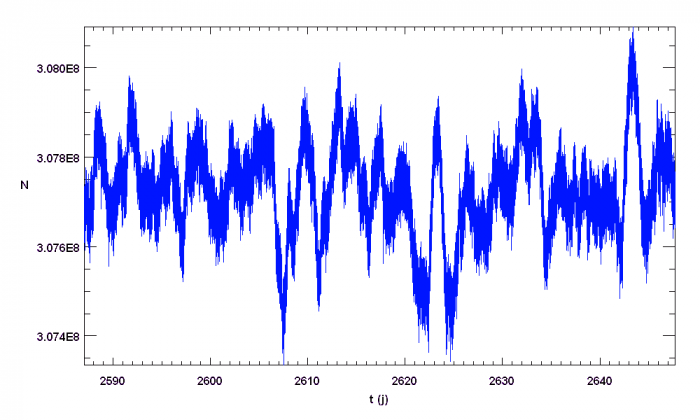
Courbe de lumière de l'étoile HD 49933. Nombre de photo-électrons collectés par seconde en fonction du temps.
Crédit :
ASM/CNES
Question 1)
Estimer l'amplitude totale du bruit du signal stellaire.
[1 points]
Repérer un intervalle de temps où le signal n'évolue pas à basse fréquence, et mesurer l'amplitude crête à crête.
Question 2)
Estimer l'écart-type du bruit
[1 points]
Revoir les propriétés du bruit poissonnien.
Question 3)
Montrer que le bruit mesuré est du même ordre de grandeur que le bruit de photons.
[1 points]
Bruit instrumental
Observer
Dérive instrumentale
Les bruits instrumentaux sont souvent dus à des dérives thermiques.
L'exemple ci-joint montre la dérive enregistrée par un astérosismomètre, observant de jour une source de laboratoire délivrant un signal de référence absolument fixe, mais dont la température de travail n'est pas fixée.
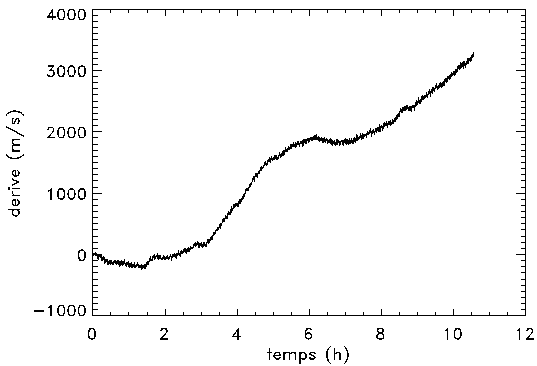
Dérive thermique enregistrée par l'instrument FTS du
CFH, observant de jour une source stabilisée. Les variations de température de la source (mal) stabilisée se traduisent en signal Doppler au cours d'une journée de test. L'inertie thermique joue le rôle de mémoire : le bruit à un instant donné dépend intimement des instants précédents.
Crédit :
ASM/CFHT
Bruit en 1/f
L'effet de mémoire occasionne un bruit instrumental dit en 1/f.
Son évolution temporelle se distingue d'un bruit blanc par une sensible dérive.
Comme le montre l'analyse de Fourier, son spectre de puissance se caractérise alors par une forte contribution aux basses fréquences, qui apparaît clairement
pour un spectre tracé en échelle logarithmique.
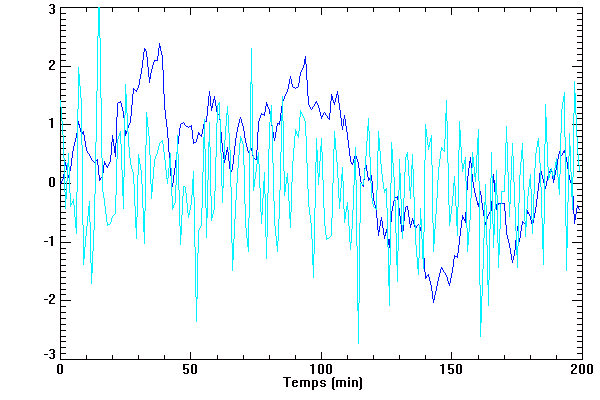
Séries temporelles, correspondant à une bruit blanc (courbe bleu ciel), de moyenne nulle, et à un bruit instrumental en 1/f (courbe bleu foncé) qui dérive.
Crédit :
ASM

Les spectres de puissance des
séries temporelles de différents types de bruits diffèrent sensiblement. Le bruit gaussien n'a pas de fréquence privilégiée, contrairement au bruit instrumental qui montre un spectre de puissance en
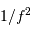
, càd un spectre de Fourier en
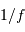
.
Crédit :
ASM
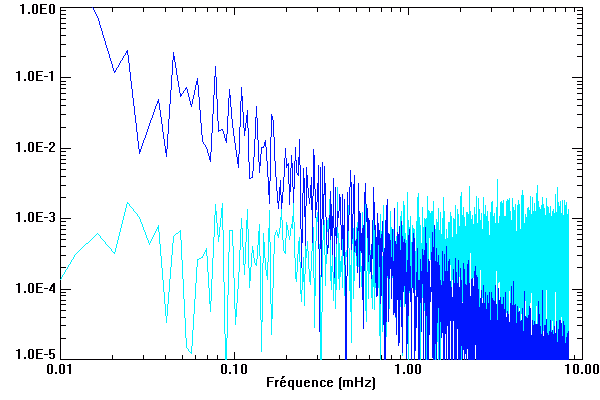
Idem, mais en double échelle logarithmique.
Crédit :
ASM
Apprendre
 Objectifs
Objectifs
Le bruit instrumental est un bruit qui "a de la mémoire". Sa signature spectrale est intense à basse fréquence.
Bruit en 1/f
Le bruit dit en 1/f, avec une dépendance spectrale variant en raison inverse de la fréquence, est typiquement d'origine instrumentale. Il apparaît lorsque les fluctuations induites sur le signal ne sont pas indépendantes, mais corrélées. C'est typiquement le cas des fluctuations thermiques : une perturbation en température à l'instant 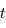 aura des conséquences à tout instant suivant.
aura des conséquences à tout instant suivant.
La transformée de Fourier de l'évolution temporelle d'un tel bruit montre un spectre en 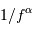 , l'exposant
, l'exposant 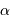 dépendant, phénoménologiquement, de la nature des corrélations au cours du temps.
dépendant, phénoménologiquement, de la nature des corrélations au cours du temps.
Analyse en fréquence d'un bruit instrumental
L'analyse de Fourier d'un bruit en 1/f se caractérise, comme son l'indique, par une forte contribution aux basses fréquences. Ceci apparaît clairement
pour un spectre tracé en échelle logarithmique.
Le critère de Shannon
Observer
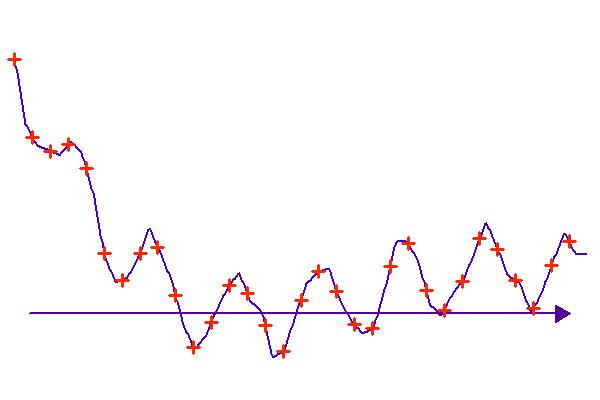
Fonction continue et signal discret associé.
Crédit :
ASM
Continu / discret
Un signal continu n'existe pas : décrire le continu nécessite une infinité de valeurs. Tout signal est échantillonné, càd décrit sur un nombre discret de valeurs.
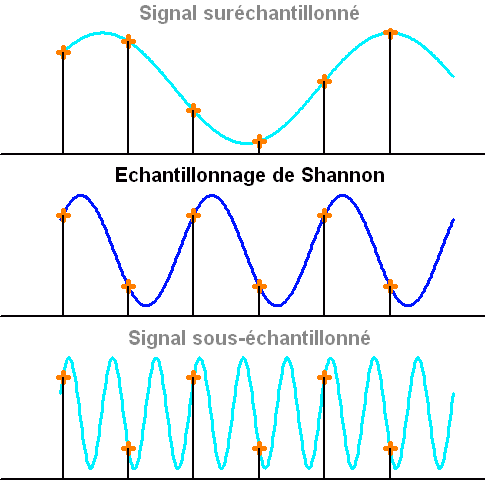
Un signal simple est échantillonné à la limite de Shannon avec 2 points par période. L'information d'un signal sous-échantillonné est perdue.
Crédit :
ASM
L'image initiale (cadre de gauche) est échantillonnée sur un nombre décroissant de pixels. Toute l'information utile est préservée dès lors que la fonction d'étalement du point est convenablement échantillonnée (=). Trop d'informations est inutile (+), et pas assez est destructif (-).
Crédit :
ASM
Échantillonnage de Shannon
Un détecteur ayant une résolution limite (spatiale ou temporelle), un signal physique est nécessairement échantillonné. Même si une observation avec ce détecteur semble prendre des valeurs continues, elle peut être traduite par une série finie de valeurs, correspondant à un échantillonnage discret.
Une bonne observation nécessite de ne pas dégrader la résolution du signal par ce phénomène d'échantillonnage, ce qu'exprime la condition d'échantillonnage de Shannon, qui s'applique aussi pour un signal 2-D.
Coupure
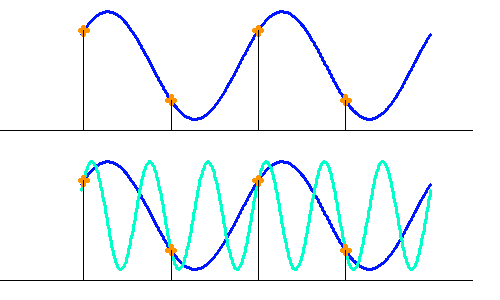
Il est nécessaire d'échantillonner au moins 2 points par période. L'échantillonnage définit ainsi une valeur maximale des fréquences analysables.
Au-delà de la fréquence de coupure, un signal de fréquence plus rapide que la fréquence de coupure peut se confondre avec un signal de pulsation moindre.
Crédit :
ASM
Echantillonnage et coupure
Le pas d'échantillonnage détermine la résolution maximale en fréquence. Au delà de la fréquence de coupure, échantillonnée sur 2 points par période, l'information est perdue. Autrement dit, la fréquence de coupure définie selon Fourier et le théorème de Shannon rendent compte du même phénomène.
Apprendre
Echantillonnage
Tout signal, spatial ou temporel, est limité en fréquence, à cause du processus d'observation. Il peut être codé sur une distribution discrète de valeurs. Ce processus de discrétisation est nommé échantillonnage.
Théorème de Shannon
Le critère de Shannon énonce qu'un signal doit avoir sa fréquence maximale échantillonnée sur au-moins 2 pixels afin de ne subir aucune dégradation.
En pratique, il faut :
- 2 acquisitions temporelles par période pour un signal temporel périodique
- 2 pixels par élément de résolution spatiale pour un signal spatial
La justification de ce critère est liée à l'analyse fréquentielle, par transformée de Fourier : en appliquant le critère de Nyquist, les fréquences sont restituées convenablement jusqu'à la fréquence de coupure.
S'exercer
 Choix d'un détecteur
Choix d'un détecteur
Difficulté : ☆
Temps : 10 min
Un télescope de la classe 4-m, dans une configuration ouverte à f/2, est installé dans un site dont le meilleur seeing est aux alentours de 0.5" en lumière visible. Une caméra CCD installée pour des programmes d'imagerie est spécifiée pour imager sans perdre d'éléments d'information.
Question 1)
Quel paramètre de la caméra est crucial pour satisfaire la spécification donnée ?
L'ouverture du faisceau est déterminée, ainsi que la résolution angulaire. Ceci permet de déterminer la résolution spatiale dans le plan focal.
Question 2)
Sur catalogue, on trouve des caméras avec des pixels de 9, 15 ou 25 microns. Quel choix effectuer ?
Question 3)
Un système d'optique adaptative permet d'atteindre la limite théorique de diffraction dans l'IR à 2 microns. Sachant qu'il n'existe pas de caméra avec des pixels plus petits que 9 micromètres, quel paramètre de la chaîne de collecte du signal doit évoluer ?
Déterminer la tache de diffraction à 2 micromètres.
Identifier les paramètres fixes, de ceux qui le sont moins...
S'évaluer
 Signal sismique
Signal sismique
Difficulté : ☆
Temps : 10 min
On cherche à caractériser un spectre d'oscillations stellaires. La période minimale des oscillations stellaires est de 4 minutes, et on souhaite distinguer des fréquences avec une résolution de 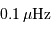 .
.
Question 1)
Estimer la durée totale nécessaire pour ce programme.
[1 points]
Question 2)
Déterminer l'échantillonnage temporel optimal, qui permette de ne pas filtrer les hautes fréquences et minimise le nombre final de données.
[1 points]
Question 3)
Les séquences d'observation du satellite COROT (projet CNES) sont-elles en accord, avec un point de mesure toutes les 32 s et 150 jours d'observation continue sur une cible stellaire ?
[1 points]
Traiter le signal
Auteur: B. Mosser
Introduction
Les signaux recherchés méritent, pour donner les meilleurs mesures possibles, des traitement appropriés. Cette section se propose d'étudier plus précisément quelques-unes des techniques de base de traitement du signal.
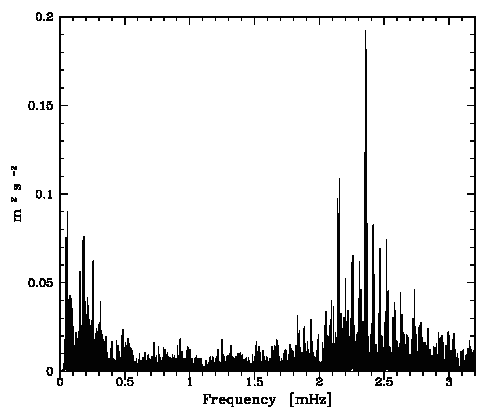
Spectre des oscillations de l'étoile
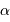
du Centaure.
Crédit : ESO
Filtrage
Observer
Pourquoi filtrer un signal ?
Dans la chaîne de traitement du signal, des
observations brutes au résultat final, une étape souvent essentielle consiste à s'affranchir de signaux parasites. C'est possible lorsque ces derniers présentent des caractéristiques différentes de celles du signal, comme p.ex. un signal à basse fréquence qui contamine un signal sismique.
Analyse d'un signal sismique
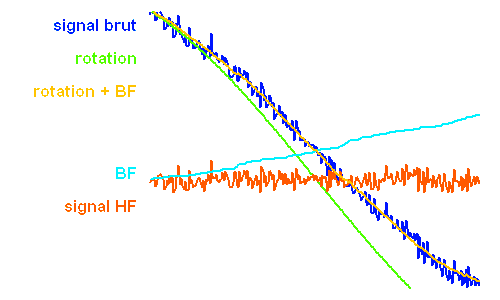
Le signal brut comprend plusieurs composantes. La rotation de la Terre, parfaitement modélisable, apporte une composante à basse fréquence (période de 24 h).
Un signal d'erreur, sur une source de référence, permet l'enregistrement d'une dérive également à basse fréquence. La correction de ces 2 termes ne comprend plus que des hautes fréquences, parmi lesquelles le signal sismique à analyser.
Crédit : ASM
Moyenne glissante
Un filtre par moyenne glissante substitue à une valeur donnée la moyenne des valeurs aux alentours, dans un intervalle de largeur 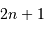 . Plus l'intervalle est grand, plus le filtrage est efficace.
. Plus l'intervalle est grand, plus le filtrage est efficace.
Ce filtrage présente des inconvénients que dévoile la transformée de Fourier.
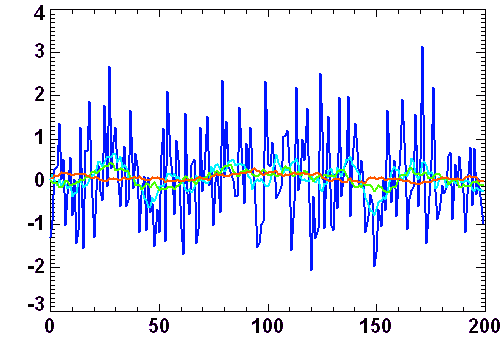
Moyennes glissantes, calculées localement sur 10 (bleu ciel), 20 (vert) ou 50 points (rouge).
Crédit : ASM
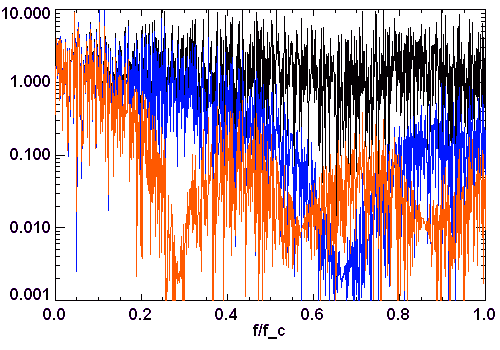
Spectre de Fourier (ordonnée en échelle logarithmique) d'une série de données non filtrée (courbe noire), ou filtrée par moyenne glissante de
sur un intervalle de largeur 3 (courbe bleue) ou 7 (courbe rouge). On s'aperçoit que le filtrage des fréquences par moyenne glissante est très irrégulier.
Crédit : ASM
Médiane
Un filtre par moyenne médiane substitue à une valeur donnée la médiane des valeurs aux alentours, dans un intervalle de largeur 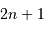 . Ce filtrage est efficace pour gommer les valeurs aberrantes.
. Ce filtrage est efficace pour gommer les valeurs aberrantes.
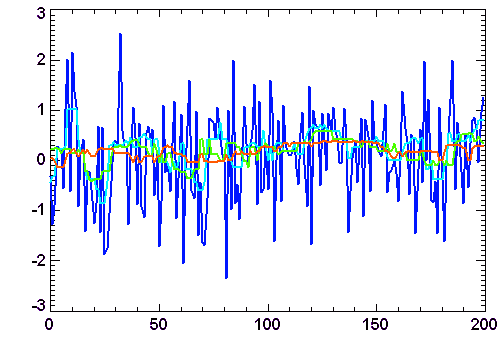
Moyennes médianes, calculées localement sur 10 (bleu ciel), 20 (vert) ou 50 points (rouge).
Crédit : ASM
Estimation linéaire
Réaliser une estimation linéaire d'une distribution de pont, c'est finalement ne décrire ce nuage de points que par 2 valeurs (ordonnée à l'origine et pente)
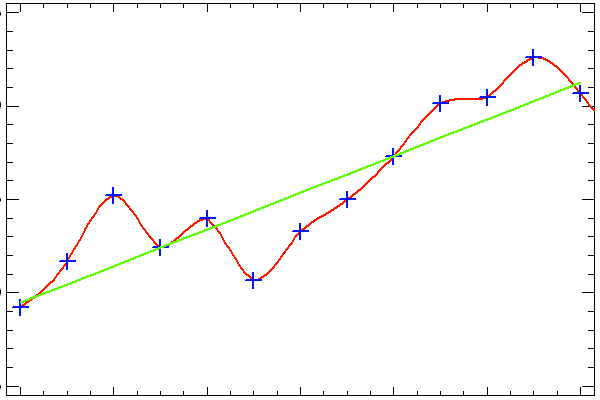
Estimation linéaire. Les hautes fréquences spatiales de la courbe rouge sont filtrées.
Crédit : ASM
Traitement d'un point aberrant
La correction de valeurs aberrantes est typiquement une opération de filtrage. Un filtrage par moyenne glissante ou par la médiane n'y parvient pas avec la même efficacité.
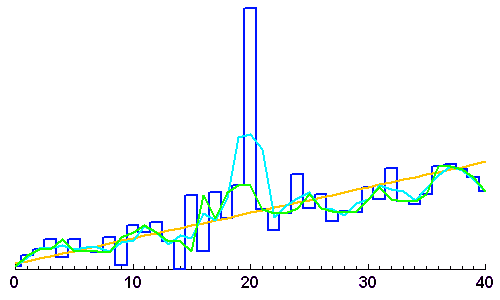
La valeur aberrante est bien corrigée par le filtre médian (vert) mais pas par la moyenne glissante (bleu ciel)
Crédit : ASM
Filtrage en fréquence
Toute série de données, dépendant de quelque paramètre que ce soit (temps, variable d'espace, autre variable), à n'importe quelle dimension, peut être décrite par ses composantes fréquentielles.
Un filtrage ad hoc peut permettre de faire ressortir le signal des autres composantes.
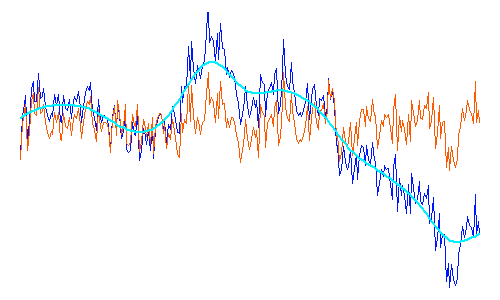
La correction par filtrage des basses fréquences (bleu ciel) permet de ne garder que le signal utile (rouge).
Crédit : ASM
Apprendre
 Prérequis
Prérequis
Analyse par transformée de Fourier
 Objectifs
Objectifs
Aborder quelques-uns des (nombreux) aspects de la transformée de Fourier.
Problématique
Il est souvent indispensable de séparer les différentes composantes en fréquences qui constituent une observation, pour extraire le signal de la contribution du bruit ou d'autres signaux, ce qui constitue un filtrage du signal.
Le but n'est pas de présenter sous forme de cours les multiples filtres possibles, mais plutôt quelques-uns de leurs effets.
Exemple de filtre temporel : l'acquisition de données
Toute acquisition de données, caractérisée par un pas de temps 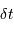 , filtre les fréquences temporelles plus rapides que
, filtre les fréquences temporelles plus rapides que 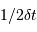 .
.
Simuler
Filtrage par moyenne glissante
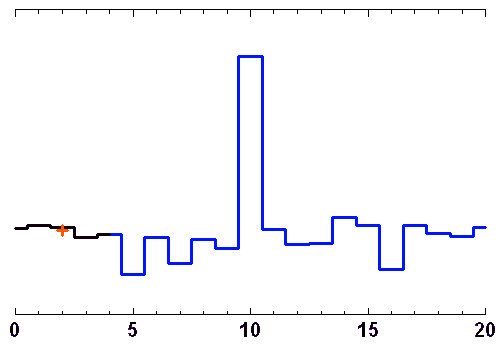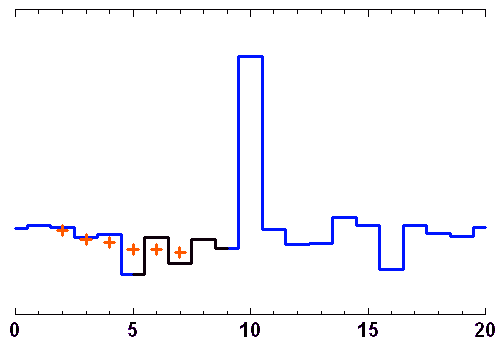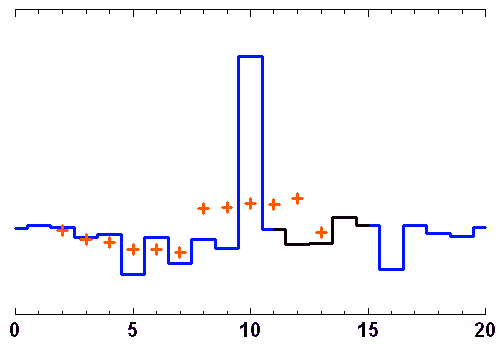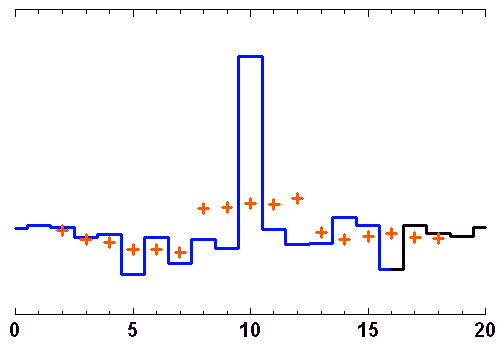
Un point donné est remplacé par la moyenne des points dans un intervalle centré autour de ce point, de plus ou moins ample largeur.
Crédit : ASM
Filtrage médian
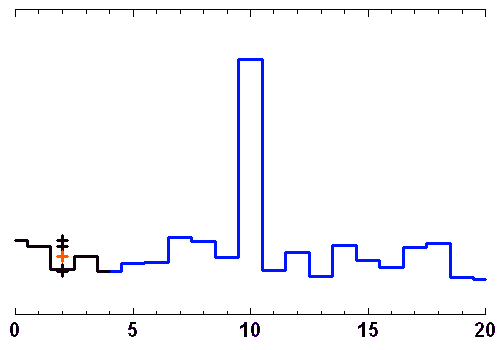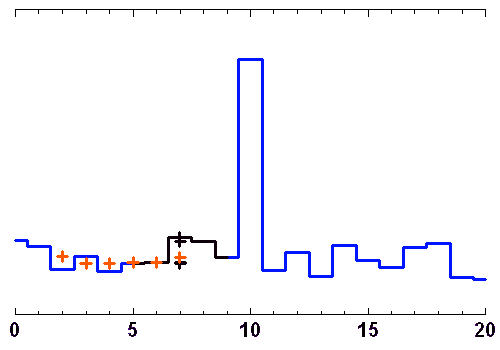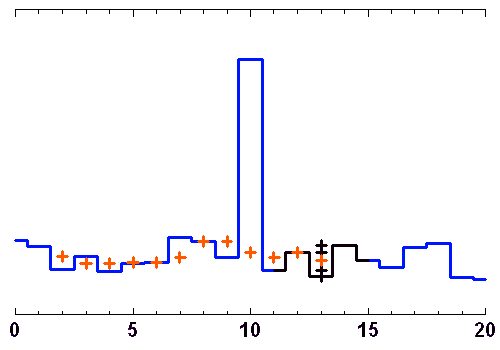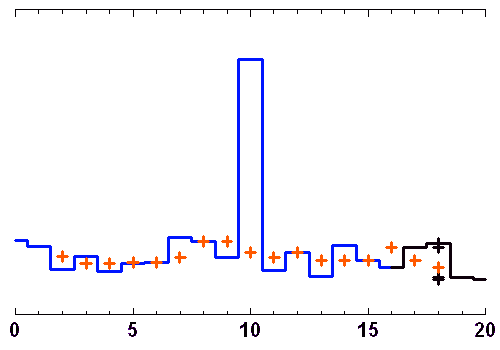
Un point donné est remplacé par la valeur médiane des points dans un intervalle centré autour de ce point, de plus ou moins ample largeur. Les points de chaque intervalle considéré ont été classés par valeur croissante, pour mettre en évidence la valeur médiane (indiquée en rouge).
Crédit : ASM
Filtrage par moyenne glissante

La série originale (en bleu) est filtrée par un filtre glissant, de largeur variable (en vert). Le nombre de points considérés pour la moyenne (en orange) a beau être de plus en plus élevé, le résultat (en rouge) présente toujours les oscillations originales, même lorsque la fenêtre est plusieurs fois plus large que la période du signal.
Crédit : ASM
Exemple de filtrage mal adapté
L'opération de filtrage n'est pas bégnine, et un filtre inadapté peut conduire à un mauvais résultat. Par exemple, le filtrage par moyenne glissante convient très mal pour un signal oscillant.
Exemple de filtrage numérique
La série temporelle ci-jointe est filtrée par filtrage numérique (algorithme de filtre à trous), avec séparation des hautes et basses fréquence. Les domaines de fréquence sont définis par rapport à une fréquence de valeur arbitraire ou mûrement réfléchie...
Filtrage numérique
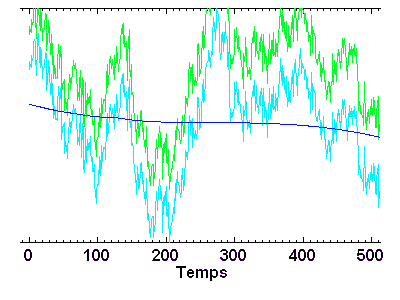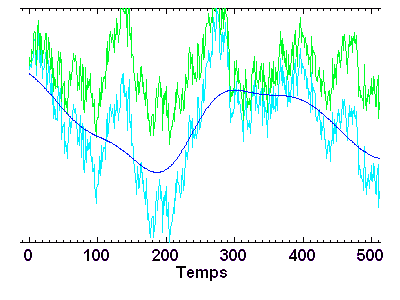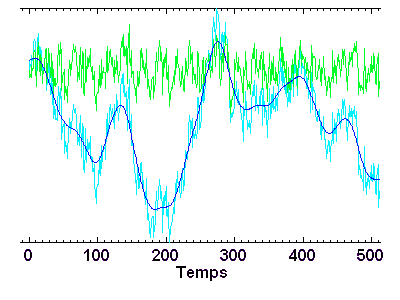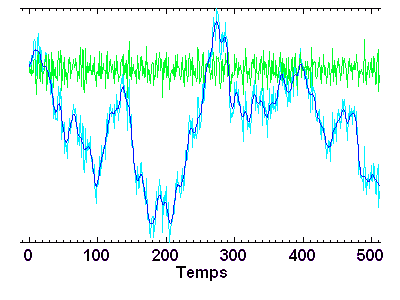
Filtrage d'un signal bruité (bleu ciel) en haute (vert) et basse (bleu foncé) fréquences, avec glissement progressif de la transition entre les définition de `haut' et `bas'.
Crédit : ASM
A la recherche de motifs
Les appliquettes ci-dessous dévoilent l'intérêt du filtrage. Elles représentent des cartes de Jupiter dans l'infrarouge thermique. Sans filtrage, c'est la structure en bandes parallèles à l'équateur qui domine l'image ; après filtrage de cette structure dominante, on voit apparaître des motifs de type ondulatoire, avec une dizaine de motifs répartis en longitude, couvrant une extension en latitude plus vaste que les bandes.
Utiliser les appliquettes pour dévoiler ces structures.


Sommation d'image
Simuler
Correction élémentaire du champ plat
A l'aide de l'appliquette ci-jointe, on se propose d'illustrer l'évolution du bruit en sommant différentes images d'un même champ.
Correction du champ plat 
- Sélectionner la 1ère image. Si besoin, adapter l'échelle de couleur avec la touche auto
- Sélection l'opération coupe, puis une ligne de coupe évitant les objets les plus brillants.
- Sélection l'opération division, puis la 1ère image et l'image de champ plat, et nommer l'image corrigée.
- Réaliser sur cette nouvelle image la coupe précédente. Comparer.
Analyse par transformée de Fourier : formalisme
Apprendre
 Prérequis
Prérequis
Approche mathématique de la transformation de Fourier
 Objectifs
Objectifs
Présentation de la transformation de Fourier, et rappel de quelques propriétés.
Propriétés
La TF est dotée de multiples propriétés (linéarité...) : se référer à un cours de maths.
L'opération inverse de la TF est notée :
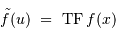 et
et
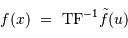 .
.
Analyse de Fourier discrète
La définition de la transformation, continue, se doit d'être amendée pour tenir compte du fait qu'un signal réel est échantillonné. L'analyse de Fourier discrète s'appuie sur un nombre fini de réalisations du signal, et donne un nombre finie de fréquences pour le décrire.
La discrétisation s'opère en douceur, car la TF d'une fonction peigne (succession équidistance de Dirac), fonction retranscrivant l'échantillonnage du signal, est une fonction peigne.
Simuler
TF et FFT
L'appliquette ci-dessous permet de calculer et visualiser le spectre de puissance de certaines fonctions. La transformée de Fourier peut calculée soit directement, soit par FFT.

Avec comme signal une sinusoïde, comme méthode la fft, visualiser
les effets :
- de la durée,
- de la période du signal,
- du nombre de points de l'échantillon.
Vérifier le lien entre la résolution en fréquence et la durée totale d'observation ; vérifier le lien entre le nombre de points et la fréquence de coupure.
S'exercer
 Conservation de l'énergie
Conservation de l'énergie
Difficulté : ☆☆
Temps : 40 min
Question 1)
Vérifier l'homogénéité de la conservation de l'énergie énoncée par le théorème de Parseval-Plancherel.
Question 2)
Pour des raisons physiques, il est commode de poser la définition de la TF d'une série temporelle bornée sur un intervalle de temps 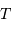 comme :
comme :
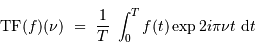
avec le changement de notation pour préciser la différence par rapport à la TF classique. Montrer l'intérêt physique de cette notation, en s'appuyant p.ex. sur un signal purement sinusoïdale.
Passer à la limite des grandes valeurs de 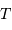 .
.
Question 3)
Pour d'autre raisons, il peut être commode de poser la définition de la TF d'une série temporelle discrète d'une manière différente :
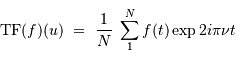
avec le changement de notation pour préciser la différence par rapport à la TF classique. Réécrire la relation de Parseval-Plancherel, et montrer que
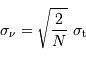
où 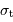 et
et 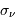 sont respectivement les écarts-types de la série temporelle et du spectre.
sont respectivement les écarts-types de la série temporelle et du spectre.
Analyse par transformée de Fourier : signal
Observer
Intérêt de la transformée de Fourier
La TF permet la recherche de composantes périodiques dans un signal.
Les signaux ci-contre sont équivalents. L'un correspond à une série temporelle, l'autre à son spectre de Fourier.
Série temporelle et son spectre
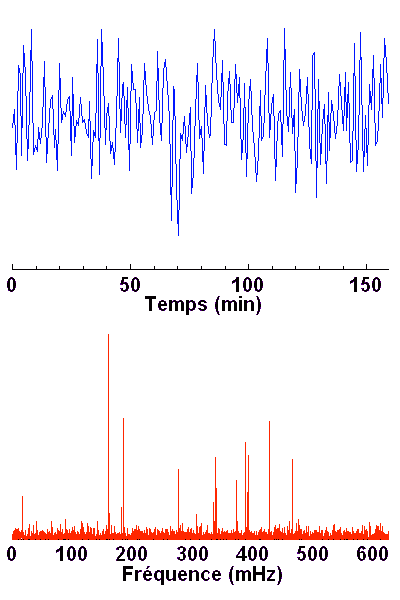
La série temporelle (extrait donné en bleu) ne montre rien de définissable. Son spectre de Fourier dévoile en revanche les fréquences propres qui constituent le signal, en les distinguant clairement du bruit.
Crédit : ASM
Exemple : signal sismique
L'astérosismologie est un sujet en plein développement, dont les observations se basent sur de longues séries temporelles, pour l'identification des modes propres d'oscillations dans le spectre de Fourier.
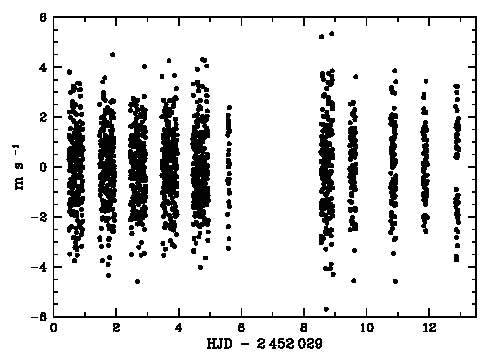
Série temporelle de données astérosismiques enregistrées à l'ESO, pendant 11 nuits, sur l'étoile
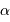
Cen.
Crédit : ESO

Spectre de Fourier de la série temporelle de données astérosismiques enregistrées à l'ESO, pendant 11 nuits, sur l'étoile alpha Cen.
Crédit : ESO
Apprendre
 Objectifs
Objectifs
Utiliser la TF pour la recherche de phénomènes périodiques.
Résolution en fréquence
Un signal observé durant une durée totale 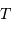 permet une résolution en fréquence
permet une résolution en fréquence 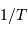 .
.
Fréquence de coupure
Un signal observé avec un échantillonnage 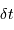 permet de suivre les fréquences jusqu'à la coupure
permet de suivre les fréquences jusqu'à la coupure 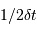 .
Le facteur 2 provient de la nécessité d'observer sur 2 mesures distinctes une demi-période négative et une demi-période positive.
.
Le facteur 2 provient de la nécessité d'observer sur 2 mesures distinctes une demi-période négative et une demi-période positive.
Echantillonnage
L'observation de phénomènes variables doit permettre :
- Un échantillonnage suffisamment rapide de la série temporelle, afin d'avoir accès aux variations les plus rapides.
- Une durée d'observation suffisamment longue pour suivre une période entière d'un phénomène périodique.
Simuler
Résolution
Pour une série temporelle, la résolution en fréquence du spectre est d'autant meilleure que la base de temps d'observation est plus longue.
TF et résolution
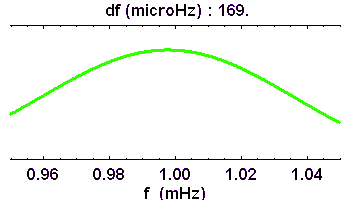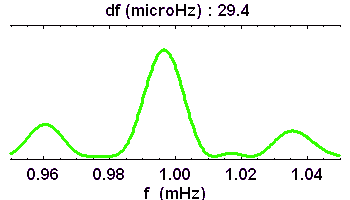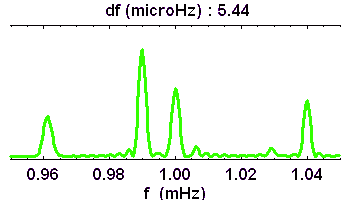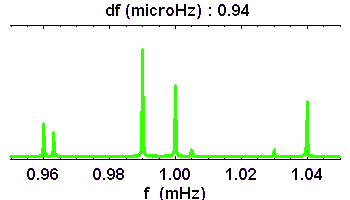
La résolution en fréquence, d'autant plus fine que la série temporelle initiale est longue, permet de dévoiler peu à peu la richesse du spectre.
Crédit : ASM
Pour une image, on relie la fréquence de coupure spatiale à la résolution spatiale .
TF et fréquence de coupure

M31, vue avec un nombre plus ou moins grand de fréquences spatiales (spectre de Fourier 2-D à gauche, image reconstruite à droite).
Crédit : ASM
S'exercer
 Pulsation de coupure
Pulsation de coupure
Difficulté : ☆☆
Temps : 30 min
On échantillonne un signal temporel avec un pas de temps 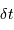 . On définit la pulsation
. On définit la pulsation 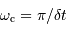 .
.
Question 1)
Montrer qu'il y a confusion entre les spectres de puissance des signaux périodiques de pulsation 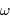 et
et
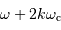 ou
ou 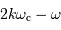 , où
, où 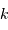 est un entier
est un entier
Courage, ce n'est qu'un peu de calculs sur les sinus.
Estimer 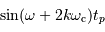 à une date
à une date 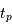 de l'échantillonnage
de l'échantillonnage
Supposer 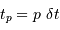
Question 2)
En déduire l'expression de la pulsation de coupure
Jusqu'à quelle fréquence n'y aura-t-il pas de confusion?
Analyse par transformée de Fourier : bruit
Observer
Bruit / signal cohérent
Une analyse par TF va traiter différemment un signal, avec un spectre donné, d'un bruit, sans signature spectrale caractéristique.
Transformée de Fourier et bruit
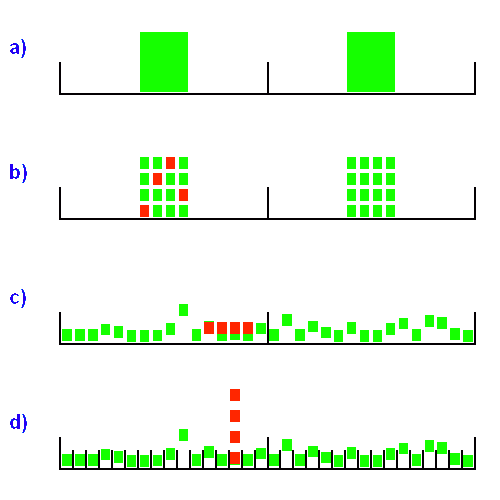
Evolution temporelle du bruit dans une TF. La durée d'observation augmentant, l'énergie du bruit se retrouve distribuée sur un nombre croissant de fréquences, contrairement au signal à fréquence bien déterminée.
Crédit : ASM
Bruit blanc
Un bruit gaussien ne montre aucune fréquence privilégiée, contrairement à un bruit en 1/f.
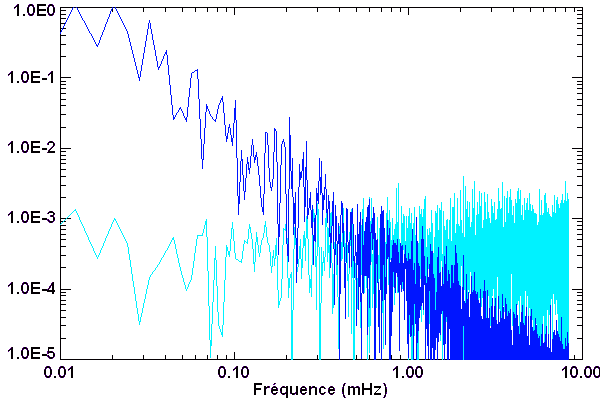
Comparaison des spectre d'un bruit en 1/f et d'un bruit gaussien, avec une représentation en
double échelle logarithmique.
Crédit : ASM
Apprendre
 Objectifs
Objectifs
Utiliser la TF pour distinguer signaux et bruits
Signal ou bruit
La dialectique est simple : un bruit ne mérite ce titre qu'en l'absence de signature spectrale définie (un bruit blanc ne présente aucune particularité spectrale; un bruit instrumental, par effet de mémoire, présente plus d'énergie aux basses fréquences qu'aux fréquences plus élevées).
La TF permet par son principe, en classant et en analysant les fréquences constitutives d'une suite de données, de distinguer la part du signal de celle du bruit.
En pratique, cela nécessite un rapport signal-à-bruit suffisant (mais qui peut être très faible).
Cohérence
Lorsque le nombre de données observationnelles
augmente,
un signal cohérent va garder une signature bien précise. En revanche, un bruit va voir son énergie diluée dans une multitude de fréquences.
La TF permet de faire ressortir du bruit un signal bien cohérent.
Simuler
Evolution temporelle des bruits et signaux
En augmentant la durée totale de la série temporelle de données, un signal périodique cohérent (càd de durée de vie supérieure à la durée d'observation) ressort peu à peu du bruit.
Comment faire taire le bruit ?
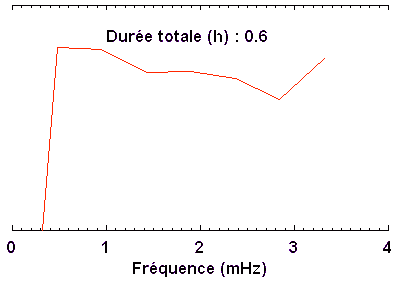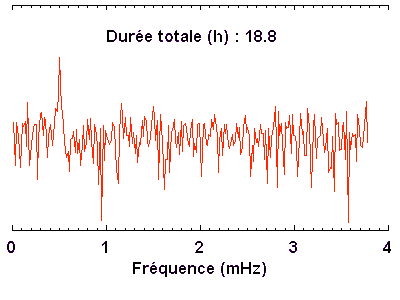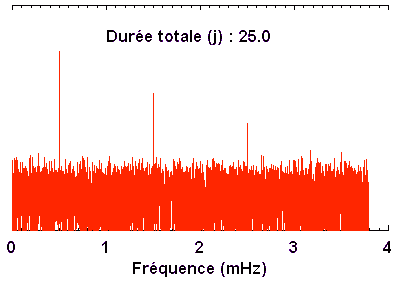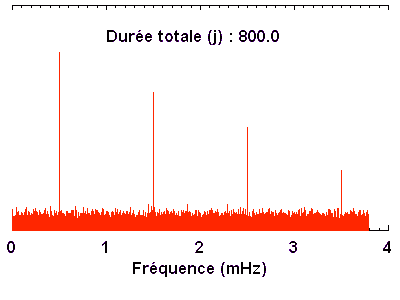
La durée d'observation augmentant, la puissance du bruit est peu à peu diluée sur un nombre croissant d'éléments spectraux, alors que le signal, supposé cohérent, s'accumule à une fréquence donnée.
Crédit : ASM
Faire taire le bruit
A l'aide de l'appliquette ci-dessous, on se propose d'évaluer comment le bruit évolue dans un spectre

Avec comme signal une sinusoïde, comme méthode la FT, et 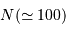 points dans l'échantillon, faire varier le niveau de bruit
points dans l'échantillon, faire varier le niveau de bruit 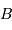 , et montrer que le signal est identifiable dans le spectre si son amplitude excède
largement
, et montrer que le signal est identifiable dans le spectre si son amplitude excède
largement 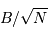 .
.
Si besoin, zoomer sur les hautes fréquences du spectre pour s'affranchir du fort signal à basse fréquence.
S'exercer
 Astérosismologie
Astérosismologie
Difficulté : ☆☆☆
Temps : 30 min
Question 1)
La documentation de HARPS indique qu'un rapport signal à bruit de 500 sur un spectre correspond à une incertitude, exprimée en vitesse, de 45 cm/s. Par ailleurs,
une cible de magnitude 5.5 conduit à un rapport signal à bruit de 200 avec des poses de 3 min. A quelle vitesse cela correspond-il ?
L'incertitude en vitesse correspond à un niveau de bruit.
Le niveau de bruit et le rapport signal à bruit sont simplement ... inversement proportionnels
Question 2)
Combien de poses élémentaires sur une telle étoile sont nécessaires pour aboutir à un bruit résiduel de 5 cm/s. A quelle durée cela correspond-il ?
Le rapport signal à bruit évole comme la racine carrée du nombre de pose élémentaire,
Question 3)
Sur la cible alphaCen B, très brillante, HARPS délivre un signal bruité à 2 cm/s, après 7 h d'observation. Les poses élémentaires étant de 1 min, quelle est la performance en vitesse sur une pose ?
7 h font combien de minutes ?
Réponses aux QCM
pages_multispectral/multispectral-sexercer.html
QCM
- Question 1
Solution : réponse 3)
pages_interferometrie-spatiale/interferometrie-spatiale-sexercer.html
QCM
- Question 1
Solution : réponse 3)
- Question 2
Solution : réponse 1)
(
A la limite du faisable actuellement
)
- Question 3
Solution : réponse 2)
- Question 4
Solution : réponse 1)
(
En effet, car D définit la tache de diffraction
)
pages_detection-quantique/detection-quantique-sexercer.html
QCM
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 3)
- Question 3
Solution : réponse 3)
pages_detection-rendement/detection-rendement-sexercer.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 2)
pages_rapport-signal-bruit/rapport-signal-bruit-sexercer.html
QCM
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 2)
pages_bruit-gaussien/bruit-gaussien-sexercer.html
QCM
- Question 1
Solution : réponse 3)
- Question 2
Solution : réponse 1)
pages_bruit-photons/bruit-photons-sexercer.html
QCM
- Question 1
Solution : réponse 3)
(
Il varie en effet comme la racine carrée du nombre de photons
)
- Question 2
Solution : réponse 3)
(
Il varie en effet comme la racine carrée du nombre de photons
)
- Question 3
Solution : réponse 3)
- Question 4
Solution : réponse 3)
pages_shannon/shannon-sexercer.html
QCM
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 3)
Réponses aux exercices
pages_collecter/elt-sexercer.html
Exercice
'Hypertélescope'
- Question 1
Aide :
Réfléchir au rôle de la diffraction par une sous-pupille,
à celui des interférences entres sous-pupilles.
Aide :
Mener l'analogie avec un réseau.
Solution :
L'analogie avec un réseau de diffraction est immédiate. Une
sous-pupille se comportant comme une fente individuelle d'un
réseau de diffraction. Chaque sous-pupille diffracte le faisceau
pour une tache image individuelle 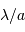 ; les
interférences entre les sous-faisceaux conduisent à une taille
angulaire
; les
interférences entre les sous-faisceaux conduisent à une taille
angulaire 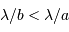 .
.
- Question 2
Aide :
Pour une comparaison aisée, imaginer que L2 et L5 ont les mêmes diamètre et focale que L1.
Solution :
La recombinaison des faisceaux par L5 conduit à un système qui aurait des caractéristiques identiques à L1, mais en remplaçant 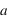 par
par 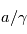 , c'est-à-dire, de façon équivalente, en remplaçant
, c'est-à-dire, de façon équivalente, en remplaçant 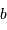 par
par 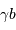 . Tout se passe comme si on avait un gruyère avec moins de trous.
. Tout se passe comme si on avait un gruyère avec moins de trous.
En exagérant la taille des lentilles L2 et L5, jusqu'à celle de
L1, on peut comparer directement les situations de
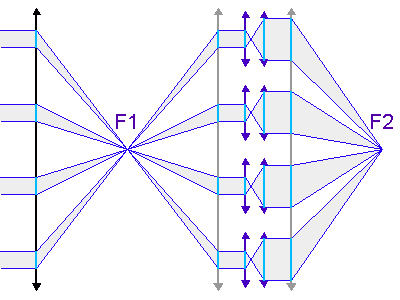
Crédit :
ASM
- Question 3
Aide :
Mener un raisonnement géométrique s'appuyant sur la figure.
Aide :
S'intéresser à la localisation de l'énergie dans les pics d'interférence.
Solution :
Lorsque 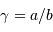 , tout se passe comme si l'on avait réuni des collecteurs de diamètre plus important et qu'il n'y avait plus de trous dans le miroir équivalent. La pupille a été densifiée.
, tout se passe comme si l'on avait réuni des collecteurs de diamètre plus important et qu'il n'y avait plus de trous dans le miroir équivalent. La pupille a été densifiée.
- Question 4
Aide :
S'intéresser à la tache de diffraction.
Aide :
S'intéresser au champ accessible, dimensionné par une tache de diffraction élémentaire
Aide :
Que devient la tache de diffraction d'une sous-pupille ?
Solution :
Le gain en termes de formation d'image est clair : on a reconstitué un plus grand miroir, et donc les images sont plus piquées (la fonction d'étalement du point est moins... étalée). Mais, comme la tache de diffraction d'une
sous-pupille a été divisée par 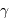 . Il en est de même du champ : le champ accessible par l'instrument a été réduit. Il y a toujours des compromis à faire.
. Il en est de même du champ : le champ accessible par l'instrument a été réduit. Il y a toujours des compromis à faire.
pages_former/astrometrie-sevaluer.html
Exercice
'Précision astrométrique et inégalité de Heisenberg'
- Question 1
Aide :
Réfléchir (!) à la formation d'image. Considérer une lentille
équivalente pour se simplifier la vie.
- Question 2
Aide :
L'échantillonnage en position se fait ici par pas de largeur 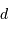 .
.
- Question 3
Aide :
Déterminer d'abord 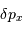 .
.
Aide :
Déterminer 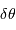 en fonction de
en fonction de 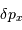 .
.
- Question 4
- Question 5
pages_former/spectrometrie-hr-sexercer.html
Exercice
'Le spectromètre HARPS'
- Question 1
Aide :
Rappel du montage afocal
Faisceau de sortie du montage afocal

Crédit :
ASM
Solution :
Le grossissement du télescope doit transformer un faisceau parallèle de diamètre 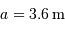 en un autre faisceau parallèle de diamètre
en un autre faisceau parallèle de diamètre 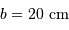 . Le grossissement doit donc vérifier :
. Le grossissement doit donc vérifier :
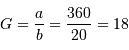
- Question 2
Aide :
Relier la déviation de 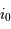 à celle de
à celle de 
Solution :
Vu le grossissement,
une déviation 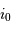 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 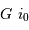 dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour
dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour 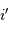 cette déviation
cette déviation 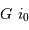 .
.
- Question 3
Aide :
Le réseau envoie la lumière préférentiellement dans la direction 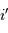 obéissant à :
obéissant à :
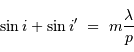
Aide :
Différencier l'expression précédente.
Solution :
Le réseau envoie la lumière préférentiellement dans la direction 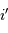 obéissant à :
obéissant à :
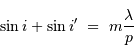
A incidence  fixée, la différentiation de la relation précédente donne :
fixée, la différentiation de la relation précédente donne :
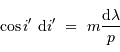
D'où la relation de dispersion :
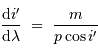
- Question 4
Aide :
Faire le lien entre 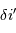 ,
, 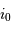 et le grossissement
et le grossissement 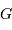 .
.
Solution :
La dispersion du réseau énonce :
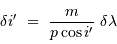
La résolution souhaitée entraîne la nécessité de distinguer des éléments spectraux de largeur :
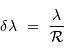
Par ailleurs, des variations de l'angle d'injection 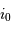 se traduisent par des variations de
se traduisent par des variations de 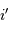 à hauteur de
à hauteur de 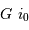 . On en déduit que les variations de l'angle
. On en déduit que les variations de l'angle 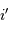 doivent être contraintes par :
doivent être contraintes par :
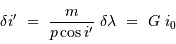
Et donc 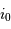 doit satisfaire :
doit satisfaire :
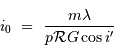
L'application numérique donne (avec 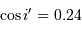 ) :
) :

On en déduit que le champ objet doit être extrêmement réduit. La fibre du spectromètre HARPS sélectionne ainsi uniquement 1" sur le ciel.
- Question 5
Aide :
Estimer la divergence en fonction de la longueur 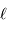 proposée et de l'angle
proposée et de l'angle 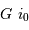 .
.
Solution :
Une déviation angulaire 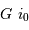 avec un bras de levier de longueur
avec un bras de levier de longueur 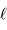 se traduit par une déviation linéaire
se traduit par une déviation linéaire 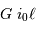 .
.
L'application numérique donne 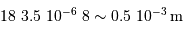 . Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.
. Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.
pages_former/spectro-imagerie-sexercer.html
Exercice
'Spectrométrie intégrale de champ : résolutions spatiale et spectrale'
- Question 1
Aide :
Pour fixer les ordres de grandeur, on peut traduire large intervalle spectral comme 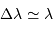 .
.
Aide :
Les définitions de 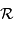 et
et 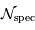 sont :
sont :
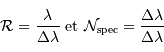
Solution :
En supposant 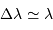 , on vérifie bien que
, on vérifie bien que
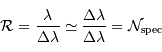
- Question 2
Aide :
Réfléchir à la signification du mot pixel. Combien d'informations spatiales élémentaires un CCD de 2k  2k peut-il traiter?
2k peut-il traiter?
Solution :
En supposant un rendement optimal, le nombre de pixels fournit le nombre d'éléments spectraux et spatiaux. Au mieux, pour un détecteur 2k  2k :
2k :
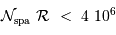
Mais comme on va souhaiter échantillonner une information spatiale ou spectrale sur au moins 2 pixels, et qu'il est prudent de laisser des pixels non éclairés entre chaque spectre, il faut plutôt compter :
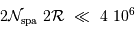
- Question 3
Aide :
Montrer que, vu les hypothèses :
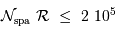
Solution :
Avec 20 pixels par information élémentaire, on a :
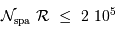
L'application numérique donne un nombre d'informations spatiales indépendantes  limité à :
limité à :
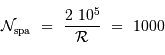
Le nombre de pixels étant limité, on ne peut pas simultanément gagner en résolutions spatiale et spectrale.
pages_former/interferometrie-spatiale-sexercer.html
Exercice
'L'interféromètre du plateau de Bure'
- Question 1
Aide :
Revoir le cours sur la diffraction
Aide :
Une fréquence de 230 GHz correspond à une longueur d'onde de 1.3 mm.
Solution :
Avec la correspondance 230 GHz / 1.3 mm, on calcule
l'extension angulaire de la diffraction :
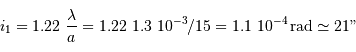
- Question 2
Solution :
Avec une base 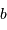 :
:
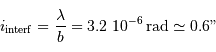
Un objet étendu de diamètre 21" est dans le premier cas visualisé sur 1 élément
de résolution, et sur 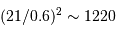 dans le second.
dans le second.
pages_detecter/detection-physique-sexercer.html
Exercice
'Principe de la détection hétérodyne'
- Question 1
Aide :
On rappelle :
![\cos a \cos b = {1\over 2} \Bigl[ \cos (a+b) + \cos (a-b) \Bigr]](../pages_detecter/equations_detection-physique/equation7.png)
Solution :
Avec 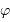 le déphasage inconnu à un instant de référence choisi comme origine, le produit des signaux est proportionnel à :
le déphasage inconnu à un instant de référence choisi comme origine, le produit des signaux est proportionnel à :
![\cos( \omega t +\varphi) \cos \omega_0 t = {1\over 2} \left[ \cos \bigl( (\omega+\omega_0) t + \varphi \bigr) + \cos \bigl( (\omega-\omega_0)t-\varphi \bigr) \right]](../pages_detecter/equations_detection-physique/equation9.png)
Les 2 pulsations étant voisines, la deuxième composante a une fréquence bien plus basse que la première.
- Question 2
Aide :
Que reste-t-il du signal précédent après élimination des hautes fréquences ?
Solution :
La partie à basse fréquence, qui porte l'information du signal scientifique, à une translation en fréquence près, devient analysable à l'aide de l'électronique ad hoc, et peut être détectée en amplitude.
pages_detecter/reponse-temporelle-sexercer.html
Exercice
'Temps de réponse'
- Question 1
Aide :
Rappel : magnitude et luminosité varient dans le rapport :
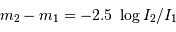
Solution :
Par application de la définition de la magnitude, le flux d'une étoile de magnitude 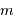 vaut
vaut 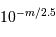 par rapport à celui d'une étoile de magnitude nulle.
par rapport à celui d'une étoile de magnitude nulle.
Le temps de pose étant limité par le flux optimal sur un pixel, une pose de durée 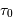 pour une magnitude nulle sera multipliée par
pour une magnitude nulle sera multipliée par 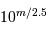 pour une magnitude
pour une magnitude 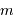 .
.
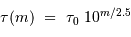
Soit 10 s pour une magnitude 2.5, 100 s pour une magnitude 5.
- Question 2
Solution :
En application de ce qui précède, une pose de 20 s correspond à la magnitude 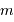 vérifiant
vérifiant
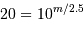 , càd
, càd 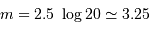 .
.
Le temps de pose pour une étoile plus brillante que la magnitude 3.25 est plus court que 20 s : le temps est majoritairement dépensé à lire le détecteur.
- Question 3
Aide :
La pose sur l'objet est nécessairement limitée à 160 s.
Solution :
En application de ce qui précède (avec des pixels bien remplis), une pose de 160 s correspond à la magnitude 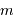 vérifiant
vérifiant
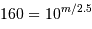 , càd
, càd 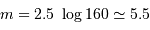 .
.
Le temps de pose pour une étoile moins brillante que la magnitude 5.5 dépasse 160 s.
En acceptant de remplir les pixels de façon très incomplète, le gain d'un facteur 10 en nombre de photoélectrons, donc de photons, correspond à un surcroît de 2.5 magnitudes. La limite en magnitude est donc de l'ordre de 8.
pages_detecter/reponse-geometrie-sexercer.html
Exercice
'Projet MEGACAM du télescope CFH'
- Question 1
Aide :
Déterminer le nombre total de pixels pour 36 CCD.
Solution :
1 CCD comporte 9 Mpx. Soit un côté équivalent de 3 kpx, s'il était de forme carrée. Donc, 6 CCD par côté représente 18 kpx.
Comme 0.94 deg vaut 3384", chaque pixel voit un champ de 0.188" de côté.
- Question 2
Aide :
1 pixel codé sur 16 bits nécessite 2 octets pour le stockage.
Solution :
Le nombre total de pixels vaut 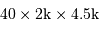 , soit 360 Mpx, d'où un taille de 720 Mo par image.
, soit 360 Mpx, d'où un taille de 720 Mo par image.
- Question 3
Solution :
D'après la question précédente, 3 images pour 3 poses dans différents filtres.
donnent 2.16 Go.
Le volume de données représentera finalement 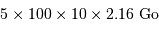 , soit 10.8 téraoctets.
, soit 10.8 téraoctets.
pages_detecter/reponse-bruits-sexercer.html
Exercice
'Numérisation'
- Question 1
Aide :
L'échantillonnage du signal requiert de coder le niveau de signal à la moitié de la plus petite variation.
Aide :
Déterminer l'amplitude relative du signal entre le niveau de codage et la valeur maximale
Solution :
Ne pas introduire de bruit nécessite de coder comme niveau de signal minimal la moitié de la plus petite variation, soit 0.05.
Le rapport entre cette valeur et l'amplitude maximale vaut 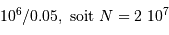 .
.
Le nombre de bits nécessaire vérifie :
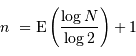
(avec E codant le symbole partie-entière).
Il faudrait donc coder le signal sur 25 bits, ce qui est beaucoup.
- Question 2
Aide :
Même démarche que précédemment.
Solution :
Le niveau de quantification requis est identique, mais l'amplitude maximale est cette fois-ci de 1000, et le rapport de 20000.
Un codage sur 15 bits suffit à rendre compte du signal filtré du continu.
pages_detecter/detection-rendement-sevaluer.html
Exercice
'Transmission atmosphérique'
- Question 1
- Question 2
Aide :
Faire un schéma montrant les couches d'atmosphère traversées avant la détection.
- Question 3
Aide :
Dans l'appliquette :
- sélectionner la 1ère case de la colonne 1-T (D1) et réaliser :
=100-C1
- sélectionner la 1ère case de la colonne (lambda^-4) (E1) et réaliser :
=(1000/A1)^4
pages_analyser/rapport-signal-bruit-sexercer.html
Exercice
'Bruit dominant'
- Question 1
Aide :
Au numérateur, on a tout simplement le signal, au dénominateur les bruits.
Aide :
Il reste à identifier le terme 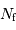 et à interpréter la somme du dénominateur.
et à interpréter la somme du dénominateur.
Solution :
Les 3 termes du dénominateur sont :
- le bruit de photons 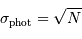 ,
,
- le bruit de fond, 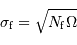 , avec
, avec 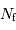 le nombre de photoélectrons par unité d'angle solide dus au fond,
le nombre de photoélectrons par unité d'angle solide dus au fond,
- le bruit de lecture.
- Question 2
Aide :
Déterminer l'importance relative des différents bruits.
Solution :
Pour un objet très brillant, le bruit de photons de la source va dominer devant les autres bruits :
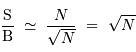
Dans le cas d'un objet peu lumineux, le bruit de photons de la source est négligeable. En l'absence d'autres données, il n'est pas possible de discriminer parmi les 2 autres sources de bruit.
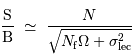
Dans un cas, 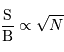 , dans l'autre
, dans l'autre 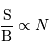 .
.
- Question 3
Aide :
Comment le nombre de photoélectrons collectés varie-t-il avec le diamètre du collecteur ou le temps de pose ?
Solution :
Si l'on note 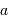 le diamètre du collecteur et
le diamètre du collecteur et 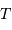 le temps de pose, il est immédiat que
le temps de pose, il est immédiat que 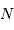 varie comme la surface collectrice
varie comme la surface collectrice 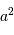 et comme
et comme 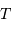 .
.
On en déduit les dépendances respectives :
| diamètre collecteur | temps de pose |
| source lumineuse | 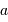 | 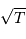 |
| source faible | 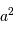 | 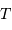 |
Dépendance envers 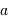 ou
ou 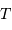 du rapport signal à bruit.
du rapport signal à bruit.
pages_analyser/bruit-photons-sexercer.html
Exercice
'Le projet COROT'
pages_analyser/bruit-photons-sevaluer.html
Exercice
'Au photon près'
- Question 1
Aide :
Repérer un intervalle de temps où le signal n'évolue pas à basse fréquence, et mesurer l'amplitude crête à crête.
- Question 2
Aide :
Revoir les propriétés du bruit poissonnien.
- Question 3
pages_analyser/shannon-sexercer.html
Exercice
'Choix d'un détecteur'
- Question 1
Aide :
L'ouverture du faisceau est déterminée, ainsi que la résolution angulaire. Ceci permet de déterminer la résolution spatiale dans le plan focal.
Solution :
L'ouverture du faisceau étant déterminée, la focale du télescope est connue (8 m) ainsi que la résolution angulaire, limité par le seeing 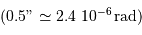 , la taille linéaire dans le plan focal est fixée :
, la taille linéaire dans le plan focal est fixée :
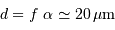
- Question 2
Solution :
La taille des pixels doit être au moins moitié moindre que la tache de seeing, il faut donc des pixels de 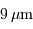 .
.
- Question 3
Aide :
Déterminer la tache de diffraction à 2 micromètres.
Aide :
Identifier les paramètres fixes, de ceux qui le sont moins...
Solution :
La tache de diffraction vaut 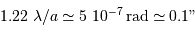 . Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.
. Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.
Comme le diamètre du télescope est fixée, de même que la taille minimale des pixels, la seule variable d'ajustement est l'ouverture du faisceau. Elle doit être diminuée d'un facteur au-moins 5, passant de f/4 à f/20.
pages_traiter/analyse-tf-sexercer.html
Exercice
'Conservation de l'énergie'
- Question 1
Aide :
Avec les notations du cours.
Poser 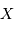 la dimension de la variable
la dimension de la variable 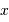 ,
, 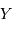 celle de la fonction
celle de la fonction 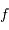 . Et en déduire les dimensions de
. Et en déduire les dimensions de 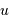 et
et 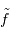
Solution :
Avec les notations du cours, et en notant entre crochets les dimensions.
![[x] = X \mathrm{\ et\ } [f] = Y](../pages_traiter/equations_analyse-tf/equation30.png) , donc la définition de la TF donne :
, donc la définition de la TF donne :
![[u] = X^{-1} \hbox{ et } [\tilde f] = XY](../pages_traiter/equations_analyse-tf/equation31.png) .
.
On en déduit l'homogénéité :
![\left [\int \left| f (x) \right|^{2} \ {\mathrm{d}} x \right] \ =\ Y^2\ X \ =\ (YX)^2 \ X^{-1} \ =\ \left [\int \left| \tilde s (u) \right|^{2} {\mathrm{d}} u \right]](../pages_traiter/equations_analyse-tf/equation32.png)
- Question 2
Aide :
Passer à la limite des grandes valeurs de 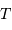 .
.
Solution :
Avec un signal purement sinusoïdal d'amplitude 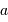 et de fréquence
et de fréquence 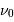 , la définition donne :
, la définition donne :
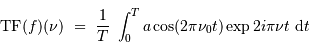
Pour 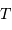 grand devant
grand devant 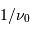 , si
, si 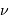 est différent de
est différent de 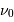 , l'intégrale tend vers 0, alors que pour
, l'intégrale tend vers 0, alors que pour 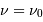 , on retrouve :
, on retrouve :
![\mathrm{TF} (f) (\nu_0) \ =\ {1\over T}\ \int_0^T {a\over 2} [\exp 2i\pi \nu_0 t + \exp -2i\pi \nu_0 t]\ \exp 2i\pi \nu_0 t \ {\mathrm{d}} t \ ={1\over T}\ \int_0^T {a\over 2} \ {\mathrm{d}} t \ = {a\over 2}](../pages_traiter/equations_analyse-tf/equation44.png)
Au facteur 1/2 près, dû au fait que la TF en 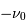 est également non nul,
la normalisation en
est également non nul,
la normalisation en 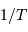 par rapport à la définition de la TF usuelle permet de retrouver dans le spectre l'amplitude du signal sinusoïdal.
par rapport à la définition de la TF usuelle permet de retrouver dans le spectre l'amplitude du signal sinusoïdal.
- Question 3
Aide :
Ecrire la relation de Parseval-Plancherel et faire le changement de variable de 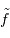 à
à 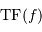 .
.
Solution :
Avec les notations analogues au cours 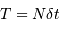 , et en tenant compte des propriétés de la TF, on a :
, et en tenant compte des propriétés de la TF, on a :
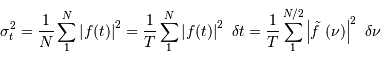
en se servant de la relation de Perseval, et du fait que l'énergie est rapportée sur 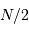 fréquences réelles entre les fréquences nulle et
fréquences réelles entre les fréquences nulle et 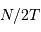 .
Avec le changement de notation :
.
Avec le changement de notation : 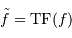 , et en tenant compte de
, et en tenant compte de 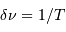 :
:
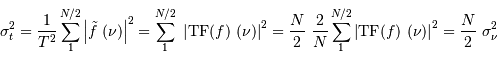
On en déduit :
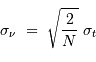
Le bruit dans le spectre de Fourier diminue comme la racine carrée du nombre de points de mesure.
pages_traiter/analyse-tf-signal-sexercer.html
Exercice
'Pulsation de coupure'
- Question 1
Aide :
Courage, ce n'est qu'un peu de calculs sur les sinus.
Aide :
Estimer 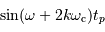 à une date
à une date 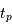 de l'échantillonnage
de l'échantillonnage
Aide :
Supposer 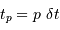
Solution :
On suppose, sans restreindre la généralité, que le signal est de forme sinusoïdale, et l'on choisit l'origine des temps de façon à avoir la p-ième date de l'échantillon vérifiant 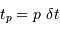 .
.
On en déduit :
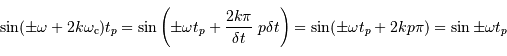
Au signe près, auquel n'est pas sensible le spectre de puissance (TF ),
cette égalité est assurée à toute date de l'échantillonnage.
),
cette égalité est assurée à toute date de l'échantillonnage.
- Question 2
Aide :
Jusqu'à quelle fréquence n'y aura-t-il pas de confusion?
Solution :
La 1ère confusion va apparaître pour les pulsations 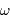 telles que
telles que
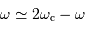 , càd bien-sûr juste au voisinage supérieur de la fréquence de coupure.
, càd bien-sûr juste au voisinage supérieur de la fréquence de coupure.
pages_traiter/analyse-tf-bruit-sexercer.html
Exercice
'Astérosismologie'
- Question 1
Aide :
L'incertitude en vitesse correspond à un niveau de bruit.
Aide :
Le niveau de bruit et le rapport signal à bruit sont simplement ... inversement proportionnels
Solution :
Le niveau de signal est inversement proportionnel au rapport signal à bruit.
La performance 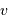 avec un rapport signal à bruit de 200 vérifie donc :
avec un rapport signal à bruit de 200 vérifie donc :
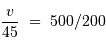
D'où le niveau de bruit : 110 cm/s.
- Question 2
Aide :
Le rapport signal à bruit évole comme la racine carrée du nombre de pose élémentaire,
Solution :
Le rapport signal à bruit évoluant comme la racine carrée du nombre 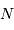 de pose élémentaire, ce dernier doit vérifier :
de pose élémentaire, ce dernier doit vérifier :
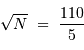
Soit 484 poses élémentaires de 3 minutes, soit environ 24 h de données. Elles ne pourront être atteintes qu'en 3 nuits environ.
- Question 3
Aide :
7 h font combien de minutes ?
Solution :
La nuit d'observation de 7 h comprend 420 poses élémentaires de 1 min. Le rapport signal à bruit évoluant comme la racine carrée du nombre de pose élémentaire, la performance en 1 min vaut :
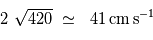



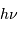 par photon est très faible dans le domaine radio.
par photon est très faible dans le domaine radio.
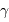 .
.








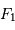 , transformant une onde plane en onde sphérique. L'hyperbole échange les 2 foyers
, transformant une onde plane en onde sphérique. L'hyperbole échange les 2 foyers 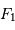 et
et 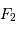 : l'onde sphérique converge alors en
: l'onde sphérique converge alors en 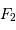 .
.





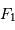 , transformant une onde plane en onde sphérique. L'hyperbole échange les 2 foyers
, transformant une onde plane en onde sphérique. L'hyperbole échange les 2 foyers 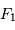 et
et 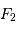 : l'onde sphérique converge alors en
: l'onde sphérique converge alors en 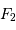 .
.







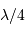 pour un dioptre usuel à
pour un dioptre usuel à 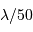 pour une optique d'interféromètre).
pour une optique d'interféromètre).




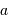 mesure le diamètre d'une sous-pupille,
mesure le diamètre d'une sous-pupille, 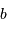 l'écartement entre 2 sous-pupilles et
l'écartement entre 2 sous-pupilles et 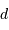 le diamètre total.
le diamètre total.

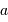 mesure le diamètre d'une sous-pupille ;
mesure le diamètre d'une sous-pupille ; 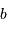 leur écartement.
leur écartement.
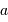 mesure le diamètre d'une sous-pupille ;
mesure le diamètre d'une sous-pupille ; 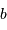 leur écartement.
leur écartement.
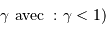 .
.
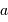 séparées d'une distance
séparées d'une distance 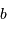 , s'étalant sur une longueur totale
, s'étalant sur une longueur totale 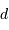 .
.
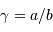 ?
?







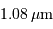 . Ce domaine spectral est sélectionné par un filtre étroit. Noter l'unité spectrale, inverse de la longueur d'onde.
. Ce domaine spectral est sélectionné par un filtre étroit. Noter l'unité spectrale, inverse de la longueur d'onde.





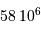
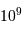
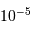
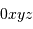 telle que le plan
telle que le plan 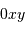 corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à
corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à 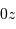 . On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
. On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
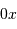 .
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe
.
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe 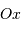 est inconnue, et que donc elle est
affublée d'une incertitude de position
est inconnue, et que donc elle est
affublée d'une incertitude de position 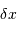 .
.
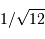 . En déduire
l'incertitude de mesure de la composant selon
. En déduire
l'incertitude de mesure de la composant selon 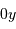 de la quantité
de mouvement du photon.
de la quantité
de mouvement du photon.
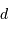 .
.
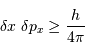
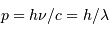 .
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
.
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
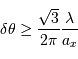
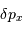 .
.
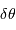 en fonction de
en fonction de 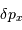 .
.
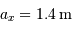 . Cela est-il
compatible avec les performances annoncées, de l'ordre de
. Cela est-il
compatible avec les performances annoncées, de l'ordre de 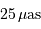 à la magnitude
à la magnitude 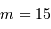 ? Pourquoi ?
? Pourquoi ?
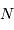 photons effectivement
détectés, l'incertitude est divisée par
photons effectivement
détectés, l'incertitude est divisée par 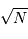 . Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
. Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.







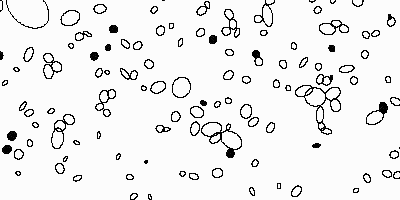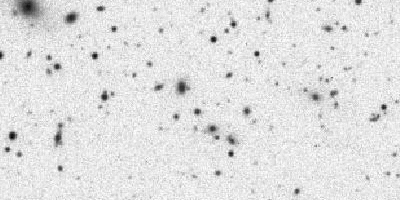



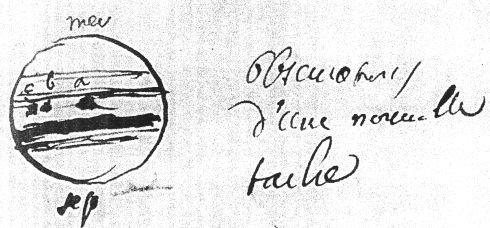

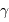 , la capacité d'imagerie des détecteurs est très limitée, et il est souvent difficile de bien localiser une source même intense. Du côté des très grandes longueurs d'onde, la tache d'Airy due à la diffraction peut atteindre une extension angulaire très grande ce qui limite la résolution spatiale.
, la capacité d'imagerie des détecteurs est très limitée, et il est souvent difficile de bien localiser une source même intense. Du côté des très grandes longueurs d'onde, la tache d'Airy due à la diffraction peut atteindre une extension angulaire très grande ce qui limite la résolution spatiale.


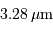 , alors que Io apparaît bien plus brillant à cette longueur d'onde.
, alors que Io apparaît bien plus brillant à cette longueur d'onde.


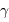 , X, visible, proche, moyen et lointain infrarouge, raie de
, X, visible, proche, moyen et lointain infrarouge, raie de 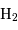 , H atomique, et radio.
, H atomique, et radio.






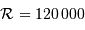 , en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une
, en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une 
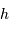 de 20 cm. Déterminer le grossissement
de 20 cm. Déterminer le grossissement 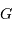 du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.

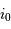 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 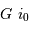 de l'angle dispersé.
de l'angle dispersé.
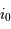 à celle de
à celle de 
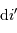 de l'angle de dispersion
de l'angle de dispersion 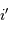 en fonction des variations de longueur d'onde
en fonction des variations de longueur d'onde 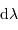 , du pas
, du pas 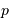 du réseau, et selon l'ordre d'interférence
du réseau, et selon l'ordre d'interférence 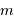 .
.
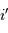 obéissant à :
obéissant à :
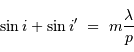
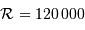 . Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
. Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
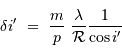
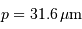 ,
, 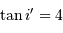 et un ordre d'interférence
et un ordre d'interférence 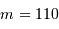 à
à 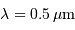 :
:
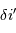 ,
, 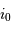 et le grossissement
et le grossissement 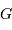 .
.
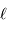 proposée et de l'angle
proposée et de l'angle 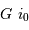 .
.







 2k (2000 fois 2000 pixels).
On note
2k (2000 fois 2000 pixels).
On note 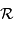 le pouvoir de résolution spectrale visé,
le pouvoir de résolution spectrale visé, 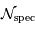 le nombre d'éléments spectraux correspondant,
le nombre d'éléments spectraux correspondant, 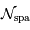 le nombre d'informations spatiales souhaité.
le nombre d'informations spatiales souhaité.
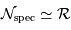 . On se place par la suite dans le cadre de cette hypothèse.
. On se place par la suite dans le cadre de cette hypothèse.
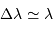 .
.
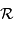 et
et 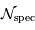 sont :
sont :
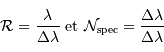
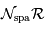 est nécessairement borné.
est nécessairement borné.
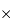 2k peut-il traiter?
2k peut-il traiter?
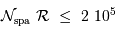



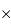 21 km
21 km






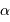 du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.
du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.

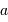 est en
est en 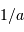 ; la tache image résultant de l'interférence sur la base
; la tache image résultant de l'interférence sur la base 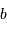 est en
est en 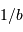 .
.


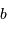 , la résolution angulaire de la tache image des faisceaux interférant à la longueur d'onde
, la résolution angulaire de la tache image des faisceaux interférant à la longueur d'onde 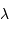 vaut
vaut 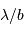 .
.
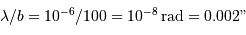 .
.
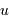 par rapport à l'image géométrique, il est utile de faire la correspondance entre la projection des lignes de bases de l'interféromètre, projetées sur le plan d'onde. Une configuration donnée, à une date donnée, va conduire à la mesure de la visibilité des franges d'interférences pour un vecteur angulaire donné
par rapport à l'image géométrique, il est utile de faire la correspondance entre la projection des lignes de bases de l'interféromètre, projetées sur le plan d'onde. Une configuration donnée, à une date donnée, va conduire à la mesure de la visibilité des franges d'interférences pour un vecteur angulaire donné 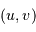 .
.


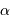 -Cen, située à 4.2 AL du Soleil, de rayon linéaire voisin de celui du soleil (750 000 km)?
-Cen, située à 4.2 AL du Soleil, de rayon linéaire voisin de celui du soleil (750 000 km)?
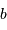 est nécessaire pour mesurer le diamètre d'une étoile de type analogue à
est nécessaire pour mesurer le diamètre d'une étoile de type analogue à 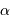 -Cen mais située à 10 pc, en faisant la mesure à une longueur d'onde de 1 micron ?
-Cen mais située à 10 pc, en faisant la mesure à une longueur d'onde de 1 micron ?
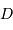 sur une base
sur une base 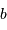 est définie par :
est définie par :





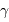 à radio auxquels s'intéressent les astrophysiciens. Les techniques de détection, tout comme les
détecteurs, sont évidemment bien différentes selon le domaine spectral.
à radio auxquels s'intéressent les astrophysiciens. Les techniques de détection, tout comme les
détecteurs, sont évidemment bien différentes selon le domaine spectral.


 4k pixels, les plus grands CCD actuels (2003) atteignant la taille 8k
4k pixels, les plus grands CCD actuels (2003) atteignant la taille 8k  8k pixels.
8k pixels.

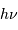 alors
qu'un détecteur cohérent voir le champ électromagnétique,
alors
qu'un détecteur cohérent voir le champ électromagnétique,
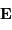 ou
ou 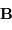 .
.
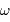 la pulsation du signal scientifique, et
la pulsation du signal scientifique, et 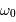 celle de la référence, cette dernière étant voisine de
celle de la référence, cette dernière étant voisine de 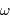 .
.
![\cos a \cos b = {1\over 2} \Bigl[ \cos (a+b) + \cos (a-b) \Bigr]](../pages_detecter/equations_detection-physique/equation7.png)
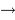 photo-électron s'appuie sur différents effets.
photo-électron s'appuie sur différents effets.
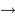 radio
radio
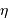 de création d'un photoélectron, souvent
appelée rendement quantique, dépend de différents paramètres, et
varie fortement avec la longueur d'onde :
de création d'un photoélectron, souvent
appelée rendement quantique, dépend de différents paramètres, et
varie fortement avec la longueur d'onde :
![\eta (\lambda) \ = \ (1-r) \ \varepsilon\ \bigl[1-\exp(-\alpha_\lambda \ell)\bigr]](../pages_detecter/equations_detection-quantique/equation4.png)
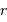
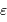
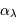
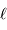
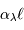 augmente, plus la probabilité d'absorption d'un photon est grande
augmente, plus la probabilité d'absorption d'un photon est grande








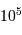 photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
photo-électrons par pixel, est que cette saturation est atteinte en environ 1 s pour une étoile de magnitude 0.
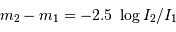
 4k.
Pour augmenter la capacité de détection, on pave le plan focal de plusieurs détecteurs, comme par exemple pour la
4k.
Pour augmenter la capacité de détection, on pave le plan focal de plusieurs détecteurs, comme par exemple pour la 
 256 px (dans l'infrarouge thermique) à 2k
256 px (dans l'infrarouge thermique) à 2k  4k pixels (dans le visible).
4k pixels (dans le visible).

 4.5k pixels. L'information d'un pixel est codé sur 16 bits. Le temps de lecture d'une image totale est de 30 secondes.
4.5k pixels. L'information d'un pixel est codé sur 16 bits. Le temps de lecture d'une image totale est de 30 secondes.

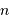 bits, ce qui permet de coder
bits, ce qui permet de coder 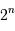 valeurs), peut rajouter du bruit au signal.
valeurs), peut rajouter du bruit au signal.


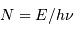 photons, la valeur moyenne
observée est
photons, la valeur moyenne
observée est 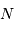 et la fluctuation
et la fluctuation 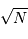 autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
autour de cette
valeur moyenne. Il s'ensuit un rapport signal à bruit déterminé
par le flux de photons égal à :
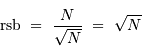
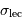 est de l'ordre de quelques photo-électrons par pixel
est de l'ordre de quelques photo-électrons par pixel
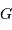 , dont la valeur n'est pas fixe mais sujette à différents bruits.
, dont la valeur n'est pas fixe mais sujette à différents bruits.
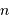 éléments d'information (bit), ce qui permet uniquement
éléments d'information (bit), ce qui permet uniquement 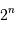 valeurs de codage.
valeurs de codage.
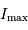 présentera, de par le codage sur
présentera, de par le codage sur 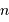 éléments d'information, une résolution minimale de
éléments d'information, une résolution minimale de 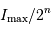 .
.
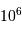
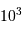
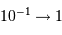


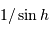 , avec
, avec 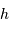 la hauteur sur l'horizon de l'objet visé)
la hauteur sur l'horizon de l'objet visé) 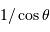 , l'angle
, l'angle 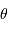 mesurant la distance angulaire entre le zénith et la direction de visée, est de la forme :
mesurant la distance angulaire entre le zénith et la direction de visée, est de la forme :
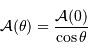








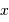 suit une loi de Poisson de moyenne
suit une loi de Poisson de moyenne 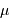 si la probabilité pour réaliser
si la probabilité pour réaliser 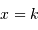 vaut
vaut 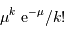
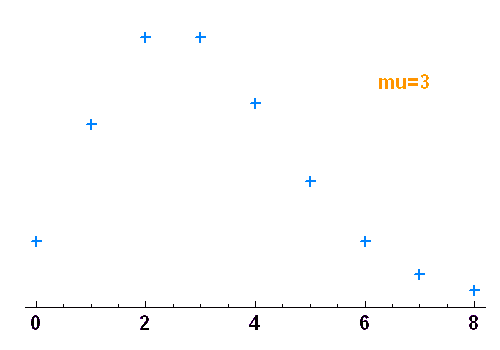
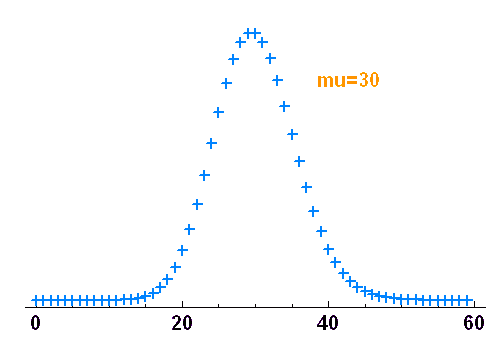





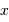 va être donnée par
va être donnée par 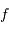 sa densité de probabilité, ou bien
sa densité de probabilité, ou bien 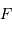 sa fonction de répartition
sa fonction de répartition 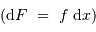 .
.
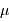 la moyenne et
la moyenne et 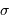 l'écart-type sont respectivement définis par :
l'écart-type sont respectivement définis par :
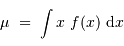
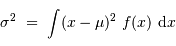
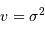 est la variance).
est la variance).


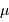 de la densité de probabilité de sa mesure
de la densité de probabilité de sa mesure 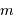 . Avec
. Avec 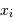 les réalisations d'une variable aléatoire, on a accès seulement à :
les réalisations d'une variable aléatoire, on a accès seulement à :
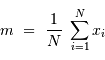
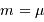 . En fait, c'est de mieux en mieux réalisé lorsque
. En fait, c'est de mieux en mieux réalisé lorsque 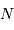 devient très grand.
devient très grand.
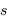 est mesurable par :
est mesurable par :
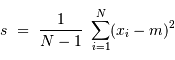
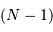 au dénominateur car
au dénominateur car 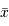 a déjà été obtenu à l'aide des
a déjà été obtenu à l'aide des 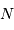 mesures, et il ne reste plus que
mesures, et il ne reste plus que 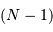 valeurs indépendantes pour estimer
valeurs indépendantes pour estimer 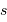 .
.
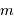 et
et 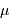 vaut typiquement
vaut typiquement 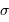 .
.

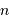 points obéissant à une loi normale de moyenne nulle et écart-type unité. Ce n'est qu'avec un très grand nombre de points que les réalisations représentent précisément la courbe théorique gaussienne.
points obéissant à une loi normale de moyenne nulle et écart-type unité. Ce n'est qu'avec un très grand nombre de points que les réalisations représentent précisément la courbe théorique gaussienne.

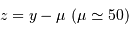 et puis
et puis 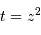 . L'ajustement donne un écart-type de 1.
. L'ajustement donne un écart-type de 1.

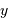 n'est pas uniforme autour d'une valeur moyenne, mais suis une relation linéaire. Il est nécessaire de soustraire la pente. On estime cette dernière avec l'appliquette, et on calcule alors la valeur centrée sur 0
n'est pas uniforme autour d'une valeur moyenne, mais suis une relation linéaire. Il est nécessaire de soustraire la pente. On estime cette dernière avec l'appliquette, et on calcule alors la valeur centrée sur 0 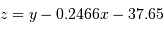 et puis
et puis 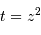 . L'ajustement donne un écart-type de 1.04.
. L'ajustement donne un écart-type de 1.04.

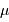 , et celle du bruit par l'écart-type
, et celle du bruit par l'écart-type 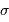 . Le rapport signal à bruit est donc :
. Le rapport signal à bruit est donc :
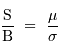
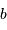 , il faut en tenir compte dans l'estimation de ce rapport, et retirer au préalable sa contribution :
, il faut en tenir compte dans l'estimation de ce rapport, et retirer au préalable sa contribution :
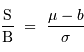
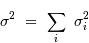
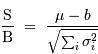


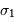 et
et 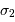 a un écart-type de :
a un écart-type de :
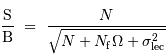
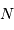 le nombre de photoélectrons reçus,
le nombre de photoélectrons reçus, 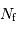 relié à un signal de fond,
relié à un signal de fond, 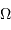 la taille angulaire de la cible, et
la taille angulaire de la cible, et 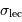 le bruit de lecture
le bruit de lecture
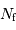 et à interpréter la somme du dénominateur.
et à interpréter la somme du dénominateur.
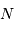 du rapport signal à bruit.
du rapport signal à bruit.
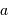 du collecteur ou le temps de pose
du collecteur ou le temps de pose 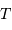 .
.

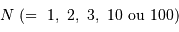 variables indépendantes, obéissant à une loi de distribution uniforme (entre 0 et 1). Lorsque
variables indépendantes, obéissant à une loi de distribution uniforme (entre 0 et 1). Lorsque 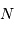 augmente, la distribution tend vers une loi gaussienne de moyenne
augmente, la distribution tend vers une loi gaussienne de moyenne 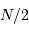 et écart type
et écart type 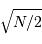 (courbe rouge). Pour
(courbe rouge). Pour 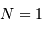 , la distribution reste bien sûr uniforme,
pour
, la distribution reste bien sûr uniforme,
pour 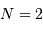 elle garde une allure triangulaire.
elle garde une allure triangulaire.

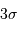

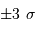 de la moyenne.
de la moyenne.
![f(x) \ = \ {1\over \sqrt{2\pi}\sigma}\ \exp \left[ -{(x-\mu)^2\over 2 \sigma^2} \right]](../pages_analyser/equations_bruit-gaussien/equation9.png)
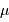 la moyenne et
la moyenne et 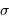 l'écart-type. Un tel bruit est dit gaussien.
l'écart-type. Un tel bruit est dit gaussien.
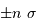 par rapport à la valeur moyenne décroît rapidement avec
par rapport à la valeur moyenne décroît rapidement avec 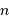 ;
99.7 % des réalisations du signal s'écartent de moins de
;
99.7 % des réalisations du signal s'écartent de moins de 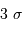 de la moyenne.
de la moyenne.
![[-n\ \sigma, \ n \ \sigma]](../pages_analyser/equations_bruit-gaussien/equation15.png) pour un bruit gaussien.
pour un bruit gaussien.
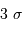 de la moyenne est sûrement dû à un signal et non à un bruit, et l'identifier comme tel ?
de la moyenne est sûrement dû à un signal et non à un bruit, et l'identifier comme tel ?


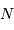 pas, il se sera éloigné du lampadaire d'une distance moyenne de
pas, il se sera éloigné du lampadaire d'une distance moyenne de 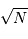 .
.

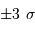 . On en déduit un niveau de bruit de l'ordre de 16/6=2.7. Le signal moyen étant d'environ 200, le rapport signal à bruit est voisin de 75.
. On en déduit un niveau de bruit de l'ordre de 16/6=2.7. Le signal moyen étant d'environ 200, le rapport signal à bruit est voisin de 75.

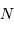 quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de
quanta par unité de temps est attendue, un détecteur idéal (rendement unité) en comptera un nombre plus ou moins voisin de 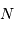 . La distribution des valeurs dépend du nombre N :
. La distribution des valeurs dépend du nombre N :
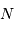 est grand, plus la
est grand, plus la 



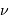 de luminosité
de luminosité 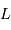 , observé pendant une durée
, observé pendant une durée 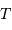 , apporte une énergie
, apporte une énergie 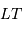 . Ce rayonnement est véhiculé par un nombre moyen de photons
. Ce rayonnement est véhiculé par un nombre moyen de photons 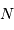 obéissant à :
obéissant à :
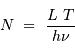
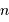 photons lorsque
photons lorsque 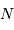 sont attendus en moyenne s'écrit :
sont attendus en moyenne s'écrit :
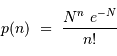
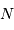 .
Il faut retenir que :
.
Il faut retenir que :
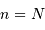 .
.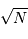 .
.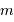 parties, suffisamment petites pour assurer qu'un seul photon peut arriver pendant l'intervalle de temps
parties, suffisamment petites pour assurer qu'un seul photon peut arriver pendant l'intervalle de temps 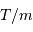 , on peut estimer la probabilité de voir arriver
, on peut estimer la probabilité de voir arriver 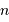 photons, en les rangeant dans les
photons, en les rangeant dans les 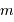 cases.
cases.
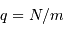 , et la probabilité opposée
, et la probabilité opposée 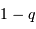 . Comme il y a
. Comme il y a 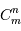 façons de ranger
façons de ranger 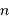 photons dans les
photons dans les 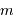 cases, on obtient finalement en développant le coefficient de combinaison :
cases, on obtient finalement en développant le coefficient de combinaison :
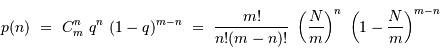
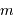 d'intervalles, on retrouve la loi énoncée :
d'intervalles, on retrouve la loi énoncée :
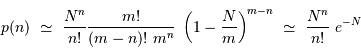
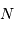 grand et
grand et 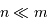 :
:
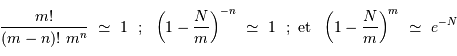
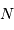 , on
, on ![p(n) \ \propto \ \exp \left[ - {(n-N)^2 \over 2 N}\right]](../pages_analyser/equations_bruit-poisson/equation32.png)
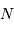 , l'écart-type vaut
, l'écart-type vaut 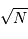 .
.
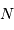 croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
croît, l'écart-type croît, mais le rapport écart-type/moyenne du signal décroît.
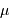 varie.
varie.



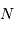 photons par intervalle de temps, la valeur moyenne observée est ...
photons par intervalle de temps, la valeur moyenne observée est ... 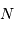 et sa fluctuation autour de cette valeur moyenne vaut
et sa fluctuation autour de cette valeur moyenne vaut 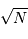 .
.
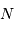 photons, est
photons, est 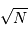 .
.
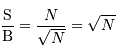
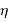 le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
le rendement, le nombre de photoélectrons détectés vaut en fonction du nombre de photons incidents sur le détecteur :
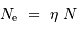
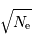 .
.
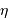 le rendement du détecteur. Le rapport signal à bruit varie comme
le rendement du détecteur. Le rapport signal à bruit varie comme 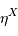 avec
avec 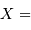 :
:
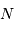 photons, le rapport signal à bruit du bruit de photons vaut
photons, le rapport signal à bruit du bruit de photons vaut 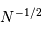 .
.
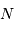 photons, on obtient seulement
photons, on obtient seulement 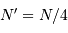 photoélectrons.
photoélectrons.



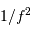 , càd un spectre de Fourier en
, càd un spectre de Fourier en 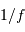 .
.

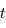 aura des conséquences à tout instant suivant.
aura des conséquences à tout instant suivant.
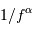 , l'exposant
, l'exposant 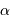 dépendant, phénoménologiquement, de la nature des corrélations au cours du temps.
dépendant, phénoménologiquement, de la nature des corrélations au cours du temps.


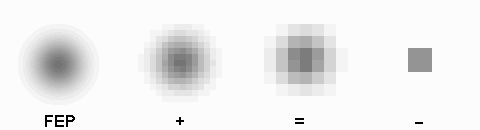

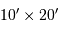 avec une résolution de 0.6",
il faut une caméra de taille (en pixels) :
avec une résolution de 0.6",
il faut une caméra de taille (en pixels) :
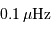 .
.

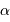 du Centaure.
du Centaure.

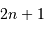 . Plus l'intervalle est grand, plus le filtrage est efficace.
. Plus l'intervalle est grand, plus le filtrage est efficace.


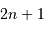 . Ce filtrage est efficace pour gommer les valeurs aberrantes.
. Ce filtrage est efficace pour gommer les valeurs aberrantes.




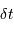 , filtre les fréquences temporelles plus rapides que
, filtre les fréquences temporelles plus rapides que 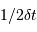 .
.
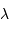 par une ouverture
par une ouverture 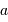 comme un filtrage des fréquences angulaires supérieures à
comme un filtrage des fréquences angulaires supérieures à 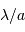 .
.




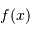 sa transformée~:
sa transformée~:
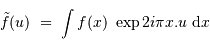
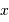 et
et 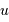 sont conjuguées. A la variable temporelle
sont conjuguées. A la variable temporelle 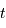 est associée la variable fréquentielle
est associée la variable fréquentielle 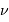 ; à la variable d'espace
; à la variable d'espace 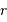 , la fréquence spatiale
, la fréquence spatiale 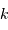 .
.
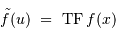 et
et
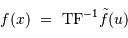 .
.
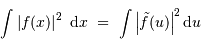
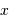
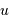
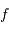
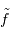
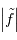
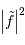
![[\mathrm{XY}]^2](../pages_traiter/equations_analyse-tf/equation18.png)
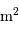
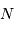 tel que
tel que 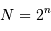 points, sinon le gain en temps est annulé, et la FFT peut
devenir
extrêmement lente si le nombre de points est premier, ou se
factorise avec de grands facteurs premiers.
points, sinon le gain en temps est annulé, et la FFT peut
devenir
extrêmement lente si le nombre de points est premier, ou se
factorise avec de grands facteurs premiers.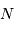 valeurs conduit à un spectre de
valeurs conduit à un spectre de 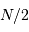 fréquences.
fréquences.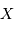 la dimension de la variable
la dimension de la variable 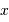 ,
, 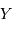 celle de la fonction
celle de la fonction 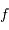 . Et en déduire les dimensions de
. Et en déduire les dimensions de 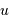 et
et 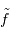
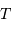 comme :
comme :
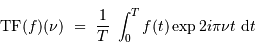
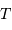 .
.
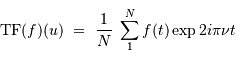
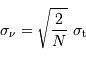
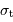 et
et 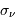 sont respectivement les écarts-types de la série temporelle et du spectre.
sont respectivement les écarts-types de la série temporelle et du spectre.
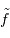 à
à 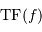 .
.


 Cen.
Cen.
 signaux, sur une durée totale
signaux, sur une durée totale  , l'analyse par transformée de Fourier se réécrit :
, l'analyse par transformée de Fourier se réécrit :
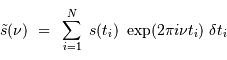
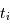 les dates individuelles et
les dates individuelles et 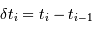 .
Si l'enregistrement est suffisamment régulier :
.
Si l'enregistrement est suffisamment régulier :
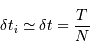
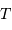 et
et 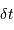 définissent les principales propriétés de l'analyse de Fourier.
définissent les principales propriétés de l'analyse de Fourier.
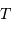 permet une résolution en fréquence
permet une résolution en fréquence 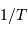 .
.
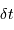 permet de suivre les fréquences jusqu'à la coupure
permet de suivre les fréquences jusqu'à la coupure 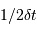 .
Le facteur 2 provient de la nécessité d'observer sur 2 mesures distinctes une demi-période négative et une demi-période positive.
.
Le facteur 2 provient de la nécessité d'observer sur 2 mesures distinctes une demi-période négative et une demi-période positive.
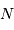 signaux, sur une durée totale
signaux, sur une durée totale 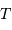 et avec un échantillonnage
et avec un échantillonnage 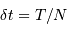 , on peut alors distinguer
sans ambiguïté
, on peut alors distinguer
sans ambiguïté 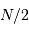 fréquences, entre
fréquences, entre 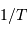 et
et 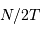 .
.


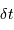 . On définit la pulsation
. On définit la pulsation 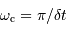 .
.
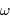 et
et
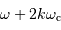 ou
ou 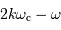 , où
, où 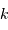 est un entier
est un entier
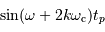 à une date
à une date 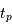 de l'échantillonnage
de l'échantillonnage
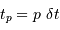



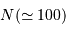 points dans l'échantillon, faire varier le niveau de bruit
points dans l'échantillon, faire varier le niveau de bruit 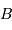 , et montrer que le signal est identifiable dans le spectre si son amplitude excède
largement
, et montrer que le signal est identifiable dans le spectre si son amplitude excède
largement 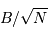 .
.
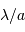 ; les
interférences entre les sous-faisceaux conduisent à une taille
angulaire
; les
interférences entre les sous-faisceaux conduisent à une taille
angulaire 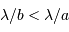 .
.
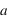 par
par 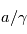 , c'est-à-dire, de façon équivalente, en remplaçant
, c'est-à-dire, de façon équivalente, en remplaçant 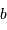 par
par 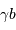 . Tout se passe comme si on avait un gruyère avec moins de trous.
. Tout se passe comme si on avait un gruyère avec moins de trous.

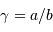 , tout se passe comme si l'on avait réuni des collecteurs de diamètre plus important et qu'il n'y avait plus de trous dans le miroir équivalent. La pupille a été densifiée.
, tout se passe comme si l'on avait réuni des collecteurs de diamètre plus important et qu'il n'y avait plus de trous dans le miroir équivalent. La pupille a été densifiée.
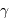 . Il en est de même du champ : le champ accessible par l'instrument a été réduit. Il y a toujours des compromis à faire.
. Il en est de même du champ : le champ accessible par l'instrument a été réduit. Il y a toujours des compromis à faire.
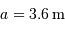 en un autre faisceau parallèle de diamètre
en un autre faisceau parallèle de diamètre 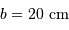 . Le grossissement doit donc vérifier :
. Le grossissement doit donc vérifier :
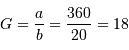
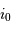 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 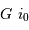 dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour
dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour 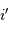 cette déviation
cette déviation 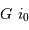 .
.
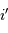 obéissant à :
obéissant à :
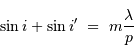
 fixée, la différentiation de la relation précédente donne :
fixée, la différentiation de la relation précédente donne :
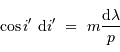
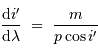
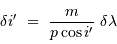
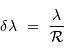
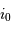 se traduisent par des variations de
se traduisent par des variations de 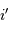 à hauteur de
à hauteur de 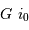 . On en déduit que les variations de l'angle
. On en déduit que les variations de l'angle 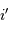 doivent être contraintes par :
doivent être contraintes par :
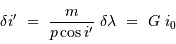
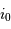 doit satisfaire :
doit satisfaire :
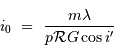
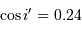 ) :
) :

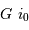 avec un bras de levier de longueur
avec un bras de levier de longueur 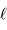 se traduit par une déviation linéaire
se traduit par une déviation linéaire 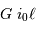 .
.
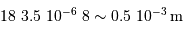 . Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.
. Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.
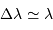 , on vérifie bien que
, on vérifie bien que
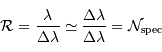
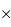 2k :
2k :
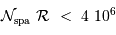
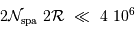
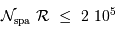
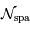 limité à :
limité à :
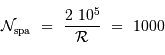
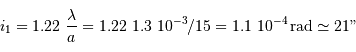
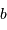 :
:
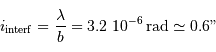
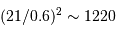 dans le second.
dans le second.
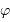 le déphasage inconnu à un instant de référence choisi comme origine, le produit des signaux est proportionnel à :
le déphasage inconnu à un instant de référence choisi comme origine, le produit des signaux est proportionnel à :
![\cos( \omega t +\varphi) \cos \omega_0 t = {1\over 2} \left[ \cos \bigl( (\omega+\omega_0) t + \varphi \bigr) + \cos \bigl( (\omega-\omega_0)t-\varphi \bigr) \right]](../pages_detecter/equations_detection-physique/equation9.png)
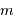 vaut
vaut 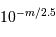 par rapport à celui d'une étoile de magnitude nulle.
par rapport à celui d'une étoile de magnitude nulle.
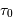 pour une magnitude nulle sera multipliée par
pour une magnitude nulle sera multipliée par 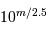 pour une magnitude
pour une magnitude 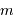 .
.
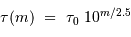
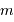 vérifiant
vérifiant
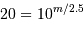 , càd
, càd 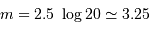 .
.
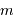 vérifiant
vérifiant
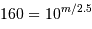 , càd
, càd 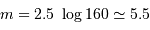 .
.
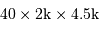 , soit 360 Mpx, d'où un taille de 720 Mo par image.
, soit 360 Mpx, d'où un taille de 720 Mo par image.
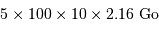 , soit 10.8 téraoctets.
, soit 10.8 téraoctets.
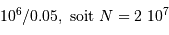 .
.
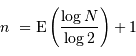
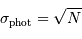 ,
,
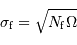 , avec
, avec 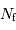 le nombre de photoélectrons par unité d'angle solide dus au fond,
le nombre de photoélectrons par unité d'angle solide dus au fond,
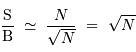
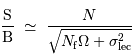
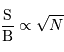 , dans l'autre
, dans l'autre 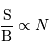 .
.
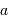 le diamètre du collecteur et
le diamètre du collecteur et 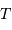 le temps de pose, il est immédiat que
le temps de pose, il est immédiat que 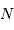 varie comme la surface collectrice
varie comme la surface collectrice 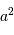 et comme
et comme 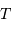 .
.
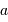
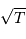
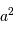
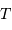
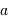 ou
ou 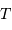 du rapport signal à bruit.
du rapport signal à bruit.
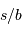 et la performance requise sont tous deux exprimés dans le même système d'unité relative. Le nombre
et la performance requise sont tous deux exprimés dans le même système d'unité relative. Le nombre 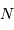 de photons doit donc vérifier :
de photons doit donc vérifier :
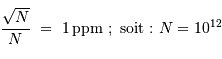
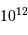 photons pour atteindre la sensibilité requise.
photons pour atteindre la sensibilité requise.
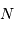 photons, on obtient seulement
photons, on obtient seulement 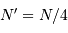 photoélectrons. L'égalité précédente doit donc être vérifiée par
photoélectrons. L'égalité précédente doit donc être vérifiée par 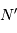 et non par
et non par 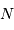 . Il faut donc collecter
. Il faut donc collecter 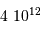 photons.
photons.
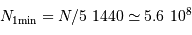
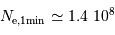 photo-électrons), la performance devient
photo-électrons), la performance devient 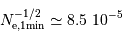 .
.
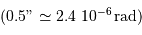 , la taille linéaire dans le plan focal est fixée :
, la taille linéaire dans le plan focal est fixée :
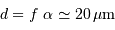
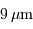 .
.
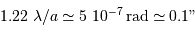 . Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.
. Le gain en résolution linéaire dans le plan focal est donc d'un facteur 5.
![[x] = X \mathrm{\ et\ } [f] = Y](../pages_traiter/equations_analyse-tf/equation30.png) , donc la définition de la TF donne :
, donc la définition de la TF donne :
![[u] = X^{-1} \hbox{ et } [\tilde f] = XY](../pages_traiter/equations_analyse-tf/equation31.png) .
.
![\left [\int \left| f (x) \right|^{2} \ {\mathrm{d}} x \right] \ =\ Y^2\ X \ =\ (YX)^2 \ X^{-1} \ =\ \left [\int \left| \tilde s (u) \right|^{2} {\mathrm{d}} u \right]](../pages_traiter/equations_analyse-tf/equation32.png)
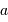 et de fréquence
et de fréquence 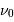 , la définition donne :
, la définition donne :
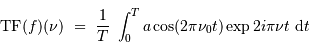
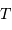 grand devant
grand devant 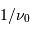 , si
, si 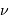 est différent de
est différent de 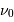 , l'intégrale tend vers 0, alors que pour
, l'intégrale tend vers 0, alors que pour 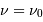 , on retrouve :
, on retrouve :
![\mathrm{TF} (f) (\nu_0) \ =\ {1\over T}\ \int_0^T {a\over 2} [\exp 2i\pi \nu_0 t + \exp -2i\pi \nu_0 t]\ \exp 2i\pi \nu_0 t \ {\mathrm{d}} t \ ={1\over T}\ \int_0^T {a\over 2} \ {\mathrm{d}} t \ = {a\over 2}](../pages_traiter/equations_analyse-tf/equation44.png)
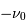 est également non nul,
la normalisation en
est également non nul,
la normalisation en 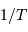 par rapport à la définition de la TF usuelle permet de retrouver dans le spectre l'amplitude du signal sinusoïdal.
par rapport à la définition de la TF usuelle permet de retrouver dans le spectre l'amplitude du signal sinusoïdal.
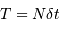 , et en tenant compte des propriétés de la TF, on a :
, et en tenant compte des propriétés de la TF, on a :
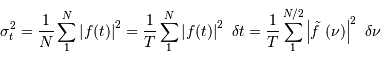
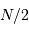 fréquences réelles entre les fréquences nulle et
fréquences réelles entre les fréquences nulle et 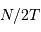 .
Avec le changement de notation :
.
Avec le changement de notation : 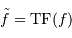 , et en tenant compte de
, et en tenant compte de 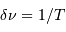 :
:
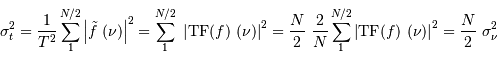
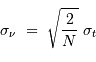
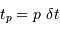 .
.
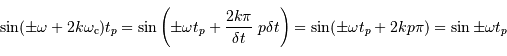
 ),
cette égalité est assurée à toute date de l'échantillonnage.
),
cette égalité est assurée à toute date de l'échantillonnage.
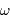 telles que
telles que
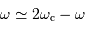 , càd bien-sûr juste au voisinage supérieur de la fréquence de coupure.
, càd bien-sûr juste au voisinage supérieur de la fréquence de coupure.
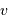 avec un rapport signal à bruit de 200 vérifie donc :
avec un rapport signal à bruit de 200 vérifie donc :
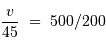
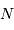 de pose élémentaire, ce dernier doit vérifier :
de pose élémentaire, ce dernier doit vérifier :