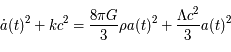Equation d'évolution du terme d'accroissement

Auteurs: Sylvain Fouquet, François Hammer

Les équations de Friedmann

Pour décrire le continuum espace-temps de l'univers, il suffit de connaître sa courbure 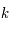et la fonction d'accroissement 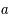qui définissent la métrique de l'univers. Ces deux quantités sont déduites des équations d'Einstein dans le cadre d'un univers isotrope et homogène. De plus, l'univers étant supposé être un fluide de masse volumique constante, l'énergie équivalente à sa densité de masse est donnée par 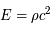$E = \rho c^2$ avec en plus une pression 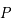. Les équations d'Einstein dans le cadre de la cosmologie furent obtenues dans les années 1920 par le mathématicien russe Alexandre Friedmann :

(a) 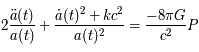$2\frac{\ddot{a}(t)}{a(t)} +\frac{\dot{a}(t)^2 + kc^2}{a(t)^2} = \frac{-8 \pi G}{c^2}P$

(b) 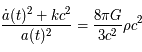$\frac{\dot{a}(t)^2+kc^2}{a(t)^2} = \frac{8 \pi G}{3c^2}\rho c^2$

où 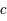est la vitesse de la lumière et 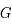la constante de la gravitation. Ces équations qui dépassent le cadre de ce cours sont seulement là pour illustrer le fait que seules les valeurs 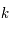de et de 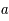sont inconnues dans ces équations. Des théorèmes mathématiques prouvent que ce système de deux équations à deux inconnues admet des solutions.

La constante cosmologique

Les équations d'Einstein ont la particularité qu'il est possible de leur ajouter une constante d'intégration, notée 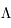$\Lambda$ . La valeur de cette constante peut avoir de grandes conséquences dans les propriétés de l'univers. Sa valeur n'a pas de réelle contrainte, si bien qu'elle peut être considérée comme un paramètre libre. Einstein, en son temps, l'avait utilisée pour faire de l'univers un univers statique. Aujourd'hui, cette constante sert à expliquer la possible accélération de l'univers. Dans le cadre de la cosmologie, les équations d'Einstein avec constante cosmologique deviennent :

(a) 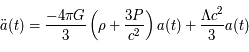$\ddot{a}(t)} = \frac{-4 \pi G}{3}\left(\rho + \frac{3P}{c^2}\right)a(t) + \frac{\Lambda c^2}{3}a(t)$

(b) $\dot{a}(t)^2+kc^2 = \frac{8 \pi G}{3}\rho a(t)^2 + \frac{\Lambda c^2}{3}a(t)^2$