Après avoir défini les concepts importants de l'évolution du continuum espace-temps, les sections qui suivent montrent des cas particuliers d'univers en fixant les paramètres cosmologiques et la constante de Hubble. Les premiers exemples d'univers sont uniquement constitués de matière. Le rayonnement est en effet négligeable durant la majeure partie de l'histoire de l'univers ; il ne joue un rôle important que pendant les premiers milliers d'années. De ce fait, l'évolution de l'univers est bien décrit même sans cette composante. La constante cosmologique,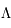 
, est supposée être nulle. Le paramètre de la courbure de l'espace se trouve donc être 
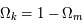< 1 car 
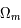est plus grand que 0. La constante de Hubble est prise valant 70 km.s-1.Mpc-1. Tous les paramètres sont alors connus, il est possible d'en déduire 
et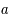 
.
L'évolution de l'univers prend trois formes différentes en fonction de la valeur de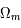 
. Si le paramètre de densité est plus grand que 1, donc si la densité de la matière est plus grande que la densité critique, alors 
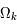est plus petit que 0 et après une phase d'expansion, l'univers s'effondrera sur lui même. La courbure de l'univers est alors positive et l'univers est fini. Si le paramètre de densité vaut 1, 
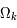= 0, l'univers est plat et l'expansion continue indéfiniment. Les galaxies s'éloigneront avec des vitesses de plus en plus faibles jusqu'à arriver à une vitesse quasi-nulle dans un temps infini. Le troisième cas offre un univers hyperbolique qui ne fera qu'enfler avec une vitesse d'expansion qui certes diminuera mais ne sera jamais nulle. Le graphique illustre les trois fonctions possibles pour le terme d'accroissement, 
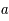. Seul le cas 
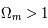admet pour un temps différent de 0 l'égalité suivante 
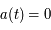. Cela représente une deuxième singularité appelé le Big Crunch.
