La métrique de l'univers

Auteurs: Sylvain Fouquet, François Hammer

Courbure de l'univers

Représentation des trois types de courbure de l'univers : plat, elliptique et hyperbolique.

Crédit : A. Füzfa (image de fond : Hubble Ultra-Deep Field, télescope spatial Hubble, NASA/ESA).

Le concept de métrique

Avant Einstein, l'espace de la physique classique était considéré comme statique et plat. Deux masses seules supposées sans interaction et sans vitesse relative, séparées dans l'espace, ne pouvaient ni s'éloigner ni se rapprocher. L'espace de la physique classique était aussi décorrélé du temps et comprenait trois dimensions. On pouvait lui joindre un repère cartésien pour donner à chaque point des coordonnées (x, y, z). 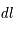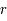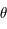Dans cet espace, la distance, , entre deux points très proches s'écrivait de la manière suivante en coordonnées cartésiennes (x, y, z) et sphériques (, $\theta$ , $\phi$ ) :

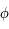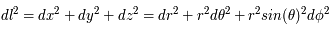
$dl^2 = dx^2 + dy^2 + dz^2 = dr^2 + r^2d\theta^2 + r^2sin(\theta)^2d\phi^2 \right)$

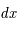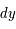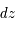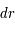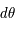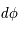où , et sont les différences de coordonnées en coordonnées cartésiennes et , $d\theta$ et $d\phi$ les différences de coordonnées en coordonnées sphériques entre les deux points. Ces deux relations sont ce que l'on appelle la métrique de l'univers dans les coordonnées cartésiennes ou sphériques car elles permettent de mesurer la distance entre deux points proches. Le temps quant à lui est séparé de l'espace et ne fait pas partie de la métrique ; il est absolu, peu importe votre référentiel pour décrire un événement, le temps de ce dernier sera toujours le même.

La relativité restreinte apporte un premier changement en mêlant espace et temps et définit pour cela une métrique en quatre dimensions notée 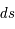. Entre deux événements E1(x1, y1, z1, t1) et E2(x2, y2, z2, t2) dans un espace à quatre dimensions, la distance est notée :

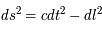ds^2 = cdt^2 - dl^2 , le même 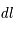qu'en physique Newtonienne, avec 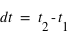dt = t_2-t_1 et 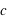étant la vitesse de la lumière.

Ce changement de définition de distance mêlant espace et temps, et surtout l'invariance de cette distance par changement de référentiel, provoque un grand changement conceptuel. L'espace et le temps sont maintenant liés et le temps perd son caractère absolu. Cette métrique de la relativité restreinte est appelée métrique de Minkowski, du nom du mathématicien Hermann Minkowski.

La métrique de notre univers

Avec la relativité générale, Einstein bouleverse encore les concepts d'espace-temps. Après avoir lié l'espace et le temps, Einstein le courbe. En effet, l'espace-temps euclidien est plat, i.e. il correspond à la géométrie euclidienne. Dans ce cas deux droites parallèles ne se croisent jamais, la somme des angles d'un triangle fait 180°, etc. Einstein comprend que la métrique de l'espace-temps n'est pas définie de manière absolue mais qu'elle dépend de la quantité de matière et de la distribution d'énergie dans l'univers. Plusieurs scientifiques, Friedmann, Lemaître, Robertson et Walker, ont aidé à la mise en place de la forme de la métrique de l'univers. En effet, le caractère isotrope et homogène de l'univers contraint la forme de sa métrique. Ainsi, la métrique déduite est appelée métrique FLWR et elle s'écrit sous la forme :

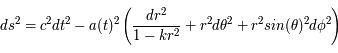
$ds^2 = c^2dt^2 - a(t)^2\left(\frac{dr^2}{1-kr^2} + r^2d\theta^2 + r^2sin(\theta)^2d\phi^2 \right)$

En comparant cette nouvelle métrique avec la métrique de la relativité restreinte, trois caractéristiques apparaissent. Premièrement, la partie temporelle ne change pas, cela implique que l'univers évolue de manière identique dans tout l'espace, c'est le principe d'équivalence temporelle. Deuxièmement, la constante 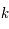peut pendre trois valeurs possibles, -1, 0 ou 1. En fonction de ces valeurs l'univers sera :

hyberbolique et infini (-1), décrit par la géométrie de Lobatchevski ;
plat et infini (0), décrit par la géométrie euclidienne ;
elliptique et refermé sur lui même donc fini (1), décrit par la géométrie de Riemann.

Troisièmement, cette nouvelle métrique a un terme d'accroissement 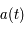a(t) . S'il augmente avec le temps, les distances sont dilatées, sinon elles sont compressées. Ce terme, s'il est constant avec le temps, traduit l'expansion de l'univers. La constante 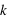et la fonction 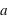doivent être déterminées par l'observation pour caractériser l'espace-temps de l'univers.