Exercice

Auteurs: Sylvain Fouquet, François Hammer

Auteur: Sylvain Fouquet

L'univers d'Einstein de Sitter

Cet exercice traite des particularités de l'univers d'Einstein-de Sitter. Bien que faux, cet univers est bien connu pour ses vertus pédagogiques ; en effet tout y est décrit analytiquement. Dans cet univers seule la matière courbe l'espace-temps, le rayonnement et la constante cosmologique sont supposés être nuls. Cet univers est de plus plat.

Question 1)

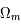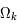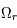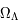Quelles sont les valeurs des quatre paramètres cosmologiques, $\Omega_m$ , $\Omega_k$ , $\Omega_r$ et $\Omega_\Lambda$ ?

Question 2)

Dans ce modèle 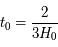$t_0 = \frac{2}{3 H_0}$ , quel est donc l'âge de l'univers ? Est-ce raisonnable ?

Question 3)

La densité vaut 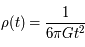$\rho(t) = \frac{1}{6\pi G t^2}$ . Que vaudrait-elle à présent et lorsque l'univers avait 380 000 ans ?

Question 4)

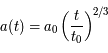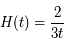Pour ce modèle, $a(t) = a_0\left(\frac{t}{t_0}\right)^{2/3}$ et $H(t) = \frac{2}{3t}$ . Est-ce cohérent avec un univers plat ? Comment seront distribuées les galaxies dans une époque très lointaine ?