Cinématique dans un univers relativiste

Auteurs: Sylvain Fouquet, François Hammer

Vitesse

La métrique de l'univers décrite précédemment conduit à des phénomènes inhabituels. Si deux masses sont supposées immobiles l'une par rapport à l'autre, leur distance relative peut tout de même changer. Elle augmente si l'univers est en expansion, elle diminue s'il se comprime. On peut ainsi définir une vitesse d'expansion. Cette vitesse n'en est pas réellement une car elle ne décrit pas le déplacement d'un objet dans l'espace au cours du temps mais le changement de l'espace lui même au cours du temps. La "vitesse d'expansion" entre deux points, distants d'une longueur 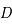, qui résulte de la métrique de l'univers, est donnée par la relation suivante :

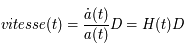$vitesse(t) = \frac{\dot{a}(t)}{a(t)}D = H(t)D$ qui est la forme générale de la Loi de Hubble (qui a été présentée au chapitre sur l'expansion de l'univers) pour un univers quelconque. Cette relation montre que la constante de Hubble n'en est pas réellement une. Actuellement, la constante de Hubble vaut près de 70 km.s^-1.Mpc^-1.

Accélération

Si nous suivons l'évolution entre deux masses sans interaction comment évoluera leur vitesse d'expansion ? Elle n'a pas de raison d'être constante car la distance entre les masses change ainsi que la valeur de 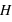avec le temps. Le terme d'accélération de l'expansion décrit ce changement de vitesse :

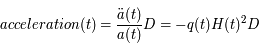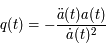
$acceleration(t) = \frac{\ddot{a}(t)}{a(t)}D = -q(t) H(t)^2D$ où $q(t) = -\frac{\ddot{a}(t)a(t)}{\dot{a}(t)^2}$

Le terme 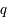(défini historiquement de la sorte) n'est pas directement l'accélération mais son signe indique s'il y a une accélération (négatif) ou une décélération (positif) car il est multiplié à un terme toujours positif 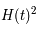H(t)^2 . Actuellement, ce terme semble être négatif et valoir -0,55 m/s². Son signe négatif implique que l'univers est en expansion accélérée.