L'astronomie s'intéresse au repérage des objets. Ce repérage dépend intimement du lieu d'observation, et son interprétation nécessite le plus souvent un changement de référentiel.

L'astronomie s'intéresse au repérage des objets. Ce repérage dépend intimement du lieu d'observation, et son interprétation nécessite le plus souvent un changement de référentiel.

Les observations du ciel sont effectuées, pour la plupart, depuis la Terre. Les mesures qui en résultent sont analysées, pour la plupart, dans un référentiel héliocentrique, le référentiel géocentrique n'offrant pas un cadre suffisamment galiléen (référentiel dans lequel un corps soumis à aucune force est en mouvement rectiligne uniforme) .
Les pages de cette section traitent des changements entre les différents référentiels utiles à l'astronomie et à l'astrophysique.
Passer des coordonnées équatoriales, données par les catalogues, aux coordonnées azimutales, liées au lieu d'observation.
En un lieu d'observation de latitude, 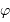 ,
les équations de passage des coordonnées équatoriales (ascension droite
,
les équations de passage des coordonnées équatoriales (ascension droite 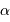 , déclinaison
, déclinaison 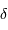 ) vers les coordonnées locales (azimut
) vers les coordonnées locales (azimut 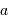 , hauteur
, hauteur 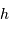 ) s'expriment par :
) s'expriment par :
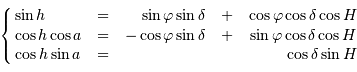
avec 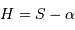 l'angle horaire,
l'angle horaire, 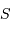 étant le temps sidéral.
étant le temps sidéral.
La visibilité d'un astre nécessite au moins 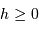 (astre au dessus de l'horizon), et en pratique
(astre au dessus de l'horizon), et en pratique 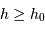 , la limite dépendant des contraintes d'observation.
, la limite dépendant des contraintes d'observation.
Les conditions posées sur l'angle horaire 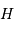 , et donc
, et donc 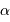 , sont estimées en exercice. Les équations précédentes montrent que le passage au méridien, l'altitude
, sont estimées en exercice. Les équations précédentes montrent que le passage au méridien, l'altitude 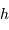 maximale, est atteint pour
maximale, est atteint pour 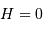 , càd
, càd 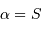 .
.
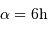 et déclinaison nulle à peu près toute la nuit (rappel :
et déclinaison nulle à peu près toute la nuit (rappel : 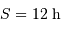 à l'équinoxe de printemps).
à l'équinoxe de printemps).
Difficulté : ☆ Temps : 40 min
D'après les équations de changement de système de coordonnées, un astre est levé si sa hauteur 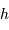 est positive, ce qui signifie :
est positive, ce qui signifie :
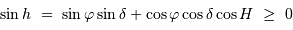
(voir la page cours pour le rappel de la définition des symboles).
Ceci conduit à une condition sur l'angle horaire :
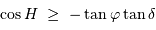
qui doit pouvoir être satisfaite.
Dans quel cas cette équation n'admet-elle jamais de solution ?
Dans quel cas cette équation admet-elle toujours une solution ?
Représenter, pour un lieu de latitude 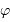 moyenne, un diagramme avec les étoiles circumpolaires (une étoile circumpolaire est suffisamment proche du pôle pour ne jamais descendre sous l'horizon) et les étoiles toujours invisibles.
moyenne, un diagramme avec les étoiles circumpolaires (une étoile circumpolaire est suffisamment proche du pôle pour ne jamais descendre sous l'horizon) et les étoiles toujours invisibles.
Un référentiel, c'est aussi une horloge. La période apparente d'un phénomène périodique dépend donc de cette horloge.
Changer de référentiel, c'est changer de point de vue !
Comme ici, les différents référentiels concernés s'appuyant sur la rotation de la Terre autour du Soleil, ou sur la rotation de la Terre sur elle-même ou sur les étoiles fixes, sont en rotation angulaire les uns par rapport aux autres, il est nécessaire de s'intéresser à la composition des vitesses angulaires.
Les mesures d'une vitesse angulaire exprimée dans deux référentiels différents 1 et 2, identifiées par les indices /1 et /2, vérifient la "relation de Chasles" :
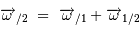
En considérant des mouvements de rotation coplanaires, l'égalité pour les périodes devient :
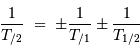
Les signes  dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
dépendent des sens respectifs des mouvements, selon que
l'entraînement, la rotation du référentiel 1 par rapport au référentiel 2, s'ajoute ou se retranche au mouvement du système considéré.
Dans les cas des référentiels terrestre tournant et sidéral, la rotation propre et la révolution étant le plus souvent sur des axes parallèles et dans le même sens, on a :
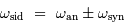
et donc :
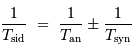
le signe 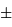 dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
dépendant de la planète considérée, d'orbite intérieure ou extérieure à la Terre.
Par exemple, on retrouve la relation entre le jour synodique moyen (temps qui sépare deux passages du Soleil au méridien) et le jour sidéral (temps pour que la Terre fasse un tour exact sur elle-même):
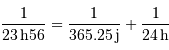
Ces 4 minutes de différence entre 23h56 et 24h00, en fait plutôt 3min56.3s, représente de l'ordre d'une fraction 1/365 de 24h.
A l'aide de l'appliquette, convertir les périodes sidérales des planètes (Tsid) en périodes synodiques (Tsyn).

L'évolution de Mercure a conduit à figer ses périodes de rotation propre et de révolution dans une résonance de type 3:2, ce qui signifie que Mercure accomplit, dans un référentiel sidéral, 3 rotations propres en 2 révolutions autour du Soleil.
Cette configuration particulière conduit, pour une hypothétique habitant mercurien (hermien), à des jours valant deux années mercuriennes (voir exercice), comme le montre l'animation.
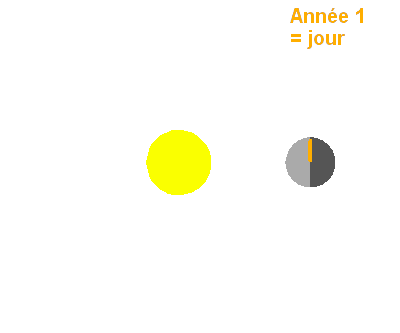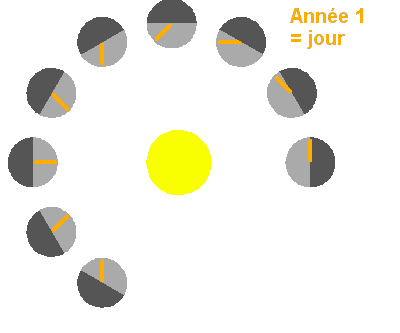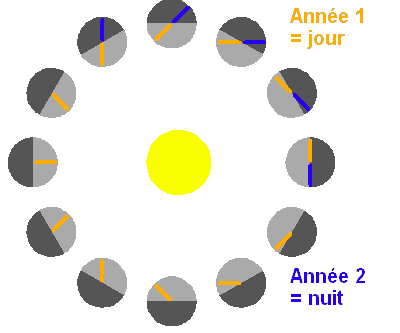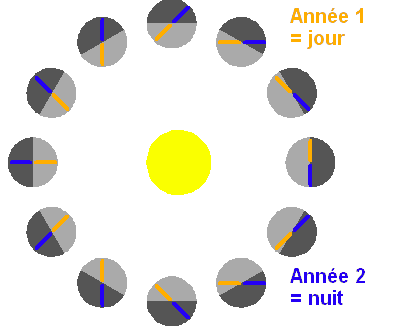
Difficulté : ☆ Temps : 20 min
Le tableau ci-joint donne les période de révolution sidérale des planètes du système solaire. On veut calculer leurs périodes de révolution synodiques.
| Planète | 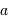 | 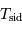 |
| UA | an | |
| Mercure | 0.3871 | 0.2408 |
| Vénus | 0.7233 | 0.6152 |
| Terre | 1.0000 | 1.0000 |
| Mars | 1.5237 | 1.8808 |
| Jupiter | 5.2026 | 11.862 |
| Saturne | 9.5547 | 29.457 |
| Uranus | 19.218 | 84.020 |
| Neptune | 30.109 | 164.77 |
Le cas des planètes internes (Mercure, Vénus) est-il analogue à celui des planètes externes?
Calculer les révolutions synodiques.
Pourquoi les périodes synodiques ci-dessus calculées tendent-elles vers un an lorsque l'on s'éloigne dans le système solaire ?
Difficulté : ☆☆☆ Temps : 20 min
En quelle durée le Soleil parcourt-il son diamètre, du fait de la rotation diurne ?
En quelle durée la Lune parcourt-elle son diamètre ?
Déterminer la durée moyenne d'une éclipse, entre les premier et dernier
contacts ? La période de révolution synodique de la Lune est de 29.5 j ; les premier et dernier contacts correspondent aux tout début et toute fin de l'éclipse (situation 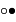 et
et  ).
).
Difficulté : ☆☆ Temps : 30 min
Déterminer la période sidérale de rotation, avec comme unité l'année hermienne sidérale.
Définir les référentiels d'étude, et l'entraînement angulaire de l'un par rapport à l'autre. Montrer alors que le jour hermien vaut 2 années sidérales.
Difficulté : ☆☆ Temps : 20 min
La période de révolution synodique de la Lune, durée s'écoulant entre deux nouvelles lunes, vaut 29 j 12 h 44 min.
Calculer la période de révolution sidérale de la Lune.
[2 points]
Déterminer l'intervalle de temps moyen entre 2 passages consécutifs de la Lune au méridien.
[2 points]
La coordonnée locale 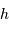 , la hauteur d'un astre, nous renseigne si un astre est levé
, la hauteur d'un astre, nous renseigne si un astre est levé
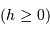 . L'angle horaire
. L'angle horaire 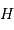 nous renseigne sur sa position par rapport au méridien (passage au méridien à
nous renseigne sur sa position par rapport au méridien (passage au méridien à 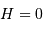 ).
).
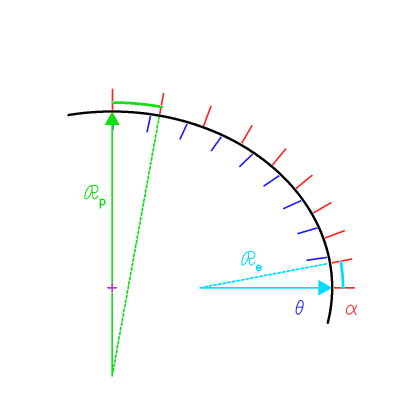
Le tracé de 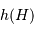 est utile pour estimer les conditions d'observations.
est utile pour estimer les conditions d'observations.
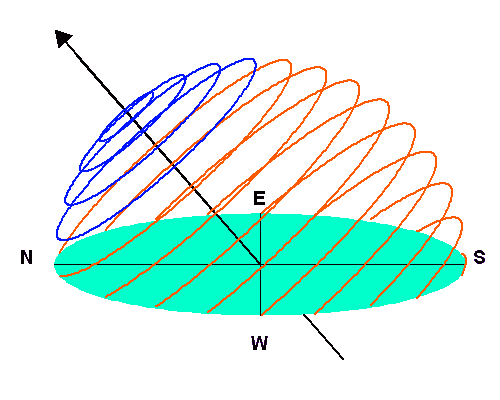
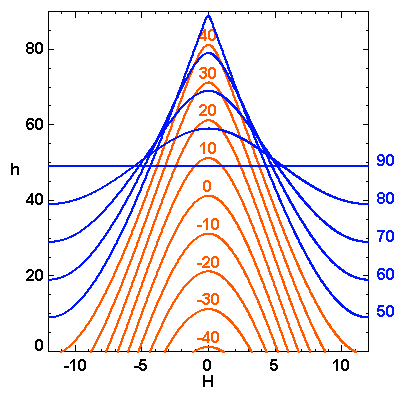
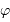 de Paris, de la hauteur
de Paris, de la hauteur 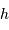 d'un astre, en fonction de l'angle horaire
d'un astre, en fonction de l'angle horaire 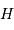 . En bleu : les astres toujours visibles, ou circumpolaires,
de déclinaison
. En bleu : les astres toujours visibles, ou circumpolaires,
de déclinaison 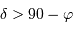 ; en rouge, ceux de déclinaison dans l'intervalle
; en rouge, ceux de déclinaison dans l'intervalle ![[\varphi-90,\ 90-\varphi]](../pages_referentiels/equations_pointer/equation10.png) , plus ou moins visibles selon l'angle horaire.
L'étoile polaire, quasi-immobile et de déclinaison proche de
, plus ou moins visibles selon l'angle horaire.
L'étoile polaire, quasi-immobile et de déclinaison proche de 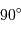 , garde bien sûr une hauteur quasi constante.
, garde bien sûr une hauteur quasi constante.
La hauteur 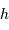 détermine si l'astre est levé, mais cela ne suffit pas pour
assurer la visibilité de l'objet : il faut que le soleil soit couché (sauf si c'est lui que l'on souhaite observer, évidemment).
détermine si l'astre est levé, mais cela ne suffit pas pour
assurer la visibilité de l'objet : il faut que le soleil soit couché (sauf si c'est lui que l'on souhaite observer, évidemment).
Cela dépend de l'ascension droite. Les éphémérides et logiciels de l'IMCCE permettent de calculer positions, visibilités...
Les objets internes du système solaire, Mercure et Vénus, mais aussi tout petit corps de périhélie inférieur à 1 UA, ne peuvent être visibles toute la nuit (le contraire signifierait que la Terre se situe entre eux et le Soleil, ce qui est contradictoire), ce qui réduit leur durée d'observation.
Ainsi, le coucher de Mercure suit de peu celui du Soleil.

Comment savoir si une étoile est visible ou non, et comment la pointer, càd diriger le télescope vers elle ? Cela dépend de ses coordonnées (ascension droite et déclinaison), mais aussi du lieu, de la date et de l'heure d'observation, comme cela a été montré aux pages traitant des coordonnées et du temps sidéral.
Observer un astre dans les meilleures conditions, c'est l'observer lorsqu'il passe au méridien à minuit, et donc lorsque son ascension droite vaut le temps sidéral de référence (Greenwich) à minuit.
Un paramètre couramment mesuré est la masse d'air, qui n'est pas une masse mais rend compte de l'épaisseur d'atmosphère traversée. C'est la tangente de la distance zénithale, distance angulaire séparant le zénith de l'altitude de l'objet.
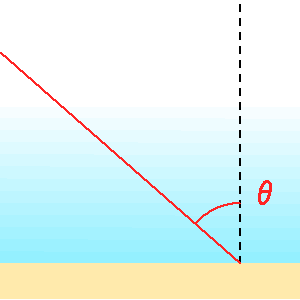
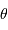 comme
comme 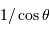 .
.
Difficulté : ☆ Temps : 20 min
Aller rechercher les coordonnées des planètes Vénus, Mars, Jupiter et Saturne sur le site de l'Institut de Mécanique Céleste (CNRS, Observatoire de Paris). Choisir l'objet, la date, et laisser de côté le reste des informations demandées.
Déterminer, pour 20h00 ce soir (heure locale), le temps sidéral (pour un observatoire de votre choix), à l'aide des données de site de l'Institut de Mécanique Céleste.
Quelles planètes seront visibles (s'il fait beau) ?
Difficulté : ☆☆ Temps : 15min
Pour une bonne qualité d'observations, on souhaite qu'une cible stellaire étudiée culmine à une hauteur supérieure à 60 deg. Quelle contrainte cela pose-t-il sur la cible, fonction de la latitude 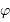 du lieu d'observation ?
du lieu d'observation ?
Interpréter le terme culmine.
Quelle contrainte cela pose-t-il sur la cible, fonction de la latitude du lieu d'observation ?
Difficulté : ☆☆☆ Temps : 40 min
Un programme d'observation à l'Observatoire de Paris, sur le campus de Meudon, comprend les cibles stellaires ci-jointes :
| nom | 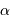 | 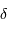 | sép. | 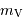 | remarque |
| (h, min) | (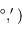 | (") | |||
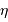 Cas Cas | 00 49.1 | 57 49 | 12.2 | 3.4, 7.5 | |
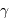 Ari Ari | 01 53.5 | 19 18 | 7.8 | 4.8, 4.8 | |
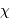 Tau Tau | 04 22.6 | 25 38 | 19.4 | 5.5, 7.6 | |
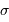 Ori Ori | 05 38.7 | -02 37 | 12.9,43 | 4,7,7.5 | quadruple en fait |
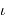 Cnc Cnc | 08 46.7 | 28 45 | 30.7 | 4.4, 6.5 | |
| 38 Lyn | 09 18.8 | 36 48 | 2.7 | 3.9, 6.6 |
Vers quelle date va-t-on pouvoir observer dans la même nuit chacune de ces cibles, dans des conditions optimales, en première partie de nuit vers 22h00 heure locale?
[2 points]
On souhaite passer 1/2 h par cible. Dans quel ordre les cibles devront-elles être observées ?
[1 points]
Pour éviter un premier quartier de Lune et tester une webcam sur la cible
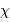 Tau, des observations en fin de nuit (4h heure locale) se sont imposées : vers quelle date l'observation a-t-elle été menée, alors que
Tau, des observations en fin de nuit (4h heure locale) se sont imposées : vers quelle date l'observation a-t-elle été menée, alors que 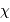 Tau culminait ?
Tau culminait ?
[1 points]
Ces pages permettent de faire le lien entre 2 étapes caractéristiques de la démarche scientifique : dans un cadre donné (p.ex. lié à la Terre entraînée autour du Soleil) mener des observations ou rendre compte de phénomènes ; puis énoncer ou valider une loi physique dans un cadre général (p.ex. dans le référentiel héliocentrique).
Les points techniques associés aux changements de référentiel ne doivent pas rebuter ; ce ne sont que des points techniques. Il existe d'ailleurs de nombreux outils qui permettent de se faciliter la tâche. Voir par exemple le serveur d'éphémérides de l'ESO (par exemple pour les étoiles), ou bien celui de l'IMCCE (par exemple pour les objets du système solaire).
Les alignements d'objet, au-delà de leur côté parfois spectaculaires, apportent des mesures inédites, précieuses pour l'astrométrie.
Cette section traite ainsi des éclipses, occultations et transits, dans l'optique (réductrice) de faire le lien entre ces phénomènes et diverses mesures de distances, de longueur ou de position.

Une éclipse totale de soleil est un événement très ponctuel géographiquement et temporellement, donc exceptionnel.
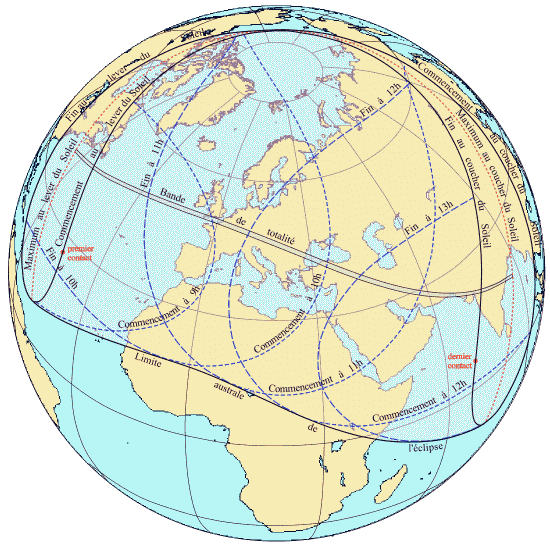
La prédiction précise des éclipses est un exercice difficile, maîtrisé par un nombre restreint d'instituts dans le monde, qui relève de la métrologie du temps et de l'espace la plus poussée.
Voir les pages de l'IMCCE.
Difficulté : ☆ Temps : 30
La durée de la rotation de la Terre est très proche de 86400 secondes (24 heures), mais sa valeur exacte est variable dans le temps. Le frottement provoqué par des effets de marées est à l'orgine d'un très lent ralentissement (de l'ordre de quelques millisecondes par siècle). Cela paraît peu, mais cumulé sur une période longue, il en resulte un décalage important.
Un des meilleurs moyens de mesurer cette variation consiste en l'étude d'observations historiques d'éclipses. Le décalage temporel (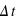 ) du moment précis d'une éclipse dû au ralentissement de la rotation de la Terre peut atteindre plusieurs heures! On trouve la relation mathématique suivante :
) du moment précis d'une éclipse dû au ralentissement de la rotation de la Terre peut atteindre plusieurs heures! On trouve la relation mathématique suivante :
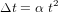 .
Ici,
.
Ici,  est la date de l'événement (compté en siècles avant 1820), et
est la date de l'événement (compté en siècles avant 1820), et  est mesuré en s par siecle2.
est mesuré en s par siecle2.
Un texte babylonien conservé au British Museum à Londres décrit une éclipse solaire totale, observée à Babylone le 15 avril de l'an 136 avant notre ère. En comparant l'heure de début et de fin décrits dans ce texte à un calcul des positions de la Terre et du Soleil, on trouve pour
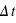 une valeur entre 11200 et 12150 secondes. Déduisez-en la valeur de la constante
une valeur entre 11200 et 12150 secondes. Déduisez-en la valeur de la constante 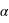 ainsi que son incertitude!
ainsi que son incertitude!
[ points]
Un autre texte décrit une observation d'une éclipse totale, en Mésopotamie, il y a 40 siècles. A priori, l'observation état plus ancienne ( plus élevé), on pourrait espérer avoir une mesure plus précise de la valeur de
plus élevé), on pourrait espérer avoir une mesure plus précise de la valeur de 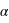 et du coup de mieux caractériser la rotation de la Terre.
et du coup de mieux caractériser la rotation de la Terre.
Le problème est que, dans ce cas, le texte ne mentionne pas le lieu d'observation. L'incertitude spatiale est de l'ordre de 1000 km le long de la bande de totalité, quasiment parallèle au parallèle de latitude 35 deg. Traduire l'incertitude spatiale en incertitude temporelle. Calculez aussi l'incertitude sur 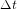 qui résulte de l'incertitude sur
qui résulte de l'incertitude sur  calculée à l'exercice précédent (1 s/siècle2).
calculée à l'exercice précédent (1 s/siècle2).
La date précise de l'éclipse est connue, par la mécanique céleste, plus précisement que la rotation de la Terre. Cette éclipse permet-elle de préciser la rotation de la Terre ?
Lorsque qu'un objet du système solaire entouré d'une atmosphère occulte une étoile, la haute atmosphère joue le rôle de lentille. La phase d'extinction présente des fluctuations d'intensité, reliées à la stratification des couches atmosphériques.
L'observation de l'occultation sur plusieurs sites permet de déterminer les positions et longueurs des diverses cordes correspondant aux conditions locales d'observation de l'occultation. On en déduit la taille et la forme de l'objet occultant.
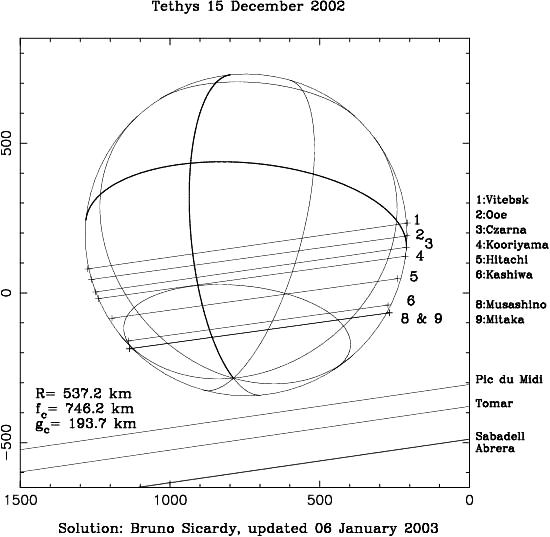
Montrer comment une occultation conduit, entre autres, à des mesures inaccessibles par ailleurs : taille et forme de l'objet occultant, sondage de son atmosphère...
Les occultations stellaires sont des phénomènes rares qui mettent en jeu le passage d'une planète ou d'un satellite devant une étoile. Pendant quelques minutes, il est alors possible de sonder avec une très grande précision l'atmosphère du corps, s'il en possède une, de détecter ses anneaux éventuels, ou de mesurer sa taille avec une précision kilométrique.
Une occultation, comme une éclipse, se caractérise par une ombre et une pénombre. La durée de l'ombre dépend essentiellement de la taille de l'objet du système solaire.
La durée de la pénombre dépend du diamètre stellaire (voir en exercice le principe de la mesure, et les échelles de temps associées). Il s'agit là d'une mesure très simple d'une grandeur par ailleurs inaccessible sans interférométrie.
La taille finie, non nulle, de l'étoile occultée implique une phase de pénombre, durant laquelle le disque stellaire disparaît ou réapparaît peu à peu.

Difficulté : ☆ Temps : 45 min
On cherche à estimer le diamètre angulaire d'une étoile occultée par un astéroïde.
On note 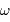 la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire,
la vitesse angulaire de déplacement sur le ciel de l'objet du système solaire, 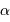 son diamètre angulaire,
son diamètre angulaire, 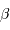 celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
celui de l'étoile. On suppose l'occultation centrale (l'étoile, l'objet occultant et la Terre parfaitement alignés au centre de l'occultation).
Dans une 1er temps, on fait l'hypothèse que le diamètre angulaire de l'étoile est négligeable. Déterminer la durée 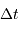 de l'occultation.
de l'occultation.
On ne suppose plus 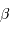 nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates
nul. Déterminer la durée des phases d'ombres et de pénombre. Déterminer les dates 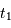 ...
... 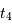 des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
des premier contact, début puis fin de la totalité, dernier contact, en les repérant par rapport à la centralité.
Tracer l'allure de la courbe d'occultation.
A quelle condition peut-on mesurer les diamètres angulaire et linéaire de l'objet, de l'étoile ?
Les objets du système solaire ont typiquement une vitesse angulaire, notée en "/h, de 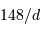 , avec
, avec 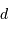 leur distance au soleil exprimée en UA.
La distance
leur distance au soleil exprimée en UA.
La distance 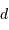 a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
a été mesurée à 9.6 UA ; en déduire le rayon de l'objet pour un transit de durée moyenne (repérée par la mi-occultation) de T=12 s.
Chaque phase de pénombre a duré 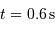 . En déduire le diamètre stellaire, l'étoile étant à
. En déduire le diamètre stellaire, l'étoile étant à 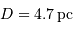 . Comparer le rayon stellaire calculé au rayon solaire.
. Comparer le rayon stellaire calculé au rayon solaire.
Les transits sont des phénomènes rares et localisés. Les observer a longtemps relevé du défi scientifique.
Un transit apparaît simplement comme une ombre chinoise.

La superposition de plusieurs clichés trace la trajectoire - une corde - du transit.

Les dernièrs transits de Mercure visible de la Terre ont eu lieu en mai 2016 et en novembre 2019. Les suivants auront lieu en 2032 et 2039.
Vénus étant plus grande et plus proche de la Terre, son ombre apparaît bien plus importante sur le Soleil. L'inclinaison des orbites de Vénus et de la Terre conduit à un nombre très limité de transits. Les derniers transits de Venus ont eu lieu en 2004 et 2012. Pour les prochains, il faudra être patient : ce ne sera que en 2117 et 2125!

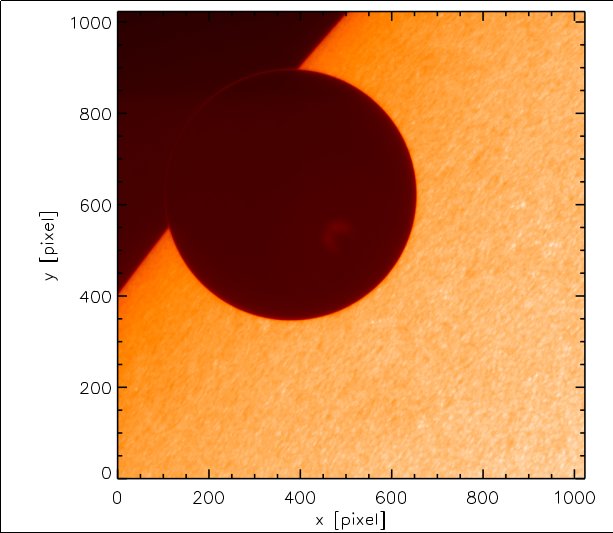
On parle de transits lorsque Mercure ou Vénus passent devant le disque du soleil. Ces événements sont, comme les éclipses, rares mais instructifs.
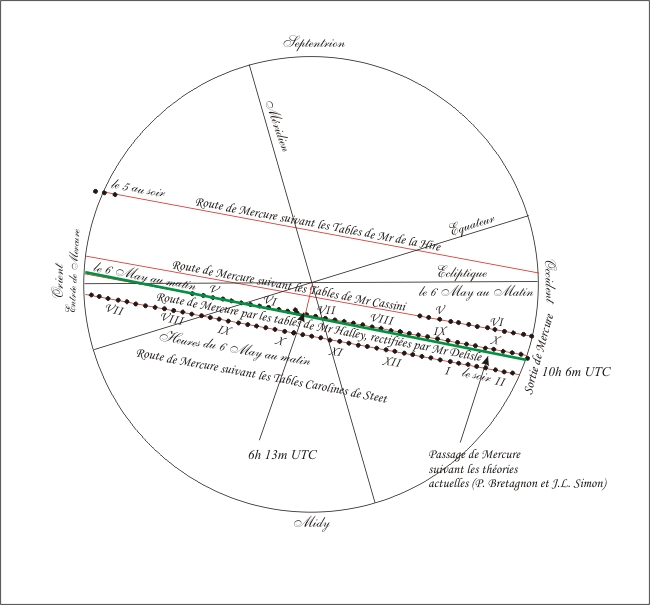
Historiquement, les transits de Mercure et Vénus ont permis la mesure de l'unité astronomique.
La trace du disque planétaire sur le disque solaire est une simple projection. Il s'ensuit que différents observateurs verront des traces différentes, mais parallèles entre elles, évoluant à la même vitesse angulaire. La différence entre les dates des premier et dernier contacts est proportionnelle à la longueur de la corde parcourue sur le disque.
Les transits ont permis la mesure de l'unité astronomique, comme l'a proposé l'astronome Halley. En effet, si la 3e loi de Kepler permet de figer le rapport entre les demi-grands axes de Vénus et de la Terre, elle ne permet pas d'en donner une mesure absolue.
Plutôt que de longs calculs, une animation montre le principe de la mesure.
Le point de vue de 2 observateurs différents permet de mettre en oeuvre le principe de mesure de distance par triangulation .

La valeur de l'UA a pu être déterminée à partir de différentes observations d'un même transit. Les observables indépendantes sont :
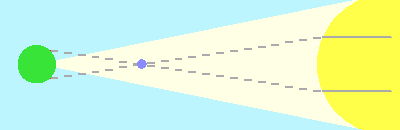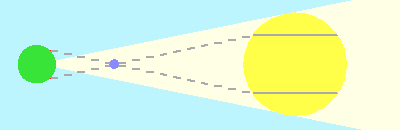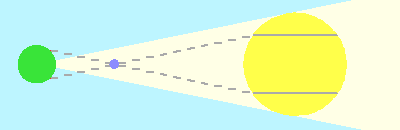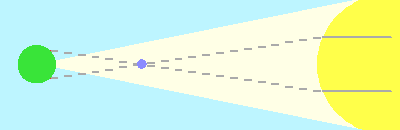
L'écartement des cordes tracées par les ombres est d'autant plus grand que la distance terre-soleil est petite. La mesure de cet écartement (repéré par les dates des début et fin de transit à une époque où la photographie n'existait pas) permet de mesurer l'unité astronomique.
Lorsque la distance Terre-Soleil, inconnue a priori, notée A, croît :
Difficulté : ☆☆ Temps : 30
Déterminer la période de révolution synodique de Vénus. En déduire sa vitesse angulaire synodique autour du Soleil, puis sa vitesse linéaire synodique 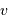 .
.
[3 points]
Quelle distance 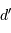 Vénus doit-elle parcourir sur son orbite pour un transit total le long du diamètre solaire
Vénus doit-elle parcourir sur son orbite pour un transit total le long du diamètre solaire 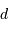 . En déduire la durée maximale d'un transit.
. En déduire la durée maximale d'un transit.
[2 points]
Estimer l'ordre de grandeur de la différence angulaire entre les traces de Vénus lors du transit du 8 juin 2004, pour 2 observateurs (l'un à Lille, l'autre à Perpignan, villes séparées de 1000 km).
[2 points]
Le transit dure 5h24min28s à Lille, et 5h24min58s à Perpignan. Situer schématiquement l'allure des cordes correspondant au transit vues de Lille ou Perpignan : passent-elles proche d'un pôle (lequel ?) ou plutôt par l'équateur.
[2 points]
Au-delà de l'aspect événementiel, éclipses, occultations et transits sont des phénomènes scientifiques utiles et utilisés en astrophysiques. Ils permettent, comme on l'a vu, des mesures astrométriques extrêmement précises.
Ouverture sur ce sujet : l'observation et l'étude des phénomènes mutuels de Jupiter et Saturne, menées à l'IMCCE.
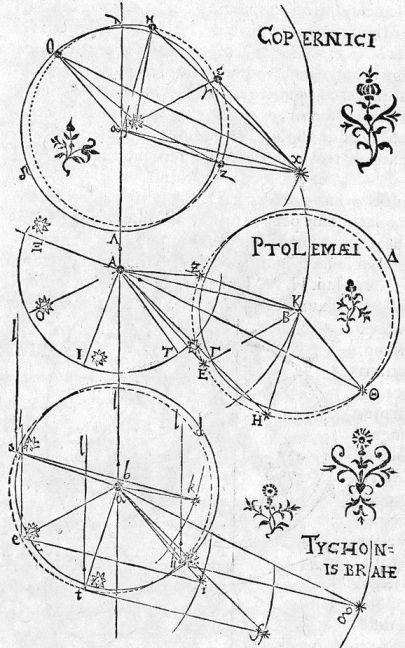
Les unités définies dans les chapitres précédents reposent sur l'observation de phénomènes périodiques, par rotation (l'année, la circonférence de la Terre...). Mais en fait, si l'on scrute ces phénomènes plus précisément, leur définition se doit d'être approfondie.
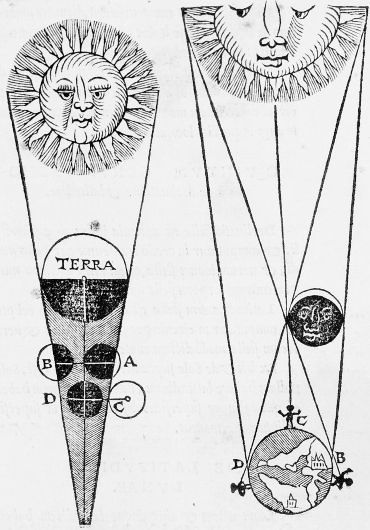
La définition du jour est basée sur la rotation de la Terre, et mesurée par le passage au méridien du soleil, qui définit un intervalle de temps de 24 heures. Et pourtant !
Si l'on repère chaque jour le passage au méridien du soleil, et que l'on repère cet instant par rapport à une valeur moyenne, on note au fil de l'année une modulation. Midi arrive en avance ou en retard, avec une amplitude de l'ordre d'un quart d'heure au plus, due à la variation du mouvement annuel de la Terre autour du Soleil. Cette modulation peut être observée à toute heure.

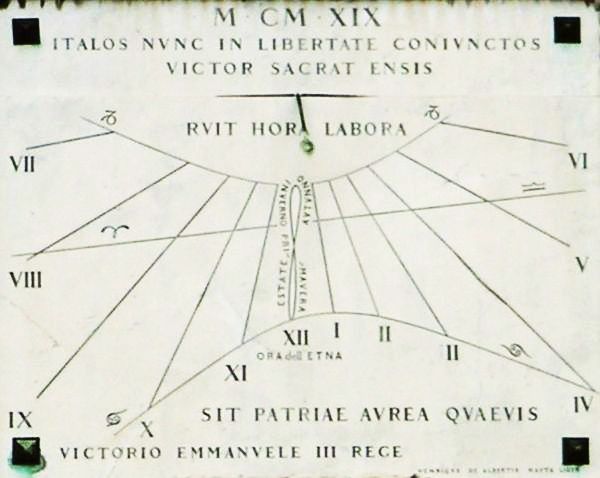
L'équation du temps correspondant à un déphasage entre midi solaire et midi local moyen, les lever et coucher du soleil sont également déphasés. Ceci est particulièrement sensible au voisinage d'un solstice. Ce n'est pas pile au solstice d'été (d'hiver) que le soleil se lève le plus tôt (tard) et se couche le plus tard (tôt)... mais c'est bien aux solstices que la durée du jour est extrêmale.
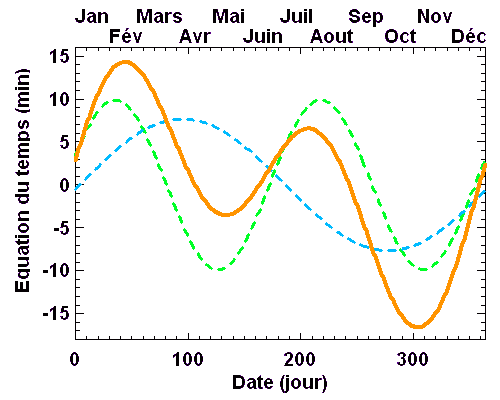
Les 24 heures séparant deux midis solaires dépendent de la rotation propre de la Terre. Comme son orbite n'est pas circulaire, l'entraînement n'est pas régulier (cf. 2ème loi de Kepler).
Il s'ensuit un phénomène appelé équation du temps : midi n'arrive pas à midi régulièrement.
Les étoiles n'ont pas la réputation d'être volages, et pourtant on voit dans la littérature des coordonnées différentes pour un même objet, repérées par des dates différentes.
Des époques standard ont été définies, pour s'y retrouver.
C'est la précession de l'axe polaire qui explique la majeure part des dérives repérées.


L'orbite de la Terre n'est ni circulaire, ni rigoureusement elliptique (malgré ce que nous a appris Newton).
L'axe de rotation de la Terre n'est pas fixe, mais animé d'un mouvement de précession (de période 26000 ans), car il
évolue sous l'effet de termes gravitationnels non inclus dans le problème à 2 corps, dus par exemple au fait que la Terre n'est pas un point matériel. Il s'ensuit que
les coordonnées angulaires d'un astre évoluent dans le temps. Elles sont données pour une époque de référence (p.ex. 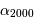 ,
, 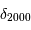 ).
).
| Epoque | 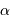 | 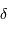 |
| 1950 | 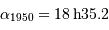 | 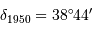 |
| 2000 | 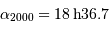 | 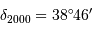 |
Coordonnées aux époques 1950 et 2000 de l'étoile Véga.
Il s'ensuit diverses définitions de l'année, selon que l'on se réfère à l'intervalle de temps entre 2 solstices, 2 périhélies, 2 passages au point vernal.
On définit ainsi des années de durées légèrement différentes. Pour plus de précision, voir le site de l'Institut de Mécanique Céleste
Les coordonnées polaires, c'est simple a priori. Sauf que faire les mesures à partir de la surface de la Terre, et non du centre, change le point de vue. La Terre n'étant pas ronde, la définition des coordonnées angulaires par rapport à la verticale locale ne coincide pas avec une définition centrale.
Difficulté : ☆☆ Temps : 30 min
Au milieu du XVIIIe siècle, les missions de La Condamine au Pérou et de Maupertuis au Laponie ont conduit à la mesure de la longueur d'un degré du méridien en Laponie (aux alentours de la latitude 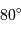 ) ainsi qu'au Pérou (vers
) ainsi qu'au Pérou (vers 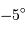 ). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
Expliquer pourquoi la longueur d'un degré le long du méridien diffère entre ces 2 régions. Faire un schéma.
La Terre étant aplatie aux pôles, le rayon de courbure local est-il plus important au pôle ou à l'équateur ? Quel degré de méridien correspond à la plus grande longueur ?
La longueur 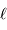 d'un arc de méridien d'ouverture
d'un arc de méridien d'ouverture 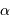 s'écrit en fonction du rayon de courbure
s'écrit en fonction du rayon de courbure 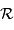 :
:
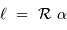
En représentation paramétrique, on repère un point de l'ellipse de révolution par
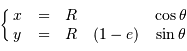
avec 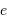 le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en
le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en 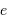 :
:
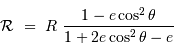
[on peut retrouver ce résultat en appliquant la définition : 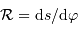 , avec
, avec 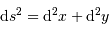 et
et 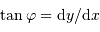 ].
].
Les mesures pour tourner de 1 degré donnant respectivement 57395 toises en Laponie, et 56735 toises au Pérou (57097 au sud de Paris), en déduire un ordre de grandeur de l'aplatissement de la Terre, exprimé comme la différence relative entre les rayons au pôle et à l'équateur.
pages_changement-spatial/changement-spatial-sexercer.html
pages_changement-temporel/changement-temporel-sexercer.html
pages_referentiels/changement-spatial-sexercer.html
Dans quel domaine de valeurs 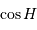 peut-il varier ?
peut-il varier ?
Comme nécessairement 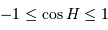 , l'inégalité précédente n'a pas de solution si
, l'inégalité précédente n'a pas de solution si 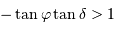 . Le cas limite est donc :
. Le cas limite est donc :
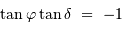
càd
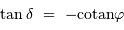
càd 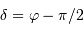 , et en tenant compte de l'inégalité, il n'y a aucune solution si
, et en tenant compte de l'inégalité, il n'y a aucune solution si
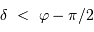
Se baser sur la question précédente
Comme nécessairement 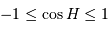 , l'inégalité précédente admet toujours une solution si
, l'inégalité précédente admet toujours une solution si 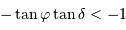 . Le cas limite est donc :
. Le cas limite est donc :
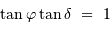
càd :
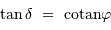
càd 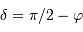 , et en tenant compte de l'inégalité, il y a toujours une solution si :
, et en tenant compte de l'inégalité, il y a toujours une solution si :
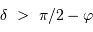
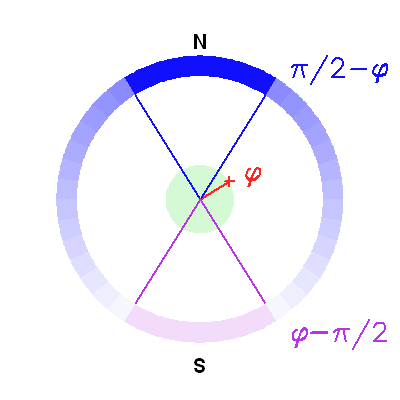
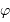 dans la région en violet.
dans la région en violet.
pages_referentiels/changement-temporel-sexercer.html
De la planète considérée et de la Terre, qui double qui ?
La période synodique vérifie
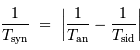
La table ci-contre donne les solutions,
| Planète | 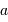 | 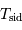 | 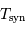 |
| UA | an | j | |
| Mercure | 0.3871 | 0.2408 | 115.88 |
| Vénus | 0.7233 | 0.6152 | 583.92 |
| Terre | 1.0000 | 1.0000 | -- |
| Mars | 1.5237 | 1.8808 | 779.94 |
| Jupiter | 5.2026 | 11.862 | 398.88 |
| Saturne | 9.5547 | 29.457 | 378.09 |
| Uranus | 19.218 | 84.020 | 369.66 |
| Neptune | 30.109 | 164.77 | 367.49 |
Plus la planète est lointaine, plus son mouvement propre est lent, et donc son évolution se rapproche peu à peu de celle d'une étoile, animée essentiellement par le mouvement apparent dû à la rotation de la Terre autour du Soleil.
pages_referentiels/changement-temporel-sexercer.html
Convertir l'unité angulaire en minute de temps
On peut arriver au résultat de 2 façons différentes.
Soit calculer la vitesse angulaire du soleil (360 degrés en 24 h, 15 degrés à l'heure), et donc un parcours de 0.5 deg prend 2 minutes.
Soit, directement, convertir le diamètre angulaire en diamètre horaire :
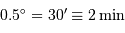 .
.
Estimer la part relative du mouvement propre de la Lune autour de la Terre et du mouvement d'entraînement dû à la rotation diurne.
Le mouvement propre de la Lune est-il vraiment important en 2 minutes ?
Comme la durée trouvée pour le Soleil est très courte devant la période de révolution synodique de la Lune (29.5 j), alors que la Lune présente le même diamètre angulaire que le Soleil, on peut négliger son mouvement. Il s'ensuit que la durée cherchée est sensiblement la même pour la Lune que pour le Soleil.
Montrer que 1 deg (2 diamètres solaires/lunaires) sépare le premier du dernier contact.
Montrer que le fait de considérer la révolution synodique de la Lune fige le mouvement du Soleil.
Pour "doubler" totalement le soleil, la lune doit
passer de la configuration 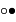 à la configuration
à la configuration
 , càd parcourir 2 diamètres, soit 1 deg.
, càd parcourir 2 diamètres, soit 1 deg.
Ceci représente 1/360ème de la période de révolution synodique (29.5 j), soit 0.082 j, càd environ 2 heures.
pages_referentiels/changement-temporel-sexercer.html
La question est peut être trop simple.
Si l'année hermienne vaut 1, le jour sidéral vaut 2/3, d'après l'énoncé, qui annonce 3 jours hermiens = 2 révolutions.
Identifier ce qui est sidéral, hermien, et la révolution de l'un par rapport à l'autre.
En unités d'année hermienne sidérale, la période de rotation propre est 2/3, et la période d'entraînement du référentiel hermien par rapport aux étoiles est 1. La relation de cours, vue avec une période synodique, s'écrit ici avec la période hermienne cherchée :
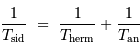
Avec 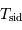 la rotation hermienne sidérale,
la rotation hermienne sidérale,
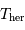 Avec
Avec 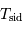 la période hermienne sidérale, la rotation hermienne,
et
la période hermienne sidérale, la rotation hermienne,
et 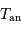 l'année hermienne sidérale.
l'année hermienne sidérale.
Donc, dans le système d'unité choisi :
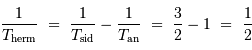
On en conclut que le jour hermien dure 2 années, comme l'illustre l'animation.
pages_referentiels/changement-temporel-sevaluer.html
Quelle rotation distingue les descriptions sidérale et synodique ?
La Lune n'est ni le Soleil, autour duquel la Terre tourne, ni les étoiles, considérées comme lointaines et fixes.
pages_referentiels/pointer-sexercer.html
Impossible de donner une solution dynamique. Mais vous trouverez la réponse sur le site de l'IMCCE, par exemple à l'entrée Observations des planètes, en choisissant l'objet et la date.
Exemple de solution, au jour où cet exercice a été rédigé : la position de Mars est de 10h37 en ascension droite, et 9°55 en déclinaison.
Ne pas oublier de passer d'abord en temps universel.
Impossible de donner une solution dynamique. Mais vous trouverez la réponse sur le site de l'IMCCE, à l'entrée Observations des planètes, en choisissant l'objet, la date, et en précisant le lieu d'observation.
Exemple de solution, au jour où cet exercice a été rédigé : à Nançay, le temps sidéral local de Mars est de 8h01.
Essayer de définir un critère simple de visibilité.
La planète doit être levée en début de soirée.
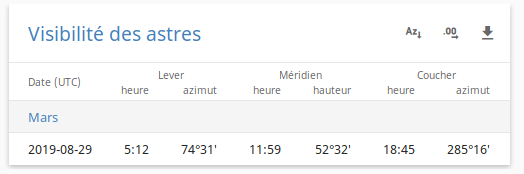
Impossible de donner une solution en temps réel. Mais vous trouverez la réponse sur le site de l'IMCCE, à l'entrée Visibilité des astres, en choisissant l'objet, la date, et en précisant le lieu d'observation.
Exemple de solution, au jour où cet exercice a été rédigé : Mars se couche vers 18h45 TU, soit 20h45 en heure locale, et n'est donc pas observable cette nuit.
pages_phenomenes-mutuels/eclipse-sexercer.html
136+1820-1 ans = 20 siècles
Pour 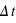 =11200 s, on trouve
=11200 s, on trouve  =28 s/siecle2.
Pour
=28 s/siecle2.
Pour 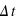 =12150 s, on trouve
=12150 s, on trouve  =30 s/siecle2.
Résultat:
=30 s/siecle2.
Résultat: 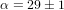 s/siecle2.
s/siecle2.
Calculer la longueur du parallèle 35 deg.
Incertitude de localisation : L'équateur mesurant 40 000 km, le parallèle à 35 deg mesure lui 32 700 km. Une bande de longueur 1000 km est parcourue par la rotation de la Terre en 24 / 32.7 = 0.73 h, soit 44 min.
Incertitude de la rotation de la Terre : 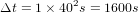 . Au bout de 40 siècles, l'incertitude est de l'ordre de 1600 s (un peu moins d'une demi-heure).
. Au bout de 40 siècles, l'incertitude est de l'ordre de 1600 s (un peu moins d'une demi-heure).
La comparaison des 2 résultats précédents montre que l'incertitude sur la localisation géographique, supérieure à l'incertitude temporelle sur la rotation de la Terre, ne permet pas de situer la Terre précisément par rapport à l'éclipse.
pages_phenomenes-mutuels/occultation-sexercer.html
N'a-t-on pas 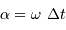 , par définition des variables ?
, par définition des variables ?
La relation entre vitesse angulaire et angle conduit à
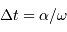 .
.
A quoi correspond la phase de pénombre ?
Quelle distance angulaire le satellite a-t-il parcouru durant l'occultation ?
La phase de pénombre débute au 1er contact entre les 2 objets, jusqu'à ce que l'étoile soit totalement occultée. Cette phase de 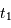 à
à 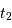 dure
dure 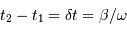 . Par symétrie,
. Par symétrie, 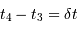 .
.
Lors de la phase de totalité, le satellite parcourt son diamètre moins celui de l'étoile. On a donc : 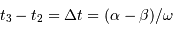 .
.
On en déduit, par rapport à la centralité 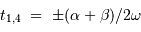 et
et 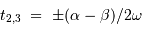 .
.
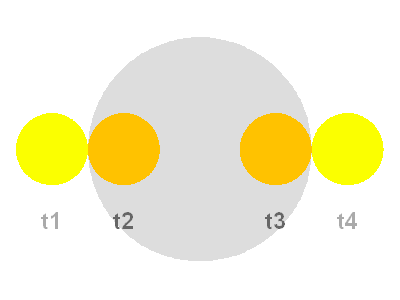
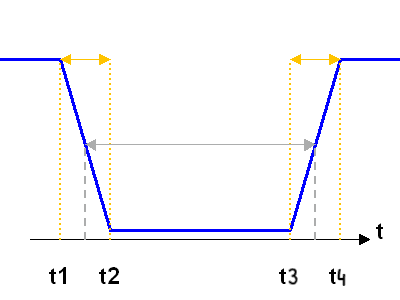
Courbe de lumière de l'occultation. La flèche grise mesure la durée moyenne.
Déterminer les inconnues et les observables : vitesse angulaire, distances...
La vitesse angulaire 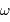 de l'objet est mesurable : les diamètres angulaires
de l'objet est mesurable : les diamètres angulaires 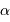 et
et 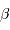 sont alors déterminés par les mesures de
sont alors déterminés par les mesures de 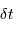 et
et 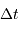 .
.
La distance au soleil de l'objet occultant peut être déduite, par application des lois de la gravitation, de son mouvement.
La mesure du diamètre linéaire de l'objet ou de l'étoile va dépendre de sa distance 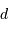 :
:
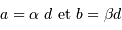
Il suffit de procéder dans l'ordre, et de calculer la vitesse angulaire, le rayon angulaire... ou de simplifier les calculs en prenant garde aux unités !
Avec une vitesse angulaire 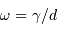 ,
, 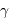 s'exprimant en UA."/h, le diamètre angulaire s'écrit
s'exprimant en UA."/h, le diamètre angulaire s'écrit
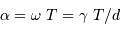 (AN : 0.05", en ayant pris soin d'exprimer le temps en heure, en accord avec l'unité de
(AN : 0.05", en ayant pris soin d'exprimer le temps en heure, en accord avec l'unité de 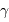 ).
).
Le diamètre linéaire 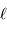 vérifie
vérifie 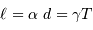 . L'application numérique donne
. L'application numérique donne 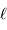 en UA."
en UA."
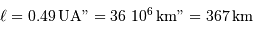 .
.
Obtenir d'abord le diamètre angulaire de l'étoile.
Pour passer du diamètre angulaire de l'étoile à son diamètre linéaire, appliquer directement la définition du parsec.
Par règle de 3 entre les durées et les distances angulaires, le diamètre angulaire vaut :
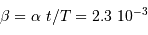 seconde d'arc.
seconde d'arc.
Passer du diamètre angulaire de l'étoile (donné en seconde d'arc) et de la distance (donnée en parsec) au diamètre linéaire de l'étoile par la définition du parsec donne le résultat simplement en UA.
A 4.7 pc, ce diamètre angulaire correspond à un diamètre linéaire 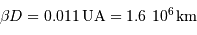 , très proche du diamètre du Soleil (1.4 millions de km).
, très proche du diamètre du Soleil (1.4 millions de km).
Remarquer que les durées à mesurer sont courtes.
pages_complements-ephemerides/coordonnee-geocentrique-sexercer.html
Réfléchir au système de coordonnées utilisé.
Les mesures sont effectuées en coordonnées géographiques, les observateurs pouvant p.ex. s'appuyer sur la verticale locale, et non sur une hypothétique et inconnue direction pointant le centre de la Terre.
En raison de la non sphéricité, le rayon de courbure local varie, et donc la mesure d'un arc d'ouverture fixée.
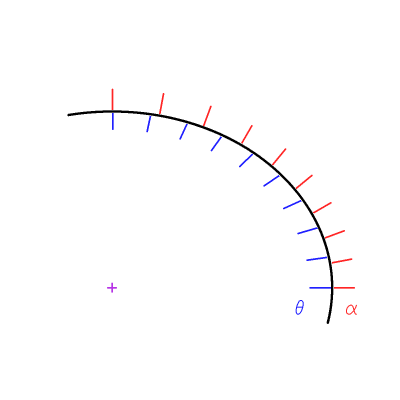
Voir la figure de la question précédente.
Comme le rayon de courbure local est plus important au pôle, une rotation d'un angle géographique de 10 degré sera plus importante au pôle.
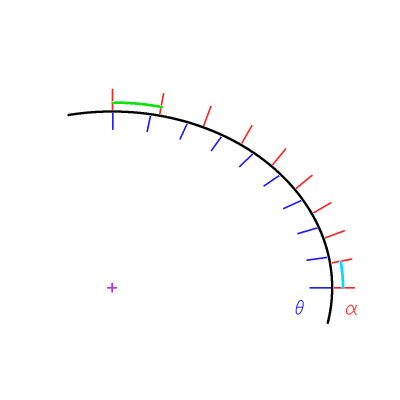
Identifier 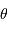 au pôle et à l'équateur, et y calculer
au pôle et à l'équateur, et y calculer 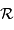 .
.
Les rayons de courbures aux pôles 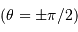 ou à l'équateur
ou à l'équateur 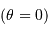 valent respectivement :
valent respectivement :
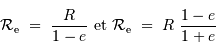
Avec l'hypothèse que 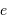 est petit, et les développements limités usuels, on trouve :
est petit, et les développements limités usuels, on trouve :
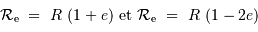
On en déduit que la différence relative des mesures, de l'ordre de 1.2%, correspond à 3 fois le paramètre 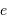 . En effet :
. En effet :
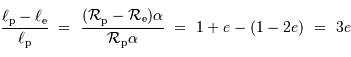
d'où l'aplatissement de la Terre, de l'ordre de 0.4%, cad 1/250.