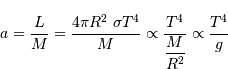La phase de formation ne représente qu'une courte étape dans la vie de la plupart des étoiles. Ensuite, l'étoile doit trouver une autre source d'énergie.
Avec une masse stellaire suffisante, de l'ordre du douzième de la masse du Soleil, la fusion de l'hydrogène peut s'amorcer, et l'étoile entre sur la séquence principale.

Cet objet du catalogue Herbig-Haro est une étoile de type T-Tauri. Sur le point d'atteindre la séquence principale, elle éjecte encore une fraction importante de sa masse sous forme de vent stellaire.
Crédit :
HST

Image en rayon X du Soleil. Quelle source d'énergie interne explique la luminosité du Soleil ?
Crédit :
NASA
Energie interne
Le Soleil présente un âge bien plus avancé que le temps de Kelvin-Helmholtz. Il possède une source d'énergie interne qui explique son rayonnement.
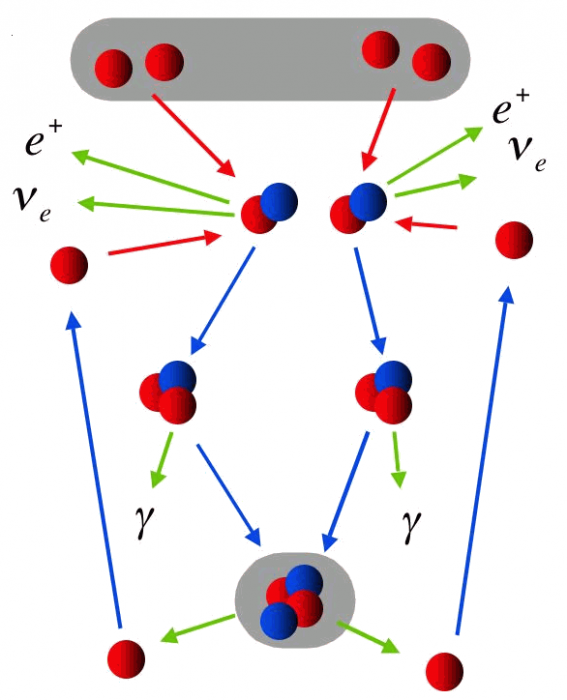
Réaction détaillée de la fusion de 4 H en 1 He.
Crédit :
ASM
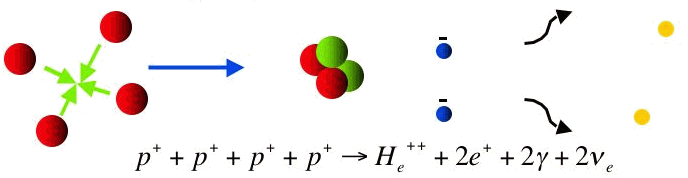
Bilan de la fusion de 4 H en 1 He.
Crédit :
ASM
Chaine proton-proton
Différentes étapes conduisent à la fusion de 4 protons en un noyau d'hélium, ne faisant intervenir que des paires de réactifs à chaque étape élémentaire.
L'étape limitante de la réaction consiste en la fusion de 2 protons vers un noyau de deutérium, avec émission d'un positron, donc un bilan réduit 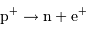 . L'interaction faible mise en jeu induit un très faible taux de réaction.
. L'interaction faible mise en jeu induit un très faible taux de réaction.
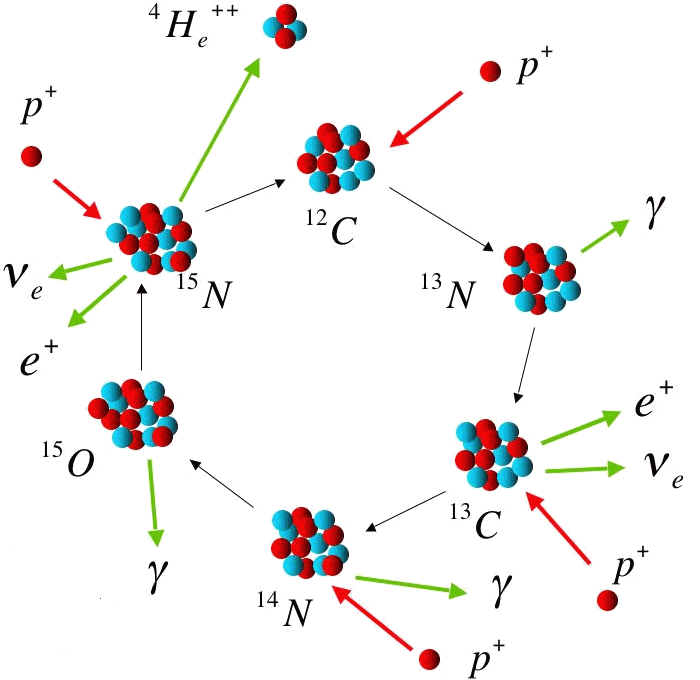
Cycle CNO.
Crédit :
ASM
Cycle CNO
A plus haute température (car les noyaux impliquées sont plus lourds, donc plus chargés), le cycle CNO peut s'avérer plus rapide que la chaîne proton-proton. Il est à l'oeuvre dans les étoiles massives. Les noyaux C, N et O participent au cycle, mais n'apparaissent pas dans le bilan final, qui reste la transformation de 4 protons en 1 noyau d'hélium.
 Objectifs
Objectifs
Définir dans quelles conditions microphysiques la fusion de l'hydrogène va s'amorcer.
Montrer que la fusion nécessite une température élevée, de l'ordre de 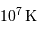 .
.

Seules les régions internes les plus chaudes peuvent être le siège de la fusion de l'hydrogène. Leur volume est limité.
Crédit :
ASM
Constante de temps nucléaire
La durée de vie à ce régime, pour une étoile comme le Soleil, est alors :
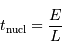
L'application numérique, avec la luminosité solaire mesurée aujourd'hui 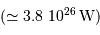 , le taux de conversion par nucléon et la masse concernée donne :
, le taux de conversion par nucléon et la masse concernée donne :
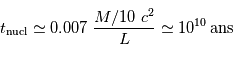
Une réaction chimique, dégageant typiquement 1 eV par nucléon, soit 1 million de fois moins que la fusion de l'hydrogène, conduirait à une durée de vie de 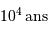 seulement.
seulement.
L'estimation de 10 milliards d'année pour le Soleil est très proche de ce que donne une modélisation plus poussée. Actuellement, avec un âge de 4.56 milliards d'années, le Soleil est à mi-parcours sur la
séquence principale.
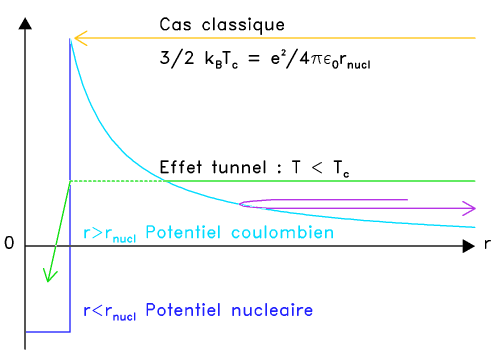
L'effet tunnel permet à un couple de protons de se rencontrer et d'interagir via l'interaction nucléaire forte, en outrepassant la barrière électrostatique.
Crédit :
ASM
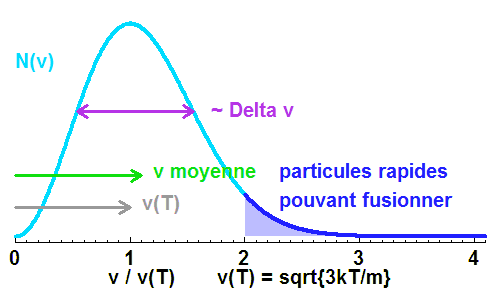
Distribution maxwellienne de vitesse, valable pour un gaz parfait. Valeur la plus probable, valeur moyenne et largeur de la distribution se valent, pour une énergie cinétique égale à 3/2 kT.
Crédit :
ASM
Interagir
Au sein d'une étoile, l'hydrogène est totalement ionisé : la matière se présente sous la forme d'un gaz de protons et d'électrons essentiellement. La réaction entre 2 protons nécessite leur rencontre à très courte distance, car l'interaction nucléaire forte n'a qu'une très courte portée, de l'ordre du femtomètre. Ceci nécessite de vaincre la répulsion électrostatique.
La barrière de potentiel pour une distance de 1 fm entre les 2 protons, peut se traduire en température : de l'ordre de 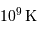 . Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
. Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
Deux phénomènes se conjuguent pour faciliter la fusion :
- L'effet tunnel conduit à tromper les électrons sur la distance exacte qui les sépare. Il exprime l'incertitude de Heisenberg : les 2 protons fonçant l'un sur l'autre ne peuvent pas avoir une position très précisément définie.
- La distribution de vitesse des protons est maxwellienne, donnée par la théorie cinétique du gaz parfait : si l'énergie cinétique moyenne est
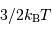 , une proportion non négligeable de protons est sensiblement plus rapide.
, une proportion non négligeable de protons est sensiblement plus rapide.
Ces points sont quantifiés en exercice.
Fusion de l'hydrogène
En pratique, la température limite de fusion de l'hydrogène est de l'ordre de 10 millions de Kelvin. Pour des températures plus faibles, seule la fusion du deutérium peut s'amorcer.
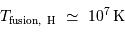
La fusion par le cycle pp domine lorsque la température n'excède pas 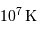 . Au delà de
. Au delà de 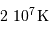 , le cycle CNO est prépondérant.
, le cycle CNO est prépondérant.
Fusion de noyaux lourds
Plus les noyaux sont lourds, plus leur fusion nécessite une température élevée. En fonction du nombre de charge  de l'élément considéré :
de l'élément considéré :
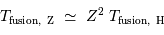
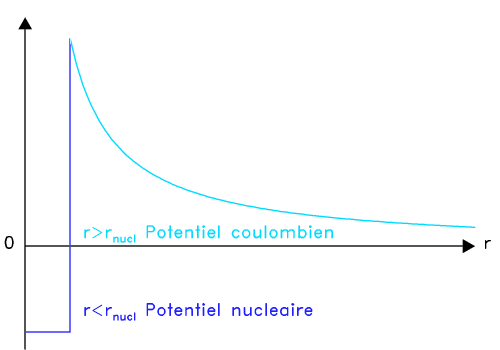
Energie potentielle d'interaction proton-proton.
Crédit :
ASM
 Température de fusion
Température de fusion
Difficulté : ☆☆
Temps : 40 min
Cet exercice a pour but de quantifier, dans un cadre classique, la température minimale qui doit régner au centre d'une étoile pour que s'amorcent les réactions nucléaires. Il se base sur la figure donnant le potentiel d'interaction entre 2 protons.
Question 1)
Mener un bilan d'énergie, pour déterminer l'énergie cinétique minimale conduisant à la fusion.
[1 points]
Exprimer l'énergie de la barrière coulombienne.
Exprimer la condition énergétique limite à remplir en 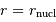
Question 2)
En déduire l'expression de la température minimale pour que la fusion puisse avoir lieu.
[2 points]
Faire le lien entre l'énergie cinétique et la température.
Question 3)
Faire l'application numérique. On donne 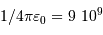 en unité SI, et
en unité SI, et 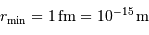 . Qu'en pensez-vous ?
. Qu'en pensez-vous ?
[2 points]
Question 4)
Comment s'écrit cette température s'il s'agit de faire fusionner non pas 2 protons, mais 2 noyaux d'une élément de charge 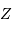 .
.
En déduire que la température de fusion des éléments lourds nécessite une température bien plus élevée que celle pour l'hydrogène.
[1 points]
Réécrire le potentiel électrostatique en fonction de 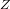 .
.
L'effet varie comme 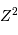
 Du rôle de l'effet tunnel et de la distribution des vitesses
Du rôle de l'effet tunnel et de la distribution des vitesses
Difficulté : ☆☆☆
Temps : 60 min
Sans effet tunnel, la
fusion de l'hydrogène nécessiterait des températures très élevées (et p.ex. non atteintes dans l'intérieur du Soleil). Cet exercice a pour but de décrire le rôle de l'effet tunnel dans le cadre d'un modèle très simplifié.
On note 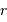 la position d'un proton par rapport à un autre et
la position d'un proton par rapport à un autre et 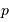 la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
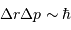
Question 1)
Relier la distance minimale d'approche des 2 protons à la quantité de mouvement incidente, puis à la température du milieu.
[1 points]
Déterminer les expressions des énergies cinétique et potentielle, ainsi que leurs valeurs particulières à grande distance ou à la distance minimale d'approche.
Question 2)
Faire l'application numérique dans le cas d'une distance d'approche de 1 fm, nécessaire pour arriver à une interaction forte entre les protons.
[1 points]
Question 3)
Dans le problème étudié, la loi de distribution des vitesses permet de confondre 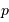 et
et 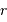 avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
On suppose que le proton incident ne sait pas localiser l'autre proton, avec une incertitude dépendant de sa quantité de mouvement incidente précédemment calculée (notée simplement 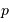 ).
).
Déterminer alors cette incertitude de position.
[3 points]
La relation d'incertitude présentée ici se traduit par
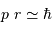
L'égalité entre l'énergie cinétique à grande distance 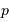 et l'énergie potentielle à distance minimale
et l'énergie potentielle à distance minimale 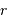 donne une autre relation entre ces 2 variables.
donne une autre relation entre ces 2 variables.
Question 4)
Faire l'application numérique (on donne 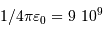 en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
[2 points]
Question 5)
La distribution des quantités de mouvement assure qu'il existe une population avec des protons 3 fois plus rapide que la valeur moyenne. En déduire la température minimale pour la fusion.
[1 points]
Estimer les conséquences de ces protons rapides en termes énergétiques, puis de température.
 Objectifs
Objectifs
Définir dans quelles conditions la fusion de l'hydrogène va s'amorcer.
 Prérequis
Prérequis
Pression au centre de l'étoile.
La compression gravitationnelle peut être équilibrée par 3 termes de
pression :
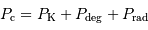
respectivement pression du gaz de matière chaud, pression de Fermi et présence du gaz de photons.
Phase de contraction
La compression gravitationnelle au centre de l'objet varie en fonction de sa masse et de son rayon comme :
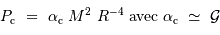
Lors de la contraction de l'objet, la température centrale varie en fonction du rayon 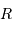 comme :
comme :
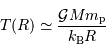
(avec 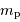 la masse du proton).
Lorsque
la masse du proton).
Lorsque 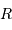 décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
Rôle des différents termes de pression
La pression cinétique présente la même dépendance en masse et rayon que la compression gravitationnelle :
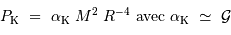
Avec ces variables, la pression de dégénérescence varie elle comme :
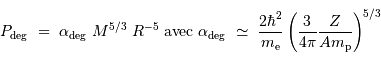
Lorsque l'objet se contracte, cette pression augmente plus vite que la compression gravitationnelle. Elle peut donc bloquer la compression, en atteignant un équilibre caractérisé par :
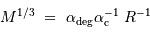
Température centrale
Dans ces conditions, la température atteinte au centre vaut (en éliminant la variable rayon des équations qui précèdent) :
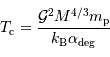
Si la température centrale atteint 10 millions de Kelvin, une étoile est née. Sinon, il s'agit d'un astre dégénéré sans amorçage des réactions nucléaires.
Masse minimale
Il est nécessaire d'avoir une masse initiale suffisante pour atteindre une température permettant d'initier la fusion de l'hydrogène. Un modèle précis donne la masse minimale pour la combustion de l'hydrogène :
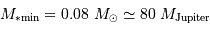
Entre 13 et 80 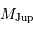 , l'objet ne peut brûler que son deutérium : il s'agit alors d'une naine brune.
, l'objet ne peut brûler que son deutérium : il s'agit alors d'une naine brune.
Masse maximale
La pression de radiation varie comme 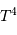 , donc :
, donc :
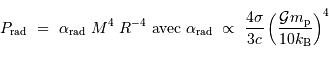
à comparer à la compression gravitationnelle 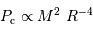 .
.
Si la masse est trop importante, la pression de radiation va conduire à souffler l'étoile. La limite d'équilibre 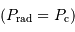 est atteinte lorsque :
est atteinte lorsque :
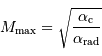
Une modélisation précise donne la valeur numérique :
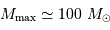
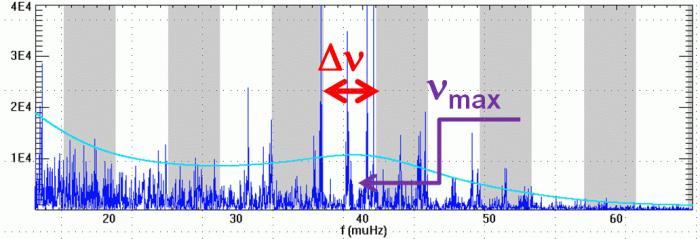
Définition des fréquences caractéristiques
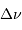
et
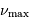
d'un
spectre d'oscillation stellaire.
Crédit :
ASM
 Masse et rayon sismiques
Masse et rayon sismiques
Difficulté : ☆☆
Temps : 30 min
L'astérosismologie, l'étude de la vibration des étoiles, est une
branche récente de la physique stellaire qui apporte de nouvelles
observables. La description globale d'un
spectre d'oscillation introduit
deux fréquences caractéristiques 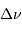 et
et 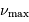 ,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse
,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse 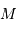 , du rayon
, du rayon 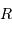 et de la température effective
et de la température effective 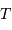 de l'étoile via les définitions :
de l'étoile via les définitions :
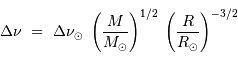
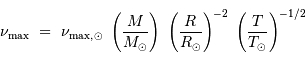
avec les valeurs solaires 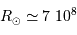 m,
m, 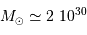 kg,
kg, 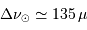 Hz,
Hz, 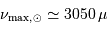 Hz, et
Hz, et 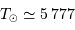 K.
K.
Question 1)
Ordonner les valeurs de 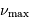 pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
[2 points]
Identifier dans l'expression de 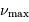 ce qui peut ressemble au
champ gravitationnel d'une étoile.
ce qui peut ressemble au
champ gravitationnel d'une étoile.
Comment se traduit le fait que l'on considère des étoiles de même
type spectral ?
Question 2)
Quelle mesure intéressante apporte 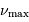 , grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
, grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
[1 points]
La réponse est quasiment à la question précédente.
Question 3)
Ordonner les valeurs de la grande séparation 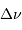 pour deux
étoiles présentant une masse volumique moyenne très différente.
pour deux
étoiles présentant une masse volumique moyenne très différente.
[1 points]
Exprimer la masse volumique moyenne en fonction des masse et
rayon stellaire.
Quel lien entre 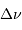 et la masse volumique moyenne ?
et la masse volumique moyenne ?
Question 4)
Calculer 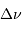 et
et 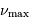 pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à
pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à 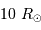 et de température
effective 4 800 K.
et de température
effective 4 800 K.
[1 points]
Faites chauffer le calcotron.
Question 5)
Montrer que l'on peut déduire de la mesure de 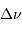 ,
, 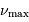 et
et
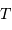 une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
[2 points]
Désolé, pas d'autre solution que retrousser ses manches et
inverser les équations de départ !
Question 6)
Énoncer un des intérêts de l'astérosismologie ?
[1 points]
 De nouvelles classes spectrales ?
De nouvelles classes spectrales ?
Difficulté : ☆☆
Temps : 5 min
Question 1)
Pourquoi peut-on penser qu'il n'y aura pas de découvertes de nouvelles classes spectrales
même si l'on met en service de nouveaux télescopes de sensibilité encore plus grande ?
Si l'on découvrait de nouvelles classes, correspondraient-elles à des étoiles très ou très peu lumineuses ?
 Objectifs
Objectifs
Estimer quelques dimensionnements des objets sur la séquence
principale à partir de la relation masse-luminosité sur séquence
principale (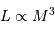 ).
).
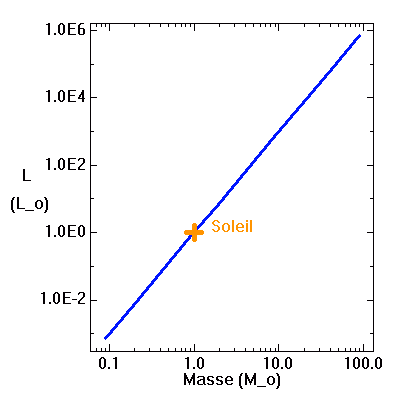
Relation masse-luminosité. Les étoiles les moins lumineuses sont intrinsèquement plus de 1000 fois moins lumineuses que le Soleil, quand les plus lumineuses atteignent 1 millions de fois la valeur solaire.
Crédit :
ASM
Relation masse luminosité
En faisant de la physique avec les mains, on démontre rapidement que la luminosité d'une étoile est reliée à sa masse par la relation :
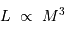
La démonstration complète est hors de portée de ce cours, car elle introduit des éléments de transfert radiatif, qui aboutissent à la relation entre masse et rayon stellaires. Notons les étapes principales.
Constante de temps radiative
La luminosité d'une étoile, commensurable à une puissance, est égale au quotient de l'énergie interne du gaz de photons à la constante de temps radiative :
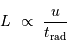
L'énergie interne du gaz de photons est proportionnelle au volume stellaire 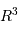 , ainsi qu'à
, ainsi qu'à 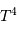 selon la loi de rayonnement du corps noir). La constante de temps radiative mesure le durée d'échappement des photons, qui résulte d'un phénomène stochastique.
selon la loi de rayonnement du corps noir). La constante de temps radiative mesure le durée d'échappement des photons, qui résulte d'un phénomène stochastique.
On suppose que le libre parcours moyen 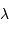 d'un photon est uniforme dans tout l'intérieur stellaire. Le processus de marche au hasard demande alors, pour parcourir une distance
d'un photon est uniforme dans tout l'intérieur stellaire. Le processus de marche au hasard demande alors, pour parcourir une distance 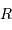 par étapes de longueur élémentaire
par étapes de longueur élémentaire 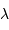 , un nombre d'étapes variant comme
, un nombre d'étapes variant comme 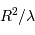 . On en déduit la constante de temps radiative :
. On en déduit la constante de temps radiative :
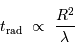
Comme le libre parcours 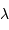 est en fait inversement proportionnel à l'encombrement, donc à la masse volumique, on a :
est en fait inversement proportionnel à l'encombrement, donc à la masse volumique, on a :
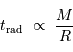
et
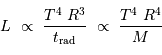
Relation masse-rayon-température-luminosité
Dans les pages précédentes,
des éléments de physique simples ont permis de calibrer les masse volumique et pression internes :
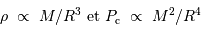
ainsi que la relation donnant la température
centrale :
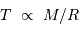
La luminosité du corps noir stellaire vérifie donc :
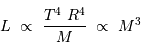
Observationnellement, l'exposant s'avère être 3.3 :
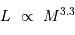
Le long de la séquence principale
Différents modèles stellaires ont été synthétisés. La masse, le rayon et la luminosité sont données en unités solaires, la température de corps noir en Kelvin (on remarquera que le modèle correspondant à 1 masse solaire n'a pas un rayon solaire : la série a été déterminée pour des conditions d'âge et de composition différentes de celles de notre Soleil).
A l'aide de l'appliquette, calculer la luminosité de corps noir Lcn, et vérifier qu'elle correspond à la luminosité modélisée.
Calculer ensuite les luminosités, masses et rayons en échelle logarithmique, et vérifier les exposants des relations de proportionnalité entre la luminosité et la masse d'une part, la luminosité et le rayon d'autre part.

 Amplitude des oscillations
Amplitude des oscillations
Difficulté : ☆☆
Temps : min
L'amplitude des oscillations de type solaire dépendent du rapport 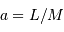 , la luminosité
, la luminosité 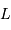 donnant la mesure de l'énergie transportée par convection, et la masse
donnant la mesure de l'énergie transportée par convection, et la masse 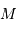 mesurant l'inertie de la réponse. Ces deux grandeurs ne peuvent être mesurées qu'indirectement : la mesure de la luminosité dépend de la distance, et la mesure de la masse nécessite un modèle de structure interne.
mesurant l'inertie de la réponse. Ces deux grandeurs ne peuvent être mesurées qu'indirectement : la mesure de la luminosité dépend de la distance, et la mesure de la masse nécessite un modèle de structure interne.
Question 1)
Montrer que l'amplitude croît avec le type spectral.
[1 points]
Comment varie la luminosité sur la séquence principale ?
Question 2)
Déterminer la dépendance 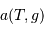 , avec
, avec 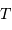 la température effective (déduit du spectre) et
la température effective (déduit du spectre) et 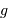 le champ gravitationnel (déduit des profils de raies).
le champ gravitationnel (déduit des profils de raies).
[1 points]
 Le long de la séquence principale
Le long de la séquence principale
Difficulté : ☆
Temps : 15 min
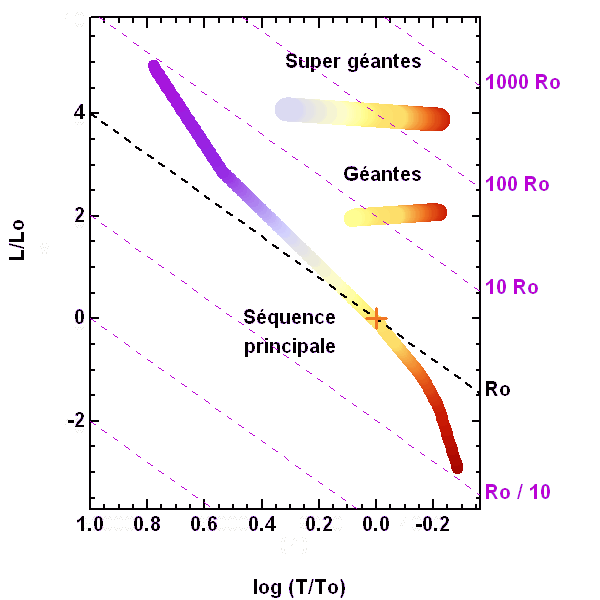
Diagramme HR.
Crédit :
ASM
Le long de la séquence principale, la luminosité d'une étoile varie approximativement comme la puissance 6 de la température, comme le rappelle le diagramme HR ci joint.
Question 1)
Montrer que l'on peut en déduire une relation masse-rayon le long de la séquence principale du type:
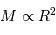
[2 points]
Question 2)
Que peut-on en déduire pour le champ gravitationnel d'une étoile de la séquence principale ?
[1 points]

Champ d'étoiles dans le Grand Nuage de Magellan (galaxie satellite de la Voie Lactée) vu par le télescope Hubble.
Crédit :
HST

Naine brune 2M1207, et son compagnon exoplanétaire, détectée par optique adaptative au VLT.
Crédit :
ESO

Naine brunes identifiées dans l'amas ouvert des Pléiades.
Crédit :
UKIDSS and Palomar Observatory Sky Survey
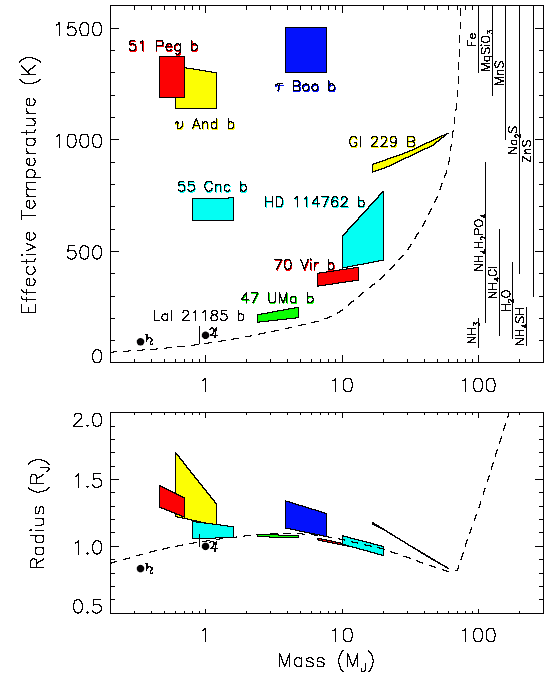
Modélisation de planètes géantes et naines brunes.
Crédit :
CNRS
Champ d'étoiles
Quels objets d'un
champ stellaire sont effectivement des étoiles, et pour quelles raisons ?
Naines brunes
Dans les années 1990, des objets présentant une très faible luminosité et un indice de couleur très rouge ont été clairement identifiés comme
naines brunes : objet de masse insuffisante pour amorcer la fusion de l'hydrogène mais de masse suffisante pour la fusion de deuterium. Les moyens observationnels actuels permettent de les détecter en grand nombre, par exemple dans un amas.
Les modèles de
structure interne montrent qu'ils présentent un rayon de l'ordre de celui de Jupiter, pour une température effective de 1000 à 1500 K pour les plus chauds.
La nature du Soleil et des étoiles
La nature du Soleil et des étoiles a été un sujet continu de questionnement au cours de l'histoire :
- Pour Anaxagore, au Ve siècle avant JC, le Soleil est un rocher incandescent.
- Pour Aristote, au IVe siècle avant JC, les corps célestes sont constitués d'une autre matière que les 4 éléments terrestres. L'Univers est éternel.
- Jean Philopon, philosophe chrétien au VIe siècle, réfute un Univers sans création. Les étoiles sont des soleils.
- Pour Giordano Bruno, fin XVe siècle, les étoiles sont des soleils entourés de planètes.
- Au XIXe siècle, l'émergence de la spectroscopie permet d'analyser la photosphère solaire.
La question énergétique
La question énergétique se pose dès le XVIIIe siècle. Comment le Soleil compense-t-il la perte d'énergie par rayonnement (Herschel, 1795) ? Pour une Terre de 6000 ans (création du monde selon la tradition biblique, ou de quelques millions d'années (Buffon), le mécanisme de
Kelvin-Helmholtz convient ; mais lorsque la géologie, par datation des roches terrestres, conduit à un âge supérieur au milliard d'années, les choses se compliquent.
- En 1804, Helmholtz suppose que le Soleil tire son énergie de sa contraction gravitationnelle.
- En 1919, Eddington suppose une origine nucléaire, par fusion de l'hydrogène.
- En 1939, le premier mécanisme de fusion de l'hydrogène est proposé par le physicien Hans Bethe.
 Objectifs
Objectifs
Établir les éléments de définition d'une étoile.
Brûler de l'hydrogène
 Définition
Définition
Une étoile passe par une phase adulte, sur la séquence principale, où elle tire son énergie de la fusion de l'hydrogène.
La masse de l'étoile étant apparue comme le paramètre crucial gouvernant sa formation puis son devenir, on récapitule ici comment varient la nature et le rayon d'un objet en fonction de sa masse.
Diagramme masse-rayon
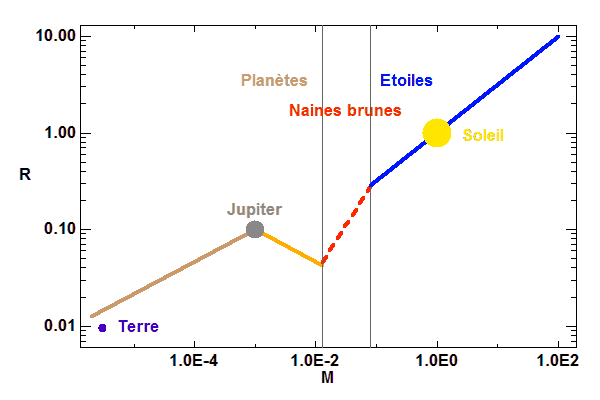
Relation masse rayon (en unités solaires), de la Terre à une étoile
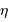
Carinae, de masse de l'ordre de 100 fois la masse du Soleil.
Crédit :
ASM
Faibles masses
Aux faibles masses (comme celle de la Terre), la matière solide est très peu compressible. La relation masse-rayon d'un simple empilement de masse volumique uniforme donne :
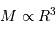
Le rayon croît avec la masse (cas d'une planète de masse inférieure à celle de Jupiter).
Pression de dégénérescence
Avec l'augmentation de la masse au-dela d’une masse critique proche de la masse de Jupiter, la pression de dégénérescence variant comme 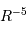 l'emporte. L'équilibre de la compression gravitationnelle
l'emporte. L'équilibre de la compression gravitationnelle 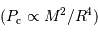 par la pression de dégénérescence
par la pression de dégénérescence 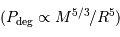 conduit à la relation masse-rayon :
conduit à la relation masse-rayon :
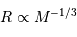
Le rayon de l'objet décroît avec la masse. Ceci n'est bien sûr pas intuitivement évident, mais c'est bien ce que l'on modélise pour les (exo)planètes géantes plus massives que Jupiter.
Relation masse rayon
Pour les étoile de la séquence principale, on a vu :
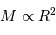
Evolution en fonction de la masse
L'étude à suivre montre l'avenir des étoiles une fois achevée leur vie sur la séquence principale.
- Une étoile de masse initiale inférieure à la masse de Chandrasekhar
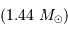 évolue vers le stade de naine blanche.
évolue vers le stade de naine blanche. - Pour une masse supérieure, elle finit comme étoile à neutrons.
- Voire comme trou noir pour une masse supérieure à 3 fois celle du Soleil.
 Populations stellaires
Populations stellaires
Temps : 30 min
Les observations photométriques menées par le satellite CoRoT ont conduit à identifier des populations d'étoiles peu brillantes pour lesquelles peu d'informations sont disponibles. Ici, on travaille avec une estimation de leurs températures effectives et gravités obtenues par suivi spectroscopique au sol. Ces estimations sont compilées dans un graphe 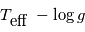 (les logarithmes sont calculés pour des gravités exprimées en cm.s-2). Le graphe montre deux populations, que l'on souhaite caractériser.
(les logarithmes sont calculés pour des gravités exprimées en cm.s-2). Le graphe montre deux populations, que l'on souhaite caractériser.
Champ CoRoT
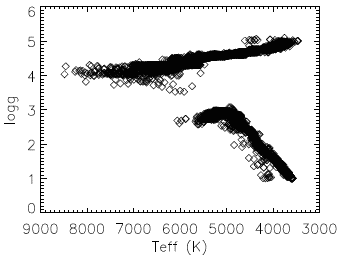
Relevé des températures effectives et gravité du champ initial observé par CoRoT.
Crédit :
CNES/ASM
Question 1)
Déterminer l'expression du champ de gravité de surface d'une étoile de masse 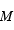 et rayon
et rayon 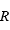 .
.
Aller raffraichir ses souvenirs de mécanique du point.
Dans le cours FSU c'est là .
Question 2)
Faire l'application numérique pour une étoile comme le Soleil et pour une géante rouge de masse identique, mais rayon 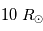 . Exprimer les résultats par la valeur
. Exprimer les résultats par la valeur 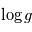 .
.
Les valeurs des masses et rayons solaires sont données par le calcotron !
Question 3)
Positionner les deux types d'objets dans le graphe et en déduire la nature des étoiles observées.
La température effective du Soleil vaut 5777 K. Compter 4800 K pour une géante de 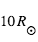
Question 4)
Identifier les deux populations.
Se servir de ce qui précède.
Question 5)
Estimer l'ordre de grandeur des plus grandes géantes observées dans l'échantillon.
Voir du côté des plus faibles gravités.
Quelle masse typique pour une géante typique ?
- Question 1
Aide :
Exprimer l'énergie de la barrière coulombienne.
Aide :
Exprimer la condition énergétique limite à remplir en 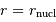
Solution :
L'énergie totale d'un proton s'écrit :
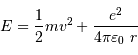
Pour passer la barrière coulombienne en 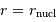 , le proton doit avoir une énergie vérifiant :
, le proton doit avoir une énergie vérifiant :
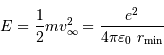
(énergie potentielle nulle à l'infini, énergie cinétique nulle au niveau de la barrière).
- Question 2
Aide :
Faire le lien entre l'énergie cinétique et la température.
Solution :
La température minimale vérifie :
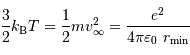
Soit :
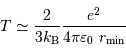
- Question 3
Solution :
Avec les valeurs proposées, on trouve :
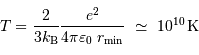
Cette valeur est surestimée, car ne prend pas en compte les phénomènes quantiques qui relaxent considérablement les conditions de fusion.
- Question 4
Aide :
Réécrire le potentiel électrostatique en fonction de 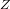 .
.
Aide :
L'effet varie comme 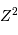
Solution :
Les équations précédentes se réécrivent avec la nouvelle énergie potentielle
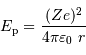
Il s'ensuit une température de fusion :
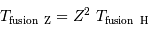
La valeur de la température est encore plus élevée que pour l'hydrogène.
- Question 1
Aide :
Déterminer les expressions des énergies cinétique et potentielle, ainsi que leurs valeurs particulières à grande distance ou à la distance minimale d'approche.
Aide :
Voir l'exercice
précédent
Solution :
L'exercice consacré à ce raisonnement donne la
solution. Avec les notations ici proposées :
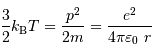
- Question 2
Aide :
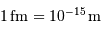
Solution :
L'application numérique donne :
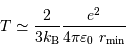
- Question 3
Aide :
La relation d'incertitude présentée ici se traduit par
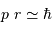
Aide :
L'égalité entre l'énergie cinétique à grande distance 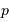 et l'énergie potentielle à distance minimale
et l'énergie potentielle à distance minimale 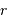 donne une autre relation entre ces 2 variables.
donne une autre relation entre ces 2 variables.
Solution :
En notant simplement 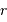 la distance minimale d'approche, et
la distance minimale d'approche, et 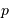 la quantité de mouvement incidente, l'équation énergétique dit :
la quantité de mouvement incidente, l'équation énergétique dit :
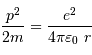
La relation d'incertitude présentée ici se traduit par
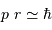 On en déduite la valeur de
On en déduite la valeur de 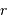 , en éliminant
, en éliminant 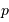 :
:
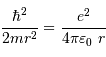
Et donc on aboutit à la nouvelle position (ou incertitude de position, d'après la présentation de l'énoncé) :
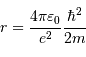
- Question 4
Solution :
L'application numérique donne :
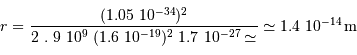
Cette distance est plus grande que 1 fm. Les protons peuvent donc se "tromper", et se croire en train de fusionner alors qu'ils sont 14 fois trop éloignés.
La température de fusion décroît de ce même facteur 14, soit de l'ordre de 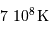 .
.
- Question 5
Aide :
Estimer les conséquences de ces protons rapides en termes énergétiques, puis de température.
Solution :
Un proton 3 fois plus rapide est 9 fois plus énergétique que la moyenne. On gagne donc ainsi un facteur 9 sur la température, soit la possibilité de fusion dès 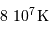 .
.
Ceci reste trop élevé, car la modélisation de l'effet tunnel est trop simpliste, mais montre comment l'estimation purement classique de la température de fusion est déjà surdimensionnée d'un facteur 120.
- Question 1
Aide :
Identifier dans l'expression de 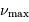 ce qui peut ressemble au
champ gravitationnel d'une étoile.
ce qui peut ressemble au
champ gravitationnel d'une étoile.
Aide :
Comment se traduit le fait que l'on considère des étoiles de même
type spectral ?
Solution :
Le champ gravitationnel d'une étoile varie en 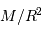 , comme
, comme
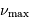 , dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et
, dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et 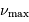 porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
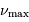 plus élevée, et réciproquement.
plus élevée, et réciproquement.
- Question 2
Aide :
La réponse est quasiment à la question précédente.
Solution :
La mesure de 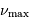 , identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
, identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
- Question 3
Aide :
Exprimer la masse volumique moyenne en fonction des masse et
rayon stellaire.
Aide :
Quel lien entre 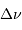 et la masse volumique moyenne ?
et la masse volumique moyenne ?
Solution :
L'examen de la définition de 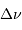 montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
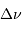 qu'une étoile plus dense.
qu'une étoile plus dense.
- Question 4
Aide :
Faites chauffer le calcotron.
Solution :
La géante, 10 fois plus grande que le Soleil, présente un volume
1000 fois plus important, donc une densité 31 fois moindre, et
donc 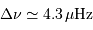 . Pour
. Pour 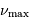 , l'application
numérique donne
, l'application
numérique donne 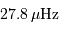 .
.
- Question 5
Aide :
Désolé, pas d'autre solution que retrousser ses manches et
inverser les équations de départ !
Solution :
L'inversion donne :
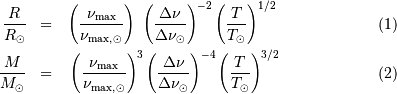
- Question 6
Solution :
Ce n'est pas tous les jours qu'une technique observationnelle
donne accès à la masse et au rayon de l'étoile relativement
précisément, et indépendamment de toute mesure de distance !



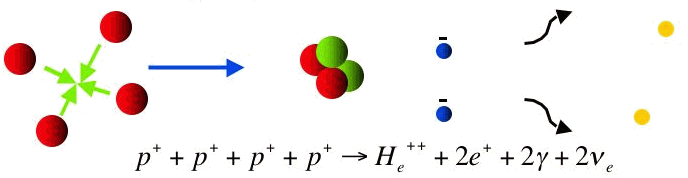
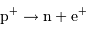 . L'interaction faible mise en jeu induit un très faible taux de réaction.
. L'interaction faible mise en jeu induit un très faible taux de réaction.

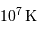 .
.

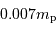 par proton. L'énergie nucléaire disponible, par fusion de l'hydrogène, est donc de
par proton. L'énergie nucléaire disponible, par fusion de l'hydrogène, est donc de 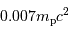 , soit 7 MeV, par nucléon, et a priori de
, soit 7 MeV, par nucléon, et a priori de 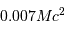 pour toute l'étoile.
pour toute l'étoile.
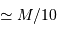 est concernée.
est concernée.
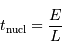
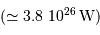 , le taux de conversion par nucléon et la masse concernée donne :
, le taux de conversion par nucléon et la masse concernée donne :
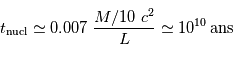
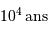 seulement.
seulement.


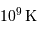 . Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
. Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
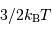 , une proportion non négligeable de protons est sensiblement plus rapide.
, une proportion non négligeable de protons est sensiblement plus rapide.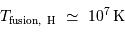
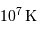 . Au delà de
. Au delà de 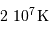 , le cycle CNO est prépondérant.
, le cycle CNO est prépondérant.
 de l'élément considéré :
de l'élément considéré :
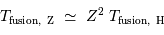

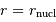
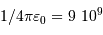 en unité SI, et
en unité SI, et 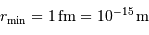 . Qu'en pensez-vous ?
. Qu'en pensez-vous ?
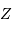 .
.
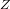 .
.
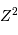
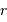 la position d'un proton par rapport à un autre et
la position d'un proton par rapport à un autre et 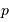 la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
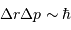
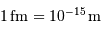
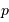 et
et 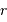 avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
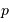 ).
).
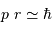
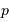 et l'énergie potentielle à distance minimale
et l'énergie potentielle à distance minimale 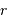 donne une autre relation entre ces 2 variables.
donne une autre relation entre ces 2 variables.
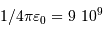 en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
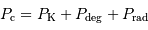
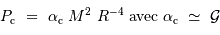
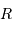 comme :
comme :
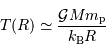
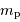 la masse du proton).
Lorsque
la masse du proton).
Lorsque 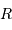 décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
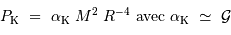
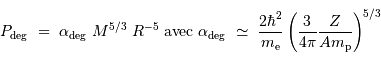
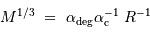
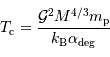
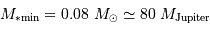
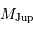 , l'objet ne peut brûler que son
, l'objet ne peut brûler que son 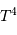 , donc :
, donc :
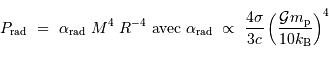
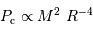 .
.
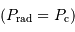 est atteinte lorsque :
est atteinte lorsque :
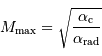
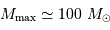

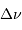 et
et 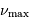 d'un
spectre d'oscillation stellaire.
d'un
spectre d'oscillation stellaire.
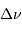 et
et 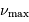 ,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse
,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse 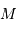 , du rayon
, du rayon 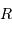 et de la température effective
et de la température effective 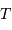 de l'étoile via les définitions :
de l'étoile via les définitions :
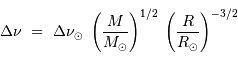
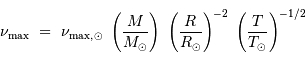
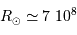 m,
m, 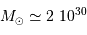 kg,
kg, 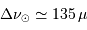 Hz,
Hz, 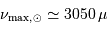 Hz, et
Hz, et 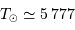 K.
K.
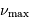 pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
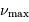 ce qui peut ressemble au
champ gravitationnel d'une étoile.
ce qui peut ressemble au
champ gravitationnel d'une étoile.
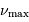 , grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
, grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
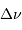 pour deux
étoiles présentant une masse volumique moyenne très différente.
pour deux
étoiles présentant une masse volumique moyenne très différente.
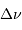 et la masse volumique moyenne ?
et la masse volumique moyenne ?
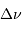 et
et 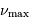 pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à
pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à 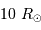 et de température
effective 4 800 K.
et de température
effective 4 800 K.
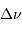 ,
, 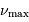 et
et
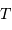 une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
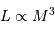 ).
).

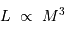
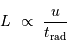
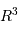 , ainsi qu'à
, ainsi qu'à 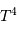 selon la loi de rayonnement du
selon la loi de rayonnement du 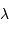 d'un photon est uniforme dans tout l'intérieur stellaire. Le processus de marche au hasard demande alors, pour parcourir une distance
d'un photon est uniforme dans tout l'intérieur stellaire. Le processus de marche au hasard demande alors, pour parcourir une distance 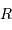 par étapes de longueur élémentaire
par étapes de longueur élémentaire 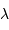 , un nombre d'étapes variant comme
, un nombre d'étapes variant comme 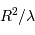 . On en déduit la constante de temps radiative :
. On en déduit la constante de temps radiative :
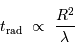
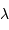 est en fait inversement proportionnel à l'encombrement, donc à la masse volumique, on a :
est en fait inversement proportionnel à l'encombrement, donc à la masse volumique, on a :
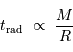
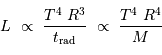
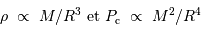
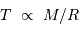
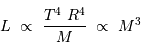
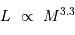
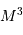 , la durée de vie stellaire varie comme :
, la durée de vie stellaire varie comme :
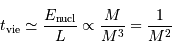
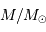
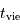 (ans)
(ans)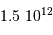
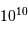
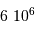

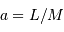 , la luminosité
, la luminosité 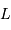 donnant la mesure de l'énergie transportée par convection, et la masse
donnant la mesure de l'énergie transportée par convection, et la masse 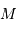 mesurant l'inertie de la réponse. Ces deux grandeurs ne peuvent être mesurées qu'indirectement : la mesure de la luminosité dépend de la distance, et la mesure de la masse nécessite un modèle de structure interne.
mesurant l'inertie de la réponse. Ces deux grandeurs ne peuvent être mesurées qu'indirectement : la mesure de la luminosité dépend de la distance, et la mesure de la masse nécessite un modèle de structure interne.
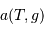 , avec
, avec 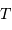 la température effective (déduit du spectre) et
la température effective (déduit du spectre) et 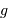 le champ gravitationnel (déduit des profils de raies).
le champ gravitationnel (déduit des profils de raies).

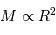





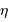 Carinae, de masse de l'ordre de 100 fois la masse du Soleil.
Carinae, de masse de l'ordre de 100 fois la masse du Soleil.
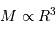
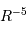 l'emporte. L'équilibre de la compression gravitationnelle
l'emporte. L'équilibre de la compression gravitationnelle 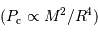 par la pression de dégénérescence
par la pression de dégénérescence 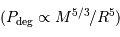 conduit à la relation masse-rayon :
conduit à la relation masse-rayon :
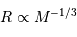
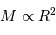
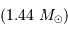 évolue vers le stade de naine blanche.
évolue vers le stade de naine blanche.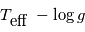 (les logarithmes sont calculés pour des gravités exprimées en cm.s-2). Le graphe montre deux populations, que l'on souhaite caractériser.
(les logarithmes sont calculés pour des gravités exprimées en cm.s-2). Le graphe montre deux populations, que l'on souhaite caractériser.

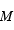 et rayon
et rayon 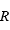 .
.
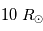 . Exprimer les résultats par la valeur
. Exprimer les résultats par la valeur 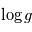 .
.
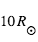
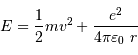
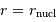 , le proton doit avoir une énergie vérifiant :
, le proton doit avoir une énergie vérifiant :
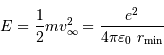
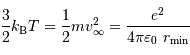
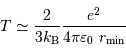
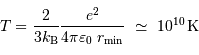
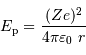
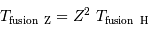
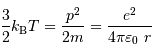
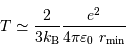
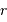 la distance minimale d'approche, et
la distance minimale d'approche, et 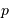 la quantité de mouvement incidente, l'équation énergétique dit :
la quantité de mouvement incidente, l'équation énergétique dit :
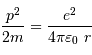
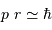 On en déduite la valeur de
On en déduite la valeur de 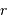 , en éliminant
, en éliminant 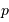 :
:
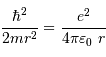
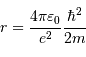
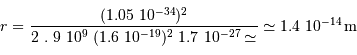
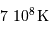 .
.
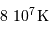 .
.
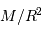 , comme
, comme
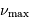 , dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et
, dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et 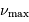 porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
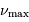 plus élevée, et réciproquement.
plus élevée, et réciproquement.
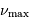 , identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
, identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
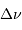 montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
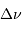 qu'une étoile plus dense.
qu'une étoile plus dense.
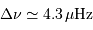 . Pour
. Pour 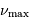 , l'application
numérique donne
, l'application
numérique donne 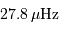 .
.
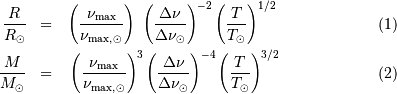
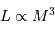 , on trouve :
, on trouve :
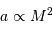 . L'amplitude des oscillations augmente vers les types spectraux plus massifs.
. L'amplitude des oscillations augmente vers les types spectraux plus massifs.