

Ex: Extinction atmosphérique |
Difficulté : ☆ Temps : 1h
Le nombre de particules atmosphériques rencontrées par un rayon de Soleil le long de son parcours est appelé densité de colonne, et est égal à :
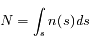
où 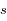 est la coordonnée le long du trajet du rayon et
est la coordonnée le long du trajet du rayon et 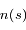 est la densité atmosphérique au point de coordonnée
est la densité atmosphérique au point de coordonnée 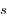 .
.
On peut approximer la densité atmosphérique à faible altitude (là où elle est la plus dense) par:
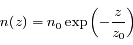
où 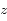 est l'altitude (mesurée verticalement),
est l'altitude (mesurée verticalement), 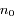 est la densité au niveau du sol, et
est la densité au niveau du sol, et 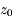 est l'échelle de hauteur caractéristique de l'atmosphère. Cette expression est une forme de la loi barométrique.
est l'échelle de hauteur caractéristique de l'atmosphère. Cette expression est une forme de la loi barométrique.
La figure ci-dessous représente la situation. Le centre de la Terre est au point C, l'observateur en O. Le point S représente le point de coordonnée 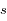 sur le trajet du rayon de Soleil, et d'altitude
sur le trajet du rayon de Soleil, et d'altitude 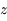 .
. 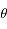 est la hauteur du Soleil sur l'horizon (vu par l'observateur) et R est le rayon de la Terre.
est la hauteur du Soleil sur l'horizon (vu par l'observateur) et R est le rayon de la Terre.
Dans le cas du Soleil couchant (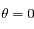 ), donner l'expression de l'altitude
), donner l'expression de l'altitude 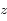 en fonction de la coordonnée
en fonction de la coordonnée 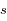 .
.
Donner l'expression de 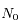 , la densité de colonne au Soleil couchant (
, la densité de colonne au Soleil couchant (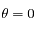 ). On remarque que la densité de particules décroît rapidement avec l'altitude et devient petite pour
). On remarque que la densité de particules décroît rapidement avec l'altitude et devient petite pour 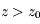 ; on peut donc tronquer l'intégrale à une altitude maximum telle que
; on peut donc tronquer l'intégrale à une altitude maximum telle que 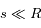 (l'atmosphère est fine par rapport à la taille de la planète).
(l'atmosphère est fine par rapport à la taille de la planète).
Reprendre les questions 1) et 2) pour donner l'expression de 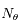 , la densité de colonne pour une position
, la densité de colonne pour une position 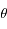 quelconque du Soleil dans le ciel. En plus de l'hypothèse précédente, on évite cette fois les situations proches de l'horizon ; on a donc
quelconque du Soleil dans le ciel. En plus de l'hypothèse précédente, on évite cette fois les situations proches de l'horizon ; on a donc 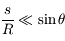 .
.
Le Soleil est au zénith quand 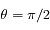 . Calculer le rapport
. Calculer le rapport 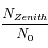 . Pour l'application numérique on prendra
. Pour l'application numérique on prendra 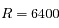 km,
km, 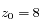 km (échelle de hauteur de l'atmosphère terrestre).
km (échelle de hauteur de l'atmosphère terrestre).
Difficulté : ☆ Temps : 30 min
Le rapport  de l'exercice précédent est appelé masse d'air en Astronomie. C'est le chemin optique parcouru dans l'atmosphère par rapport à la position zénitale. Suffisamment loin de l'horizon, on a en bonne approximation
de l'exercice précédent est appelé masse d'air en Astronomie. C'est le chemin optique parcouru dans l'atmosphère par rapport à la position zénitale. Suffisamment loin de l'horizon, on a en bonne approximation 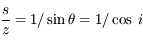 , où i est l'angle zénital (compté à partir de la verticale). Cette valeur correspond à l'approximation plan-paralléle. On cherche toujours à observer les astres sous faible masse d'air (< 2) pour limiter l'extinction atmosphérique.
, où i est l'angle zénital (compté à partir de la verticale). Cette valeur correspond à l'approximation plan-paralléle. On cherche toujours à observer les astres sous faible masse d'air (< 2) pour limiter l'extinction atmosphérique.
On veut maintenant calculer exactement la longueur du chemin optique parcouru par les rayons lumineux dans l'atmosphère pour étudier la validité de l'approximation précédente.
Reprendre la question 3 de l'exercice précédent : dériver une relation entre l'altitude 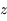 et la coordonnée
et la coordonnée 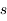 pour une hauteur
pour une hauteur 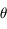 quelconque.
quelconque.
On exprimera cette relation en fonction de l'angle zénital  (compté à partir de la verticale locale).
(compté à partir de la verticale locale).
Résoudre en 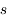 .
.
Tracer 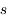 en fonction de l'angle zénital
en fonction de l'angle zénital  et comparer avec l'approximation usuelle en sécante (
et comparer avec l'approximation usuelle en sécante (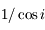 ).
).
Quel est le domaine de validité de l'approximation en sécante ? Quels autres phénomènes affectent la diffusion dans ces conditions ? Conclusion ?