Outils
Auteur: B. Mosser
- Introduction
- Un peu d'optique géométrique
- Introduction
- Foyer primaire
- Observer
- Apprendre
- Simuler
- S'exercer
- Système afocal
- Champ et ouverture
- Observer
- Apprendre
- Simuler
- S'exercer
- S'évaluer
- Diffraction et formation d'image
- Introduction
- Fonction de transfert
- Diffraction et tache image
- Observer
- Apprendre
- Simuler
- S'exercer
- S'évaluer
- Diffraction et résolution
- Observer
- Apprendre
- S'exercer
- Résolution angulaire
- Observer
- Apprendre
- Simuler
- S'exercer
- S'évaluer
- Interférences et spectrométrie
- Introduction
- Résolution spectrale
- Observer
- Apprendre
- Simuler
- S'exercer
- Le réseau : diffraction et interférences
- Le réseau de diffraction : dispersion
- Observer
- Apprendre
- Simuler
- S'exercer
- Le réseau blazé
- Observer
- Apprendre
- S'exercer
- Le réseau et son optique
- Observer
- Apprendre
- S'exercer
- S'évaluer
- Compléments d'optique
- Introduction
- Aberrations géométriques
- Étendue de faisceau
- Apprendre
- S'exercer
- S'évaluer
- Diaphragmes de champ et d'ouverture
- Observer
- Apprendre
- Simuler
- S'exercer
- S'évaluer
- Diffraction par une pupille circulaire
- Diffraction et transformée de Fourier
- Cohérence temporelle
- Observer
- Apprendre
- Simuler
- S'exercer
- Cohérence spatiale
- Observer
- Apprendre
- Simuler
- S'exercer
- Cohérence spatiale et interférométrie
- Observer
- Apprendre
- S'exercer
Introduction
Le chapitre Outils reprend quelques grandes lignes de l'optique géométrique et de l'optique physique, dans une approche clairement astrophysique (les objets sont p.ex. vraiment à l'infini !), nécessaires à la compréhension de la formation des images en astrophysique.

Aperçu du ciel au travers de la trappe d'un télescope.
Crédit :
ESO
Un peu d'optique géométrique
Auteur: B. Mosser
Introduction
Quelques notions d'optique de base sont rappelées, afin de comprendre dans les grandes lignes les principes instrumentaux les plus couramment mis en oeuvre pour acquérir une image en astronomie.

Télescope de Herschel, de diamètre 40 pouces (1798).
Crédit :
Bibliothèque de l'Observatoire de Paris
Foyer primaire
Observer
Observation grand champ

Image du programme de cartographie des amas ouverts du télescope
CFH. Un tel programme nécessite l'observation d'un
champ de grande taille. Amas NGC2099
Crédit :
CFHT
Foyer primaire

La caméra MEGACAM au foyer primaire du télescope CFH.
Crédit :
CFHT
Imagerie grand champ
Les images de grands champs stellaires sont typiquement obtenues par observation au foyer primaire d'un télescope, càd au foyer du miroir primaire collecteur de photons.
Pour en savoir plus :
projet MEGACAM du télescope CFH
Apprendre
 Prérequis
Prérequis
Optique géométrique : vocabulaire de l'optique géométrique, image d'un objet à l'infini.
 Objectifs
Objectifs
Formation d'image au foyer primaire d'un télescope.
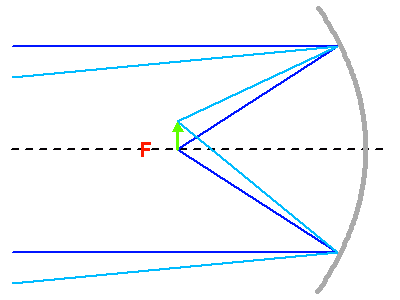
Observation au foyer primaire d'un télescope.
Crédit :
ASM
Collecteur de photons
Le collecteur de photons le plus couramment utilisé est le miroir parabolique, qui convertit après réflection une onde plane en une onde sphérique convergente. Un miroir parabolique conjugue ainsi les sources de lumière situées à l'infini au foyer de la parabole.
Un tel collecteur est équivalent à une lentille de diamètre et focale identique. Une lentille fonctionne en transmission et non en réflexion comme un miroir, mais le principe de fonctionnement est le même. Une lentille transforme une onde plane en onde sphérique, et concentre ainsi la lumière provenant d'une étoile lointaine située sur son axe optique en son foyer.
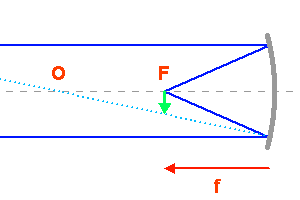
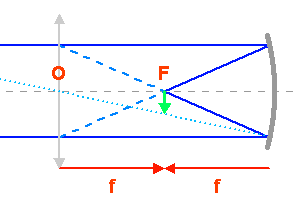
Analogie optique entre un télescope (avec miroir parabolique) et une lunette (lentille). La lentille équivalente est placée au centre du miroir parabolique.
Crédit :
ASM
Lentille équivalente
Tous les systèmes optiques donnant une image réelle d'un objet réel peuvent se résumer en un système comprenant une seule lentille, équivalant au système entier. Dans le cas de l'observation astronomique où, mis à part l'observation in situ apportée par les atterrisseurs des sondes planétaires, l'objet est à l'infini, l'observation a donc lieu au foyer image de cette lentille équivalente.
Simuler

Quelques éléments d'une monture
Localisation du foyer primaire, et donnée de quelques éléments d'un télescope en monture équatoriale.
Convergence au foyer primaire
La parabole a pour propriété de ramener l'ensemble des rayons lumineux en provenance d'une source située à l'infini sur son axe optique (l'onde incidente est alors plane) en un même point : son foyer. On parle alors de conjugaison optique entre le foyer de la parabole et l'infini.
Ceci n'est en fait rigoureusement vrai que pour un rayon incident parallèle à l'axe de la parabole. Un faisceau de rayons parallèles inclinés sur l'axe optique ne va pas converger en un foyer unique, ce qui conduit à l'aberration de sphéricité : le plan focal est en fait incurvé.
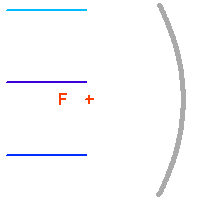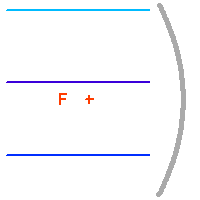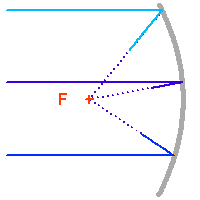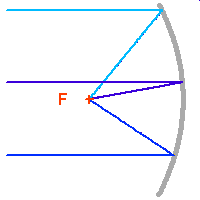
Convergence au foyer primaire : l'onde plane est transformée en onde sphérique.
Crédit :
ASM

Lentille équivalente
L'appliquette ci-jointe montre comment déterminer la lentille simple équivalente à un montage optique recueillant un faisceau provenant de l'infini. Elle se situe à l'intersection des rayons incidents d'une part, et convergeant vers le détecteur d'autre part.

Si besoin est...
L'appliquette ci-jointe rappelle, si besoin est, les règles pour localiser l'image par une lentille d'un objet à distance finie.
S'exercer
Système afocal
Apprendre
 Prérequis
Prérequis
Image d'un objet à l'infini, image d'un objet au foyer.
 Objectifs
Objectifs
L'étude d'un montage optique particulièrement utile en astronomie, le montage afocal, montre que la taille angulaire du champ sur le ciel (champ objet) et le diamètre du faisceau lumineux en sortie de l'instrument sont liés de façon simple au grossissement du système.
Intérêt
Que ce soit pour observer à l'oeil nu, ou pour alimenter un spectromètre, le collecteur a pour fonction de transformer un faisceau à l'infini en un autre faisceau à l'infini.
L'objectif (la lentille ou le miroir côté objet) forme de l'objet à l'infini une image au foyer. L'oculaire (si le détecteur est l'oeil) ou l'optique de chambre permet de regarder cet objet à l'infini.
Montage afocal
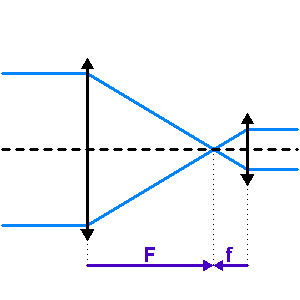
Le montage afocal réunit 2 lentilles (ou équivalents) partageant un foyer : le foyer image de l'une est foyer objet de l'autre.
Crédit :
ASM
Montage afocal
L'association de 2 optiques, l'objectif (côté objet) et l'oculaire (côté oeil) de foyer commun, transforme un faisceau parallèle en un autre faisceau parallèle.
Grossissement du montage afocal
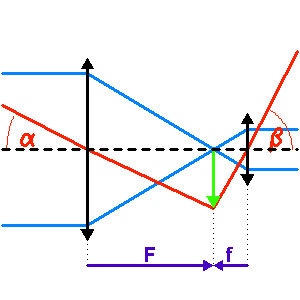
Le grossissement du montage afocal dépend du rapport des focales.
Crédit :
ASM
Grossissement
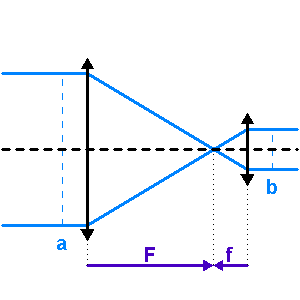
En effet, l'image intermédiaire au foyer commun a pour taille linéaire 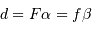 .
.
Faisceau de sortie du montage afocal
Le rapport des diamètres des faisceaux dépend du rapport des focales du montage afocal.
Crédit :
ASM
Taille du faisceau
En effet, l'inclinaison du faisceau entre les foyers s'écrit, dans l'hypothèse des petits angles (pour laquelle 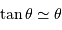 ) :
) : 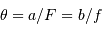 .
.
Champ et dimension
Le diamètre du faisceau en sortie est d'autant plus important que le champ objet est grand.
De ce qui précède, on déduit qu'en sortie d'un montage afocal, une instrumentation de taille réduite (dimensionnée par 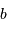 ) va nécessiter un grossissement élevé, et donc ne pourra porter que sur un champ objet de taille restreinte.
) va nécessiter un grossissement élevé, et donc ne pourra porter que sur un champ objet de taille restreinte.
La notion d'étendue de faisceau généralise cette idée.
S'exercer
Champ et ouverture
Observer
Champ d'étoiles

Aperçu d'une portion du ciel austral au travers de la trappe d'ouverture d'un télescope. On distingue le miroir secondaire et son support.
Crédit :
ASM
La galaxie M31 dans la constellation d'Andromède

Grand champ autour de la galaxie M31. M31, galaxie jumelle de la Voie Lactée, est l'un des rares objets extragalactiques visibles à l'oeil nu).
Crédit :
ASM
La galaxie M31

Petit champ autour de M31, obtenu avec un fort grossissement.
Crédit :
ASM
Viser !
Viser un objet, c'est arriver à positionner précisément un collecteur et son instrument d'analyse. Ensuite, selon les objectifs scientifiques, on s'intéresse à un champ plus ou moins grand. La taille du champ est reliée aux propriétés du collecteur et de l'instrumentation.

Lunette ancienne. Le tube focal est très long par rapport au diamètre de la lentille primaire.
Crédit :
Bibliothèque de l'Observatoire de Paris

Télescope infrarouge VISTA de l'ESO, très ouvert d'après son aspect très ramassé.
Crédit :
ESO

Antenne de 30-m de l'
IRAM.
Crédit :
IRAM
Angle d'ouverture
L'angle d'ouverture d'un collecteur de lumière mesure le rapport entre le diamètre du collecteur et la focale résultante.
Les instruments anciens et les lunettes présentent des angles d'ouverture fermés : le tube focal, de longueur très voisine de la focale résultante, est long et grand devant le diamètre collecteur. Les collecteurs récents et/ou de grand diamètre présentent de grands angles d'ouverture, pour limiter leur longueur. Il en est de même des antennes submillimétriques.

Plan focal du satellite Kepler, pour la recherche d'exoplanètes sur un grand champ d'observation (de l'ordre de 10 deg de côté).
Crédit :
NASA
Plan focal
L'observation sur un grand champ nécessite un grand détecteur. Ceci est aujourd'hui réalisé par la juxtaposition de plusieurs détecteurs bidimensionnels de lumière comme les CCD ou les CMOS.
Apprendre
 Prérequis
Prérequis
Optique géométrique
 Objectifs
Objectifs
Former une image dans de 'bonnes' conditions nécessite de bien dimensionner une optique ; le champ est l'une des grandeurs importantes à considérer. Il dépend des propriétés d'ouverture du collecteur.
Ouverture d'un télescope
Un télescope se caractérise par sa focale résultante 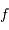 et par le diamètre
et par le diamètre 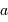 du collecteur.
du collecteur.
 Définition
Définition
L'angle d'ouverture d'un instrument est le rapport entre le diamètre et la focale résultante, soit, avec les notations proposées, 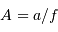 .
.
Le nombre d'ouverture d'un télescope est le rapport inverse.
Comme en photographie, on parle d'un instrument ouvert à 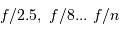 avec respectivement les nombres d'ouverture
avec respectivement les nombres d'ouverture 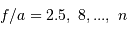 .
.
Exemples typiques d'ouverture : de 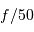 à
à 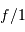 .
.
Plus le nombre d'ouverture est petit, plus le télescope est ouvert (grand angle d'ouverture) et admet des rayons de grande inclinaison. Un petit nombre d'ouverture correspond à une courte focale, ou à un grand diamètre.
Les télescopes les plus récents (télescopes optiques, radiotélescopes), de par leur grand diamètre collecteur, sont en général très ouverts, afin de limiter la longueur de leur focale, et donc leur encombrement.
Champ objet
Le champ objet est la région du ciel effectivement observée dans de bonnes conditions (stigmatisme suffisant pour la qualité d'image requise ; éclairement du champ uniforme, sans vignetage). Son extension dépend du collecteur, et de l'instrumentation et de son grossissement.
Avec 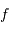 la focale résultante d'un collecteur et
la focale résultante d'un collecteur et 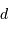 la taille du détecteur effectivement éclairée, le champ objet
la taille du détecteur effectivement éclairée, le champ objet 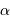 s'écrit simplement (dans l'approximation des petits angles) :
s'écrit simplement (dans l'approximation des petits angles) :
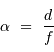
Comme l'angle d'ouverture, le champ objet décroît si la focale 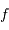 du télescope augmente.
du télescope augmente.
Simuler
Ouverture d'un faisceau
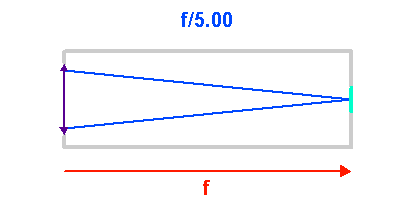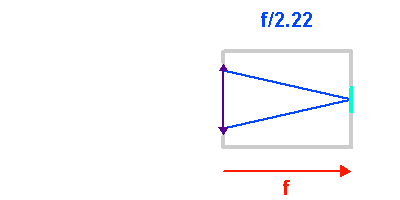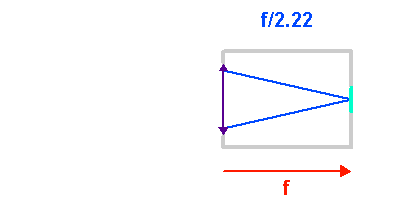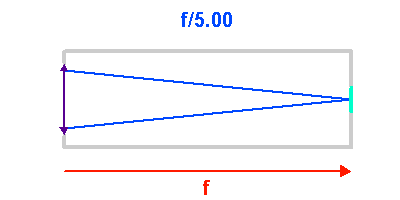
A diamètre collecteur fixé, plus la focale est courte, plus l'ouverture géométrique du télescope est importante (et corrélativement le nombre d'ouverture petit).
Crédit :
ASM
Ouverture du faisceau
L'animation illustre comment l'ouverture géométrique d'un télescope varie avec la focale d'un collecteur. Plus le télescope est ouvert, plus l'inclinaison des rayons dans le télescope est importante.
Champ objet
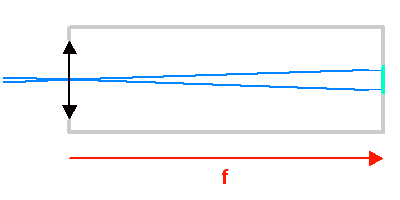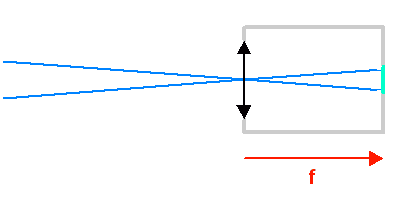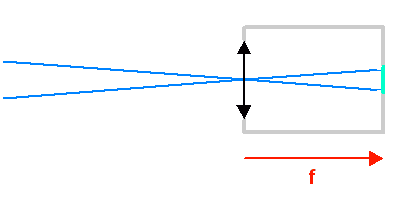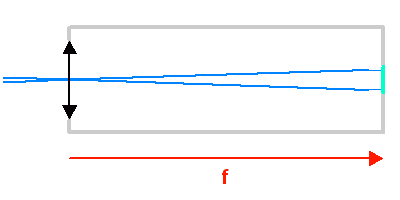
La taille linéaire de l'image dans le plan focal étant fixée (ici par un détecteur au foyer), plus la focale est courte, plus le champ de vue est important.
Crédit :
ASM
Champ objet
L'animation illustre comment la taille du champ objet varie avec la focale du collecteur.
Mesure du champ
Les données de l'appliquette ci-jointe reportent les mesures effectuées par un groupe d'étudiants observant au télescope de 60 cm du campus de Meudon de l'Observatoire de Paris. Le but de l'observation, premier contact avec le télescope, consiste à prendre conscience que le champ accessible au pointage est restreint, et qu'il est nécessaire pour pouvoir pointer un objet de garantir une précision angulaire, exprimée en seconde de temps et non d'angle, meilleure que 30 s.
Traversée du champ 
L'entraînement du télescope étant arrêté, les étoiles défilent dans le champ : les durées T1 et T2 mesurent la traversée du diamètre du champ par des étoiles brillantes, pour deux grossissements différents.
- Vérifier à l'aide de l'appliquette que la durée de traversée pour une cible de déclinaison
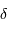 est proportionnelle à
est proportionnelle à 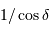
- En déduire la mesure du diamètre angulaire du champ dans chacun des cas.
S'exercer
 Champ objet
Champ objet
Difficulté : ☆
Temps : 10 min
Question 1)
Déterminer la focale équivalente d'un télescope de diamètre
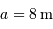 ouvert à f/3.75.
ouvert à f/3.75.
Application de la définition de l'ouverture d'un télescope.
Question 2)
L'image est formée sur une matrice CCD de 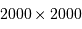 pixels, avec des pixels carrés de côté
pixels, avec des pixels carrés de côté 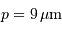 .
Quel champ voit un pixel ? Déterminer le champ de vue total dans
le ciel.
.
Quel champ voit un pixel ? Déterminer le champ de vue total dans
le ciel.
Faire un schéma de l'image au foyer d'un faisceau incliné d'un angle 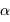 .
.
 Observation à la table équatoriale de Meudon
Observation à la table équatoriale de Meudon
Difficulté : ☆
Temps : 20 min
Le télescope T60, installé sur la table équatoriale du campus de
Meudon de l'Observatoire de Paris, présente un miroir primaire de
diamètre 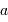 =60 cm.
=60 cm.
Question 1)
Déterminer son nombre d'ouverture, sachant que sa focale
résultante vaut F = 9 m.
Application directe de la définition de l'ouverture.
Question 2)
Quel grossissement est obtenu avec des oculaires de distance focale 45 ou 30 mm ?
Si l'on parle d'oculaire, c'est pour observer à l'oeil, ceci conditionne le montage optique.
Le montage doit être afocal.
Question 3)
L'ouverture du faisceau image étant de toutes façons inférieure au champ de vision de l'oeil (environ 60 degrés), déterminer le diamètre maximal du champ objet pour un oculaire de focale 45 ou 30 mm.
Revoir l'expression du grossissement.
S'évaluer
 Mesure du champ
Mesure du champ
Difficulté : ☆☆
Temps : 30 min
Cet exercice s'appuie sur les données de l'appliquette "mesure du champ". Il est préférable d'avoir auparavant traité la section Systèmes de coordonnées .
Question 1)
Montrer par un schéma qu'une étoile de déclinaison 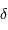 possède, du fait de la rotation diurne, une vitesse angulaire proportionnelle à
possède, du fait de la rotation diurne, une vitesse angulaire proportionnelle à 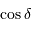 .
.
[2 points]
Question 2)
L'étoile traverse le champ de l'instrument, de diamètre angulaire 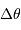 en une durée
en une durée 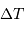 . Montrer que l'on a :
. Montrer que l'on a :
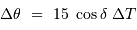
si le champ est mesuré en seconde d'arc et la durée en seconde de temps.
[2 points]
Question 3)
Vérifier la relation précédente avec les données de l'appliquette (pour tracer la fonction 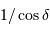 : sélectionner la 1ère ligne de la 3ème colonne (C1), et demander le calcul : = 1./15./cos(pi * B1 / 180.))
: sélectionner la 1ère ligne de la 3ème colonne (C1), et demander le calcul : = 1./15./cos(pi * B1 / 180.))
[1 points]
Question 4)
Avec les données de l'appliquette, déterminer dans les 2 cas (avec des grossissements différents) le diamètre angulaire du champ objet.
[1 points]
Question 5)
Les grossissements, dépendants de l'oculaire utilisé, valent respectivement 140 et 300. Montrer que les champs images ont une taille analogue au champ de vue de l'oeil humain, de l'ordre de 60 degrés.
[1 points]
Diffraction et formation d'image
Auteur: Benoît Mosser
Introduction
Que l'observation astrophysique serait facile si l'image d'un point était un point !
Dans le meilleur des cas, l'image d'une étoile est une tache de diffraction, mais le plus souvent, c'est une structure spatialement et temporellement bien plus complexe.
Le but de cette section est de comprendre et d'interpréter la structure spatiale d'une image simple.

Représentation des Pléiades, à l'époque néo-babylonienne, en 200 avant JC. Les étoiles ont une forme... d'étoile
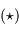
!
Crédit :
ASM
Fonction de transfert
Observer
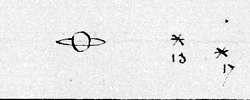
Saturne, et ses satellites, observés par
J.D. Cassini en 1673, confondus avec des étoiles.
Crédit :
Bibliothèque de l'Observatoire de Paris
Le mot étoile codé en écriture cunéiforme.
Crédit :
ASM

Mizar, dans la Grande Ourse : diffraction, turbulence, surexposition, réflexions parasites s'ajoutent et s'emmêlent.
Crédit :
CDS
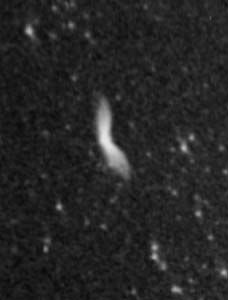
Le défaut de coma apparaît en tout point éloigné du centre optique. L'image d'un tel point s'allonge ; elle apparaît telle une petite comète, d'où le nom de cette aberration optique.
Crédit :
D. Césari
L'image d'un point
L'astrophysique nous apprend que les étoiles sont des sphères gazeuses, tellement lointaines qu'il est impossible dans la plupart des cas de les résoudre spatialement. Pourquoi alors les représente-t-on et les voit-on avec diverses formes tellement différentes d'un point ou d'un cercle, mais le plus souvent proches du symbole  ?
?
En fait, plusieurs phénomènes se conjuguent pour aboutir à ces formes
et les expliquer :
- Les aberrations optiques diverses, qui déforment l'image géométrique perçue : coma, défaut de mise au point.
- La diffraction, qui fait que l'image d'un point ne peut pas être un point
- La turbulence atmosphérique, qui brouille l'information spatiale
- Les propriétés des récepteurs.

Exemple de fonction d'étalement du point de l'instrument NAOS. Avec correction d'optique adaptative, la FEP se rapproche d'une figure d'Airy.
Crédit :
LESIA
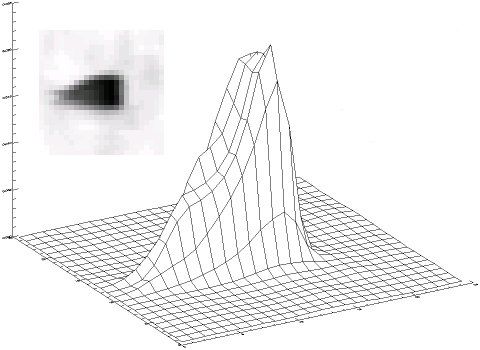
Fonction d'étalement du point de la voie exoplanète du satellite CoRoT.
Crédit :
CNES
Fonction d'étalement du point
L'image d'un objet ponctuel, non ponctuelle, est donnée par la fonction de transfert de la chaîne de détection. Cette fonction de transfert, dans ce cas précis, s'appelle fonction d'étalement du point, soit FEP en français ou PSF en anglais (point spread function).
Connaître ou estimer la fonction d'étalement du point est une étape indispensable pour le traitement d'image. Autre exemple : la FEP d'une image obtenue par le satellite CoRoT.
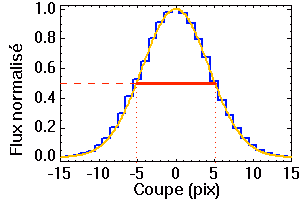
Définition de la largeur à mi-hauteur.
Crédit :
ASM
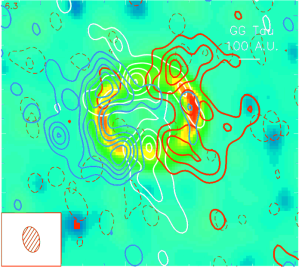
La tache image est explicitement indiquée sur l'
image de la
source GG Tauri enregistrée dans la raie de
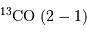
. Cette source correspond à un système stellaire binaire en formation. Le flux millimétrique à 1.3 mm codé en fausse couleur montre une structure en anneau.
Crédit :
IRAM
Largeur à mi-hauteur
On rend compte d'une fonction d'étalement du point simple par sa largeur à mi-hauteur.
Souvent, les images obtenues dans les longueurs d'onde millimétriques ou radio
mentionnent explicitement l'extension à mi-hauteur de la tache image élémentaire.

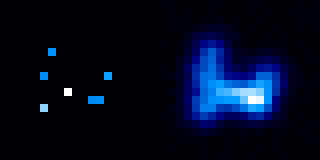
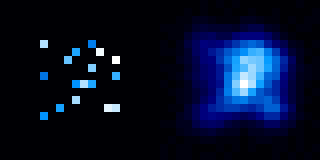
Simulation de champs stellaires. L'étalement de l'image de plusieurs sources ponctuelles bien distinctes peut conduire à l'apparence d'une source étendue.
Crédit :
ASM
FEP et résolution spatiale
La résolution spatiale dépend intimement de la FEP : distinguer les détails d'un champ s'avère impossible aux échelles plus petites que la largeur à mi-hauteur de la FEP.
Apprendre
 Objectifs
Objectifs
La fonction de transfert, l'image d'un objet ponctuel, transcrit la qualité de la formation d'image.

Fragment d'image, et estimation de sa fonction d'étalement du point.
Les différentes images des sources stellaires correspondent à la convolution de l'image idéale stellaire par la
FEP.
Crédit :
ASM
Fonction de transfert/fonction d'étalement du point
La fonction de transfert de la chaîne de collecte du signal, ou fonction d'étalement du point, rend compte de l'image non ponctuelle d'un objet ponctuel. Cette fonction de transfert relate toutes les modifications apportées à l'image idéale.
Par définition, l'image d'une source ponctuelle est la fonction de transfert, au bruit près.
L'image d'une source non ponctuelle est son image géométrique idéale convoluée par la fonction de transfert. Au mieux, la fonction de transfert rend compte de la diffraction. Mais elle inclut aussi tous les autres défauts de la chaîne de détection.
Résolution, et largeur à mi-hauteur
Le lien entre la fonction de transfert et la résolution est immédiat : il n'est pas possible d'obtenir de détails plus fins que la fonction de transfert.
Il est souvent suffisant de rendre compte de la fonction de transfert, si elle présente la symétrie circulaire, par sa largeur à mi-hauteur.
Contributions à la fonction d'étalement du point
Les pages suivantes décrivent la contribution de la diffraction à la fonction de transfert. Les aberrations optiques ne sont pas abordées. Le rôle de la turbulence atmosphérique est traité dans une section à part.
Simuler
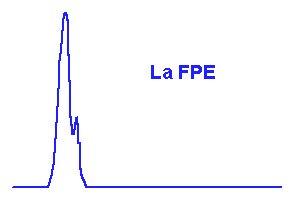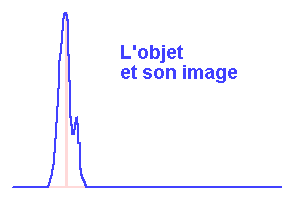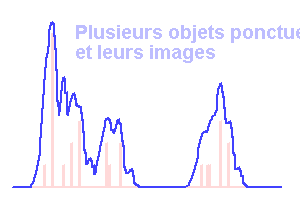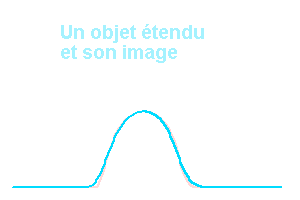
FPE, objets et images.
Crédit :
ASM
La fonction d'étalement du point à l'oeuvre
L'animation ci-dessous décompose, dans un cas unidimensionnel, la transformation d'un objet en son image via la FPE.
Diffraction et tache image
Observer

Image d'une étoile de l'amas ouvert NGC 188. Cet amas d'étoiles a servi pour l'étalonnage de la fonction d'étalement du point du télescope spatial Hubble. La tache image rend essentiellement compte de la figure de diffraction d'une source ponctuelle.
Crédit :
HST



Différentes tailles de collecteur, et taches de diffraction associées : l'extension de la tache de diffraction est inversement proportionnelle au diamètre du collecteur.
Crédit :
ASM
Influence du secondaire

Le front d'onde incident, avec l'occultation par le miroir secondaire, et la figure de diffraction associée. A la figure de diffraction du miroir primaire se superpose celle de l'occultation secondaire.
Crédit :
ASM
Influence du miroir secondaire
Le plus souvent, le miroir secondaire occulte le faisceau incident.
Le front d'onde initial n'est pas seulement découpé par le miroir primaire, il est aussi amputé de sa partie centrale. La tache de diffraction d'un télescope possédant un miroir secondaire sur son axe optique est moins lumineuse mais plus étendue que celle du miroir primaire considéré seul. La perte de flux lumineux est due à l'occultation par le miroir secondaire d'une partie du faisceau.
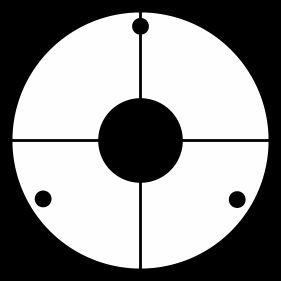
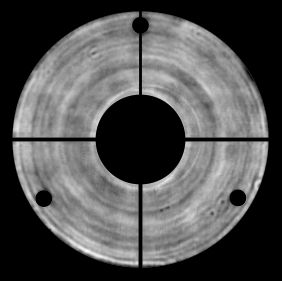
Pupille du télescope HST (théorique et observée), avec obstruction centrale du miroir secondaire, et support de celui-ci par une araignée à 4 branches.
Crédit :
IRAM
Influence de l'araignée
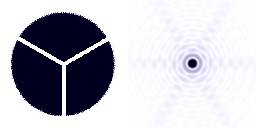
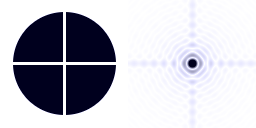

Le support du miroir secondaire, également appelé araignée, qui occulte le faisceau primaire, rajoute sa signature à la figure de diffraction.
Crédit :
ASM
Influence du support du miroir secondaire
L'araignée, le support du miroir secondaire, occulte également la pupille. Sa signature apparaît clairement pour une source brillante.
Étoile ou galaxie ?

Champ galactique avec des étoiles au premier plan. Les objets étendus, dont celui dans le coin inférieur droit, ne semblent pas présenter d'aigrettes de diffraction, contrairement aux objets ponctuels.
Crédit :
HST
Objet ponctuel ou non
Sur une image, certains objets semblent soumis à la diffraction, avec de belles aigrettes de diffraction, alors que d'autres non. Les premiers sont des objets non résolus (typiquement une étoile), alors que les seconds sont étendus (typiquement une galaxie). Les contributions des différents points sources d'un objet étendu, non superposées, sont diluées et ne se distinguent pas.
Apprendre
 Prérequis
Prérequis
Diffraction de Fraunhofer. Diffraction par une fente rectiligne.
 Objectifs
Objectifs
Déterminer et dimensionner le rôle de la diffraction dans la formation d'image.
Tache image pour un collecteur de section circulaire
Le facteur 1.22 est d'origine géométrique (dans le cas d'une fente rectiligne de largeur 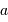 , le facteur est 1) ; c'est la première valeur qui annule la fonction de Bessel qui rend compte de la diffraction par une pupille circulaire.
, le facteur est 1) ; c'est la première valeur qui annule la fonction de Bessel qui rend compte de la diffraction par une pupille circulaire.
Il est physiquement impossible de distinguer des détails plus petits que cette tache image : la diffraction fixe la résolution ultime d'un collecteur unique.
Pour comparer la tache de diffraction au diamètre angulaire des objets étudiés, il est utile de connaître l'ordre de grandeur :
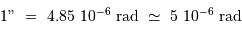
et aussi
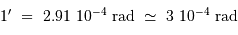
De l'intérêt d'un collecteur de grand diamètre
La relation entre la taille angulaire de la tache image et le diamètre du collecteur montre directement l'intérêt d'augmenter ce dernier : cela permet d'avoir des images angulairement mieux résolues.
Simuler

Diffraction d'une onde mécanique
L'appliquette ci-jointe montre la diffraction d'une vague de surface par une ouverture étroite.

Influence du support du miroir secondaire
Le support du miroir secondaire, appelé araignée, occulte le faisceau primaire, et rajoute sa signature à la figure de diffraction, surtout pour les objets brillants.

Taches images
L'appliquette ci-dessous calcule la tache image de divers collecteurs.
Visualiser l'influence, avec un seul collecteur (avec circulaire comme choix de pupille) :
- du diamètre du collecteur,
- de la longueur d'onde (identifier la pleine échelle de la tache image, exprimée en unité angulaire),
- de l'éventuelle occultation par un miroir secondaire,
Visualiser l'influence, avec un collecteur et une occultation du secondaire (avec circ+ obst. second. comme choix de pupille) :
- de l'éventuelle occultation par un miroir secondaire,
- de la taille relative de cette occultation
Visualiser l'influence, avec plusieurs collecteurs (avec 2 circulaires ou bien croix d'Angel):
- du rapport entre leur diamètre et leur éloignement,
- de la configuration des collecteurs.
S'exercer
Ciel profond

Champ de galaxies.
Crédit :
HST
 Diffraction or not diffraction ?
Diffraction or not diffraction ?
Difficulté : ☆
Temps : 10 min
L'appliquette ci-jointe montre l'étoile double Mizar, dont les 2 composantes sont séparées de 14.4", observées dans le rouge à 800 nm, par un télescope de la classe 1-m.

Question 1)
Déterminer l'échelle de l'image, en "/pixel.
Établir l'échelle en se repérant par rapport au système double.
Question 2)
Déterminer le rayon des anneaux concentriques entourant chaque étoile.
Travailler avec l'outil cercle
Question 3)
Ces anneaux peuvent-ils être dus à la diffraction par le miroir primaire, secondaire (ces anneaux se situent à 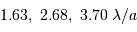 ) ?
) ?
Calculer la tache de diffraction.
S'évaluer
 Dans quel sens ?
Dans quel sens ?
Difficulté : ☆
Temps : 20 min

Radiotélescope de Nançay : vue grand angle de l'ensemble. Le miroir plan orientable, à gauche, vise dans la direction méridienne ; le faisceau est renvoyé vers le miroir sphérique, à droite, qui le focalise au centre.
Crédit :
Observatoire de Paris

Radiotélescope de Nançay : l'antenne sphérique
Crédit :
Observatoire de Paris

Radiotélescope de Nançay : les 3 cornets de l'ancien chariot focal (en service jusqu'en 2000).
Crédit :
Observatoire de Paris
Les figures ci-jointes montrent le miroir primaire et l'ancien foyer (utilisé jusqu'en 2000) du grand radiotélescope de Nançay (Observatoire de Paris).
Question 1)
L'antenne principale a une taille de 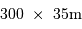 .
Estimer le profil de la tache angulaire de diffraction, pour les trois longueurs d'onde de travail 9, 18 et 21 cm (raie de couplage spin-orbite de l'hydrogène atomique).
.
Estimer le profil de la tache angulaire de diffraction, pour les trois longueurs d'onde de travail 9, 18 et 21 cm (raie de couplage spin-orbite de l'hydrogène atomique).
[2 points]
Question 3)
Discuter de la forme et de l'orientation de ces cornets.
[1 points]
Diffraction et résolution
Observer
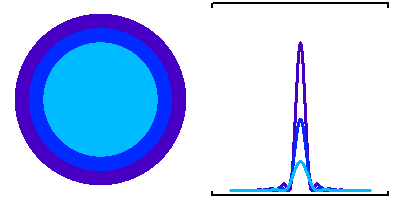
Différentes tailles de collecteur, et taches de diffraction associées.
Le flux reçu par unité d'élément d'image varie comme la puissance quatrième du diamètre collecteur.
Crédit :
ASM
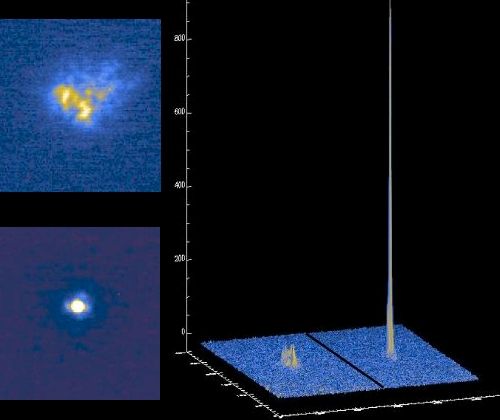
Image enregistrée sans ou avec optique adaptative.
Crédit :
ESO
De l'intérêt d'arriver à la tache de diffraction
Il est utile de s'attacher à récupérer une forte densité de flux sur les pixels, comme le montre cet exemple de traitement par optique adaptative.
Critère de Rayleigh

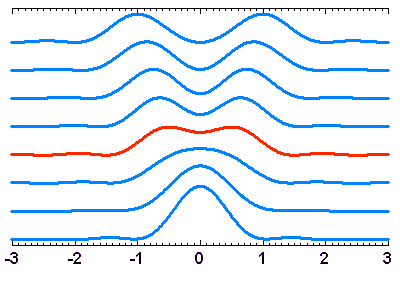
Le critère de Rayleigh ; la résolution des 2 sources (images, et coupes de ces images) nécessite une séparation de l'ordre de
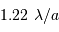
.
L'abscisse du profil en coupe est directement donnée en unité
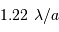
.
Crédit :
ASM
Le critère de Rayleigh
Les schémas ci-joints illustrent le critère de Rayleigh, qui définit la condition pour distinguer 2 objets de magnitude identique angulairement voisins.
Apprendre
 Prérequis
Prérequis
Diffraction de Fraunhofer.
 Objectifs
Objectifs
Montrer le lien entre la diffraction et la résolution ultime d'un système optique.
Critère de Rayleigh
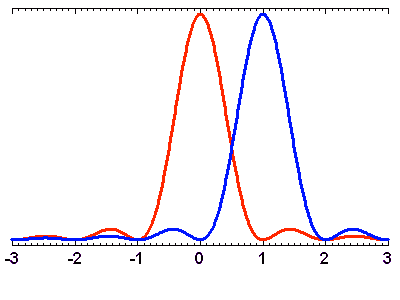
Le critère de Rayleigh ; l'abscisse est ici directement en unité
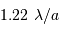
Crédit :
ASM
Critère de Rayleigh
Le critère de Rayleigh permet de préciser à quelle condition
on peut distinguer 2 sources ponctuelles : il faut que le premier zéro
de la figure de diffraction de l'une corresponde au maximum de l'autre.
S'exercer
 Bonnes résolutions
Bonnes résolutions
Difficulté : ☆
Temps : 10 min
On cherche à résoudre différents objets, en lumière visible. Déterminer le diamètre minimal du collecteur nécessaire, la résolution angulaire étant limitée par la diffraction, dans les cas suivants.
Question 1)
Un cratère de 20 km sur la Lune (distante de 380 000 km).
Estimer la taille angulaire du cratère, et la comparer à la résolution limitée par la seule diffraction : 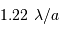
Question 2)
Une étoile double, dont les composantes sont séparées de 0.2".
Résolution angulaire
Observer
Une histoire d'anneaux
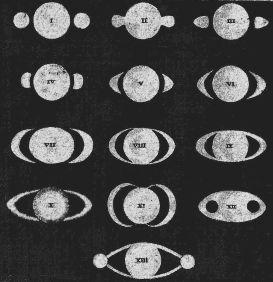
Diverses interprétations rendant compte des observations des anneaux de Saturne
(compilation d'observations de Galilée, Hévélius, Gassendi) : 2 satellites, des protubérances, des anses...
Crédit :
Bibliothèque de l'Observatoire de Paris
Cratères lunaires

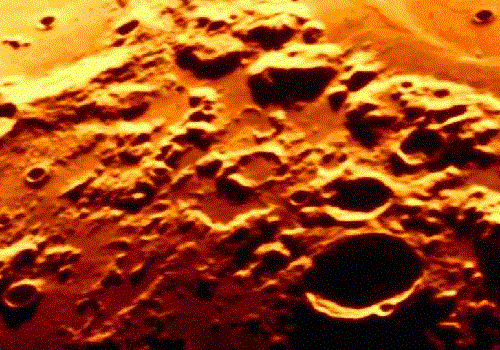
La Lune observée avec une lunette de 70 mm, et avec la caméra grand champ du télescope
CFH.
Crédit :
CFHT
Résolution angulaire et qualité d'image
L'apparence d'un objet dépend intimement de la finesse des détails les plus fins. Ainsi, l'identité des anneaux de Saturne n'a été dévoilée que lorsque des observations de qualité suffisante ont permis de trancher parmi les multiples interprétations alors discutées.
Le gain en résolution angulaire permet une meilleure identification des images ;
par exemple pour la Lune observée avec un petit collecteur, ou bien un grand collecteur corrigé des premiers ordres de la turbulence.
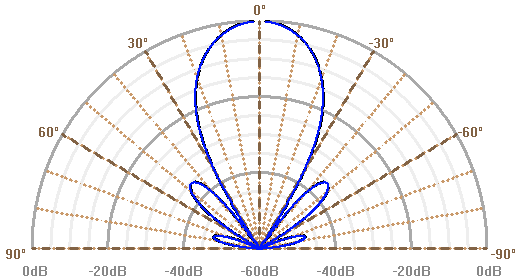
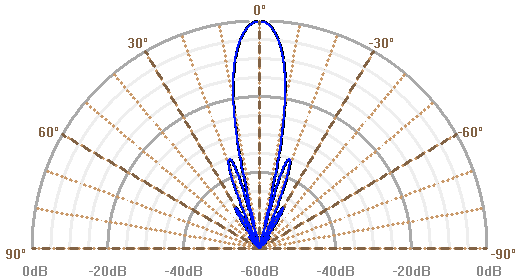
Lobes d'antenne, en diagramme polaire. L'amplitude du lobe est donnée en échelle logarithmique, mesurée en dB d'atténuation par rapport à la réponse dans l'axe.
Crédit :
ASM
Résolution angulaire et longueur d'onde
A grande longueur d'onde, la diffraction empêche une vision spatialement bien résolue, sauf à avoir un collecteur de très grande taille. Pour une antenne radio unique, circulaire de diamètre correspondant à un nombre limité de longueurs d'onde, le lobe d'antenne apparaît très étendu.
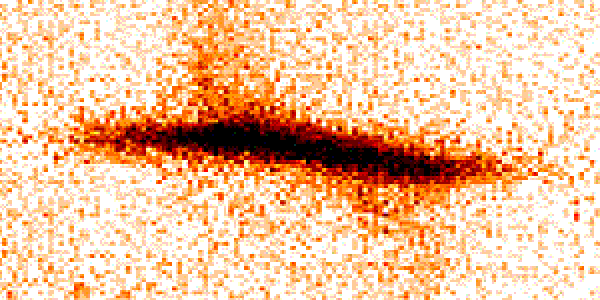
L'objet NGC7782, vu par le spectroimageur UVES du VLT (couleur en vidéo inverse). La pixélisation apparaît clairement.
Crédit :
ESO
Résolution angulaire et taille d'un élément d'image
Il est important, pour enregistrer une image en respectant sa résolution angulaire, d'avoir des éléments d'image ou pixels convenablement dimensionnés.
Apprendre
Vers la haute résolution angulaire
La quête de résolution angulaire de plus en plus fine nécessite des bases de collecte d'observation de plus en plus étendues. Comme la taille d'un élément collecteur est limitée (en 2018 : à 8 m en mono-pupille pour les télescopes du VLT, Gemini Nord et Sud, Subaru ; 10 m en pupille segmentée pour les 2 télescopes Keck; bientôt 39 mètres pour l'ELT européen de l'ESO), on se tourne vers l'interférométrie.
La pixélisation
La résolution angulaire ne dépend pas uniquement des conditions de collecte du signal, avec un collecteur de diamètre plus ou moins grand ; elle dépend aussi de la façon dont l'image est finalement enregistrée.
L'enregistrement du signal, aujourd'hui quasi uniquement sous forme numérique, doit être adapté à la résolution.
Afin que la taille finie des pixels ne limite pas la résolution, le critère de Shannon énonce qu'il faut au moins 2 pixels par élément de résolution.
Par exemple, si la résolution visée est de 0.4", un pixel doit couvrir 0.2".
S'il est plus gros, sa taille va limiter la résolution.
S'il est plus petit, le signal sera suréchantillonné spatialement, sans gain d'information spatiale.
Simuler
Résolution angulaire variable

Animation montrant l'aspect de la galaxie M31 à diverses résolutions spatiales, balayant les différents aspects avec un appareil très peu résolvant, jusqu'à un bon télescope.
Crédit :
ASM
Résolution angulaire
L'aspect de galaxie M31 (d'Andromède) dépend de la résolution angulaire instrumentale. Plus elle est élevée, plus les détails observables sont fins.
Taille du pixel variable
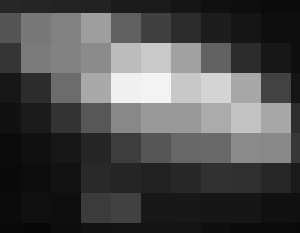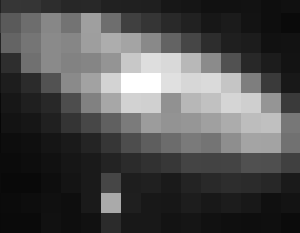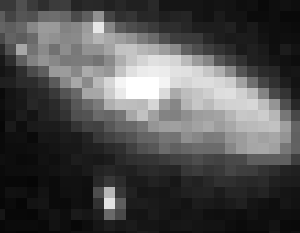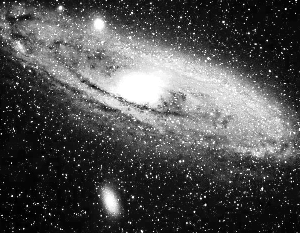
Animation montrant la galaxie M31, à divers niveaux de pixélisation. Plus la taille du
pixel est petite, meilleure est la résolution angulaire, donc la résolution spatiale.
Crédit :
ASM
Résolution angulaire et taille d'un élément d'image
La résolution est également limitée par la pixélisation, qui conditionne la FEP.
S'exercer
 Choix d'une caméra
Choix d'une caméra
Difficulté : ☆
Temps : 20 min
Dans le cadre du développement d'un instrument, on cherche à choisir la caméra optimale, càd celle qui réalisera les performances demandées, pour un coût minimal. Un constructeur propose
des caméras de taille 1k 1k (1000 px par 1000 px), 1k
1k (1000 px par 1000 px), 1k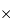 2k,
2k
2k,
2k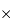 2k, et 2k
2k, et 2k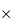 4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
Question 1)
Le collecteur présente un diamètre de 3.6 m, pour une ouverture f/3.3
En déduire la focale équivalente, puis le lien entre la taille physique 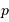 du pixel et le champ
du pixel et le champ 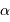 qu'il couvre.
qu'il couvre.
Revoir la relation entre ouverture, focale et diamètre.
Si 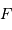 est la focale, alors
est la focale, alors 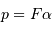
Question 2)
Le champ doit couvrir 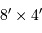 , avec une résolution de
, avec une résolution de 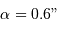 .
En déduire la caméra appropriée.
.
En déduire la caméra appropriée.
Déterminer la taille angulaire d'un pixel.
S'évaluer
 Saturne et ses anneaux
Saturne et ses anneaux
Difficulté : ☆☆
Temps : 15 min

Géométrie simplifiée.
Crédit :
ASM
L'identification de la nature des anneaux de Saturne ne fut pas sans peine. Le but de l'exercice est de déterminer la résolution angulaire nécessaire permettant de le faire.
A l'opposition, Saturne s'approche à 8.5 UA de la Terre. Le rayon planétaire vaut 60 000 km, les rayons interne et externe des principaux anneaux respectivement 90 000 et 140 000 km. On suppose que les anneaux sont observés sous grand incidence (l'incidence maximale est de l'ordre de 26 deg), pour être dans un cas favorable (lorsque la Terre passe dans le plan des anneaux... on ne les voit simplement pas). Néanmoins, pour simplifier les calculs, on s'intéresse au seul problème 1-D portant sur la seule variable radiale, selon la géométrie de la figure jointe.
Question 1)
Refaire à l'échelle schéma de Saturne et de ses anneaux. Déterminer le plus petit élément bien contrasté à observer pour pouvoir identifier les anneaux.
[1 points]
Question 2)
La résolution devant être au-moins d'un facteur 2 plus précis que la taille du plus petit élément à identifier, déterminer la résolution nécessaire.
[2 points]
Interférences et spectrométrie
Auteur: Benoît Mosser
Introduction
Analyser spectralement la lumière est à la base de l'astrophysique. Cette section a pour but de rappeler quelques principes de physique permettant une analyse spectrale efficace. L'instrumentation nécessaire s'appuie sur le réseau de diffraction, bien plus efficace pour disperser la lumière qu'un prisme. Mais la mise en oeuvre du réseau nécessite un environnement précis.
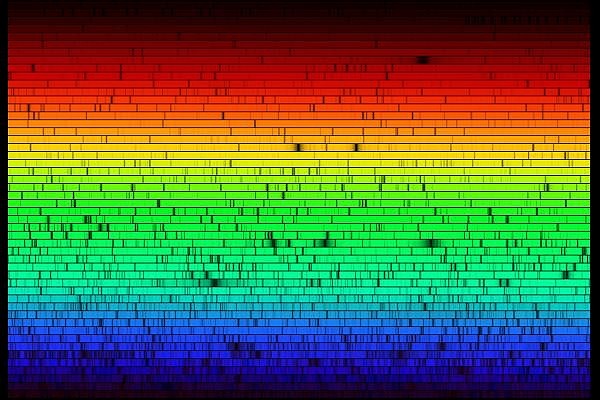
Le spectre solaire à haute résolution spectrale, obtenu avec un spectromètre échelle. Les couleurs comme l'aspect du spectre résultent d'un traitement d'image complexe.
Crédit :
NOAO
Résolution spectrale
Observer
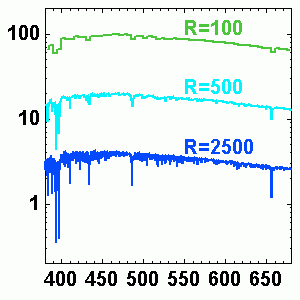
Spectre stellaire visible théorique à diverses résolutions spectrales
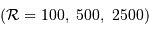
. La luminosité par intervalle spectral (unité arbitraire) est inversement proportionnelle à la résolution.
Crédit :
ASM
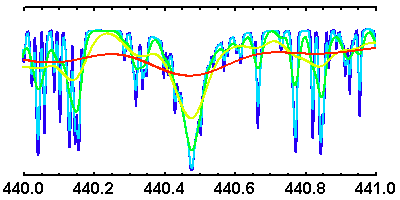
Échantillon d'un spectre stellaire observé à diverses résolutions spectrales
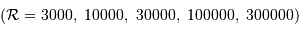
, avec renormalisation du flux.
Crédit :
ASM
Résolution spectrale
Plus la résolution d'un spectre stellaire théorique est élevée :
Apprendre
 Objectifs
Objectifs
Définir les notions de résolution spectrale : élément de résolution ; pouvoir de résolution ; intervalle spectral élémentaire.
Le pouvoir de résolution
Le pouvoir de résolution spectrale mesure la capacité à distinguer deux longueurs d'onde différentes 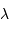 et
et 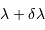 . Il est mesuré par la quantité :
. Il est mesuré par la quantité :
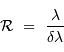
Le pouvoir de résolution est d'autant plus élevé que l'élément de résolution 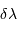 (également appelé résolution spectrale élémentaire ou élément spectral) est petit.
(également appelé résolution spectrale élémentaire ou élément spectral) est petit.
Conversions
Le pouvoir de résolution peut être exprimé avec les diverses grandeurs spectrales (longueur d'onde 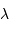 , fréquence
, fréquence 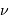 ) :
) :
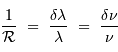
Il peut également être traduit en une vitesse, via l'équivalent Doppler:
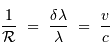
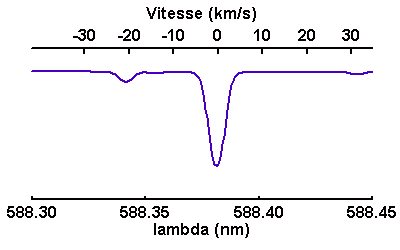
Raie stellaire représentée en fonction de la longueur d'onde ou de la vitesse repérée par rapport au centre de la raie.
Crédit :
ASM
Diverses résolutions
| Instrument | Pouvoir de résolution typique | 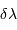 @ 500 nm (nm) @ 500 nm (nm) | vitesse (km/s) |
| Prisme | 500 | 1 | 600 |
| Réseau | 5000 | 0.1 | 60 |
| Réseau blazé | 50000 | 0.01 | 6 |
Simuler
Le doublet du sodium
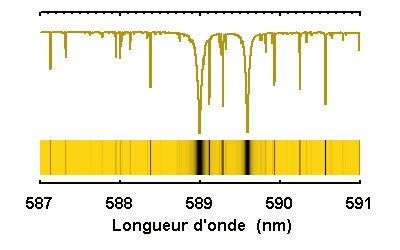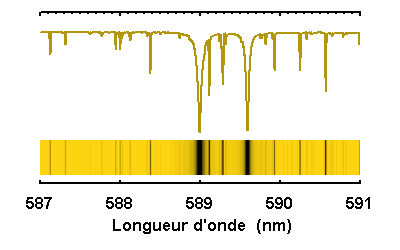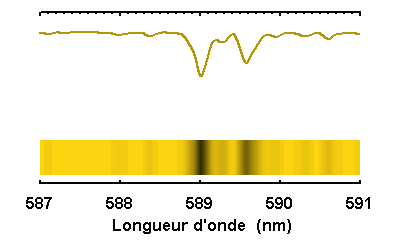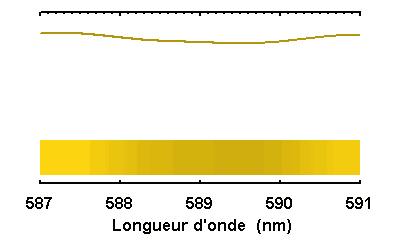
Le doublet jaune du sodium du spectre solaire,
simulé à diverses résolutions spectrales.
Crédit :
ASM
Résolution variable
Selon la résolution spectrale, des raies bien marquées, comme celles du sodium à 589.0 et 589.6 nm, apparaîtront plus ou moins clairement, avec l'identification de raies fines entre les 2 éléments du doublet, ou bien noyées dans le flux continu.
S'exercer
 Résolution et variable spectrale
Résolution et variable spectrale
Difficulté : ☆
Temps : 10 min
Un spectromètre assure un pouvoir de résolution 25 000 dans le visible à 500 nm.
Question 1)
Déterminer la largeur d'un élément spectral élémentaire.
 Quelle résolution ?
Quelle résolution ?
Difficulté : ☆
Temps : 20 min
Le spectre ci-joint (voir l'appliquette) a été enregistré aux
alentours de 440.5 nm. Il s'agit d'estimer sa résolution, en fait
limitée par la résolution instrumentale.

Question 1)
Vaut-il mieux effectuer la mesure sur une raie fine ou une raie large ?
Réfléchir aux causes d'élargissement de la raie.
Question 2)
Estimer alors la résolution instrumentale
Estimer la largeur d'une raie à mi-hauteur
Le réseau : diffraction et interférences
Apprendre
 Prérequis
Prérequis
Même s'il reprend les bases théoriques, ce cours suppose que le réseau a déjà été étudié en physique. Un réseau est alimenté en faisceau parallèle par une fente source, et en donne une série d'images colorées.
 Objectifs
Objectifs
Caractériser les interférences constructives d'un réseau ; voir la distribution de l'énergie dans la figure d'interférence.
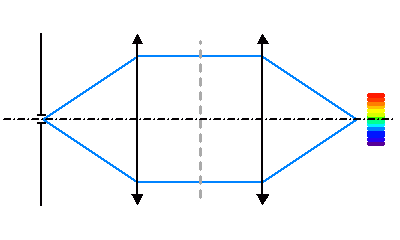
Le réseau donne une série d'images colorées de la fente source.
Crédit :
ASM
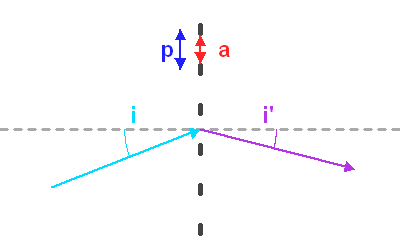
Paramètres du réseau, et définition des angles des faisceaux incident et diffracté.
Crédit :
ASM
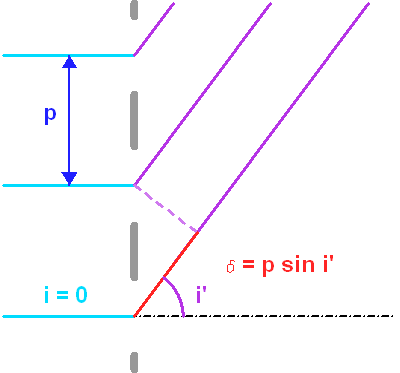
À incidence nulle, la différence de marche entre 2 rayons consécutifs, vaut
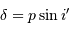
. Elle correspond au déphasage
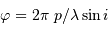
.
Crédit :
ASM
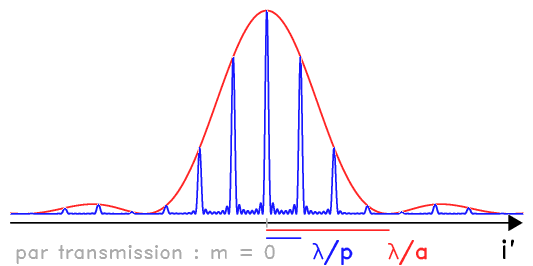
Les interférences se construisent principalement dans le lobe principal de la tache de diffraction d'une fente du réseau (en rouge).
Crédit :
ASM
Le rôle de la diffraction puis des interférences
La diffraction par une fente du réseau détermine les différentes directions vers lesquelles la lumière est envoyée, chacun des fentes du réseau se comportant comme une source secondaire.
Les interférences entre ces différentes sources secondaires construisent les franges d'interférences, d'autant plus fines que le réseau comporte un nombre important de traits (cf. calcul de l'intensité de la figure d'interférence).
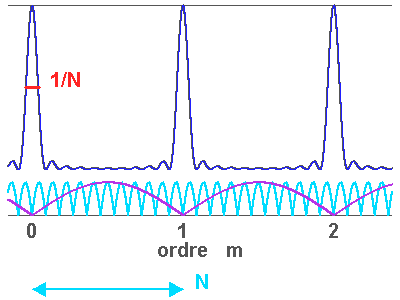
Représentation des numérateur (bleu ciel) et dénominateur (violet) de l'intensité diffractée par le réseau (en bleu). Les pics d'interférence apparaissent pour chaque annulation du terme
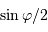
du dénominateur. La finesse des pics d'interférence augmente avec le nombre de traits
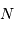
.
Crédit :
ASM
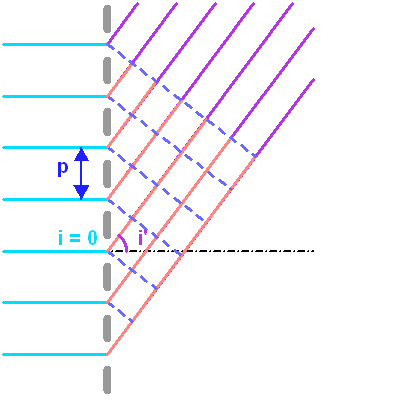
Sommation des différentes amplitudes.
Crédit :
ASM
Intensité de la figure d'interférence
L'intensité de la figure d'interférence est issue du double effet de la
diffraction par une seule fente et des interférences par 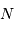 fentes. On s'intéresse dans un premier temps au phénomène d'interférence seul.
On note
fentes. On s'intéresse dans un premier temps au phénomène d'interférence seul.
On note 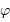 le déphasage entre 2 fentes consécutives, et
le déphasage entre 2 fentes consécutives, et 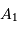 l'amplitude complexe. On mène les calculs dans l'approximation de
Fraunhofer, pour montrer que l'intensité diffractée vaut :
l'amplitude complexe. On mène les calculs dans l'approximation de
Fraunhofer, pour montrer que l'intensité diffractée vaut :
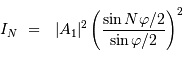
 Démonstration
Démonstration
La sommation des amplitudes conduit à :
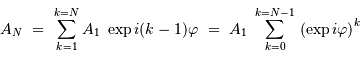
Le traitement de la somme des termes d'une suite en progression géométrique
donne :
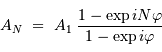
On calcule l'intensité en factorisant le numérateur et le dénominateur
par l'exponentielle complexe de l'angle moitié (de module unité), pour
aboutir à :
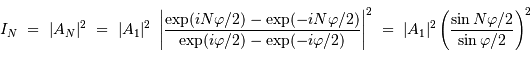
Le terme d'intensité est important uniquement lorsque le dénominateur s'annule. Dans ce cas, le numérateur s'annule également et, par continuité du rapport,
le pic d'intensité tend vers 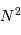 . Chaque pic correspond à un ordre d'interférence. La largeur de ce pic est donnée par les variations du numérateur, qui oscille
. Chaque pic correspond à un ordre d'interférence. La largeur de ce pic est donnée par les variations du numérateur, qui oscille 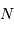 fois plus rapidement que le dénominateur ; elle est donc
fois plus rapidement que le dénominateur ; elle est donc 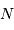 fois inférieure à la largeur entre 2 ordres consécutifs.
fois inférieure à la largeur entre 2 ordres consécutifs.
Inefficacité du réseau par transmission
L'inconvénient du réseau par transmission ici décrit est qu'il n'est a priori pas efficace : l'essentiel de l'énergie passe dans l'ordre 0, inintéressant pour la dispersion. Un concept technologique spécifique pare cet inconvénient : le réseau blazé.
Le réseau de diffraction : dispersion
Observer
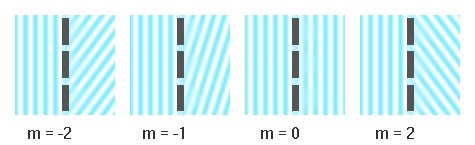
Variation de l'angle de dispersion en fonction de l'ordre d'interférence.
Crédit :
ASM
Dispersion du réseau / ordre d'interférence
La déviation des ordres diffractés par le réseau dépend de l'ordre d'interférence.

Variation de l'angle de dispersion en fonction de la couleur de l'onde plane monochromatique incidente.
Crédit :
ASM
Dispersion du réseau / couleur
La déviation des ordres diffractés par le réseau dépend de la longueur d'onde de l'onde plane
incidente.
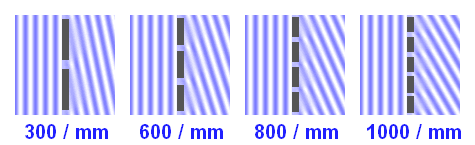
Variation de l'angle de dispersion en fonction du nombre de traits du réseau, donné en traits par millimètre, l'ordre (ici m = 1) et la longueur d'onde étant fixés.
Crédit :
ASM
Apprendre
 Prérequis
Prérequis
Etude du réseau en physique.
 Objectifs
Objectifs
Caractériser la dispersion d'un réseau, càd sa capacité à distinguer les différentes couleurs.
Relation du réseau
Rappel : la condition d'interférences constructives s'écrit :
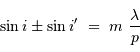
avec 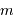 l'ordre d'interférence (entier),
l'ordre d'interférence (entier), 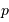 le pas du réseau,
le pas du réseau, 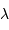 la longueur d'onde d'étude.
la longueur d'onde d'étude.
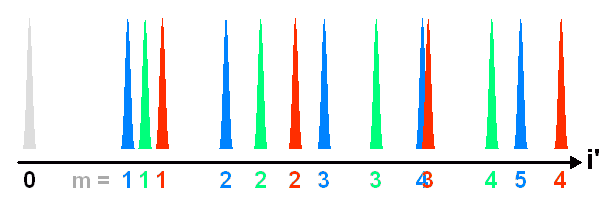
Les ordres d'interférences des différentes couleurs progressent d'autant plus vite que la longueur d'onde est petite. Très rapidement, les différents ordres des différentes couleurs se mêlent.
Crédit :
ASM
Ordres d'interférences
A couleur fixée, mais ordre d'interférence 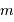 variable, la différentiation de la relation constitutive du réseau s'écrit :
variable, la différentiation de la relation constitutive du réseau s'écrit :
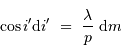
Un pas d'interférence, correspondant à 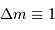 , correspond à un
intervalle angulaire :
, correspond à un
intervalle angulaire :
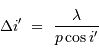
Ce pas varie directement avec la couleur de l'onde considérée.
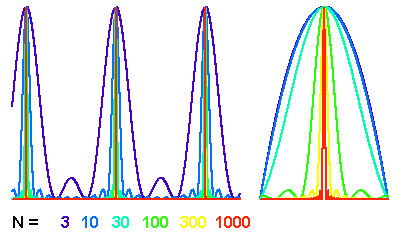
Diffraction et interférences à
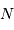
ondes
![(N = [3, 10, 30, 100, 300, 1000])](../pages_interference/equations_reseau-dispersion/equation20.png)
. La largeur de la tache principale varie comme
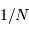
. La figure de droite
zoome sur un ordre donné.
Crédit :
ASM
Le pouvoir de résolution théorique
Le nombre 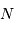 de traits du réseau
fixe la largeur angulaire de la tache image : la figure d'interférence envoie la lumière de façon significative dans un intervalle angulaire
de traits du réseau
fixe la largeur angulaire de la tache image : la figure d'interférence envoie la lumière de façon significative dans un intervalle angulaire 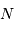 fois moindre qu'un ordre :
fois moindre qu'un ordre :
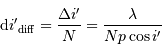
Le pouvoir de résolution théorique du réseau s'écrit, s'il est limité par la seule diffraction, en application de ce qui précède 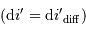 :
:
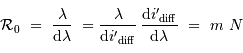
Le pouvoir de résolution théorique augmente avec le nombre de traits éclairés et avec l'ordre d'interférence.
AN : avec un réseau blazé de 100 mm, 100 traits/mm et travaillant à l'ordre 40, le pouvoir de résolution théorique atteint 400 000.
Inefficacité du réseau par transmission
L'inconvénient du réseau par transmission ici décrit est qu'il n'est toujours pas efficace : la dispersion spectrale est d'autant plus grande que l'ordre du réseau est élevé, mais l'essentiel de l'énergie reste dans l'ordre 0, inintéressant pour la dispersion. De plus, la superposition des ordres mélange les couleurs.
Simuler

Lumière rouge, ordre 1
Crédit :
ASM

Lumière verte, ordre 1
Crédit :
ASM

Lumière bleue, ordre 1
Crédit :
ASM

Lumière verte, ordre 2
Crédit :
ASM

Lumière verte, ordre -1
Crédit :
ASM

Lumière verte, ordre 1, grand pas
Crédit :
ASM

Lumière verte, ordre 1, petit pas
Crédit :
ASM
La déviation du réseau
Les animations montrent la création des ordres d'interférence par interférences constructives, pour différents ordres et couleurs.
Attention : ces animations supposent indûment valide à courte distance l'approximation de Fraunhofer, qui décrit la diffraction uniquement à grande distance de l'objet diffractant.
Voir comme la déviation varie avec :
- l'ordre d'interférence : cf animations pour différents ordres,
1,
2 ,
-1
- la longueur d'onde : cf animations pour différentes couleurs,
rouge,
vert,
bleu
- le pas du réseau : cf animations pour différents pas,
grand, ou
petit
S'exercer
Le réseau blazé
Observer

Le double réseau de l'instrument HARPS (ESO, télescope de 3.6 m). Les 2 réseaux côte à côte couvrent une surface de
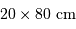
.
Crédit :
HARPS/ESO
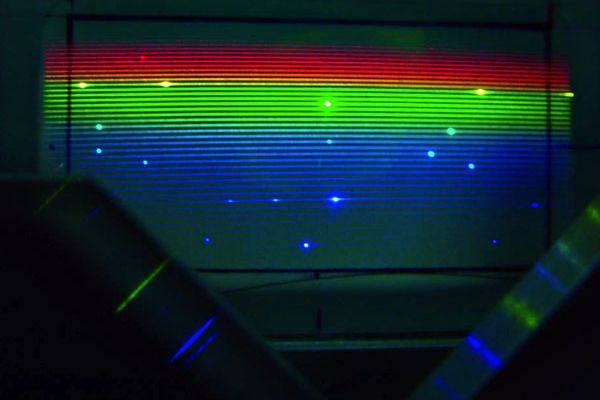
Image projetée sur un écran translucide d'un spectre-échelle
obtenu avec un spectromètre (SOPHIE, OHP) incluant un réseau blazé
et un post-disperseur.
Crédit :
OHP/CNRS
Un réseau efficace
Un réseau-échelle ou réseau blazé (a blaze of color =
resplendissant de couleur) traite efficacement la dispersion : il envoie la puissance lumineuse incidente dans des ordres élevés du spectre, avec une grande dispersion spectrale. Il s'agit d'un réseau par réflexion, très couramment utilisé en instrumentation astrophysique.

Image d'un
spectre-échelle à haute résolution spectrale obtenu avec une caméra CCD. Le spectre de l'étoile apparaît ici sous l'aspect de bandes sombres. L'étalonnage en longueur d'onde est apporté par les raies en émission d'une lampe spectrale (Thorium Argon), dont le spectre est intercalé avec celui de l'étoile, et enregistré simultanément.
Crédit :
ESO/ASM
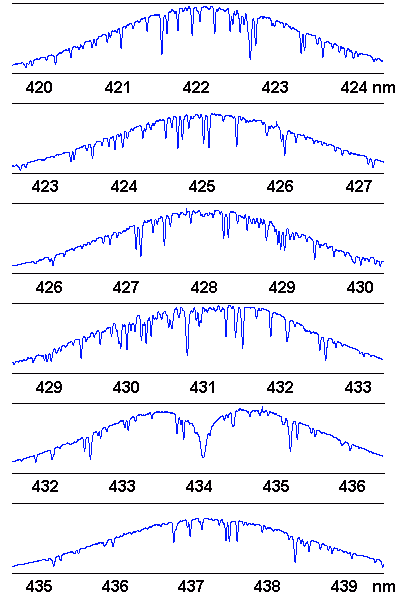
Aperçu de 6 ordres du spectre obtenu avec le spectromètre Harps. La diffraction par chaque trait du réseau est responsable du profil d'étalement du flux ; la séparation des ordres est obtenue grâce à un deuxième élément dispersif, dans une direction perpendiculaire à celle du premier réseau.
Crédit :
ESO/ASM

La dispersion croisée du spectromètre Harps est assurée par un
grisme, qui correspond à un réseau par transmission gravé sur un
prisme.
Crédit :
ESO
Les ordres d'un réseau blazé
Une deuxième dispersion, dite
dispersion croisée, des ordres diffractés par un
réseau blazé permet d'obtenir un spectre sur un large intervalle
spectral divisé en plusieurs
ordres.
L'intensité dans chaque
ordre est modulée par la fonction d'Airy de la fente d'entrée.
Apprendre
 Objectifs
Objectifs
Introduire les propriétés du réseau blazé, dont l'intérêt est d'envoyer l'énergie diffractée dans un ordre d'interférence non nul.
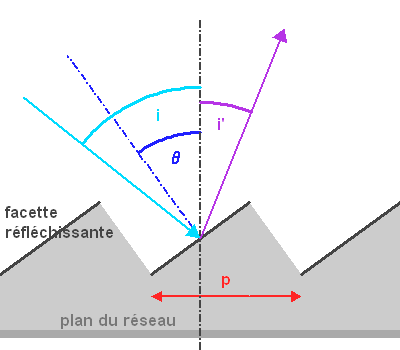
Profil d'un réseau blazé ou réseau échelle, et définition des angles. Les facettes réfléchissantes du réseau sont gravées avec une inclinaison
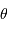
par rapport au plan du réseau. La diffraction envoie une intensité maximale dans un ordre d'interférence non nul, pour
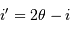
. Les angles

et
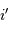
restent définis par rapport au plan du réseau.
Crédit :
ASM
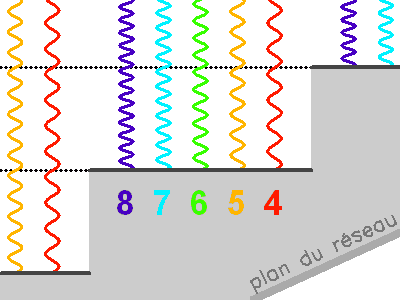
Le maximum d'énergie renvoyée (dans la direction de l'optique géométrique) correspond à un ordre non nul, d'autant plus grand que la longueur d'onde est petite. Dans la pratique, l'inclinaison du faisceau est le plus souvent très proche de la normale aux facettes.
Crédit :
ASM
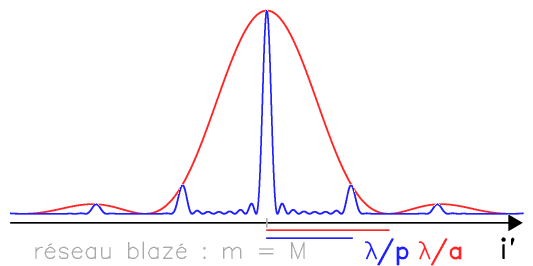
Pour un réseau blazé, les interférences se construisent principalement dans le lobe principal de la tache de diffraction, centré sur une frange d'ordre non nul.
Crédit :
ASM
Le réseau blazé
Le réseau par transmission n'est pas efficace. La diffraction envoie essentiellement l'énergie dans l'ordre 0, qui n'est pas dispersif, ce qui n'est guère intéressant.
L'intérêt du réseau blazé est d'envoyer le flux dans un ordre d'interférence non nul dans les conditions de l'optique géométrique (les conditions usuelles d'utilisation sont proches du cas 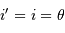 , où
, où 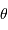 est l'angle de blaze). Cet ordre dépend de la couleur étudié.
est l'angle de blaze). Cet ordre dépend de la couleur étudié.
D'un point de vue énergétique, le montage optique d'un réseau blazé s'arrange pour voir essentiellement la tache de diffraction du réseau (déterminée par une facette élémentaire).
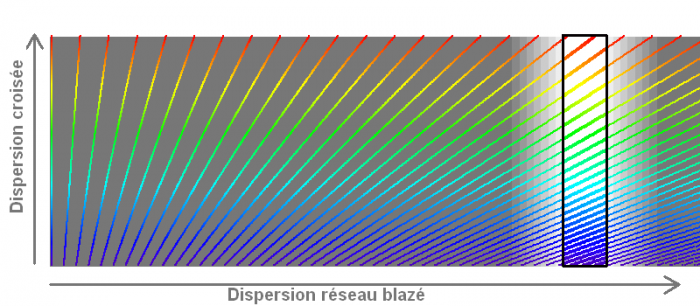
Avec un réseau blazé, l'image diffractée de la fente d'entrée correspond à un ordre d'interférences non nul. Cet ordre d'interférence varie d'une couleur à l'autre. Une dispersion à basse résolution spectrale, perpendiculaire à la haute résolution apportée par le réseau blazé, permet de séparer ces ordres et d'obtenir une image d'un large intervalle spectral constitué d'une succession d'ordres.
Crédit :
ASM
Nécessité d'une dispersion croisée
Par rapport au réseau par transmission, le réseau blazé permet un
travail dans un ordre d'interférence élevé, assurant un pouvoir de
résolution théorique élevé. Mais, à lui seul, le réseau blazé
n'assure pas une dispersion optimale : les ordres restent
superposés, aboutissant à la confusion des couleurs si chèrement
dispersées. Il faut adjoindre au
réseau blazé un deuxième
élément dispersif, assurant une dispersion dans une direction
perpendiculaire, qui permet de distinguer les différents ordres.
Avec 2 dispersions à angle droit, la source doit nécessairement
être ponctuelle (en pratique, souvent une fibre).
S'exercer
Le réseau et son optique
Observer
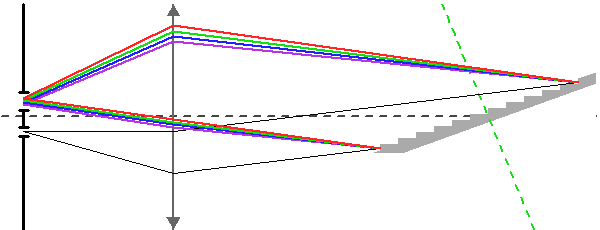
Montage de Littrow avec réseau blazé. Le plan du réseau est incliné par rapport à l'axe optique de telle sorte que les facettes du réseau sont quasi perpendiculaires à l'axe optique.
Crédit :
ASM

Le réseau donne une série d'images colorées de la fente source.
Crédit :
ASM
Montage de principe
Le réseau est alimenté en faisceau parallèle par une fente source ou un trou source. Le
montage de principe est donc simplement un montage conjuguant la source à son image en passant via 2 lentilles équivalentes par un faisceau parallèle. Le réseau donne en fait une série d'images colorées de la
fente source.
Spectromètre et réseau
En pratique, c'est évidemment plus complexe.
L'insertion du réseau dans le spectromètre nécessite :
- Une fente d'entrée, ou tout dispositif réduisant le champ (un trou source dans le cas du réseau blazé).
- Une bonne illumination de la fente ou du trou source.
- Une optique assurant un bon éclairement du réseau.
L'appliquette ci-joint permet de lire le schéma optique de l'instrument CRIRES
(CRyogenic high-resolution IR Echelle Spectrometer) du VLT.

Montage de Littrow
Un montage optique couramment utilisé avec un réseau blazé est celui de type Littrow, où une optique unique alimente le réseau en lumière parallèle et collecte le faisceau dispersé. Les facettes du réseau blazé sont éclairées sous une incidence quasi-nulle (mais correspondant à une incidence élevée par rapport au plan du réseau).
Apprendre
 Prérequis
Prérequis
Etude du réseau en physique.
 Objectifs
Objectifs
Lier le pouvoir de résolution spectrale d'un instrument disperseur avec réseau aux conditions de formation d'image.
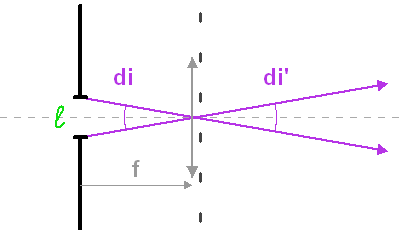
Fente du réseau et collimation.
Crédit :
ASM
La taille de la fente d'entrée
Le rôle de l'optique géométrique ne doit pas être oublié : il peut dimensionner la résolution effective du réseau. Avec 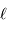 la largeur de la fente et
la largeur de la fente et 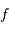 la focale du miroir collimateur, la taille angulaire de la fente vue dans l'espace image est :
la focale du miroir collimateur, la taille angulaire de la fente vue dans l'espace image est :
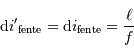
Le pouvoir de résolution limité par la largeur de la fente d'entrée 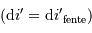 s'écrit :
s'écrit :
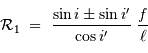
où subsistent les conditions géométriques de l'éclairement du réseau. Dans les conditions d'un réseau blazé éclairé quasi normalement aux facettes, 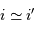 et avec le signe + correspondant au réseau par réflexion :
et avec le signe + correspondant au réseau par réflexion :
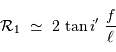
Un pouvoir de résolution optimal nécessite une source de petite taille et une grande focale. Avec une focale de l'ordre du mètre, une fente de 100 micromètres (en fait une fibre), et 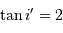 , le pouvoir de résolution géométrique vaut 40 000.
, le pouvoir de résolution géométrique vaut 40 000.
La finesse de la fente d'entrée assure la finesse des images monochromatiques ; mais fermer la fente est réalisé au détriment de la luminosité. Assurer une longue focale nécessite un grand réseau, ce qui a un coût.
S'exercer
S'évaluer
 Le réseau du spectromètre HARPS
Le réseau du spectromètre HARPS
Difficulté : ☆☆
Temps : 20 min
Question 1)
Le montage du spectromètre HARPS assure un pouvoir de résolution
de l'ordre de 120 000. La focale de l'optique de chambre valant
1.56 m, en déduire la taille de la fente d'entrée, sachant que par
ailleurs l'illumination du réseau a lieu dans les conditions 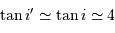 .
.
[1 points]
Question 2)
Le flux collecté par le télescope a un diamètre de 3.6 m, qui devient dans l'instrument 20 cm. En déduire le grossissement.
[1 points]
Question 3)
Déduire de ce qui précède l'ordre de grandeur du champ de vue sur le ciel.
[2 points]
Compléments d'optique
Auteur: B. Mosser
Introduction
Cette section propose des développements plus ardus, au-delà d'un programme de niveau L2 ou L3, mais bien utiles, concernant divers points d'optique.
- La notion d'étendue de faisceau permet, sans décrire complètement un faisceau, de connaître rapidement certaines propriétés spatiales.
- La diffraction par une pupille circulaire est établie en bonne et due forme.
- Une introduction à l'optique de Fourier est proposée.
- Les notions de cohérence temporelle et cohérence spatiale sont exposées.
- ...

Ça se complique.
Crédit :
ASM
Aberrations géométriques
Observer
Aberration de sphéricité
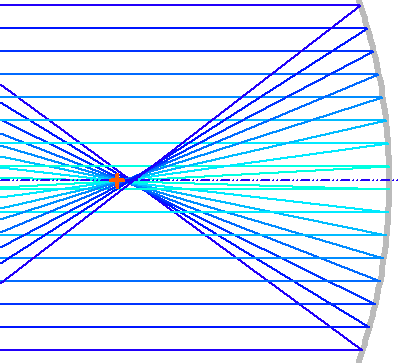
Programme de tracé de rayons.
Les rayons les plus éloignés de l'axe de révolution d'un miroir sphérique convergent plus près du miroir que les rayons paraxiaux. Des couleurs différentes sont utilisées uniquement pour permettent de distinguer les rayons entre eux.
Crédit :
ASM
Aberration sphérique
Un miroir sphérique est beaucoup plus simple à tailler qu'un miroir parabolique. Mais il ne rend pas les mêmes services, car il concentre la lumière imparfaitement ; plus le rayon est éloigné de l'axe optique, plus il va converger en avant du foyer. On parle d'aberration de sphéricité.
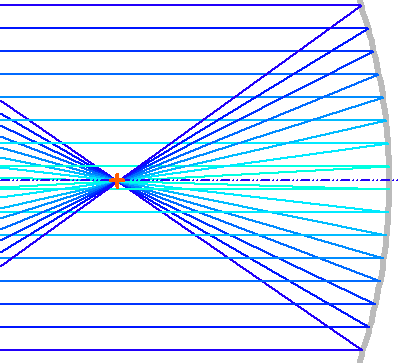
Contrairement au miroir sphérique, le miroir parabolique concentre parfaitement tous les rayons provenant d'un objet sur l'axe à l'infini.
Crédit :
ASM

Même pour un miroir parabolique, l'image d'un objet à l'infini hors axe n'est pas parfaitement ponctuelle. L'effet est analogue à l'aberration de sphéricité présentée par un miroir sphérique.
Crédit :
ASM
Aberration de coma
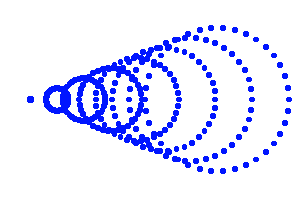
Diagramme de tracé de rayon montrant l'allure de la coma : l'image d'un point devient une petite tache allongée. comme une aigrette.
Crédit :
ASM
Coma
Un miroir parabolique est exempt de cette aberration de sphéricité, mais uniquement pour un objet centré sur l'axe et non hors axe . On parle dans ce cas d'aberration de coma, qui rend donc compte de l'aberration de sphéricité hors axe.
Apprendre
 Objectifs
Objectifs
Brièvement décrire les aberrations géométriques
Stigmatisme
La définition de la justesse de la formation d'image s'appelle le stigmatisme. Le stigmatisme idéal est atteint lorsque tous les rayons issus d'un point de l'objet convergent en un seul point de l'image.
Cette situation idéale n'est pas opérationnelle : il faut en pratique définir les conditions dans lesquelles la convergence est suffisante (p.ex. avec une précision dans le plan focal meilleure que la taille d'un pixel). Ces conditions sont d'autant mieux réalisées que l'on est proche de l'axe optique du système.
Aberration de coma
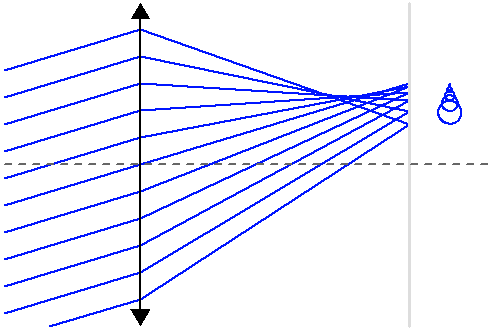
L'aberration de coma affecte tout rayon hors axe.
Crédit :
ASM
Distorsion
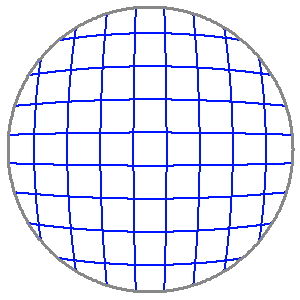
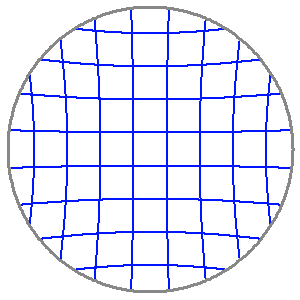
La distorsion transforme une grille rectangulaire en une grille en forme de barillet ou de coussinet.
Crédit :
ASM
Aberration chromatique
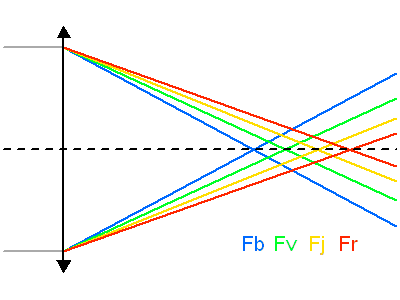
L'aberration chromatique apparaît pour une lentille simple, dont la focale dépend de la couleur.
Crédit :
ASM
Aberrations chromatiques
L'aberration chromatique apparaît pour une lentille simple : comme l'indice du matériau varie avec la longueur d'onde, la focale varie également. En règle générale, l'indice bleu, plus élevé donne une distance focale bleue plus courte.
Cette aberration est corrigée par l'utilisation de systèmes de lentilles (doublet, triplet...), avec des verres d'indices différents pour obtenir une focale équivalent quasiment identique pour toutes les longueurs d'onde considérées.
Les miroirs présentent l'avantage de ne pas induire d'aberrations
chromatiques (la lumière ne traverse pas le miroir). Leur
coefficient de réflexion, qui dépend intimement du traitement de
surface, est néanmoins chromatique.
Simuler
Comparaison de diverses aberrations
Aberrations 
Les différents défauts géométriques cohabitent joyeusement, et les
distinguer n'est pas toujours facile, comme le montre le
diaporama ci-joint.
Étendue de faisceau
Apprendre
 Prérequis
Prérequis
Notion d'angle solide.
 Objectifs
Objectifs
Définir l'étendue de faisceau ; mais surtout montrer la conservation de l'étendue de faisceau.
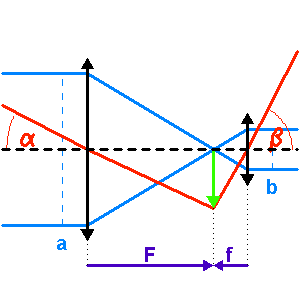
Le montage afocal transforme un faisceau de diamètre
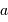
en un faisceau de diamètre
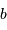
, avec un grossissement angulaire
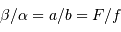
.
Crédit :
ASM
Exemple : montage afocal
Un montage afocal transforme un faisceau plan en un autre faisceau plan. Les rapports des diamètres des faisceaux et des inclinaisons en entrée et sortie sont intimement liés au grossissement.
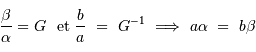
Le produit est un invariant, ce qui relate une relation physique plus générale : la conservation de l'énergie du faisceau.
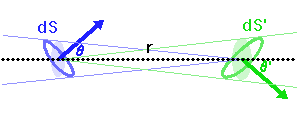
Conservation de l'étendue de faisceau, de l'élément émetteur
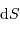
à l'aire collectrice
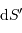
.
Crédit :
ASM
Faisceau, étendue de faisceau et conservation de l'énergie
La puissance (ou luminosité )
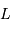 transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la luminance
transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la luminance 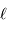 , à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
, à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
Un jeu d'écriture sur les grandeurs photométriques, avec les données de la figure, conduit à exprimer la conservation de la puissance lumineuse comme la conservation de l'étendue géométrique de faisceau. On définit cette étendue de faisceau, pour un faisceau traversant sans être collimaté (= sans perte d'énergie) un élément optique de section 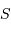 , occupant un angle solide
, occupant un angle solide 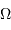 , dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit
, dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit 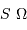 , qui se conserve le long du faisceau.
, qui se conserve le long du faisceau.
Pour les systèmes stigmatiques (càd, très grossièrement, donnant des images avec des aberrations limitées), la conservation de l'énergie se traduit par la conservation de l'étendue de
faisceau :
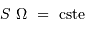
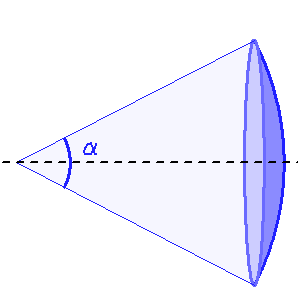
Faisceau divergeant d'une source quasi ponctuelle, collimaté : son énergie est localisée dans un cône.
Crédit :
ASM
Faisceau conique peu ouvert
Un faisceau conique d'ouverture totale 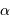 couvre un angle solide :
couvre un angle solide :
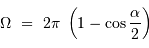
Si l'angle 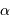 est petit, cet angle solide se réécrit simplement :
est petit, cet angle solide se réécrit simplement :
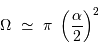
Au travers d'une optique de diamètre 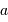 , la conservation du produit
, la conservation du produit 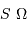 devient, pour ce faisceau conique :
devient, pour ce faisceau conique :
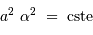
On retrouve donc le résultat obtenu dans le cadre du montage afocal.
Quelques conséquences
Comme conséquences importantes, on note que :
- Plus le faisceau collecté passe par un diamètre fin, plus il est divergent.
- Plus l'aire du collecteur est grande, plus l'étendue de faisceau est grande, plus les instruments doivent également être de grande taille pour offrir un grand diamètre au faisceau mis en forme.
- La surface du détecteur et l'angle solide qu'il peut voir (de l'ordre de l'angle d'ouverture du télescope) limitent nécessairement la taille angulaire du champ objet.
Etendue de faisceau cohérente
Un faisceau monochromatique est cohérent sur une étendue égale à 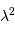 .
La justification est donnée en exercice.
.
La justification est donnée en exercice.
S'exercer
 Imagerie grand champ
Imagerie grand champ
Difficulté : ☆
Temps : 20 min
Le but d'une caméra est de réaliser un programme de cartographie, par imagerie grand champ. Les caractéristiques du détecteur sont fixées (taille du capteur CCD et caractéristiques de son optique), que l'on traduit par le produit 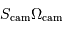 . Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
. Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
Question 1)
Comment varie la taille angulaire du champ objet en fonction de la surface 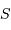 du collecteur ?
du collecteur ?
Se servir la conservation de l'étendue de faisceau
Question 2)
Le temps de pose est fixé par le rapport signal à bruit des observations, qui dépend essentiellement du nombre de photons collectés. Comment le temps de pose varie-t-il avec la surface du collecteur ?
Comment varie le nombre de photons collectés avec la surface collectrice ?
Question 3)
Y'a-t-il un intérêt particulier à utiliser un grand collecteur pour réaliser cette cartographie ? Quel usage peut-on conseiller à un télescope de la classe 4-m qui doit motiver son existence par rapport aux télescopes de nouvelle génération plus grands ?
Se servir des 2 questions précédentes.
Comparer la dépendance vis à vis de la surface collectrice 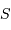 de la taille du champ élémentaire et du temps de pose élémentaire.
de la taille du champ élémentaire et du temps de pose élémentaire.
 Sur les 2 tableaux
Sur les 2 tableaux
Difficulté : ☆☆
Temps : 20 min

Le montage optique réel de CoRoT. Les 2 miroirs paraboliques hors-axe sont notés Primary mirror et M2. Lens correspond à l'optique de chambre ; Focal box aux détecteurs CCD.
Crédit :
CNES
CoRoT est un satellite du CNES lancé en décembre 2006, qui poursuit 2 objectifs scientifiques : la recherche d'exoplanètes par la méthode des transits d'une part, l'étude sismique de quelques étoiles de type solaire d'autre part. Ces 2 objectifs s'appuient sur la capacité de CoRoT à mener des observations de photométrie très précises. Le montage optique retenu consiste en l'association de 2 miroirs paraboliques confocaux (confocal 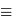 même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
Question 1)
Faire à l'échelle un schéma de principe le plus simple possible du système équivalent à l'ensemble miroirs + optique de chambre avec 3 lentilles équivalentes pour respectivement les 2 miroirs et l'optique de chambre.
Revoir la page sur le montage afocal.
Question 2)
Le diamètre du premier miroir vaut 30 cm ; les focales des miroirs primaire et secondaire sont dans un rapport de 3 à 1. Que peut-on en déduire concernant les lentilles de l'optique de chambre ? En quoi consiste l'un des intérêts de ce montage ?
Revoir (encore !) la page sur le montage afocal.
Question 3)
Reprendre le schéma de principe, en respectant l'ouverture du faisceau à 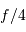 vu par la caméra, Calculer la focale
vu par la caméra, Calculer la focale 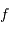 équivalente et la focale
équivalente et la focale 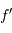 de l'optique de chambre.
de l'optique de chambre.
Question 4)
La question précédente met en évidence un gain sur l'optique de chambre. Mettre en évidence la contrainte associée, qui dérive de la conservation de l'étendue de faisceau. Conclure.
Simple application de la conservation de l'étendue de faisceau.
 Étendue cohérente
Étendue cohérente
Difficulté : ☆☆
Temps : 10 min
Un collecteur de diamètre 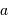 délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur)
délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur) 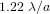 . On cherche à en déduire l'étendue de faisceau cohérente.
. On cherche à en déduire l'étendue de faisceau cohérente.
Question 1)
Justifier que l'étendue cohérente correspond au pic central de la diffraction.
Pourquoi le premier anneau de la tache de diffraction est-il noir? Que cela signifie-t-il ?
Question 2)
Déterminer l'étendue de faisceau cohérente. Montrer qu'elle est très voisine de
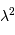 .
.
Revenir à la définition : exprimer 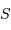 et
et 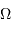 .
.
S'évaluer
 D'un collecteur de 8 m à une fibre
D'un collecteur de 8 m à une fibre
Difficulté : ☆
Temps : 5 min
Un instrument du VLT (collecteur de diamètre 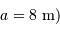 est alimenté par un faisceau de fibres de diamètre
est alimenté par un faisceau de fibres de diamètre 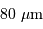 .
.
Question 1)
L'alimentation optimale de la fibre se fait à 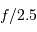 . En déduire l'ouverture angulaire du faisceau en entrée de fibre.
. En déduire l'ouverture angulaire du faisceau en entrée de fibre.
[1 points]
Question 2)
Que vaut le champ objet admissible sur le ciel ? L'exprimer en seconde d'angle.
[1 points]
 Observation au foyer et étendue de faisceau
Observation au foyer et étendue de faisceau
Difficulté : ☆☆
Temps : 15 min
On se propose de retrouver par l'application de la conservation de l'étendue de faisceau l'expression de la taille linéaire de l'image d'un objet à l'infini de diamètre angulaire 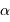 par un collecteur de diamètre
par un collecteur de diamètre 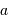 et de focale
et de focale 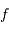 . On considère le seul cas où l'angle
. On considère le seul cas où l'angle 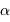 est petit. On note
est petit. On note 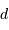 ladite taille linéaire.
ladite taille linéaire.
Question 1)
Exprimer le produit 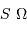 côté source, en fonction des données.
côté source, en fonction des données.
[1 points]
Question 2)
Rappeler l'expression de l'ouverture angulaire du collecteur, et exprimer le produit 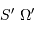 côté détecteur.
côté détecteur.
[2 points]
Question 3)
Exprimer la conservation de l'étendue de faisceau. Retrouve-t-on le résultat attendu ?
L'objet ayant une taille angulaire 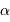 , quelle est la taille linéaire
, quelle est la taille linéaire 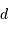 de son image.
de son image.
[2 points]
Diaphragmes de champ et d'ouverture
Observer
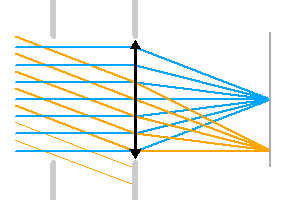
Illustration du phénomène de vignetage. Une partie du faisceau inclinés (en orange) est bloquée, alors que la totalité du faisceau d'incidence nulle (en bleu) est transmise : l'image sera moins lumineuse au bord.
Crédit :
ASM

Champ vigneté : les sources les plus éloignées se retrouvent éteintes.
Crédit :
ASM
Le vignetage
Le vignetage apparaît lorsque qu'un diaphragme coupe indûment le faisceau optique. Les bords de l'image ne sont alors plus suffisamment éclairés.
Apprendre
 Prérequis
Prérequis
Optique géométrique ; tracé de rayons.
 Objectifs
Objectifs
Bien accepter ou bien stopper les photons (sans trop rentrer dans les détails).
Champ et diaphragme
Le champ d'un instrument d'optique est la partie de l'espace dont cet instrument fournit une image acceptable.
Un diaphragme, c'est par définition ce qui limite un faisceau. En pratique, les montures des pièces optiques, la taille d'un détecteur sont des diaphragmes. La suite précise cette notion.
Diaphragme de champ
Un diaphragme de champ limite la taille angulaire du faisceau. Il est dimensionné pour assurer :
- Un champ aux dimensions voulues.
- Une bonne qualité optique dans le champ.
- Un éclairement uniforme.
Le détecteur, de taille finie, peut jouer le rôle de diaphragme de champ.
Diaphragme d'ouverture
Dans un système optique centré, le diaphragme d'ouverture est le diaphragme matériel qui limite
l'ouverture d'un faisceau centré. C'est donc le diaphragme vu de puis l'objet sous le plus petit angle ; c'est souvent la monture de la première lentille.
Un diaphragme d'ouverture limite l'éclairement. Il est essentiellement dimensionné pour assurer le niveau d'éclairement voulu. Il joue sur l'extension linéaire du faisceau : un grand diaphragme nécessite des pièces optiques de grande taille... dont la qualité doit suivre.
Pupilles
La pupille d'entrée d'un instrument est l'image géométrique du diaphragme d'ouverture par les lentilles placées en avant ce diaphragme.
La pupille de sortie est l'image géométrique de la pupille d'entrée. C'est aussi l'image géométrique du diaphragme d'ouverture par les lentilles placées après ce diaphragme.
Simuler
Diaphragme de champ
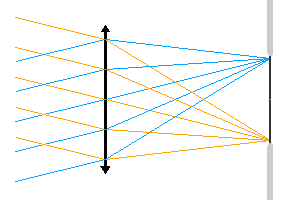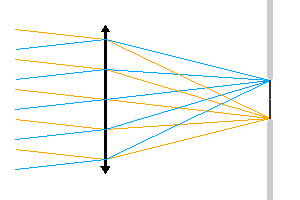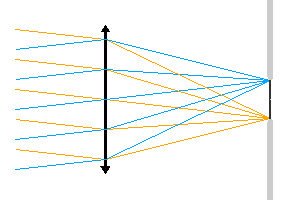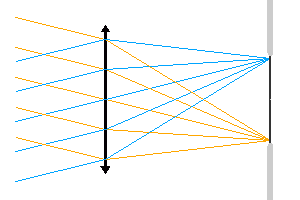
Relation entre la taille du détecteur, faisant office de diaphragme de champ, et le champ accessible.
Crédit :
ASM
Diaphragme de champ
Un diaphragme de champ limite l'ouverture angulaire du faisceau. Dans l'animation proposée, c'est la taille du détecteur qui limite le champ accessible : le détecteur joue le rôle de diaphragme de champ.
Diaphragme d'ouverture
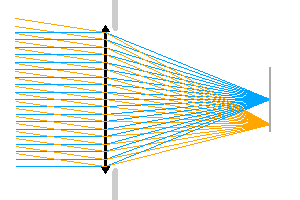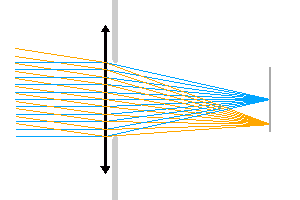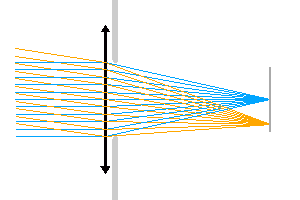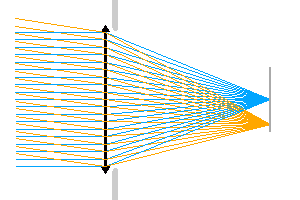
Relation entre le diaphragme d'ouverture et l'éclairement au foyer.
Crédit :
ASM
Diaphragme d'ouverture
Un diaphragme d'ouverture limite l'éclairement. Dans l'animation proposée, le diaphragme d'ouverture limite l'éclairement au foyer.
S'exercer
 Diaphragme d'ouverture
Diaphragme d'ouverture
Difficulté : ☆
Temps : 10 min
On propose d'utiliser un montage afocal, avec les lentilles L1 et L2 de caractéristiques respectives (focales et diamètres) :
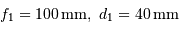 ;
;
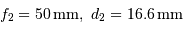 .
.
Question 1)
Sous quelle ouverture sont vues les lentilles depuis leur foyer commun ?
[1 points]
Question 2)
En déduire la lentille qui joue le rôle de diaphragme d'ouverture.
[1 points]
La question précédente suffit pour apporter la réponse.
S'évaluer
 Pupille d'entrée de CoRoT
Pupille d'entrée de CoRoT
Difficulté : ☆☆
Temps : 30 min
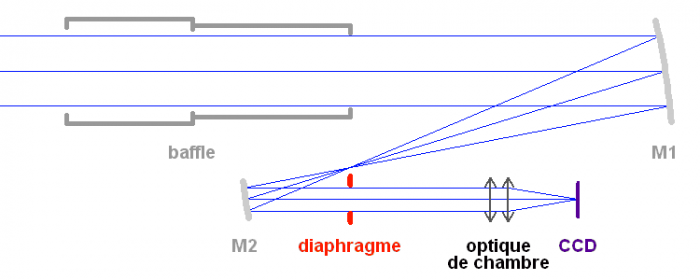
Schéma optique de CoRoT.
Crédit :
ASM
La figure représente le montage optique du collecteur du
satellite CoRoT. Il comporte un baffle de grande taille dont le
rôle est de protéger le signal de toute perturbation extérieure,
pour une étude photométrique extrêmement précise. Le montage
collecteur (miroirs M1 et M2) est hors-axe, afin d'éviter toutes
les réflexions parasites qu'apporterait le miroir secondaire M2
avec sa structure dans le cas d'un montage axial.
Question 1)
D'après le schéma optique, à quelle configuration correspond l'ensemble des miroirs collecteurs M1 et M2 ? Quelles sont les propriétés du faisceau après passage par M2, en terme de diamètre, ouverture et étendue de faisceau comparées aux mêmes valeurs en amont de M1 ?
[2 points]
Examiner le tracé de rayons.
Identitifier la nature des rayons incidents, émergents. Que se passe-t-il entre les miroirs M1 et M2?
Question 2)
Le diaphragme 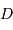 est positionné en aval de M2, à une distance du miroir égale à la focale de M2. En déduire la position de la pupille d'entrée
est positionné en aval de M2, à une distance du miroir égale à la focale de M2. En déduire la position de la pupille d'entrée 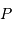 . Faire un schéma justifiant la réponse.
. Faire un schéma justifiant la réponse.
[2 points]
Le diaphragme 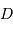 est un diaphragme d'ouverture.
est un diaphragme d'ouverture.
Se rappeler la définition de la pupille d'entrée, et le lien avec le diaphragme 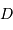 .
.
Question 3)
Que peut-on dire d'un photon qui passe par la pupille d'entrée ?
[1 points]
Quel lien encore entre diaphragme d'ouverture et diaphragme de champ ?
Question 4)
En fonction de ce qui précède, reformuler le rôle du baffle de protection.
[1 points]
Diffraction par une pupille circulaire
Observer
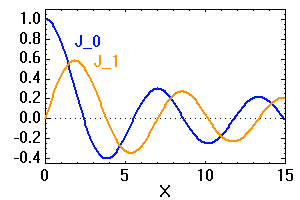
Les 2 premières fonctions de Bessel,
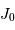
et
.
Crédit :
ASM
Fonctions de Bessel
La figure de diffraction d'une pupille circulaire introduit les fonctions de Bessel.
Coupe de la figure de diffraction, en représentation logarithmique et unité
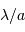
. Le premier zéro est à l'abscisse 1.22.
Crédit :
ASM
Apprendre
 Prérequis
Prérequis
Diffraction de Fraunhofer.
 Objectifs
Objectifs
(Page à n'aborder qu'en deuxième lecture).
Introduire, pour une pupille circulaire, les fonctions de Bessel, qui justifient le facteur 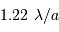 qui dimensionne la tache de diffraction.
qui dimensionne la tache de diffraction.
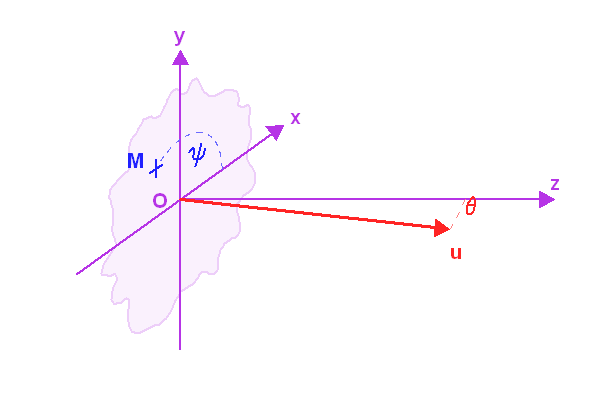
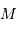
est un point courant de la pupille, de coordonnées polaires
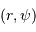
, et
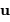
porte la direction pour laquelle on recherche l'amplitude de l'onde diffractée.
Crédit :
ASM
Pupille circulaire
La pupille étant circulaire, de rayon 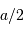 , il est préférable de décrire les coordonnées du point
, il est préférable de décrire les coordonnées du point 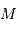 et de la direction de diffraction
et de la direction de diffraction 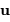 en coordonnées polaires, avec les notations suivantes :
en coordonnées polaires, avec les notations suivantes :
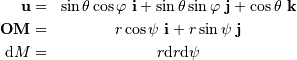
(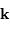 est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction
est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction 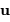 faisant un angle
faisant un angle 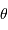 avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
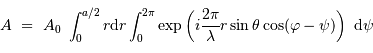
On introduit les fonctions de Bessel, dont les 2 premiers termes sont, par définition :
![\begin{eqnarray*} J_0 (X) =& \displaystyle{{1\over 2\pi} \int_0^{2\pi} \exp \bigl[-iX \cos v \bigr]\ {\mathrm{d}} v}\\ J_1 (X) =& \displaystyle{{1\over X}\ \int_0^{X} u J_0 (u)\ {\mathrm{d}} u}\\ \end{eqnarray*}](../pages_rayon/equations_diffraction-pupille/equation25.png)
L'amplitude diffractée dans une direction faisant un petit angle 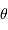 par rapport à l'axe optique, devient :
par rapport à l'axe optique, devient :
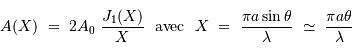
 Démonstration
Démonstration
Les calculs passent par les changements de variables
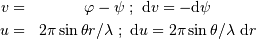
L'intensité diffractée dans la direction 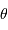 s'écrit donc :
s'écrit donc :
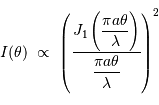
Zéros, anneaux et largeur à mi-hauteur
Pour 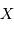 voisin de 0,
voisin de 0, 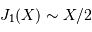 . Par ailleurs,
le premier zéro de la fonction
. Par ailleurs,
le premier zéro de la fonction 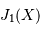 est pour
est pour 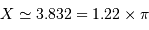 .
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille
.
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille 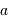 et de la longueur d'onde
et de la longueur d'onde 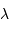 :
:
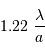
La figure de diffraction s'annule ensuite pour les rayons 2.23, 3.23, 4.24, 5.24.... en unité 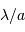 . Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...
. Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...
Diffraction et transformée de Fourier
Observer

Pupille d'entrée et sa transformée de Fourier.
Crédit :
ASM
La TF de la pupille
La figure de diffraction d'une pupille, quelle qu'elle soit, est identique à sa
transformée de Fourier.
Apprendre
 Prérequis
Prérequis
Cours sur la diffraction de Fraunhofer.
 Objectifs
Objectifs
(Page à n'aborder qu'en 2eme lecture.)
Mettre en regard le formalisme décrivant la diffraction à l'infini par une pupille et le formalisme de la transformation de Fourier.
Diffraction et filtrage
On peut utiliser les propriétés de la TF pour réécrire les caractéristiques de la diffraction.
Une pupille de taille caractéristique 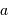 filtre les hautes fréquences, càd l'information angulaire plus fine typiquement que
filtre les hautes fréquences, càd l'information angulaire plus fine typiquement que 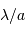 .
.
Plus la pupille est grande, moins elle filtre angulairement.
Simuler
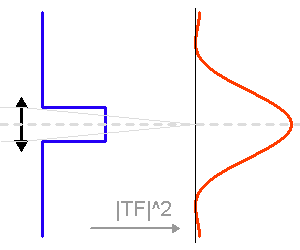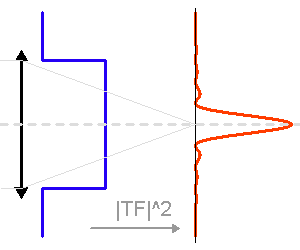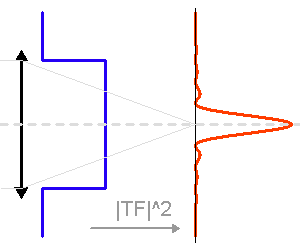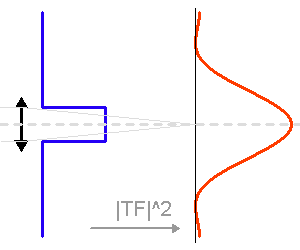
Pupille d'entrée et sa tache d'Airy : module carré de sa transformée de Fourier.
Crédit :
ASM
La TF de la pupille
La tache image due à la seule diffraction dépend du diamètre du télescope. Plus ce dernier est grand, plus la tache d'Airy est piquée.
Cohérence temporelle
Observer
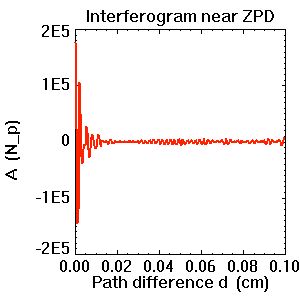
Portion de la partie modulée d'un interférogramme. Le contraste des franges s'écroule dès lors que l'on s'éloigne de la différence de marche nulle.
Crédit :
ASM
Interférogramme
Un interféromètre de Michelson permet de tracer l'interférogramme d'une source, càd la figure d'interférence obtenue après déphasage de l'une des 2 voies de l'interféromètre d'une différence de marche 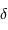 .
L'interférogramme du
spectre d'une source réelle, délimitée par un intervalle spectral
fini, illustre le phénomène de cohérence temporelle : le signal
d'interférence chute dès lors que la différence de marche devient
grande.
.
L'interférogramme du
spectre d'une source réelle, délimitée par un intervalle spectral
fini, illustre le phénomène de cohérence temporelle : le signal
d'interférence chute dès lors que la différence de marche devient
grande.
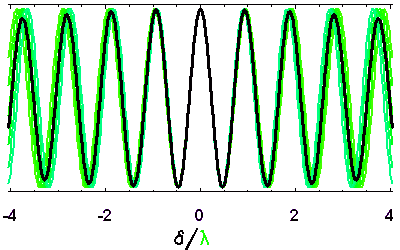
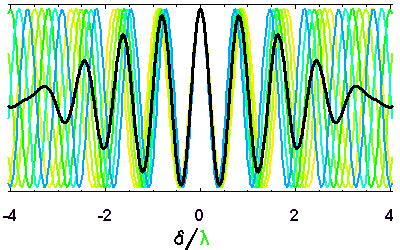
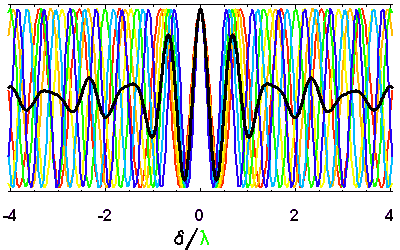
Evolution de la longueur de cohérence temporelle en fonction de la largeur spectrale. Plus l'intervalle spectral accepté est large, plus vite le signal est moyenné dès lors que la différence de marche s'éloigne de la valeur nulle.
Crédit :
ASM
Cohérence temporelle et intervalle spectral
La cohérence temporelle décroît d'autant plus rapidement que le spectre de la source présente une gamme de longueurs d'onde importante.
Apprendre
 Objectifs
Objectifs
Le cas d'une source rigoureusement ponctuelle et monochromatique est
souvent évoqué pour aborder l'optique géométrique et physique. Une source ne sera jamais totalement monochromatique,
même si son spectre présente des raies d'émission très étroites, ou si
par dispersion ou filtrage on sélectionne un très fin domaine
spectral. La cohérence temporelle d'une onde rend compte de sa chromaticité.
Une approche rigoureuse passe par le théorème de Wiener-Khintchine.
 Prérequis
Prérequis
Interféromètre de Michelson
Cohérence temporelle
Tout phénomène d'interférence avec une source monochromatique conduit à une modulation de l'amplitude résultante fonction de la longueur d'onde du rayonnement.
Pour une source polychromatique, mélanger les couleurs revient donc à mélanger des périodes différentes : la cohérence temporelle du signal est prise en défaut.
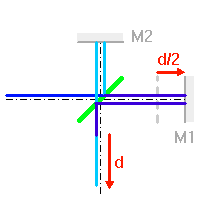
Interféromètre de Michelson : les 2 faisceaux, après recombinaison, sont décalés d'une différence de marche
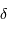
.
Crédit :
ASM
Exemple : interférométrie par transformée de Fourier
(Ne pas hésiter à aller voir les pages dédiées au spectromètre par TF).
L'exemple d'un interféromètre par transformée de Fourier (réglé en anneau) présente la problématique :
la visibilité des franges décroît d'autant plus rapidement que le
domaine spectral accepté est vaste.
Pour une raie monochromatique, l'interférogramme se développe, en fonction de la différence de marche, comme :
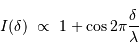
Pour une raie réelle, présentant une largeur non infiniment fine, il faut tenir compte de la contribution des différentes composantes spectrales.
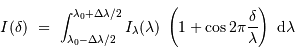
L'intégration, fonction du profil spectral 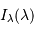 de la raie, conduit à :
de la raie, conduit à :
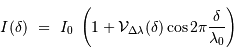
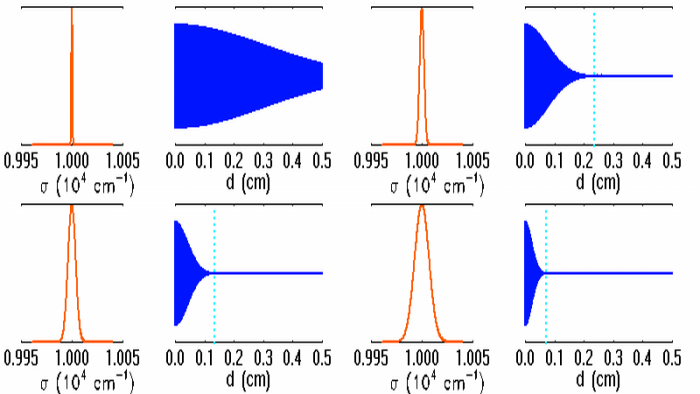
Profils de raie et visibilités associées.
Crédit :
ASM
L'expression de la fonction de visibilité des franges 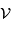 dépend de l'intégration du profil spectral
dépend de l'intégration du profil spectral 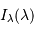 , et n'est pas nécessairement simple. La visibilité :
, et n'est pas nécessairement simple. La visibilité :
- a une extension inversement proportionnelle à
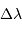 ; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles.
; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles. - décroît avec la différence de marche
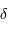 .
.
Un exemple de démonstration, dans un cas simplifié, est donné en exercice.
Définition de la cohérence temporelle
Dans le cas général, le degré de cohérence d'une source polychromatique, complexe, s'écrit :
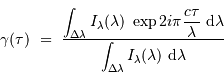
La démonstration résulte du théorème de Wiener-Khintchine.
La longueur de cohérence 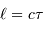 , qui mesure l'étendue du degré de cohérence, vérifie approximativement :
, qui mesure l'étendue du degré de cohérence, vérifie approximativement :
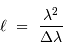
Simuler
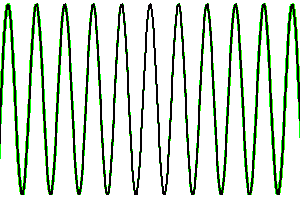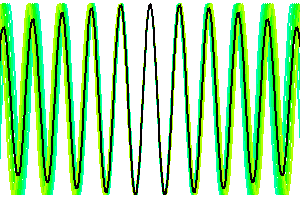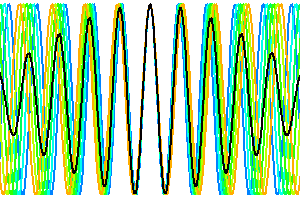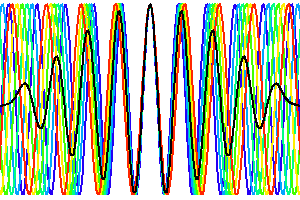
Evolution de la longueur de cohérence temporelle en fonction de la largeur spectrale.
Crédit :
ASM
Visibilité fonction de l'intervalle spectral
La visibilité des franges d'interférences dépend de la largeur de l'intervalle spectral considéré. La superposition de franges de couleurs différentes, donc de périodes différentes, conduit à un signal d'interférence en moyenne nulle.
S'exercer
Cohérence spatiale
Observer
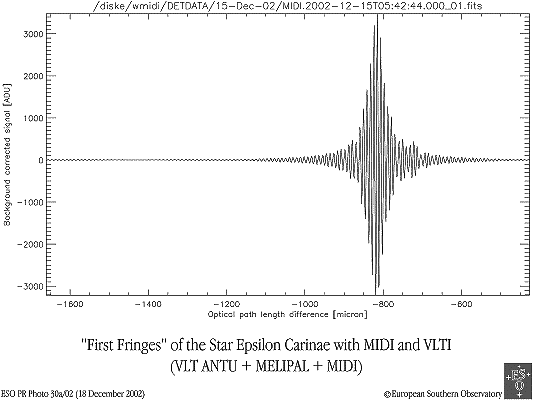
Enregistrement de franges d'interférence. La cohérence spatiale est limitée par la taille angulaire de la source.
Crédit :
ESO
Mesure de visibilité
Un interféromètre enregistre des franges d'interférence, pour en déterminer la visibilité. Celle-ci décroît rapidement dès que l'interférogramme s'écarte de la différence de marche correspondant au déphasage nul entre les 2 signaux.
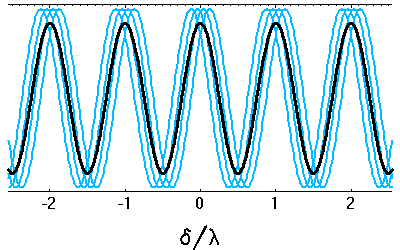
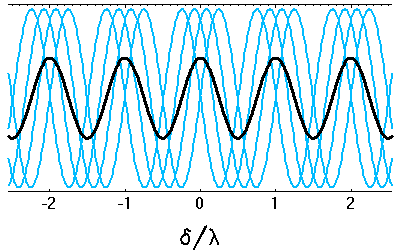
Cohérence spatiale : la superposition des différentes contributions déphasées amoindrit la visibilité des franges.
Crédit :
ASM
Source étendue
La cohérence spatiale entre 2 points d'un écran dépend de l'étendue angulaire de la source.

Tache de diffraction récupérée par optique adaptative (NACO/VLT) en bande K.
Crédit :
ESO
Source ponctuelle
L'image d'une source ponctuelle n'est pas un point : c'est la diffraction qui le veut... c'est un cas particulier de la notion de cohérence spatiale.
Apprendre
 Objectifs
Objectifs
Le cas d'une source rigoureusement ponctuelle et monochromatique est
souvent évoqué pour aborder l'optique (géométrique ou physique). Une source réelle en astrophysique peut être
approximativement ponctuelle, du fait d'un très grand éloignement, mais ce
n'est pas toujours le cas.
La cohérence spatiale rend compte de l'étendue angulaire de la source.
Une analyse détaillée des phénomènes peut se traiter par une formalisme
mathématique et s'appuie sur le théorème Zernike Van-Cittert.
Cohérence spatiale
Les sources astrophysiques ne sont pas naturellement cohérentes. Leur
étendue angulaire va conduire à dégrader la cohérence du rayonnement : l'onde collectée mélange diverses directions incidentes, présentant différentes phases, dont le mélange dégrade la cohérence.
Pour modéliser ce phénomène, on s'intéresse à la cohérence du champ sur un écran illuminé par une source à grande distance ; cet écran illustre le rôle que joue un plan d'onde intermédiaire ou bien une pupille.
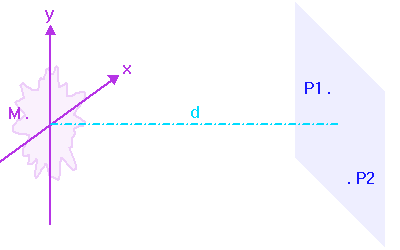
Cohérence du champ vu depuis 2 points P1 et P2 d'un écran E.
Crédit :
ASM
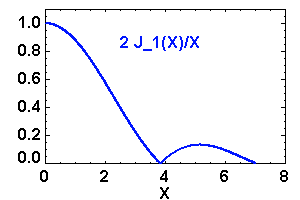
Cohérence du rayonnement d'une source circulaire.
Crédit :
ASM
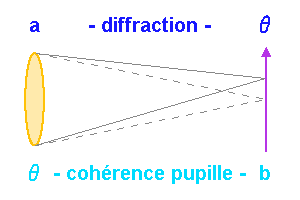
Ce schéma montre l'analogie entre le calcul de la tache de diffraction par une pupille circulaire de rayon
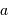
, et la cohérence du champ d'une source de diamètre
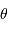
entre 2 points d'un écran séparés de
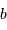
.
Crédit :
ASM
Rappel sur la diffraction de Fraunhofer
Le résultat précédent ressemble furieusement à celui de la diffraction. Est-ce un hasard ?
La tache d'Airy résultant de la diffraction par une pupille circulaire rend compte de la contribution de toutes les sources secondaires à considérer sur la pupille. Plus la pupille est grande, plus les déphasages s'accumulent dès lors que l'on s'éloigne de la position centrale de l'image géométrique. Il s'ensuit que la tache de diffraction est d'autant plus piquée que la pupille est grande.
En terme de cohérence, plus une pupille est grande, plus le degré de cohérence entre 2 points de cette pupille diminue.
Une autre manière de reformuler ceci dérive de l'analyse de Fourier :
plus on possède d'information sur un signal, moins ce signal est localisé.
Le principe d'incertitude de Heisenberg ne dit pas autre chose : la détermination précise d'une grandeur nécessite que sa grandeur conjuguée soit étendue, la moins localisée possible.
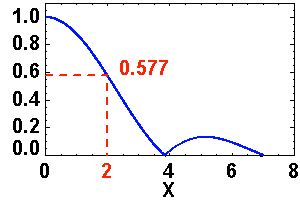
Etendue de cohérence : la valeur à mi-hauteur est obtenue pour
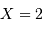
.
Crédit :
ASM
Simuler
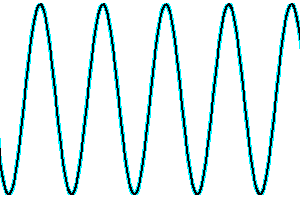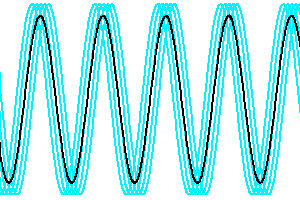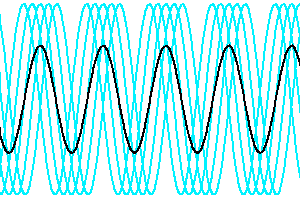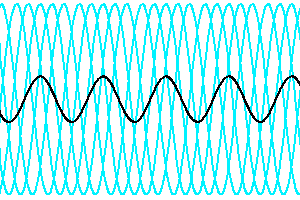
Evolution de la cohérence spatiale en fonction des déphasage des faisceaux issus de différents points de la source.
Crédit :
ASM
Visibilité fonction du degré de cohérence de la pupille
La visibilité du signal d'interférence dépend des déphasages entre les faisceaux issus des différents points de la source. Plus ces déphasages augmentent, moins le signal est cohérent.
S'exercer
Cohérence spatiale et interférométrie
Observer

Disque solaire, en lumière visible. Sa brillance n'est pas tout à fait uniforme : le phénomène d'assombrissement centre-bord rend compte des conditions différentes de transfert de rayonnement entre le centre et le limbe.
Crédit :
Observatoire de Paris
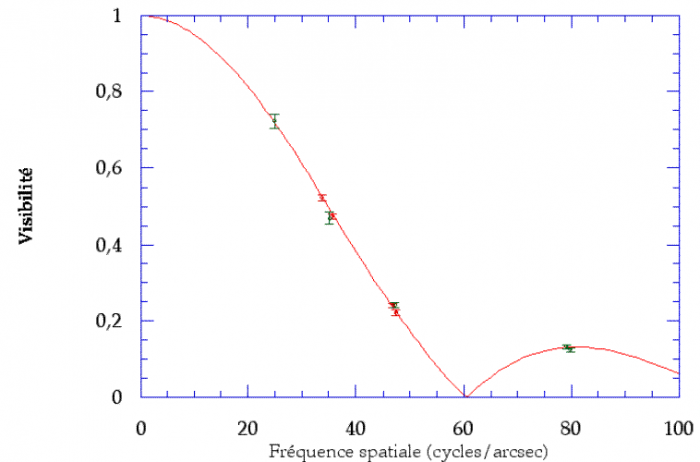
La mesure du diamètre angulaire de l'étoile
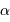
du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.
Crédit :
Observatoire de Paris
Diamètre stellaire
L'immense majorité des disques stellaires ne peut pas être résolue par imagerie avec un seul collecteur. Il est nécessaire, pour pallier cet effet, de recourir à la technique d'interférométrie.
La visibilité des franges d'interférence d'une source stellaire conduit alors de à la mesure de son diamètre.
Apprendre
 Objectifs
Objectifs
Nombre de sources astrophysiques présentent un diamètre angulaire qui ne peut pas être résolu par une pupille unique. Mais l'interférométrie permet d'affiner la résolution angulaire, et de mesurer des diamètres stellaires.
Source ponctuelle étendue
Le diamètre d'une étoile du proche environnement solaire sous-tend un
angle de l'ordre d'une milliseconde d'arc. Ce diamètre est, sauf exception,
très inférieur à la largeur de la tache de diffraction dans le visible d'un télescope, même de grand diamètre. En revanche, par interférométrie, on peut avoir accès indirectement à ce diamètre, si l'on dispose d'une base suffisamment grande.
On suppose une source de brillance uniforme, circulaire de diamètre angulaire
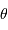 , observée par 2 télescopes identiques séparés d'une base
, observée par 2 télescopes identiques séparés d'une base
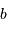 (base projetée dans le plan perpendiculaire à la source) que l'on fait interférer.
(base projetée dans le plan perpendiculaire à la source) que l'on fait interférer.
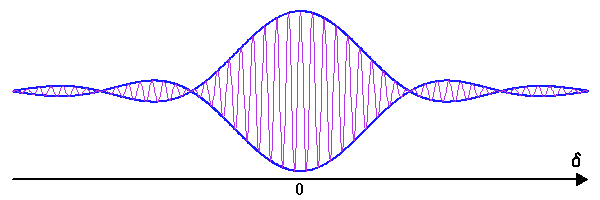
Franges d'interférence (en violet) et fonction de visibilité (courbe rouge).
Crédit :
ASM
Visibilité et mesure du diamètre stellaire
Le facteur de cohérence
établi dans le cas général est usuellement dénommé visibilité. La fonction de visibilité s'écrit :
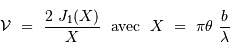
où 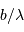 est la fréquence spatiale.
est la fréquence spatiale.
Chaque base 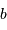 conduit à une mesure de la visibilité pour la fréquence spatiale
conduit à une mesure de la visibilité pour la fréquence spatiale 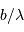 . Dans le cadre du modèle, où une étoile est un disque de brillance uniforme, la visibilité s'annule pour
. Dans le cadre du modèle, où une étoile est un disque de brillance uniforme, la visibilité s'annule pour 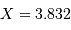 , et donc pour une relation entre le diamètre angulaire stellaire et la fréquence spatiale telle que :
, et donc pour une relation entre le diamètre angulaire stellaire et la fréquence spatiale telle que :
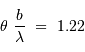
Finalement, une mesure du diamètre stellaire 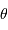 revient à une mesure de visibilité de la figure d'interférence.
revient à une mesure de visibilité de la figure d'interférence.
Le calcul précédent a supposé que la source présente un profil de brillance uniforme : en fait le phénomène d'assombrissement centre-bord complique un peu l'analyse.
Le rôle de la diffraction ne peut bien sûr pas être négligé : toute mesure de visibilité doit être corrigée de la fonction d'appareil des collecteurs (dont la diffraction), que l'on détermine expérimentale sur une source vraiment ponctuelle (en pratique : très lointaine).
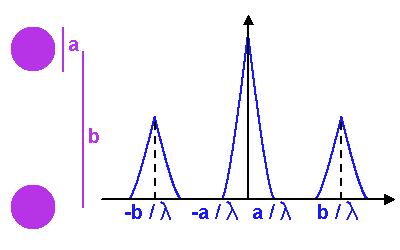
Diagramme donnant intensité en fonction de la fréquence spatiale, pour un interféromètre à 2 télescopes, de diamètre
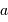
, sur une base
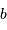
. L'autocorrélation de la pupille donne accès aux hautes fréquences spatiales
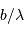
.
Crédit :
ASM
Résolution angulaire
Une pupille unique est un filtre passe-bas, coupant à la fréquence spatiale 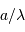 , et donnant une résolution angulaire de
, et donnant une résolution angulaire de 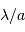 .
.
Un interféromètre est donc un filtre passe-bande, qui fournit une information à la fréquence 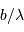 ; sa résolution angulaire est
; sa résolution angulaire est 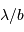 .
.
On retrouve ces propriétés par une analyse en terme de Fourier : le théorème de Wiener-Khintchine relie la fonction de transfert optique à la TF inverse de l'autocorrélation de la pupille.
Synthèse d'ouverture
Une mesure du facteur de cohérence complexe fournit une composante de fréquence spatiale de la source. La mesure de ce facteur à plusieurs fréquences spatiales permet la reconstruction de la distribution spatiale d'intensité de la source.
S'exercer
 QCM
QCM
 Diamètre stellaire
Diamètre stellaire
Difficulté : ☆☆
Temps : 20 min
Les figures ci-jointes illustrent la mesure de visibilité de franges d'interférence.
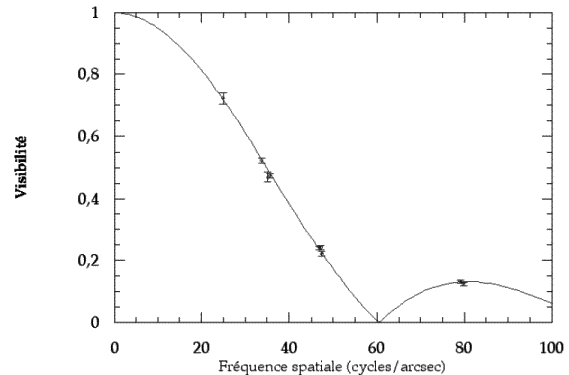
Courbe de visibilité de l'étoile
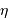
du Bouvier.
Crédit :
Observatoire de Paris
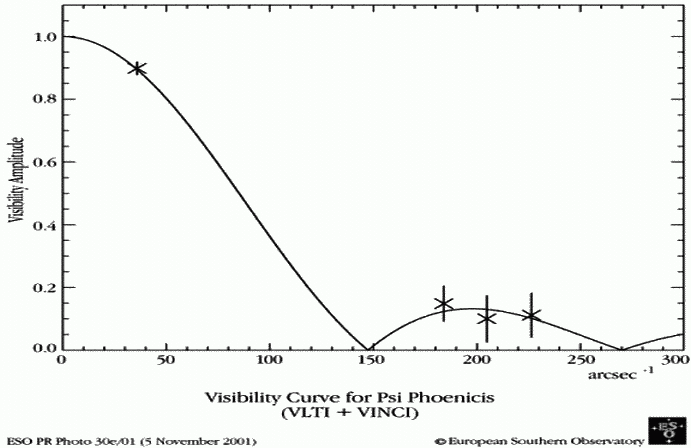
Courbe de visibilité de l'étoile
de la constellation du Phénix.
Crédit :
ESO
Courbe de visibilité de l'étoile
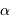
de la constellation d'Hercule.
Crédit :
ESO
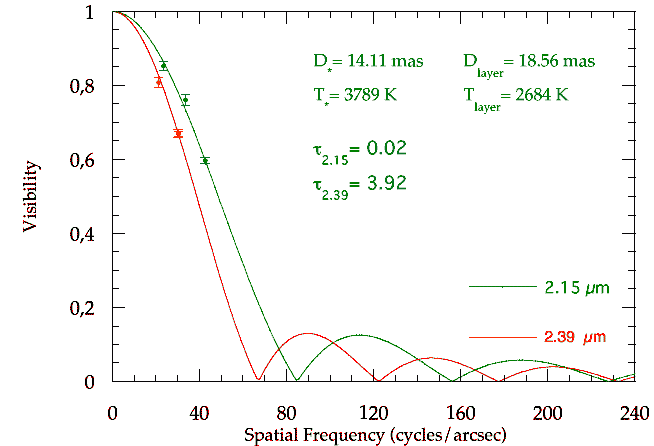
Courbes de visibilité de l'étoile
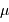
de Céphée.
Crédit :
Observatoire de Paris
Question 1)
Déduire des courbes le diamètre angulaire des sources stellaires 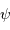 Phe et
Phe et 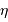 Boo.
Boo.
Rechercher le premier minimum de la fonction de visibilité.
Question 2)
Quelle raison physique peut expliquer que la courbe de visibilité de
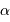 d'Hercule ne s'annule pas.
d'Hercule ne s'annule pas.
Quelle hypothèse sous-tend le résultat ?
Question 4)
Discuter les courbes de la figure concernant l'étoile 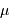 Cep.
Cep.
Est-ce normal d'avoir 2 courbes de visibilité différentes à 2 longueurs d'onde différentes ?
Que signifie la détermination de 2 diamètres stellaires différents pour 2 longueurs d'onde différentes ?
Réponses aux QCM
pages_foyer-primaire/foyer-primaire-sexercer.html
QCM
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 2)
- Question 3
Solution : réponse 2)
pages_afocal/afocal-sexercer.html
QCM
- Question 1
Solution : réponse 2)
(
L'oeil regarde ainsi à l'infini
)
- Question 2
Solution : réponse 1)
- Question 3
Solution : réponse 3)
pages_champ-ouverture/champ-ouverture-sexercer.html
QCM
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 2)
pages_diffraction-image/diffraction-image-sexercer.html
QCM
- Question 1
Solution : réponse 2)
(
Essayer de résoudre 1 cheveu à 10 m (l'oeil humain ne peut pas le faire)
)
- Question 2
Solution : réponse 2)
(
Mais il faut aussi que toute la chaîne de mesure assure une résolution de 1.2", ce qui n'est pas aisé
)
- Question 3
Solution : réponse 3)
(
Il y en a sûrement plus, mais on ne les distingue pas
)
- Question 4
Solution : réponse 1)
pages_resolution-spatiale/resolution-spatiale-sexercer.html
QCM
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 3)
(
effet supérieur à la diffraction et à la pixélisation
)
pages_resolution-spectrale/resolution-spectrale-sexercer.html
QCM
- Question 1
Solution : réponse 3)
- Question 2
Solution : réponse 2)
- Question 3
Solution : réponse 2)
pages_reseau-dispersion/reseau-dispersion-sexercer.html
QCM
- Question 1
Solution : réponse 3)
- Question 2
Solution : réponse 1)
(
Les interférences vont construire un seul pic dans la tache de diffraction
)
- Question 3
Solution : réponse 2)
(
Il ne dépend en effet pas de la longueur d'onde
)
- Question 4
Solution : réponse 2)
pages_reseau-blaze/reseau-blaze-sexercer.html
QCM
- Question 1
Solution : réponse 3)
(
Seule réponse possible, pour tenir compte d'une longueur d'onde dans le bleu plus courte que dans le vert
)
- Question 2
Solution : réponse 1)
(
C'est en effet la valeur entière la plus proche du résultat
)
pages_spectro-reseau/spectro-reseau-sexercer.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 1)
- Question 3
Solution : réponse 1)
pages_coherence-temporelle/coherence-temporelle-sexercer.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 2)
- Question 3
Solution : réponse 3)
pages_coherence-spatiale/coherence-spatiale-sexercer.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 1)
pages_coherence-interferometrie/coherence-interferometrie-sexercer.html
QCM
- Question 1
Solution : réponse 3)
- Question 2
Solution : réponse 3)
Réponses aux exercices
pages_optiquegeo/champ-ouverture-sexercer.html
Exercice
'Champ objet'
- Question 1
Aide :
Application de la définition de l'ouverture d'un télescope.
Solution :
Par définition, la focale 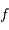 d'un télescope muni d'un miroir primaire de diamètre
d'un télescope muni d'un miroir primaire de diamètre 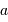 ouvert à
ouvert à 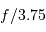 vaut :
vaut :
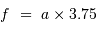
et donc 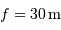
- Question 2
Aide :
Faire un schéma de l'image au foyer d'un faisceau incliné d'un angle 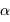 .
.
Solution :
Un pixel voit un champ 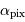 vérifiant :
vérifiant :
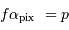
L'application numérique donne :
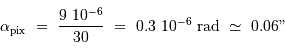
Le champ total, 2000 px, couvre une largeur de 120", soit 2'.
pages_optiquegeo/champ-ouverture-sexercer.html
Exercice
'Observation à la table équatoriale de Meudon'
- Question 1
Aide :
Application directe de la définition de l'ouverture.
Solution :
L'ouverture est f/15, car 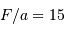 .
.
- Question 2
Aide :
Si l'on parle d'oculaire, c'est pour observer à l'oeil, ceci conditionne le montage optique.
Aide :
Le montage doit être afocal.
Solution :
Le montage étant afocal, le grossissement est simplement :
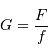
avec 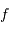 le focale de l'oculaire.
le focale de l'oculaire.
L'application numérique donne 200 et 300 respectivement, pour les oculaires de focale 45 et 30 mm.
- Question 3
Aide :
Revoir l'expression du grossissement.
Solution :
Dans le montage afocal, avec un angle du champ image 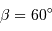 , l'angle du champ objet vérifie :
, l'angle du champ objet vérifie :
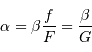
Les applications numériques donnent :
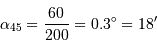
et
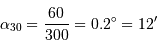
Ceci représente respectivement un peu plus ou un peu moins de la moitié du diamètre lunaire.
pages_diffraction/diffraction-image-sexercer.html
Exercice
'Diffraction or not diffraction ?'
- Question 1
Aide :
Établir l'échelle en se repérant par rapport au système double.
Solution :
Le seul repère donné est la séparation des 2 composantes. Une mesure seule est entachée d'erreur. Plusieurs mesures, avec l'outil ligne donnent en pixels : 60.4 ; 59.5 ; 59.8 ; 58.2 ; 59.5 ... soit de l'ordre de  .
.
On en déduit l'échelle 0.24"/pix, ou 4.13 pix/".
- Question 2
Aide :
Travailler avec l'outil cercle
Solution :
Les mesures, avec l'outil cercle, donnent en pixels, pour l'anneau entourant la composante faible 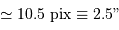 pour les anneaux entourant la composante brillante
pour les anneaux entourant la composante brillante 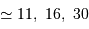 , soit respectivement 2.6, 4.1 et 7.3".
, soit respectivement 2.6, 4.1 et 7.3".
- Question 3
Aide :
Calculer la tache de diffraction.
Solution :
La tache de diffraction vaut 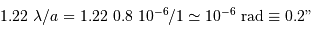 .
.
Elle est bien inférieure aux anneaux mesurés. Ils ne peuvent pas être dus à la diffraction par le miroir primaire. Ils ne semblent pas être liés à la diffraction par le miroir secondaire (de diamètre caractéristique 10 cm dans ce cas, pour coïncider au premier anneau), car leurs rayons ne progressent pas de la bonne manière. De toutes façons, la diffraction ne peut pas expliquer le fort contraste du grand anneau entourant la composante brillante ; par conséquent, des réflexions parasites sont suspectées.
pages_diffraction/diffraction-resolution-sexercer.html
Exercice
'Bonnes résolutions'
- Question 1
Aide :
Estimer la taille angulaire du cratère, et la comparer à la résolution limitée par la seule diffraction : 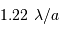
Solution :
La taille angulaire du cratère représente 20/380 000 rad, soit 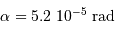 , soit environ 11".
, soit environ 11".
Cette valeur est à comparer à 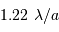 ; soit le diamètre :
; soit le diamètre :
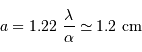
- Question 2
Solution :
Le cheminement pour arriver au résultat est analogue à la question précédente. Il faut un collecteur
de diamètre 60 cm.
pages_diffraction/resolution-spatiale-sexercer.html
Exercice
'Choix d'une caméra'
- Question 1
Aide :
Revoir la relation entre ouverture, focale et diamètre.
Aide :
Si 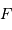 est la focale, alors
est la focale, alors 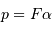
Solution :
Une ouverture de 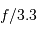 pour un collecteur de 3.6 m représente une focale de
pour un collecteur de 3.6 m représente une focale de
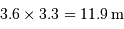 .
.
- Question 2
Aide :
Déterminer la taille angulaire d'un pixel.
Solution :
Bien échantillonner la résolution nécessite un pixel couvrant 0.3" (la moitié de la résolution de 0.6").
Le champ de 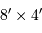 , ou
, ou 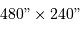 , devient, traduit en pixel,
, devient, traduit en pixel,
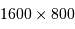 .
.
Avec la focale résultante 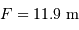 , la résolution de 0.3", cad
, la résolution de 0.3", cad 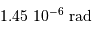 , correspond à une dimension physique de
, correspond à une dimension physique de 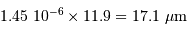 .
.
D'où la caméra choisie : 1k 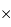 2k, avec des pixels de
2k, avec des pixels de 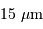 .
.
pages_interference/resolution-spectrale-sexercer.html
Exercice
'Résolution et variable spectrale'
- Question 1
Aide :
Appliquer la définition.
Solution :
L'application numérique donne :
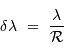
soit 0.02 nm.
- Question 2
Aide :
Pour calculer 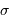 , c'est simple. Pour
, c'est simple. Pour 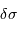 , il faut revenir à la définition.
, il faut revenir à la définition.
Aide :
Avec 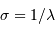 , calculer la différentielle
, calculer la différentielle 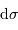 .
.
Solution :
La définition de 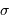 donne :
donne :
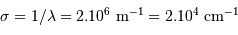
Mais écrire
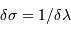
est faux (faire l'application numérique pour s'en convaincre !). En revanche,
la différentiation logarithmique s'écrit :
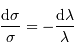
Et alors l'application de la définition donne :
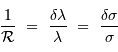
On en déduit :
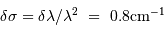
pages_interference/resolution-spectrale-sexercer.html
Exercice
'Quelle résolution ?'
- Question 1
Aide :
Réfléchir aux causes d'élargissement de la raie.
Solution :
La raie large est élargie par d'autres phénomènes que la résolution spectrale de l'instrument. La résolution instrumentale doit être mesurée sur une raie fine.
- Question 2
Aide :
Estimer la largeur d'une raie à mi-hauteur
Solution :
La solution est graphique.
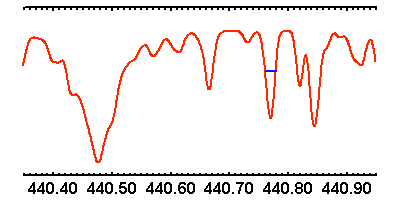
Crédit :
ASM
La largeur à mi-hauteur est de l'ordre de 0.020 nm, la résolution est donc de l'ordre de :
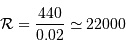
pages_rayon/etendue-faisceau-sexercer.html
Exercice
'Imagerie grand champ'
- Question 1
Aide :
Se servir la conservation de l'étendue de faisceau
Solution :
Si l'optique est bien conçue (sans diaphragme gênant), l'étendue
de faisceau se conserve. La traduction de 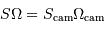 donne un angle solide objet
donne un angle solide objet
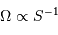
. Plus la
surface du collecteur est grande, plus le champ objet est réduit.
- Question 2
Aide :
Comment varie le nombre de photons collectés avec la surface collectrice ?
Solution :
Le nombre de photons collectés varie linéairement avec la surface collectrice. Le temps de pose varie donc en raison inverse :
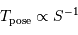
.
Plus la surface du collecteur est grande, plus le temps de pose est réduit.
- Question 3
Aide :
Se servir des 2 questions précédentes.
Aide :
Comparer la dépendance vis à vis de la surface collectrice 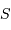 de la taille du champ élémentaire et du temps de pose élémentaire.
de la taille du champ élémentaire et du temps de pose élémentaire.
Solution :
La taille angulaire du champ élémentaire accessible varie comme 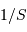 , la surface collectrice. Le temps de pose élémentaire varie comme
, la surface collectrice. Le temps de pose élémentaire varie comme 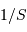 . Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée
. Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée 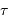 avec un petit collecteur sera observée par
avec un petit collecteur sera observée par 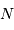 poses de durées
poses de durées 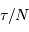 avec un grand.
avec un grand.
Notons que le télescope CFH, ouvert en 1980 avec un diamètre du collecteur de 3.6 m, s'est converti à partir des années 2000 vers l'imagerie grand champ.
pages_rayon/etendue-faisceau-sexercer.html
Exercice
'Sur les 2 tableaux'
- Question 1
Aide :
Revoir la page sur le montage afocal.
Solution :
Le schéma équivalent correspond à un montage afocal suivi de l'optique de chambre
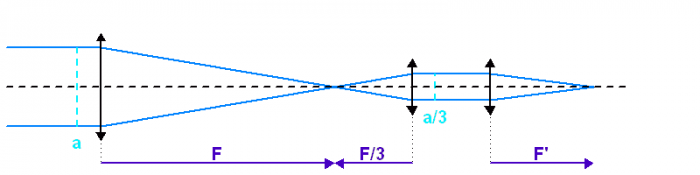
Ce montage afocal tient ici déjà compte de la suite, concernant le dimensionnement du miroir secondaire.
Crédit :
ASM
Remarque : pourquoi l'emploi des deux adjectifs, afocal et confocal, pour un même concept ? En fait, tout dépend du point de vue : si l'on s'intéresse aux dioptres, ils partagent un même foyer, d'où la dénomination confocale. Mais si l'on s'intéresse au faisceau, il passe de l'infini à l'infini, d'où la dénomination afocale.
- Question 2
Aide :
Revoir (encore !) la page sur le montage afocal.
Solution :
Par application directe des propriétés du montage afocal, le diamètre de la 2ème parabole comme celui des lentilles vaut le tiers de celui du primaire, soit 10 cm. Ce montage permet de réduire la taille des 6 lentilles de l'optique de chambre (intéressant en terme de poids et de coût). Mais, par conservation de l'étendue de faisceau, ces optiques travaillent sur des rayons d'inclinaison triplée.
- Question 3
Solution :
Le schéma équivalent demande 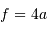 . L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
. L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
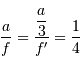
L'application numérique donne : 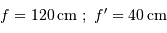
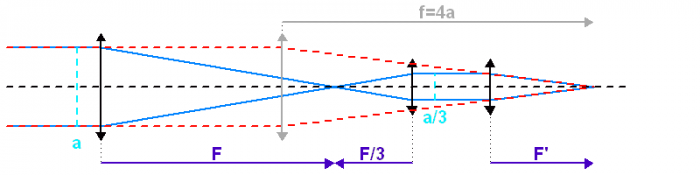
Le schéma équivalent demande
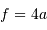
.
Crédit :
ASM
- Question 4
Aide :
Simple application de la conservation de l'étendue de faisceau.
Solution :
Par conservation de l'étendue de faisceau, la diminution du diamètre du faisceau par un facteur 3 s'accompagne par un accroissement dans un même facteur de l'ouverture.
Ainsi, le gain en taille doit être compensée par une meilleure qualité optique de ces lentilles travaillant avec rayons plus inclinés sur l'axe optique.
pages_rayon/etendue-faisceau-sexercer.html
Exercice
'Étendue cohérente'
- Question 1
Aide :
Pourquoi le premier anneau de la tache de diffraction est-il noir? Que cela signifie-t-il ?
Solution :
Le premier anneau sombre de diffraction est dû à une anticoïncidence de l'information collectée. Le faisceau est donc juste cohérent sur le pic central de diffraction.
- Question 2
Aide :
Revenir à la définition : exprimer 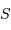 et
et 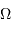 .
.
Solution :
La tache de diffraction, de taille angulaire 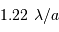 , couvre un angle solide de l'ordre de :
, couvre un angle solide de l'ordre de :
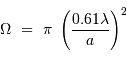
(dans l'approximation, éminemment valide, des petits angles).
Elle résulte de la collecte via un collecteur de surface :
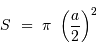
L'étendue de faisceau s'écrit alors :
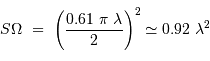
Ce qui est bien du même ordre de grandeur que 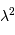 .
.
pages_rayon/diaphragmes-sexercer.html
Exercice
'Diaphragme d'ouverture'
- Question 1
Aide :
Faire un schéma.
Aide :
Revoir la notion de nombre d'ouverture.
Solution :
En confondant un angle et sa tangente, la lentille L1 est vue sous un nombre d'ouverture 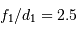 , la lentille L2 sous
, la lentille L2 sous 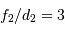 .
.
- Question 2
Aide :
La question précédente suffit pour apporter la réponse.
Solution :
La lentille L2 est vue sous un angle plus fermé. C'est elle qui limite l'ouverture du faisceau.
pages_rayon/diaphragmes-sevaluer.html
Exercice
'Pupille d'entrée de CoRoT'
- Question 1
Aide :
Examiner le tracé de rayons.
Aide :
Identitifier la nature des rayons incidents, émergents. Que se passe-t-il entre les miroirs M1 et M2?
- Question 2
Aide :
Le diaphragme 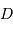 est un diaphragme d'ouverture.
est un diaphragme d'ouverture.
Aide :
Se rappeler la définition de la pupille d'entrée, et le lien avec le diaphragme 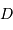 .
.
- Question 3
Aide :
Quel lien encore entre diaphragme d'ouverture et diaphragme de champ ?
- Question 4
pages_rayon/coherence-interferometrie-sexercer.html
Exercice
'Diamètre stellaire'
- Question 1
Aide :
Rechercher le premier minimum de la fonction de visibilité.
Solution :
Les diamètres stellaires sont respectivement :
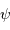 Phe : 1/147 = 6.8 mas
Phe : 1/147 = 6.8 mas
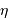 Boo : 1/61 = 16.4 mas
Boo : 1/61 = 16.4 mas
- Question 2
Aide :
Quelle hypothèse sous-tend le résultat ?
Solution :
Un profil de type d'Airy suppose que le disque stellaire présente une brillance uniforme.
Ici, ce n'est visiblement pas le cas.
- Question 3
Aide :
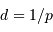 donne directement la distance en parsec si la parallaxe
donne directement la distance en parsec si la parallaxe 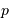 est mesurée en seconde d'arc.
est mesurée en seconde d'arc.
Solution :
Les distances de ces étoiles, sont alors, en parsec puis en unité métrique :
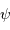 Phe : 99 pc,
Phe : 99 pc, 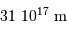 .
.
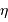 Boo : 11 pc, 3.5 ...
Boo : 11 pc, 3.5 ...
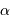 Her : 118 pc, 36 ...
Her : 118 pc, 36 ...
On en déduit ensuite les diamètres, en unité 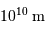 , puis en diamètre solaire et unité astronomique :
, puis en diamètre solaire et unité astronomique :
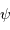 Phe : 10.4, soit 74 fois le diamètre solaire, ou 0.70 UA.
Phe : 10.4, soit 74 fois le diamètre solaire, ou 0.70 UA.
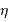 Boo : 2.9, ... 20.5 ... 0.19
Boo : 2.9, ... 20.5 ... 0.19
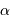 Her : 42, ... 300 ... 2.8
Her : 42, ... 300 ... 2.8
Il s'agit là d'étoiles géantes ou supergéantes, et non de naines.
- Question 4
Aide :
Est-ce normal d'avoir 2 courbes de visibilité différentes à 2 longueurs d'onde différentes ?
Aide :
Que signifie la détermination de 2 diamètres stellaires différents pour 2 longueurs d'onde différentes ?
Solution :
La visibilité dépend a priori de la longueur d'onde d'observation. Mais, dans la cas représenté, l'abscisse du graphe étant la fréquence spatiale, plus aucun paramètre ne dépend de la longueur d'onde. On en déduit que le diamètre stellaire sondé varie avec la longueur d'onde.
Pour cette étoile, la photosphère, de diamètre de l'ordre de 14 mas, est entourée d'une couche de diamètre 18.6 mas transparente à 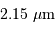 mais opaque à
mais opaque à 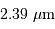 .
.







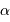 . Au foyer du miroir primaire du télescope, cet objet donne une image de taille linéaire
. Au foyer du miroir primaire du télescope, cet objet donne une image de taille linéaire 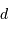 telle que
telle que 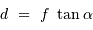 , avec
, avec 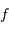 la focale du collecteur. L'angle
la focale du collecteur. L'angle 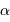 est le plus souvent très petit, et donc confondu avec sa tangente. On garde, avec
est le plus souvent très petit, et donc confondu avec sa tangente. On garde, avec 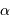 compté en radian :
compté en radian :
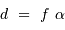

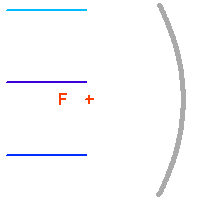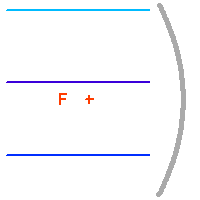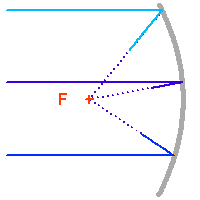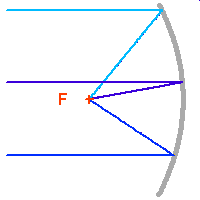
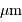 , au foyer d'un télescope de 12 m de focale ?
, au foyer d'un télescope de 12 m de focale ?
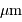 couvre sur le ciel un champ de 0.1". En déduire la focale du collecteur
couvre sur le ciel un champ de 0.1". En déduire la focale du collecteur


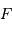 et
et 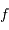 , le
, le 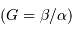 , vaut en valeur absolue :
, vaut en valeur absolue :
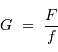
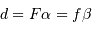 .
.

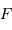 et
et 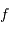 , le rapport des
, le rapport des 
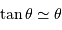 ) :
) : 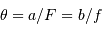 .
.
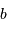 ) va nécessiter un grossissement élevé, et donc ne pourra porter que sur un champ objet de taille restreinte.
) va nécessiter un grossissement élevé, et donc ne pourra porter que sur un champ objet de taille restreinte.
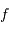 du secondaire est courte, plus le
grossissement est :
du secondaire est courte, plus le
grossissement est :







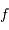 et par le diamètre
et par le diamètre 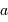 du collecteur.
du collecteur.
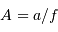 .
.
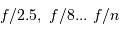 avec respectivement les nombres d'ouverture
avec respectivement les nombres d'ouverture 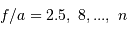 .
.
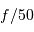 à
à 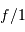 .
.
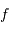 la focale résultante d'un collecteur et
la focale résultante d'un collecteur et 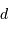 la taille du détecteur effectivement éclairée, le champ objet
la taille du détecteur effectivement éclairée, le champ objet 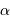 s'écrit simplement (dans l'approximation des petits angles) :
s'écrit simplement (dans l'approximation des petits angles) :
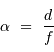
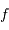 du télescope augmente.
du télescope augmente.


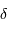 est proportionnelle à
est proportionnelle à 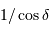
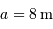 ouvert à f/3.75.
ouvert à f/3.75.
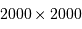 pixels, avec des pixels carrés de côté
pixels, avec des pixels carrés de côté 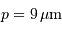 .
Quel champ voit un pixel ? Déterminer le champ de vue total dans
le ciel.
.
Quel champ voit un pixel ? Déterminer le champ de vue total dans
le ciel.
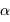 .
.
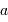 =60 cm.
=60 cm.
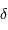 possède, du fait de la rotation diurne, une vitesse angulaire proportionnelle à
possède, du fait de la rotation diurne, une vitesse angulaire proportionnelle à 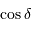 .
.
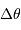 en une durée
en une durée 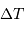 . Montrer que l'on a :
. Montrer que l'on a :
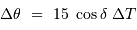
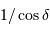 : sélectionner la 1ère ligne de la 3ème colonne (
: sélectionner la 1ère ligne de la 3ème colonne (
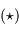 !
!
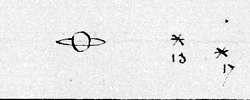



 ?
?




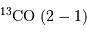 . Cette source correspond à un système stellaire binaire en formation. Le flux millimétrique à 1.3 mm codé en fausse couleur montre une structure en anneau.
. Cette source correspond à un système stellaire binaire en formation. Le flux millimétrique à 1.3 mm codé en fausse couleur montre une structure en anneau.


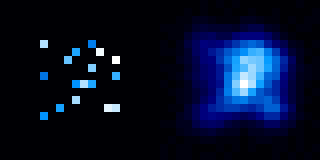













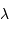 pour un collecteur de diamètre
pour un collecteur de diamètre 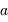 vaut :
vaut :
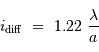
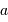 , le facteur est 1) ; c'est la première valeur qui annule la
, le facteur est 1) ; c'est la première valeur qui annule la 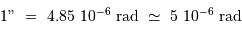
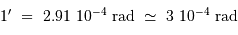

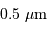 , il faut un collecteur de taille au-moins égale à
, il faut un collecteur de taille au-moins égale à
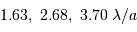 ) ?
) ?



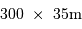 .
Estimer le profil de la tache angulaire de diffraction, pour les trois longueurs d'onde de travail 9, 18 et 21 cm (raie de couplage spin-orbite de l'hydrogène atomique).
.
Estimer le profil de la tache angulaire de diffraction, pour les trois longueurs d'onde de travail 9, 18 et 21 cm (raie de couplage spin-orbite de l'hydrogène atomique).
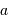
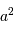
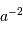
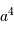




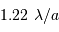 .
L'abscisse du profil en coupe est directement donnée en unité
.
L'abscisse du profil en coupe est directement donnée en unité 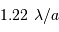 .
.
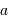
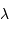
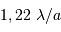

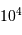

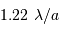
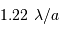







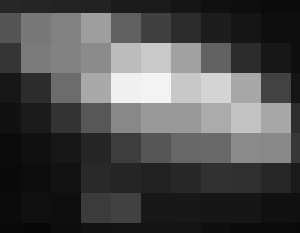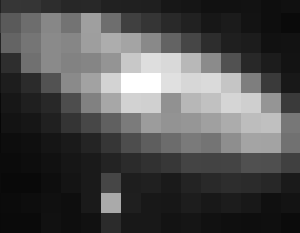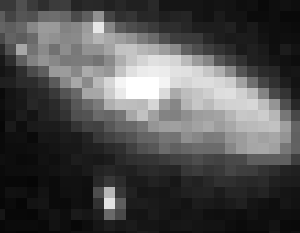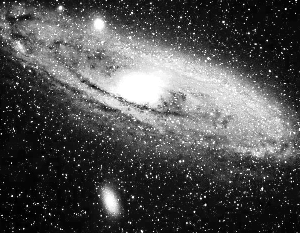
 1k (1000 px par 1000 px), 1k
1k (1000 px par 1000 px), 1k 2k,
2k
2k,
2k 2k, et 2k
2k, et 2k 4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
4k, avec pixels carrés de 20, 15 ou 9 micromètres de côté.
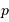 du pixel et le champ
du pixel et le champ 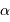 qu'il couvre.
qu'il couvre.
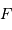 est la focale, alors
est la focale, alors 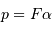
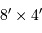 , avec une résolution de
, avec une résolution de 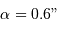 .
En déduire la caméra appropriée.
.
En déduire la caméra appropriée.



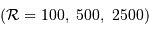 . La luminosité par intervalle spectral (unité arbitraire) est inversement proportionnelle à la résolution.
. La luminosité par intervalle spectral (unité arbitraire) est inversement proportionnelle à la résolution.

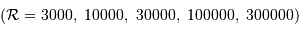 , avec renormalisation du flux.
, avec renormalisation du flux.
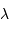 et
et 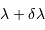 . Il est mesuré par la quantité :
. Il est mesuré par la quantité :
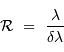
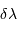 (également appelé résolution spectrale élémentaire ou élément spectral) est petit.
(également appelé résolution spectrale élémentaire ou élément spectral) est petit.
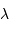 , fréquence
, fréquence 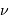 ) :
) :
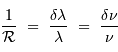
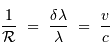

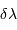 @ 500 nm (nm)
@ 500 nm (nm) 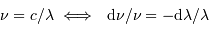 .
.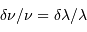 .
.
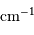 . Exprimer le nombre d'onde
. Exprimer le nombre d'onde 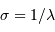 et la résolution
et la résolution 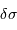 dans ce système d'unité.
dans ce système d'unité.
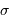 , c'est simple. Pour
, c'est simple. Pour 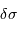 , il faut revenir à la définition.
, il faut revenir à la définition.
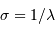 , calculer la différentielle
, calculer la différentielle 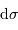 .
.



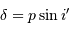 . Elle correspond au déphasage
. Elle correspond au déphasage 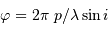 .
.
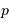 la
la 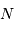 le nombre de traits,
le nombre de traits, 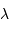 la longueur d'onde étudiée.
La condition d'interférences constructives s'écrit :
la longueur d'onde étudiée.
La condition d'interférences constructives s'écrit :
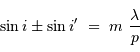
 , entier, l'ordre d'interférence. Le signe
, entier, l'ordre d'interférence. Le signe  dans cette relation concerne un réseau par transmission, le signe
dans cette relation concerne un réseau par transmission, le signe  un réseau par réflexion. C'est ce dernier cas qui nous intéresse, car il correspond au cas du
un réseau par réflexion. C'est ce dernier cas qui nous intéresse, car il correspond au cas du 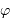 entre les amplitudes complexes issues de 2 traits consécutifs, vaut
entre les amplitudes complexes issues de 2 traits consécutifs, vaut 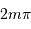 (ou bien, de façon équivalente, que la différence de marche vaut
(ou bien, de façon équivalente, que la différence de marche vaut 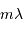 ).
).


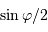 du dénominateur. La finesse des pics d'interférence augmente avec le nombre de traits
du dénominateur. La finesse des pics d'interférence augmente avec le nombre de traits 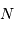 .
.

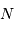 fentes. On s'intéresse dans un premier temps au phénomène d'interférence seul.
On note
fentes. On s'intéresse dans un premier temps au phénomène d'interférence seul.
On note 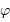 le déphasage entre 2 fentes consécutives, et
le déphasage entre 2 fentes consécutives, et 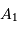 l'amplitude complexe. On mène les calculs dans l'approximation de
Fraunhofer, pour montrer que l'intensité diffractée vaut :
l'amplitude complexe. On mène les calculs dans l'approximation de
Fraunhofer, pour montrer que l'intensité diffractée vaut :
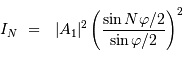
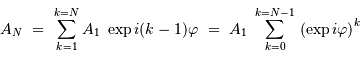
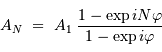
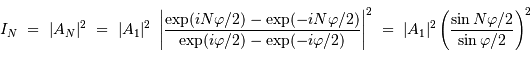
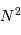 . Chaque
. Chaque 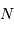 fois plus rapidement que le dénominateur ; elle est donc
fois plus rapidement que le dénominateur ; elle est donc 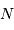 fois inférieure à la largeur entre 2 ordres consécutifs.
fois inférieure à la largeur entre 2 ordres consécutifs.



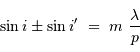
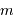 l'ordre d'interférence (entier),
l'ordre d'interférence (entier), 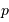 le pas du réseau,
le pas du réseau, 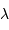 la longueur d'onde d'étude.
la longueur d'onde d'étude.
 fixée, les variations de
l'angle de sortie
fixée, les variations de
l'angle de sortie 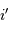 avec
avec 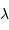 . Elle est obtenue par différentiation de la relation du réseau :
. Elle est obtenue par différentiation de la relation du réseau :
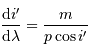
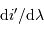 croît avec l'ordre
croît avec l'ordre 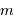 et la fréquence spatiale du réseau
et la fréquence spatiale du réseau 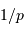 .
La résolution
.
La résolution 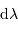 dépend des paramètres du réseau, mais aussi de la précision
dépend des paramètres du réseau, mais aussi de la précision 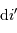 avec laquelle on peut déterminer l'angle
avec laquelle on peut déterminer l'angle 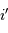 .
.

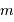 variable, la différentiation de la
variable, la différentiation de la 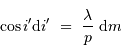
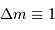 , correspond à un
intervalle angulaire :
, correspond à un
intervalle angulaire :
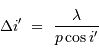

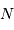 ondes
ondes ![(N = [3, 10, 30, 100, 300, 1000])](../pages_interference/equations_reseau-dispersion/equation20.png) . La largeur de la tache principale varie comme
. La largeur de la tache principale varie comme 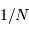 . La figure de droite
zoome sur un ordre donné.
. La figure de droite
zoome sur un ordre donné.
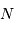 de traits du réseau
de traits du réseau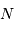 fois moindre qu'un ordre :
fois moindre qu'un ordre :
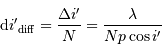
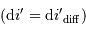 :
:
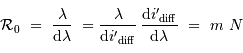







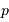 et la largeur de fente
et la largeur de fente 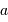 sont très proches pourra travailler efficacement dans combien d'ordres :
sont très proches pourra travailler efficacement dans combien d'ordres :

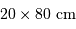 .
.





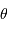 par rapport au plan du réseau. La diffraction envoie une intensité maximale dans un ordre d'interférence non nul, pour
par rapport au plan du réseau. La diffraction envoie une intensité maximale dans un ordre d'interférence non nul, pour
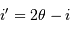 . Les angles
. Les angles  et
et 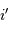 restent définis par rapport au plan du réseau.
restent définis par rapport au plan du réseau.


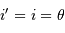 , où
, où 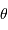 est l'angle de blaze). Cet ordre dépend de la couleur étudié.
est l'angle de blaze). Cet ordre dépend de la couleur étudié.

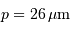 et d'angle
et d'angle 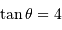 observe dans le rouge (600 nm) dans l'ordre
observe dans le rouge (600 nm) dans l'ordre


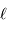 la largeur de la fente et
la largeur de la fente et 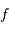 la focale du miroir collimateur, la taille angulaire de la fente vue dans l'espace image est :
la focale du miroir collimateur, la taille angulaire de la fente vue dans l'espace image est :
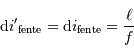
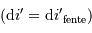 s'écrit :
s'écrit :
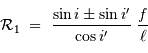
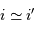 et avec le signe + correspondant au réseau par réflexion :
et avec le signe + correspondant au réseau par réflexion :
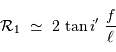
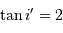 , le pouvoir de résolution géométrique vaut 40 000.
, le pouvoir de résolution géométrique vaut 40 000.
![{\cal R} \ = \mathrm{min}\ [ {\cal R}_0, \ {\cal R}_1]](../pages_interference/equations_spectro-reseau/equation9.png)
 du réseau, inférieur au pouvoir de résolution théorique, dépend :
du réseau, inférieur au pouvoir de résolution théorique, dépend :
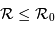 , qui varie comme
, qui varie comme 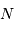
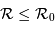 , qui varie comme
, qui varie comme 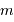
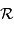 varie comme
varie comme 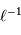
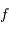 de l'optique et la largeur
de l'optique et la largeur 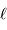 de la fente d'entrée comme
de la fente d'entrée comme
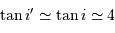 .
.








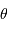 entre un point de l'objet et le point de l'objet centré sur l'axe optique ; la distance
entre un point de l'objet et le point de l'objet centré sur l'axe optique ; la distance 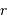 , sur la
, sur la 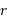 . Elle est d'autant plus grande que l'ouverture de l'optique est grande.
. Elle est d'autant plus grande que l'ouverture de l'optique est grande.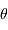 , indépendamment de la taille de l'optique. La
, indépendamment de la taille de l'optique. La 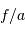 et de la distance angulaire
et de la distance angulaire 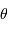 .
.

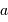 en un faisceau de diamètre
en un faisceau de diamètre 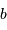 , avec un grossissement angulaire
, avec un grossissement angulaire 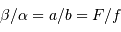 .
.
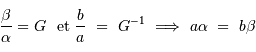

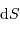 à l'aire collectrice
à l'aire collectrice 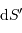 .
.
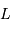 transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la
transportée par un faisceau lumineux, émise par l'élément de surface S et reçue par S' se conserve (sorte de tautologie, le faisceau étant défini par l'ensemble des rayons lumineux, càd la totalité de la puissance lumineuse). Cette puissance est proportionnelle à la 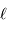 , à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
, à l'élément de surface émetteur et à l'élément d'angle solide d'émission.
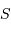 , occupant un angle solide
, occupant un angle solide 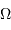 , dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit
, dans un milieu d'indice unité (comme le vide ou comme l'air à peu de chose près), par le produit 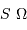 , qui se conserve le long du faisceau.
, qui se conserve le long du faisceau.
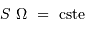
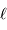 à la puissance lumineuse nécessite de s'appuyer sur le produit d'un élément de surface émetteur
à la puissance lumineuse nécessite de s'appuyer sur le produit d'un élément de surface émetteur 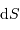 et d'un angle solide d'émission
et d'un angle solide d'émission 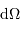 .
La luminosité élémentaire s'écrit :
.
La luminosité élémentaire s'écrit :
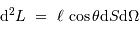
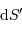 à la distance
à la distance 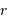 telle que :
telle que :
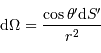
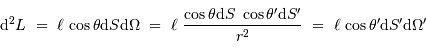
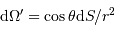 l'angle solide sous lequel est vue la source depuis la surface réceptrice. On remarque que le rôle des éléments émetteur et récepteur est symétrique. Le produit
l'angle solide sous lequel est vue la source depuis la surface réceptrice. On remarque que le rôle des éléments émetteur et récepteur est symétrique. Le produit 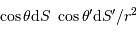 introduit l'étendue géométrique élémentaire.
introduit l'étendue géométrique élémentaire.
 angle solide
angle solide 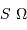 .
.

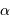 couvre un angle solide :
couvre un angle solide :
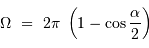
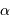 est petit, cet angle solide se réécrit simplement :
est petit, cet angle solide se réécrit simplement :
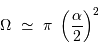
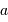 , la conservation du produit
, la conservation du produit 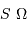 devient, pour ce faisceau conique :
devient, pour ce faisceau conique :
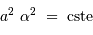
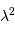 .
La justification est donnée en
.
La justification est donnée en 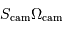 . Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
. Le but de l'exercice est de déterminer quel collecteur optimal utiliser pour réaliser ce programme.
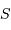 du collecteur ?
du collecteur ?
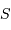 de la taille du champ élémentaire et du temps de pose élémentaire.
de la taille du champ élémentaire et du temps de pose élémentaire.

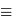 même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
même foyer) hors axe, suivis par une optique de chambre conjuguant le faisceau issu des 2 paraboles avec le détecteur CCD. En pratique, pour les respecter les specifications de la formation d'image, cette optique de chambre est constituée de 6 lentilles.
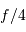 vu par la caméra, Calculer la focale
vu par la caméra, Calculer la focale 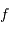 équivalente et la focale
équivalente et la focale 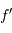 de l'optique de chambre.
de l'optique de chambre.
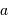 délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur)
délivre une tache de diffraction d'ouverture (définie comme largeur à mi-hauteur) 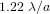 . On cherche à en déduire l'étendue de faisceau cohérente.
. On cherche à en déduire l'étendue de faisceau cohérente.
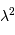 .
.
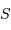 et
et 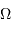 .
.
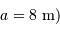 est alimenté par un faisceau de fibres de diamètre
est alimenté par un faisceau de fibres de diamètre 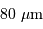 .
.
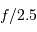 . En déduire l'ouverture angulaire du faisceau en entrée de fibre.
. En déduire l'ouverture angulaire du faisceau en entrée de fibre.
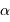 par un collecteur de diamètre
par un collecteur de diamètre 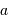 et de focale
et de focale 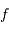 . On considère le seul cas où l'angle
. On considère le seul cas où l'angle 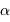 est petit. On note
est petit. On note 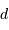 ladite taille linéaire.
ladite taille linéaire.
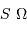 côté source, en fonction des données.
côté source, en fonction des données.
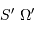 côté détecteur.
côté détecteur.
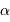 , quelle est la taille linéaire
, quelle est la taille linéaire 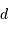 de son image.
de son image.




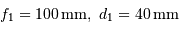 ;
;
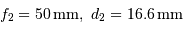 .
.

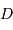 est positionné en aval de M2, à une distance du miroir égale à la focale de M2. En déduire la position de la pupille d'entrée
est positionné en aval de M2, à une distance du miroir égale à la focale de M2. En déduire la position de la pupille d'entrée 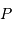 . Faire un schéma justifiant la réponse.
. Faire un schéma justifiant la réponse.
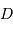 est un diaphragme d'ouverture.
est un diaphragme d'ouverture.
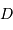 .
.

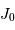 et
et 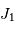 .
.

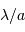 . Le premier zéro est à l'abscisse 1.22.
. Le premier zéro est à l'abscisse 1.22.
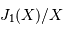 , avec
, avec 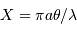 , avec
, avec 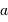 le diamètre de la pupille,
le diamètre de la pupille, 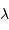 la longueur d'onde et
la longueur d'onde et 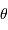 la direction d'observation.
la direction d'observation.
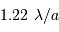 qui dimensionne la tache de diffraction.
qui dimensionne la tache de diffraction.
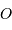 , et l'on note
, et l'on note 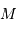 un point de la pupille. Cette pupille est éclairée par une onde plane uniforme, monochromatique, en incidence normale. L'amplitude de l'onde diffractée dans une direction repérée par le vecteur directeur
un point de la pupille. Cette pupille est éclairée par une onde plane uniforme, monochromatique, en incidence normale. L'amplitude de l'onde diffractée dans une direction repérée par le vecteur directeur 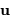 s'écrit :
s'écrit :
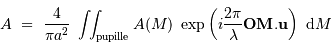

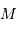 est un point courant de la pupille, de coordonnées polaires
est un point courant de la pupille, de coordonnées polaires 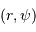 , et
, et 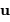 porte la direction pour laquelle on recherche l'amplitude de l'onde diffractée.
porte la direction pour laquelle on recherche l'amplitude de l'onde diffractée.
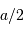 , il est préférable de décrire les coordonnées du point
, il est préférable de décrire les coordonnées du point 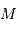 et de la direction de diffraction
et de la direction de diffraction 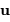 en coordonnées polaires, avec les notations suivantes :
en coordonnées polaires, avec les notations suivantes :
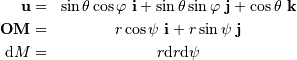
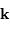 est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction
est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction 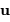 faisant un angle
faisant un angle 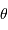 avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
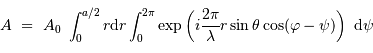
![\begin{eqnarray*} J_0 (X) =& \displaystyle{{1\over 2\pi} \int_0^{2\pi} \exp \bigl[-iX \cos v \bigr]\ {\mathrm{d}} v}\\ J_1 (X) =& \displaystyle{{1\over X}\ \int_0^{X} u J_0 (u)\ {\mathrm{d}} u}\\ \end{eqnarray*}](../pages_rayon/equations_diffraction-pupille/equation25.png)
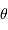 par rapport à l'axe optique, devient :
par rapport à l'axe optique, devient :
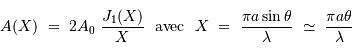
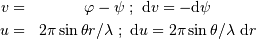
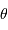 s'écrit donc :
s'écrit donc :
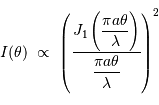
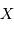 voisin de 0,
voisin de 0, 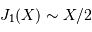 . Par ailleurs,
le premier zéro de la fonction
. Par ailleurs,
le premier zéro de la fonction 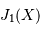 est pour
est pour 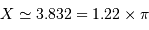 .
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille
.
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille 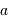 et de la longueur d'onde
et de la longueur d'onde 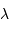 :
:
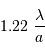
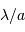 . Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...
. Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...

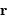 , la fonction
, la fonction 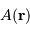 caractérisant l'éclairement sur la pupille, l'amplitude diffractée
dans une direction angulaire de vecteur directeur
caractérisant l'éclairement sur la pupille, l'amplitude diffractée
dans une direction angulaire de vecteur directeur 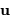 s'écrit :
s'écrit :
![\begin{eqnarray*} A ( \mathbf{u})\ &=&\ \int\!\!\!\int_{\mathrm{ pupille }} A( \mathbf{r} ) \exp\left[ -2i\pi \mathbf{u}. { \mathbf{r} \over \lambda} \right] \ \ { {\mathrm{d}} \mathbf{r}\over \lambda^2}\\ &=& \ \int\!\!\!\int {\cal P}( \mathbf{r})\ I( \mathbf{r} ) \exp\left[ -2i\pi \mathbf{u}. { \mathbf{r} \over \lambda} \right]\ \ { {\mathrm{d}} \mathbf{r}\over \lambda^2}\\ \end{eqnarray*}](../pages_rayon/equations_diffraction-fourier/equation4.png)
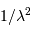 introduit pour normaliser l'élément de surface
introduit pour normaliser l'élément de surface 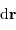 , et
, et
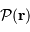 la pupille d'entrée, qui limite la fraction de l'onde plane
émise par la source à l'infini. Pour un éclairement uniforme en incidence normale,
la pupille d'entrée, qui limite la fraction de l'onde plane
émise par la source à l'infini. Pour un éclairement uniforme en incidence normale, 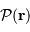 est typiquement une fonction porte à 2 dimensions.
est typiquement une fonction porte à 2 dimensions.
![\tilde f ( \mathbf{u}) \ =\ \int\!\!\!\int f( \mathbf{r} ) \exp\left[ -2i\pi \mathbf{u} . \mathbf{r} \right] \ \ {\mathrm{d}} \mathbf{r}](../pages_rayon/equations_diffraction-fourier/equation9.png)
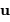 est donnée par la transformée de Fourier de la fonction
de pupille
est donnée par la transformée de Fourier de la fonction
de pupille 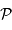 , la variable de position étant normalisée en unité de longueur d'onde :
, la variable de position étant normalisée en unité de longueur d'onde :
![A ( \mathbf{u})\ =\ A_0 \ \int\!\!\!\int {\cal P}( \mathbf{r})\ \exp\left[ -2i\pi \mathbf{u}. { \mathbf{r} \over \lambda} \right]\ \ { {\mathrm{d}} \mathbf{r}\over \lambda^2}](../pages_rayon/equations_diffraction-fourier/equation12.png)
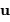 , et
, et 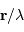 la variable spatiale décrivant la pupille rapportée à la longueur d'onde.
la variable spatiale décrivant la pupille rapportée à la longueur d'onde.
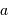 filtre les hautes fréquences, càd l'information angulaire plus fine typiquement que
filtre les hautes fréquences, càd l'information angulaire plus fine typiquement que 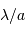 .
.


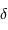 .
L'
.
L'



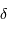 .
.
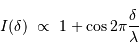
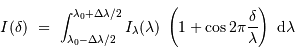
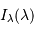 de la raie, conduit à :
de la raie, conduit à :
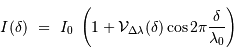

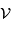 dépend de l'intégration du profil spectral
dépend de l'intégration du profil spectral 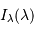 , et n'est pas nécessairement simple. La visibilité :
, et n'est pas nécessairement simple. La visibilité :
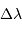 ; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles.
; plus l'intervalle spectral est grand, moins les franges de l'interférogramme seront visibles.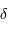 .
.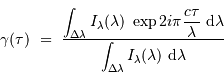
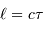 , qui mesure l'étendue du degré de cohérence, vérifie approximativement :
, qui mesure l'étendue du degré de cohérence, vérifie approximativement :
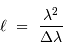






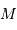 de la source par le rayon vecteur
de la source par le rayon vecteur 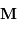 de coordonnées
de coordonnées 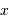 et
et 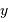 . On compare la cohérence entre 2 points
. On compare la cohérence entre 2 points 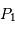 et
et 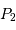 de l'écran.
Pour une source à grande distance (
de l'écran.
Pour une source à grande distance (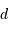 très grand par rapport aux autres dimensions), on définit le degré de cohérence comme une fonction du profil de brillance
très grand par rapport aux autres dimensions), on définit le degré de cohérence comme une fonction du profil de brillance 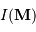 :
:
![\gamma_{1,2} \ = \ \gamma (\mathbf{P_1P_2}) \ = \ { \displaystyle{\int _{\mathrm{source}} I( \mathbf{M})\ \exp \left[ -2i\pi\ { \mathbf{M} \over d}. {\mathbf{P_1P_2} \over \lambda} \right] \ {\mathrm{d}}^2 \mathbf{M}} \over \displaystyle{\int _{\mathrm{source}} I( \mathbf{M}) \ {\mathrm{d}}^2 \mathbf{M}} }](../pages_rayon/equations_coherence-spatiale/equation9.png)

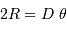 ,
de brillance uniforme, observée à distance
,
de brillance uniforme, observée à distance 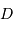 . La brillance peut être représentée par une fonction porte
. La brillance peut être représentée par une fonction porte 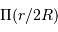 . On traite alors ce cas particulier en s'appuyant sur sa géométrie cylindrique, et
l'on réécrit la cohérence entre le centre
. On traite alors ce cas particulier en s'appuyant sur sa géométrie cylindrique, et
l'on réécrit la cohérence entre le centre 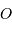 de l'écran (centre repéré sur la normale à l'écran vers la source) et un point
de l'écran (centre repéré sur la normale à l'écran vers la source) et un point 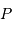 tel
tel 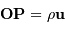 :
:
![\begin{eqnarray*} \gamma_{1,2} \ =& { \displaystyle{\int _{\mathrm{source}} \ \Pi{\left({D \mathbf{u}\over 2R } \right)}\exp\left[ -2i\pi\ \mathbf{u} . {\mathbf{\rho} \over \lambda}\right] \ {\mathrm{d}} \mathbf{u}} \over \displaystyle{\int _{\mathrm{source}} \Pi{\left({D \mathbf{u}\over 2R } \right)}\ {\mathrm{d}} \mathbf{u}} }\\ \propto & \displaystyle{\int_0^\theta \ \exp\left[ -2i\pi\ \mathbf{u} . {\mathbf{\rho} \over \lambda}\right] \ {\mathrm{d}} \mathbf{u}} \ = \ \displaystyle{ 2 J_1 \left( 2\pi\theta \displaystyle{\rho\over \lambda}\right) \over 2\pi\theta \displaystyle{\rho\over \lambda}}\\ = & \displaystyle{ 2 J_1 (X) \over X} \ \ \mathrm{avec} \ \ X\ =\ 2\pi\theta \displaystyle{\rho\over \lambda} \end{eqnarray*}](../pages_rayon/equations_coherence-spatiale/equation16.png)
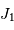 .
.

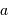 , et la cohérence du champ d'une source de diamètre
, et la cohérence du champ d'une source de diamètre 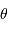 entre 2 points d'un écran séparés de
entre 2 points d'un écran séparés de 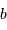 .
.

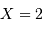 .
.
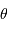 est vue depuis l'écran sous un angle solide
est vue depuis l'écran sous un angle solide 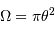 . Une surface
. Une surface 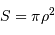 de l'écran correspond à une
de l'écran correspond à une 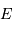 telle que :
telle que :
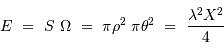
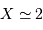 : on choisit cette valeur pour définir le rayon de l'étendue de cohérence.
: on choisit cette valeur pour définir le rayon de l'étendue de cohérence.
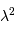 .
.



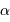 du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.
du Bouvier (Arcturus) résulte de la visibilité des franges d'interférence obtenues par interférométrie.
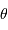 , observée par 2 télescopes identiques séparés d'une base
, observée par 2 télescopes identiques séparés d'une base
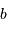 (base projetée dans le plan perpendiculaire à la source) que l'on fait interférer.
(base projetée dans le plan perpendiculaire à la source) que l'on fait interférer.

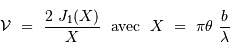
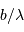 est la fréquence spatiale.
est la fréquence spatiale.
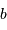 conduit à une mesure de la
conduit à une mesure de la 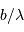 . Dans le cadre du modèle, où une étoile est un disque de brillance uniforme, la visibilité s'annule pour
. Dans le cadre du modèle, où une étoile est un disque de brillance uniforme, la visibilité s'annule pour 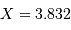 , et donc pour une relation entre le diamètre angulaire stellaire et la fréquence spatiale telle que :
, et donc pour une relation entre le diamètre angulaire stellaire et la fréquence spatiale telle que :
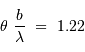
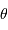 revient à une mesure de visibilité de la figure d'interférence.
revient à une mesure de visibilité de la figure d'interférence.

 , sur une base
, sur une base  . L'autocorrélation de la pupille donne accès aux hautes fréquences spatiales
. L'autocorrélation de la pupille donne accès aux hautes fréquences spatiales 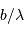 .
.
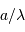 , et donnant une résolution angulaire de
, et donnant une résolution angulaire de 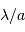 .
.
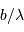 ; sa résolution angulaire est
; sa résolution angulaire est 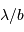 .
.
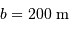 apporte à
apporte à 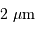 une résolution angulaire de :
une résolution angulaire de :
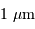 , sera résolue pour une base de :
, sera résolue pour une base de :

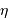 du Bouvier.
du Bouvier.

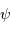 de la constellation du Phénix.
de la constellation du Phénix.

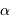 de la constellation d'Hercule.
de la constellation d'Hercule.

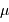 de Céphée.
de Céphée.
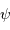 Phe et
Phe et 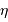 Boo.
Boo.
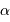 d'Hercule
d'Hercule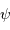 Phe,
Phe, 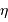 Boo et
Boo et 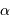 Her sont estimées à respectivement 10.1, 88.2, 8.5 mas. En déduire la distance de chaque étoile, puis son diamètre linéaire.
Her sont estimées à respectivement 10.1, 88.2, 8.5 mas. En déduire la distance de chaque étoile, puis son diamètre linéaire.
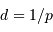 donne directement la distance en parsec si la parallaxe
donne directement la distance en parsec si la parallaxe 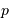 est mesurée en seconde d'arc.
est mesurée en seconde d'arc.
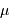 Cep
Cep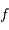 d'un télescope muni d'un miroir primaire de diamètre
d'un télescope muni d'un miroir primaire de diamètre 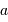 ouvert à
ouvert à 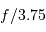 vaut :
vaut :
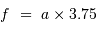
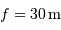
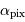 vérifiant :
vérifiant :
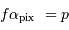
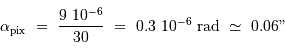
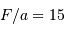 .
.
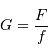
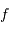 le focale de l'oculaire.
le focale de l'oculaire.
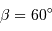 , l'angle du champ objet vérifie :
, l'angle du champ objet vérifie :
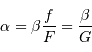
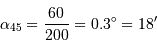
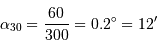
 .
.
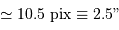 pour les anneaux entourant la composante brillante
pour les anneaux entourant la composante brillante 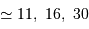 , soit respectivement 2.6, 4.1 et 7.3".
, soit respectivement 2.6, 4.1 et 7.3".
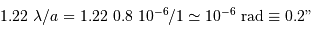 .
.
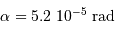 , soit environ 11".
, soit environ 11".
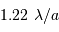 ; soit le diamètre :
; soit le diamètre :
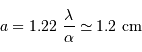
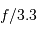 pour un collecteur de 3.6 m représente une focale de
pour un collecteur de 3.6 m représente une focale de
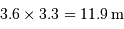 .
.
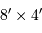 , ou
, ou 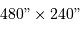 , devient, traduit en pixel,
, devient, traduit en pixel,
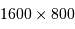 .
.
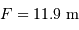 , la résolution de 0.3", cad
, la résolution de 0.3", cad 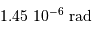 , correspond à une dimension physique de
, correspond à une dimension physique de 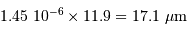 .
.
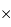 2k, avec des pixels de
2k, avec des pixels de 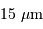 .
.
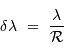
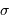 donne :
donne :
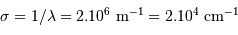
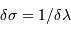
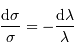
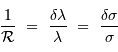
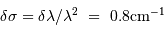

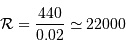
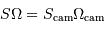 donne un angle solide objet
donne un angle solide objet
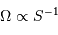
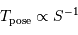
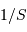 , la surface collectrice. Le temps de pose élémentaire varie comme
, la surface collectrice. Le temps de pose élémentaire varie comme 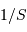 . Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée
. Pour couvrir un champ donné, la durée totale ne dépend donc pas de la taille du télescope : le champ couvert en 1 pose de durée 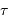 avec un petit collecteur sera observée par
avec un petit collecteur sera observée par 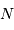 poses de durées
poses de durées 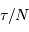 avec un grand.
avec un grand.

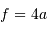 . L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
. L'étendue du faisceau s'écrit dont de 2 façons différentes, selon que l'on considère le montage réel ou le montage équivalent :
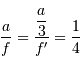
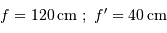

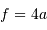 .
.
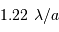 , couvre un angle solide de l'ordre de :
, couvre un angle solide de l'ordre de :
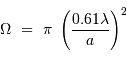
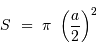
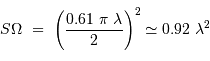
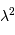 .
.
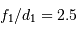 , la lentille L2 sous
, la lentille L2 sous 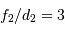 .
.
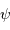 Phe : 1/147 = 6.8 mas
Phe : 1/147 = 6.8 mas
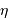 Boo : 1/61 = 16.4 mas
Boo : 1/61 = 16.4 mas
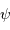 Phe : 99 pc,
Phe : 99 pc, 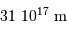 .
.
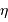 Boo : 11 pc, 3.5 ...
Boo : 11 pc, 3.5 ...
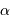 Her : 118 pc, 36 ...
Her : 118 pc, 36 ...
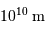 , puis en diamètre solaire et unité astronomique :
, puis en diamètre solaire et unité astronomique :
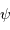 Phe : 10.4, soit 74 fois le diamètre solaire, ou 0.70 UA.
Phe : 10.4, soit 74 fois le diamètre solaire, ou 0.70 UA.
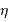 Boo : 2.9, ... 20.5 ... 0.19
Boo : 2.9, ... 20.5 ... 0.19
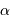 Her : 42, ... 300 ... 2.8
Her : 42, ... 300 ... 2.8
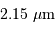 mais opaque à
mais opaque à 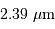 .
.