Définitions : Variance et Ecart-type

Il est souvent intéressant de savoir si les valeurs sont très dispersées ou si elles sont proches de la moyenne E(X). On est tentés de calculer la moyenne des valeurs de x_i-E(X), de la même façon qu'on calcule la moyenne des valeurs, c'est à dire .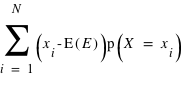

Les valeurs de x_i-E(X) peuvent être négatives ou positives, donc cette moyenne peut valoir 0 même si les valeurs sont très dispersés. La solution est de calculer la moyenne des (x_i-E(X))² , qui sont toujours positive :

La Variance est V(X) ou 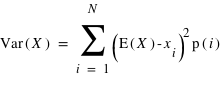. On peut voir que c'est aussi la différence entre la moyenne des carrés des valeurs et le carré de la moyenne des valeurs,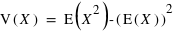

(standard deviation en anglais), σ, est la racine carré de la Variance: 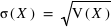.