Définitions : Loi Binomiale

La loi binomiale est la loi de probabilité de l'expérience de N épreuves à deux choix (gagné/perdu, pile/face...). Si les deux choix ne sont pas équivalents, et que la probabilité de l'un est p , la probabilité de l'autre choix est donc (1-p). On dit qu'il s'agit d'une loi binomiale de paramètres N et p. La v.a. X qui définit la probabilité d'avoir k fois le choix de probabilité p (et donc N-k fois le choix de probabilité (1-p)), est donnée par 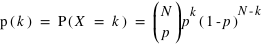où 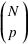est la combinaison de k éléments parmi N.

Quand N devient grand, on remplace la variable aléatoire entière par une variable aléatoire réelle. La loi binomiale devient la loi normale.

Il est important, dans les calculs de statistiques, de savoir combien on peut faire de combinaisons différentes de N éléments.

Par exemple, combien y a-t-il de permutations de 3 éléments, a, b et c ?

Il y a 3 choix pour la première lettre, 2 choix pour la deuxième lettre et 1 seul choix pour la troisième. Le nombre total de choix est 3x2x1 = 6 possibilités : (a-b-c), (a-c-b), (b-a-c), (b-c-a), (c-a-b), (c-b-a).

Combien y a-t-il de classements possibles de 52 cartes? Il y a 52 choix pour la première carte, puis 51 choix pour la deuxième carte, etc.... Le nombre de classements possibles est 52x51x50x49.........x3x2x1 qui s'écrit 52! (factorielle 52)

S'il n'y a que deux sortes d'éléments dans les N, par exemple k fois G (Gagné) et N-k fois P (Perdu), il y aura N! permutations mais beaucoup seront semblables. Combien y aura-t-il de permutations distinctes?

Parmi les N! permutations, celles qui échangent seulement les G sont identiques. Il y a k! permutations de cette sorte. De même, il y a (n-k)! permutations qui sont identiques parce-qu'elles permutent des P.

Il y aura donc 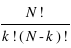permutations distinctes de N éléments avec k éléments d'une sorte et N-k d'une autre sorte.

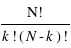s'écrit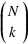

Par exemple, si en tirant 10 fois à Pile ou Face, on trouve 7 Pile et 3 Face, il y a 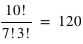permutations distinctes.

Un autre type de combinaisons est le nombre de "mains" de 13 cartes quand on distribue 52 cartes entre 4 joueurs, au bridge par exemple. Avec le même raisonnement qu'au dessus, on compte 52x51x...43x42x40 soit 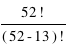combinaisons possibles si elles sont rangées. Si on ne tient pas compte de l'ordre, il faut diviser par 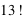, le nombre de mains avec les mêmes cartes rangées dans des ordres différents. On obtient , soit 635 013 559 600.