Systèmes binaires et multiples
- Introduction
- Les systèmes stellaires multiples
- Introduction
- Etoiles doubles
- Binarité et astrophysique
- Les étoiles doubles visuelles
- Les étoiles doubles spectroscopiques
- Les étoiles binaires à éclipse
- Binaires visuelles
- Introduction
- Les étoiles binaires visuelles
- Observer
- Apprendre
- S'exercer
- La trajectoire apparente
- La reconstruction de l'orbite vraie
- Apprendre
- Simuler
- S'évaluer
- Masse des deux composantes
- Binaires à éclipse ou photométriques
- Introduction
- Les paramètres de l'orbite et la courbe de lumière
- Observer
- Apprendre
- Simuler
- S'exercer
- S'évaluer
- Binarité et température stellaire
- Apprendre
- Simuler
- S'exercer
- S'évaluer
- Binaires spectroscopiques
- Introduction
- Les courbes de vitesse radiale
- Les masses des deux composantes
- Apprendre
- S'exercer
- S'évaluer
- Planètes extrasolaires
- Introduction
- Historique
- Caractéristiques
- Détection des planètes extrasolaires par la méthode des vitesses radiales
- Observer
- Apprendre
- Simuler
- S'exercer
- Courbes de vitesses radiales
- Limitations de la méthode des vitesses radiales
- Méthode de détection par transit
- Observer
- Apprendre
- Simuler
- S'exercer
- Limitations de la méthode par transit
- Observer
- Apprendre
- S'exercer
- Détection par mesure astrométrique
- Observer
- Apprendre
- S'exercer
- Performance de détection
- Observer
- Apprendre
- S'évaluer
- Conclusion
Introduction
Les sections sur les lois de Kepler et Newton ont montré l'importance astrophysique du système à 2 corps. On se propose, dans ce sous-chapitre, de parcourir les nombreux cas où l'étude de systèmes multiples permet de faire de la belle astrophysique, en balayant les systèmes stellaires doubles et les planètes extrasolaires.
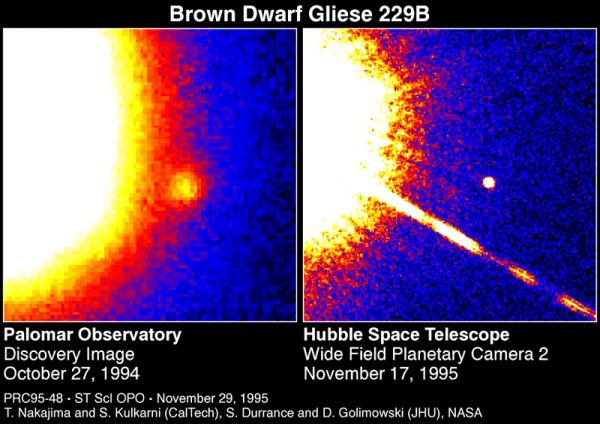
La naine brune Gliese 229 B, compagnon de ... Gliese 229 A.
Crédit :
Palomar Observatory/HST
L'image de l'étoile Gliese 229 montre à elle-seule l'intérêt d'observer le voisinage d'une étoile : on y a découvert une naine brune.
Les systèmes stellaires multiples
Auteurs: M. Gerbaldi, G. Theureau
Introduction
Le phénomène d'étoile double est très commun : on estime en effet que plus de la moitié des étoiles appartiennent à des systèmes binaires ou multiples.
Certaines des paires observées résultent de l'alignement fortuit de deux étoiles sur la ligne de visée, alors que les deux composantes sont en réalité à des années lumières l'une de l'autre (on parle alors de couples optiques), mais la grande majorité sont de réels systèmes binaires, les deux étoiles étant liées gravitationnellement.
Les mouvements de ces objets sont képlériens, chaque étoile décrivant une ellipse autour du centre de masse commun. Ce sont en fait les caractéristiques du mouvement qui permettent de distinguer les couples optiques des vraies étoiles doubles.
L'étude des systèmes doubles est précieuse pour de nombreuses mesures : masses, rayons....

L'étoile double epsilon de la constellation de la Lyre (en fait, elle est double-double i.e. chacune des deux étoile est double)
Crédit :
CDS
Etoiles doubles
Observer
Exemples de systèmes multiples
Les étoiles binaires ou multiples sont majoritaires.

L'étoile double sigma de la constellation d'Orion, entourée de 4 autres compagnons orbitant à plus grande distance.
Crédit :
CDS
Proxima Centauri
L'étoile la plus proche du Soleil, Proxima Centauri, à 1.3 pc, est une étoile triple. Les deux composantes les plus brillantes A et B ont une séparation maximale de 35", correspondant à un demi-grand axe de 23.5 UA et une période de révolution de 80 ans. Ce sont deux étoiles de la séquence principale de types spectraux respectifs G2 et K1. Le mouvement de la troisième composante (C) n'est pas connu avec une précision suffisante pour conclure définitivement, mais l'on pense qu'elle est physiquement associée aux deux autres, car elle partage les mêmes parallaxe et mouvement propre. Elle est située à 2.2 deg des deux autres, avec une période orbitale d'au moins 250 000 ans...
Apprendre
Systèmes binaires ou multiples
De nombreux systèmes multiples, avec deux, trois étoiles ou plus, forment un système gravitationnellement lié. De tels systèmes ont tendance à former une paire centrale, les autres composantes jouant un rôle de perturbateur par rapport au mouvement orbital de celle-ci.
Sur 3 étoiles, 2 sont dans un système multiple.
Formation stellaire et binarité
Les étoiles se forment suite à l'effondrement d'un nuage de matière interstellaire. Celui-ci, de masse très supérieure à la masse stellaire moyenne, conduit à une formation d'un groupe d'étoiles. Ce processus favorise la binarité.
Classification
La classification des étoiles doubles est essentiellement liée aux moyens observationnels qui ont servi à leur découverte.
On parle ainsi de binaires visuelles ou astrométriques, de binaires à éclipse et de binaires spectroscopiques, selon qu'elles ont été découvertes ou étudiées à partir de leur mouvement apparent sur le ciel, des variations de leur éclat ou des caractéristiques de leur spectre.
Binarité et astrophysique
Apprendre
De l'intérêt de l'étude
L'étude des étoiles doubles apporte un grand nombre d'informations importantes sur les étoiles, en particulier en termes de masse, de rotation, de rayon, de densité, de luminosité et de température superficielle. Ces informations, elles sont souvent les seules à pouvoir nous les donner, et leur étude est par là même indispensable pour comprendre la formation et l'évolution stellaire.
La reconstitution des orbites
Dans le cas des étoiles binaires visuelles, si la parallaxe du système est connue, la reconstitution de l'orbite de l'une des deux étoiles et de son demi-grand axe permet de calculer la somme des masses des deux composantes.
Si, par ailleurs, on est capable de repérer le mouvement de chacune des deux composantes par rapport au centre de masse du système, on est alors en mesure de calculer la masse de chaque étoile.
La courbe de lumière et la variation du spectre
L'analyse de la forme des courbes de lumière des étoiles binaires à éclipse permet de connaître certains paramètres physiques de l'atmosphère des étoiles du système. Lors d'une éclipse totale, on peut déterminer le rapport des températures effectives des deux composantes, sous couvert d'une modélisation réaliste du profil de brillance pour chacun des disques stellaires.
Si l'orbite est circulaire, on peut accéder au rapport des rayons des étoiles, ou aux rayons eux-mêmes si l'on connaît également, grâce à l'analyse de leur spectre, la courbe de variation des vitesses radiales. Ce type de situation est très rare puisqu'il faut que l'étoile soit à la fois binaire à éclipse et binaire spectroscopique. Les rayons n'ont ainsi pu être mesurés en valeur absolue que pour un très petit nombre d'étoiles, et cette mesure est fondamentale car c'est, avec l'interférométrie, le seul moyen de mesurer directement des rayons stellaires.
Des analyses plus fines
Certains systèmes particuliers permettent une analyse plus fine de l'atmosphère d'une des composantes. C'est le cas par exemple de l'étoile zeta Aurigae qui est un système formé d'une étoile géante de type K (245 fois la taille du Soleil) et d'une étoile naine de type B appartenant à la séquence principale. L'étoile de type B, la plus lumineuse, est périodiquement éclipsée par l'étoile géante dont l'atmosphère est très étendue et très diffuse, en particulier dans ses régions les plus externes. L'analyse spectroscopique de l'étoile B, vue par transparence au travers de l'atmosphère de l'étoile K permet une analyse fine des différentes couches de cette dernière. L'analyse détaillée de la courbe de lumière peut parfois donner la vitesse de rotation de l'étoile éclipsée.
Les étoiles doubles visuelles
Observer

L'étoile double epsilon de la constellation de la Lyre
Crédit :
CDS
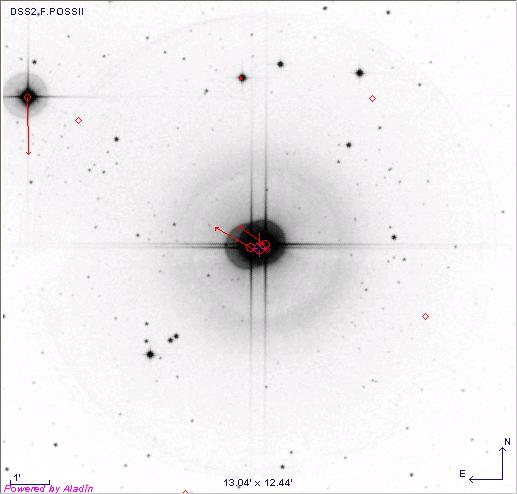
Les 2 composantes principales de l'étoile multiple
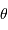
Serpentis partagent des parallaxes identiques (0.0248"). Malgré leur mouvement orbital, leurs mouvements propres (flèches rouges) apparaissent voisins. La 3ème composante, dans le coin supérieur gauche du cliché, possède également une parallaxe identique.
Crédit :
CDS
Vous voyez double ?
Hasard des alignements, ou système double ? Une image seule ne suffit pas à répondre.
Signatures
Deux figures de diffraction signent également la présence de deux objects non résolus... mais ça ne suffit pas pour conclure sur la binarité. Une bonne signature, en plus de la proximité angulaire, est fournie par des parallaxes communes.
Apprendre
Définition
On appelle binaire visuelle un couple d'étoiles qui peut être résolu en deux composantes au moyen d'un télescope, qui montrent des paramètres communs (parallaxe, ou mouvement propre typiquement). Typiquement, ce sont des étoiles relativement éloignées l'une de l'autre, dont la période orbitale varie entre un an et plusieurs milliers d'années.
Ici, et dans la plupart du chapitre, on parle uniquement d’étoiles, mais la majorité des reflexions s’appliquent également aux exoplanètes.
Binaires astrométriques
Un cas particulier de binaire visuelle est celui des binaires astrométriques. Il s'agit d'étoiles doubles dont on ne voit qu'une des deux composantes : c'est le mouvement apparent périodique de l'étoile visible qui permet de détecter indirectement l'existence d'un compagnon. Celui-ci est très peu lumineux et en général de faible masse.
Ce type d'étude très fine du mouvement apparent est un terrain propice pour la découverte de nouveaux systèmes planétaires.
Simuler
Ballets
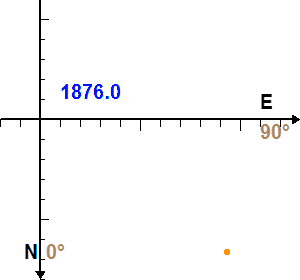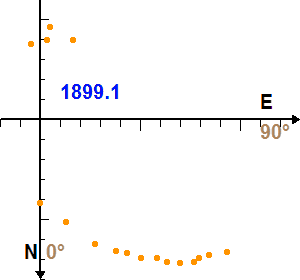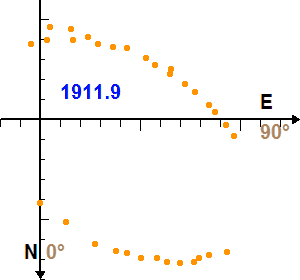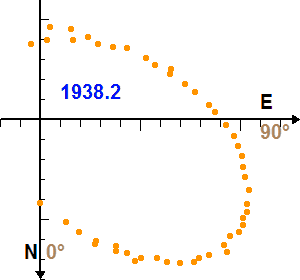
Mouvement de Sirius B autour de Sirius A. La date est indiquée en bleu, en année décimale.
Crédit :
ASM
Le mouvement orbital du couple Sirius A et B, composé au mouvement propre, conduit à de jolis festons.
Les étoiles doubles spectroscopiques
Observer
Spectre du système 57 Cyg
Les raies du spectre de 57 Cyg présentent un dédoublement périodique. Ceci est interprété comme la signature d'un système double.
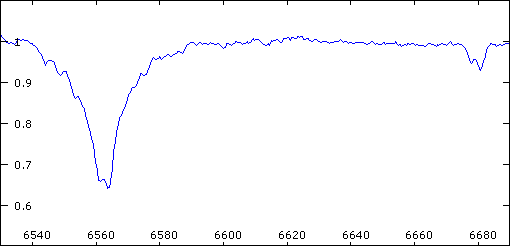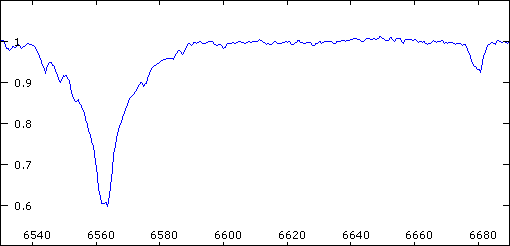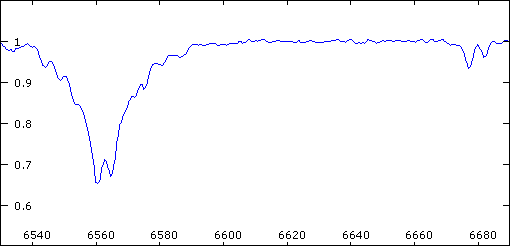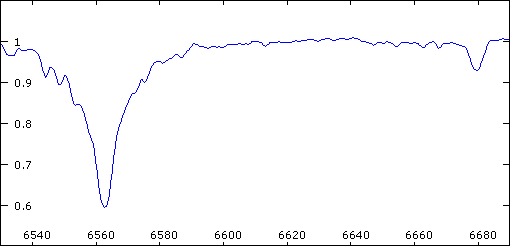
Crédit :
Christian Buil
Déplacement des raies
Si le rapport des luminosités est important, seule l'une des composantes est visible. Ses raies apparaissent modulées au cours de la période orbitale. Cette modulation n'est pas à confondre avec celle liée au mouvement annuel de la Terre autour du Soleil.

Déplacement au cours du temps des raies d'une étoile appartenant à un système binaire spectroscopique.
Crédit :
U. Texas
Apprendre
Définition
Les étoiles binaires spectroscopiques forment des couples en général très serrés, constituant une image unique au foyer d'un télescope. Elles sont détectées grâce à l'analyse de leur spectre, où l'on observe un déplacement périodique des raies.
Binaires de type 1 ou 2
Deux composantes suffisamment brillantes ou de type spectral semblable constituent un système à doubles raies, mais il arrive souvent que l'on n'observe qu'une seule des deux composantes. Comme dans le cas des binaires astrométriques, ceci permet de deviner indirectement la présence du compagnon. Les binaires spectroscopiques ont typiquement des périodes orbitales de quelques heures à quelques mois.
Simuler
Dédoublement de raies
Si les 2 composantes sont de type spectral identique, le dédoublement de la binaire spectroscopique apparaît très symétrique. Mais ce n'est pas nécessairement le cas : deux étoiles de type spectral ou magnitude différentes vont montrer un dédoublement non symétrique, voire pas de dédoublement mais une simple modulation si seulement la composante la plus brillante est visible.
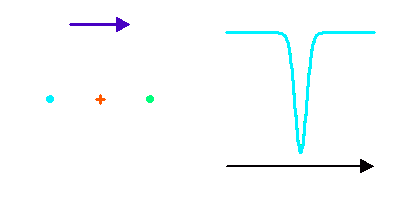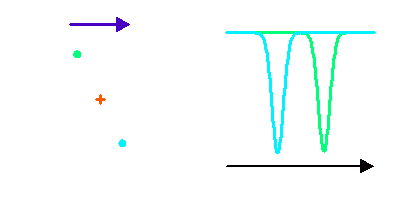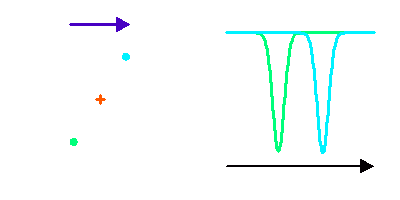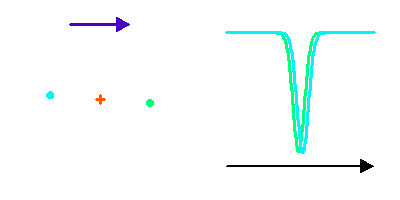
Dédoublement symétrique de raies dans un système double spectroscopique.
Crédit :
ASM
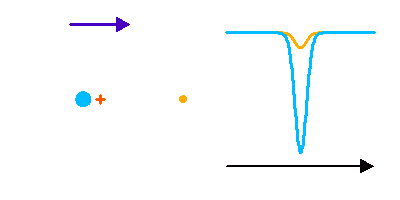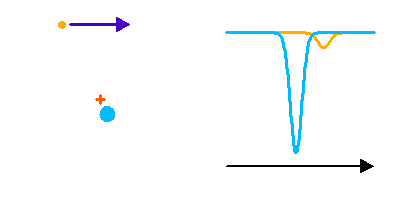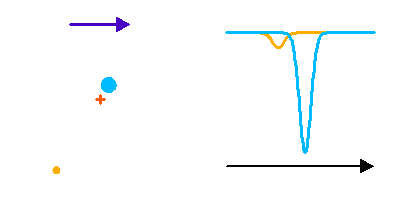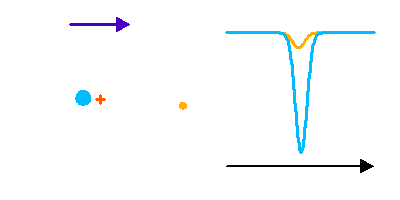
Dédoublement non symétrique de raies dans un système double spectroscopique.
Crédit :
ASM
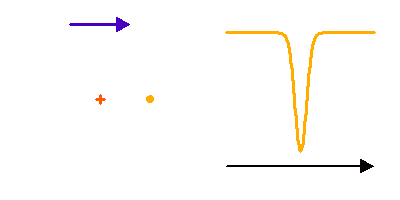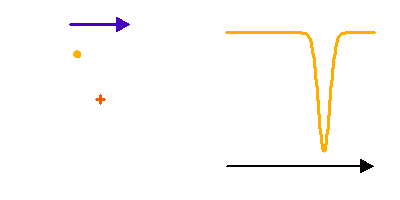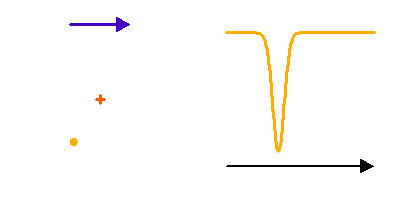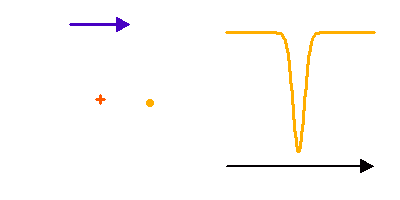
Pas de dédoublement de raies dans un système double spectroscopique, mais une simple modulation, lorsque le rapport des luminosités stellaire est très déséquilibré.
Crédit :
ASM
Les étoiles binaires à éclipse
Observer
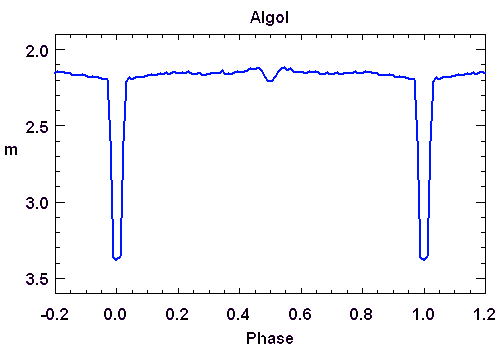
Courbe de lumière d'Algol.
Crédit :
ASM
Eclipses
Un système double peut être dévoilé par analyse de sa courbe de lumière, par la présence d'éclipses.
Apprendre
Définition
Un système binaire à éclipse est un système où les deux composantes s'éclipsent mutuellement et périodiquement au cours de leur mouvement orbital. Ce que l'on observe est alors une courbe de lumière correspondant à la variation périodique de la magnitude apparente du système. On qualifie aussi ces étoiles de binaires photométriques.
S'il y a occultation, l'observateur se trouve forcément au voisinage du plan de l'orbite.
Le phénomène est le même que les transits de planètes ou d'exoplanètes.
Simuler
Courbe de lumière
La forme de la courbe de lumière dépend :
- de l'inclinaison du système : la condition d'éclipse impose une très faible inclinaison ;
- de la distance entre les 2 composantes ;
- du rapport des flux et rayons.
L'appliquette ci-jointe permet de faire varier ces paramètres. Examiner dans différents cas (binaire composée d'une géante rouge et naine bleue, ou composée de naines rouge et bleue) les phénomènes suivants concernant l'allure conjointe du mouvement et de la courbe de lumière (lancer la visualisation avec la commande Figure+Graphe) :
- Influence de l'inclinaison du système
- Influence de la température de la primaire
- Influence de la température de la secondaire
- Influence de la distance
Vous devez ensuite pouvoir répondre aux questions :
- Que se passe-t-il si les 2 composantes ont des températures identiques ?
- Comment les extinctions des deux eclipses se comparent-elle selon les températures des 2 composantes ?
- Que se passe-t-il si la distance entre les 2 composantes est décuplée ?

Type Algol ou W Ursae
Les binaires de type Algol sont nettement séparées, alors que celles de type W Ursae sont très proches.

Courbe de lumière d'une binaire à éclipse de type Algol.
Crédit :
ASM
Courbe de lumière d'une binaire à éclipse de type W Ursae
Crédit :
ASM
Binaires visuelles
Auteurs: M. Gerbaldi, G. Theureau
Introduction
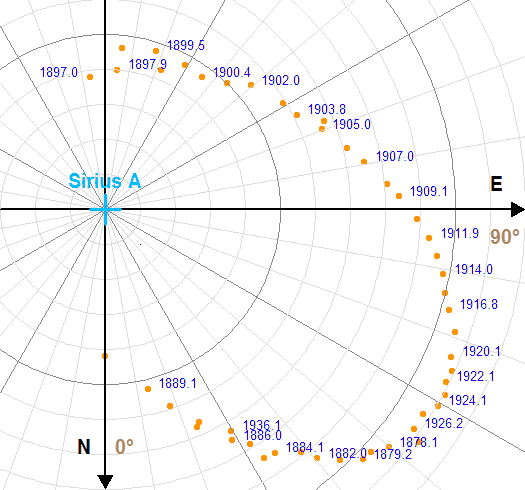
L'orbite de Sirius B autour de Sirius A.
Crédit :
ASM
Les étoiles binaires visuelles
Observer

Crédit :
ESO
Séparation
L'observation des étoiles binaires visuelles est limitée par la qualité d'image des observations au sol. La plus petite séparation angulaire détectable depuis le sol est d'environ 1 seconde d'arc. Cette limite imposée par la turbulence atmosphérique est améliorée grâce à l'optique adaptative. L'interférométrie sur les VLT permet d'atteindre une séparation de quelques millièmes de seconde d'arc.
Apprendre
Sélection
L'effet de sélection dans l'observation de ces couples est très important. Deux catégories d'objets sont en particulier très difficile à observer : les binaires à longue période d'une part, et d'autre part les étoiles qui forment au contraire un système très serré.
La séparation caractéristique de tels couples varie d'une fraction d'unité astronomique à quelques centaines d'unités astronomiques, quand leurs périodes s'échelonnent de quelques années à plus d'un siècle. Les périodes plus longues (quelques siècles) ou les orbites plus grandes sont très difficiles à mettre en évidence, essentiellement pour des raisons de recul dans le temps.
S'exercer
 Binaire visuelle
Binaire visuelle
Difficulté : ☆
Temps : 30 min
On observe une étoile double visuelle dont les caractéristiques observées sont les suivantes :
| séparation angulaire maximum | 5" |
| séparation angulaire minimum | 1" |
parallaxe 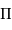 | 0.1" |
période de révolution 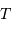 | 30 ans |
L'étoile primaire 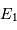 se trouve au foyer de l'orbite observée ; le compagnon est observé à une distance du barycentre 5 fois plus grande que celle de l'étoile primaire.
se trouve au foyer de l'orbite observée ; le compagnon est observé à une distance du barycentre 5 fois plus grande que celle de l'étoile primaire.
Question 1)
Montrer que l'inclinaison  du plan de l'orbite est nulle.
du plan de l'orbite est nulle.
Question 2)
Déterminer le rapport des masses des deux étoiles.
Question 3)
Exprimer la loi du mouvement des deux corps (troisième loi de Kepler) en prenant comme unités de masse, la masse du Soleil, de temps, l'année, et de distance, la distance Terre-Soleil (unité astronomique).
Question 4)
Calculer la distance en parsec à partir de la parallaxe, puis le demi-grand axe en UA.
Question 5)
Déterminer la masse de chaque composante en unité de masse solaire.
La trajectoire apparente
Observer
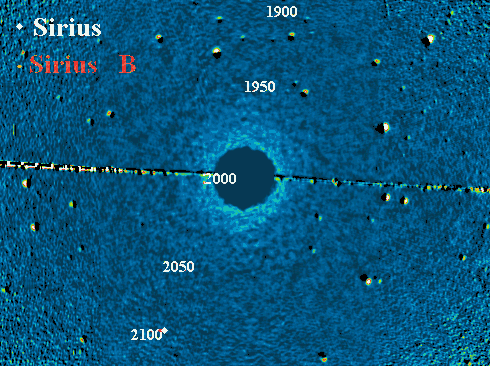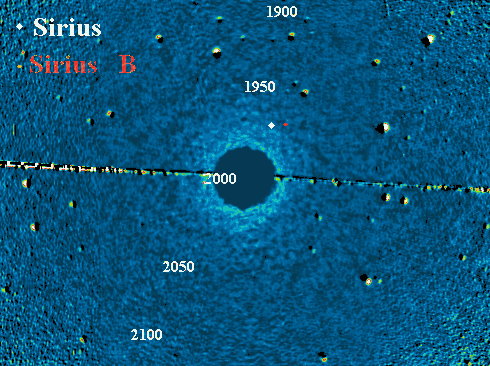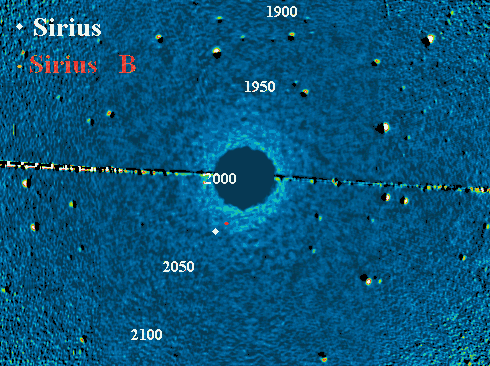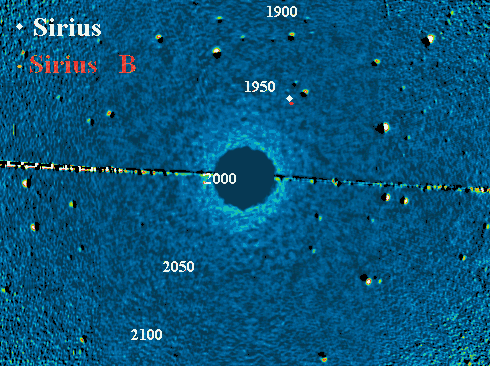
Sirius A et B. Simulation superposée à une vue du ciel, avec Sirius A masqué par
coronographie
Crédit :
Observatoire du Pic du Midi
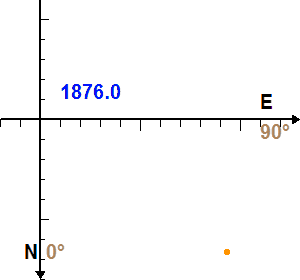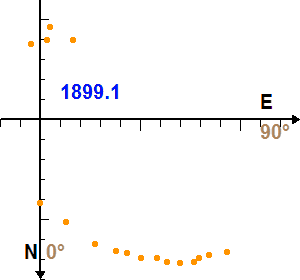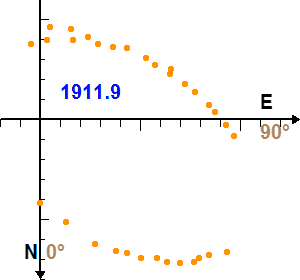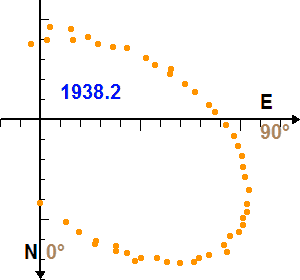
Mouvement de Sirius B autour de Sirius A. La date est indiquée en bleu, en année décimale.
Crédit :
ASM
Mouvements
Dans le cas des binaires visuelles, on observe à chaque instant la séparation angulaire apparente 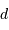 entre les deux composantes et l'angle de position
entre les deux composantes et l'angle de position 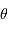 de la composante la plus faible par rapport à une direction de référence (celle de la direction du pôle céleste Nord) passant par l'étoile la plus brillante et repérée par rapport aux autres étoiles.
de la composante la plus faible par rapport à une direction de référence (celle de la direction du pôle céleste Nord) passant par l'étoile la plus brillante et repérée par rapport aux autres étoiles.
Trajectoire apparente
Trajectoire apparente de Sirius B autour de Sirius A, et animation correspondante.
Orbite projetée
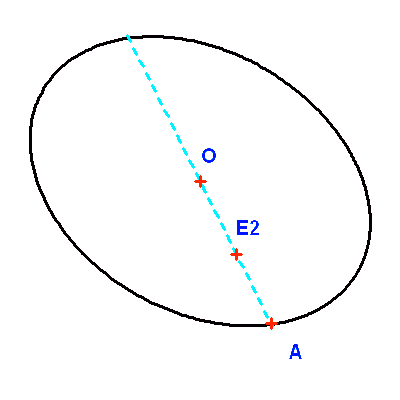
La projection d'une ellipse reste une ellipse, mais la projection du foyer n'est pas le foyer de l'ellipse projetée. Le demi-grand axe initial (tireté bleu) n'est pas le demi-grand axe de l'orbite projeté.
Crédit :
ASM
Projection
Ce que voit en général l'observateur, ce n'est pas l'orbite elle-même mais sa projection sur un plan perpendiculaire à la ligne de visée. Dans cette projection, les orbites sont toujours des ellipses et la loi des aires est conservée. Par contre, le foyer de l'ellipse projetée (ou orbite apparente) n'est pas la projection du foyer de l'orbite vraie et le demi-grand axe apparent n'est pas non plus la projection du demi-grand axe vrai. Pour remonter aux paramètres de l'orbite réelle, il est donc nécessaire de reconstituer cette orbite à partir de l'ellipse observée.
La reconstruction de l'orbite vraie
Apprendre
 Objectifs
Objectifs
Reconstituer les éléments géométriques de l'orbite vraie du système.
 Prérequis
Prérequis
Eléments géométriques définissant une trajectoire elliptique.
Demi-grand axe
L'observation donne une série de positions relatives des deux étoiles sur le ciel. En choisissant l'étoile la plus brillante (E2) comme origine des coordonnées, les positions de l'étoile la plus faible (E1) s'agencent sur une ellipse, mais il apparaît que E2 n'est pas au foyer de l'orbite projetée.

Ellipse et grand axe vus de biais.
Crédit :
ASM
Soit O le centre de l'ellipse apparente et A à l'intersection de la droite OE2 avec l'ellipse, au plus proche de E2 ; O est la projection du centre de l'orbite vraie et A est la projection de son périgée. Le segment [OA] est alors la projection du demi-grand axe de l'orbite vraie.
Excentricité
L'excentricité 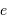 n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).
n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).
Cercle principal
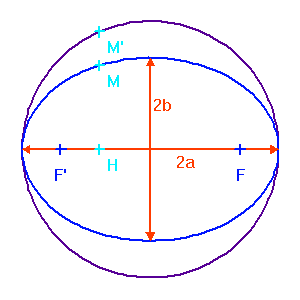
Ellipse et son cercle principal.
Crédit :
ASM
Simuler
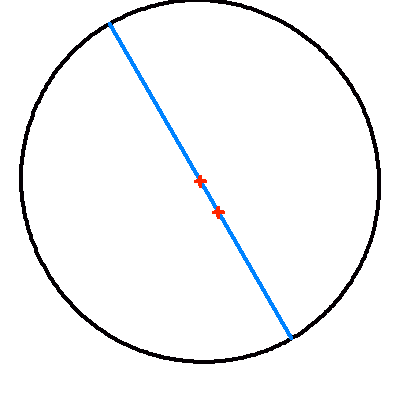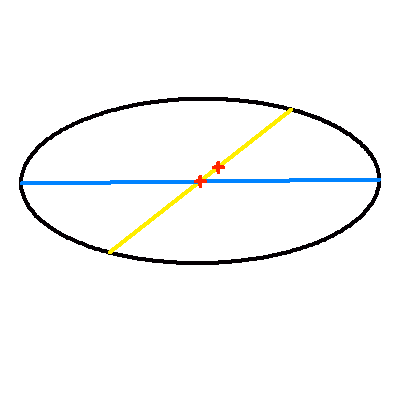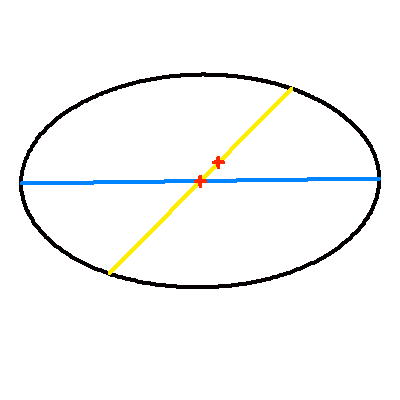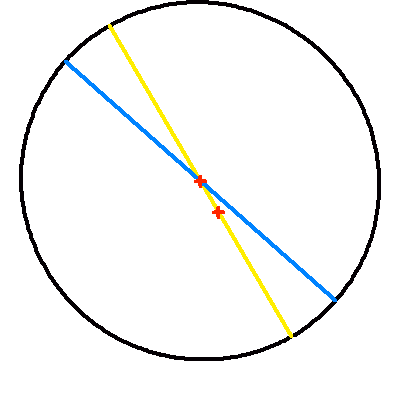
Projection dans le plan du ciel d'une orbite elliptique d'excentricité 0.2.
La droite jaune représente la projection du vrai demi-grand axe ; elle contient le centre et le foyer (occupé par la composante principale choisie comme origine). Le demi-grand axe apparent en en bleu.
Crédit :
ASM
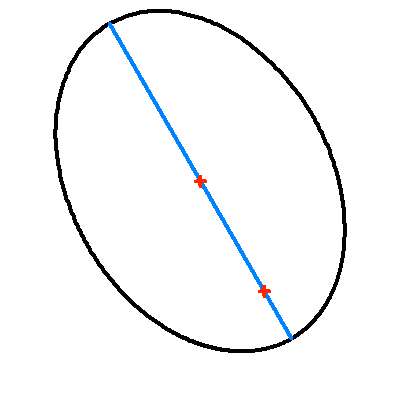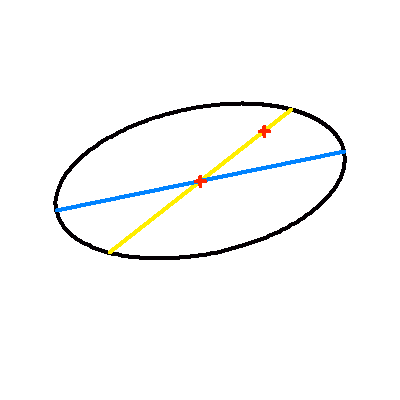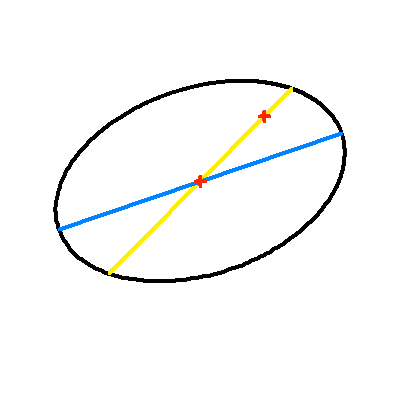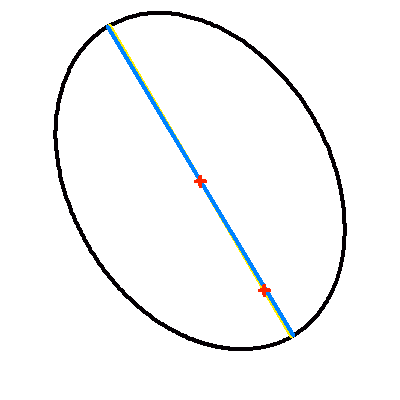
Projection dans le plan du ciel d'une orbite elliptique d'excentricité 0.7.
La droite jaune représente la projection du vrai demi-grand axe ; elle contient le centre et le foyer (occupé par la composante principale choisie comme origine). Le demi-grand axe apparent en en bleu.
Crédit :
ASM
Effet de projection
La projection du plan de l'orbite sur le plan du ciel modifie les paramètres de l'orbite apparente. Si le centre de l'ellipse est conservé par projection (la projection du centre de l'ellipse est égale au centre de l'ellipse projeté), le foyer ne l'est point : le demi-grand axe apparent se distingue (sauf dans certains cas très particuliers) de la projection du demi-grand axe.
L'animation met ce phénomène en évidence : elle montre l'apparence de la projection dans le plan du ciel d'une orbite elliptique, pour différentes inclinaisons. Étonnamment, l'effet est moins marqué dans le cas d'une excentricité plus grande.

L'orbite
L'appliquette donne la position de Sirius B par rapport à Sirius A.
- Tracer la trajectoire.
- Peut-on estimer directement les paramètres de la trajectoire ?
S'évaluer
 Paramètres de l'orbite
Paramètres de l'orbite
Difficulté : ☆☆
Temps : 30 min
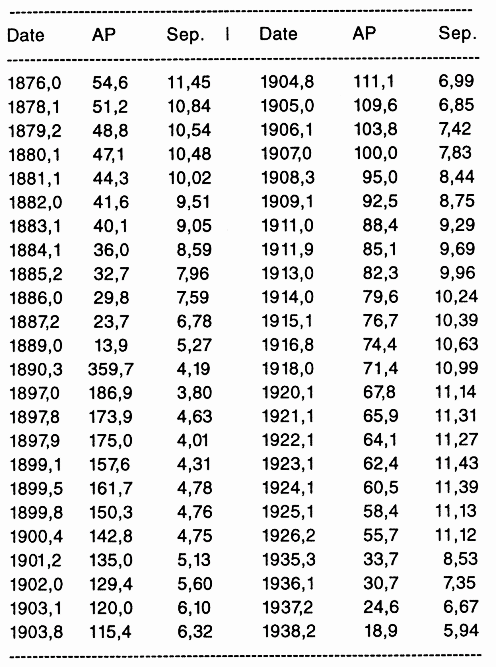
Angle de phase (en degré) et séparation (en "), en fonction de la date
Crédit :
ASM
En 1844, F.W. Bessel découvrit que Sirius présentait un mouvement propre, non linéaire, mais dont la modulation ressemblait à celle d'une étoile double visuelle. Il en conclut que le mouvement propre de Sirius était affecté par l'interaction gravitationnelle avec une seconde étoile de luminosité trop faible pour être observée. Ce compagnon fut observé pour la première fois en 1862 par A.G. Clark : cette étoile appelée Sirius B a une magnitude de 8.7 alors que celle de Sirius A vaut -1.4.

- L'appliquette ci-jointe donne les positions observées de Sirius B par rapport à Sirius A de 1876 à 1938, mesurées sur une suite de clichés photographiques. Chaque position est repérée par la séparation angulaire (en ") des deux étoiles et l'angle de position de la direction de Sirius B compté à partir de la direction Nord et dans le sens direct (0 deg pour la direction Nord et 90 deg pour la direction Est).
- Les positions successives ainsi reportées tracent l'orbite apparente de Sirius B par rapport à Sirius A, c'est-à-dire l'orbite telle qu'elle est observée sur le ciel.
- Les paramètres de l'ellipse représentant l'orbite apparente sont calculés par la méthode des moindres carrés. L'ellipse qui s'ajuste au mieux parmi les points observés est décrite par les paramètres du tableau.
| demi-grand axe | 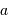 | 7.24" |
| excentricité | 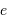 | 0.765 |
| distance entre les foyers | 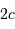 | 11.08" |
Question 1)
Sirius A, à l'intersection des axes, est-il au foyer de l'ellipse apparente ? Quelle conséquence en tire-t-on pour le plan de l'orbite ?
[1 points]
Question 2)
Déterminer la valeur de la période (en années).
[1 points]
Question 3)
Déterminer graphiquement le grand axe de l'ellipse vraie (il contient le centre de l'ellipse projetée (le centre est conservé par projection) et bien sûr Sirius A).
Déterminer les positions apparentes P et A du périastre et de l'apoastre et les dates qui leur correspondent.
[2 points]
Question 4)
Déterminer l'excentricité de l'orbite vraie.
[1 points]
Masse des deux composantes
S'exercer
 Sirius A et Sirius B
Sirius A et Sirius B
Difficulté : ☆☆
Temps : 30 min

La figure trace le mouvement vrai de la composante Sirius B par rapport à Sirius A dans le plan orbital.
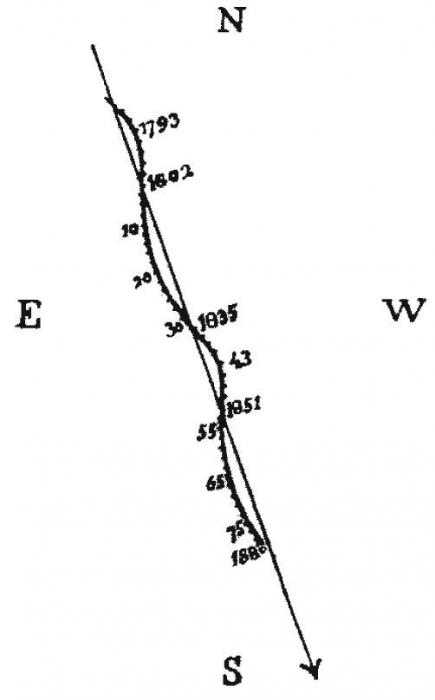
Mouvement de Sirius dans le plan du ciel, reporté par Camille Flammarion au XIXe siècle.
Crédit :
ASM
Question 1)
Etalonner la figure de l'appliquette, en tenant compte du fait que les portions de cercle centrés sur Sirius A sont espacés de 1 seconde d'angle, et définir le rapport d'unité permettant de lire directement des secondes d'angle sur la figure.
Activité soit l'outil 'ligne', soit l'outil 'cercle'.
Faire une règle de trois et définir le rapport d'unité.
Question 2)
Estimer le demi-grand axe de l'orbite relative et la période.
Pour le demi-grand axe : repérer les projections des péri- et apoastre.
Pour la période : s'appuyer sur les valeurs au voisinage de l'apoastre.
Question 3)
La parallaxe du système vaut 0.379". En déduire la somme des masses des deux composantes (en unités de masse solaire).
Traduire la parallaxe en distance.
De la valeur angulaire du demi-grand axe et de la distance, déterminer le demi-grand axe en UA.
Utiliser la 3ème loi de Kepler
Question 4)
Le mouvement de Sirius A par rapport au barycentre présente une demi-amplitude de 2.35" au cours d'une orbite (corrigée de la projection du plan orbital sur le plan du ciel). Comparer cette amplitude au mouvement relatif des 2 composantes, et en déduire la masse de chaque composante.
La demi-amplitude est à comparer au demi-grand axe.
Binaires à éclipse ou photométriques
Auteurs: M.Gerbaldi, G.Theureau
Introduction
Quand l'orbite d'une étoile double est vue par la tranche ou sous un angle très petit, et que l'on a affaire à un couple relativement serré, chacune des étoiles s'interpose périodiquement entre l'observateur et l'autre composante. Un phénomène d'éclipse, ou plus exactement d'occultation, se produira donc pour l'observateur qui reçoit la lumière de la binaire sans pouvoir séparer les deux composantes stellaires. On détecte ainsi ces étoiles doubles par la variation périodique de la magnitude apparente du système.
Du fait que les deux composantes sont très proches, les binaires à éclipse sont aussi très souvent en même temps des binaires spectroscopiques. Dans ce cas, l'étude de la variation d'éclat permet de calculer le rapport des rayons, et l'étude du spectre, s'il est à doubles raies, donne la vitesse orbitale de chaque composante. On peut alors calculer le rayon des deux composantes, mais aussi leurs masses et la distance qui les sépare, sans faire aucune mesure de diamètre apparent.
La première binaire à éclipse qui a été observée est Algol (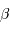 Persei). Ses variations d'éclat sont connues depuis 1670 par les observations de Geminiano Montanari. La première étude systématique a été faite par John Goodricke en 1783. On connaît actuellement plus de 4000 systèmes de binaires à éclipse. Les périodes de ces systèmes sont en général courtes, variant de quelques heures à une dizaine de jours. La plus petite période actuellement mesurée est celle de WZ Sagittae (1h22min), et la plus longue est celle de
Persei). Ses variations d'éclat sont connues depuis 1670 par les observations de Geminiano Montanari. La première étude systématique a été faite par John Goodricke en 1783. On connaît actuellement plus de 4000 systèmes de binaires à éclipse. Les périodes de ces systèmes sont en général courtes, variant de quelques heures à une dizaine de jours. La plus petite période actuellement mesurée est celle de WZ Sagittae (1h22min), et la plus longue est celle de 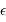 Aurigae avec ses 9883 jours (27 ans).
Aurigae avec ses 9883 jours (27 ans).
Il est maintenant possible, avec les télescopes de la classe des 8 mètres, de mesurer les paramètres des binaires à éclipse extragalactiques, ce qui améliore la précision sur la mesure de la distance de ces galaxies.
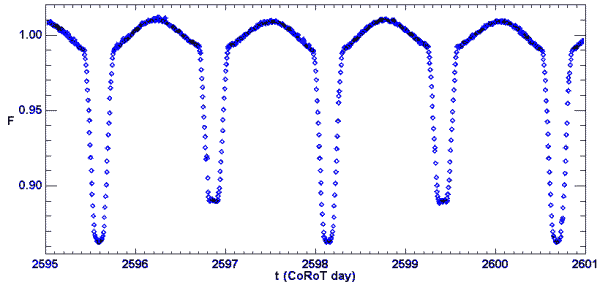
Courbe de lumière d'une binaire à éclipse observée par le satellite CoRoT. Remarquer les différences entre les minima principaux et secondaires.
Crédit :
CNES
Les paramètres de l'orbite et la courbe de lumière
Observer
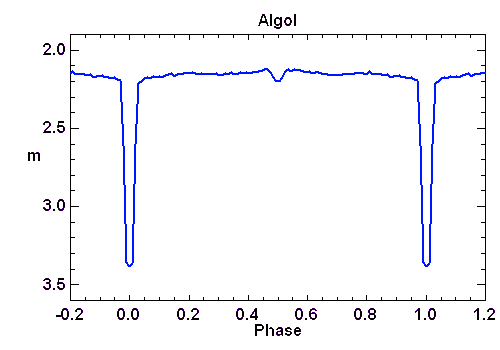
Courbe de lumière d'Algol.
Crédit :
ASM
La courbe de lumière d'Algol
Algol, dont le nom vient de l'arabe Al Guhl esprit changeant est l'étoile 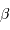 de la constellation de Persée (
de la constellation de Persée (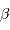 Persei). Son comportement est connu depuis plusieurs siècles car ses variations d'éclat sont spectaculaires et particulièrement visibles à l'oeil nu.
Persei). Son comportement est connu depuis plusieurs siècles car ses variations d'éclat sont spectaculaires et particulièrement visibles à l'oeil nu.
Sa luminosité totale diminue en effet en quelques heures jusqu'au tiers de sa valeur habituelle, puis remonte pour rester quasiment stable pendant deux jours et demi. Puis le cycle recommence... Algol est un couple de binaires à éclipse, dont la plus brillante est de type spectral B (blanc bleuté), et la plus faible est de type K (jaune orangé).
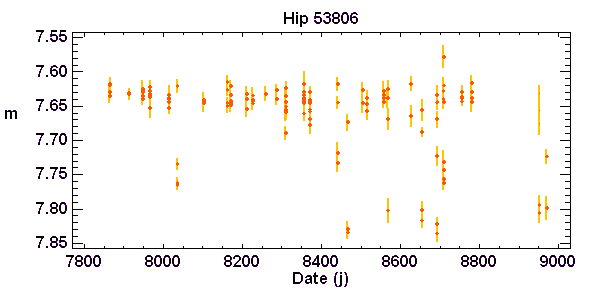
Magnitude d'une binaire à éclipse de type Algol en fonction du temps. Observations du satellite européen Hipparcos
Crédit :
Hipparcos/ASM
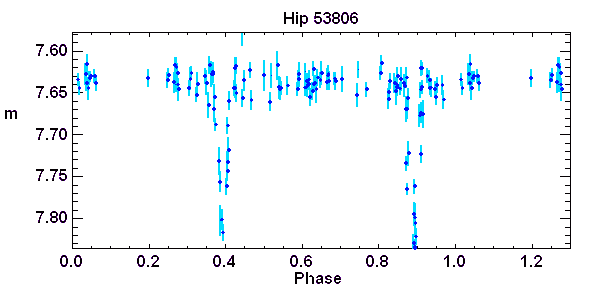
Courbe de lumière d'une binaire à éclipse de type Algol. Observations du satellite européen Hipparcos
Crédit :
Hipparcos/ASM
Binaires à éclipse de type Algol
Les observations de la courbe de lumière donne la magnitude totale du système en fonction du temps. La périodicité de la série temporelle est analysée, pour conduire à la courbe de lumière en fonction de la phase.
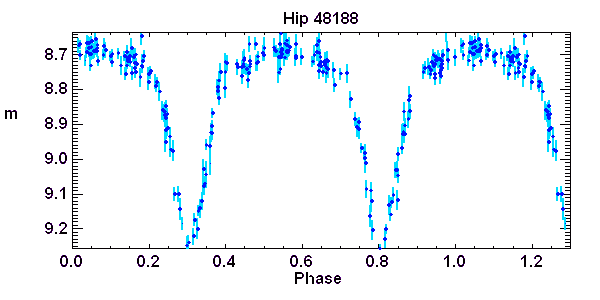
Courbe de lumière d'une étoile de type Beta Lyrae. Observations du satellite européen Hipparcos
Crédit :
Hipparcos/ASM
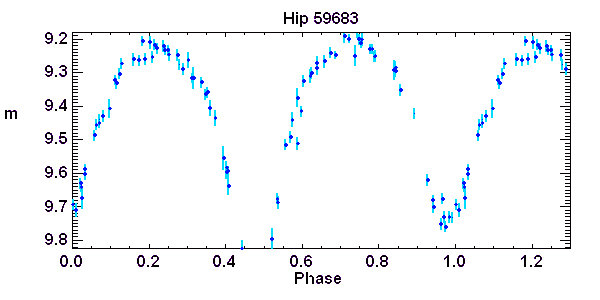
Courbe de lumière d'une étoile de type W Ursae. Observations du satellite européen Hipparcos
Crédit :
Hipparcos/ASM
Binaires à éclipse serrées
classes de binaires correspondent à des couples très serrées, présentant alors des périodes très courtes, bien plus rapides que le type Algol, telles les variables de type Beta Lyrae ou
W Ursae Majoris. Ces dernières, moins massives, sont le plus souvent tellement proches l'une de l'autre qu'elles remplissent leur lobe de Roche, et échangent de la matière.

Image du disque solaire en lumière visible montrant l'assombrissement du disque dans les régions proches du limbe.
Crédit :
ASM
Assombrissement centre bord
Le profil des courbes de lumière, arrondi, dévoile que les étoiles ne sont pas des disques de brillance uniforme. En effet, comme pour le Soleil, les régions visibles proches du limbe sont sondées à des altitudes plus élevées, où la température est plus froide.
Apprendre
Courbe de lumière
Les variations de la magnitude en fonction du temps donnent la courbe de lumière. L'étude de la forme de cette courbe permet en principe de reconstituer les paramètres de l'orbite. On notera cependant que ces couples d'étoiles étant serrés, la courbe de lumière peut parfois être déformée par les interactions entre les deux composantes : par exemple des effets de réflexion de lumière entre les deux étoiles ou des déformations des étoiles elles-mêmes qui, sous l'effet des forces de marées, ne sont plus sphériques.
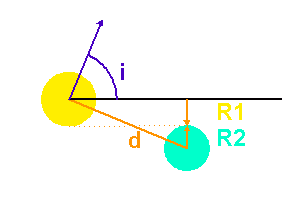
Paramètres de l'éclipse.
Crédit :
ASM
Occultation
L'occultation sera partielle ou totale selon les diamètres relatifs des étoiles et l'inclinaison du plan de l'orbite par rapport à la ligne de visée : il y a en effet éclipse (partielle ou totale) lorsque la distance 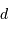 entre les étoiles est telle que
entre les étoiles est telle que
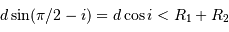
où 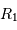 et
et 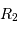 sont les rayons de chaque étoile.
sont les rayons de chaque étoile.
Dans le cas où 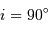 , les deux éclipses sont centrales, l'une étant totale (quand la plus grosse passe devant la plus petite), l'autre étant annulaire. On remarquera par ailleurs que lorsqu'il y a éclipse totale les minima de la courbe de lumière montrent un plateau, qui correspond à la durée effective de totalité de l'éclipse ou de l'occultation.
, les deux éclipses sont centrales, l'une étant totale (quand la plus grosse passe devant la plus petite), l'autre étant annulaire. On remarquera par ailleurs que lorsqu'il y a éclipse totale les minima de la courbe de lumière montrent un plateau, qui correspond à la durée effective de totalité de l'éclipse ou de l'occultation.
Orbite circulaire
On reconnaît que l'orbite est circulaire quand les deux éclipses se produisent exactement toutes les demi-périodes. Dans ce cas, il est alors possible de déterminer l'inclinaison et les rayons relatifs des étoiles 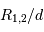 .
.
Simuler
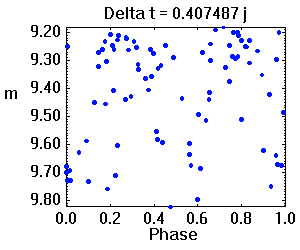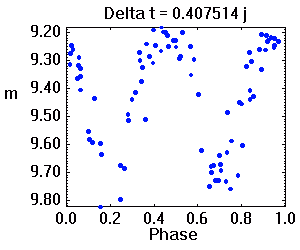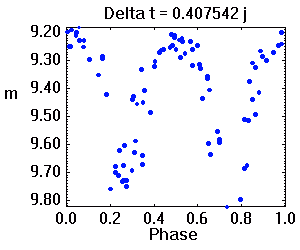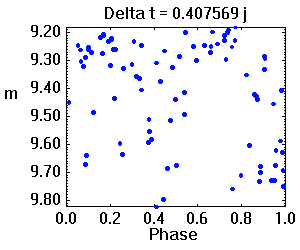
Tracé de la courbe de lumière repliée sur diverses périodes. La période adéquate assure une moindre dispersion des valeurs.
Crédit :
ASM
De la série temporelle à la phase
L'animation ci-jointe montre l'évolution de la série temporelle à la phase orbitale, par balayage de la période. La période adéquate est celle qui assure une moindre dispersion des valeurs.

Courbe de lumière d'une binaire à éclipse de type Algol.
Crédit :
ASM
Courbe de lumière d'une binaire à éclipse de type W Ursae Majoris
Crédit :
ASM
Courbe de lumière
Les binaires de type Algol sont nettement séparées, alors que celles de type W Ursae Majoris sont très proches. Les membres d'un couple W Ursae Majoris présentent un profil déformé par le champ gravitationnel du compagnon ; la courbe de lumière présente des formes très arrondies.
S'exercer
 Système binaire et courbe de lumière
Système binaire et courbe de lumière
Difficulté : ☆
Temps : 30 min

Courbe de lumière schématique : variation de l'éclat en fonction du temps.
Crédit :
ASM
On observe un système binaire à éclipse 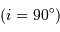 dont les orbites sont circulaires. La courbe de lumière correspond à la figure ci-dessus. Soient
dont les orbites sont circulaires. La courbe de lumière correspond à la figure ci-dessus. Soient 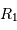 et
et 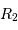 les rayons des deux étoiles,
les rayons des deux étoiles, 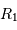 étant le rayon de la plus grosse. On notera
étant le rayon de la plus grosse. On notera 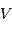 la vitesse relative du mouvement orbital de la plus petite par rapport à la plus grosse.
la vitesse relative du mouvement orbital de la plus petite par rapport à la plus grosse.
Question 2)
La période P du mouvement orbital est de 2 jours et 22 heures. La durée de chaque éclipse est par ailleurs de 18h00min, et la totalité dure 7h19min. En déduire le rapport des rayons 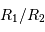 .
.
Question 4)
Montrer que, d'après la figure, l'étoile la plus chaude est la plus petite.
A quoi correspond le minimum arrondi ?
S'évaluer
 Durée d'une éclipse
Durée d'une éclipse
Difficulté : ☆☆
Temps : 30 min
Cet exercice s'intéresse à mesurer la durée d'une éclipse dans un système stellaire binaire. Pour simplifier, on suppose l'orbite circulaire. Les observables sont : la période orbitale 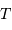 et la durée du transit
et la durée du transit 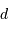 .
.
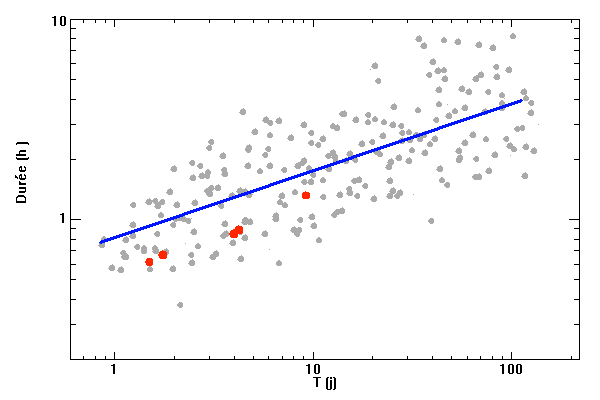
Durée d'un transit, fonction de la période orbitale du système double. Les points gris rapportent des événements de binaires à éclipses. Les points rouges rapportent des transits exoplanétaires observés par CoRoT.
Crédit :
ASM
Question 1)
Montrer que la durée d'un transit est inversement proportionnelle à la vitesse orbitale.
[1 points]
On fera l'hypothèse que les étoiles ont un rayon moyen voisin du rayon solaire.
Question 2)
Montrer que la durée 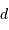 d'un transit varie comme
d'un transit varie comme 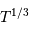 .
.
[1 points]
S'intéresser à la vitesse orbitale.
Question 3)
Expliquer la dispersion des points sur la courbe jointe.
[1 points]
S'intéresser aux rayons stellaires.
Question 4)
Pourquoi les planètes découvertes par CoRoT ont-elles des durées de transit légèrement inférieures ?
[1 points]
Comparer les tailles des objets.
Binarité et température stellaire
Apprendre
Maxima
En supposant la brillance de chaque disque uniforme, dans les cas où l'éclipse est totale, la comparaison du maximum principal et du maximum secondaire de la courbe de lumière permet de déterminer le rapport des températures des deux étoiles.
Simuler
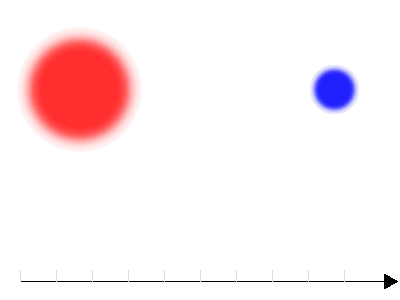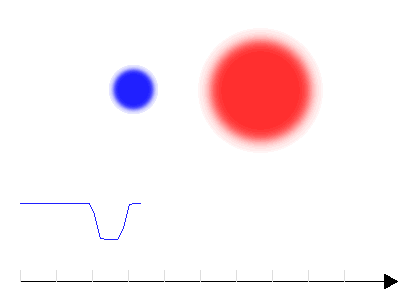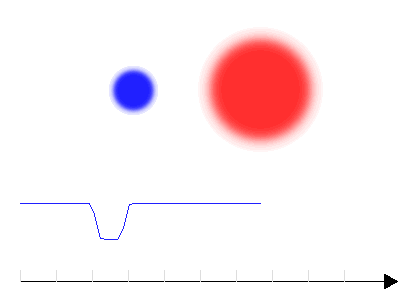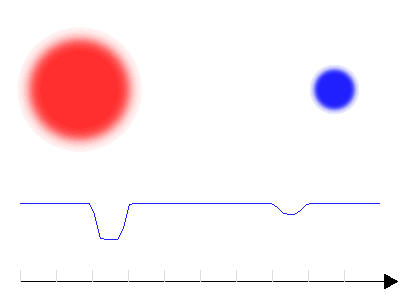
Courbe de lumière d'une binaire à éclipse avec 2 composantes présentant un fort contraste en température
Crédit :
ASM
Courbe de lumière
Lorsque le contraste en température est marqué, les minima des deux éclipses diffèrent sensiblement ; la baisse de flux est plus forte lorsque la composante chaude est occultée.
Forme des minima, températures rayons stellaires

L'allure des minima apporte des renseignements comparatifs sur les 2 composantes.
La première appliquette explicite les arguments permettant de comparer les tailles : lorsque la plus petite étoile du couple disparaît, le flux est uniformément bas.

La deuxième appliquette explicite les arguments permettant de comparer les températures : lorsque c'est l'étoile la plus chaude du couple qui disparaît, le minimum est plus profond.
S'exercer
 Système binaire et températures
Système binaire et températures
Difficulté : ☆
Temps : 30 min
Une des composantes d'une binaire à éclipse a une température effective de 15000 K, l'autre de 5000 K. La plus froide est une géante de rayon 4 fois plus grand que celui de la plus chaude.
Question 1)
Quel est le rapport des luminosités des deux étoiles ?
Question 2)
Quelle est l'étoile éclipsée au minimum primaire ?
Question 3)
Le minimum principal correspond-il à une éclipse totale ou à une éclipse annulaire ?
Question 4)
Quel est le rapport de profondeur entre les minima ?
S'évaluer
 AR Lacertae : forme de la courbe de lumière
AR Lacertae : forme de la courbe de lumière
Difficulté : ☆
Temps : 30 min
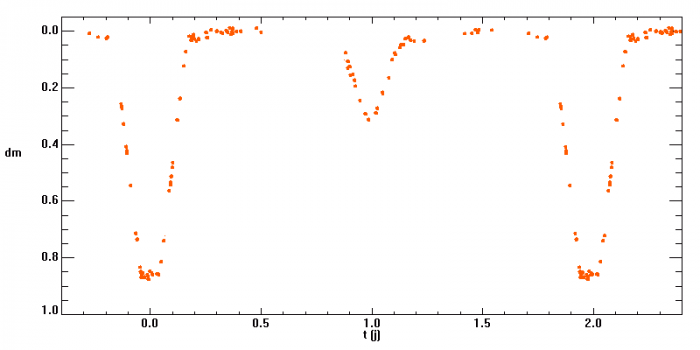
Courbe de lumière de AR Lacertae.
Crédit :
ASM
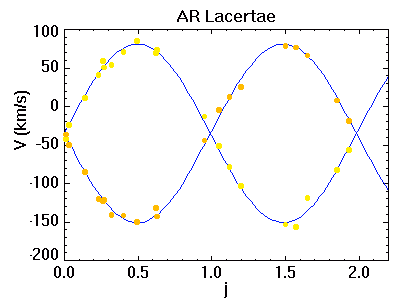
Courbe de vitesse radiale de AR Lacertae
Crédit :
ASM
On considère l'étoile double AR Lacertae, dont on a observé la courbe de lumière et les vitesses radiales des deux composantes. La période du système vaut 1.983 j.

Question 1)
Commenter la forme des deux minima. Les températures des 2 étoiles peuvent-elles être identiques ?
[3 points]
Question 2)
Justifier que l'inclinaison est proche de 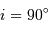 et que les orbites sont circulaires.
et que les orbites sont circulaires.
[3 points]
Question 3)
Représenter schématiquement les positions de l'étoile compagnon sur l'orbite relative en fonction des phases d'éclipse observées sur la courbe de lumière.
[2 points]
Question 4)
A l'aide de l'appliquette, estimer la durée de la phase de totalité, celle de l'éclipse principale dans son ensemble, ainsi que la profondeur (en magnitude) du minimum primaire.
[2 points]
 AR Lacertae : mesure des paramètres physiques
AR Lacertae : mesure des paramètres physiques
Difficulté : ☆
Temps : 30 min
On se propose d'analyser la courbe de lumière de AR Lacertae pour en déduire les paramètres physiques des deux composantes : rayons, températures, éclats apparents et luminosités intrinsèques...
Question 2)
Préciser laquelle des deux étoiles est la plus chaude.
[1 points]
Question 3)
Déterminer le rapport des luminosités 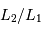 des deux étoiles. Commenter.
des deux étoiles. Commenter.
[2 points]
Question 4)
L'étude spectroscopique de l'étoile 1 indique que son type spectral est K0 et sa classe de luminosité IV (sous-géante). Sa magnitude absolue peut donc être estimée à 3. Déterminer la luminosité 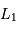 de l'étoile 1 et celle
de l'étoile 1 et celle 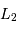 de l'autre composante en unité solaire (la magnitude absolue visuelle
de l'autre composante en unité solaire (la magnitude absolue visuelle 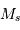 du Soleil vaut 4.8).
du Soleil vaut 4.8).
[1 points]
Binaires spectroscopiques
Auteurs: M.Gerbaldi, G.Theureau
Introduction
Le premier système d'étoiles binaires spectroscopique fut découvert en 1889 par Antonia C. Maury, qui remarqua un dédoublement des raies dans le spectre de l'étoile 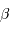 Aurigae. Les positions de ces raies, en longueur d'onde, varient au cours du temps, témoins de la variation de la vitesse radiale de chaque composante, par suite de leur mouvement orbital relatif.
Aurigae. Les positions de ces raies, en longueur d'onde, varient au cours du temps, témoins de la variation de la vitesse radiale de chaque composante, par suite de leur mouvement orbital relatif.
Les étoiles doubles spectroscopiques sont très nombreuses : on estime qu'en moyenne une étoile sur trois ou quatre est une double spectroscopique. Leurs périodes observées s'échelonnent entre quelques heures et quelques années. A partir de l'étude de la courbe de vitesse radiale, on peut calculer les paramètres définissant l'orbite elliptique d'une étoile par rapport à l'autre. Cette détermination se fait toutefois à l'effet de projection près, car on ne connaît pas a priori l'orientation du plan orbital dans l'espace. Actuellement, on connaît précisément les paramètres orbitaux pour environ un millier de ces objets.
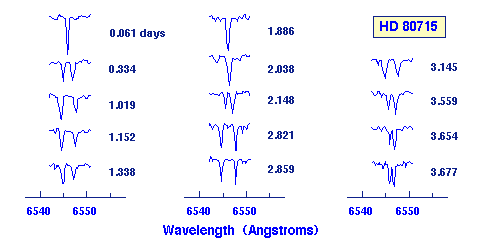
Dédoublement de raies de l'étoile
HD 80715
Crédit :
ASM
Les courbes de vitesse radiale
Observer
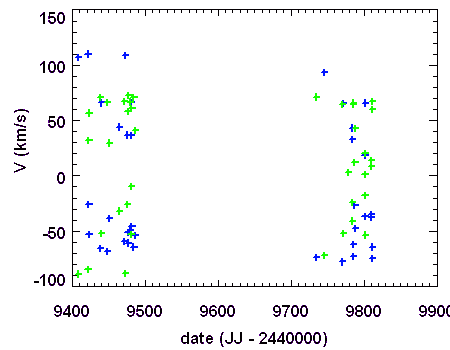
Série temporelle : mesure des vitesses radiales des 2 composantes de l'étoile 55 Uma
Crédit :
ASM
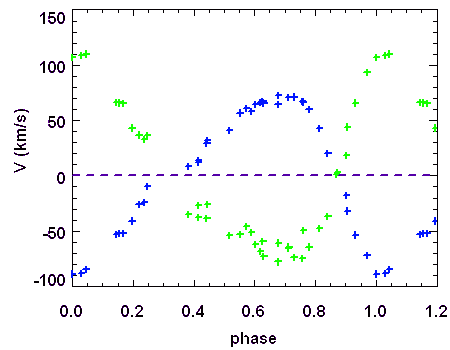
Courbe de vitesses radiales des 2 composantes de l'étoile double 55 Uma
Crédit :
ASM
Apprendre
Paramètres du mouvement
On peut ainsi représenter la variation de la vitesse des deux composantes (ou d'une seule, si une seule est détectable) en fonction du temps. Selon la forme de l'orbite et son orientation dans l'espace, les caractéristiques de la courbe de vitesse radiale observée seront différentes. L'analyse de cette courbe permet de remonter aux paramètres du mouvement et aux masses des composantes.
Simuler
Les masses des deux composantes
Apprendre
Masses
Par définition du centre de masse : 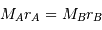 . On obtient alors le rapport des masses :
. On obtient alors le rapport des masses :
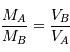
qui est donné par le rapport des amplitudes des deux courbes. D'autre part, d'après la troisième loi de Kepler, on a :
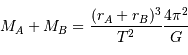
On obtient :
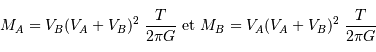
Si l'inclinaison  est différente de
est différente de 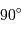 , l'amplitude de la courbe de vitesse radiale est diminuée d'un facteur
, l'amplitude de la courbe de vitesse radiale est diminuée d'un facteur 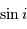
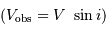 .
.
Dans les équations précédentes, 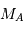 est donc remplacé par
est donc remplacé par 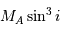 (respectivement
(respectivement 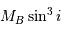 ).
).
Orbite elliptique
Si l'orbite n'est pas circulaire mais elliptique avec une excentricité 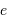 non nulle, les courbes de vitesse radiale ne sont pas sinusoïdales, bien que toujours en opposition de phase et avec un rapport d'amplitude égal au rapport des masses.
non nulle, les courbes de vitesse radiale ne sont pas sinusoïdales, bien que toujours en opposition de phase et avec un rapport d'amplitude égal au rapport des masses.
S'exercer
 Observabilité
Observabilité
Difficulté : ☆
Temps : 5 min
Question 1)
Comment se révèle à l'observation une étoile double spectroscopique dans le cas où 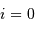 ?
?
 Résolution spectrale
Résolution spectrale
Difficulté : ☆☆
Temps : 20 min
On cherche à analyse un spectre d'étoile spectroscopique double, enregistré avec une résolution dans le domaine visible 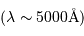 de l'ordre de
de l'ordre de 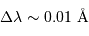 .
.
Question 1)
Quelle limitation cela impose-t-il sur les vitesses radiales que l'on peut effectivement mesurer ?
Voir le cours sur l'effet Doppler issues de mesures spectrométriques.
Question 2)
Observer des grandes vitesses orbitales favorise-t-il ou non les systèmes serrés ?
 Inclinaison de l'orbite
Inclinaison de l'orbite
Difficulté : ☆
Temps : 10 min
Question 1)
Comment peut-on vérifier que l'hypothèse 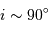 est vraie ou non ?
est vraie ou non ?
Question 2)
Quand l'inclinaison est inconnue, peut-on obtenir des limites inférieures ou supérieures pour les masses des deux composantes ?
S'évaluer
 L'étoile double AR Lacertae
L'étoile double AR Lacertae
Difficulté : ☆
Temps : 30 min
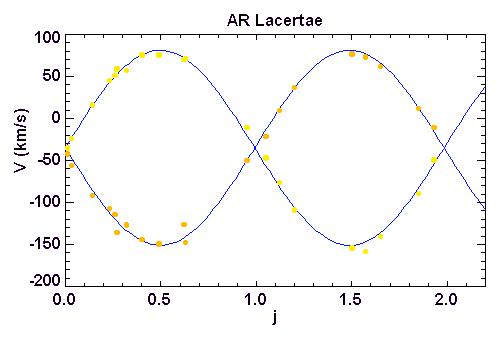
Courbe de vitesse radiale de AR Lacertae
Crédit :
ASM
On considère l'étoile double AR Lacertae, dont on a observé les courbes des vitesses radiales des deux composantes. La période du système vaut 1.983 j.
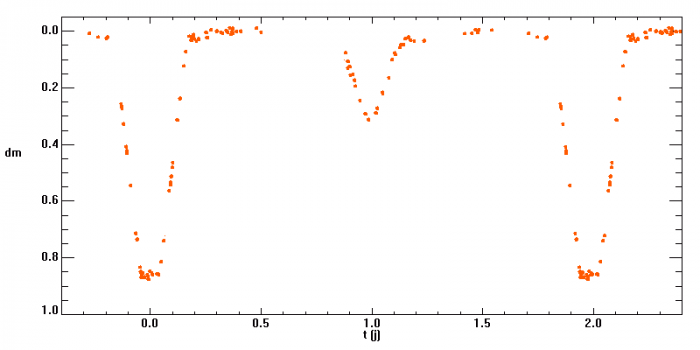
Courbe de lumière de AR Lacertae
Crédit :
ASM
Question 1)
Commenter les courbes. Que dire des caractéristiques du mouvement des deux étoiles ?
[1 points]
Question 2)
Quelle est la vitesse radiale du barycentre ?
[1 points]
Question 3)
Trouver le rapport des masses des deux composantes.
[1 points]
Question 4)
Trouver la séparation (en km) des deux composantes.
[1 points]
Question 5)
Déterminer la masse de chaque composante en unité solaire
[1 points]
Question 6)
Dans quel cas serait-il possible de calculer les rayons de chaque étoile ?
[1 points]
Planètes extrasolaires
Auteurs: G. Catherine, B. Mosser
Introduction
La découverte d'exoplanètes, planètes orbitant autour d'une étoile autre que le Soleil, a constitué l'un des principaux événements astronomiques de la fin du XXe siècle. Cette section aborde la quête des exoplanètes sous deux angles : les propriétés de ces exoplanètes, et les techniques instrumentales utilisées pour les détecter et les étudier.
Courbe de vitesse radiale de 51 Peg A
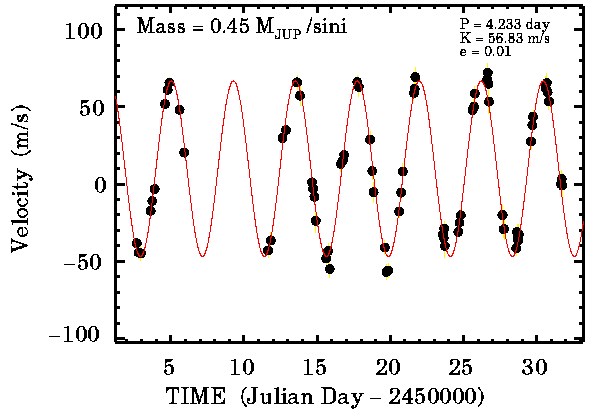
Mesure de vitesse radiale de l'étoile 51Peg, première exoplanète découverte autour d'une étoile de type solaire, en 1995, à l'Observatoire de Haute Provence par les astrophysiciens suisses Michel Mayor et Didier Queloz.
Crédit :
Butler & Marcy
Historique
Apprendre
 Objectifs
Objectifs
Ces pages présentent une grande découverte des années 90, les planètes
extrasolaires, et décrivent :
- les principales caractéristiques de ces objets ;
- les différentes techniques mises au point afin de détecter la
présence de planète(s) autour d'étoiles de type solaire, proche de la
Terre.
Ces méthodes sont basées sur l'observation des
perturbations produites sur le mouvement de l'étoile par ses compagnons planétaires, ou sur la baisse du flux stellaire occulté par un compagnon. C'est à partir de ces perturbations que l'on est capable d'obtenir certaines des caractéristiques de la planète.
Les premières tentatives
Les tentatives de détection de compagnons planétaires ont été nombreuses... dès le début du XXe siècle, par astrométrie, et non moins nombreuses furent les tentatives infructueuses. Une planète est par essence très peu massive par rapport à son étoile, et excessivement moins lumineuse...
Diverses détections ont été annoncées en 1988 puis démenties. Certaines ont été confirmées depuis (autour de 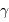 Ceph,
Ceph, 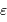 Eri)... En 1989, Latham et ses collègues identifièrent un compagnon d'environ dix fois la masse de Jupiter, autour de HD 114762. Mais ces auteurs évoquèrent alors la détection d'une naine brune et non d'une planète.
Eri)... En 1989, Latham et ses collègues identifièrent un compagnon d'environ dix fois la masse de Jupiter, autour de HD 114762. Mais ces auteurs évoquèrent alors la détection d'une naine brune et non d'une planète.
En 1992, trois planètes furent détectées sans ambiguïté par Wolszczan & Frail, autour du pulsar PSR 1257+12. Mais l'environnement d'un pulsar ne laisse guère espérer que des planètes brûlées par l'évolution de leur étoile.
Evolution du nombre d'exoplanètes détectées par année.
Autour de 51 Peg
En 1995, on retient la découverte de la première planète extrasolaire autour d'une étoile semblable à notre Soleil, par Michel Mayor et Didier Queloz, de
l'Observatoire de Genève. Elle fut détectée à l'Observatoire de
Haute-Provence, et immédiatement confirmée par Geoff Marcy et Paul
Butler, des Universités de San Francisco et Berkeley, qui eux l'avaient
observée à l'Observatoire Lick en Californie.
Ces mesures ont vraiment lancé l'un des grands sujets de
l'astrophysique actuelle : la quête des exoplanètes. Depuis, plusieurs milliers de
planètes ont été recensées. Ce nombre est en constante
augmentation, les projets de recherche se multipliant, si bien que tenir un décompte précis est impossible.
La découverte de ces planètes apporte aux astrophysiciens des données permettant de mieux comprendre
la formation des systèmes planétaires, avec d'autres exemples que notre
système solaire.
Que voit-on ?
Plusieurs dizaines de planètes ont été vues directement, mais la plupart des découvertes sont basées sur des détections indirectes, soit la détection de l'influence gravitationnelle de la planète sur l'étoile soit la baisse de luminosité de l'étoile due au passage de la planète sur sa ligne de visée.
Méthodes de détection
A ce jour (2018), cinq méthodes ont permis de découvrir ou redécouvrir l'essentiel des exoplanètes :
- Vitesse radiale de l'étoile hôte perturbée par la planète
- Transit de la planète devant son étoile
- Transit secondaire de la planète derrière son étoile
- Variation de l'instant de transit
- Effet de microlentille
- Chronométrage (autour d'un pulsar)
- Imagerie
Les méthodes de
vitesse radiale et
transit, les plus productives, sont décrites plus loin, ainsi que la méthode par astrométrie.
Un sujet à la mode
Les exoplanètes sont un sujet à la mode, pour les raisons que l'on devine aisément. Désolé si ces pages n'annoncent pas en temps réel les dernières découvertes !
Caractéristiques
Observer
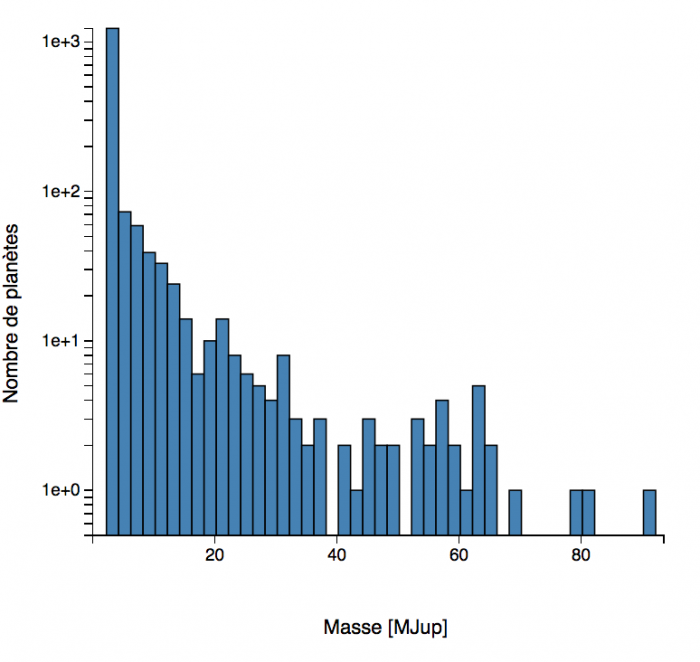
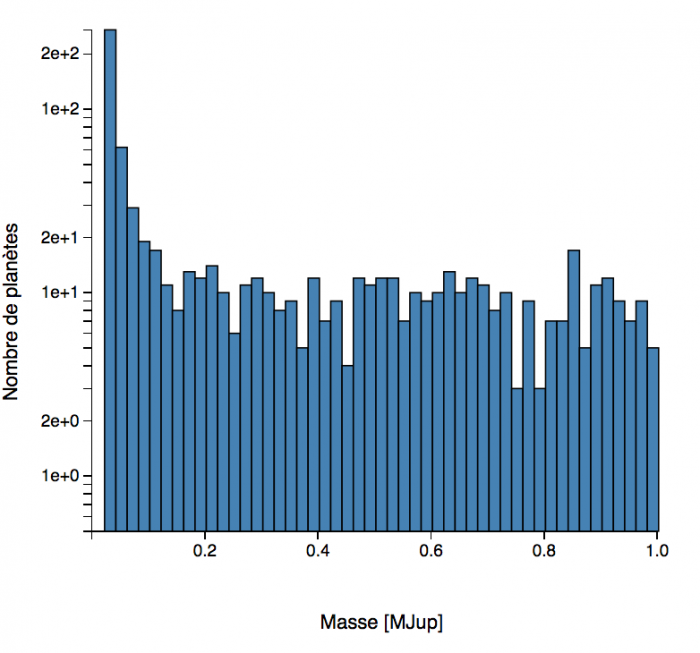
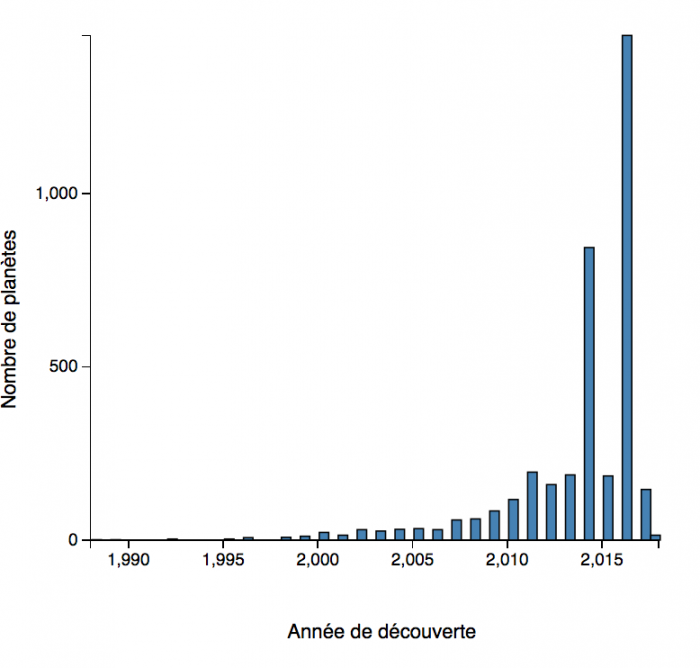
Décompte des masses des exoplanètes, ou plus exactement des
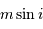
, l'inclinaison

n'étant pas une
observable (septembre 2018).
Deux échelles de masse permettent de distinguer les
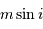
plus petits que la masse de Jupiter, et la distribution totale jusqu'à 15 masses de Jupiter.
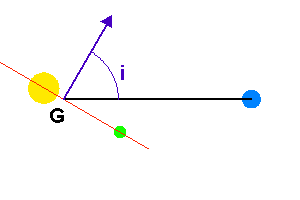
Définition de l'angle entre la normale au plan orbital et l'axe de visée. Avec les paramètres usuels, le barycentre G du système est à l'intérieur de l'étoile.
Crédit :
ASM
Masse
L'histogramme
des masses montre que la très grande majorité des planètes découvertes sont des planètes géantes.
Cela n'est pas dû au caractère unique de la présence de planètes
telluriques dans notre système solaire, mais au fait que les méthodes de
détection favorisent les fortes masses planétaires.
La limite à 13 fois la masse de Jupiter est une limite physique : au-delà,
l'objet commence à brûler son deutérium, c'est alors une naine brune.
Stricto sensu, les masses ici considérées sont affectées d'un facteur de
projection inconnu, égal au sinus de l'angle entre la normale au plan orbital et l'axe de visée. On parle non de masse 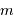 , mais de
, mais de 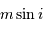 .
.
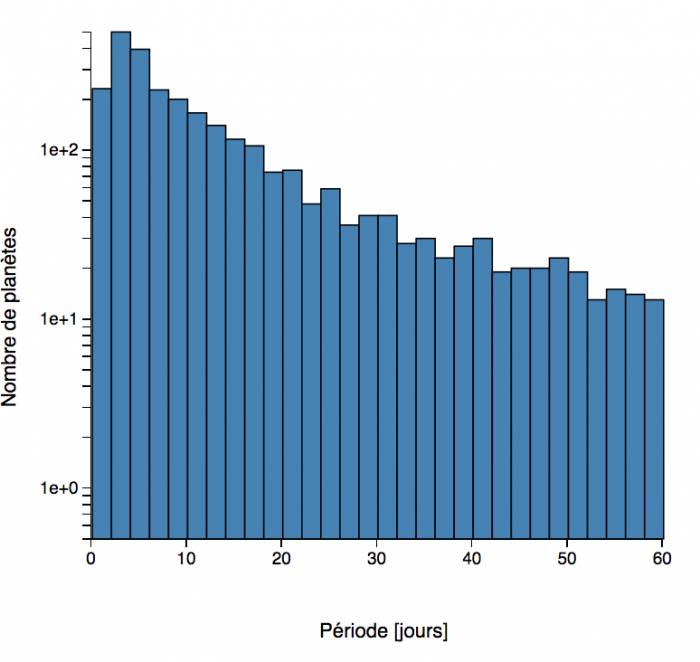
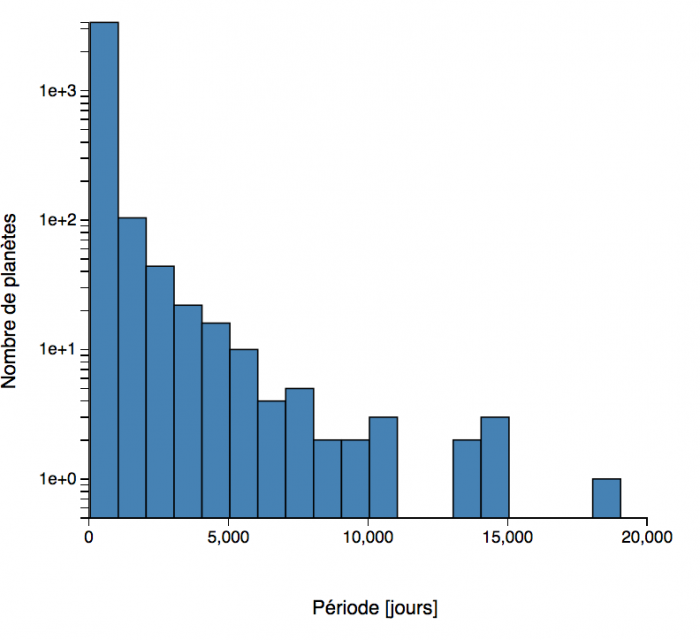
Histogrammes des périodes orbitales des exoplanètes. Zoom sur les périodes courtes (en échelle linéaire), et aperçu général (avec le décompte en échelle logarithmique) (septembre 2018).
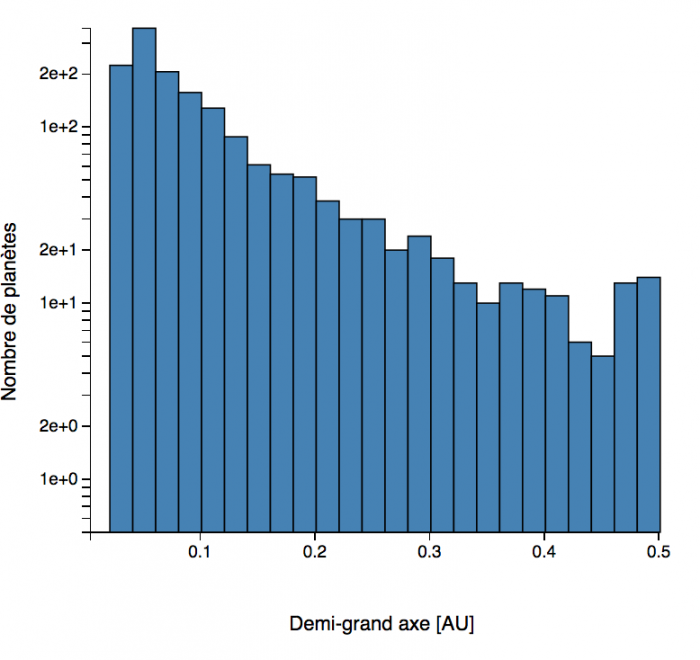
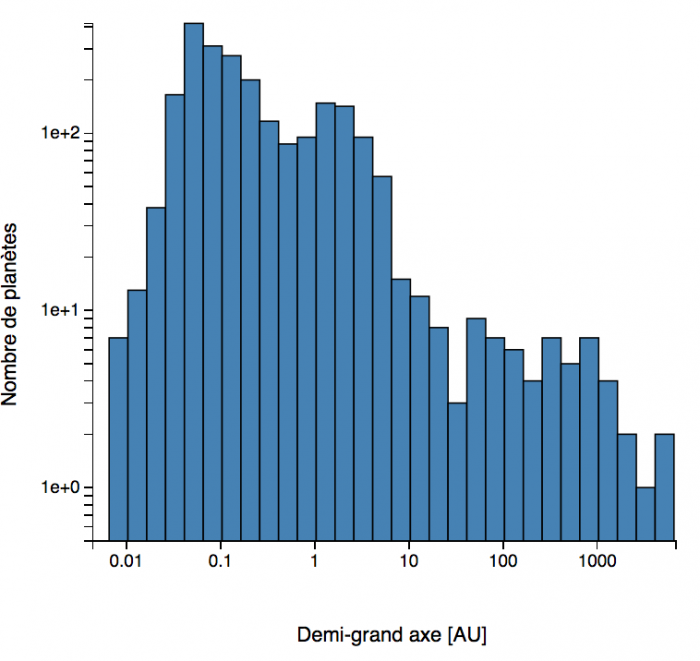
Histogrammes des demi-grands axes de l'orbite des exoplanètes. Zoom sur les demi-grands axes inférieurs à 1 UA, et aperçu général.(septembre 2018)
Demi-grand axe et période de l'orbite
L'histogramme
des demi-grands axes montre qu'ont préférentiellement été découvertes des
planètes orbitant très près de leur étoile, bien plus près que Mercure
dans le cas du système solaire. Là encore, ce sont les méthodes de détection et la 3ème loi de Kepler qui favorisent cette situation. Une nouvelle classe d'objets a été mise en évidence : les planètes géantes chaudes.
L'histogramme
des périodes orbitales aboutit à la même analyse.
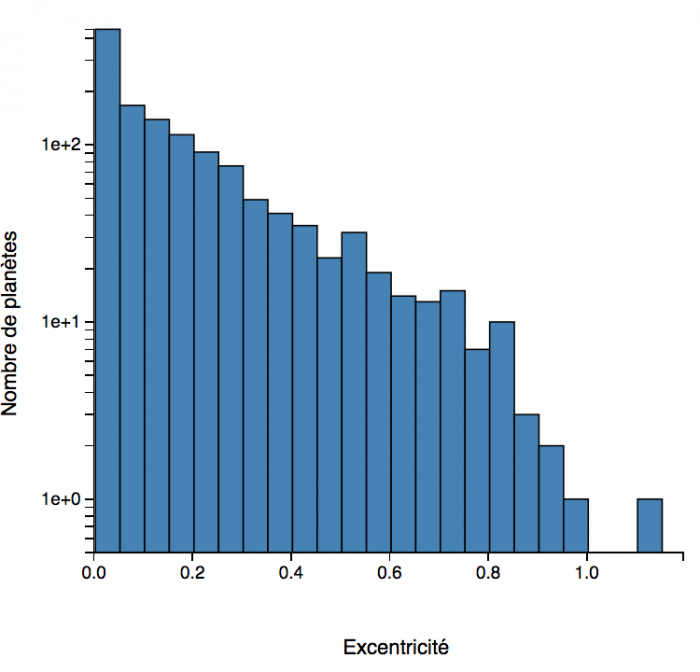
Histogramme des excentricités des exoplanètes. (septembre 2018)
Excentricité de l'orbite
L'histogramme
des excentricités orbitales dévoile une très grande variabilité de ce
paramètre. Contrairement au cas du système solaire, où les planètes
présentent des excentricités quasi nulles, les exoplanètes peuvent
suivre des orbites très excentrées. Et contrairement aux effets précédents, ceci est un phénomène réel et non un biais observationnel, qui dénote une grande variété dans la formation et l'évolution des systèmes planétaires.
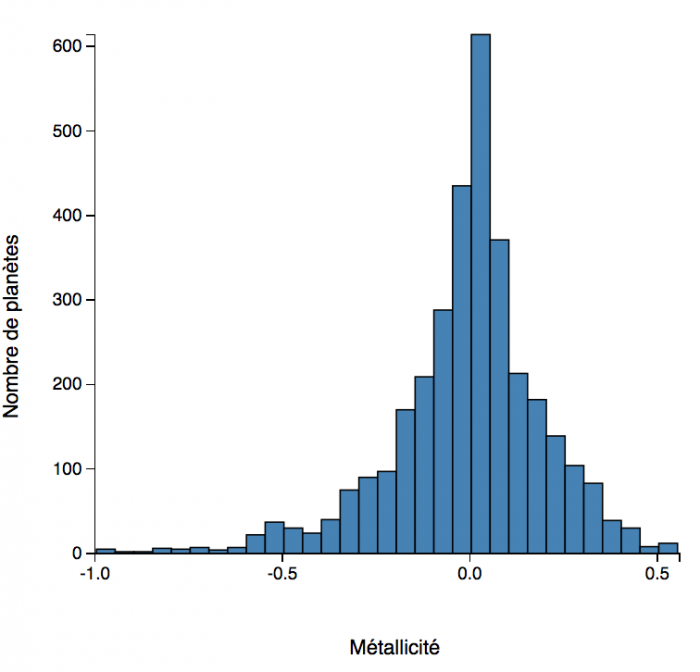
Histogramme de la métallicité des étoiles à exoplanètes. La métallicité est donnée en échelle logarithmique relative ; elle compare l'abondance de l'élément Fe dans l'étoile par rapport à celle dans le Soleil (0 = valeur solaire). (septembre 2018)
Métallicité de l'étoile hôte
L'histogramme
de la métallicité de l'étoile hôte montre qu'une metallicité solaire favorise la présence d'une planète autour d'une étoile.
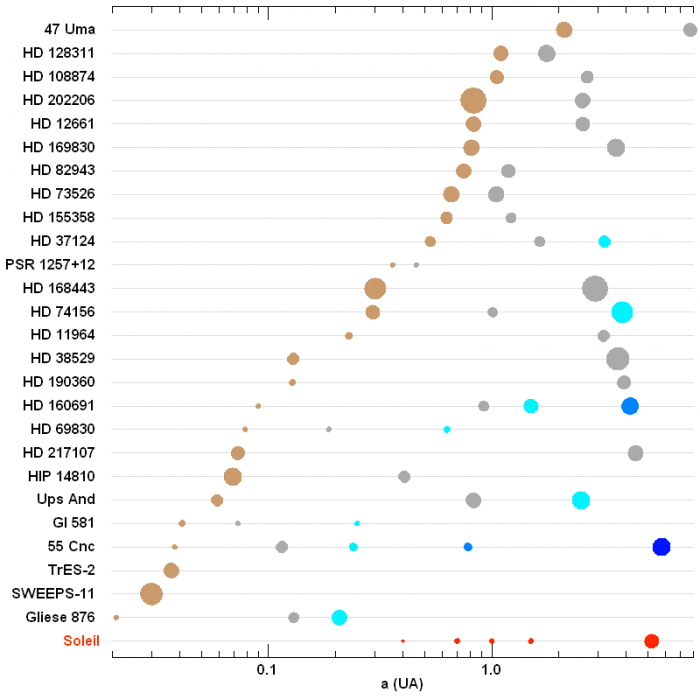
Quelques systèmes exoplanétaires. La couleur code le rang de la planète.
La plupart de ces systèmes sont plus tassés et plus massifs que le système solaire.
Crédit :
ASM
Systèmes planétaires
À ce jour, un grand nombre de systèmes planétaires ont été identifiés, présentant des caractéristiques différentes de notre système solaire. Les planètes les moins massives sont détectées par les perturbations qu'elles exercent sur les plus massives.
Détection des planètes extrasolaires par la méthode des vitesses radiales
Observer
Méthode des vitesses radiales
Considérons un système binaire constitué d'une étoile et d'une planète.
Chacun des objets décrit une orbite elliptique dont le foyer est le
centre de masse du système.
Effet Doppler dû à l'oscillation de l'étoile
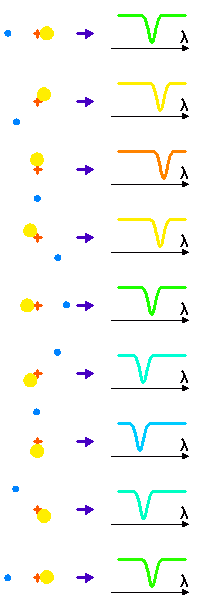
Dans son mouvement, l'étoile tantôt se rapproche, tantôt s'éloigne de l'observateur.
Une raie spectrale est alternativement décalée vers le bleu ou vers le
rouge, selon la vitesse relative entre l'étoile et l'observateur (direction indiquée par une flèche violette).
Crédit :
ASM
Les raies spectrales stellaires qui nous parviennent (à travers un
spectromètre) sont en conséquence tantôt décalées vers le bleu (longueur d'onde plus courte), tantôt vers le rouge (longueur d'onde plus grande), par effet Doppler.
Apprendre
L'orbite de la planète et l'axe de visée

L'angle

est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
Crédit :
ASM
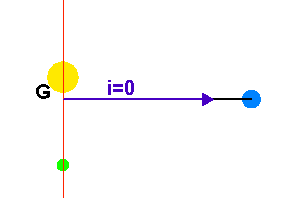
Cas particulier où l'angle

est nul. Pas de mouvement détectable.
Crédit :
ASM
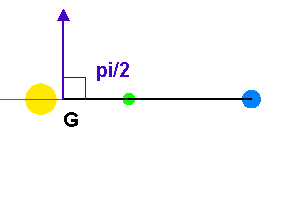
Cas particulier où l'angle

vaut
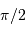
.
Crédit :
ASM
Courbe de vitesse radiale de 51 Peg A

Mesure de vitesse radiale de l'étoile 51Peg.
Crédit :
Butler & Marcy
Simuler
Vitesse radiale
Animation des mouvements orbitaux planétaires et stellaires, et signature spectrale due à la vitesse radiale de l'étoile.
Effet Doppler dû au mouvement de l'étoile
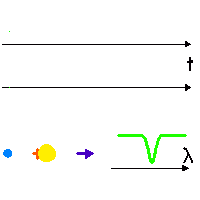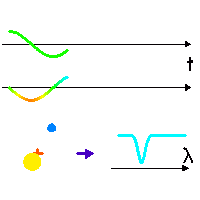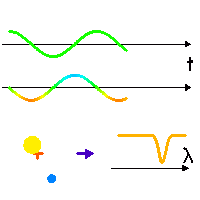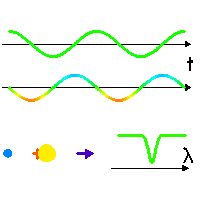
Dans son mouvement (séquence animée), l'étoile en rotation autour du barycentre (croix rouge, fixe) tantôt se rapproche, tantôt s'éloigne (courbe verte) de l'observateur (direction indiquée par la flèche bleu foncé), avec une vitesse donnée par la courbe du milieu (couleur modifiée selon une convention de type
effet Doppler .
Une raie spectrale (courbe du bas) est alternativement décalée vers le bleu ou vers le rouge, selon la vitesse relative entre l'étoile et l'observateur.
Crédit :
ASM
S'exercer

L'angle

est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
Crédit :
ASM
 QCM
QCM
 Le paramètre m sin i
Le paramètre m sin i
Difficulté : ☆☆
Temps : 20 min
On s'intéresse à la distribution du facteur multiplicatif 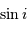 qui intervient dans la détermination de la masse
qui intervient dans la détermination de la masse 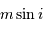 .
.
Question 1)
Rappeler la définition de l'angle 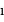 .
.
Question 2)
Statistiquement, trouve-t-on plus de systèmes avec 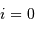 ou bien
ou bien
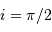 ?
?
Faire un schéma. A quelle condition sur le plan orbital a-t-on
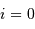 ou
ou 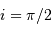 ?
?
Y'a-t-il autant de plans avec 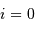 ou
ou 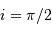 ?
?
Question 3)
Montrer, en faisant un schéma, que la probabilité de voir un
système sous une inclinaison  est proportionnelle à
est proportionnelle à 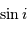 .
.
Question 4)
Calculer la valeur moyenne de 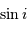 .
.
La définition d'une valeur moyenne conduit à :
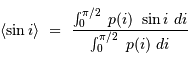
avec 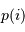 la loi de probabilité associée.
la loi de probabilité associée.
 La vélocimétrie Doppler
La vélocimétrie Doppler
Difficulté : ☆☆
Temps : 45 min
Cette technique permet la détection de planètes, via la perturbation en vitesse (vitesse réflexe) qu'elles induisent sur leur étoile.
On observe un système constitué d'une planète de masse 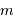 , en orbite circulaire autour d'une étoile de masse
, en orbite circulaire autour d'une étoile de masse 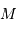 . La composante de vitesse de l'étoile
. La composante de vitesse de l'étoile 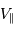 , parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse
, parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse 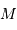 de l'étoile est supposée connue.
de l'étoile est supposée connue.
Schéma du système
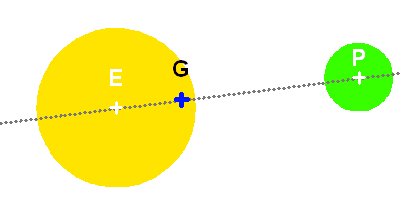
On note respectivement
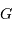
,
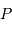
et
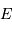
les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
Crédit :
ASM
Question 1)
Définir la position du barycentre du système étoile-planète.
Montrer que, dans le référentiel barycentrique, les vitesses 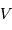 de l'étoile et
de l'étoile et 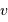 de la planète satisfont à la relation :
de la planète satisfont à la relation :
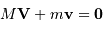
Définir la position du barycentre.
Le barycentre 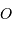 du système obéit à:
du système obéit à:
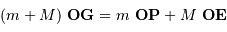
Différencier cette relation pour obtenir l'information en vitesse.
Question 4)
Quelle information inédite apporte cette relation?
Reformulation de la question :
quelle grandeur non directement observable peut finalement être ainsi mesurée ?
Question 5)
Substituer à l'observable 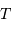 la variable
la variable 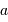 , et montrer que l'on aboutit à l'égalité suivante entre les variables
, et montrer que l'on aboutit à l'égalité suivante entre les variables 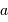 et
et 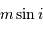 :
:
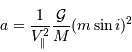
Commencer par réécrire la 3ème loi de Kepler.
Courbes de vitesses radiales
Observer
Série temporelle
La mesure de ce décalage spectral est traduite en une vitesse. Ce décalage, apparaissant comme un phénomène périodique
et d'amplitude bien inférieure à ce que l'on attendrait d'une perturbation due à un compagnon stellaire, s'interprète comme la signature d'une perturbation due à la présence de la planète autour de l'étoile.
Vitesse radiale de l'étoile en fonction du temps

Le décalage Doppler du spectre est mesuré puis traduit en vitesse
radiale
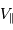
. On obtient une série temporelle de vitesse radiale, qui
semble présenter des variations répétitives.
Crédit :
Butler &Marcy
Sur une période
Vitesse radiale rapportée sur une période
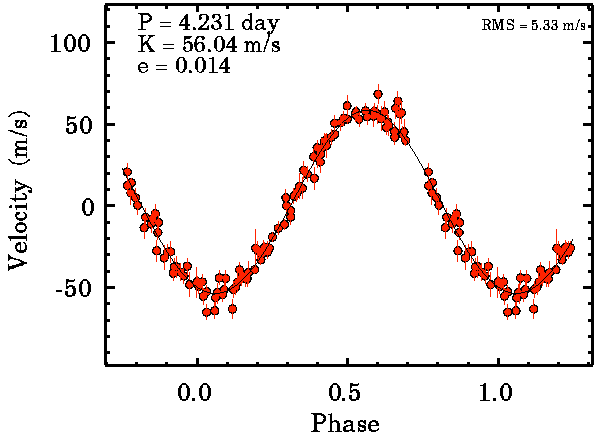
Une longue série temporelle, plus longue qu'une période,
donne accès à la période de
rotation du système, ici visualisée par repliement : la variable temporelle est la phase, et non plus la date d'observation.
Crédit :
Butler & Marcy
Lorsque l'orbite de la planète est quasi-circulaire, le graphe de la
vitesse a la forme d'une sinusoïde. L'excentricité de l'orbite a pour effet de déformer cette sinusoïde.
Graphe de vitesse de HD 108147
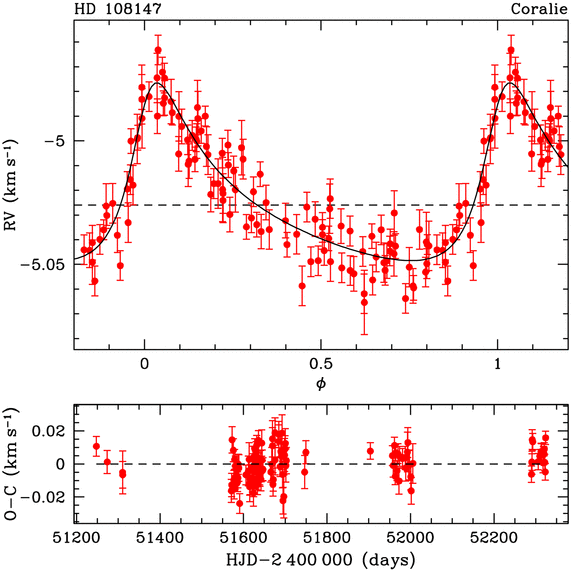
L'excentricité de l'orbite, voisine de 0.5, et la géométrie de l'observation conduisent à une telle courbe de vitesse radiale. Le schéma du dessous représente les résidus entre les valeur observées et la courbe de vitesse modélisée.
Crédit :
Observatoire de Genève
Système multiple
Lorsque l'étoile réagit à plusieurs compagnons planétaires, la complexité de la courbe de vitesse radiale s'accroît.
Dans certain cas, comme pour le système observé autour de HD 82943, on observe une résonance, avec pour ce système des périodes orbitales planétaires dans un rapport 1:2.
Graphe de vitesse de HD 168443
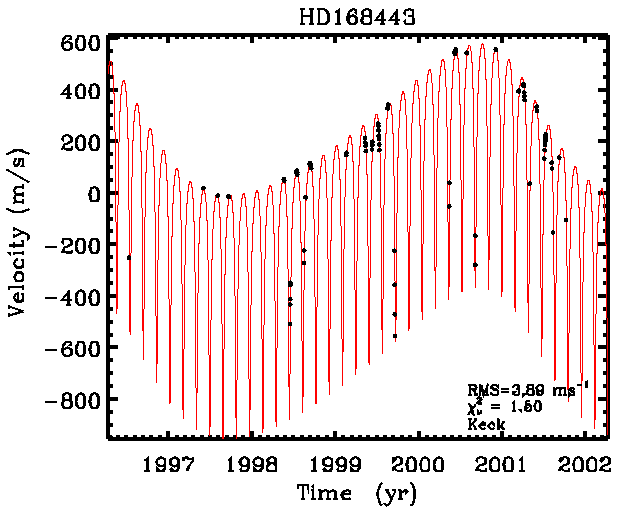
La courbe de vitesse radiale de l'étoile
HD 168443présente 2 composantes, dues à 2 compagnons planétaires. Les orbites des deux planètes détectées autour de HD 168443 ont des périodes d'ordres de grandeur bien distincts et une excentricité élevée (0.53 et 0.23)
Crédit :
Butler & Marcy
Graphe de vitesse de HD 82943
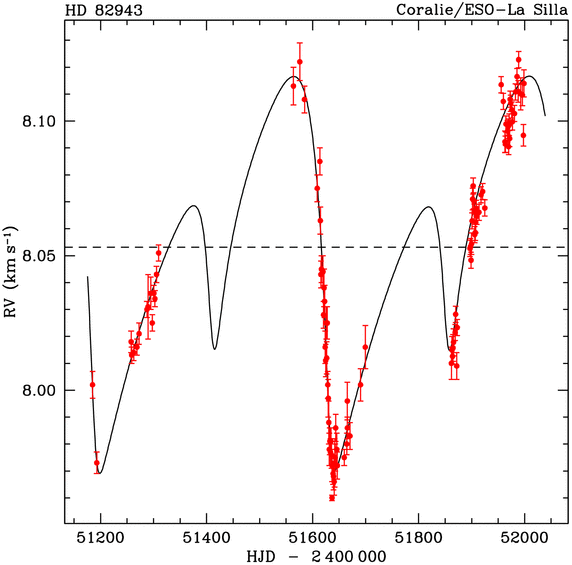
Les 2 périodes (respectivement 222 et 444 j) sont multiples l'une de l'autre, dans un rapport 2.
Crédit :
Observatoire de Genève
Limitations de la méthode des vitesses radiales
Apprendre
Diagramme a-m sin i
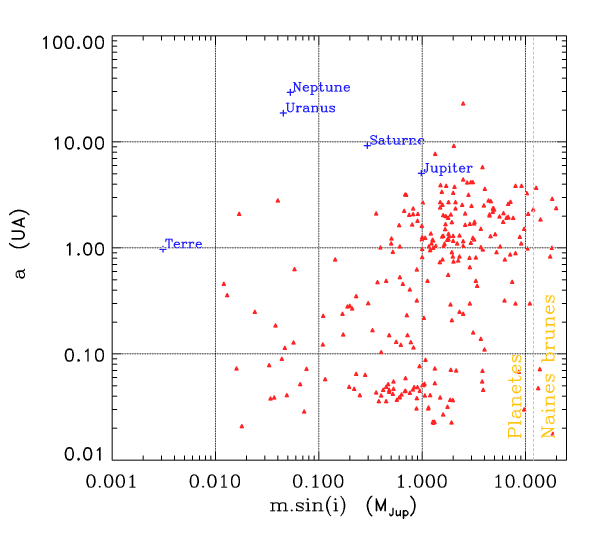
Diagramme msini-a des exoplanètes et des planètes du système solaire. Au delà de 13 fois la masse de Jupiter, on considère qu'il ne s'agit plus de planètes, mais de
naines brunes.
Crédit :
ASM
Systèmes pouvant être détectés par cette méthode
La méthode des vitesses radiales ne permet d'obtenir qu'une limite
inférieure de la masse des planètes, 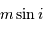 , car l'angle sous lequel
le système est observé,
, car l'angle sous lequel
le système est observé,  , reste en général inconnu. Cela a bien sûr
été un obstacle à l'interprétation du premier cas qui annonçait la
découverte d'une d'exoplanète. Cependant, une centaine d'objets avec
une masse
, reste en général inconnu. Cela a bien sûr
été un obstacle à l'interprétation du premier cas qui annonçait la
découverte d'une d'exoplanète. Cependant, une centaine d'objets avec
une masse 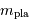 les rangeant dans la catégorie des planètes ont
été détectés, et, statistiquement, la masse réelle de la plupart
d'entre eux est bien une masse planétaire.
Cette méthode est biaisée, car elle favorise la détection des planètes
massives et relativement proches de leur étoile. En effet :
les rangeant dans la catégorie des planètes ont
été détectés, et, statistiquement, la masse réelle de la plupart
d'entre eux est bien une masse planétaire.
Cette méthode est biaisée, car elle favorise la détection des planètes
massives et relativement proches de leur étoile. En effet :
- Plus la planète est massive, plus l'étoile est perturbée, car
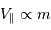 .
. - Plus la planète est proche, plus la période est courte et
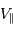 important, car
important, car 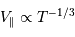 .
.
Il est commode de réécrire 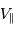 sous la forme :
sous la forme :
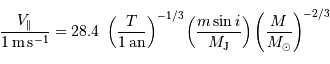
où 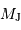 et
et 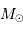 sont, respectivement, les masses de Jupiter et du Soleil.
sont, respectivement, les masses de Jupiter et du Soleil.
On rappelle, qu'avec les mêmes unités :
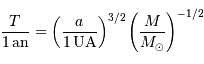
où 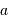 est exprimé en unité astronomique.
est exprimé en unité astronomique.
Limite de détection par la méthode des vitesses radiales
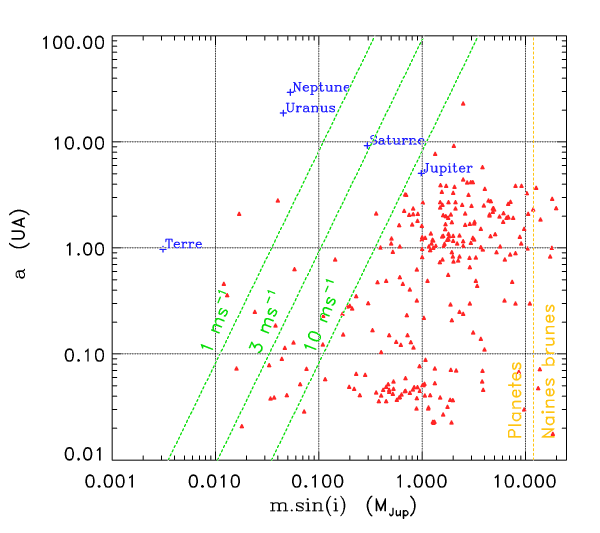
Cette méthode permet de détecter des variations de vitesse de
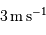
. Il faut également observer les étoiles longtemps pour avoir accès aux plus longues périodes. Les exoplanètes les moins massives n'ont pas été détectées par mesure Doppler, mais par la méthode des
transits.
Crédit :
ASM
Limite de détection
La limite de détection des instruments utilisés actuellement est de l'ordre de 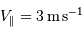 . Cela ne signifie qu'une planète similaire à la Terre autour d'une étoile de type solaire induisant une modulation de vitesse
. Cela ne signifie qu'une planète similaire à la Terre autour d'une étoile de type solaire induisant une modulation de vitesse 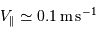 reste largement indétectable.
reste largement indétectable.
Néanmoins, il ne suffit pas que la vitesse réflexe de l'étoile soit supérieure à cette limite pour détecter une planète. En effet, une planète de masse égale à la masse de Jupiter va induire un effet Doppler de cet ordre pour une distance étoile-planète de 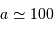 UA. Cependant, la période de révolution d'une telle planète est de 1000 ans, et il est donc exclu de l'observer ! Notons que la même planète située à la distance de Jupiter
UA. Cependant, la période de révolution d'une telle planète est de 1000 ans, et il est donc exclu de l'observer ! Notons que la même planète située à la distance de Jupiter 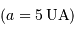 entraîne
entraîne 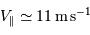 , ce qui est largement observable.
, ce qui est largement observable.
Les mesures de vitesses radiales pour la recherche de planètes extrasolaires sont menées systématiquement depuis 1995. Ceci limite la détection aux planètes de période orbitale inférieure à 15 ans en 2010, 30 ans en 2025...
Jusqu'à ce jour, la plupart des planètes extrasolaires détectées l'ont été par cette méthode.
Un exercice traite de cette limite de détection.
S'évaluer
 Limite de détection
Limite de détection
Difficulté : ☆☆☆
Temps : 45 min
Un exercice précédent a montré que la vitesse réflexe de l'étoile dépend de la masse et de l'orbite de la planète via la relation :
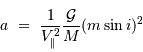
Un graphe (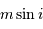 - rayon orbital
- rayon orbital 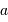 ) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse
) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse 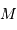 de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.
de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.
Diagramme m sin i - a
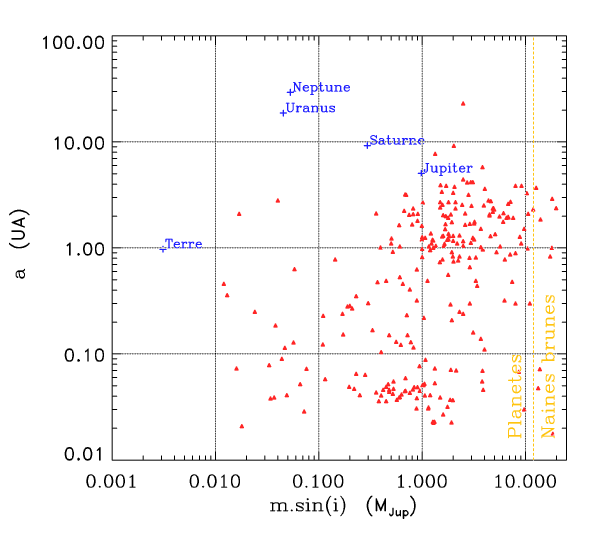
Crédit :
ASM
Données numériques
| objet | masse (kg) |
|---|
| Soleil | 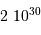 |
| Jupiter | 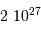 |
| la Terre | 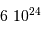 |
| 1 UA | 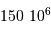 km km |
Question 1)
Les mesures en 2000 atteignaient une précision en vitesse de l'ordre de
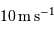 . En déduire la relation numérique entre les variables
. En déduire la relation numérique entre les variables 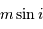 et
et 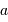 correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et
correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et 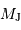 .
.
[3 points]
Faire le calcul en SI, puis passer aux unités demandées.
Question 2)
Reporter la relation trouvée sur le diagramme masse-distance, avec comme unités la masse de Jupiter pour 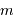 , et l'unité astronomique pour
, et l'unité astronomique pour 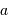 .
Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de
.
Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de 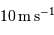 ) ?
) ?
[3 points]
Les axes du diagramme sont en échelle logarithmique décimale. Il faut prendre le logarithme de l'équation précédente pour tracer des droites sur le diagramme. En échelle log-log, l'origine du repère est en (a=1, et msin i=1).
Question 3)
Même question, si l'on parvient à détecter des amplitudes en vitesse de 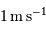 .
.
[1 points]
Question 4)
Montrer que Saturne, de période orbitale sidérale de l'ordre de 30 ans, ne pourrait tout de même pas être détecté avant l'année 2025.
[1 points]
Les observations ont vraiment débuté en 1995.
Question 5)
Montrer que cette technique d'observation comporte un biais, car elle favorise la détection de planète ayant des paramètres orbitaux particuliers.
[1 points]
Méthode de détection par transit
Observer
Détection par transit
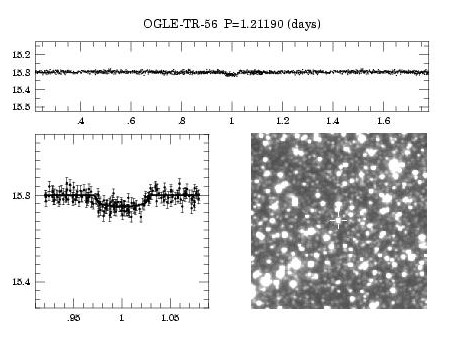
Occultation détectée par la campagne d'observation OGLE (Optical Gravitational Lensing Experiment ; Warsaw Telescope (1.3 m) installé à l'Observatoire de Las Campanas au Chili). L'aperçu de la courbe de lumière, et le zoom autour du transit montre combien la signature de ce dernier est ténue. Le champ stellaire localise la cible, de faible magnitude (V = 16).
Le temps est donné en unité de la période orbitale.
Crédit :
OGLE
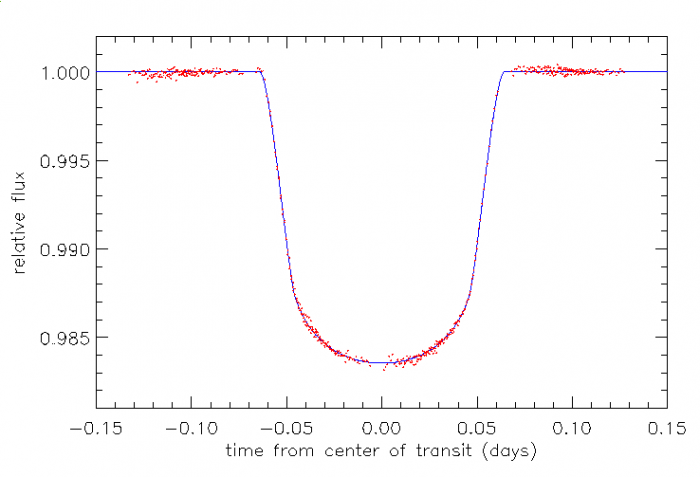
Occultation de
HD209458 par sa planète, vue par le télescope spatial Hubble. Le profil d'assombrissement du centre au bord de l'étoile occasionne la concavité du fond du transit.
Crédit :
HST
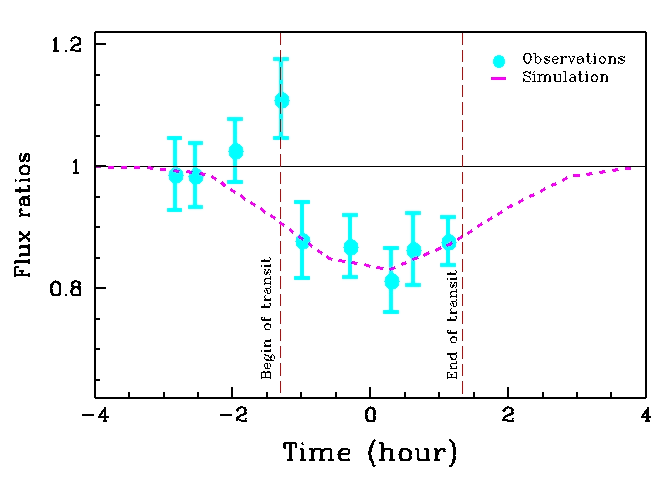
Occultation de HD209458 par sa planète, vue dans le filtre étroit de la raie Lyman alpha de l'hydrogène. L'augmentation du flux est due à la composante planétaire, et dénote vraisemblablement une atmosphère planétaire étendue.
Crédit :
HST
Transit
Le passage répété d'une planète devant son étoile provoque une diminution périodique de la luminosité de l'étoile. La forme de la figure de transit dépend du diamètre relatif de la
planète par rapport à celui de l'étoile, de l'inclinaison du système
par rapport à la ligne de visée, de l'épaisseur et de la composition de
l'éventuelle atmosphère de la planète.
Mesures orbitales
On retire des observations : la période orbitale, le demi-grand axe, et surtout l'inclinaison de l'orbite (voisine de 90°). Cette dernière n'est pas mesurable par la méthode des vitesses radiales.
L'atmosphère planétaire
Potentiellement, la comparaison des mesures spectroscopiques de l'étoile avant et pendant le transit peut donner accès à la composition de l'atmosphère planétaire.
Le transit de l'étoile HD 209458 a conduit à la détection d'une atmosphère planétaire étendue, qui explique l'allure de la courbe d'occultation dans la raie Lyman alpha de l'hydrogène.
Apprendre
Transit d'une planète devant son étoile

Crédit :
ASM
Méthode de détection d'éléments chimiques dans une atmosphère
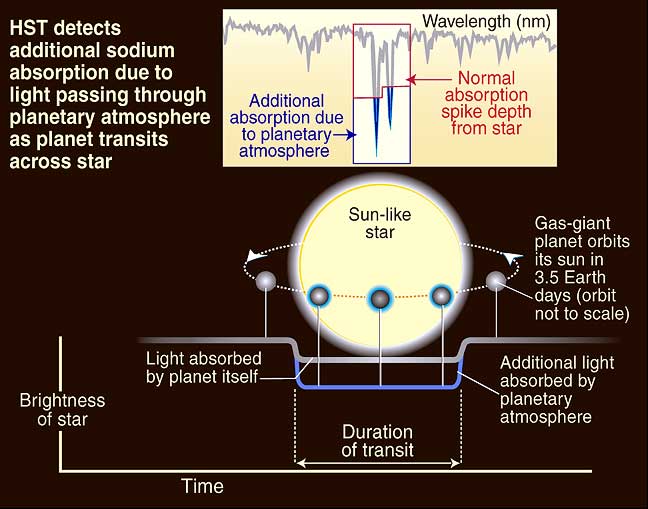
Crédit :
HST
Baisse de flux
Le passage récurrent d'une planète devant son étoile parente provoque une diminution périodique du flux reçu de l'étoile si le système est observé sous un angle adéquat, i.e. si la planète traverse la ligne de visée de l'observateur.
La diminution relative du flux émis par l'étoile dans la direction de l'observateur lors du transit de la planète est :
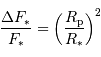
où 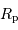 est le rayon de la planète et
est le rayon de la planète et 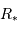 celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en exercice).
celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en exercice).
Ordres de grandeurs
Les systèmes les plus facilement détectables, avec une planète de type Jupiter chaud, ont un rayon de l'ordre de 10 à 20% du rayon stellaire d'une étoile froide de la séquence principale. Ils induisent des baisses de flux de l'ordre de quelques pourcents.
La variation relative de flux pour un système de type Soleil-Jupiter est de 1%, et de 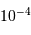 pour un système tel que Soleil-Terre.
pour un système tel que Soleil-Terre.
Sondage atmosphérique
Une information essentielle pourra également être apportée par cette méthode : la présence ou non d'une atmosphère autour de la planète, reliée à la pente de l'extinction du flux, progressive en présence d'une atmosphère. Cette détection est extrêmement importante, car on peut connaître la composition de cette atmosphère en comparant les mesures spectroscopiques de l'étoile avant et pendant le transit.
Il est en principe possible de rechercher des signes d'activités exobiologiques en détectant des composants gazeux dont l'abondance est un indice de la présence d'organismes vivants... mais hors de portée des moyens actuels.
Simuler
Occultations
Animation reliant la courbe de lumière à l'évolution temporelle de la géométrie du système. L'inclinaison du plan orbital planétaire est un paramètre crucial.
La signature photométrique diffère selon que l'inclinaison est
très proche ou
voisine de 90 degrés, ou
trop éloignée.

Transit planétaire, avec une inclinaison proche de 90 degrés. La signature photométrique reste ténue. Le rapport des luminosités stellaire et planétaire est tel que l'occultation de la planète par l'étoile reste n'est pas observable.
Crédit :
ASM

Transit planétaire. L'inclinaison, voisine de 90 deg, ne conduit qu'à une occultation partielle, et donc une très faible signature photométrique.
Crédit :
ASM

Pas de transit planétaire, l'inclinaison différant trop de 90 deg. Aucune occultation, et donc aucune signature photométrique.
Crédit :
ASM
S'exercer
 Transit de HD 209458
Transit de HD 209458
Difficulté : ☆
Temps : 20 min
HD 209458 est une des nombreuses étoiles hébergeant une exoplanète. On cherche à caractériser le transit de cette dernière. Les notations sont les mêmes que celles des pages précédentes.
Question 1)
Retrouver l'expression de la diminution relative de luminosité 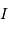 :
:
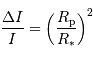
On suppose le flux (équivalent à une luminosité, ou puissance, surfacique) stellaire 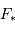 uniforme :
uniforme :
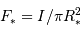 .
.
Estimer la différence de luminosité avec et sans éclipse, fonction de la
surface stellaire visible, variable, et du flux surfacique, fixe.
Question 3)
Calculer la masse volumique 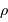 de l'exoplanète, sachant que sa masse
de l'exoplanète, sachant que sa masse 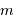 vaut
vaut 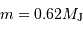 . Quelle remarque vous inspire ce résultat ?
. Quelle remarque vous inspire ce résultat ?
Limitations de la méthode par transit
Observer

Fraction d'un champ stellaire observée par le satellite CoRoT. Au total, plusieurs milliers de cibles sont suivies simultanément.
Crédit :
CoRoT/CNES
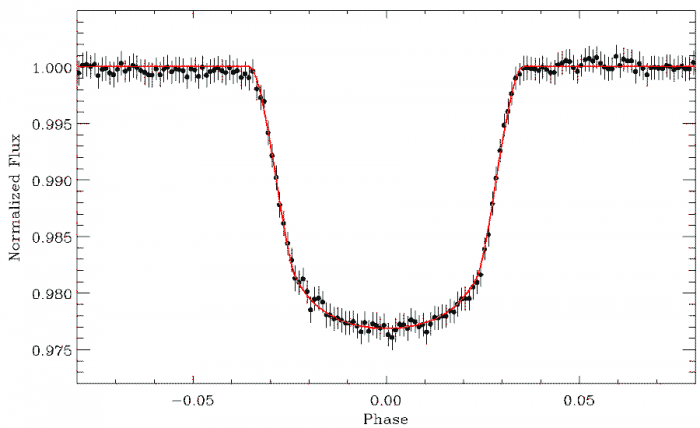
Détecter et identifier un transit nécessite une grande précision photométrique, telle que l'apporte CoRoT, la première mission dédiée à ce thème de recherche.
Crédit :
CoRoT/CNES
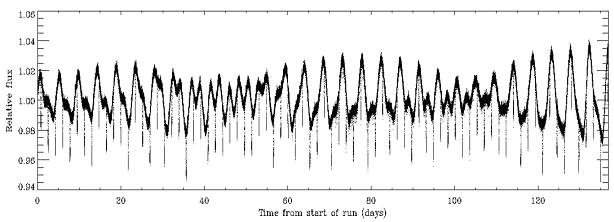
Les transits, ici événements très fins de profondeur relative 4%, se superposent à un flux stellaire éminemment variable.
Crédit :
CoRoT/CNES
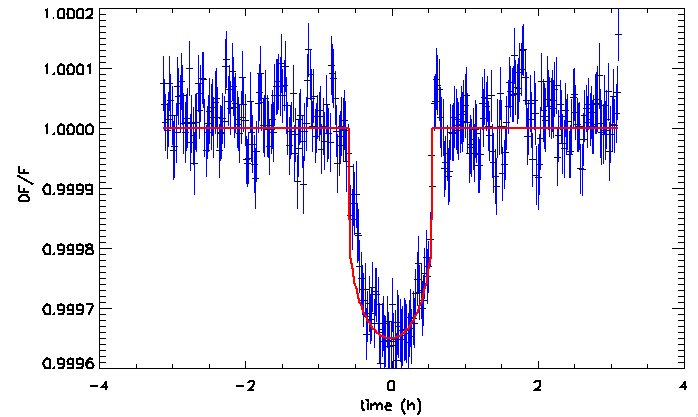
Transit profond de seulement 0.4% observé par CoRoT (planète CoRoT-Exo-7b, de rayon égal à 1.8 fois celui de la Terre).
Crédit :
CoRoT/CNES
Observer beaucoup d'étoiles
La probabilité de détection d'une planète étant faible, un programme de détection par transits doit nécessairement suivre simultanément un
grand nombre de cibles, ce que permet la photométrie.
Observer longtemps
Un transit seul n'apporte pas d'information, et peut être confondu avec un événement non planétaire. Les séquences d'observation de CoRoT durent 5 mois, et la répétition de trois événements est attendue.
Observer précisément
Distinguer un transit planétaire des multiples autres sources possibles de
variation du flux stellaire n'est pas toujours simple.
Les planètes les moins massives détectées, par transit et donc sans l'ambiguïté du facteur de projection 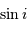 , ont été observées par le satellite CoRoT puis Kepler.
, ont été observées par le satellite CoRoT puis Kepler.
Apprendre
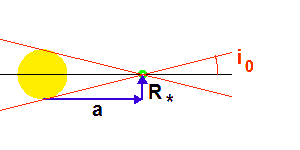
Le rayon planétaire étant négligé devant le rayon stellaire, l'angle séparant le plan orbital de l'axe de visée doit être inférieur à une valeur limite pour qu'il y ait occultation.
Crédit :
ASM
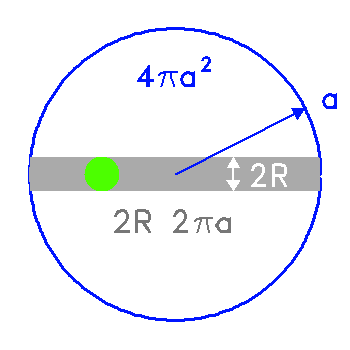
La probabilité de transit
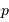
est obtenue par le rapport de l'aire balayée par la planète à l'aire de la sphère de rayon égal au demi-grand axe planétaire :
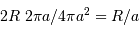
.
Crédit :
ASM
Précision photométrique
Le deuxième facteur limitant est photométrique. En effet, depuis le sol il est difficile d'obtenir une précision photométrique meilleure que 1 % (c'est-à-dire 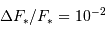 ) en raison de l'agitation atmosphérique. Les observations depuis l'espace, en revanche, permettent d'atteindre une précision aussi bonne que
) en raison de l'agitation atmosphérique. Les observations depuis l'espace, en revanche, permettent d'atteindre une précision aussi bonne que 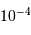 , et donc de détecter des planètes de type tellurique.
, et donc de détecter des planètes de type tellurique.
Limite de détection par la méthode des transits
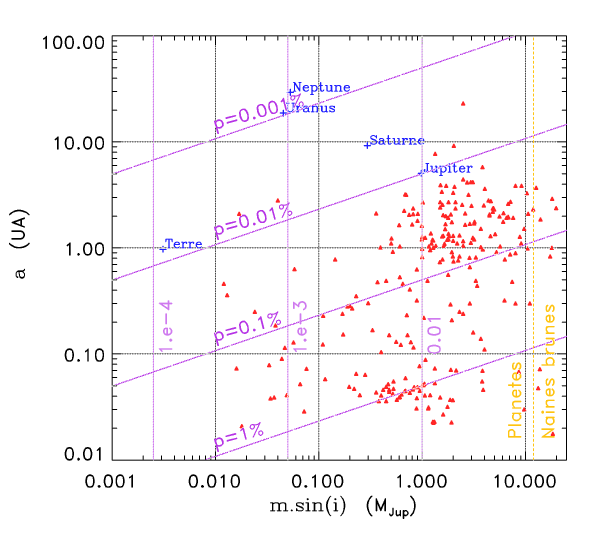
La détection des planètes les moins massives nécessite une
excellente précision photométrique. La probabilité de détection
décroît fortement avec l'évolution du demi-grand axe.
Crédit :
ASM
Observation de transits
Il s'ensuit que, pour être efficace, les projets de détection
d'exoplanètes par transit doivent observer un très grand nombre de
cibles, avec la meilleure précision
photométrique possible. De plus, pour éviter tout effet
stroboscopique, il faut observer continûment. L'espace est l'endroit idéal pour ceci, comme l’ont démontré les mission CoRoT et Kepler.
Confirmation des observations
Plusieurs artefacts observationnels peuvent imiter la signature
d'un transit planétaire. Les plus courants sont l'observation d'un
système stellaire double, ou d'une binaire à éclipses présente
dans le champ d'observation de l'étoile principale. Dans ces deux
cas, la baisse de flux peut être faible et confondue avec celle
d'une hypothétique planète. Une vérification a posteriori s'impose
pour déterminer les éventuels faux positifs, menée le plus souvent
en vélocimétrie Doppler, et parfois par imagerie en optique adaptative.
S'exercer
 Limitation de la méthode du transit
Limitation de la méthode du transit
Difficulté : ☆☆
Temps : 30 min
Avant les missions spatiales CoRoT et Kepler, peu de transits avaient été observés ; leur nombre a ensuite explosé. L'exercice se propose de déterminer la probabilité 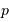 d'un tel événement, fonction du rayon de l'étoile
d'un tel événement, fonction du rayon de l'étoile 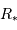 et du rayon orbital de la planète
et du rayon orbital de la planète 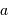 , et d'établir
, et d'établir
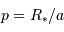 .
.

Crédit :
ASM
Question 1)
L'angle  de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum
de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum 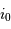 pour lequel une éclipse peut être observée, en fonction de
pour lequel une éclipse peut être observée, en fonction de 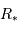 et
et 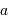 , en supposant le rayon planétaire négligeable.
, en supposant le rayon planétaire négligeable.
Faire un schéma, basé sur la figure de l'énoncé.
Question 2)
En vous aidant des propriétés de symétrie du système, déterminer de quelle(s) variable(s) dépend 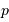 .
.
Question 3)
La probabilité 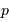 de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet
de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet 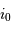 .
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet
.
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet  .
.
Définition de la mesure d'un angle solide (unité stéradian):
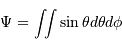
avec 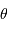 et
et 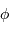 les angles d'Euler.
les angles d'Euler.
Dans le cas étudié, il y a symétrie de révolution autour de l'axe de
révolution du système.
Question 4)
Exprimer 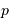 en fonction de
en fonction de 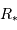 et
et 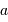 .
.
La probabilité 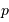 mesure la non-appartenance au cône précédemment
défini.
mesure la non-appartenance au cône précédemment
défini.
Question 5)
Application numérique pour le cas l'exoplanète 51 Peg.
Données : 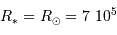 km, et
km, et 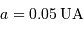 .
.
Détection par mesure astrométrique
Observer
Astrométrie
Il est possible de détecter le mouvement de l'étoile perpendiculairement à la ligne de visée, c'est-à-dire sur
la sphère céleste, et d'en déduire les caractéristiques de
la planète et de son orbite.
Déplacement astrométrique du Soleil dû à Jupiter
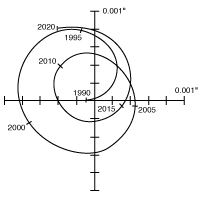
Déplacement du Soleil sous l'effet des mouvements planétaires (Jupiter et Saturne principalement), vu à une distance de 10 pc.
L'amplitude de ce déplacement est de 500 microsecondes d'arc (
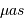
). Le déplacement dû à la Terre présenterait une amplitude de
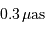
à la même distance.
Crédit :
NASA
Apprendre
 Objectifs
Objectifs
L'astrométrie s'intéresse à la position des astres sur la sphère céleste. Cette technique peut être sensible à la modulation de la position d'une étoile légèrement perturbée par la présence d'une planète.
Astrométrie
Il est possible de détecter le mouvement de l'étoile
perpendiculairement à la ligne de visée, c'est-à-dire sur
la sphère céleste, et d'en déduire les caractéristiques de la
planète et de son orbite.
On se limite au cas d'une orbite
circulaire, mais bien sûr cette méthode s'applique aussi à la détection
de planètes sur des orbites elliptiques. Le mouvement de l'étoile
projeté sur le plan du ciel, c'est-à-dire sur le plan perpendiculaire à
la ligne de visée, est une ellipse de demi-grand axe 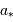 . Comme
la distance
. Comme
la distance 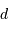 à l'étoile est grande devant
à l'étoile est grande devant 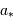 , la déviation
angulaire correspondante est
, la déviation
angulaire correspondante est 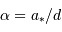 , ou encore :
, ou encore :
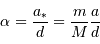
avec 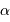 exprimé
seconde d'arc,
exprimé
seconde d'arc, 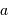 le
rayon de l'orbite de la planète (en UA) et
le
rayon de l'orbite de la planète (en UA) et 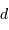 la distance
Soleil-étoile. La masse
la distance
Soleil-étoile. La masse 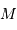 de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire
de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire 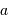 de la périodicité du
mouvement, et donc la masse de la planète
de la périodicité du
mouvement, et donc la masse de la planète 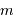 de la mesure de
de la mesure de 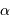 .
.
En pratique, la variation de la position d'un astre sur la sphère céleste n'est pas mesurée de façon absolue, mais différentiellement par rapport à un objet du champ, angulairement proche mais très lointain en distance, dont la position reste fixe.

Diagramme masse-distance, montrant les performances de la détection astrométrique, fonction de la précision de mesure (respectivement 10, 1 et 0.05 milliseconde d'arc). Les triangles rouges marquent les exoplanètes déjà détectées.
Crédit :
ASM
Systèmes pouvant être détectés par cette méthode
Les mesures faites à l'heure actuelle depuis le sol ont une précision d'une milliseconde d'arc (mas), et devraient atteindre 10 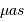 dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des zones habitables (i.e.
dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des zones habitables (i.e. 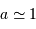 UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
S'exercer
 Petite révision sur la formation d'image
Petite révision sur la formation d'image
Difficulté : ☆
Temps : 30 min
Un astronome extraterrestre regarde notre système solaire à une distance de 10 AL de notre Soleil. On souhaite dimensionner le télescope dont il aurait besoin pour distinguer Jupiter autour du Soleil.
On suppose le pouvoir de résolution de l'appareil limité par la seule diffraction : la tache de diffraction vaut angulairement 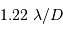 radian, où
radian, où 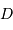 est le diamètre du télescope.
est le diamètre du télescope.
Pour la suite, on prendra 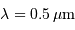 .
.
Question 1)
Déterminer la distance angulaire maximale 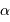 entre le soleil et Jupiter
entre le soleil et Jupiter 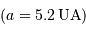 .
.
Rappel : 1 AL = 63 000 UA.
Question 2)
Déterminer 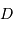 , le diamètre minimum du collecteur nécessaire.
, le diamètre minimum du collecteur nécessaire.
Un objet est résolu spatialement si sa taille angulaire est supérieure à la taille de la tache de diffraction.
Question 3)
Cela est-il suffisant?
S'intéresser au rapport des flux respectifs du Soleil et de Jupiter.
 Astrométrie
Astrométrie
Difficulté : ☆☆
Temps : 40 min
Le mouvement apparent d'une étoile voisine du soleil, corrigé de la parallaxe annuelle, est a priori rectiligne uniforme en l'absence de perturbation. On cherche à quantifier l'influence d'un compagnon planétaire.
On observe un système binaire composé d'une étoile de masse 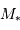 et d'une planète de masse
et d'une planète de masse 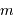 ( avec
( avec 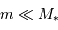 ) de rayon orbital
) de rayon orbital 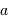 .
.
Question 1)
Justifier le caractère rectiligne et uniforme du mouvement stellaire, en l'absence de compagnon.
Un mouvement rectiligne uniforme est un mouvement non perturbé par quoi
que ce soit.
Question 2)
Exprimer l'amplitude de la perturbation angulaire maximale 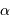 de la position de l'étoile, située à une distance
de la position de l'étoile, située à une distance 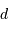 du Soleil.
du Soleil.
Question 3)
Retrouver l'expression :
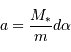
Définir le centre de masse.
Etablir 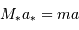
Question 4)
A quelle distance 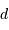 se situe l'étoile si sa parallaxe annuelle vaut 0.1" ?
se situe l'étoile si sa parallaxe annuelle vaut 0.1" ?
Le parsec est défini comme étant la distance d'une étoile ayant une parallaxe de 1".
Question 5)
Quelles planètes du système solaire, supposé vu à 10 pc, pourrait-on détecter, si l'on est capable de mesurer des variations de position à 0.01" ou 0.001" près ?
Compléter le diagramme ci-joint, positionnant les objets en fonction de leur masse 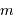 et de leur demi-grand axe
et de leur demi-grand axe 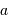 , en définissant la frontière qui marque la limite de détectabilité
(rappel
, en définissant la frontière qui marque la limite de détectabilité
(rappel 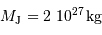 ).
).
Diagramme a-msin i

Crédit :
ASM
Traduire la relation établie précédemment entre 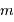 et
et 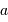 , et l'exprimer dans le système d'unités (UA, masse de Jupiter).
, et l'exprimer dans le système d'unités (UA, masse de Jupiter).
Question 6)
A terme, on imagine être capable de mesurer des écarts de position 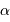 avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme
avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme 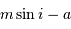 , pour un système à 10 pc et
, pour un système à 10 pc et 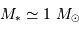 .
.
C'est la même chose que précédemment. Seule l'application numérique change.
Question 7)
Quelles planètes du système solaire deviennent ainsi détectables ?
Si les graphes ont été dressés, la réponse n'est plus qu'une question de domaine.
Performance de détection
Observer

GQ Lupi A et son compagnon froid b.
Crédit :
ESO
Une exoplanète attrapée au vol
Alors que les méthodes de détection par transit et vélocimétrie Doppler donnent de plus en plus de résultats, plusieurs objets ont été détectés en imagerie directe. Cette population comprend des planètes flottantes ou des naines brunes sans qu'il soit facile/possible de faire la différence.
Un des premier objets décourts est GQ Lupi b qui orbite autour de l'étoile QG Lupi A. A une distance d'environ 100 UA, 270 fois moins brillant que GQ Lupi A, GQ Lupi b a une masse entre une et 30 fois la masse du Jupiter. Ni les observations, ni leur modélisation ne permettent de conclure à l'heure actuelle sur la nature exacte de cet objet.
Apprendre
Observables
L'examen des différentes méthodes de détection montre qu'elles ne donnent pas accès aux mêmes observables, et qu'elles ne subissent pas les mêmes biais observationnels. Ces différentes méthodes (et il y en a d'autres) sont donc complémentaires : le sujet astrophysique est d'ailleurs suffisamment important pour motiver de nombreux projets observationnels, au sol ou spatiaux.
Performance de détection
La méthode des vitesses radiales favorise la détection des planètes massives et proches de l'étoile, alors que l'astrométrie favorise les planètes massives et de grands rayons orbitaux. Là encore, les méthodes apparaissent complémentaires.
Planètes détectables
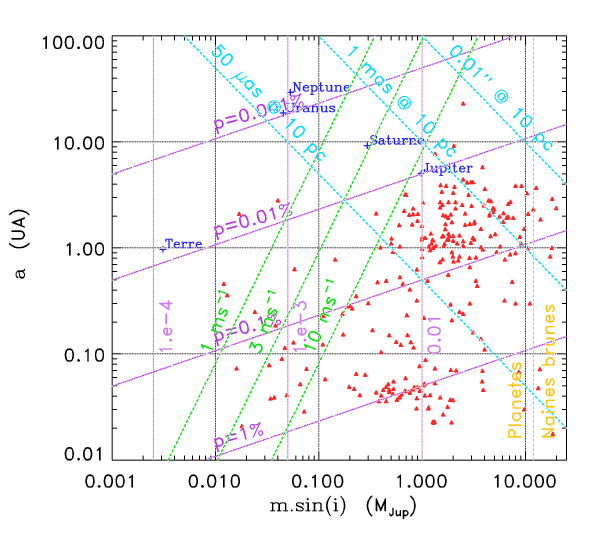
Les triangles rouges marquent les exoplanètes déjà détectées. Les limites en violet concernent la détection par transit, en vert par mesure Doppler, en bleu par astrométrie.
Crédit :
ASM
Détections
L'existence de spectromètres performants et stables a favorisé jusqu'à ce jour la détection par vitesse radiale. L'accroissement
du nombre de projets de recherche par transit fait augmenter le nombre de telles détections.
Nombre d'exoplanètes détectées par les différentes méthodes (octobre 2018)
| Méthode | Planètes | Systèmes planétaires |
|---|
| Vitesse radiale | 771 | 574 |
| Transit | 2847 | 2127 |
| Microlentille | 82 | 79 |
| Imagerie | 100 | 82 |
| Chronométrage | 29 | 23 |
S'évaluer
 Discours de la méthode
Discours de la méthode
Difficulté : ☆
Temps : 30 min
Question 1)
Distinguer les différentes techniques en fonction de leurs biais respectifs portant sur 1) la masse de la planète 2) son demi-grand axe 3) l'inclinaison orbitale.
[3 points]
Question 2)
Quelle technique est à votre avis la plus facilement spatialisable ?
[1 points]
Conclusion
L'étude des exoplanètes, champ de l'astrophysique en pleine effervescence, appartient de plain-pied à ces domaines scientifiques qui éveillent en chacun un intérêt qui n'est pas que purement scientifique.
De nombreux grands projets sont développés pour mieux détecter ou, plus difficile, voir directement les exoplanètes (ce qui demande alors d'éteindre la lumière stellaire avec une excellente efficacité, et motive des projets instrumentaux alliant interférométrie et coronographie).
Deux grands projets spatiaux ont apporté une moisson importante d'observations par transits. Le suivi au sol des candidats exoplanétaires doit se poursuivre avec des observations au sol pour vérifier qu'il s'agit bien de planètes vues en transit et non d'autres objets.
Différents observatoires ont mené des campagnes intensives de recherche d'exoplanètes par vitesse radiale :
- Spectromètre HARPS au 3.6-m de l'ESO au Chili,
- Spectomètre équivalent télescope Keck,
- HARPS nord, clone de l'instrument HARPS sud.
Lister tous les projets en cours et oeuvrant prochainement est une tâche ardue tant la discipline progresse rapidement. On note :
- Projet SPHERE pour imager avec un grand contraste de l'environnement stellaire,
- Mission spatiale TESS de la NASA pour la recherche d'exoterres,
- Caractérisation des atmosphères exoplanétaires avec la mission JWST de la NASA,
- Mission spatiale PLATO de l'ESA pour la caractérisation des systèmes étoiles-planètes
- ...
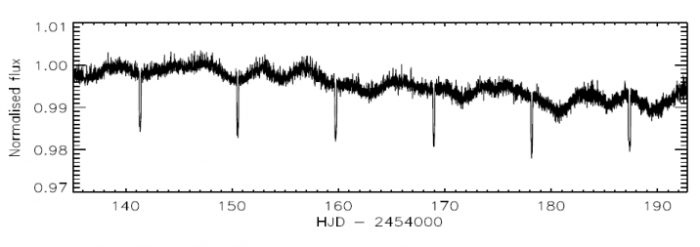
Courbe de transit d'une exoplanète détectée par la mission CoRoT.
Crédit :
CNES
Une technique prometteuse pour l'observation directe d'une planète est l'interférométrie annulante, où l'étoile est éteinte par interférométrie (ou là) destructive, quand la planète apparaît en revanche en opposition de phase.
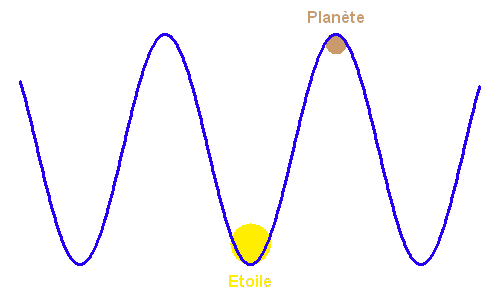
Le flux de l'étoile, positionnée sur une frange d'interférence destructive, apparaît éteint par rapport à celui de la planète.
Crédit :
ASM
Réponses aux QCM
pages_vitesse-radiale-extrasolaire/vitesse-radiale-extrasolaire-sexercer.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 1)
(
En effet
)
Réponses aux exercices
pages_visuelles/intro-binaires-visuelles-sexercer.html
Exercice
'Binaire visuelle'
- Question 1
Solution :
On appelle  le centre de l'ellipse observée et A l'intersection de la demi-droite [0E) avec l'ellipse. Comme l'excentricité
le centre de l'ellipse observée et A l'intersection de la demi-droite [0E) avec l'ellipse. Comme l'excentricité 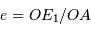 est invariante par projection, le fait que l'étoile primaire soit au foyer de l'orbite projetée montre que le grand axe de l'orbite projetée correspond à la projection du grand axe, ce qui ne peut avoir lieu que si
est invariante par projection, le fait que l'étoile primaire soit au foyer de l'orbite projetée montre que le grand axe de l'orbite projetée correspond à la projection du grand axe, ce qui ne peut avoir lieu que si 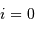 ...
...
- Question 2
Solution :
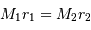 et
et 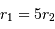 implique un rapport de masse
implique un rapport de masse 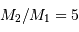
- Question 3
Solution :
La troisième loi de Kepler, en unités, UA, année, masse solaire, s'exprime :
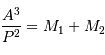
- Question 4
Solution :
La parallaxe étant de 0.1", le système double est situé à 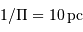 de nous et qu'une unité astronomique y est vue sous un angle de 0,1".
de nous et qu'une unité astronomique y est vue sous un angle de 0,1".
Le demi-grand axe apparent est égal à 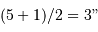 ; le demi-grand axe est donc de 30 UA.
; le demi-grand axe est donc de 30 UA.
- Question 5
Solution :
On applique la troisième loi de Kepler pour calculer la somme des masses :
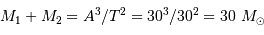 .
.
et on obtient 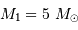 et
et 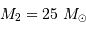
pages_visuelles/masse-sirius-sexercer.html
Exercice
'Sirius A et Sirius B'
- Question 1
Aide :
Activité soit l'outil 'ligne', soit l'outil 'cercle'.
Aide :
Faire une règle de trois et définir le rapport d'unité.
Solution :
Avec l'outil 'cercle' centré sur Sirius A, 10" correspondent à 350 unités. On définit le rapport d'unité : 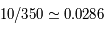
- Question 2
Aide :
Pour le demi-grand axe : repérer les projections des péri- et apoastre.
Aide :
Pour la période : s'appuyer sur les valeurs au voisinage de l'apoastre.
Solution :
D'après la figure, on déduit la période 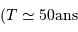 et le demi-grand axe de l'orbite relative
et le demi-grand axe de l'orbite relative 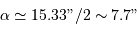
- Question 3
Aide :
Traduire la parallaxe en distance.
Aide :
De la valeur angulaire du demi-grand axe et de la distance, déterminer le demi-grand axe en UA.
Aide :
Utiliser la 3ème loi de Kepler
Solution :
Si 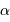 est le demi-grand axe mesuré en secondes d'arc et
est le demi-grand axe mesuré en secondes d'arc et 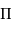 la parallaxe, le demi-grand axe linéaire
la parallaxe, le demi-grand axe linéaire 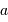 , mesuré en UA est alors égal à
, mesuré en UA est alors égal à 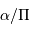 , soit
, soit 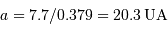 .
.
D'après la troisième loi de Kepler, on a par ailleurs :
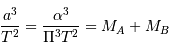
où 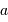 est exprimé en UA,
est exprimé en UA, 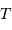 en années, et
en années, et 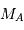 et
et 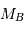 en masse solaire. Ce qui donne :
en masse solaire. Ce qui donne :
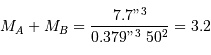
- Question 4
Aide :
Définir le barycentre.
Aide :
La demi-amplitude est à comparer au demi-grand axe.
Solution :
La définition du barycentre G donne :
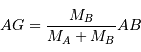
On peut ainsi comparer la demi-amplitude de AG au demi-grand axe, pour obtenir le rapport 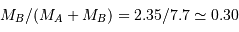 .
.
On en déduit les masses respectives : 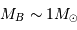 et
et 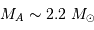 .
.
pages_eclipses/orbite-courbe-lumiere-sexercer.html
Exercice
'Système binaire et courbe de lumière'
- Question 1
Aide :
Ecrire une relation entre 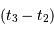 ,
, 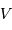 ,
, 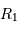 et
et 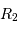 ; puis entre
; puis entre 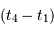 ,
, 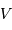 ,
, 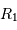 et
et 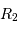 .
.
Solution :
Le trajet de la petite étoile pour aller de la position 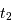 à la position
à la position 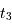 est égal à
est égal à 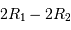 . De la même façon, le trajet de la petite étoile pour aller de la position
. De la même façon, le trajet de la petite étoile pour aller de la position 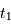 à la position
à la position 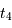 est égal à
est égal à 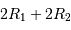 . Si l'on assimile la corde de l'arc de cercle de la trajectoire à une droite, ce qui revient à dire que l'orbite est grande vis à vis des rayons des étoiles, on obtient :
. Si l'on assimile la corde de l'arc de cercle de la trajectoire à une droite, ce qui revient à dire que l'orbite est grande vis à vis des rayons des étoiles, on obtient :
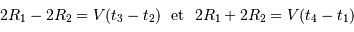
D'où 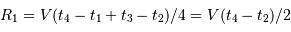 et
et 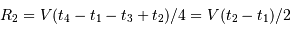
- Question 2
Solution :
On a 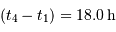 et
et 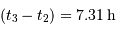 , d'où
, d'où 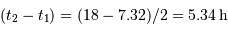 et
et 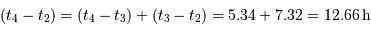 et donc, d'après le résultat de la question précédente :
et donc, d'après le résultat de la question précédente :
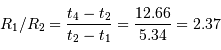
- Question 3
Solution :
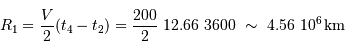
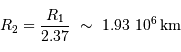
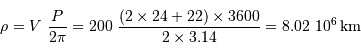
- Question 4
Aide :
A quoi correspond le minimum arrondi ?
Aide :
Voir la loi de rayonnement du corps noir.
Solution :
La même aire est occultée à chaque éclipse, que la petite étoile passe devant ou derrière la plus grosse.
En vertu de la loi de rayonnement du corps noir, c'est lorsque l'étoile la plus chaude est occultée que le minimum est le plus profond.
C'est lorsque la plus petite étoile est éclipsée que le fond du minimum est plat durant un certain laps de temps ; lorsque la plus grande est éclipsée, l'assombrissement du centre au bord arrondit la courbe de lumière. Ici, c'est donc la plus petite étoile qui est la plus chaude.
pages_eclipses/orbite-courbe-lumiere-sevaluer.html
Exercice
'Durée d'une éclipse'
- Question 1
Aide :
On fera l'hypothèse que les étoiles ont un rayon moyen voisin du rayon solaire.
- Question 2
Aide :
S'intéresser à la vitesse orbitale.
- Question 3
Aide :
S'intéresser aux rayons stellaires.
- Question 4
Aide :
Comparer les tailles des objets.
pages_eclipses/binaires-temperatures-sexercer.html
Exercice
'Système binaire et températures'
- Question 1
Aide :
Voir le rayonnement du corps noir
Solution :
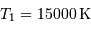 ,
, 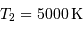 , donc
, donc 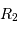 le rayon de la plus froide est égal à 4
le rayon de la plus froide est égal à 4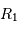 .
.
D'après la loi de rayonnement du corps noir, on a : 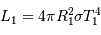 et
et 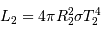 .
.
D'où :
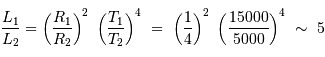
- Question 2
Aide :
voir la page loi de Stefan.
Solution :
La surface occultée est toujours égale à celle de la plus petite étoile (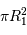 ). Conséquence de la loi de rayonnement du corps noir, le minimum principal correspond donc à l'occultation de l'étoile la plus chaude, ici en l'occurrence, la plus petite...
). Conséquence de la loi de rayonnement du corps noir, le minimum principal correspond donc à l'occultation de l'étoile la plus chaude, ici en l'occurrence, la plus petite...
- Question 3
Solution :
La plus petite étoile est occultée, il s'agit donc d'une éclipse totale
- Question 4
Aide :
Voir le paragraphe sur les mesures de température
Solution :
Le rapport des profondeurs est de 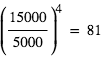
pages_eclipses/binaires-temperatures-sevaluer.html
Exercice
'AR Lacertae : mesure des paramètres physiques'
pages_spectroscopiques/binaires-masse-sexercer.html
Exercice
'Observabilité'
- Question 1
Solution :
Lorsque l'inclinaison du plan de l'orbite par rapport à la ligne de visée est nulle, les composantes radiales des vitesses orbitales sont nulles et les raies des deux étoiles se superposent... Mais si les deux étoiles sont de type spectral différent, ce qui est le cas le plus général, on verra dans le spectre des familles de raies correspondant à deux températures superficielles différentes, témoignant de la présence de deux objets distincts.
pages_spectroscopiques/binaires-masse-sexercer.html
Exercice
'Résolution spectrale'
- Question 1
Aide :
Voir le cours sur l'effet Doppler issues de mesures spectrométriques.
Solution :
La mesure en vitesse est limitée par la résolution
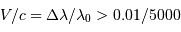
soit la valeur limite  .
.
- Question 2
Aide :
Penser à Kepler
Solution :
La 3eme loi de Kepler, reliant la vitesse 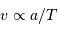 au demi-grand axe s'exprime :
au demi-grand axe s'exprime :
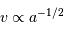
Dans le cas d'un binaire spectroscopique, le système double n'est pas résolu en ses deux composantes, et les deux étoiles entrent dans la fente du même spectrographe, ce qui implique une proximité spatiale et donc une limitation à des périodes orbitales courtes, et des vitesses élevées.
pages_spectroscopiques/binaires-masse-sexercer.html
Exercice
'Inclinaison de l'orbite'
- Question 1
Solution :
Les binaires spectroscopiques étant des couples serrés, si l'inclinaison est proche de 90°, la binaire est forcément aussi à éclipse. Ce qui se vérifie aisément par l'observation.
- Question 2
Solution :
D'après les expressions de la page masses des composantes , la masse étant inversement proportionnelle à 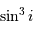 , on obtient bien une limite inférieure pour la masse de chaque composante.
, on obtient bien une limite inférieure pour la masse de chaque composante.
pages_spectroscopiques/binaires-masse-sevaluer.html
Exercice
'L'étoile double AR Lacertae'
pages_exoplanete/vitesse-radiale-extrasolaire-sexercer.html
Exercice
'Le paramètre m sin i'
- Question 1
Aide :
Revoir le cours !
Solution :
C'est l'angle entre la normale au plan orbital et l'axe de visée.
- Question 2
Aide :
Faire un schéma. A quelle condition sur le plan orbital a-t-on
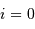 ou
ou 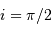 ?
?
Aide :
Y'a-t-il autant de plans avec 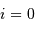 ou
ou 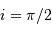 ?
?
Solution :
Il y a un seul plan perpendiculaire à la ligne de visée (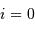 ),
mais une infinité qui la contiennent (
),
mais une infinité qui la contiennent (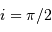 ).
).
- Question 3
Aide :
Il faut estimer toutes les directions  , et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture
, et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture  et
et 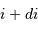 .
.
Solution :
La probabilité est mesurée par l'ouverture du cône de demi-angle
au sommet  . Son angle solide est
. Son angle solide est 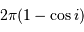 . Le rayon
d'ouverture du cône, proportionnel à
. Le rayon
d'ouverture du cône, proportionnel à 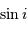 , permet d'estimer
comment la probabilité cherchée varie avec
, permet d'estimer
comment la probabilité cherchée varie avec  .
.
La différentielle de l'angle solide aboutit au même résultat.
On retrouve intuitivement que le cas 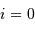 est peu probable.
est peu probable.
- Question 4
Aide :
La définition d'une valeur moyenne conduit à :
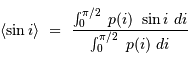
avec 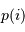 la loi de probabilité associée.
la loi de probabilité associée.
Solution :
Avec 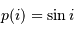 la loi de probabilité, la définition de la valeur moyenne de la variable
la loi de probabilité, la définition de la valeur moyenne de la variable 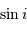 conduit à :
conduit à :
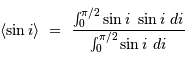
Le numérateur vaut 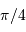 , car il est égal à la moyenne sur le même intervalle, de largeur
, car il est égal à la moyenne sur le même intervalle, de largeur 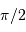 , de
, de 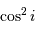 , et que la somme des carrés des sinus et cosinus vaut 1.
, et que la somme des carrés des sinus et cosinus vaut 1.
Le dénominateur vaut 1.
La valeur moyenne est donc :
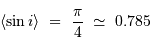
pages_exoplanete/vitesse-radiale-extrasolaire-sexercer.html
Exercice
'La vélocimétrie Doppler'
- Question 1
Aide :
Définir la position du barycentre.
Aide :
Le barycentre 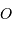 du système obéit à:
du système obéit à:
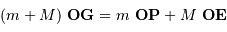
Différencier cette relation pour obtenir l'information en vitesse.
Solution :
Par définition du barycentre, 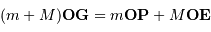 , avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
, avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
Dans le référentiel du centre de masse :
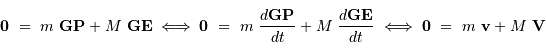
- Question 2
Aide :
Commencer par faire le schéma, pour estimer 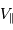 dans les cas
dans les cas  nul ou angle droit.
nul ou angle droit.
Solution :
La relation entre 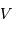 , le module de
, le module de 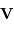 et
et 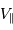 s'écrit :
s'écrit :
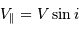
- Question 3
Solution :
La troisième loi de Kepler appliquée à la planète s'écrit :
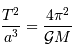
Par ailleurs, la définition du périmètre de l'orbite donne le demi-grand axe en fonction de la période et de la vitesse :
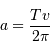
On en déduit :
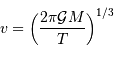
Et on en tire :
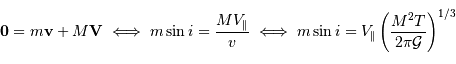
- Question 4
Aide :
Reformulation de la question :
quelle grandeur non directement observable peut finalement être ainsi mesurée ?
Solution :
A partir des observables, 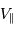 et
et 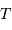 , et de la masse stellaire
, et de la masse stellaire 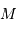 déduite des modèles stellaires, on a accès, au facteur
déduite des modèles stellaires, on a accès, au facteur 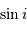 près,
à la masse de la planète... inaccessible par ailleurs.
près,
à la masse de la planète... inaccessible par ailleurs.
- Question 5
Aide :
Commencer par réécrire la 3ème loi de Kepler.
Solution :
La 3ème loi de Kepler... toujours elle, permet d'écrire :
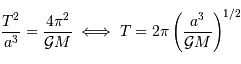
![\Rightarrow m\sin i = V _{\mathrm{\parallel}}\left[{M^{2}\over 2\pi{\cal G}}2\pi\left({a^{3}\over {\cal G}M}\right)^{1/2}\right]^{1/3} = V _{\mathrm{\parallel}}\left({Ma\over {\cal G}}\right)^{1/2}](../pages_exoplanete/equations_vitesse-radiale-extrasolaire/equation105.png)
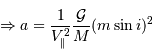
pages_exoplanete/limite-vitesse-radiale-sevaluer.html
Exercice
'Limite de détection'
- Question 1
Aide :
Faire le calcul en SI, puis passer aux unités demandées.
- Question 2
Aide :
Les axes du diagramme sont en échelle logarithmique décimale. Il faut prendre le logarithme de l'équation précédente pour tracer des droites sur le diagramme. En échelle log-log, l'origine du repère est en (a=1, et msin i=1).
- Question 3
- Question 4
Aide :
Les observations ont vraiment débuté en 1995.
- Question 5
pages_exoplanete/methode-transit-sexercer.html
Exercice
'Transit de HD 209458'
- Question 1
Aide :
Estimer la différence de luminosité avec et sans éclipse, fonction de la
surface stellaire visible, variable, et du flux surfacique, fixe.
Solution :
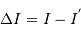 avec
avec 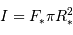 , et
, et 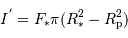 . Donc :
. Donc :
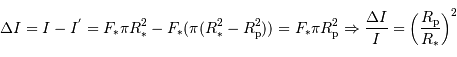
- Question 2
Aide :
Il s'agit d'une simple application numérique
Solution :
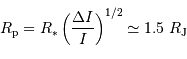
- Question 3
Solution :
En reliant la masse à la masse volumique et au volume, on trouve :
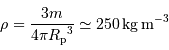
Cette planète est bien moins dense que Saturne ( ). C'est une géante gazeuse. Et si l'on trouvait un océan suffisamment grand, la planète y flotterait ...
). C'est une géante gazeuse. Et si l'on trouvait un océan suffisamment grand, la planète y flotterait ...
pages_exoplanete/limite-methode-transit-sexercer.html
Exercice
'Limitation de la méthode du transit'
- Question 1
Aide :
Faire un schéma, basé sur la figure de l'énoncé.
Solution :
Le triangle étoile-diamètre planétaire permet d'écrire, le rayon de la planète étant supposé très petit :
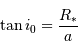
- Question 2
Solution :
Le problème est à symétrie de révolution. La position de la ligne de visée autour de l'étoile ne joue aucun rôle, la seule variable pertinente est l'angle  .
.
- Question 3
Aide :
Définition de la mesure d'un angle solide (unité stéradian):
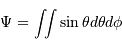
avec 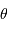 et
et 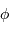 les angles d'Euler.
les angles d'Euler.
Dans le cas étudié, il y a symétrie de révolution autour de l'axe de
révolution du système.
Solution :
Mesure de l'angle solide d'un hémisphère :
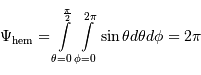
Mesure de l'angle solide d'un cône de demi-angle au sommet 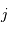 :
:
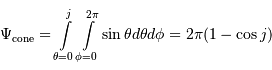
- Question 4
Aide :
La probabilité 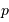 mesure la non-appartenance au cône précédemment
défini.
mesure la non-appartenance au cône précédemment
défini.
Solution :
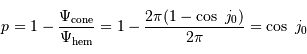
Les angles 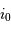 et
et 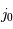 sont complémentaires :
sont complémentaires : 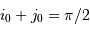 . On en tire :
. On en tire :
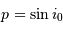
Comme de plus le rayon stellaire est petit devant le rayon de la trajectoire de l'exoplanète, l'angle 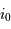 est petit, et l'on peut le confondre avec son sinus ou sa tangente.
est petit, et l'on peut le confondre avec son sinus ou sa tangente.
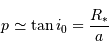
- Question 5
Solution :
Application numérique directe :
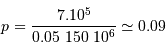
pages_exoplanete/astrometrie-extrasolaire-sexercer.html
Exercice
'Petite révision sur la formation d'image'
- Question 1
Aide :
Rappel : 1 AL = 63 000 UA.
Solution :
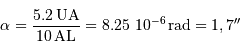
- Question 2
Aide :
Un objet est résolu spatialement si sa taille angulaire est supérieure à la taille de la tache de diffraction.
Solution :
Le diamètre minimum 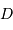 du collecteur est atteint lorsque la tache de diffraction est égale la distance angulaire maximum
du collecteur est atteint lorsque la tache de diffraction est égale la distance angulaire maximum 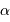 entre le soleil et Jupiter :
entre le soleil et Jupiter :
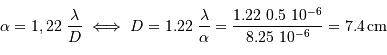
Pour tout télescope de diamètre supérieur, l'astronome extraterrestre peut résoudre Jupiter autour du Soleil.
- Question 3
Aide :
S'intéresser au rapport des flux respectifs du Soleil et de Jupiter.
Solution :
Le rapport des flux est tellement disproportionné qu'il faut un meilleur pouvoir séparateur de l'instrument ou une plus grande distance entre les 2 objets pour espérer voir la planète.
pages_exoplanete/astrometrie-extrasolaire-sexercer.html
Exercice
'Astrométrie'
- Question 1
Aide :
Un mouvement rectiligne uniforme est un mouvement non perturbé par quoi
que ce soit.
Solution :
L'étoile observée est isolée, et donc elle obéit au principe de Galilée.
- Question 2
Aide :
Faire un schéma.
Solution :
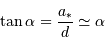
avec 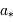 étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
- Question 3
Aide :
Définir le centre de masse.
Aide :
Etablir 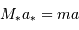
Solution :
D'après la définition du barycentre 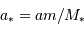 . Alors :
. Alors :
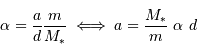
- Question 4
Aide :
Le parsec est défini comme étant la distance d'une étoile ayant une parallaxe de 1".
Solution :
Une étoile ayant une parallaxe de 0.1" est, par définition, à 10 pc.
- Question 5
Aide :
Traduire la relation établie précédemment entre 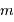 et
et 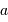 , et l'exprimer dans le système d'unités (UA, masse de Jupiter).
, et l'exprimer dans le système d'unités (UA, masse de Jupiter).
Aide :
Le produit 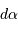 , avec
, avec 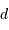 en pc et
en pc et 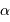 en seconde d'arc, donne directement une distance en UA.
en seconde d'arc, donne directement une distance en UA.
Solution :
On traite l'équation :
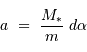
en tenant en compte que le produit 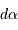 , avec
, avec 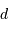 en pc et
en pc et 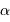 en " donne une distance en UA directement, par définition. En prenant
en " donne une distance en UA directement, par définition. En prenant 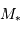 directement en masse jovienne (
directement en masse jovienne (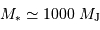 ), on obtient dans le système d'unités (UA,
), on obtient dans le système d'unités (UA, 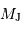 ), pour
), pour 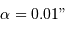 :
:
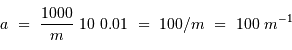
En échelle logarithmique, cette équation définit une droite de pente -1 ; elle passe par le point 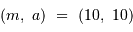 .
.
Pour une précision de 1 mas (1 millième de seconde d'arc), la courbe obtenue est définie par :
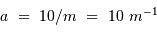
Parallèle à la précédente, elle contient le point
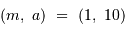 .
.
Comme le montre le diagramme ci-joint, aucune planète du système solaire n'est ainsi détectable à ce niveau de précision astrométrique.
Diagramme a-msin i
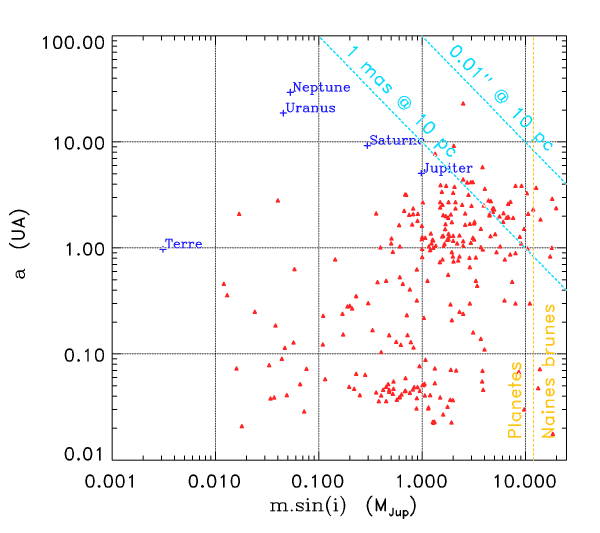
Crédit :
ASM
- Question 6
Aide :
C'est la même chose que précédemment. Seule l'application numérique change.
Solution :
Par rapport au cas précédent, le gain en précision d'un facteur 20 déplace la
limite vers les faibles masses, passant p.ex. par le point
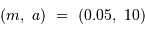 .
.
Planètes détectables
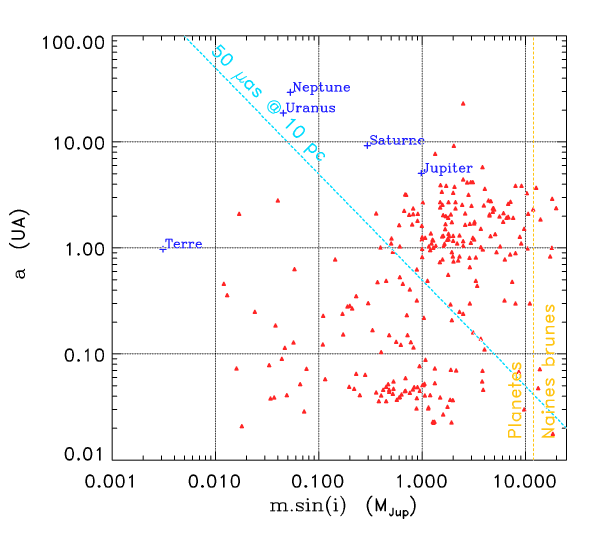
Crédit :
ASM
- Question 7
Aide :
Si les graphes ont été dressés, la réponse n'est plus qu'une question de domaine.
Solution :
Planètes détectables : Jupiter, Saturne, Uranus et Neptune. Seules les planètes géantes sont donc détectables, pas la Terre !
Planètes détectables
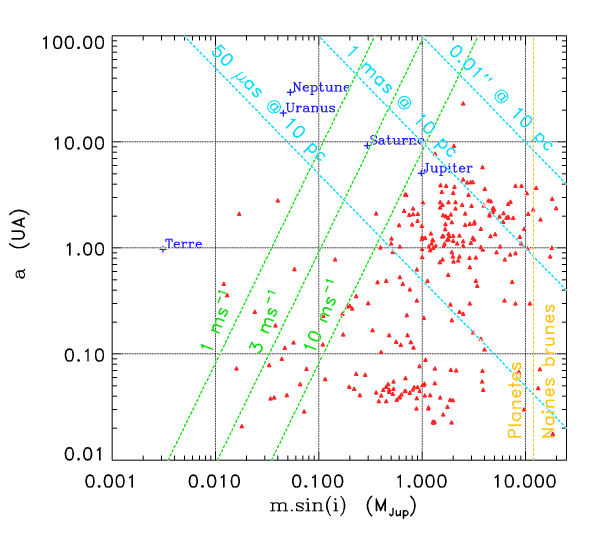
Crédit :
ASM




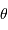 Serpentis partagent des parallaxes identiques (0.0248"). Malgré leur mouvement orbital, leurs mouvements propres (flèches rouges) apparaissent voisins. La 3ème composante, dans le coin supérieur gauche du cliché, possède également une parallaxe identique.
Serpentis partagent des parallaxes identiques (0.0248"). Malgré leur mouvement orbital, leurs mouvements propres (flèches rouges) apparaissent voisins. La 3ème composante, dans le coin supérieur gauche du cliché, possède également une parallaxe identique.












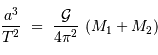
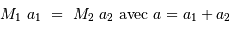
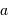 représente le demi-grand axe de l'orbite relative du corps de masse
représente le demi-grand axe de l'orbite relative du corps de masse 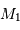 par rapport au corps de masse
par rapport au corps de masse 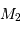 et
et 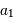 et
et 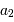 sont les demi-grands axes des orbites absolues de chacun des corps par rapport au barycentre
sont les demi-grands axes des orbites absolues de chacun des corps par rapport au barycentre 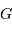 du système.
du système.
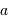 ,
, 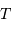 et de la position du barycentre du système (c'est-à-dire des demi-grands axes
et de la position du barycentre du système (c'est-à-dire des demi-grands axes 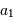 et
et 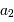 ) permet alors de déterminer
) permet alors de déterminer 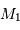 et
et 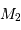 .
.
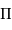
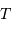
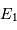 se trouve au foyer de l'orbite observée ; le compagnon est observé à une distance du barycentre 5 fois plus grande que celle de l'étoile primaire.
se trouve au foyer de l'orbite observée ; le compagnon est observé à une distance du barycentre 5 fois plus grande que celle de l'étoile primaire.
 du plan de l'orbite est nulle.
du plan de l'orbite est nulle.


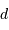 entre les deux composantes et l'angle de position
entre les deux composantes et l'angle de position 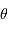 de la composante la plus faible par rapport à une direction de référence (celle de la direction du pôle céleste Nord) passant par l'étoile la plus brillante et repérée par rapport aux autres étoiles.
de la composante la plus faible par rapport à une direction de référence (celle de la direction du pôle céleste Nord) passant par l'étoile la plus brillante et repérée par rapport aux autres étoiles.

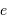 n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).
n'est pas plus conservée par la projection que le demi-grand axe, mais la détermination de l'excentricité de l'orbite réelle découle directement des paramètres de l'orbite projetée. Cette excentricité est en effet définie par la distance du foyer (E2) au centre (O), rapportée au demi-grand axe (0A). Ce rapport se mesure directement par OE2/OA, qui est conservé par la projection (par application du théorème de Thalès).

 de l'orbite vraie avec le plan du
ciel en reconstituant la projection du cercle principal de
l'ellipse vraie : ce cercle se projette suivant une ellipse dont
le rapport d'axes est égal à
de l'orbite vraie avec le plan du
ciel en reconstituant la projection du cercle principal de
l'ellipse vraie : ce cercle se projette suivant une ellipse dont
le rapport d'axes est égal à 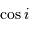 .
.
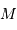 de l'ellipse coupe le cercle
principal en un point
de l'ellipse coupe le cercle
principal en un point 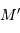 et le grand axe en un point
et le grand axe en un point 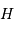 , tels
que
, tels
que 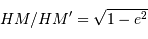 . Cette propriété se conservant par
projection on peut donc reconstituer l'ellipse projection du
cercle principal point par point à partir de la trajectoire
observée et de la direction conjuguée, i.e. la direction de la
tangente à l'ellipse observée aux points
. Cette propriété se conservant par
projection on peut donc reconstituer l'ellipse projection du
cercle principal point par point à partir de la trajectoire
observée et de la direction conjuguée, i.e. la direction de la
tangente à l'ellipse observée aux points 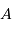 et
et 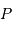 .
.
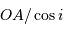 .
.



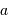
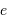
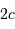

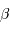 Persei). Ses variations d'éclat sont connues depuis 1670 par les observations de Geminiano Montanari. La première étude systématique a été faite par John Goodricke en 1783. On connaît actuellement plus de 4000 systèmes de binaires à éclipse. Les périodes de ces systèmes sont en général courtes, variant de quelques heures à une dizaine de jours. La plus petite période actuellement mesurée est celle de WZ Sagittae (1h22min), et la plus longue est celle de
Persei). Ses variations d'éclat sont connues depuis 1670 par les observations de Geminiano Montanari. La première étude systématique a été faite par John Goodricke en 1783. On connaît actuellement plus de 4000 systèmes de binaires à éclipse. Les périodes de ces systèmes sont en général courtes, variant de quelques heures à une dizaine de jours. La plus petite période actuellement mesurée est celle de WZ Sagittae (1h22min), et la plus longue est celle de 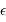 Aurigae avec ses 9883 jours (27 ans).
Aurigae avec ses 9883 jours (27 ans).


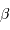 de la constellation de Persée (
de la constellation de Persée (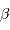 Persei). Son comportement est connu depuis plusieurs siècles car ses
Persei). Son comportement est connu depuis plusieurs siècles car ses 





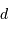 entre les étoiles est telle que
entre les étoiles est telle que
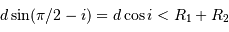
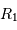 et
et 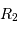 sont les rayons de chaque étoile.
sont les rayons de chaque étoile.
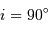 , les deux éclipses sont centrales, l'une étant totale (quand la plus grosse passe devant la plus petite), l'autre étant annulaire. On remarquera par ailleurs que lorsqu'il y a éclipse totale les minima de la courbe de lumière montrent un plateau, qui correspond à la durée effective de totalité de l'éclipse ou de l'occultation.
, les deux éclipses sont centrales, l'une étant totale (quand la plus grosse passe devant la plus petite), l'autre étant annulaire. On remarquera par ailleurs que lorsqu'il y a éclipse totale les minima de la courbe de lumière montrent un plateau, qui correspond à la durée effective de totalité de l'éclipse ou de l'occultation.
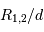 .
.




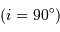 dont les orbites sont circulaires. La courbe de lumière correspond à la figure ci-dessus. Soient
dont les orbites sont circulaires. La courbe de lumière correspond à la figure ci-dessus. Soient 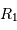 et
et 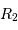 les rayons des deux étoiles,
les rayons des deux étoiles, 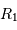 étant le rayon de la plus grosse. On notera
étant le rayon de la plus grosse. On notera 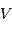 la vitesse relative du mouvement orbital de la plus petite par rapport à la plus grosse.
la vitesse relative du mouvement orbital de la plus petite par rapport à la plus grosse.
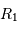 et
et 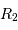 en fonction des dates
en fonction des dates 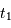 ,
, 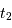 ,
, 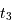 et
et 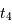 et de la vitesse relative des deux étoiles.
et de la vitesse relative des deux étoiles.
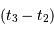 ,
, 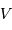 ,
, 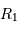 et
et 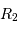 ; puis entre
; puis entre 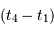 ,
, 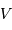 ,
, 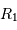 et
et 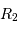 .
.
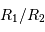 .
.
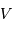 est de 200 km/s. Calculer
est de 200 km/s. Calculer 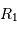 ,
, 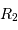 et la distance
et la distance 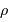 entre les deux étoiles.
entre les deux étoiles.
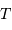 et la durée du transit
et la durée du transit 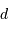 .
.

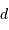 d'un transit varie comme
d'un transit varie comme 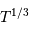 .
.
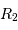 est le rayon de la plus petite étoile, les deux minima se produisent lorsque la même aire
est le rayon de la plus petite étoile, les deux minima se produisent lorsque la même aire 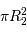 est occultée. Lorsque l'aire occultée appartient à l'étoile la plus chaude, de température
est occultée. Lorsque l'aire occultée appartient à l'étoile la plus chaude, de température 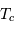 , la courbe de lumière passe par son minimum principal. De même, lorsque la surface occultée appartient à l'étoile la plus froide, de température
, la courbe de lumière passe par son minimum principal. De même, lorsque la surface occultée appartient à l'étoile la plus froide, de température 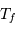 , la courbe de lumière passe par son minimum secondaire. Ainsi, si
, la courbe de lumière passe par son minimum secondaire. Ainsi, si 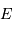 est l'éclat apparent correspondant à la phase où les deux étoiles sont visibles simultanément et sans occultation,
est l'éclat apparent correspondant à la phase où les deux étoiles sont visibles simultanément et sans occultation, 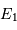 l'éclat du minimum principal et
l'éclat du minimum principal et 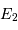 celui du minimum secondaire, on a :
celui du minimum secondaire, on a :
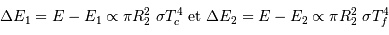
![{\Delta E_1 \over \Delta E_2} = \frac{E-E_1}{E-E_2} = \left[ \frac{T_c}{T_f}\right]^4](../pages_eclipses/equations_binaires-temperatures/equation9.png)
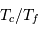 .
.



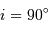 et que les orbites sont circulaires.
et que les orbites sont circulaires.
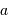 mesurant la séparation des deux étoiles,
mesurant la séparation des deux étoiles, 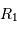 le rayon de la plus grosse,
le rayon de la plus grosse, 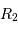 celui de la plus petite, déterminer
celui de la plus petite, déterminer 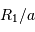 et
et 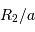 à partir de la figure.
à partir de la figure.
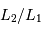 des deux étoiles. Commenter.
des deux étoiles. Commenter.
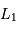 de l'étoile 1 et celle
de l'étoile 1 et celle 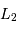 de l'autre composante en unité solaire (la magnitude absolue visuelle
de l'autre composante en unité solaire (la magnitude absolue visuelle 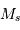 du Soleil vaut 4.8).
du Soleil vaut 4.8).
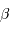 Aurigae. Les positions de ces raies, en longueur d'onde, varient au cours du temps, témoins de la variation de la vitesse radiale de chaque composante, par suite de leur mouvement orbital relatif.
Aurigae. Les positions de ces raies, en longueur d'onde, varient au cours du temps, témoins de la variation de la vitesse radiale de chaque composante, par suite de leur mouvement orbital relatif.



 de l'orbite sur le ciel n'est pas nulle, produit des variations périodiques de la vitesse radiale (vitesse projetée le long de la ligne de visée) des deux étoiles par rapport à l'observateur. L'effet
de l'orbite sur le ciel n'est pas nulle, produit des variations périodiques de la vitesse radiale (vitesse projetée le long de la ligne de visée) des deux étoiles par rapport à l'observateur. L'effet 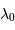 observée des raies émises à
observée des raies émises à 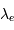 par le couple d'étoiles.
par le couple d'étoiles.
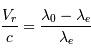
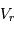 est la vitesse radiale d'une des composantes et
est la vitesse radiale d'une des composantes et 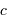 est la vitesse de la lumière.
est la vitesse de la lumière.
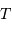 est un peu inférieure à 3 jours.
est un peu inférieure à 3 jours.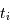 , estimer une phase du type
, estimer une phase du type 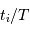 .
.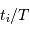 (fonction
(fonction 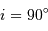 (le plan de l'orbite contient la ligne de visée). Les deux courbes de vitesse radiale sont alors des sinusoïdes qui oscillent en opposition de phase, autour de la vitesse
(le plan de l'orbite contient la ligne de visée). Les deux courbes de vitesse radiale sont alors des sinusoïdes qui oscillent en opposition de phase, autour de la vitesse 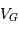 de leur barycentre, avec une même période
de leur barycentre, avec une même période 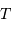 .
.
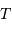 autour de G, les vitesses
autour de G, les vitesses 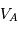 et
et 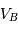 sont liées aux distances
sont liées aux distances 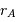 et
et 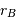 par les relations :
par les relations :
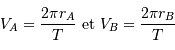
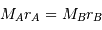 . On obtient alors le rapport des masses :
. On obtient alors le rapport des masses :
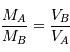
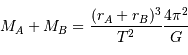
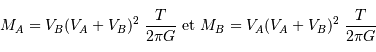
 est différente de
est différente de 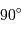 , l'amplitude de la courbe de vitesse radiale est diminuée d'un facteur
, l'amplitude de la courbe de vitesse radiale est diminuée d'un facteur 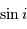
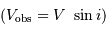 .
.
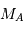 est donc remplacé par
est donc remplacé par 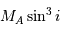 (respectivement
(respectivement 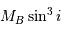 ).
).
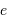 non nulle, les courbes de vitesse radiale ne sont pas sinusoïdales, bien que toujours en opposition de phase et avec un rapport d'amplitude égal au rapport des masses.
non nulle, les courbes de vitesse radiale ne sont pas sinusoïdales, bien que toujours en opposition de phase et avec un rapport d'amplitude égal au rapport des masses.
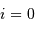 ?
?
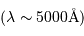 de l'ordre de
de l'ordre de 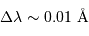 .
.
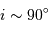 est vraie ou non ?
est vraie ou non ?



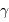 Ceph,
Ceph, 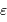 Eri)... En 1989, Latham et ses collègues identifièrent un compagnon d'environ dix fois la masse de Jupiter, autour de HD 114762. Mais ces auteurs évoquèrent alors la détection d'une
Eri)... En 1989, Latham et ses collègues identifièrent un compagnon d'environ dix fois la masse de Jupiter, autour de HD 114762. Mais ces auteurs évoquèrent alors la détection d'une 


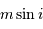 , l'inclinaison
, l'inclinaison  n'étant pas une
n'étant pas une 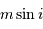 plus petits que la masse de Jupiter, et la distribution totale jusqu'à 15 masses de Jupiter.
plus petits que la masse de Jupiter, et la distribution totale jusqu'à 15 masses de Jupiter.

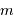 , mais de
, mais de 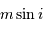 .
.








 est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.

 est nul. Pas de mouvement détectable.
est nul. Pas de mouvement détectable.

 vaut
vaut 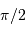 .
.
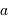 .
.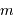 la masse de la planète, et
la masse de la planète, et 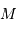 celle de l'étoile.
celle de l'étoile. . Mais une variable reste inconnue :
. Mais une variable reste inconnue : 
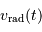 .
Ce type d'observation spectrométrique fournit deux
.
Ce type d'observation spectrométrique fournit deux 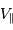 , parallèle à l'axe de visée (car
, parallèle à l'axe de visée (car 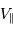 ).
).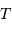 de rotation du système.
de rotation du système.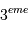 loi de Kepler appliquée au couple planète-étoile relie le rayon de l'orbite à la période de rotation :
loi de Kepler appliquée au couple planète-étoile relie le rayon de l'orbite à la période de rotation :
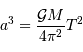
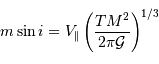
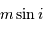 est la masse de la planète
est la masse de la planète 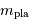 affectée du facteur
géométrique
affectée du facteur
géométrique 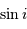 , inconnu.
Le calcul complet est proposé en
, inconnu.
Le calcul complet est proposé en  dépend de l'ouverture du cône de demi-angle au sommet
dépend de l'ouverture du cône de demi-angle au sommet  : elle vaut
: elle vaut 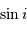 .
La probabilité de voir un système
.
La probabilité de voir un système 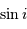 vaut
vaut 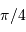 ;
ce calcul est proposé en
;
ce calcul est proposé en 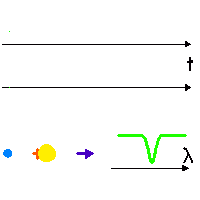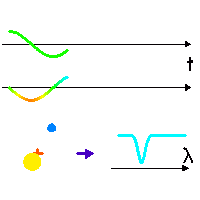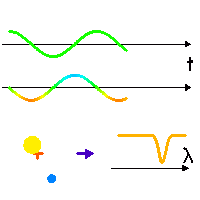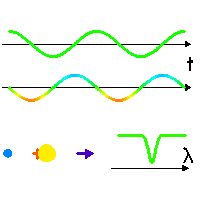
 est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
est défini entre la normale au plan de la trajectoire (vu par la tranche, trace rouge) et l'axe de visée.
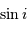 qui intervient dans la détermination de la masse
qui intervient dans la détermination de la masse 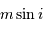 .
.
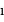 .
.
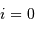 ou bien
ou bien
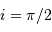 ?
?
 ou
ou 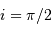 ?
?
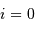 ou
ou 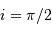 ?
?
 est proportionnelle à
est proportionnelle à 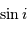 .
.
 , et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture
, et pour cela estimer
l'angle solide compris entre les cônes centrés sur l'axe de visée
et d'ouverture  et
et 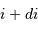 .
.
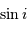 .
.
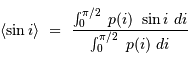
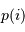 la loi de probabilité associée.
la loi de probabilité associée.
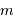 , en orbite circulaire autour d'une étoile de masse
, en orbite circulaire autour d'une étoile de masse 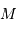 . La composante de vitesse de l'étoile
. La composante de vitesse de l'étoile 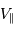 , parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse
, parallèle à l'axe de visée, ainsi que la période de rotation du système découlent de l'observation. La masse 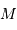 de l'étoile est supposée connue.
de l'étoile est supposée connue.

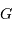 ,
, 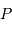 et
et 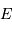 les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
les positions du barycentre du système, du centre de masse de la planète et du centre de masse de l'étoile.
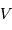 de l'étoile et
de l'étoile et 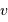 de la planète satisfont à la relation :
de la planète satisfont à la relation :
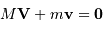
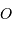 du système obéit à:
du système obéit à:
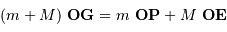
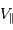 au module
au module 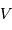 de la vitesse de l'étoile et à l'angle
de la vitesse de l'étoile et à l'angle  entre l'axe de visée et la normale au plan de rotation du système. Faire un schéma.
entre l'axe de visée et la normale au plan de rotation du système. Faire un schéma.
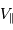 dans les cas
dans les cas  nul ou angle droit.
nul ou angle droit.
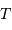 et
et 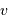 , puis montrer que la masse de la planète s'exprime en fonction des
, puis montrer que la masse de la planète s'exprime en fonction des 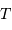 et
et 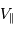 par :
par :
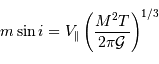
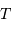 la variable
la variable 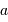 , et montrer que l'on aboutit à l'égalité suivante entre les variables
, et montrer que l'on aboutit à l'égalité suivante entre les variables 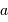 et
et 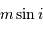 :
:
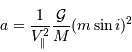
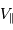 . On obtient une série temporelle de vitesse radiale, qui
semble présenter des variations répétitives.
. On obtient une série temporelle de vitesse radiale, qui
semble présenter des variations répétitives.





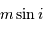 , car l'angle sous lequel
le système est observé,
, car l'angle sous lequel
le système est observé,  , reste en général inconnu. Cela a bien sûr
été un obstacle à l'interprétation du premier cas qui annonçait la
découverte d'une d'exoplanète. Cependant, une centaine d'objets avec
une masse
, reste en général inconnu. Cela a bien sûr
été un obstacle à l'interprétation du premier cas qui annonçait la
découverte d'une d'exoplanète. Cependant, une centaine d'objets avec
une masse 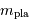 les rangeant dans la catégorie des planètes ont
été détectés, et, statistiquement, la masse réelle de la plupart
d'entre eux est bien une masse planétaire.
Cette méthode est biaisée, car elle favorise la détection des planètes
massives et relativement proches de leur étoile. En effet :
les rangeant dans la catégorie des planètes ont
été détectés, et, statistiquement, la masse réelle de la plupart
d'entre eux est bien une masse planétaire.
Cette méthode est biaisée, car elle favorise la détection des planètes
massives et relativement proches de leur étoile. En effet :
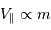 .
.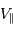 important, car
important, car 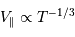 .
.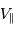 sous la forme :
sous la forme :
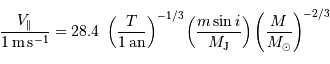
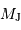 et
et 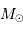 sont, respectivement, les masses de Jupiter et du Soleil.
sont, respectivement, les masses de Jupiter et du Soleil.
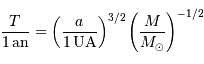
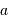 est exprimé en unité astronomique.
est exprimé en unité astronomique.

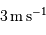 . Il faut également observer les étoiles longtemps pour avoir accès aux plus longues périodes. Les exoplanètes les moins massives n'ont pas été détectées par mesure Doppler, mais par la méthode des
. Il faut également observer les étoiles longtemps pour avoir accès aux plus longues périodes. Les exoplanètes les moins massives n'ont pas été détectées par mesure Doppler, mais par la méthode des 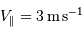 . Cela ne signifie qu'une planète similaire à la Terre autour d'une étoile de type solaire induisant une modulation de vitesse
. Cela ne signifie qu'une planète similaire à la Terre autour d'une étoile de type solaire induisant une modulation de vitesse 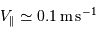 reste largement indétectable.
reste largement indétectable.
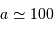 UA. Cependant, la période de révolution d'une telle planète est de 1000 ans, et il est donc exclu de l'observer ! Notons que la même planète située à la distance de Jupiter
UA. Cependant, la période de révolution d'une telle planète est de 1000 ans, et il est donc exclu de l'observer ! Notons que la même planète située à la distance de Jupiter 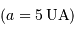 entraîne
entraîne 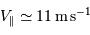 , ce qui est largement observable.
, ce qui est largement observable.
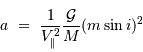
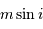 - rayon orbital
- rayon orbital 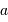 ) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse
) est utile afin de déterminer quel type de planète est détectable par vélocimétrie Doppler. La masse 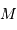 de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.
de l'étoile étant de l'ordre d'une masse solaire, le champ de planètes détectables dépend essentiellement de la sensibilité des instruments de recherche.

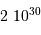
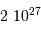
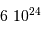
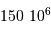 km
km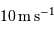 . En déduire la relation numérique entre les variables
. En déduire la relation numérique entre les variables 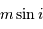 et
et 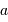 correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et
correspondant à la limite de détection, et pour une étoile d'une masse solaire. Exprimer le résultat en UA et 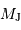 .
.
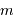 , et l'unité astronomique pour
, et l'unité astronomique pour 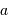 .
Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de
.
Quelles planètes de notre système solaire sont détectables au vu de cette ancienne performance de 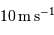 ) ?
) ?
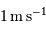 .
.





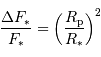
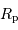 est le rayon de la planète et
est le rayon de la planète et 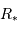 celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en
celui de l'étoile. On suppose ici que le flux était uniforme à la surface de l'étoile (le détail du calcul est traité en 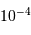 pour un système tel que Soleil-Terre.
pour un système tel que Soleil-Terre.
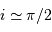 . La masse
. La masse 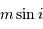 est donc dans ce cas égale à la masse réelle
est donc dans ce cas égale à la masse réelle 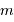 . Le transit permet également de déterminer le rayon de la planète, le rayon de l'étoile étant estimé par une autre méthode.
. Le transit permet également de déterminer le rayon de la planète, le rayon de l'étoile étant estimé par une autre méthode.


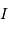 :
:
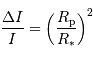
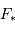 uniforme :
uniforme :
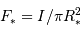 .
.
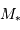
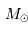
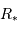
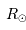
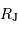
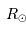

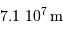
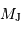
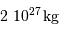
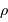 de l'exoplanète, sachant que sa masse
de l'exoplanète, sachant que sa masse 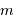 vaut
vaut 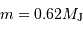 . Quelle remarque vous inspire ce résultat ?
. Quelle remarque vous inspire ce résultat ?




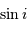 , ont été observées par le satellite
, ont été observées par le satellite 

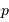 est obtenue par le rapport de l'aire balayée par la planète à l'aire de la sphère de rayon égal au demi-grand axe planétaire :
est obtenue par le rapport de l'aire balayée par la planète à l'aire de la sphère de rayon égal au demi-grand axe planétaire : 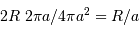 .
.
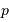 d'un tel événement vaut
d'un tel événement vaut 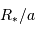 ,
, 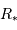 étant le rayon stellaire, et
étant le rayon stellaire, et 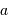 le demi-grand axe de l'orbite planétaire. Ce résultat est démontré par un calcul complet en
le demi-grand axe de l'orbite planétaire. Ce résultat est démontré par un calcul complet en 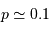 pour
pour 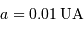 , c'est-à-dire pour les planètes détectées à ce jour qui sont sur les orbites les plus serrées. Cette probabilité décroît avec l'augmentation du demi-grand axe.
, c'est-à-dire pour les planètes détectées à ce jour qui sont sur les orbites les plus serrées. Cette probabilité décroît avec l'augmentation du demi-grand axe.
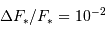 ) en raison de l'
) en raison de l'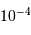 , et donc de détecter des planètes de type
, et donc de détecter des planètes de type 
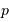 d'un tel événement, fonction du rayon de l'étoile
d'un tel événement, fonction du rayon de l'étoile 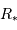 et du rayon orbital de la planète
et du rayon orbital de la planète 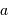 , et d'établir
, et d'établir 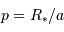 .
. de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum
de visée est défini comme l'angle entre la normale au plan de révolution de l'orbite et la ligne de visée.
Exprimer l'angle maximum 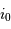 pour lequel une éclipse peut être observée, en fonction de
pour lequel une éclipse peut être observée, en fonction de 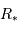 et
et 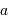 , en supposant le rayon planétaire négligeable.
, en supposant le rayon planétaire négligeable.
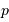 .
.
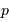 de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet
de détecter un transit est égale à la probabilité que la ligne de visée ne se trouve pas dans le demi-cône d'axe perpendiculaire au plan de l'orbite et de demi-angle au sommet 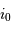 .
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet
.
Calculer la mesure de l'angle solide d'un hémisphère et d'un cône de demi-angle au sommet 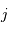 .
.
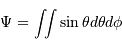
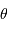 et
et 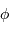 les angles d'Euler.
les angles d'Euler.
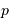 en fonction de
en fonction de 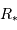 et
et 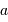 .
.
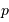 mesure la non-appartenance au cône précédemment
défini.
mesure la non-appartenance au cône précédemment
défini.
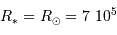 km, et
km, et 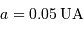 .
.

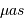 ). Le déplacement dû à la Terre présenterait une amplitude de
). Le déplacement dû à la Terre présenterait une amplitude de 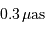 à la même distance.
à la même distance.
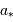 . Comme
la distance
. Comme
la distance 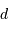 à l'étoile est grande devant
à l'étoile est grande devant 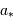 , la déviation
angulaire correspondante est
, la déviation
angulaire correspondante est 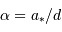 , ou encore :
, ou encore :
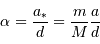
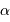 exprimé
seconde d'arc,
exprimé
seconde d'arc, 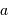 le
rayon de l'orbite de la planète (en UA) et
le
rayon de l'orbite de la planète (en UA) et 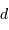 la distance
Soleil-étoile. La masse
la distance
Soleil-étoile. La masse 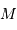 de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire
de l'étoile et sa distance à la Terre
étant connues par ailleurs, on peut déduire 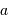 de la périodicité du
mouvement, et donc la masse de la planète
de la périodicité du
mouvement, et donc la masse de la planète 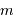 de la mesure de
de la mesure de 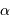 .
.

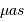 dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des
dans le futur proche sur des champs d'observation réduits. Il ne sera donc pas possible de détecter des planètes semblables à la Terre, orbitant dans des 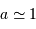 UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
UA), puisque les étoiles observées sont à une distance d'au moins quelque parsecs de la Terre. L'astrométrie est plus adaptée à la détection de planètes géantes et de rayon orbital grand.
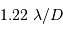 radian, où
radian, où 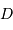 est le diamètre du télescope.
est le diamètre du télescope.
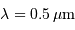 .
.
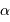 entre le soleil et Jupiter
entre le soleil et Jupiter 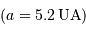 .
.
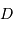 , le diamètre minimum du collecteur nécessaire.
, le diamètre minimum du collecteur nécessaire.
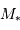 et d'une planète de masse
et d'une planète de masse  ( avec
( avec 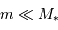 ) de rayon orbital
) de rayon orbital 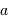 .
.
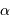 de la position de l'étoile, située à une distance
de la position de l'étoile, située à une distance 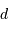 du Soleil.
du Soleil.
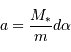
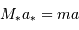
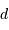 se situe l'étoile si sa
se situe l'étoile si sa 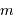 et de leur demi-grand axe
et de leur demi-grand axe 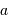 , en définissant la frontière qui marque la limite de détectabilité
(rappel
, en définissant la frontière qui marque la limite de détectabilité
(rappel 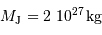 ).
).
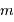 et
et 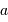 , et l'exprimer dans le système d'unités (UA, masse de Jupiter).
, et l'exprimer dans le système d'unités (UA, masse de Jupiter).
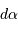 , avec
, avec 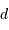 en pc et
en pc et 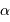 en seconde d'arc, donne directement une distance en UA.
en seconde d'arc, donne directement une distance en UA.
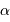 avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme
avec une précision de l'ordre de 50 millionièmes de seconde d'arc. En déduire le domaine observable dans le diagramme 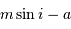 , pour un système à 10 pc et
, pour un système à 10 pc et 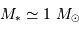 .
.




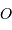 le centre de l'ellipse observée et A l'intersection de la demi-droite [0E) avec l'ellipse. Comme l'excentricité
le centre de l'ellipse observée et A l'intersection de la demi-droite [0E) avec l'ellipse. Comme l'excentricité 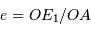 est invariante par projection, le fait que l'étoile primaire soit au foyer de l'orbite projetée montre que le grand axe de l'orbite projetée correspond à la projection du grand axe, ce qui ne peut avoir lieu que si
est invariante par projection, le fait que l'étoile primaire soit au foyer de l'orbite projetée montre que le grand axe de l'orbite projetée correspond à la projection du grand axe, ce qui ne peut avoir lieu que si 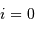 ...
...
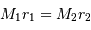 et
et 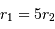 implique un rapport de masse
implique un rapport de masse 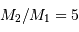
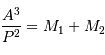
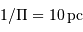 de nous et qu'une unité astronomique y est vue sous un angle de 0,1".
de nous et qu'une unité astronomique y est vue sous un angle de 0,1".
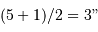 ; le demi-grand axe est donc de 30 UA.
; le demi-grand axe est donc de 30 UA.
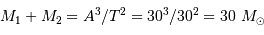 .
.
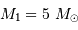 et
et 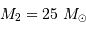
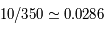
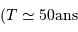 et le demi-grand axe de l'orbite relative
et le demi-grand axe de l'orbite relative 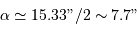
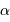 est le demi-grand axe mesuré en secondes d'arc et
est le demi-grand axe mesuré en secondes d'arc et 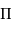 la parallaxe, le demi-grand axe linéaire
la parallaxe, le demi-grand axe linéaire 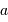 , mesuré en UA est alors égal à
, mesuré en UA est alors égal à 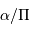 , soit
, soit 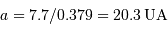 .
.
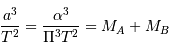
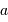 est exprimé en UA,
est exprimé en UA, 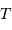 en années, et
en années, et 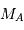 et
et 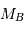 en masse solaire. Ce qui donne :
en masse solaire. Ce qui donne :
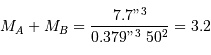
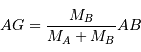
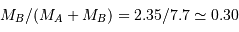 .
.
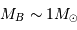 et
et 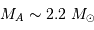 .
.
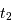 à la position
à la position 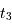 est égal à
est égal à 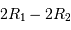 . De la même façon, le trajet de la petite étoile pour aller de la position
. De la même façon, le trajet de la petite étoile pour aller de la position 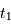 à la position
à la position 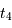 est égal à
est égal à 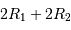 . Si l'on assimile la corde de l'arc de cercle de la trajectoire à une droite, ce qui revient à dire que l'orbite est grande vis à vis des rayons des étoiles, on obtient :
. Si l'on assimile la corde de l'arc de cercle de la trajectoire à une droite, ce qui revient à dire que l'orbite est grande vis à vis des rayons des étoiles, on obtient :
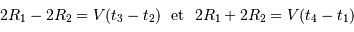
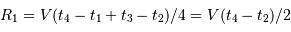 et
et 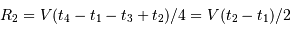
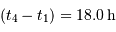 et
et 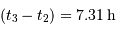 , d'où
, d'où 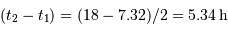 et
et 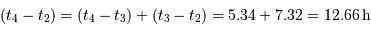 et donc, d'après le résultat de la question précédente :
et donc, d'après le résultat de la question précédente :
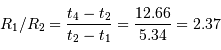
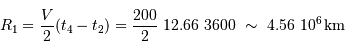
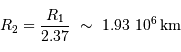
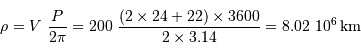
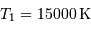 ,
, 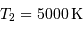 , donc
, donc 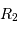 le rayon de la plus froide est égal à 4
le rayon de la plus froide est égal à 4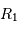 .
.
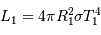 et
et 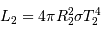 .
.
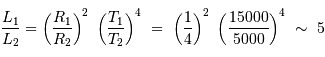
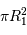 ). Conséquence de la loi de rayonnement du corps noir, le minimum principal correspond donc à l'occultation de l'étoile la plus chaude, ici en l'occurrence, la plus petite...
). Conséquence de la loi de rayonnement du corps noir, le minimum principal correspond donc à l'occultation de l'étoile la plus chaude, ici en l'occurrence, la plus petite...
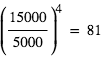
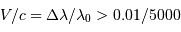
 .
.
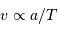 au demi-grand axe s'exprime :
au demi-grand axe s'exprime :
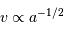
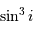 , on obtient bien une limite inférieure pour la masse de chaque composante.
, on obtient bien une limite inférieure pour la masse de chaque composante.
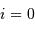 ),
mais une infinité qui la contiennent (
),
mais une infinité qui la contiennent (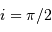 ).
).
 . Son angle solide est
. Son angle solide est 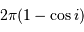 . Le rayon
d'ouverture du cône, proportionnel à
. Le rayon
d'ouverture du cône, proportionnel à 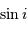 , permet d'estimer
comment la probabilité cherchée varie avec
, permet d'estimer
comment la probabilité cherchée varie avec  .
.
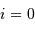 est peu probable.
est peu probable.
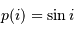 la loi de probabilité, la définition de la valeur moyenne de la variable
la loi de probabilité, la définition de la valeur moyenne de la variable 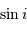 conduit à :
conduit à :
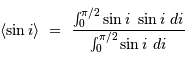
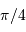 , car il est égal à la moyenne sur le même intervalle, de largeur
, car il est égal à la moyenne sur le même intervalle, de largeur 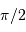 , de
, de 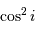 , et que la somme des carrés des sinus et cosinus vaut 1.
, et que la somme des carrés des sinus et cosinus vaut 1.
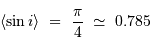
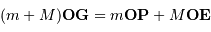 , avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
, avec O, un point fixe quelconque d'un repère galiléen.
PG est la distance de la planète au centre de masse.
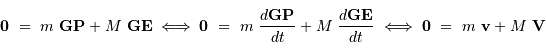
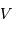 , le module de
, le module de 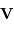 et
et 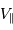 s'écrit :
s'écrit :
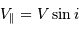
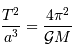
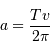
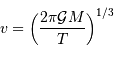
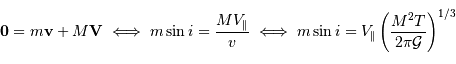
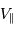 et
et 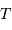 , et de la masse stellaire
, et de la masse stellaire 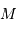 déduite des modèles stellaires, on a accès, au facteur
déduite des modèles stellaires, on a accès, au facteur 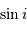 près,
à la masse de la planète... inaccessible par ailleurs.
près,
à la masse de la planète... inaccessible par ailleurs.
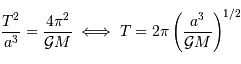
![\Rightarrow m\sin i = V _{\mathrm{\parallel}}\left[{M^{2}\over 2\pi{\cal G}}2\pi\left({a^{3}\over {\cal G}M}\right)^{1/2}\right]^{1/3} = V _{\mathrm{\parallel}}\left({Ma\over {\cal G}}\right)^{1/2}](../pages_exoplanete/equations_vitesse-radiale-extrasolaire/equation105.png)
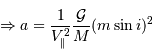
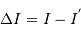 avec
avec 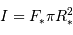 , et
, et 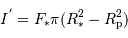 . Donc :
. Donc :
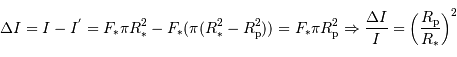
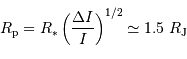
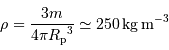
 ). C'est une géante gazeuse. Et si l'on trouvait un océan suffisamment grand, la planète y flotterait ...
). C'est une géante gazeuse. Et si l'on trouvait un océan suffisamment grand, la planète y flotterait ...
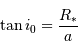
 .
.
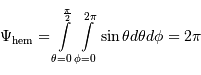
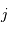 :
:
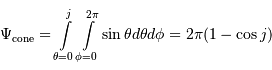
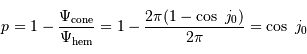
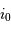 et
et 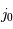 sont complémentaires :
sont complémentaires : 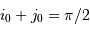 . On en tire :
. On en tire :
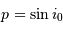
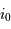 est petit, et l'on peut le confondre avec son sinus ou sa tangente.
est petit, et l'on peut le confondre avec son sinus ou sa tangente.
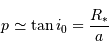
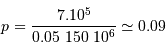
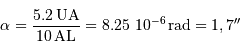
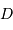 du collecteur est atteint lorsque la tache de diffraction est égale la distance angulaire maximum
du collecteur est atteint lorsque la tache de diffraction est égale la distance angulaire maximum 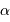 entre le soleil et Jupiter :
entre le soleil et Jupiter :
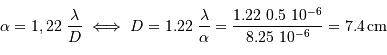
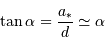
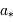 étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
étant la distance du centre de l'étoile au centre de masse du système (étoile-planète)
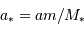 . Alors :
. Alors :
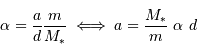
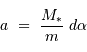
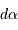 , avec
, avec 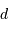 en pc et
en pc et 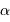 en " donne une distance en UA directement, par définition. En prenant
en " donne une distance en UA directement, par définition. En prenant 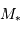 directement en masse jovienne (
directement en masse jovienne (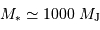 ), on obtient dans le système d'unités (UA,
), on obtient dans le système d'unités (UA, 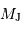 ), pour
), pour 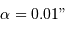 :
:
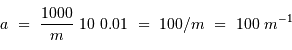
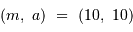 .
.
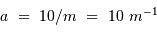
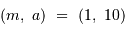 .
.

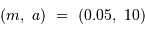 .
.

