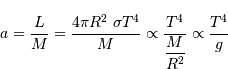Evolution stellaire
Auteur: B. Mosser
- Introduction
- Gravitation, pression et température
- Introduction
- Le gaz parfait
- La compression gravitationnelle au centre d'une étoile
- Observer
- Apprendre
- Simuler
- S'exercer
- Pression cinétique, pression de dégénérescence, pression de radiation
- Apprendre
- Simuler
- S'exercer
- Énergie potentielle d'interaction gravitationnelle
- Observer
- Apprendre
- S'exercer
- Accrétion et réchauffement
- Observer
- Apprendre
- S'exercer
- Théorème du viriel
- Observer
- Apprendre
- S'exercer
- S'évaluer
- Naissance des étoiles
- Introduction
- Le milieu interstellaire
- Observer
- Apprendre
- Simuler
- S'exercer
- Critère de Jeans
- Observer
- Apprendre
- S'exercer
- S'évaluer
- Constantes de temps
- Apprendre
- S'exercer
- S'évaluer
- Disques
- Amas d'étoiles
- Observer
- Apprendre
- S'évaluer
- Vie
- Introduction
- Fusion nucléaire
- Observer
- Apprendre
- S'exercer
- Masse d'une étoile
- Apprendre
- S'exercer
- S'évaluer
- Relation masse-luminosité
- Apprendre
- Simuler
- S'exercer
- S'évaluer
- Finalement, qu'est-ce qu'une étoile ?
- Observer
- Apprendre
- S'évaluer
- Mort des étoiles
- Introduction
- Après la séquence principale
- Naine blanche
- Observer
- Apprendre
- S'évaluer
- Masse de Chandrasekhar
- Etoile à neutrons
- Supernova
- Trou noir
- Etoiles massives et nucléosynthèse
- Evolution
- Introduction
- Evolution stellaire dans le diagramme HR
- Apprendre
- Simuler
- S'évaluer
- Age des amas
Introduction
Le but de ce sous-chapitre est de présenter différents outils qui permettent de comprendre les bases de l'évolution des étoiles, avec de la physique simple et juste.
Simplicité et justesse n'impliquent malheureusement pas la précision nécessaire
pour rendre compte des phénomènes observées. Elles donnent néanmoins des idées qualitativement correctes, quantitativement raisonnables, que l'on sera amener à préciser en tenant compte des résultats obtenus par des moyens autrement plus précis... mais impossibles à présenter dans ce cours.
La première section introduit des notions physiques utiles pour la suite, dont une est essentielle : la compression gravitationnelle.
En 3 étapes sont ensuite abordées la naissance, la vie et la mort des étoiles, essentiellement sous l'angle des processus physiques à l'oeuvre. La dernière section introduit les résultats de physique stellaire induits par les processus précédemment décrits, pour décrire l'évolution stellaire à partir de modélisations plus précises.
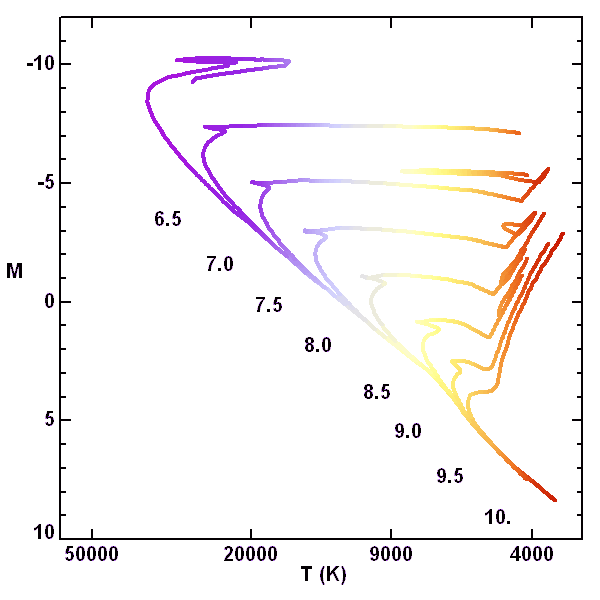
Isochrones stellaires. L'axe vertical est le logarithme de l'âge en milliard d'années.
Crédit :
ASM
Gravitation, pression et température
Auteur: B. Mosser
Introduction
Différents éléments physiques sont introduits, qui vont conduire à comprendre dans quelles conditions fonctionne une étoile, et à montrer le rôle crucial de la gravitation.
C'est la masse de l'étoile qui pilote son évolution, mais il n'y a pas incohérence avec le plan total du cours ; on entre dans un domaine où la masse, si elle conditionne l'essentiel, n'explique pas tout. On est bien... dans le chapitre Température.

La nébuleuse de la Tête de Cheval, dans la constellation d'Orion à 1500 AL du Soleil, regroupe les différents ingrédients intervenant lors de la genèse stellaire : région dense de gaz et de poussières, région d'hydrogène ionisé HII, étoiles en cours de formation.
Crédit :
ESO
Le gaz parfait
Apprendre
 Prérequis
Prérequis
Éléments de théorie cinétique du gaz parfait.
Gaz parfait 
Gaz parfait
Rappel : un gaz est dit parfait si les interactions entre particules se réduisent à des chocs élastiques.
Pour un gaz parfait usuel, non dégénéré (c'est à dire non soumis à des effets quantique) et classique (c'est à dire non relativiste), l'équation d'état s'écrit :
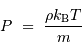
avec 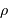 la masse volumique, et
la masse volumique, et 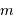 la masse d'une particule élémentaire du gaz.
la masse d'une particule élémentaire du gaz.
Un gaz parfait est dit chaud s'il est dominé par l'agitation thermique. Les effets quantiques sont dans ce cas négligeables.
Un gaz parfait est dit froid lorsque les effets thermiques ne
jouent plus aucun rôle. Son incompressibilité provient du
tassement de la matière : les cortèges électroniques se repoussent
en raison de la nature quantique (fermionique) des électrons.
Température
Pour que la température d'un système soit définie, il faut que ce système soit à l'équilibre, et que ses composantes échangent assez d'informations, via des collisions, pour se thermaliser.
Dans un milieu non collisionnel, il y a peu de chances que l'on puisse définir une température qui vaille... mais on ne s'intéresse pas la suite qu'à des milieux à l'équilibre thermodynamique local, où localement la température est bien définie.
Densité particulaire
La densité particulaire est une grandeur couramment utilisée pour mesurer l'abondance de matériau disponible dans un milieu. Elle est comptée en particules (souvent des électrons, ou des atomes ou molécules d'hydrogène) par unité de volume. Par exemple : 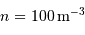 .
.
La compression gravitationnelle au centre d'une étoile
Observer
Autogravitation et forme sphérique
Une étoile présente une forme sphérique, pas évidente à voir vu la petitesse du rayon stellaire devant la distance entre elle et le Soleil. Le disque stellaire d'une étoile ne peut être imagé que si cette étoile est une géante du proche voisinage solaire.
Un noyau de comète, tel celui de la comète de Halley, n'est pas assez massif pour être façonné par sa propre gravitation. Sa forme n'est pas sphérique.
Atmosphère de Bételgeuse

Atmosphère de l'étoile supergéante rouge Bételgeuse. Cette géante
rouge, de diamètre 800 fois celui du Soleil, est suffisamment
proche (130 pc) pour que son disque puisse être imagé.
Crédit :
HST
Noyau de la comète de Halley

Noyau de la comète de Halley, vue en 1986 par la sonde européenne Giotto, lors d'un survol à 600 km (mais avec une vitesse relative de 70 km/s. Ce noyau cométaire n'est pas assez massif pour acquérir une forme sphérique.
Crédit :
ESA
Apprendre
 Objectifs
Objectifs
Exprimer sous forme d'une pression (la pression centrale) l'autogravitation d'une étoile.
Autogravitation
On qualifie d'autogravitant un objet soumis à sa propre gravitation et façonné par elle. Le Soleil, la Terre sont des objets autogravitants. Toi, lecteur, tu n'es pas un objet auto-gravitant (tout au plus sujet à un peu d'embonpoint).
Rien n'interdit à un objet autogravitant de graviter autour d'un autre astre, comme la Terre autour du Soleil ou la Lune autour de la Terre.
Un objet autogravitant est de forme sphérique si sa rotation propre n'est pas trop importante, ou ovoïde aplatie dans le cas contraire.
Équilibre
Comme cette pression rend compte de l'interaction gravitationnelle, attractive, on l'appellera par la suite compression. Il va falloir lui trouver, au sein d'un astre, une contrepartie répulsive pour assurer l'équilibre d'une étoile.
Simuler
Rotation et aplatissement
La rotation de Saturne est suffisamment rapide pour conduire à un aplatissement sensible.
Le mesurer à l'aide de l'appliquette ci-contre, en déterminant le rapport 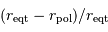 .
.
Montrer que l'inclinaison sous laquelle on voit la planète, estimée à partir des anneaux, ne perturbe pas significativement la mesure précédente.
Saturne 
S'exercer
 Compression gravitationnelle
Compression gravitationnelle
Difficulté : ☆☆☆
Temps : 30 min
Le but de l'exercice est d'estimer la constante de proportionnalité de la compression gravitationnelle. Pour dépasser l'approximation d'une masse volumique uniforme, et rendre compte d'une distribution de masse volumique plus piquée vers le centre, tout en gardant des calculs acceptablement légers, on suppose le modèle suivant :
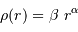 .
.
On s'intéresse à des exposants légèrement négatifs, conduisant à une singularité au centre, qui ne prête pas à conséquence.
Question 1)
Déterminer la relation entre la masse totale 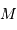 et le rayon extérieur
et le rayon extérieur 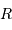 . En déduire l'expression du coefficient
. En déduire l'expression du coefficient 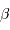 en fonction de ces grandeurs.
en fonction de ces grandeurs.
[2 points]
Pour cette distribution sphérique :
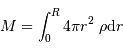
Question 2)
En déduire la masse 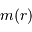 et le champ gravitationnel en un point de rayon
et le champ gravitationnel en un point de rayon 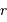 . Quelle condition sur l'exposant
. Quelle condition sur l'exposant 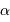 garantit que le champ ne diverge pas ?
garantit que le champ ne diverge pas ?
[2 points]
Pour des calculs plus simples, on écrit :
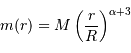
Par définition :
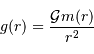
Question 3)
L'équilibre hydrostatique donne le gradient de pression :
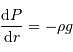
En déduire la pression centrale.
[2 points]
Mener le calcul, du centre vers la surface :
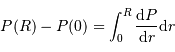
Question 4)
Discuter de la forme du résultat précédent. Que se passe-t-il pour une distribution uniforme ?
[1 points]
Traduire l'uniformité de la masse volumique sur l'exposant 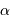 .
.
Est-il normal de retrouver 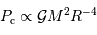 ?
?
 Ainsi fond, fond, fond...
Ainsi fond, fond, fond...
Difficulté : ☆☆
Temps : 30 min
Limbe lunaire : la hauteur des plus hauts reliefs reste petite devant le rayon.

Relief sur le limbe lunaire.
Crédit :
ASM
Le but de cet exercice est de modéliser la hauteur limite d'une montagne sur une planète de masse 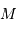 et rayon
et rayon 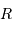 , pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
, pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
On suppose très hardiment la montagne de forme cylindrique, section 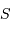 et hauteur
et hauteur 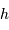 , dans le champ gravitationnel uniforme de la planète.
, dans le champ gravitationnel uniforme de la planète.
Question 2)
En déduire la valeur limite de la hauteur 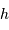 , pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches
, pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches 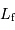 . Faire l'application numérique pour la Terre, avec
. Faire l'application numérique pour la Terre, avec 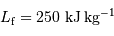 .
.
[2 points]
Comparer les énergies en jeu.
Question 3)
Les plus hautes montagnes atteignent 8.8 km sur Terre (l'Everest) et 27 sur Mars (le Mont Olympe). A l'aide des données du calcotron, vérifier si l'estimation précédente est correcte.
[1 points]
Question 4)
En supposant toujours valable le résultat précédent, et en notant 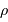 la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de
la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de 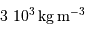 .
.
[2 points]
Ne pas se laisser désarçonner par les hypothèses, qui restent en ordre de grandeur très convenables.
Pression cinétique, pression de dégénérescence, pression de radiation
Apprendre
 Prérequis
Prérequis
Notion de gaz parfait.
 Objectifs
Objectifs
Une étoile peut exister sous réserve d'être dans un état d'équilibre. La compression d'origine gravitationnelle, qui tend à condenser l'étoile, doit être balancée par une autre source de pression : pression cinétique (ou thermique), pression de dégénérescence (ou quantique), pression de rayonnement.
Pression cinétique
Aussi appelée pression thermique, cette pression est celle du gaz parfait chaud. Dans le cas classique, non relativiste, cette pression s'exprime pour un gaz de masse volumique
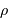 à la température
à la température 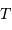 , composé de particules de masse
, composé de particules de masse 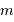 :
:
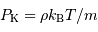
En fonction de la densité particulaire 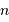 , la définition devient :
, la définition devient :
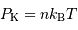
Pression de dégénérescence, ou pression de Fermi, ou pression quantique
La pression de dégénérescence est la pression dans un gaz parfait dit froid. Dans un milieu froid ou dense, les termes cinétiques peuvent devenir négligeables et les interactions entre nuages électroniques des atomes présents prépondérantes. La pression est alors dominée par la pression de dégénérescence 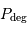 des électrons (s'il y a des électrons).
Ce terme de pression révèle la nature quantique de la matière : les électrons sont des fermions. Quand ces effets quantiques apparaissent, c'est que la densité de matière devient suffisamment importante pour négliger dans un premier temps l'agitation cinétique.
des électrons (s'il y a des électrons).
Ce terme de pression révèle la nature quantique de la matière : les électrons sont des fermions. Quand ces effets quantiques apparaissent, c'est que la densité de matière devient suffisamment importante pour négliger dans un premier temps l'agitation cinétique.
La pression de dégénérescence s'écrit alors (dans le cas non relativiste) :
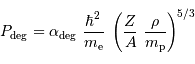
avec 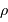 la masse volumique, et
la masse volumique, et 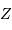 et
et 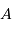 respectivement la charge et le nombre de masse des atomes en présence. La constante
respectivement la charge et le nombre de masse des atomes en présence. La constante 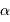 est un nombre : le calcul précis donne
est un nombre : le calcul précis donne 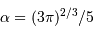 .
.
Dans certains cas, tel l'intérieur d'une étoile à neutrons, il peut ne plus y avoir d'électrons pour assurer la pression. On trouve alors des neutrons, qui sont toujours des fermions, et la pression de dégénérescence des neutrons s'écrit :
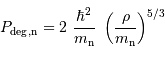
Quel terme de pression domine en fonction de la température ?
La nature est complexe, si bien que ce qui suit n'est pas toujours vrai, mais en général :
- Dans un milieu dense et froid, c'est la pression de dégénérescence qui domine. Ex : au centre de la Terre d'une planète, ou d'une étoile de masse inférieure à 1 masse solaire.
- Dans un milieu plus chaud, la pression cinétique mène la danse. Par exemple : au centre d'une étoile telle le Soleil ou plus massive. La pression de dégénérescence intervient dans les stades ultimes de l'évolution stellaire.
- Ce n'est qu'aux températures extrêmes atteinte au centre des étoiles les plus massives que la pression de radiation l'emporte.
Supporter la gravitation
Dans tous les cas, l'un des 3 termes de pression, ou l'association de 2 d'entre eux, doit permettre d'équilibrer la compression gravitationnelle.
Si, on le verra plus loin, la source énergétique essentielle pour l'étoile adulte, dans la séquence principale, est l'énergie nucléaire, c'est la gravitation qui pilote l'évolution stellaire via la masse de l'objet.
Simuler
S'exercer
 Pression de Fermi
Pression de Fermi
Difficulté : ☆☆☆
Temps : 60 min
Cet exercice a pour but d'expliciter l'expression de la pression de Fermi, qui s'exerce lorsque la nature fermionique des composants est mise en évidence. Comme il s'agit de physique complexe, ce sont seulement les ordres de grandeur qui sont importants.
Question 1)
Rappeler la relation d'incertitude de Heisenberg entre la position 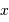 d'une particule sur un axe et sa quantité de mouvement
d'une particule sur un axe et sa quantité de mouvement 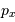 .
.
[1 points]
Question 2)
Relier l'incertitude de position 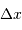 à la densité particulaire
à la densité particulaire 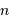 .
.
[1 points]
Faire le lien entre la densité particulaire 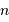 et le volume moyen par particule.
et le volume moyen par particule.
S'intéresser à l'encombrement au sein du gaz, en estimant qu'une particule occupe un volume de l'ordre de 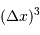 .
.
Question 3)
Montrer que, pour un gaz avec une distribution de vitesse typique, maxwellienne, la distribution de vitesse donne une valeur moyenne et une largeur de distribution du même ordre de grandeur.
[1 points]
La distribution de vitesse maxwellienne varie comme
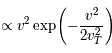 avec
avec 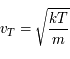
Question 4)
On rappelle que la pression est un flux de quantité de mouvement
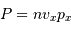
De ce qui précède (en admettant aussi que 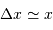 ), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
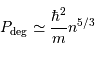
[2 points]
Pour un gaz classique : 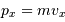 .
.
Éliminer des relations précédentes les variables de quantité de mouvement et de position au profit de la densité particulaire.
Question 5)
Montrer que la pression électronique domine par rapport à la pression des protons.
[1 points]
Comparer les masses en jeu.
Question 6)
En déduire l'expression de la pression de dégénérescence donnée dans le
cours.
[1 points]
Se servir de la neutralité électrique.
L'essentiel de la masse se retrouve dans les nucléons.
Énergie potentielle d'interaction gravitationnelle
Observer

Amas Messier 35 et NGC2158. Tous deux sont des amas ouverts, mais l'un, âgé de 100 millions d'années, présente beaucoup d'étoiles jeunes, lorsque, 6 fois plus distant et 10 fois plus âgé, ne peut plus contenir d'étoiles jeunes.
Crédit :
CFHT
Système lié
L'observation de groupes stellaires formant apparemment un
système lié semble indiquer une origine commune. L'estimation des
énergies cinétique et potentielle permet d'estimer l'énergie
mécanique totale. Si les termes cinétiques dominent, l'amas est
ouvert.
Apprendre
 Objectifs
Objectifs
Mesurer l'énergie que représente l'accrétion d'un corps dense.
Analyse dimensionnelle
On s'intéresse à un corps autogravitant de masse 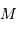 et rayon
et rayon 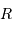 . Quelle énergie peut-on lui associer de par sa gravitation ?
. Quelle énergie peut-on lui associer de par sa gravitation ?
L'analyse dimensionnelle apporte une première réponse à cette question. Avec les caractéristiques de l'objet et la constante gravitationnelle 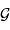 :
:
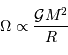
Pour s'en convaincre, il suffit de revenir à la définition de l'interaction gravitationnelle.
Énergie potentielle d'interaction gravitationnelle
Avec un peu de physique, on peut se convaincre d'un supplément d'information :
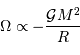
L'interaction en jeu étant attractive, nécessairement l'énergie associée à un corps dense est négative : en effet, pour défaire ce corps, il faudrait lui fournir un travail positif, pour éparpiller très loin chacune de ses particules.
L'énergie potentielle d'interaction gravitationnelle d'un objet est d'autant plus négative qu'il est massif et/ou condensé.
Le calcul complet de cette énergie potentielle est proposé en exercice.
S'exercer
 Calcul de l'énergie potentielle
Calcul de l'énergie potentielle
Difficulté : ☆☆☆
Temps : 45 min
Cet exercice un peu technique s'adresse surtout aux étudiants en licence ou maîtrise scientifique ; sinon, se contenter de suivre l'approche qualitative.
L'exercice s'attelle à la construction d'un objet stellaire. On part de rien. On y met un chouïa de matière, puis un peu plus, puis encore plus, jusqu'à constituer un corps de rayon 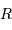 et masse
et masse 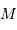 . Dans cette modélisation, on suppose qu'à tout moment la masse volumique
. Dans cette modélisation, on suppose qu'à tout moment la masse volumique 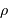 est uniforme.
est uniforme.
Question 1)
On imagine être à une étape intermédiaire caractérisée par un rayon 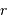 et une masse
et une masse 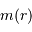 . Déterminer cette masse, ainsi que son champ gravitationnel.
. Déterminer cette masse, ainsi que son champ gravitationnel.
[2 points]
Rappel : la masse volumique est supposée uniforme.
Question 2)
Déterminer le travail d'un opérateur qui amènerait un surcroît de
masse 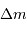 depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
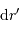 ):
):
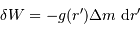
[2 points]
Le travail total est la somme des contributions des travaux de l'infini à la surface de l'objet
Question 4)
En déduire le travail total pour créer le corps, somme de toutes les contributions.
[2 points]
Accrétion et réchauffement
Observer
IC1396 en infrarouge

Nuage interstellaire (dans la nébuleuse IC1396), d'apparence bien développée dans le proche infrarouge, hébergeant de nombreuses étoiles en formation. L'aspect filamentaire provient des effets d'érosion du vent stellaire d'une étoile massive (hors champ, sur la gauche du cliché).
Crédit :
NASA/Spitzer
IC1396 en lumière visible

Même région qu'à la
figure
précédente, mais en lumière visible et non infrarouge.
On y distingue les résidus du nuage interstellaire ayant conduit à
une genèse stellaire. En effet, en lumière visible, les régions
les plus denses du nuage apparaissent totalement obscures, ou
réfléchissant le rayonnement intense des étoiles jeunes
nouvellement formées.
Crédit :
NASA/Spitzer
Contraste
Le milieu interstellaire montre des régions de matière très froide (typiquement 10 K) et très peu dense (quelques particules 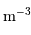 ), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement
), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement 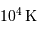 en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement
en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement 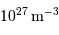 ).
).
Comble du contraste : les étoiles jeunes se situent au sein de ces régions, ou ce qu'il en reste dès lors que le rayonnement de l'étoile parvient à percer.
Apprendre
Etat initial
On suppose le nuage initialement très peu dense et très froid. Il ne possède ni énergie cinétique (il est trop froid), ni énergie potentielle d'interaction (la matière est beaucoup trop diluée). On résume la situation par une énergie mécanique totale quasi nulle (plus précisément : ces énergies sont initialement totalement négligeables par rapport aux énergies cinétiques et potentielles à venir) :
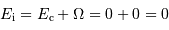
Etat final
Dans un état condensé, l'énergie cinétique qui relate l'agitation thermique n'est plus négligeable. Si 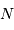 atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de
atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de 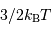 par nucléon :
par nucléon :
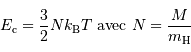
L'énergie potentielle rend compte de la très énergique interaction gravitationnelle des 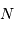 atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours
atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours 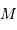 la masse concernée, et
la masse concernée, et 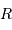 le rayon final de l'objet condensé.
le rayon final de l'objet condensé.
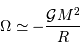
L'énergie totale s'exprime alors :
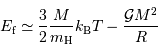
Effondrement et échauffement
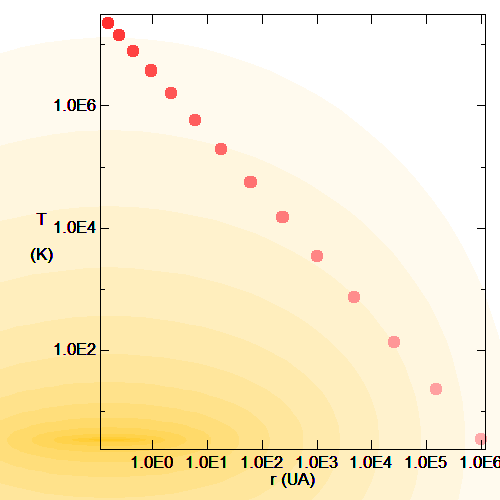
Lorsque le nuage se contracte, il se réchauffe.
Crédit :
ASM
Et la rotation ?
La conservation du moment cinétique et les collisions entre particules conduit à aplatir le système. En effet, par suite des collisions, les composantes de vitesse parallèles au moment cinétique vont peu à peu s'annuler, en gardant une valeur moyenne nulle, quand les vitesses perpendiculaires se thermalisent. Ceci est traité plus en détail à la page consacrée aux disques d'accrétion.
S'exercer
Théorème du viriel
Observer
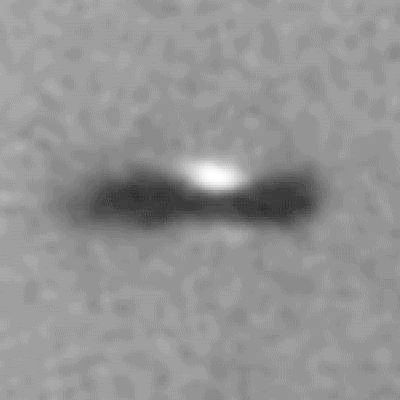
Disque protoplanétaire dans la constellation d'Orion. Au centre du nuage, l'élévation de température conduit à un objet brillant qui commence à rayonner.
Crédit :
HST
Fiat lux
La contraction du nuage l'échauffe en son centre, et donc la proto-étoile se met à rayonner. De l'énergie, initialement sous forme uniquement mécanique, a été convertie en énergie lumineuse.
Apprendre
 Objectifs
Objectifs
Par rapport au modèle d'effondrement purement mécanique, il faut tenir compte du rayonnement de la proto-étoile qui s'effondre et s'échauffe. Le théorème du viriel montre que la moitié seulement de l'énergie gagnée par l'effondrement est convertie en énergie thermique, l'autre moitié est directement rayonnée par l'objet condensé qui se réchauffe.
Conservation de l'énergie
Le modèle étudié précédemment suppose, à juste titre, la conservation de l'énergie, mais à tort que toute cette énergie est sous forme mécanique. Le milieu qui se densifie s'échauffe, et rayonne de l'énergie.
Energie rayonnée
Le théorème du viriel, ici accepté, énonce que l'énergie interne thermique ne représente que la moitié de l'énergie
interne gravitationnelle : un bilan énergétique de l'évolution vers un état à
l'équilibre hydrostatique implique que la moitié de l'énergie interne est évacuée par radiation.
Lors de la formation d'une étoile, il y a échauffement et
obligatoirement perte d'énergie par radiation, à parts égales :
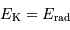 .
.
Conséquence du théorème du viriel
On peut donc réécrire la loi de conservation de l'énergie :
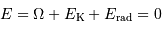
Avec l'égalité entre les énergies rayonnée et cinétique :
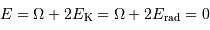
Ceci conduit à une estimation de la température interne de moitié moindre à celle obtenue en omettant l'énergie rayonnée.
Puissance rayonnée
La luminosité de l'étoile est reliée au taux de variation de l'énergie rayonnée :
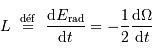
Il s'ensuite que :
- Une proto-étoile brille déjà, avant même d'avoir allumé ses réactions nucléaires.
- Entre 2 états à l'équilibre hydrostatique, une contraction du rayon implique une perte d'énergie par radiation.
Remarques
De manière plus générale, à tout champ de force correspond une forme particulière du viriel.
Pour un champ linéaire (de type ressort), énergies potentielle et cinétique moyennes sont égales. Pour un champ newtonien, elles sont respectivement dans un rapport -2.
S'exercer
 Démonstration du théorème du viriel, dans un cas simplement modélisé
Démonstration du théorème du viriel, dans un cas simplement modélisé
Difficulté : ☆☆☆
Temps : 1 h
Cet exercice a pour but d'établir le théorème du viriel, dans un cas simple. On suppose qu'à tout instant, l'astre, sous forme déjà condensée de rayon 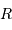 , obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
, obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
Question 1)
Dans le cadre du modèle, avec les notations du cours, on écrit l'énergie cinétique comme une intégrale :
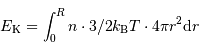 .
Réécrire cette intégrale en fonction de la pression.
.
Réécrire cette intégrale en fonction de la pression.
[1 points]
Il suffit d'introduire l'équation d'état du gaz parfait chaud.
Question 2)
L'équilibre hydrostatique énonce que le gradient de la pression évolue comme :
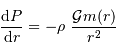
Montrer, à l'aide de cette égalité, que l'énergie gravitationnelle 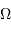 peut s'écrire sous la forme d'une intégrale du gradient de la pression.
peut s'écrire sous la forme d'une intégrale du gradient de la pression.
[3 points]
On peut par exemple commencer par écrire l'énergie potentielle sous forme intégrale
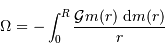
Question 3)
Estimer le lien entre 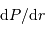 et
et 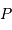 en procédant à l'intégration par parties du terme :
en procédant à l'intégration par parties du terme :
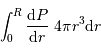
[2 points]
L'intégration par parties donne
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation22.png)
Montrer que l'un des 2 termes de l'intégration par parties est nul.
Question 4)
En déduire l'égalité vérifiée entre 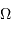 et
et 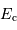 .
.
[2 points]
Tout le travail est fait, il n'y a plus qu'à comparer.
S'évaluer
 Energie d'accrétion
Energie d'accrétion
Difficulté : ☆☆
Temps : 20 min
Le but de cet exercice est d'estimer le rayonnement d'une planète géante encore en train de se contracter. On supposera, dans le cas d'un objet de masse volumique uniforme. L'énergie potentielle est :
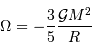
Question 1)
Relier la luminosité de l'objet à sa vitesse de contraction.
[2 points]
La vitesse de contraction est 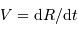 .
.
Par définition, 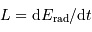 .
.
Le théorème du viriel donne , 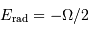 .
.
Question 2)
Quelle puissance rayonne une planète comme Jupiter qui se contracterait de 1 mm/an ? On donne : 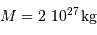 et
et 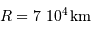 . Comparer le résultat à la puissance lumineuse reçue du Soleil par Jupiter, de l'ordre de
. Comparer le résultat à la puissance lumineuse reçue du Soleil par Jupiter, de l'ordre de 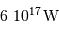 .
.
[1 points]
Naissance des étoiles
Auteur: B. Mosser
Introduction
N'est-il pas émouvant de se pencher sur le berceau de jeunes êtres débutant sur la scène de la vie ?
Cette section s'intéresse aux mécanismes qui expliquent la formation des étoiles. Le critère de Jeans fournit la condition d'effondrement d'un nuage. L'estimation du temps de Kelvin-Helmholtz mesure la durée cette phase, pendant laquelle une étoile se forme et commence à rayonner.
Bien des points sont laissés de côté par cette étude, tels la distribution de masse des étoiles juste formées, la formation de systèmes binaires ou multiples (2 étoiles sur 3 sont dans un système multiple), qui insistent sur les mécanismes physiques de base pour expliquer les grandes étapes de la formation stellaire.
Nébuleuse d'Orion
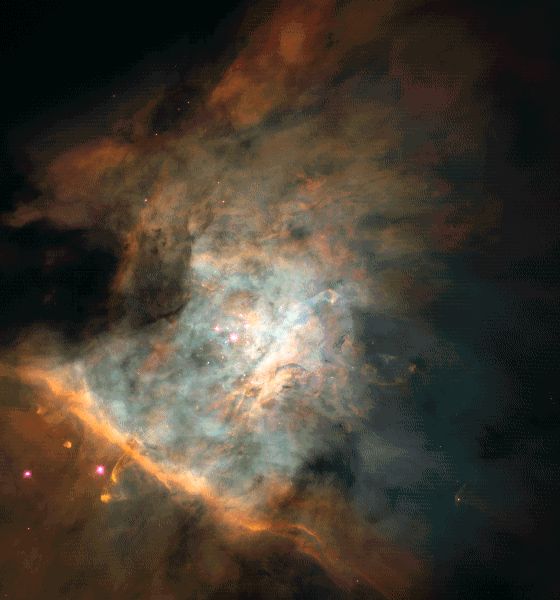
Une pépinière d'étoiles dans la nébuleuse d'Orion.
Crédit :
HST
Le milieu interstellaire
Auteur: Benoît Mosser
Observer

La galaxie dite du sombrero (M104) présente un important disque de poussières. Comme le milieu est fortement collisionnel, sa distribution est essentiellement plane. Seules les étoiles du bulbe, dans un régime non collisionnel, dessinent une distribution sphérique.
Les anneaux de poussières abritent de nombreuses étoiles jeunes et brillantes.
Crédit :
ESO

La galaxie dite du sombrero (M104) vu par le télescope Spitzer. Image composite à partir d'observations à 3.6 (traduit en bleu), 4.5 (vert), 5.8 (orange), and 8.0 (rouge) micromètres. La contribution stellaire des étoiles les plus rouges a été retranchée des images pour mettre en évidence la poussière.
Crédit :
NASA/Spitzer
Le milieu interstellaire
Le milieu interstellaire, bien visible sur un image de
galaxie, contient des poussières et du gaz concentrés dans un disque étroit marquant le plan moyen de la galaxie.
La composante gazeuse est principalement constituée d'hydrogène, l'élément le plus abondant de l'Univers ; ce dernier existe sous forme atomique ou moléculaire. Le gaz interstellaire contient aussi quelques traces d'éléments plus lourds, également sous la forme d'atomes ou de molécules.
La poussière interstellaire, fortement absorbante, correspond à des régions sombres en lumière visible, ou bien brillantes en infrarouge.
Elle se présente sous la forme de grains extrêmement petits, d'une taille typique de l'ordre d'une fraction de micron. La composition chimique de ces grains est variée : graphite, silicates, carbonates.

Région de formation stellaire NGC 6914. Les régions les plus obscurcies correspondent aux parties les plus denses et froides du nuage, qui bloquent le rayonnement visible.
La lumière bleutée de certaines régions provient de la diffusion du flux des étoiles chaudes nouvellement formées. La lumière rouge correspond à la raie atomique
H alpha excitée par ionisation sous le rayonnement UV également dû aux objets jeunes.
Crédit :
CFHT
Régions froides
Les nuages moléculaires ont une masse qui peut se chiffrer en millions de masse solaire. De ce fait, ils contiennent une grande partie de la masse du milieu interstellaire. Leur taille, qui peut dépasser 50 pc (150 années de lumière), s'accompagne d'une densité de l'ordre de la centaine de molécules par centimètre cube, pour une température interne de seulement de 10 K environ.
Principalement constitués de gaz et de poussières, ces nuages moléculaires peuvent héberger des étoiles en formation ou bien juste formées.
Globules de Bok

Globules de Bok dans IC2944.
Crédit :
HST
Globule de Bok
Les étoiles en formation se retrouvent cachées au sein de leur nuage.
Les régions de gaz denses qui hébergent ces nouvelles étoiles apparaissent sombres. On les appelle globules de Bok, du nom de l'astronome qui a imaginé leur rôle.
Un globule de Bok représente typiquement une dizaine de masses solaires, concentrée en environ 1 AL.

Zoom sur la nébuleuse M20. Le nuage non condensé est sculpté par le rayonnement ultraviolet d'étoiles jeunes et massives du voisinage. Les globules de Bok, plus denses, bloquent ce rayonnement, et leur `ombre' protège alors de fines régions du nuage.
Crédit :
HST
Régions ionisées
Le fort rayonnement ultraviolet des étoiles jeunes et chaudes conduit à ioniser le gaz environnant. L'émission est dominée par la raie H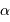 de l'hydrogène, à 656.3 nm. Il en découle la couleur rougeâtre caractéristique de ces régions.
de l'hydrogène, à 656.3 nm. Il en découle la couleur rougeâtre caractéristique de ces régions.
Evolution stellaire
Les différents stades d'évolution stellaire se côtoient couramment. Des globules de Bok avoisinent des régions HII, le tout balayé par le rayonnement des étoiles déjà formées.
Apprendre
 Objectifs
Objectifs
Distinguer les principales composantes du milieu interstellaire (MIS).
Gaz et poussière
Le milieu interstellaire (MIS), composé essentiellement de gaz (99%) et de poussières (1%), se caractérise, loin des sources stellaires, par des températures plutôt froides par rapport aux étoiles et des densités particulaires très faibles. Mais le MIS est intimement associé aux étoiles, soit qu'il en constitue le cocon au sein de laquelle elles se forment et évoluent, soit qu'il corresponde à de la matière éjectée par une étoile en fin de vie.
La principale source de poussières sont les étoiles géantes rouges, sur la branche asympotique. À ce stade d'évolution, ces étoiles synthétisent des éléments lourds, les expulsent par des vents violents, où ces éléments lourds s'agrègent en poussières.
Les nuages protostellaires et les enveloppes circumstellaires peuvent présenter des différences notables. Le but de cette page n'est pas d'en décrire les géographies complexes, mais au-moins de mettre un peu d'ordre. Les composantes sont présentées par densité croissante.
Régions HI
Cette composante du MIS correspond à des régions froides et peu denses essentiellement composés d'hydrogène atomique (forme neutre HI).
Nuages moléculaires
La matière froide et dense y est présente sous forme moléculaire. On y décèle la molécule CO et des poussières, jouant un rôle important dans l'équilibre thermique du nuage.
Régions HII
Aux alentours des étoiles en formation, le gaz est chauffé sous l'action du rayonnement stellaire, et ionisé (forme ionisée HII de l'hydrogène). Les régions HII ne sont pas confinées sous leur propre gravitation, mais en expansion.
Différentes régions
| hydrogène | | densité particulaire 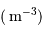 | température (K) |
|---|
| atomique | HI froid | 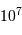 | 100 |
| HI tiède | 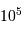 | 8000 |
| moléculaire | | 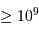 | 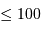 |
|
ionisé | HII | 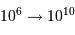 | 10000 |
| diffus | 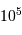 | 10000 |
| chaud | 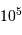 | 500 000 |
Ordre de grandeur de la température et de la densité particulaire.
Simuler


Différentes régions
Les appliquettes ci-jointes décrivent différentes
régions du
milieu interstellaire.

Le nuage Barnard 68 à diverses longueurs d'onde (en bande B, V, I, J, H et K). Les propriétés de l'interaction rayonnement-matière font que ce nuage apparaît d'autant plus absorbant que la longueur d'onde d'observation est courte.
Crédit :
ESO
De l'influence de la longueur d'onde
L'allure d'un nuage dépend de la longueur d'onde d'observation.
S'exercer
 QCM
QCM
Critère de Jeans
Observer

Cet amas sombre, Barnard 68, à 130 pc du Soleil, se détache très
distinctement du fond stellaire en lumière visible. A la limite de
la perte d'équilibre, il est soumis aux perturbation de vents
stellaires et du rayonnement UV de jeunes étoiles. Sa température
est estimée à 16 K, sa masse à 2 masses solaires, pour un diamètre de 12500 UA.
Crédit :
ESO
Hors équilibre
L'estimation des masse, taille et densité d'un
nuage peut dévoiler qu'il
n'est pas à l'équilibre. Sa contraction va conduire à une genèse
stellaire.

Région de formation stellaire dans le Grand Nuage de Magellan.
Crédit :
ESO
Naissance multiple
La formation des étoiles est un phénomène de
groupe. Un nuage
de matière interstellaire donne naissance à de multiples étoiles.
La contraction de ce nuage est un phénomène complexe, dans un
milieu hétérogène, turbulent...
Apprendre
 Objectifs
Objectifs
À quelles conditions un nuage se condense-t-il ? Le critère de Jeans donne une réponse liant la masse ou le rayon limite du nuage à sa densité particulaire et sa température.
Perturbation
Un nuage s'effondre si, perturbé, son énergie mécanique devient négative :
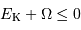
On en déduit une relation sur la masse limite du nuage, fonction de la température (pour l'agitation cinétique) et de la densité (pour la tendance à la contraction). Une masse supérieure à cette masse limite va conduire à la contraction du nuage.
On suppose le milieu homogène et uniforme, et donc le lien entre masse et rayon est simplement 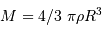 . On en déduit, quand il y a effondrement, l'inégalité sur les énergies cinétique et potentielle :
. On en déduit, quand il y a effondrement, l'inégalité sur les énergies cinétique et potentielle :
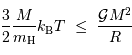
On poursuit le calcul en ne s'intéressant qu'à la dépendance en fonction des variables (ceci permet d'alléger les calculs, et de s'affranchir des constantes numériques qui ne sont de toutes façons pas correctement estimées dans une approche simplifiée). En substituant 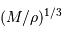 à
à 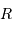 , le cas limite de l'égalité précédente donne une dépendance :
, le cas limite de l'égalité précédente donne une dépendance :
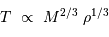
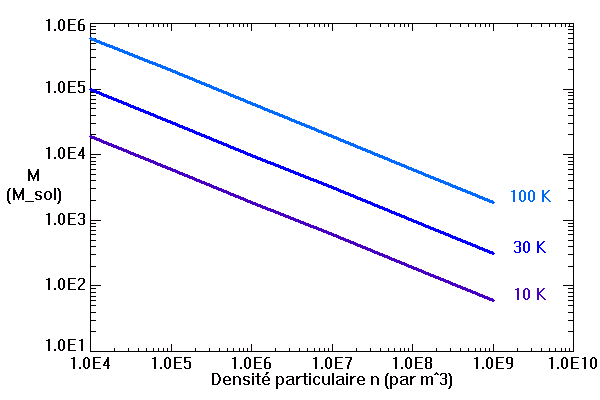
Masse de Jeans, en masse solaire, en fonction de la densité particulaire, pour 3 températures moyennes de nuage.
Crédit :
ASM
Masse de Jeans
On en déduit la masse limite du nuage, appelée masse de Jeans, qui dépend de la température et de la densité du nuage, au-delà de laquelle un nuage est amené à s'effondrer :
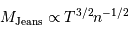
Plus le nuage est chaud, plus il peut être massif avant de s'effondrer : la pression cinétique l'aide à se maintenir. A contrario, plus il est dense, plus la masse de Jeans baisse, en raison d'un potentiel gravitationnel, attractif, croissant avec la masse.
En unité de masse solaire, la masse de Jeans devient :
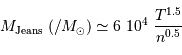
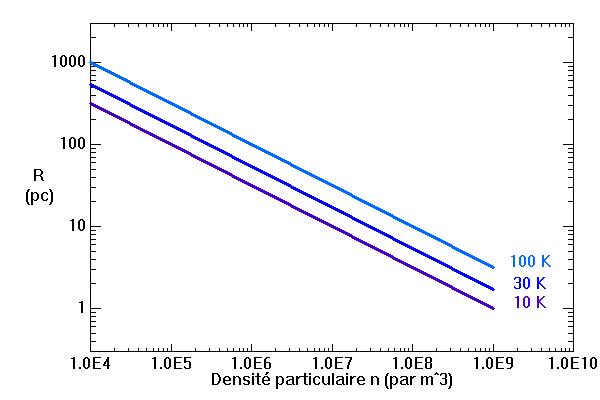
Rayon de Jeans en fonction de la densité particulaire, en parsec.
Crédit :
ASM
Rayon de Jeans
La limite d'effondrement peut également s'exprimer via le rayon du nuage, toujours en fonction de la température du nuage et de sa densité.
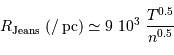
S'exercer
S'évaluer

L'amas Barnard 68 n'est plus opaque dans l'infrarouge.
Crédit :
ESO
 Rayon de Jeans
Rayon de Jeans
Difficulté : ☆
Temps : 20 min
Question 1)
Exprimer le rayon de Jeans en fonction de la masse de Jeans et de la masse volumique d'un nuage.
[2 points]
Question 2)
En déduire comment le rayon de Jeans varie en fonction de la température et de la densité particulaire.
[2 points]
 Barnard 68
Barnard 68
Difficulté : ☆
Temps : 15 min
On s'intéresse au nuage Barnard 68, ici vu en infrarouge. Sa température est estimée à 16 K, sa masse à 2 fois la masse du Soleil, pour un diamètre de 12500 UA.
Question 1)
Déterminer la densité particulaire moyenne du nuage (nombre d'atome H par unité de volume).
[2 points]
Question 2)
En déduire que ce nuage est à la limite de stabilité.
[2 points]
Constantes de temps
Apprendre
 Objectifs
Objectifs
On s'intéresse à différents temps caractéristiques d'un nuage de matière protostellaire. Le temps de chute libre mesure la durée caractéristique de l'accrétion d'un nuage ; le temps de Kelvin-Helmholtz mesure la durée maximale pendant laquelle un objet peut rayonner par simple contraction gravitationnelle.
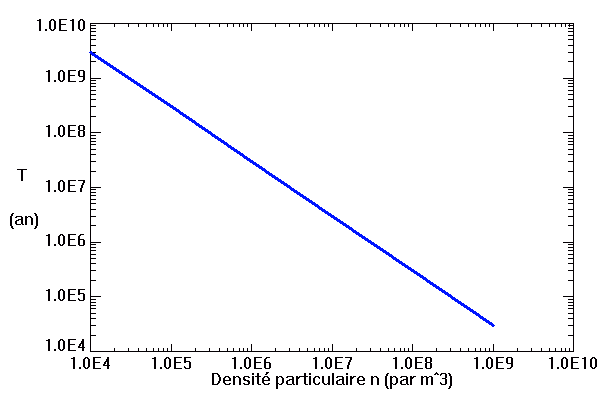
Temps de chute libre, fonction de la densité particulaire d'un nuage.
Crédit :
ASM
Temps de chute libre
En supposant que le nuage s'effondre sans rencontrer de résistance, le temps de chute libre correspond à la durée d'effondrement sous l'effet de l'autogravitation du nuage. Le nuage parcourt son rayon sous son propre champ gravitationnel en une durée 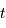 vérifiant :
vérifiant :
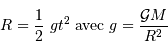
Pour un corps autogravitant de masse 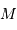 et rayon
et rayon 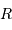 , l'analyse dimensionnelle impose :
, l'analyse dimensionnelle impose :
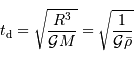
où 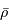 est la masse volumique moyenne du corps.
Comme l'on considère seulement l'interaction gravitationnelle, en négligeant toute résistance, la température du nuage ne joue aucun rôle. En fonction de la densité particulaire, le temps de chute libre s'exprime :
est la masse volumique moyenne du corps.
Comme l'on considère seulement l'interaction gravitationnelle, en négligeant toute résistance, la température du nuage ne joue aucun rôle. En fonction de la densité particulaire, le temps de chute libre s'exprime :
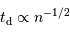
Temps de Kelvin-Helmholtz
La contraction d'un nuage s'accompagne, d'après le
théorème du viriel d'une
puissance rayonnée correspondant au taux de variation de l'énergie potentielle d'interaction gravitationnelle :
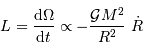
La phase de luminosité uniquement due à la contraction gravitationnelle peut se poursuivre sur une durée, appelée temps de Kelvin-Helmholtz, définie par le rapport :
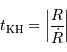
En fonction de ce qui précède, on en déduit que cette constante de temps caractéristique s'exprime :
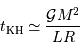
Elle augmente avec la masse (le réservoir d'énergie) et diminue avec la puissance rayonnée (la perte d'énergie).
Pour le Soleil (avec une puissance rayonnée 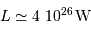 et les masse et rayon actuels) la constante de temps est de l'ordre de 30 millions d'années. Ceci signifie que, par simple contraction gravitationnelle, le Soleil peut rayonner pendant cette durée, sans autre source d'énergie.
et les masse et rayon actuels) la constante de temps est de l'ordre de 30 millions d'années. Ceci signifie que, par simple contraction gravitationnelle, le Soleil peut rayonner pendant cette durée, sans autre source d'énergie.
S'exercer
S'évaluer
 Constante de temps de Kelvin-Helmholtz
Constante de temps de Kelvin-Helmholtz
Difficulté : ☆☆
Temps : 10 min
Question 1)
Que mesure la constante de temps de Kelvin-Helmholtz ? De quel phénomène important rend-elle compte
[1 points]
Disques
Observer

Galaxie spirale NGC 4565. Ainsi vue par la tranche, elle
présente une distribution de matière essentiellement plane.
Crédit :
CFHT

Galaxie elliptique Messier 87 (à 20 Mpc, dans l'amas de la Vierge). Elle présente une distribution de matière tridimensionnelle.
Crédit :
CFHT
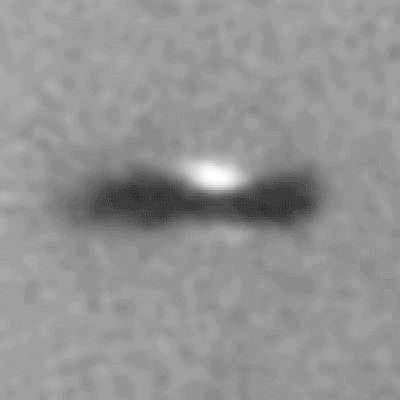
Disque protoplanétaire dans Orion, vu par la tranche.
Crédit :
HST

Disque d'accrétion de l'étoile
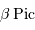
.
Crédit :
HST
Distribution plane ou sphérique
A toute échelle dans l'Univers, on observe des objets présentant une morphologie plutôt bidimensionnelle ou bien plutôt sous forme de tridimensionnelle.
Cette morphologie dévoile l'histoire du système, avec un rôle important ou non des collisions.
Disques d'accrétion
Le processus d'effondrement d'un nuage et de formation stellaire n'échappe pas à cette règle. Le nuage s'aplatit et forme un disque d'accrétion, qui entoure la jeune étoile.

Disque et jet de l'étoile HH30 (HH = Herbig Haro).
Crédit :
HST
Jets
Le plus souvent, le phénomène d'accrétion s'accompagne de l'émission de
jets, émis depuis la région centrale et perpendiculairement au plan du disque.
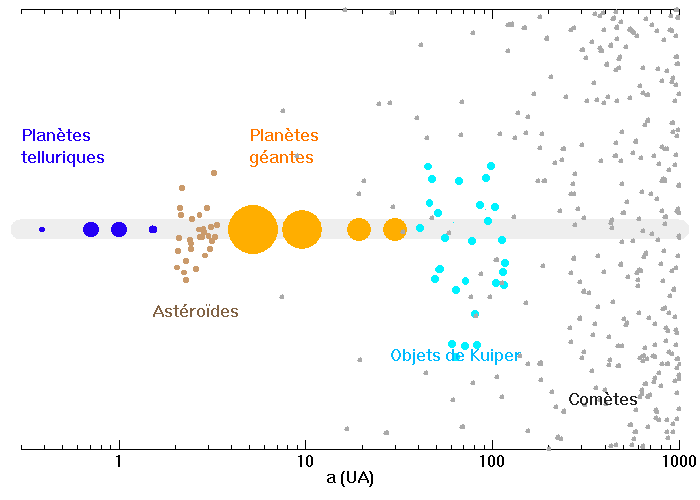
Présentation schématique de notre système solaire. Les objets les plus massifs, résultant d'un phénomène d'accrétion soutenu, se retrouvent dans le plan de l'écliptique.
Crédit :
HST
Et dans notre système solaire ?
On observe que la distribution des principaux objets du système solaire est plane. Ce plan coïncide avec le plan équatorial du Soleil : il a été défini lors de sa phase d'accrétion. Seuls les objets ayant peu interagi par collisions avec les autres - les comètes - présentent une distribution sphérique.
Apprendre
 Objectifs
Objectifs
Expliquer simplement la tendance des systèmes à s'aplatir dans la phase d'accrétion.
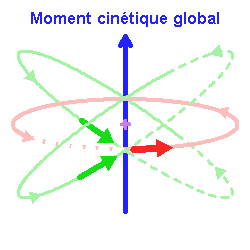
Le moment cinétique, en bleu, marque la rotation d'ensemble du système.
Les collisions ont lieu de façon privilégiée entre objets ayant des composantes de vitesse opposées selon la direction du moment cinétique. Cette composante de vitesse est alors réduite après le choc, contrairement à la composante de vitesse orthogonale. Par collisions, la rotation d'ensemble est préservée, mais le système va s'aplatir.
Crédit :
ASM
Disque protostellaire
Suite aux nombreuses collisions, le nuage s'aplatit dans sa dimension parallèle au moment cinétique, pour former un disque perpendiculaire au moment cinétique initial.
Disque protoplanétaire
Ce n'est finalement pas un hasard si les principaux composants d'un système planétaire se retrouve dans une distribution relativement plane. Seuls les membres ayant le moins participé à l'accrétion, les plus petits, les comètes, gardent une distribution sphérique uniforme.
Ejection de vent
Une autre conséquence de la conservation du moment cinétique conduit à la créations de jets, collimatés parallèlement perpendiculairement au disque, et donc parallèlement au moment cinétique.
Régime collisionnel ou non
L'aplatissement d'un système suppose l'interaction et l'accrétion de ces composants. Un système qui ne collisionne pas et n'a jamais été en régime collisionnel reste essentiellement sphérique.
C'est le cas des amas globulaires, des galaxies elliptiques.
Simuler
M15

Avant et après une collision (en bleu : le vecteur du moment cinétique représente la rotation d'ensemble du système).
Crédit :
ASM
Collisions
Les collisions conduisent à l'aplatissement du système, par annulation des composantes de vitesse parallèles au moment cinétique.
Amas d'étoiles
Observer
M80

Amas globulaire NGC 6093 (M80) dans la constellation du Scorpion, relativement compact. Les étoiles de l'amas ont une magnitude moyenne de l'ordre de 14.
Crédit :
HST
M15

Amas d'étoiles M15, l'un des plus denses recensés. Sa masse atteint 360 000 fois celle du Soleil, dans un volume sphérique de diamètre 120 AL
(la magnitude visuelle globale de 6.2 rend M15 facilement observable avec un petit télescope, dans la constellation de Pégase).
Crédit :
HST
Amas fermé (ou amas globulaire)
L'observation d'une concentration d'étoiles bien regroupées laisse à penser que les objets sont gravitationnellement liées. Nées ensemble d'un même nuage interstellaire, elles évoluent ensemble. Il s'agit d'un amas fermé, regroupant un grand nombre d'étoiles avec une symétrie sphérique et une forte
densité stellaire piquée au centre de l'amas.
Double amas de Persée

Double amas ouvert dans la constellation de Persée. Situés à plus de 2 kpc, ces deux amas sont très jeunes (environ 10 millions d'années). Ils hébergent des étoiles très chaudes et bleues qui n'ont pas encore évolué en supernovæ.
Crédit :
NOAO
Amas ouvert
Les étoiles d'un amas ouvert ne présentent pas cette forte densité stellaire. Les étoiles ne sont plus liées et s'éloignent peu à peu les unes des autres.

Le nuage moléculaire BHR 71. Le jet serait dû à la formation d'une étoile double à l'intérieur du nuage.
Crédit :
ESO
Influence d'un couple sur un groupe
La formation d'un système double dans un amas peut changer son identité : le système double pouvant
phagocyter l'essentiel de l'énergie de liaison gravitationnelle, libérant ainsi les autres membres du groupes.
Apprendre
 Objectifs
Objectifs
Les étoiles naissent en groupe. Elles évoluent ensuite chacune selon leur masse. Dans un amas fermé, elles restent proches les unes des autres.
 Prérequis
Prérequis
Potentiel gravitationnel, énergie mécanique.
Des nuages aux étoiles et aux amas d'étoiles
Un nuage donne naissance à plusieurs étoiles : en effet, en raison de la turbulence et des inhomogénéités du nuage initial, des sous-régions plus denses sont apparues. Les conditions très variées de masse, température et densité du nuage initial conduisent à des étoiles aux masses très différentes, et aux amas de tailles très variées également.
Amas fermé (ou amas globulaire)
Les amas fermés présentent une énergie mécanique totale négative : leurs étoiles, gravitationnellement liées comme l'était le nuage initial, sont amenées à subir un avenir commun.
Le fait d'observer une distribution sphérique indique que, malgré la forte densité d'étoiles, les collisions sont très improbables. En effet, un régime collisionnel conduirait à l'aplatissement du disque.
La dénomination 'amas fermé' a une explication physique. La dénomination 'amas globulaire' provient simplement de leur aspect.
Amas ouvert
Un amas ouvert possède une énergie mécanique totale positive. Cela peut paraître surprenant, vu qu'il est issu d'un nuage qui, pour exister, devait être gravitationnellement lié, donc avec une énergie mécanique totale initiale négative.
En fait, un amas peut devenir ouvert lorsque une part importante de son énergie d'interaction gravitationnelle, négative, est accaparée lors de la formation d'une binaire très serrée. Le reste de l'énergie à distribuer pour le reste de l'amas est alors positif.
En distinguant a priori les 2 étoiles qui vont évoluer en système binaire :
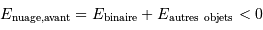
Si le système binaire est serré :
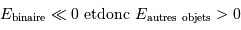
Les composantes de l'amas vont alors peu à peu se quitter.
Le mécanisme est complexe, car lié à la dynamique d'un système à N corps. On comprend que, pour former une binaire serrée, les 2 composantes ont besoin d'interagir avec le groupe. Sinon, dans le cadre du système à 2 corps décrit par la mécanique képlérienne, l'orbite des 2 étoiles n'a aucune raison d'évoluer.

Amas des Hyades, à 151 AL du Soleil (ce qui est très proche), âgé d'environ 600 millions d'années. Il s'étend sur toute la constellation du Taureau.
Crédit :
CDS
Intérêt de l'étude des amas
Les raisons motivant l'étude des amas stellaires sont très nombreuses :
- Les étoiles d'un amas sont nées à la même date, à la durée du processus de formation près, mais qui s'avère très courte devant la durée de vie des étoiles. Elles ont donc le même âge.
- Elles sont toutes à la même distance du Soleil, la dimension de l'amas étant petite devant leur distance moyenne (sauf pour l'amas le plus proche, les
Hyades). Elles ont donc le même module de distance.
- Elles présentent des compositions chimiques initiales très voisines, vu qu'elles proviennent du même nuage géniteur.
S'évaluer
 Jeune et ouvert ; vieux et fermé
Jeune et ouvert ; vieux et fermé
Difficulté : ☆☆
Temps : 10 min
Question 1)
Pourquoi les amas ouverts sont-ils en moyenne plus jeunes que les amas fermés ?
Comment les amas évoluent-ils ?
Vie
Auteur: Benoît Mosser
Introduction
La phase de formation ne représente qu'une courte étape dans la vie de la plupart des étoiles. Ensuite, l'étoile doit trouver une autre source d'énergie.
Avec une masse stellaire suffisante, de l'ordre du douzième de la masse du Soleil, la fusion de l'hydrogène peut s'amorcer, et l'étoile entre sur la séquence principale.

Cet objet du catalogue Herbig-Haro est une étoile de type T-Tauri. Sur le point d'atteindre la séquence principale, elle éjecte encore une fraction importante de sa masse sous forme de vent stellaire.
Crédit :
HST
Fusion nucléaire
Observer

Image en rayon X du Soleil. Quelle source d'énergie interne explique la luminosité du Soleil ?
Crédit :
NASA
Energie interne
Le Soleil présente un âge bien plus avancé que le temps de Kelvin-Helmholtz. Il possède une source d'énergie interne qui explique son rayonnement.
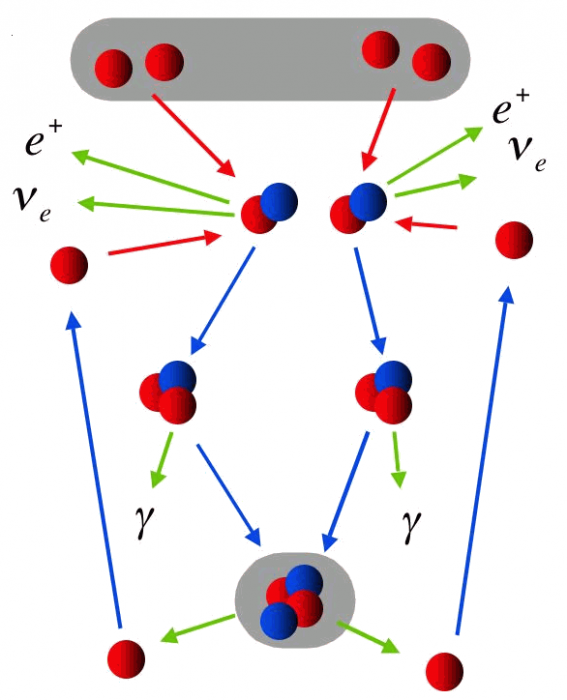
Réaction détaillée de la fusion de 4 H en 1 He.
Crédit :
ASM
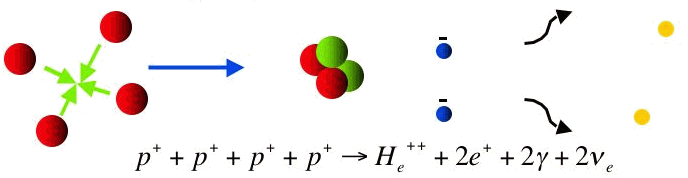
Bilan de la fusion de 4 H en 1 He.
Crédit :
ASM
Chaine proton-proton
Différentes étapes conduisent à la fusion de 4 protons en un noyau d'hélium, ne faisant intervenir que des paires de réactifs à chaque étape élémentaire.
L'étape limitante de la réaction consiste en la fusion de 2 protons vers un noyau de deutérium, avec émission d'un positron, donc un bilan réduit 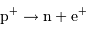 . L'interaction faible mise en jeu induit un très faible taux de réaction.
. L'interaction faible mise en jeu induit un très faible taux de réaction.
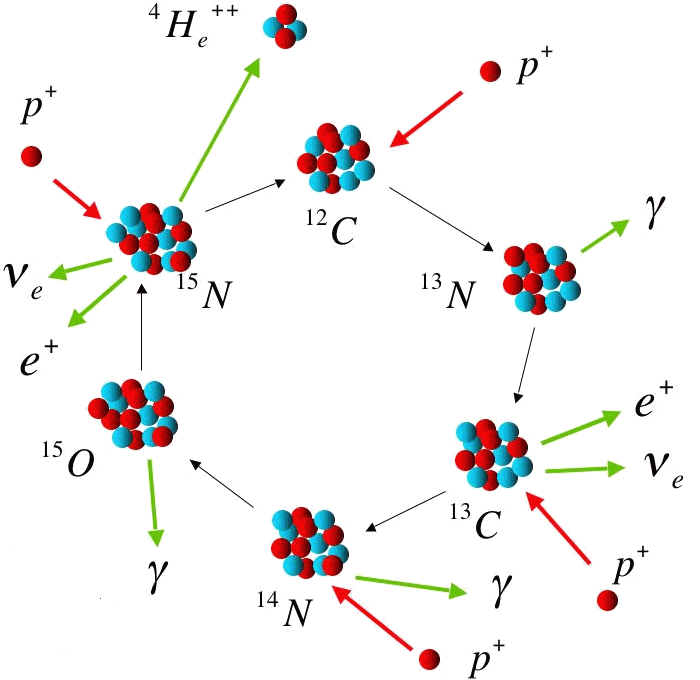
Cycle CNO.
Crédit :
ASM
Cycle CNO
A plus haute température (car les noyaux impliquées sont plus lourds, donc plus chargés), le cycle CNO peut s'avérer plus rapide que la chaîne proton-proton. Il est à l'oeuvre dans les étoiles massives. Les noyaux C, N et O participent au cycle, mais n'apparaissent pas dans le bilan final, qui reste la transformation de 4 protons en 1 noyau d'hélium.
Apprendre
 Objectifs
Objectifs
Définir dans quelles conditions microphysiques la fusion de l'hydrogène va s'amorcer.
Montrer que la fusion nécessite une température élevée, de l'ordre de 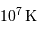 .
.

Seules les régions internes les plus chaudes peuvent être le siège de la fusion de l'hydrogène. Leur volume est limité.
Crédit :
ASM
Constante de temps nucléaire
La durée de vie à ce régime, pour une étoile comme le Soleil, est alors :
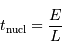
L'application numérique, avec la luminosité solaire mesurée aujourd'hui 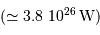 , le taux de conversion par nucléon et la masse concernée donne :
, le taux de conversion par nucléon et la masse concernée donne :
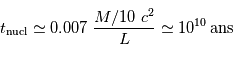
Une réaction chimique, dégageant typiquement 1 eV par nucléon, soit 1 million de fois moins que la fusion de l'hydrogène, conduirait à une durée de vie de 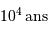 seulement.
seulement.
L'estimation de 10 milliards d'année pour le Soleil est très proche de ce que donne une modélisation plus poussée. Actuellement, avec un âge de 4.56 milliards d'années, le Soleil est à mi-parcours sur la
séquence principale.
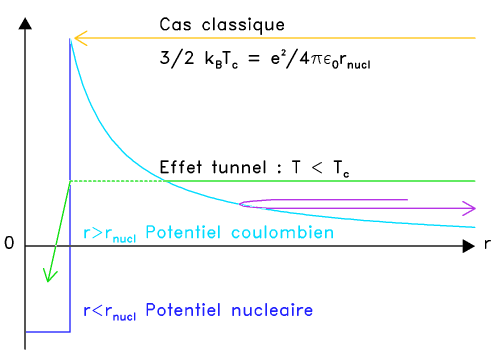
L'effet tunnel permet à un couple de protons de se rencontrer et d'interagir via l'interaction nucléaire forte, en outrepassant la barrière électrostatique.
Crédit :
ASM
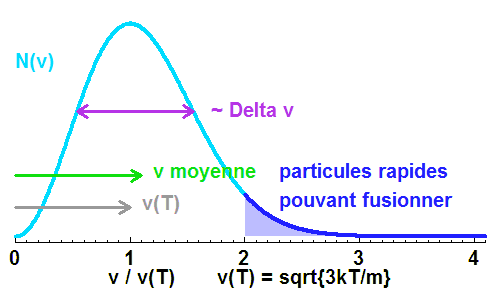
Distribution maxwellienne de vitesse, valable pour un gaz parfait. Valeur la plus probable, valeur moyenne et largeur de la distribution se valent, pour une énergie cinétique égale à 3/2 kT.
Crédit :
ASM
Interagir
Au sein d'une étoile, l'hydrogène est totalement ionisé : la matière se présente sous la forme d'un gaz de protons et d'électrons essentiellement. La réaction entre 2 protons nécessite leur rencontre à très courte distance, car l'interaction nucléaire forte n'a qu'une très courte portée, de l'ordre du femtomètre. Ceci nécessite de vaincre la répulsion électrostatique.
La barrière de potentiel pour une distance de 1 fm entre les 2 protons, peut se traduire en température : de l'ordre de 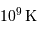 . Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
. Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
Deux phénomènes se conjuguent pour faciliter la fusion :
- L'effet tunnel conduit à tromper les électrons sur la distance exacte qui les sépare. Il exprime l'incertitude de Heisenberg : les 2 protons fonçant l'un sur l'autre ne peuvent pas avoir une position très précisément définie.
- La distribution de vitesse des protons est maxwellienne, donnée par la théorie cinétique du gaz parfait : si l'énergie cinétique moyenne est
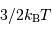 , une proportion non négligeable de protons est sensiblement plus rapide.
, une proportion non négligeable de protons est sensiblement plus rapide.
Ces points sont quantifiés en exercice.
Fusion de l'hydrogène
En pratique, la température limite de fusion de l'hydrogène est de l'ordre de 10 millions de Kelvin. Pour des températures plus faibles, seule la fusion du deutérium peut s'amorcer.
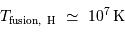
La fusion par le cycle pp domine lorsque la température n'excède pas 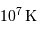 . Au delà de
. Au delà de 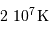 , le cycle CNO est prépondérant.
, le cycle CNO est prépondérant.
Fusion de noyaux lourds
Plus les noyaux sont lourds, plus leur fusion nécessite une température élevée. En fonction du nombre de charge  de l'élément considéré :
de l'élément considéré :
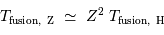
S'exercer
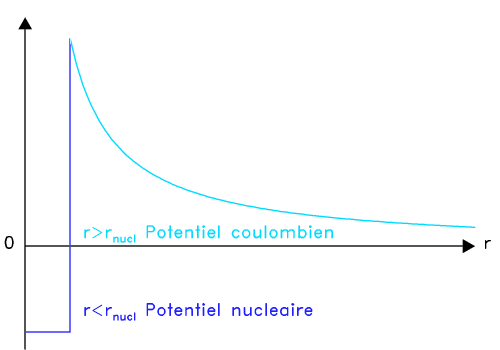
Energie potentielle d'interaction proton-proton.
Crédit :
ASM
 Température de fusion
Température de fusion
Difficulté : ☆☆
Temps : 40 min
Cet exercice a pour but de quantifier, dans un cadre classique, la température minimale qui doit régner au centre d'une étoile pour que s'amorcent les réactions nucléaires. Il se base sur la figure donnant le potentiel d'interaction entre 2 protons.
Question 1)
Mener un bilan d'énergie, pour déterminer l'énergie cinétique minimale conduisant à la fusion.
[1 points]
Exprimer l'énergie de la barrière coulombienne.
Exprimer la condition énergétique limite à remplir en 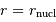
Question 2)
En déduire l'expression de la température minimale pour que la fusion puisse avoir lieu.
[2 points]
Faire le lien entre l'énergie cinétique et la température.
Question 3)
Faire l'application numérique. On donne 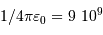 en unité SI, et
en unité SI, et 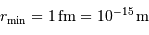 . Qu'en pensez-vous ?
. Qu'en pensez-vous ?
[2 points]
Question 4)
Comment s'écrit cette température s'il s'agit de faire fusionner non pas 2 protons, mais 2 noyaux d'une élément de charge 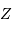 .
.
En déduire que la température de fusion des éléments lourds nécessite une température bien plus élevée que celle pour l'hydrogène.
[1 points]
Réécrire le potentiel électrostatique en fonction de 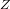 .
.
L'effet varie comme 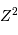
 Du rôle de l'effet tunnel et de la distribution des vitesses
Du rôle de l'effet tunnel et de la distribution des vitesses
Difficulté : ☆☆☆
Temps : 60 min
Sans effet tunnel, la
fusion de l'hydrogène nécessiterait des températures très élevées (et p.ex. non atteintes dans l'intérieur du Soleil). Cet exercice a pour but de décrire le rôle de l'effet tunnel dans le cadre d'un modèle très simplifié.
On note 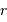 la position d'un proton par rapport à un autre et
la position d'un proton par rapport à un autre et 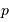 la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
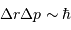
Question 1)
Relier la distance minimale d'approche des 2 protons à la quantité de mouvement incidente, puis à la température du milieu.
[1 points]
Déterminer les expressions des énergies cinétique et potentielle, ainsi que leurs valeurs particulières à grande distance ou à la distance minimale d'approche.
Question 2)
Faire l'application numérique dans le cas d'une distance d'approche de 1 fm, nécessaire pour arriver à une interaction forte entre les protons.
[1 points]
Question 3)
Dans le problème étudié, la loi de distribution des vitesses permet de confondre 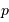 et
et 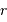 avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
On suppose que le proton incident ne sait pas localiser l'autre proton, avec une incertitude dépendant de sa quantité de mouvement incidente précédemment calculée (notée simplement 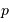 ).
).
Déterminer alors cette incertitude de position.
[3 points]
La relation d'incertitude présentée ici se traduit par
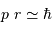
L'égalité entre l'énergie cinétique à grande distance 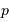 et l'énergie potentielle à distance minimale
et l'énergie potentielle à distance minimale 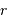 donne une autre relation entre ces 2 variables.
donne une autre relation entre ces 2 variables.
Question 4)
Faire l'application numérique (on donne 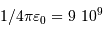 en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
[2 points]
Question 5)
La distribution des quantités de mouvement assure qu'il existe une population avec des protons 3 fois plus rapide que la valeur moyenne. En déduire la température minimale pour la fusion.
[1 points]
Estimer les conséquences de ces protons rapides en termes énergétiques, puis de température.
Masse d'une étoile
Apprendre
 Objectifs
Objectifs
Définir dans quelles conditions la fusion de l'hydrogène va s'amorcer.
 Prérequis
Prérequis
Pression au centre de l'étoile.
La compression gravitationnelle peut être équilibrée par 3 termes de
pression :
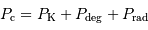
respectivement pression du gaz de matière chaud, pression de Fermi et présence du gaz de photons.
Phase de contraction
La compression gravitationnelle au centre de l'objet varie en fonction de sa masse et de son rayon comme :
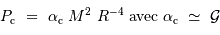
Lors de la contraction de l'objet, la température centrale varie en fonction du rayon 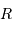 comme :
comme :
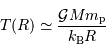
(avec 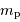 la masse du proton).
Lorsque
la masse du proton).
Lorsque 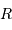 décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
Rôle des différents termes de pression
La pression cinétique présente la même dépendance en masse et rayon que la compression gravitationnelle :
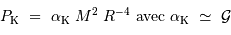
Avec ces variables, la pression de dégénérescence varie elle comme :
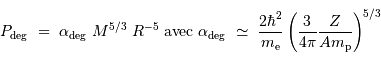
Lorsque l'objet se contracte, cette pression augmente plus vite que la compression gravitationnelle. Elle peut donc bloquer la compression, en atteignant un équilibre caractérisé par :
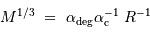
Température centrale
Dans ces conditions, la température atteinte au centre vaut (en éliminant la variable rayon des équations qui précèdent) :
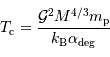
Si la température centrale atteint 10 millions de Kelvin, une étoile est née. Sinon, il s'agit d'un astre dégénéré sans amorçage des réactions nucléaires.
Masse minimale
Il est nécessaire d'avoir une masse initiale suffisante pour atteindre une température permettant d'initier la fusion de l'hydrogène. Un modèle précis donne la masse minimale pour la combustion de l'hydrogène :
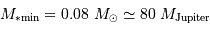
Entre 13 et 80 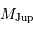 , l'objet ne peut brûler que son deutérium : il s'agit alors d'une naine brune.
, l'objet ne peut brûler que son deutérium : il s'agit alors d'une naine brune.
Masse maximale
La pression de radiation varie comme 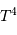 , donc :
, donc :
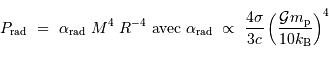
à comparer à la compression gravitationnelle 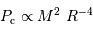 .
.
Si la masse est trop importante, la pression de radiation va conduire à souffler l'étoile. La limite d'équilibre 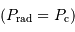 est atteinte lorsque :
est atteinte lorsque :
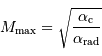
Une modélisation précise donne la valeur numérique :
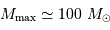
S'exercer
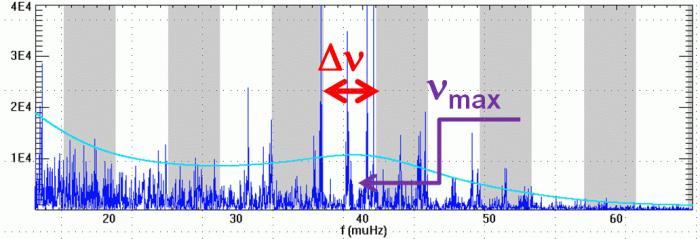
Définition des fréquences caractéristiques
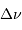
et
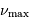
d'un
spectre d'oscillation stellaire.
Crédit :
ASM
 Masse et rayon sismiques
Masse et rayon sismiques
Difficulté : ☆☆
Temps : 30 min
L'astérosismologie, l'étude de la vibration des étoiles, est une
branche récente de la physique stellaire qui apporte de nouvelles
observables. La description globale d'un
spectre d'oscillation introduit
deux fréquences caractéristiques 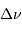 et
et 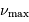 ,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse
,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse 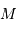 , du rayon
, du rayon 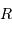 et de la température effective
et de la température effective 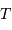 de l'étoile via les définitions :
de l'étoile via les définitions :
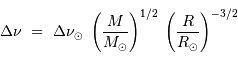
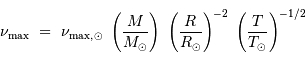
avec les valeurs solaires 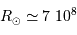 m,
m, 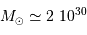 kg,
kg, 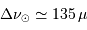 Hz,
Hz, 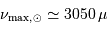 Hz, et
Hz, et 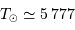 K.
K.
Question 1)
Ordonner les valeurs de 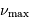 pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
[2 points]
Identifier dans l'expression de 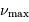 ce qui peut ressemble au
champ gravitationnel d'une étoile.
ce qui peut ressemble au
champ gravitationnel d'une étoile.
Comment se traduit le fait que l'on considère des étoiles de même
type spectral ?
Question 2)
Quelle mesure intéressante apporte 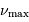 , grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
, grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
[1 points]
La réponse est quasiment à la question précédente.
Question 3)
Ordonner les valeurs de la grande séparation 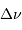 pour deux
étoiles présentant une masse volumique moyenne très différente.
pour deux
étoiles présentant une masse volumique moyenne très différente.
[1 points]
Exprimer la masse volumique moyenne en fonction des masse et
rayon stellaire.
Quel lien entre 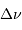 et la masse volumique moyenne ?
et la masse volumique moyenne ?
Question 4)
Calculer 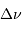 et
et 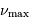 pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à
pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à 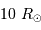 et de température
effective 4 800 K.
et de température
effective 4 800 K.
[1 points]
Faites chauffer le calcotron.
Question 5)
Montrer que l'on peut déduire de la mesure de 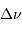 ,
, 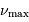 et
et
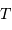 une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
[2 points]
Désolé, pas d'autre solution que retrousser ses manches et
inverser les équations de départ !
Question 6)
Énoncer un des intérêts de l'astérosismologie ?
[1 points]
S'évaluer
 De nouvelles classes spectrales ?
De nouvelles classes spectrales ?
Difficulté : ☆☆
Temps : 5 min
Question 1)
Pourquoi peut-on penser qu'il n'y aura pas de découvertes de nouvelles classes spectrales
même si l'on met en service de nouveaux télescopes de sensibilité encore plus grande ?
Si l'on découvrait de nouvelles classes, correspondraient-elles à des étoiles très ou très peu lumineuses ?
Relation masse-luminosité
Apprendre
 Objectifs
Objectifs
Estimer quelques dimensionnements des objets sur la séquence
principale à partir de la relation masse-luminosité sur séquence
principale (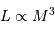 ).
).
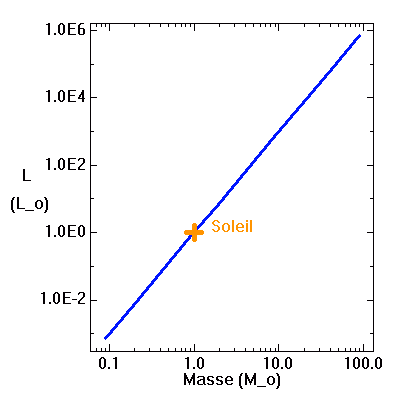
Relation masse-luminosité. Les étoiles les moins lumineuses sont intrinsèquement plus de 1000 fois moins lumineuses que le Soleil, quand les plus lumineuses atteignent 1 millions de fois la valeur solaire.
Crédit :
ASM
Relation masse luminosité
En faisant de la physique avec les mains, on démontre rapidement que la luminosité d'une étoile est reliée à sa masse par la relation :
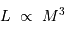
La démonstration complète est hors de portée de ce cours, car elle introduit des éléments de transfert radiatif, qui aboutissent à la relation entre masse et rayon stellaires. Notons les étapes principales.
Constante de temps radiative
La luminosité d'une étoile, commensurable à une puissance, est égale au quotient de l'énergie interne du gaz de photons à la constante de temps radiative :
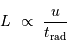
L'énergie interne du gaz de photons est proportionnelle au volume stellaire 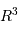 , ainsi qu'à
, ainsi qu'à 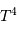 selon la loi de rayonnement du corps noir). La constante de temps radiative mesure le durée d'échappement des photons, qui résulte d'un phénomène stochastique.
selon la loi de rayonnement du corps noir). La constante de temps radiative mesure le durée d'échappement des photons, qui résulte d'un phénomène stochastique.
On suppose que le libre parcours moyen 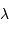 d'un photon est uniforme dans tout l'intérieur stellaire. Le processus de marche au hasard demande alors, pour parcourir une distance
d'un photon est uniforme dans tout l'intérieur stellaire. Le processus de marche au hasard demande alors, pour parcourir une distance 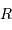 par étapes de longueur élémentaire
par étapes de longueur élémentaire 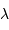 , un nombre d'étapes variant comme
, un nombre d'étapes variant comme 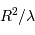 . On en déduit la constante de temps radiative :
. On en déduit la constante de temps radiative :
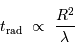
Comme le libre parcours 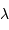 est en fait inversement proportionnel à l'encombrement, donc à la masse volumique, on a :
est en fait inversement proportionnel à l'encombrement, donc à la masse volumique, on a :
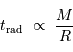
et
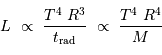
Relation masse-rayon-température-luminosité
Dans les pages précédentes,
des éléments de physique simples ont permis de calibrer les masse volumique et pression internes :
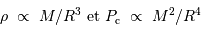
ainsi que la relation donnant la température
centrale :
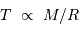
La luminosité du corps noir stellaire vérifie donc :
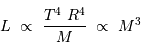
Observationnellement, l'exposant s'avère être 3.3 :
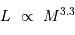
Simuler
Le long de la séquence principale
Différents modèles stellaires ont été synthétisés. La masse, le rayon et la luminosité sont données en unités solaires, la température de corps noir en Kelvin (on remarquera que le modèle correspondant à 1 masse solaire n'a pas un rayon solaire : la série a été déterminée pour des conditions d'âge et de composition différentes de celles de notre Soleil).
A l'aide de l'appliquette, calculer la luminosité de corps noir Lcn, et vérifier qu'elle correspond à la luminosité modélisée.
Calculer ensuite les luminosités, masses et rayons en échelle logarithmique, et vérifier les exposants des relations de proportionnalité entre la luminosité et la masse d'une part, la luminosité et le rayon d'autre part.

S'exercer
 Amplitude des oscillations
Amplitude des oscillations
Difficulté : ☆☆
Temps : min
L'amplitude des oscillations de type solaire dépendent du rapport 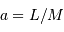 , la luminosité
, la luminosité 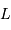 donnant la mesure de l'énergie transportée par convection, et la masse
donnant la mesure de l'énergie transportée par convection, et la masse 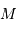 mesurant l'inertie de la réponse. Ces deux grandeurs ne peuvent être mesurées qu'indirectement : la mesure de la luminosité dépend de la distance, et la mesure de la masse nécessite un modèle de structure interne.
mesurant l'inertie de la réponse. Ces deux grandeurs ne peuvent être mesurées qu'indirectement : la mesure de la luminosité dépend de la distance, et la mesure de la masse nécessite un modèle de structure interne.
Question 1)
Montrer que l'amplitude croît avec le type spectral.
[1 points]
Comment varie la luminosité sur la séquence principale ?
Question 2)
Déterminer la dépendance 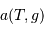 , avec
, avec 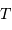 la température effective (déduit du spectre) et
la température effective (déduit du spectre) et 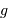 le champ gravitationnel (déduit des profils de raies).
le champ gravitationnel (déduit des profils de raies).
[1 points]
S'évaluer
 Le long de la séquence principale
Le long de la séquence principale
Difficulté : ☆
Temps : 15 min
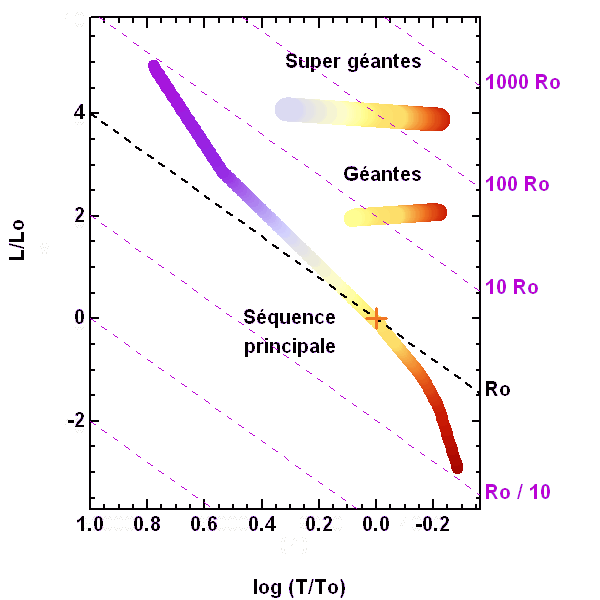
Diagramme HR.
Crédit :
ASM
Le long de la séquence principale, la luminosité d'une étoile varie approximativement comme la puissance 6 de la température, comme le rappelle le diagramme HR ci joint.
Question 1)
Montrer que l'on peut en déduire une relation masse-rayon le long de la séquence principale du type:
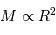
[2 points]
Question 2)
Que peut-on en déduire pour le champ gravitationnel d'une étoile de la séquence principale ?
[1 points]
Finalement, qu'est-ce qu'une étoile ?
Auteur: B. Mosser
Observer

Champ d'étoiles dans le Grand Nuage de Magellan (galaxie satellite de la Voie Lactée) vu par le télescope Hubble.
Crédit :
HST

Naine brune 2M1207, et son compagnon exoplanétaire, détectée par optique adaptative au VLT.
Crédit :
ESO

Naine brunes identifiées dans l'amas ouvert des Pléiades.
Crédit :
UKIDSS and Palomar Observatory Sky Survey
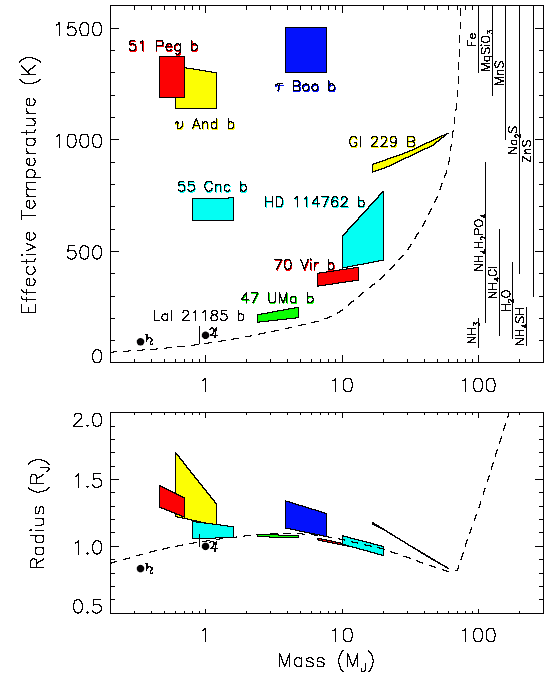
Modélisation de planètes géantes et naines brunes.
Crédit :
CNRS
Champ d'étoiles
Quels objets d'un
champ stellaire sont effectivement des étoiles, et pour quelles raisons ?
Naines brunes
Dans les années 1990, des objets présentant une très faible luminosité et un indice de couleur très rouge ont été clairement identifiés comme
naines brunes : objet de masse insuffisante pour amorcer la fusion de l'hydrogène mais de masse suffisante pour la fusion de deuterium. Les moyens observationnels actuels permettent de les détecter en grand nombre, par exemple dans un amas.
Les modèles de
structure interne montrent qu'ils présentent un rayon de l'ordre de celui de Jupiter, pour une température effective de 1000 à 1500 K pour les plus chauds.
La nature du Soleil et des étoiles
La nature du Soleil et des étoiles a été un sujet continu de questionnement au cours de l'histoire :
- Pour Anaxagore, au Ve siècle avant JC, le Soleil est un rocher incandescent.
- Pour Aristote, au IVe siècle avant JC, les corps célestes sont constitués d'une autre matière que les 4 éléments terrestres. L'Univers est éternel.
- Jean Philopon, philosophe chrétien au VIe siècle, réfute un Univers sans création. Les étoiles sont des soleils.
- Pour Giordano Bruno, fin XVe siècle, les étoiles sont des soleils entourés de planètes.
- Au XIXe siècle, l'émergence de la spectroscopie permet d'analyser la photosphère solaire.
La question énergétique
La question énergétique se pose dès le XVIIIe siècle. Comment le Soleil compense-t-il la perte d'énergie par rayonnement (Herschel, 1795) ? Pour une Terre de 6000 ans (création du monde selon la tradition biblique, ou de quelques millions d'années (Buffon), le mécanisme de
Kelvin-Helmholtz convient ; mais lorsque la géologie, par datation des roches terrestres, conduit à un âge supérieur au milliard d'années, les choses se compliquent.
- En 1804, Helmholtz suppose que le Soleil tire son énergie de sa contraction gravitationnelle.
- En 1919, Eddington suppose une origine nucléaire, par fusion de l'hydrogène.
- En 1939, le premier mécanisme de fusion de l'hydrogène est proposé par le physicien Hans Bethe.
Apprendre
 Objectifs
Objectifs
Établir les éléments de définition d'une étoile.
Brûler de l'hydrogène
 Définition
Définition
Une étoile passe par une phase adulte, sur la séquence principale, où elle tire son énergie de la fusion de l'hydrogène.
La masse de l'étoile étant apparue comme le paramètre crucial gouvernant sa formation puis son devenir, on récapitule ici comment varient la nature et le rayon d'un objet en fonction de sa masse.
Diagramme masse-rayon
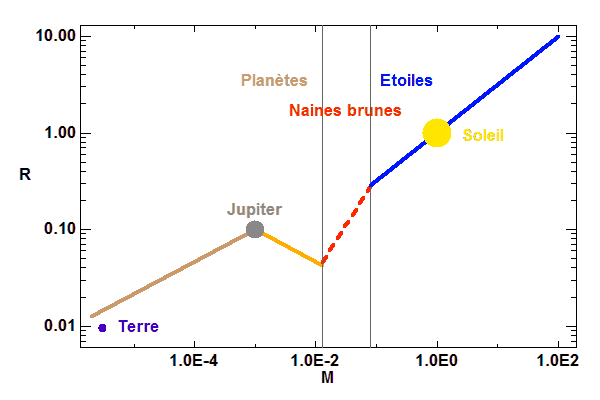
Relation masse rayon (en unités solaires), de la Terre à une étoile
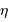
Carinae, de masse de l'ordre de 100 fois la masse du Soleil.
Crédit :
ASM
Faibles masses
Aux faibles masses (comme celle de la Terre), la matière solide est très peu compressible. La relation masse-rayon d'un simple empilement de masse volumique uniforme donne :
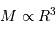
Le rayon croît avec la masse (cas d'une planète de masse inférieure à celle de Jupiter).
Pression de dégénérescence
Avec l'augmentation de la masse au-dela d’une masse critique proche de la masse de Jupiter, la pression de dégénérescence variant comme 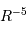 l'emporte. L'équilibre de la compression gravitationnelle
l'emporte. L'équilibre de la compression gravitationnelle 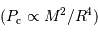 par la pression de dégénérescence
par la pression de dégénérescence 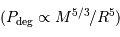 conduit à la relation masse-rayon :
conduit à la relation masse-rayon :
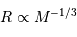
Le rayon de l'objet décroît avec la masse. Ceci n'est bien sûr pas intuitivement évident, mais c'est bien ce que l'on modélise pour les (exo)planètes géantes plus massives que Jupiter.
Relation masse rayon
Pour les étoile de la séquence principale, on a vu :
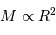
Evolution en fonction de la masse
L'étude à suivre montre l'avenir des étoiles une fois achevée leur vie sur la séquence principale.
- Une étoile de masse initiale inférieure à la masse de Chandrasekhar
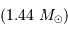 évolue vers le stade de naine blanche.
évolue vers le stade de naine blanche. - Pour une masse supérieure, elle finit comme étoile à neutrons.
- Voire comme trou noir pour une masse supérieure à 3 fois celle du Soleil.
S'évaluer
 Populations stellaires
Populations stellaires
Temps : 30 min
Les observations photométriques menées par le satellite CoRoT ont conduit à identifier des populations d'étoiles peu brillantes pour lesquelles peu d'informations sont disponibles. Ici, on travaille avec une estimation de leurs températures effectives et gravités obtenues par suivi spectroscopique au sol. Ces estimations sont compilées dans un graphe 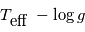 (les logarithmes sont calculés pour des gravités exprimées en cm.s-2). Le graphe montre deux populations, que l'on souhaite caractériser.
(les logarithmes sont calculés pour des gravités exprimées en cm.s-2). Le graphe montre deux populations, que l'on souhaite caractériser.
Champ CoRoT
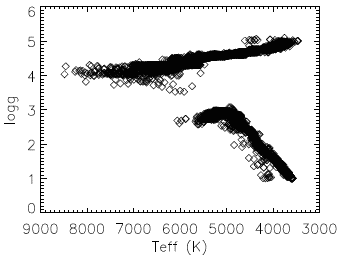
Relevé des températures effectives et gravité du champ initial observé par CoRoT.
Crédit :
CNES/ASM
Question 1)
Déterminer l'expression du champ de gravité de surface d'une étoile de masse 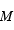 et rayon
et rayon 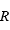 .
.
Aller raffraichir ses souvenirs de mécanique du point.
Dans le cours FSU c'est là .
Question 2)
Faire l'application numérique pour une étoile comme le Soleil et pour une géante rouge de masse identique, mais rayon 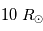 . Exprimer les résultats par la valeur
. Exprimer les résultats par la valeur 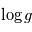 .
.
Les valeurs des masses et rayons solaires sont données par le calcotron !
Question 3)
Positionner les deux types d'objets dans le graphe et en déduire la nature des étoiles observées.
La température effective du Soleil vaut 5777 K. Compter 4800 K pour une géante de 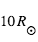
Question 4)
Identifier les deux populations.
Se servir de ce qui précède.
Question 5)
Estimer l'ordre de grandeur des plus grandes géantes observées dans l'échantillon.
Voir du côté des plus faibles gravités.
Quelle masse typique pour une géante typique ?
Mort des étoiles
Auteur: B. Mosser
Introduction
La mort des étoiles survient lorsque le carburant nucléaire principal, l'hydrogène, fait défaut au centre.

Nébuleuse de l'oeuf. Phase rapide de la mort d'une étoile de la classe du Soleil, entre les stades de géante rouge puis de nébuleuse planétaire, avec une importante éjection de matière.
Crédit :
HST
Après la séquence principale
Observer

Image infrarouge à 90 micromètres de l'étoile géante rouge U Hydrae, entourée d'un imposant nuage de poussière. Ce nuage s'étend jusqu'à 0.3 année de lumière de l'étoile. Il a dû apparaître lors de poussées de vents violents ayant débuté il y a environ 10 000 ans.
Crédit :
JAXA
Géante rouge
Le stade de géante rouge est atteint par une étoile telle le
Soleil en fin de vie. La contraction du noyau, à la recherche
d'une source d'énergie autre que la fusion de l'hydrogène,
s'accompagne de l'extension de l'enveloppe externe, et de vents
stellaires importants, conduisant à l'apparition d'un nuage de
poussières
circumstellaires.
Nébuleuse de la Lyre

Nébuleuse planétaire de la Lyre. Le diamètre de l'enveloppe
représente 1.3 AL. L'étoile centrale, à peine visible ici, atteint
une température effective de 100 000 K. La composante rouge du
rayonnement est due à l'hydrogène, les autres composantes colorées
à des raies de l'oxygène et de l'azote.
Crédit :
HST
Nébuleuse planétaire
Une nébuleuse planétaire n'a rien à voir avec une planète, sinon qu'historiquement ce nom a été donnée par confusion observationnelle due à un manque de résolution angulaire.
Une étoile de masse inférieure à 1.5 masse solaire ayant fini de
consommer tout son hydrogène, puis son hélium, voit son cœur
s'effondrer et se transforme en naine blanche. Les couches
externes, expulsées par la pression de radiation, s'étendent
autour de l'étoile à une vitesse d'expansion de plusieurs dizaines
de kilomètres par seconde. Cette région est ionisée sous l'action
des photons ultraviolets émis par l'étoile devenue très chaude ( ).
).
Atmosphère de Bételgeuse

Atmosphère de l'étoile supergéante rouge Bételgeuse. Le diamètre
stellaire vaut 800 fois celui du Soleil, portant la luminosité à
10000 fois la luminosité solaire.
Crédit :
HST
Supergéante rouge
Les étoiles les plus massives atteignent le stade de supergéante
rouge, telle
Bételgeuse. Leur
atmosphère, réagissant à la fusion des éléments de plus en plus
lourds, atteint des tailles considérables, d'où leur dénomination.
Apprendre
 Objectifs
Objectifs
Décrire l'évolution d'une étoile de faible masse (comme le Soleil).
L'hydrogène est épuisé
En fin de séquence principale, la plupart des enveloppes
stellaires autour du noyau ne sont pas convectives, mais
radiatives : l'énergie est évacuée par les photons, sans transport
de matière, donc sans mélange. Dès lors, il est inéluctable que,
l'hydrogène central arrive à épuisement. L'étoile quitte la séquence principale.
Les sous-géantes
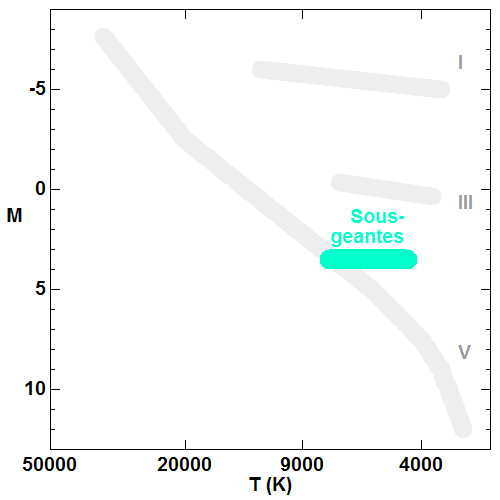
Localisation des sous-géantes dans le diagramme HR.
Crédit :
ASM
En fait durant cette phase, comme la suivante, l'hydrogène continue à brûler, mais en une fine couche autour du noyau d'hélium.
L'étoile se déplace dans le diagramme HR vers les faibles températures. La baisse de température et l'augmentation du rayon se compensent approximativement : l'évolution a lieu à luminosité quasi constante. C'est la phase de sous-géante.
La rupture de production d'énergie conduit à un déséquilibre de
structure, et le noyau d'hélium se contracte pour tenter de retrouver un
équilibre. En se contractant, il se réchauffe, et par réaction
l'enveloppe extérieure s'étend, et bien sûr la détente
s'accompagne d'un refroidissement.
Les branche des géantes rouges
Les étoiles de masse comparable à celle du Soleil voient leur atmosphère se dilater de plusieurs ordres de grandeur (en réponse au cœur d'hélium inerte qui se contracte, et toujours avec une couche d'hydrogène en fusion entre le cœur et l'enveloppe). La
luminosité s'accroît considérablement : l'étoile parcourt la
branche des géantes rouges.
Durant cette phase, l'étoile redevient entièrement convective, ce
qui extrait les éléments lourds produits dans les couches internes
vers les couches extérieures. C'est aussi une phase d'instabilité
atmosphérique, s'accompagnant au sommet de la branche des géantes
d'un fort taux d'éjection de masse, qui peut atteindre
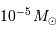 par an avec des vitesses d'éjection de l'ordre
de 5 à
par an avec des vitesses d'éjection de l'ordre
de 5 à 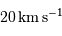 . Cette perte de masse apparaît quand la gravité de surface de l'étoile est devenue très faible : les couches périphériques de l'enveloppe stellaire ne sont plus que très (trop) faiblement liées à l'étoile. L'étoile résiduelle a
d'autant plus maigri qu'elle était peu massive au départ, ce qui
conduit à des géantes rouges aussi peu massive 0.6 masse solaire après la
perte de masse.
. Cette perte de masse apparaît quand la gravité de surface de l'étoile est devenue très faible : les couches périphériques de l'enveloppe stellaire ne sont plus que très (trop) faiblement liées à l'étoile. L'étoile résiduelle a
d'autant plus maigri qu'elle était peu massive au départ, ce qui
conduit à des géantes rouges aussi peu massive 0.6 masse solaire après la
perte de masse.
Au sommet de la branche des étoiles, les étoiles ont un rayon typiquement entre 100 et 200 fois le rayon solaire, un cœur d'hélium de plus en plus dense et chaud, et une masse allégée.
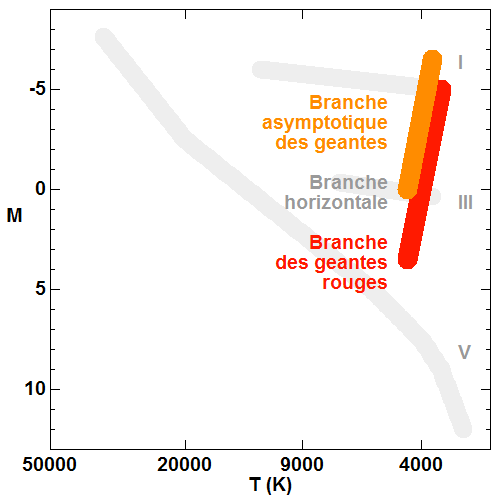
Branche des géantes rouges (avant la fusion de l'hélium du cœur) et branche asymptotique des géantes rouges (après). Le bas de la branche des géantes rouges est uniquement peuplé d'étoiles peu massives (
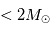
) . Les étoiles plus massives la rejoignent à plus grand luminosité.
Crédit :
ASM
La fusion de l'hélium
La contraction du noyau d'hélium conduit à son fort réchauffement. Dès 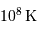 , la fusion de l'hélium peut conduire au carbone, par la réaction bilan :
, la fusion de l'hélium peut conduire au carbone, par la réaction bilan : 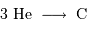 . L'étoile, retrouvant une source d'énergie, retrouve donc une situation d'équilibre. L'apport d'énergie de fusion de l'hélium provoque la dilatation du cœur et l'effondrement de l'enveloppe.
. L'étoile, retrouvant une source d'énergie, retrouve donc une situation d'équilibre. L'apport d'énergie de fusion de l'hélium provoque la dilatation du cœur et l'effondrement de l'enveloppe.
La fusion de l'hélium démarre dans des conditions différentes
selon la masse de l'étoile. Une étoile peu massive présente un
cœur dégénéré. Cette
dégénérescence bloque la fusion de l'hélium, qui ne peut démarrer
que dans des conditions brutales, le flash de l'hélium, dès lors
qu'une température critique est atteinte. Les étoiles plus
massives (de l'ordre de 2 fois la masse du Soleil) ont un cœur
plus chaud, non dégénéré, et peuvent commencer la fusion de
l'hélium graduellement.
Les étoiles qui brûlent leur hélium
central s'accumulent sur le clump, l'extrémité la plus froide de la branche horizontale des géantes. Leur rayon vaut typiquement 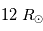 .
.
La branche asymptotique des géantes rouges
Lorsque l'hélium est épuisé dans le cœur, l'équilibre de l'étoile est perturbé. Sans source d'énergie interne, le cœur se contracte, et donc l'enveloppe recommence à s'étendre. Le mécanisme qui associe le contraction (dilatation) du cœur et la dilatation (contraction) conjointe de l'enveloppe est identique à celui à l'œuvre sur la branche des géantes.
Ce mécanisme de miroir comporte trois ingrédients : un cœur qui produit peu ou pas de l'énergie, une enveloppe essentiellement convective, et à l'interface une couche d'hydrogène en fusion. Si le cœur se contracte, la couche d'hydrogène voit sa température augmenter, et ceci provoque la dilation de l'enveloppe, et réciproquement.
Dans le diagramme HR, la branche asymptotique est parallèle à la branches des géantes rouges, un peu plus chaude. L'avenir de l'étoile dépend de sa masse. La perte de masse est aussi cruciale pour cette phase d'évolution.
La perte de masse pouvant durer jusqu'à un million d'années,
ces étoiles de la branche asymptotique s'entourent progressivement d'une enveloppe qui
peut atteindre plusieurs masses solaires, et des dimensions
importantes, de l'ordre d'une année de lumière, contribuant ainsi
à l'enrichissement du milieu interstellaire, avec des éléments
plus lourds que l'hydrogène et l'hélium.
Fusion des éléments lourds
Si la masse de l'étoile (plus précisément, de ce qu'il en reste, car la perte de masse est importante au sommet de la branche asymptotique) est assez importante, le cœur pourra se contracter, à l'épuisement des éléments les plus légers, pour démarrer la fusion des éléments plus lourds.
La fusion du carbone ensuite conduit au néon, à l'oxygène. Tous les éléments
jusqu'au fer peuvent ainsi être
produits par fusion dans les étoiles les plus massives : une étoile massive est une usine à éléments lourds.
Nébuleuse planétaire
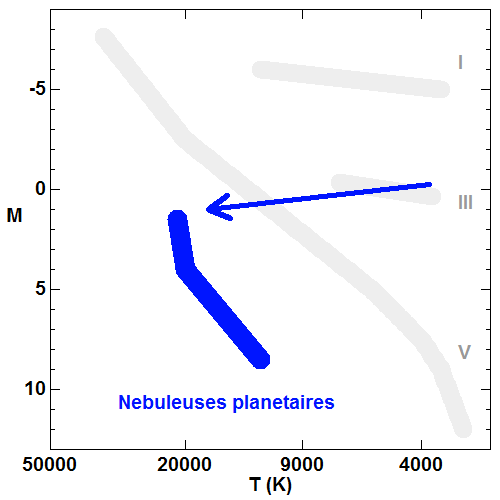
Position des étoiles centrales de nébuleuses planétaires dans le diagramme HR, issues de géantes rouges.
Crédit :
ASM
Si la masse de l'étoile n'est pas trop importante, arrive un moment où la température centrale limitée ne permet plus de trouver de nouvelle source d'énergie. Seule subsiste la pression de dégénérescence des électrons pour soutenir l'étoile.
Ses régions internes se contractent jusqu'à former une naine blanche, tandis que les couches externes expulsées par la pression de radiation donnent naissance à une nébuleuse planétaire.
Simuler
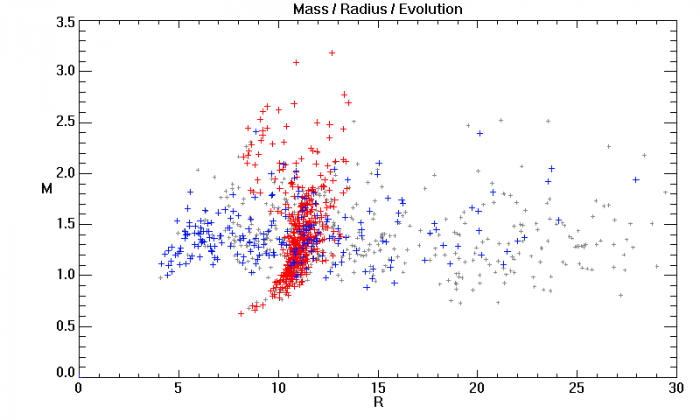
Diagramme masse-rayon d'étoiles géantes rouges observées par le
satellite Kepler de la NASA. En bleu : membres de la première
branche des géantes rouge, qui brûlent l'hydrogène en couche ; en
rouge : membres du clump, qui brûlent l'hélium du cœur ; en gris
: statut évolutif indéterminé.
Crédit :
Kepler/ASM

Perte de masse
La perte de masse des étoiles géantes rouges est perceptible dans un diagramme
rayon-masse obtenu par les données astérosismiques, d'après lesquelles on peut
distinguer les étoiles montant la première branche des géantes rouges de celles qui, passées par le sommet de la branche des
géantes et l'épisode correspondant de perte de masse, se retrouvent sur le clump et brûlent l'hélium. Alors que les
étoiles qui montent la branche ont des masses de 1 à 2 fois la masse du Soleil, celles du clump peuvent avoir des masses plus
petites. C'est la signature de la perte de masse.
Evolution d'une supergéante 
Evolution des supergéantes
L'énergie gravitationnelle des étoiles les plus massives leur
permet d'aborder la
fusion des éléments
les plus lourds.
Naine blanche
Observer
Naines blanches

Naines blanches dans l'amas M4. Privées de source d'énergie, elles sont très peu lumineuses, et s'éteignent peu à peu.
Crédit :
HST
Sirius A et B

Sirius A et B (le petit point lumineux sous l'aigrette inférieure gauche de diffraction de Sirius A). Sirius A est une étoile de la séquence principale, accompagnée d'une naine blanche
10 magnitudes moins brillante. La taille de Sirius B est comparable à celle de la Terre, sa masse étant approximativement solaire.
Crédit :
HST
Petites et chaudes
L'examen d'un champ stellaire peut mettre en évidence des objets de très petit rayon mais très chauds, des naines blanches.
Le contraste de luminosité avec une étoile de la séquence principale est très marqué.
Apprendre
 Objectifs
Objectifs
Caractériser les naines blanches dans l'évolution stellaire : l'état de naine blanche constitue l'étape ultime de l'évolution des étoiles peu massives.
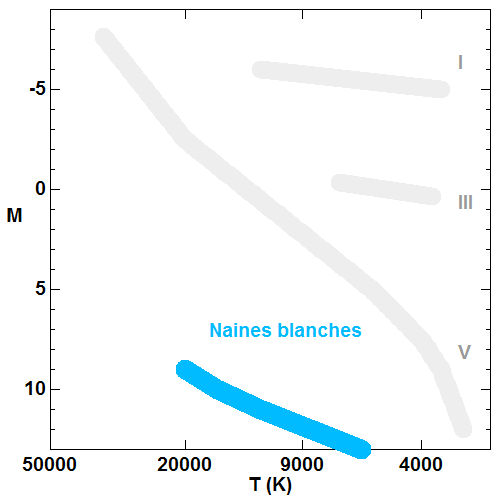
Position des naines blanches dans le diagramme HR.
Crédit :
ASM
La fin de la fusion de l'hydrogène
En l'absence de carburant nucléaire, l'hydrogène étant épuisé au centre de l'étoile, le noyau se contracte, pour atteindre une température centrale plus élevée par le processus de Kelvin-Helmholtz. L'étoile atteint le stage de naine blanche : blanche, car très chaude, et naine car réduite par rapport au rayon qu'elle avait sur la séquence principale.
Rayon d'une naine blanche
Le rayon d'une naine blanche provient de l'équilibre entre
la compression gravitationnelle et la pression de dégénérescence électronique, qui s'écrit :
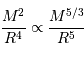
Le rayon d'une naine blanche devient :
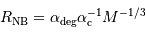
Ce rayon décroît avec la masse ! Pour une étoile de masse solaire, en s'appuyant sur un modèle précis, on trouve que le rayon est de l'ordre de 7000 km (soit environ 1/100 du rayon initial et de l'ordre de grandeur du rayon terrestre).
Masse volumique
Dans ces conditions, la masse volumique d'une naine blanche de masse solaire atteint 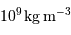 , ce qui représente environ 1 million de fois la masse volumique initiale.
, ce qui représente environ 1 million de fois la masse volumique initiale.
Nova
Dans un système double, l'accrétion de la matière du compagnon par une naine blanche donne le phénomène de nova.
S'évaluer
 Champ gravitationnel et vitesse de libération
Champ gravitationnel et vitesse de libération
Difficulté : ☆
Temps : 15 min
Question 1)
Déterminer le champ gravitationnel d'une naine blanche de masse 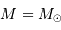 et de rayon
et de rayon 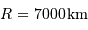 .
.
[2 points]
Question 2)
Déterminer sa vitesse de libération.
[2 points]
Masse de Chandrasekhar
Apprendre
 Objectifs
Objectifs
Lorsque la masse du noyau de l'étoile dépasse 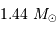 , il arrive un stade de l'évolution où la pression de Fermi des électrons ne parvient plus à soutenir l'étoile.
, il arrive un stade de l'évolution où la pression de Fermi des électrons ne parvient plus à soutenir l'étoile.
Pression de dégénérescence relativiste
Lorsque la masse d'une naine blanche croît, et donc avec un rayon de plus en plus petit, sa masse volumique et sa température croissent également. Il faut alors considérer les électrons comme relativistes. Leur pression, toujours définie comme flux de quantité de mouvement, devient
dans ce cas (avec 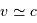 ) :
) :
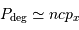
Pression de dégénérescence relativiste
On en déduit l'expression de la pression de dégénérescence relativiste.
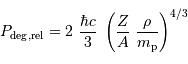
où 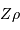 représente la charge volumique, et
représente la charge volumique, et 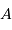 le nombre de masse des atomes en présence.
le nombre de masse des atomes en présence.
Effondrement
L'équilibre de l'objet doit être réalisé entre la pression de dégénérescence relativiste et la compression gravitationnelle :
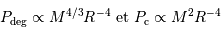
Ces 2 termes présentent la même dépendance en fonction du rayon :
contrairement au cas classique, une diminution de rayon ne permet plus à la pression de Fermi de soutenir l'étoile. En revanche, la dépendance en fonction de la masse est en défaveur de la pression de Fermi : si la masse de l'objet devient trop importante, cette pression ne fait plus l'affaire pour soutenir l'étoile.
Masse de Chandrasekhar
L'application numérique montre qu'au-delà de 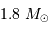 , l'étoile n'est plus soutenue. Un calcul plus précise donne pour cette masse limite, dite masse de Chandrasekhar, au-delà de laquelle l'étoile va s'effondrer faute du soutien de la pression de dégénérescence des électrons, la valeur :
, l'étoile n'est plus soutenue. Un calcul plus précise donne pour cette masse limite, dite masse de Chandrasekhar, au-delà de laquelle l'étoile va s'effondrer faute du soutien de la pression de dégénérescence des électrons, la valeur :
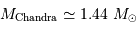
Une étoile dont la masse du noyau central est supérieure à cette valeur s'effondre vers une étoile à neutrons.
Etoile à neutrons
Observer
Etoiles à neutrons
Etoile à neutrons RX J185635-3754. Elle a été découverte d'abord par son émission X, puis identifiée par le télescope Hubble. Sa magnitude apparente visible est de 25. Estimation du diamètre : 28 km ; de la température : 600 000 K.
Crédit :
HST
Etoile à neutrons
Un objet simultanément très chaud (plusieurs centaines de milliers de Kelvin, soit bien plus qu'une étoile de la séquence principale) et très peu lumineux ne peut être, d'après la loi de rayonnement du corps noir, qu'extrêmement petit. C'est ainsi qu'ont été identifiées les étoiles à neutrons, rayonnant l'essentiel de leur énergie dans les domaines X et gamma.
Pulsar

Pulsar du Crabe, résidu de la supernova de 1054.
Crédit :
HST
Pulsars
Un pulsar (de l'anglais pulsating radio source) correspond à une étoile à neutrons dont on observe le rayonnement électromagnétique modulé par la rotation rapide. La rapidité de la période de rotation observée provient du très petit rayon de l'étoile à neutrons.
Le faisceau du pulsar correspond au rayonnement synchrotron des électrons accélérés le long des lignes de champ magnétique. C'est ce phénomène de pulsar qui a conduit à la découverte des premières étoiles à neutrons.
Apprendre
 Objectifs
Objectifs
Décrire simplement cet objet hors du commun qu'est une étoile à neutrons.
Neutron et étoiles à neutron
L'existence des étoiles à neutrons a été supposée dès
l'identification du neutron, comme résidus de supernova.
Bousculade
Au delà de la masse de Chandrasekhar, la pression de Fermi des électrons ne peut plus soutenir l'étoile. La contraction conduit les électrons à flirter intensément avec les protons. L'interaction nucléaire faible est alors sollicitée : elle transforme un proton et un électron en un neutron.
Neutronisation
Néanmoins, la réaction de neutronisation :
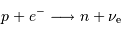
est impossible au repos, car le bilan de masse ne lui est pas favorable. En effet, l'énergie de masse de l'électron (0.5 MeV) apparaît bien inférieure à la différence d'énergie de masse entre proton et neutron (1.3 MeV).
Néanmoins, lorsque les électrons deviennent relativistes, leur énergie totale peut dépasser ce niveau nécessaire de 1.3 MeV (atteint pour une vitesse de 0.92 c). La réaction de neutronisation devient alors possible. C'est cette condition sur la vitesse des électrons qui se traduit par le seuil de masse correspondant à la masse de Chandrasekhar.
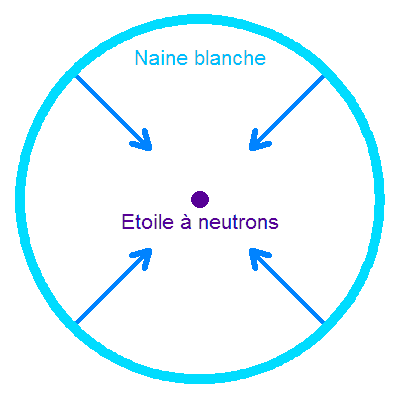
Effondrement d'une naine blanche vers une étoile à neutrons, lorsqu'a lieu la réaction de neutronisation.
Crédit :
ASM
Conséquences
Les neutrons, qui sont aussi des fermions, prennent la relève pour assurer l'équilibre de l'étoile. En effet, comme ils sont beaucoup plus massifs, ils ne sont pas relativistes, et leur pression de Fermi s'exprime comme :
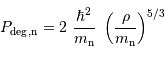
Elle varie donc en fonction du rayon comme 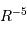 . On assiste alors à un nouvel équilibre, atteint pour un rayon bien plus petit que pour une naine blanche, en raison du facteur
. On assiste alors à un nouvel équilibre, atteint pour un rayon bien plus petit que pour une naine blanche, en raison du facteur 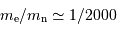 .
.
Ce nouvel équilibre se caractérise par un rayon, estimé en km :
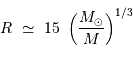
Masse volumique
Dans ces conditions, la masse volumique atteint des valeurs gigantesques :
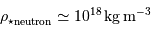
On retrouve en fait la masse volumique de la matière nucléaire. L'étoile à neutrons est analogue à une noyau surdimensionné de nombre de masse 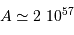 .
.
Supernova
Observer

Supernova SN 1994 D (de type I), observée dans la galaxie NGC 4526. Sa magnitude apparente (en visible) de 11.8 donne, en tenant compte du
module de distance de 30.4, une magnitude absolue de -18.6.
Crédit :
NASA
Une débauche d'énergie
De temps à autre, un point extrêmement brillant apparaît dans une galaxie lointaine. Un noyau stellaire s'effondre.
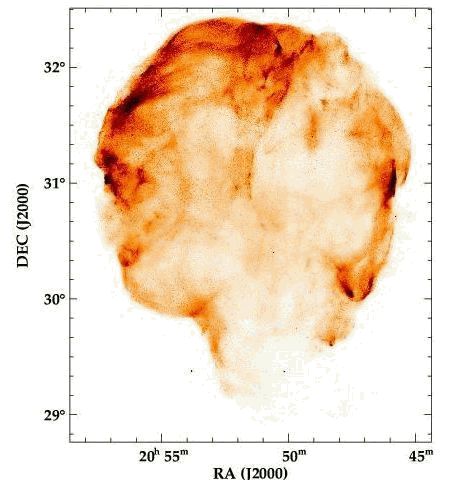
La boucle du Cygne, résidu de supernova, observée par le satellite X ROSAT.
Crédit :
NASA
Un essaimage
Chaque supernova sème dans le milieu interstellaire l'essentiel de son enveloppe stellaire.
Apprendre
 Objectifs
Objectifs
Le passage d'une naine blanche à une étoile à neutrons s'accompagne d'une débauche d'énergie : une supernova de type II.
Neutronisation
La réaction de neutronisation s'accompagne d'un effondrement de l'étoile :
- En l'absence d'électrons, plus de pression de Fermi de leur part.
- Les neutrinos emportent toute l'énergie produite.
- Les réactions de fusion au-delà du fer deviennent endothermiques.
La chute libre de l'objet qui se retrouve hors équilibre se déroule en une durée très brève,
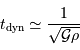
de l'ordre de quelques secondes.

Effondrement d'une naine blanche vers une étoile à neutrons : le rayon stellaire diminue brutalement d'un facteur de l'ordre de 500.
Crédit :
ASM
Energie libérée
L'énergie mise en jeu lors de l'effondrement est gigantesque ; le rapport des rayons est tellement disproportionné que l'on peut écrire :
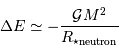
Soit une débauche de l'ordre de 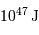 :
:
- 99% part avec les neutrinos.
- 1% en énergie cinétique de l'enveloppe.
- 0.1% en lumière (magnitude absolue
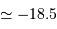 )
)
L'essentiel du pic lumineux est émis en un mois. Il s'ensuit qu'une supernova de type II rayonne durant ce laps de temps quasiment autant qu'une galaxie entière.
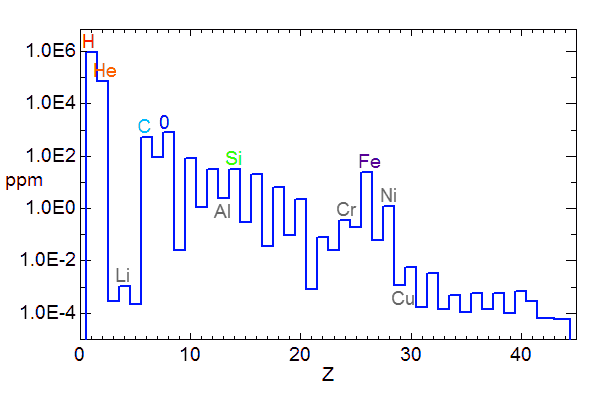
Abondance des éléments, en parties par millions (ppm). Le pic du fer signe le fait que la fusion jusqu'au fer est exothermique, puis endothermique.
Crédit :
ASM
Supernova de type I
Une supernova de type I correspond à un autre événement violent, au sein d'une binaire évoluée où l'un des membres (la primaire) a déjà atteint le stade de naine blanche. Lorsque l'étoile secondaire atteint le stade de géante rouge, un violent transfert de masse peut se créer vers la primaire. Si le taux d'accrétion est suffisamment grand, la primaire atteint la masse limite de Chandrasekhar et finit par exploser en fusionnant carbone et oxygène jusqu'à former les éléments du
pic du fer. Contrairement à une supernova de type II, aucun débris ne subsiste : la totalité des éléments produits va enrichir le milieu interstellaire.
Supernovae type I ou II
| Supernova | Type I | Type II |
| Cause | accrétion | effondrement du cœur |
| Magnitude absolue | -19.5 | -18.5 |
| Spectre | métaux | hydrogène et continu |
| Régions | systèmes stellaires âgés | régions de formation d'étoiles |
| Précurseur | naine blanche dans un système binaire | étoile très massive |
| Déclenchement | transfert de masse du compagnon | effondrement du cœur stellaire |
| Mécanisme | explosion thermonucléaire du cœur carbone/oxygène qui fusionne pour former du fer | onde de choc de rebond de la surface de l'étoile à neutrons |
| Résidu | rien | étoile à neutrons ou trou noir |
| Débris expulsés | principalement du fer | tous les éléments lourds et beaucoup d'hydrogène |
Distinction entre supernova de type I ou II
Trou noir
Observer
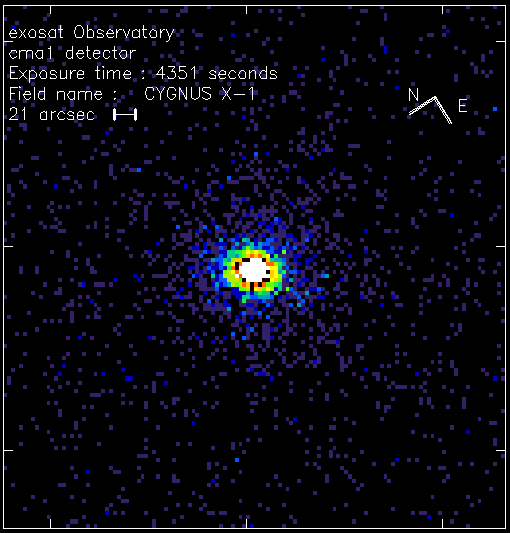
Un candidat trou noir observé par le satellite Exosat de l'ESA, en rayon X.
Crédit :
ESA
Candidats
Les trous noirs stellaires se cachent mieux que les trous noirs au centre d'une galaxie. De nombreux candidats trous noirs stellaire sont recensés. Leur observation reste difficile, associée en fait à des régions d'émissions très énergétiques, mais cachées car de très petit volume.
Le premier candidat,
Cygnus X-1, fut découvert par le satellite Uhuru en lumière X.
Apprendre
 Objectifs
Objectifs
Une étoile de masse centrale supérieure à environ 3 fois la masse du Soleil évolue vers le stade trou noir.
Rayon de Schwarzschild
Le rayon d'une étoile à neutrons diminuant avec la masse
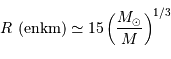
il s'ensuit une masse volumique et une vitesse de libération énormes. La limite 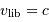 correspond au rayon dit de Schwarzschild
correspond au rayon dit de Schwarzschild
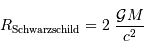 .
.
Le stade de trou noir est atteint : le rayonnement est piégé par
le champ gravitationnel. Un trou noir se signale alors par le
formidable gradient de champ gravitationnel qu'il induit dans son entourage.
Masse d'un trou noir
Pour arriver au stage de trou noir stellaire, une étoile doit
au-moins posséder un noyau de masse centrale supérieure à 3 masses solaires. Ceci correspond à une masse progénitrice initialement bien plus élevée (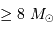 ), mais diminuée des pertes par vent stellaire.
), mais diminuée des pertes par vent stellaire.
Etoiles massives et nucléosynthèse
Observer

L'étoile
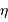
de la Carène, est tellement massive (de l'ordre de 100 fois la masse du Soleil) et lumineuse (5 millions de fois le Soleil), qu'elle sera bientôt en fin de vie, quand bien même elle réside encore dans la nébuleuse qui l'a formée.
Crédit :
ESO/VLT
Etoiles super-massives
Les étoiles les plus massives quittent la séquence principale alors même qu'elles ne sont pas sorties du nuage de matière interstellaire qui les a créées.
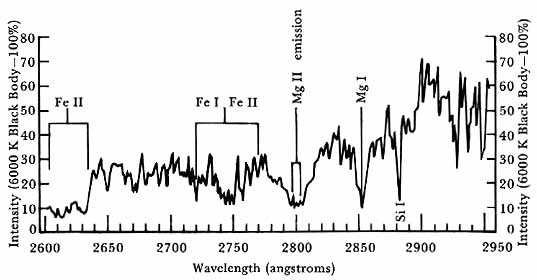
Échantillon du spectre solaire dans l'UV, entre 260 et 295 nm, avec identification des raies.
Crédit :
NASA

Matière éjectée autour de V838, supergéante rouge à 6 kpc du Soleil. La séquence ne montre pas l'expansion de la matière, mais son illumination par une bouffée de photons émis lors d'un sursaut stellaire de l'étoile centrale, qui éclaire séquentiellement l'environnement stellaire.
Crédit :
HST
Eléments chimiques
Un spectre stellaire montre une abondance de raies, avec la signature chimique de tous les éléments de la classification périodique. Ces éléments ont été pour l'essentiel créés lors de l'évolution des étoiles les plus massives, qui les essaiment sous l'influence d'un fort vent stellaire accéléré par la
pression de radiation.

Wolf-Rayet 124. L'enveloppe d'hydrogène est expulsée par le vent stellaire.
Crédit :
HST
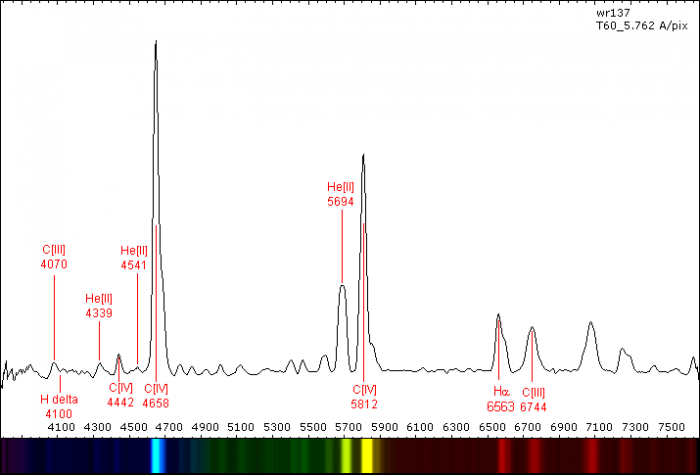
Spectre de l'étoile Wolf-Rayet WR137, avec des raies intenses en émission.
Crédit :
Observatoire du Pic du Midi
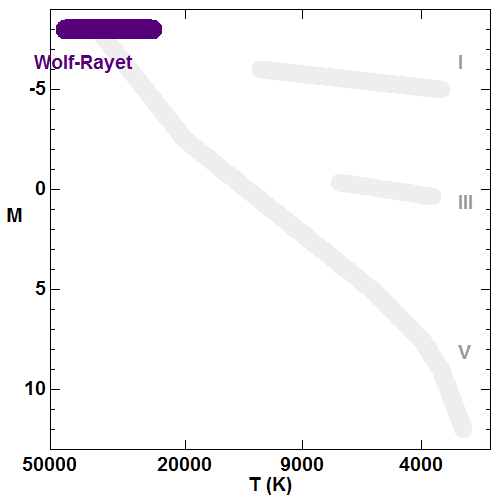
Position des étoiles Wolf-Rayet dans le diagramme HR.
Crédit :
ASM
Wolf-Rayet
Un exemple d'étoiles avec fort vent stellaire est la classe des étoiles de
Wolf-Rayet, de type spectral O, très chaudes. L'intense pression radiative souffle leur enveloppe d'hydrogène et génère une perte de masse importante.
L'enveloppe très chaude d'une Wolf-Rayet produit un spectre en
émission. La diversité des vitesses des couches sondées donne des raies très élargies par effet Doppler-Fizeau.
Apprendre
 Objectifs
Objectifs
Aperçu sur les réactions nucléaires à l'oeuvre dans une étoile très massive.
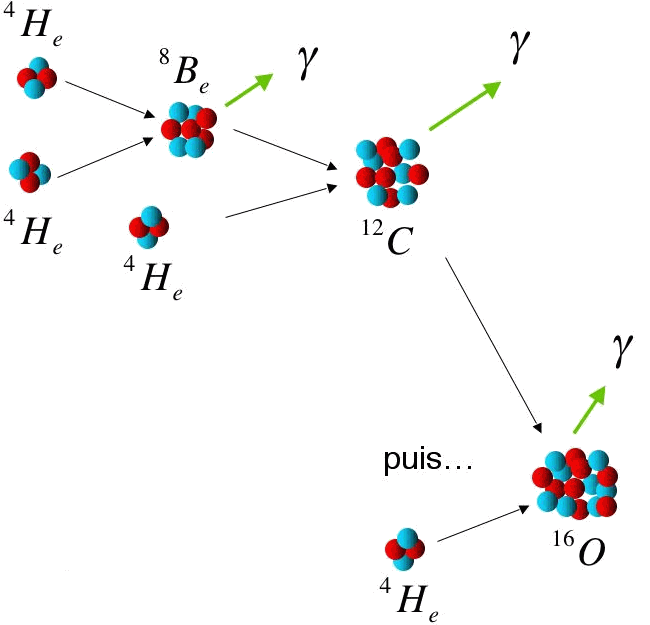
Synthèse triple alpha : 3 hélium donnent 1 carbone.
Crédit :
ASM
Synthèse des éléments lourds
Les hautes températures rencontrées durant les phases énergétiques de la fin de vie des étoiles les plus massives permettent la fusion des éléments jusqu'au fer. Ainsi, la synthèse triple 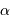 conduit, à partir de 3 noyaux d'hélium, à un noyau de carbone.
conduit, à partir de 3 noyaux d'hélium, à un noyau de carbone.
La température d'ignition augmente avec le nombre de charge des réactifs de la fusion. En revanche, les réactions sont de moins en moins exothermiques, jusqu'au fer.
Etapes
| Etape | Température (K) | Masse volumique (kg/m3) | Durée |
|---|
| Fusion H | 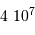 | 5000 | 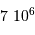 ans ans |
| Fusion He | 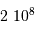 | 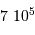 | 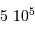 ans ans |
| Fusion C | 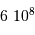 | 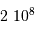 | 600 ans |
| Fusion O | 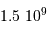 | 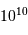 | 6 mois |
| Fusion Si | 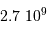 | 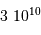 | 1 jour |
| Effondrement du cœur | 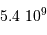 | 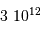 | 1/4 s |
Les étapes de fusion sont de plus en plus courtes, et à forte température.
La limite du fer
Au delà du fer (Z=26, A =56), le bilan des énergies de liaison entre nucléons est défavorable : d'exothermique, la fusion devient endothermique. La forte stabilité du noyau du fer conduit à son pic d'abondance.
Les éléments plus lourds que le fer résultent de phénomène d'addition de neutrons, transmuant des noyaux déjà massifs en éléments encore plus massifs (plomb, or, jusqu'à l'uranium). La lenteur du processus, et les conditions thermodynamiques défavorables, expliquent la faible abondance relative de ces éléments plus lourds que le fer.
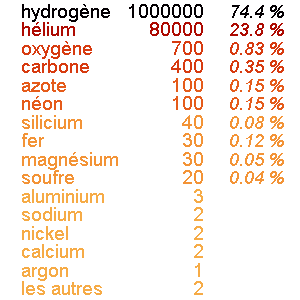
Abondance des différents éléments créés lors du big-bang (H et He essentiellement) puis par nucléosynthèse stellaire.
Crédit :
ASM
Poussières d'étoiles
La pression de radiation générée par les températures élevées conduit à un fort vent stellaire, qui souffle l'enveloppe extérieur (comme pour les étoiles Wolf-Rayet par exemple), et donc conduit à essaimer les matériaux lourds synthétisés dans la forge stellaire. Peu à peu, l'Univers s'enrichit en éléments plus lourds que l'hydrogène et l'hélium créés lors du big-bang.
Evolution
Auteur: B. Mosser
Introduction
Les sections précédentes ont décrit les processus physiques à l'oeuvre au sein des étoiles au cours de leur évolution. Celle-ci présente des résultats issus de modélisations numériques détaillées, et s'intéresse à l'évolution des étoiles de différentes masses dans le diagramme HR.
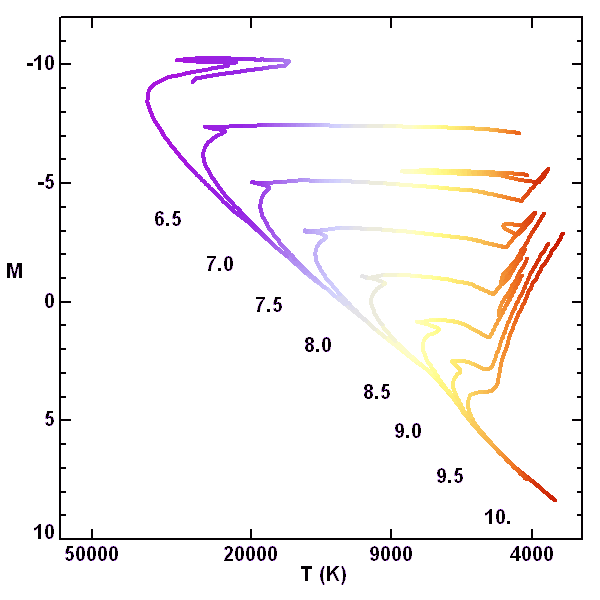
Isochrones d'évolution stellaire.
Crédit :
ASM
Evolution stellaire dans le diagramme HR
Apprendre
Les âges dans le diagramme HR
Lorsqu'une étoile naît à partir de l'effondrement gravitationnel d'un nuage de gaz et que les premières réactions nucléaires démarrent en son coeur et fournissent son processus de rayonnement, elle se retrouve très rapidement sur la séquence principale.
On décrit alors l'étoile comme un système en équilibre entre la gravitation (force d'attraction en direction du centre de l'étoile) et la pression du gaz et du rayonnement (qui pousse vers l'extérieur).
Plus l'étoile est massive, plus elle est chaude et lumineuse (en haut à gauche du diagramme), et plus elle est petite, plus elle se trouve au contraire dans la partie basse, sur la droite du diagramme.
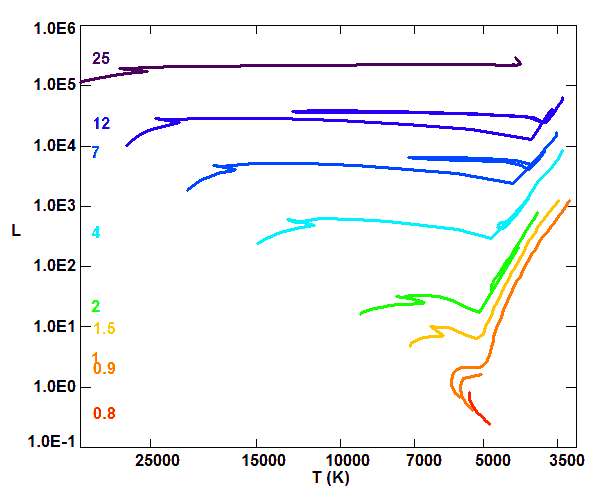
Tracé d'évolution dans le diagramme HR, fonction de la masse stellaire.
Crédit :
ASM
Evolution des étoiles de très faible masse
Pour des étoiles de masse inférieure à la moitié de la masse du Soleil, également appelées naines froides, il n'y a pas de fusion d'éléments plus lourds après la fusion de l'hydrogène. La durée de vie de ces étoiles sur la séquence principale est supérieure à l'âge actuel de l'Univers (environ 14 milliards d'années). Les modèles d'évolution stellaire prévoient que ces étoiles finissent en naines blanches d'hélium... mais il est encore trop tôt pour en observer.
Evolution des étoiles de masse intermédiaire
Entre 0,5 et 7 masses solaires, seuls l'hydrogène puis l'hélium vont pouvoir fusionner dans l'étoile. Sur la séquence principale, il y aura d'abord fusion de l'hydrogène dans le coeur. Puis l'hydrogène va fusionner dans une couche autour du coeur d'hélium.
L'enveloppe de l'étoile se dilate et refroidit : l'étoile devient une géante rouge. La diminution de la température est suffisamment compensée par l'augmentation simultanée du rayon pour faire croître la luminosité. L'étoile monte dans le diagramme HR.
La fusion de l'hélium du coeur peut alors démarrer. L'étoile se recontracte. La fusion de l'hélium va alors produire du carbone et de l'oxygène d'abord dans le coeur. L'étoile redescend dans le diagramme HR.
La fusion du carbone nécessite une température centrale d'environ 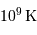 , non atteinte pour ces masses intermédiaires.
, non atteinte pour ces masses intermédiaires.
L'étoile finit en nébuleuse planétaire avec formation au centre d'une naine blanche de carbone et d'oxygène.
Evolution des étoiles les plus massives
À partir de la séquence principale, les éléments de plus en plus massifs fusionnent au coeur de l'étoile. Les éléments moins massifs continuent de fusionner en couches, enrichissant les couches plus profondes en produits de fusion. De forts vents stellaires sont observés.
Lorsque le noyau de fer dépasse la masse limite de Chandrasekhar,
il s'effondre. Le vide créé aspire la matière de l'étoile qui
rebondit et crée une onde de choc qui expulse violemment toutes
les couches externes : c'est une supernova de type II. Le résidu
du coeur de fer effondré forme une étoile à neutrons ou un trou
noir selon sa masse.
Durée de l'évolution
La rapidité de l'évolution et des différentes phases de fusion
nucléaire dépend essentiellement de sa masse et de sa composition chimique initiale. Ainsi une étoile de 1 masse solaire passera environ 10 milliards d'années sur la séquence
principale, contre 20 à 30 milliards d'années pour une étoile d'un dixième de masse solaire,
et seulement quelques millions d'années pour une étoile très massive de 50 masses solaires.
| Masse initiale (en unité de masse solaire) | Fusion | Evolution | Stade final |
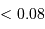 | D | Naine brune, et non étoile | Naine brune |
| 0.08 - 0.5 | H | Evolution très lente, sur une durée de vie supérieure à l'âge de l'Univers | Naine blanche d'hélium (?) |
| 0.5 - 7 | H, puis He | Fin en nébuleuse planétaire | Naine blanche C, O |
| 8 - 25 | H, puis He, puis C et O | Fusion de H sur la séquence principale puis fusion He, C, O... lors de la phase de supergéante rouge. Structure en couche avec un coeur de fer entouré d'éléments de plus en plus légers en train de fusionner | Supernova de type II, puis étoile à neutrons |
|
25+ | idem | idem | Supernova de type II, puis trou noir |
Récapitulatif de l'évolution stellaire.
Simuler

Tracé d'évolution
L'appliquette ci-jointe décrit les étapes de l'évolution d'une étoile en fonction de sa masse : séquence principale de l'âge 0 à la contraction du noyau d'hélium, stade géante rouge...
Le film de l'évolution
Le trajet d'évolution d'une étoile dans le diagramme HR dépend intimement de sa masse. Plusieurs cas sont représentés, pour diverses masses (unité = masse solaire) :
0.8,
1.5,
2,
4,
7,
25  .
.
L'échelle de temps, adaptée à chaque cas en fonction de la rapidité de l'évolution, n'est pas linéaire. Les étoiles, sauf les plus massives, vont longtemps stationner sur la séquence principale, puis plus rapidement évoluer vers les stades ultimes lorsque la réserve d'énergie s'épuise.
Evolution d'une étoile de 0.8 masse solaire dans le diagramme HR. Son évolution est très lente, et elle quitte à peine la séquence principale... à un âge supérieur à celui de l'Univers.
Crédit :
ASM
Evolution d'une étoile de 1.5 masse solaire dans le diagramme HR, qui évolue vers le stade de géante rouge (puis nébuleuse planétaire, non représentée sur l'animation)
Crédit :
ASM
Evolution d'une étoile de 2 masses solaires dans le diagramme HR. L'évolution est rapide (durée de vie sur la séquence principale de l'ordre du milliard d'années). En fin de vie, l'étoile brûle de l'hélium.
Crédit :
ASM
Evolution d'une étoile de 4 masses solaires dans le diagramme HR. L'évolution est très rapide (durée de vie sur la séquence principale de l'ordre de 150 millions d'années). En fin de vie, l'étoile brûle de l'hélium.
Crédit :
ASM
Evolution d'une étoile de 7 masses solaires dans le diagramme HR. Evolution très rapide, et fin de vie comme supergéante brûlant de l'hélium.
Crédit :
ASM
Evolution d'une étoile de 25 masses solaires dans le diagramme HR. Evolution extrêmement rapide. L'étoile en fin de vie, supergéante rouge, fusionne tous les éléments jusqu'au fer.
Crédit :
ASM
S'évaluer
 Population stellaire
Population stellaire
Difficulté : ☆
Temps : 15 min
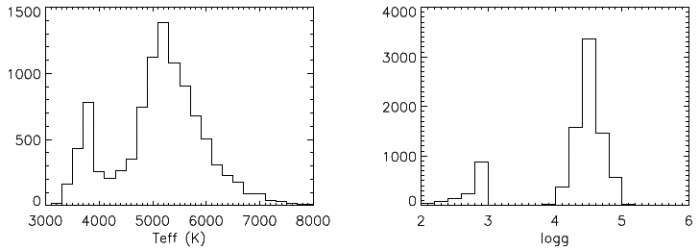
Histogrammes des températures effectives et du champ de gravité de surface (traduit par la valeur
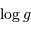
(avec
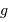
en g cm
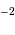
) d'étoiles observées par CoRoT.
Crédit :
CoRoT/CNES
Le satellite CoRoT observe différents champs stellaires. Une modélisation des cibles conduit aux histogrammes de leur température effective et de leur champ de gravité de surface (traduit par la valeur 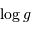 (avec
(avec 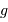 en cm s
en cm s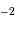 ).
).
Question 1)
Rappeler comment sont déterminées observationnellement les paramètres considérés.
[2 points]
Question 2)
Identifier les 2 populations stellaires qui dominent les observations.
[2 points]
Déterminer la valeur de log g pour le Soleil peut être utile.
Pour le Soleil, dans les unités choisies, 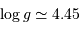 .
.
Question 3)
On s'intéresse au pic principal de la distribution. Expliquer les raisons de la décroissance aux plus faibles et plus fortes températures.
[2 points]
2 pistes à étudier : 1) les performances de tout collecteur, nécessairement limité vers les faibles luminosités 2) la durée de vie des étoiles.
Age des amas
Observer
Isochrones

Diagramme HR représentatif d'un amas d'étoiles, en fonction de son âge (donné via le logarithme de l'âge exprimé en années).
Crédit :
ASM
M67

Amas ouvert M67, d'âge avancé.
Crédit :
Catalogue NGC
NGC2363

Amas ouvert NGC 2362, entourant l'étoile tau de la constellation du Grand Chien.
Crédit :
Catalogue NGC
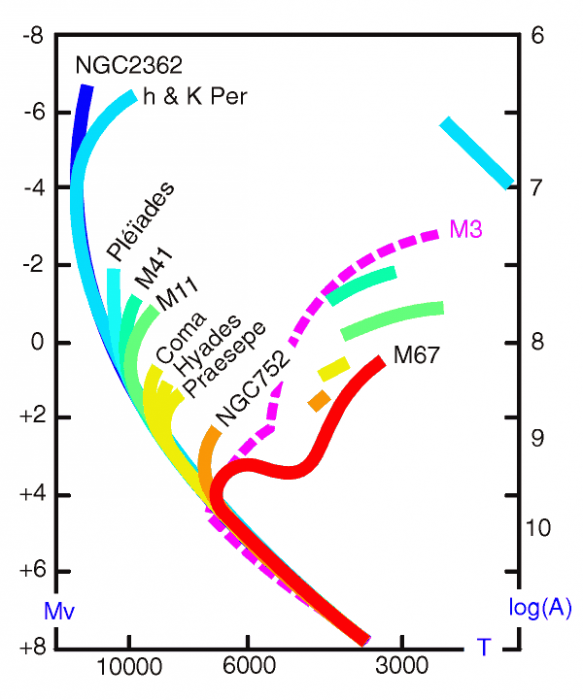
Evolution de différents amas. M67, âgé, ne comprend plus aucune étoile bleue ; NGC2363 est en revanche un amas très jeune, avec de nombreuses étoiles massives et brillantes.
Crédit :
Université de Lyon
Evolution
Les étoiles d'un amas, nées simultanément, évoluent différentiellement selon leur masse. Les courbes isochrones (de même âge) le montrent clairement : les plus massives atteignent très rapidement leur stade ultime, et donc quittent rapidement la séquence principale, quand les moins massives y restent sur une durée plus longue que l'âge actuel de l'Univers. Un amas âgé ne contiendra donc pas d'étoiles jeunes, contrairement à un amas jeune.
Amas plus ou moins jeunes
L'allure du diagramme HR d'un
amas renseigne donc sur son âge.
L'absence d'étoiles bleues et chaudes signe un âge avancé.
Apprendre
 Objectifs
Objectifs
Les étoiles d'un amas ayant le même âge. Par ailleurs elles évoluent en fonction de leur masse. L'étude de la population des amas permet la détermination de leur âge.
Evolution
Au cours de leur évolution, les amas se dépeuplent des étoiles les plus massives. Il s'ensuit que le diagramme HR d'un amas âgé montre une séquence principale uniquement peuplée d'étoiles froides, et de géantes rouges : plus un amas est âgé, plus il est dépeuplé en étoiles chaudes.
Simuler
Evolution
Les étoiles d'un amas, nées simultanément, évoluent différentiellement selon leur masse. Les plus massives atteignent très rapidement leur stade ultime, quand les moins massives ne quittent pas la séquence principale.
Diagramme HR représentatif d'un amas, en fonction de son âge (donné via le logarithme de l'âge exprimée en années).
Crédit :
ASM
Mesure de l'âge d'un amas par ajustement de séquence principal
Voir les simulations proposées à la page.
Réponses aux QCM
pages_accretion-echauffement/accretion-echauffement-sexercer.html
QCM
- Question 1
Solution : réponse 1)
(
En effet
)
- Question 2
Solution : réponse 3)
(
OK
)
- Question 3
Solution : réponse 2)
(
OK
)
pages_milieu-interstellaire/milieu-interstellaire-sexercer.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 1)
pages_critere-jeans/critere-jeans-sexercer.html
QCM
- Question 1
Solution : réponse 1)
(
Grâce à la pression cinétique
)
- Question 2
Solution : réponse 2)
(
En effet
)
- Question 3
Solution : réponse 2)
(
En effet, plus il est massif, plus il aura envie de s'effondrer sous sa propre gravitation.
)
- Question 4
Solution : réponse 3)
(
En effet, on ne peut pas décider, vu les rôles antagonistes de la température et de la densité.
)
pages_temps-evolution/temps-evolution-sexercer.html
QCM
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 1)
(
En effet, mais avec beaucoup d'hypothèses
)
- Question 3
Solution : réponse 2)
(
En effet, car le processus de rayonnement enclanche tout ce qui suit
)
- Question 4
Solution : réponse 2)
- Question 5
Solution : réponse 3)
- Question 6
Solution : réponse 3)
- Question 7
Solution : réponse 1)
Réponses aux exercices
pages_physique-evolution/pression-centrale-sexercer.html
Exercice
'Compression gravitationnelle'
- Question 1
Aide :
Pour cette distribution sphérique :
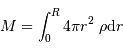
Solution :
Par application de la définition de la masse totale :
![M = \int_0^R 4\pi r^2\ \rho {\mathrm{d}} r = 4\pi \beta \ \int_0^R r^{\alpha+2} {\mathrm{d}} r = 4\pi \beta \ \left[ {r^{\alpha+3}\over \alpha+3} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation27.png)
Si 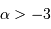 , alors :
, alors :
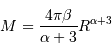
D'où l'expression demandée :
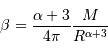
- Question 2
Aide :
Pour des calculs plus simples, on écrit :
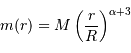
Aide :
Par définition :
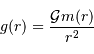
Solution :
De l'expression de la masse totale trouvée précédemment, on peut déduire de la même façon :
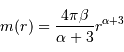
(seule la borne d'intégration supérieure a changé). On en déduit :
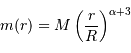
Ensuite, la définition du champ gravitationnel donne :
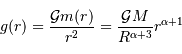
Il semble nécessaire d'avoir un exposant 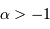 , afin d'éviter que le champ ne diverge au centre.
, afin d'éviter que le champ ne diverge au centre.
- Question 3
Aide :
Mener le calcul, du centre vers la surface :
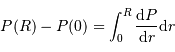
Solution :
On cherche à intégrer la pression du centre 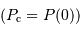 vers la surface
vers la surface 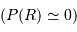 :
:
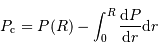
On suppose la pression de surface totalement négligeable. Il reste alors, en fonction de ce qui précède :
![P _{\mathrm{c}} = \int_0^R \rho g\ {\mathrm{d}} r = \int_0^R \beta r^\alpha \ { {\cal G} M \over R^{\alpha+3}} r^{\alpha+1} {\mathrm{d}} r = \beta { {\cal G} M \over R^{\alpha+3}} \int_0^R r^{2\alpha+1} {\mathrm{d}} r = {\alpha+3 \over 4\pi}\ { {\cal G} M^2 \over R^{2\alpha+6}} \left[ {r^{2\alpha+2}\over 2\alpha+2} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation45.png)
L'expression du champ a conduit à la restriction 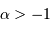 ; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
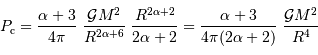
- Question 4
Aide :
Traduire l'uniformité de la masse volumique sur l'exposant 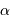 .
.
Aide :
Est-il normal de retrouver 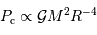 ?
?
Solution :
Retrouver 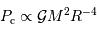 est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel
est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel 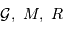 .
.
Si la masse volumique est uniforme, c'est à dire si 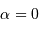 , on trouve :
, on trouve :
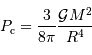
Si la masse volumique pointe vers le centre, c'est àdire 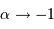 , on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la partie cours, dans le cas du Soleil.
, on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la partie cours, dans le cas du Soleil.
pages_physique-evolution/pression-centrale-sexercer.html
Exercice
'Ainsi fond, fond, fond...'
- Question 1
Aide :
Le champ gravitationnel vaut 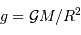 .
.
Solution :
Monter d'une hauteur 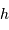 la masse considérée coûte en énergie, dans le champ
la masse considérée coûte en énergie, dans le champ 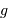 supposé uniforme :
supposé uniforme :
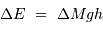
- Question 2
Aide :
Comparer les énergies en jeu.
Solution :
L'énergie gravitationnelle comparée à l'énergie de fusion montre que la dépense énergétique peut faire fondre la base si
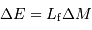 , et donc si :
, et donc si :
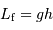
AN: 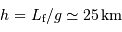
- Question 3
Solution :
A un facteur 3 près, ça semble se tenir.
- Question 4
Aide :
Ne pas se laisser désarçonner par les hypothèses, qui restent en ordre de grandeur très convenables.
Solution :
L'égalité dans le cas limite, 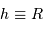 , et la définition de la masse pour une masse volumique uniforme
, et la définition de la masse pour une masse volumique uniforme
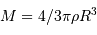 conduisent à :
conduisent à :
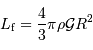
soit
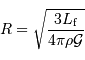
AN : 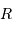 de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.
de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.
pages_physique-evolution/pressions-sexercer.html
Exercice
'Pression de Fermi'
- Question 1
Solution :
La relation de Heisenberg s'écrit, en notant 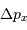 et
et 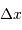 les incertitudes respectives.
les incertitudes respectives.
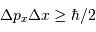
Pour la suite, on considèrera le cas
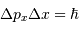
- Question 2
Aide :
Faire le lien entre la densité particulaire 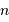 et le volume moyen par particule.
et le volume moyen par particule.
Aide :
S'intéresser à l'encombrement au sein du gaz, en estimant qu'une particule occupe un volume de l'ordre de 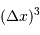 .
.
Solution :
Une densité particulaire 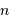 correspond à un volume par particule
correspond à un volume par particule 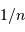 .
Ce volume par particule est lui-même de l'ordre de
.
Ce volume par particule est lui-même de l'ordre de 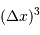 . On en déduit :
. On en déduit :
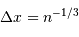
- Question 3
Aide :
La distribution de vitesse maxwellienne varie comme
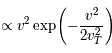 avec
avec 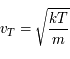
Aide :
Faire un schéma.
Solution :
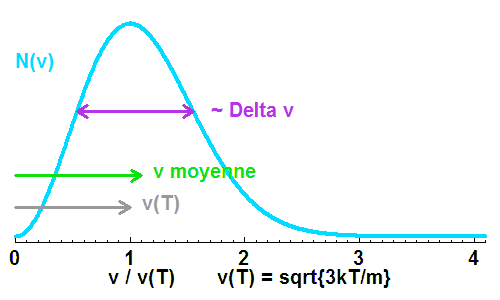
Distribution de vitesse maxwellienne.
Crédit :
ASM
L'examen de la figure montre que vitesse moyenne et écart-type sont du même ordre de grandeur. On confond donc 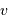 et
et 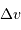 .
.
- Question 4
Aide :
Pour un gaz classique : 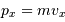 .
.
Aide :
Éliminer des relations précédentes les variables de quantité de mouvement et de position au profit de la densité particulaire.
Solution :
Pour un gaz classique, la quantité de mouvement s'écrit 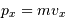 .
.
De 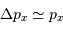 et
et 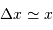 on tire :
on tire :
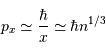
Puis
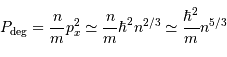
- Question 5
Aide :
Comparer les masses en jeu.
Solution :
Comme le rapport des masses entre le proton et l'électron vaut 2000, s'il y a des électrons, la pression électronique domine largement.
- Question 6
Aide :
Se servir de la neutralité électrique.
Aide :
L'essentiel de la masse se retrouve dans les nucléons.
Solution :
La neutralité électrique assure 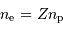 .
.
L'essentiel de la masse se retrouve dans les nucléons : 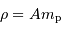 .
.
On retrouve alors le résultat du cours.
pages_physique-evolution/energie-potentielle-gravitationnelle-sexercer.html
Exercice
'Calcul de l'énergie potentielle'
- Question 1
Aide :
Rappel : la masse volumique est supposée uniforme.
Solution :
Par définition :
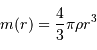
Le champ gravitationnel créé par cette masse à une distance 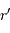 vaut :
vaut :
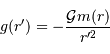
Le signe négatif rend compte de l'attraction gravitationnelle, et il faut bien distinguer les variables 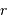 , rayon actuel de l'objet en cours de formation, et
, rayon actuel de l'objet en cours de formation, et 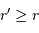 , distance à cet objet.
, distance à cet objet.
- Question 2
Aide :
Le travail total est la somme des contributions des travaux de l'infini à la surface de l'objet
Solution :
À partir d'une étape élémentaire, on somme pour obtenir le travail
total :
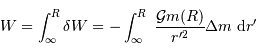
L'intégration donne :
![W = + \left[ { {\cal G} m(M) \over r'}\ \Delta m \right]_\infty^R](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation20.png)
On en tire
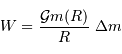
Le travail de l'opérateur est l'opposé de la variation d'énergie potentielle de l'objet entre les 2 états considérés.
- Question 3
Aide :
2 moyens de procéder au calcul, en interprétant l'usage de la notation différentielle, ou bien en raisonnant géométriquement.
Aide :
L'usage de la notation différentielle doit permettre de passer de 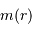 à
à 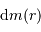 .
.
Solution :
L'accroissement de la masse 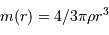 s'écrit par différentiation :
s'écrit par différentiation :
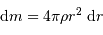
on y reconnaît la masse d'une coquille d'épaisseur 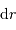 et de surface
et de surface 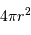 .
.
On a donc :
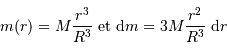
- Question 4
Solution :
De l'expression du travail élémentaire qui précède, on tire l'expression de la variation d'énergie potentielle d'interaction gravitationnelle sur une étape élémentaire :
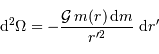
Avec 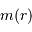 la masse accrétée au rayon
la masse accrétée au rayon 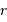 et
et 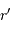 une position entre
une position entre 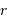 et
et 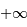 . Une première étape d'intégration conduit à apporter la masse
. Une première étape d'intégration conduit à apporter la masse 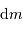 de l'infini à la surface :
de l'infini à la surface :
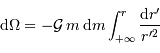
Le calcul de l'intégrale donne ![\left[ - \displaystyle{1\over r'}\right]_\infty^r = - \displaystyle{1\over r}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation46.png) . D'où la variation de potentiel :
. D'où la variation de potentiel :
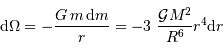
après avoir remplacé 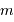 et
et 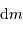 par leur valeurs.
Et donc finalement :
par leur valeurs.
Et donc finalement :
![\Omega = \int_0^R {\mathrm{d}} \Omega = \left[ - 3 { {\cal G} M^2\over R^6} {r^5\over 5} \right]_0^R = -{3\over 5} { {\cal G} M^2\over R}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation50.png)
On retrouve ce résultat classique. L'expression est homogène ; le signe négatif rappelle que la formation d'une concentration de matière a dégagé de l'énergie (ou qu'il faut en dépenser pour démonter l'objet).
pages_physique-evolution/theoreme-viriel-sexercer.html
Exercice
'Démonstration du théorème du viriel, dans un cas simplement modélisé'
- Question 1
Aide :
Il suffit d'introduire l'équation d'état du gaz parfait chaud.
Solution :
Avec l'équation d'état du gaz parfait 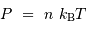 , on introduit simplement la pression, pour obtenir :
, on introduit simplement la pression, pour obtenir :
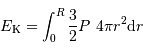
- Question 2
Aide :
On peut par exemple commencer par écrire l'énergie potentielle sous forme intégrale
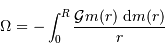
Aide :
On a aussi besoin de la définition de la masse d'une coquille d'épaisseur 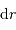 au rayon
au rayon 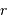 :
:
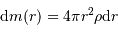
Solution :
La définition de l'énergie potentielle est :
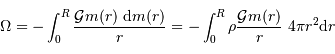
On introduit le gradient de pression, via ce que donne l'équilibre
hydrostatique, sans oublier au passage que 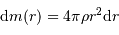 :
:
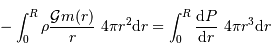
On en déduit :
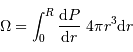
- Question 3
Aide :
L'intégration par parties donne
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation22.png)
Aide :
Montrer que l'un des 2 termes de l'intégration par parties est nul.
Solution :
Par parties :
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation23.png)
Le terme tout intégré est nul, car nul aux 2 bornes (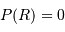 ).
).
- Question 4
Aide :
Tout le travail est fait, il n'y a plus qu'à comparer.
Solution :
On a vu pour l'énergie cinétique :
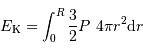
Et pour l'énergie potentielle :
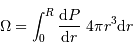
L'égalité trouvée précédemment :
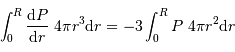
conduit alors à :
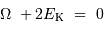
On retrouve donc le théorème du viriel dans un cas particulier.
pages_physique-evolution/theoreme-viriel-sevaluer.html
Exercice
'Energie d'accrétion'
pages_naissance/amas-stellaire-sevaluer.html
Exercice
'Jeune et ouvert ; vieux et fermé'
pages_vie/fusion-nucleaire-sexercer.html
Exercice
'Température de fusion'
- Question 1
Aide :
Exprimer l'énergie de la barrière coulombienne.
Aide :
Exprimer la condition énergétique limite à remplir en 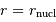
Solution :
L'énergie totale d'un proton s'écrit :
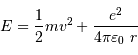
Pour passer la barrière coulombienne en 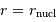 , le proton doit avoir une énergie vérifiant :
, le proton doit avoir une énergie vérifiant :
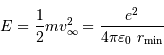
(énergie potentielle nulle à l'infini, énergie cinétique nulle au niveau de la barrière).
- Question 2
Aide :
Faire le lien entre l'énergie cinétique et la température.
Solution :
La température minimale vérifie :
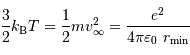
Soit :
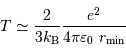
- Question 3
Solution :
Avec les valeurs proposées, on trouve :
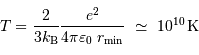
Cette valeur est surestimée, car ne prend pas en compte les phénomènes quantiques qui relaxent considérablement les conditions de fusion.
- Question 4
Aide :
Réécrire le potentiel électrostatique en fonction de 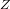 .
.
Aide :
L'effet varie comme 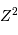
Solution :
Les équations précédentes se réécrivent avec la nouvelle énergie potentielle
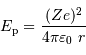
Il s'ensuit une température de fusion :
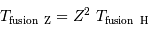
La valeur de la température est encore plus élevée que pour l'hydrogène.
pages_vie/fusion-nucleaire-sexercer.html
Exercice
'Du rôle de l'effet tunnel et de la distribution des vitesses'
- Question 1
Aide :
Déterminer les expressions des énergies cinétique et potentielle, ainsi que leurs valeurs particulières à grande distance ou à la distance minimale d'approche.
Aide :
Voir l'exercice
précédent
Solution :
L'exercice consacré à ce raisonnement donne la
solution. Avec les notations ici proposées :
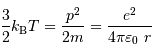
- Question 2
Aide :
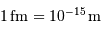
Solution :
L'application numérique donne :
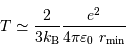
- Question 3
Aide :
La relation d'incertitude présentée ici se traduit par
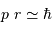
Aide :
L'égalité entre l'énergie cinétique à grande distance 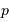 et l'énergie potentielle à distance minimale
et l'énergie potentielle à distance minimale 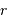 donne une autre relation entre ces 2 variables.
donne une autre relation entre ces 2 variables.
Solution :
En notant simplement 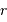 la distance minimale d'approche, et
la distance minimale d'approche, et 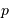 la quantité de mouvement incidente, l'équation énergétique dit :
la quantité de mouvement incidente, l'équation énergétique dit :
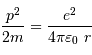
La relation d'incertitude présentée ici se traduit par
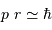 On en déduite la valeur de
On en déduite la valeur de 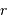 , en éliminant
, en éliminant 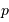 :
:
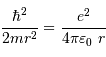
Et donc on aboutit à la nouvelle position (ou incertitude de position, d'après la présentation de l'énoncé) :
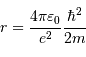
- Question 4
Solution :
L'application numérique donne :
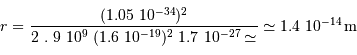
Cette distance est plus grande que 1 fm. Les protons peuvent donc se "tromper", et se croire en train de fusionner alors qu'ils sont 14 fois trop éloignés.
La température de fusion décroît de ce même facteur 14, soit de l'ordre de 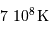 .
.
- Question 5
Aide :
Estimer les conséquences de ces protons rapides en termes énergétiques, puis de température.
Solution :
Un proton 3 fois plus rapide est 9 fois plus énergétique que la moyenne. On gagne donc ainsi un facteur 9 sur la température, soit la possibilité de fusion dès 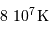 .
.
Ceci reste trop élevé, car la modélisation de l'effet tunnel est trop simpliste, mais montre comment l'estimation purement classique de la température de fusion est déjà surdimensionnée d'un facteur 120.
pages_vie/masse-etoile-sexercer.html
Exercice
'Masse et rayon sismiques'
- Question 1
Aide :
Identifier dans l'expression de 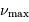 ce qui peut ressemble au
champ gravitationnel d'une étoile.
ce qui peut ressemble au
champ gravitationnel d'une étoile.
Aide :
Comment se traduit le fait que l'on considère des étoiles de même
type spectral ?
Solution :
Le champ gravitationnel d'une étoile varie en 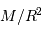 , comme
, comme
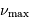 , dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et
, dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et 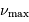 porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
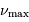 plus élevée, et réciproquement.
plus élevée, et réciproquement.
- Question 2
Aide :
La réponse est quasiment à la question précédente.
Solution :
La mesure de 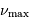 , identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
, identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
- Question 3
Aide :
Exprimer la masse volumique moyenne en fonction des masse et
rayon stellaire.
Aide :
Quel lien entre 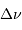 et la masse volumique moyenne ?
et la masse volumique moyenne ?
Solution :
L'examen de la définition de 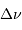 montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
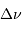 qu'une étoile plus dense.
qu'une étoile plus dense.
- Question 4
Aide :
Faites chauffer le calcotron.
Solution :
La géante, 10 fois plus grande que le Soleil, présente un volume
1000 fois plus important, donc une densité 31 fois moindre, et
donc 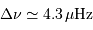 . Pour
. Pour 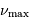 , l'application
numérique donne
, l'application
numérique donne 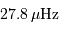 .
.
- Question 5
Aide :
Désolé, pas d'autre solution que retrousser ses manches et
inverser les équations de départ !
Solution :
L'inversion donne :
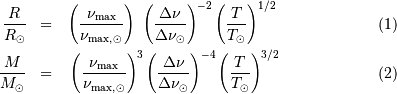
- Question 6
Solution :
Ce n'est pas tous les jours qu'une technique observationnelle
donne accès à la masse et au rayon de l'étoile relativement
précisément, et indépendamment de toute mesure de distance !
pages_vie/masse-etoile-sevaluer.html
Exercice
'De nouvelles classes spectrales ?'
pages_vie/masse-luminosite-sexercer.html
Exercice
'Amplitude des oscillations'
- Question 1
Aide :
Comment varie la luminosité sur la séquence principale ?
Solution :
Avec, sur la séquence principale, 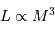 , on trouve :
, on trouve :
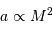 . L'amplitude des oscillations augmente vers les types spectraux plus massifs.
. L'amplitude des oscillations augmente vers les types spectraux plus massifs.
- Question 2
Solution :
La luminosité du corps noir donne directement :
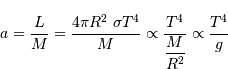
pages_vie/definition-etoile-evaluer.html
Exercice
'Populations stellaires'
- Question 1
Aide :
Aller raffraichir ses souvenirs de mécanique du point.
Aide :
Dans le cours FSU c'est là .
- Question 2
Aide :
Les valeurs des masses et rayons solaires sont données par le calcotron !
Aide :
Attention aux unités !
- Question 3
- Question 4
Aide :
Se servir de ce qui précède.
- Question 5
Aide :
Voir du côté des plus faibles gravités.
Aide :
Quelle masse typique pour une géante typique ?
pages_mort/naine-blanche-sevaluer.html
Exercice
'Champ gravitationnel et vitesse de libération'
pages_evolutionstellaire/evolution-stellaire-hr-sevaluer.html
Exercice
'Population stellaire'
- Question 1
Aide :
Pour la température effective, voir le cours correspondant sur les types spectraux.
Pour log g, voir le cours correspondant sur les classes de luminosité.
- Question 2
Aide :
Déterminer la valeur de log g pour le Soleil peut être utile.
Aide :
Pour le Soleil, dans les unités choisies, 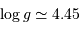 .
.
- Question 3
Aide :
2 pistes à étudier : 1) les performances de tout collecteur, nécessairement limité vers les faibles luminosités 2) la durée de vie des étoiles.



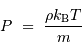
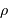 la masse volumique, et
la masse volumique, et 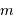 la masse d'une particule élémentaire du gaz.
la masse d'une particule élémentaire du gaz.
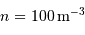 .
.
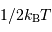 par degré de liberté. L'énergie cinétique de translation vaut
par degré de liberté. L'énergie cinétique de translation vaut 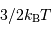 . Pour une collection de
. Pour une collection de 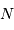 particules, l'énergie cinétique totale se monte tout simplement à
particules, l'énergie cinétique totale se monte tout simplement à 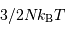 .
.
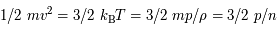 .
avec
.
avec 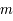 la masse d'une particule et
la masse d'une particule et 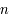 la densité particulaire. On en déduit :
la densité particulaire. On en déduit :
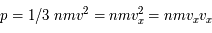 avec
avec 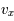 la composante de la vitesse selon un seul axe (le milieu étant supposé homogène et isotrope :
la composante de la vitesse selon un seul axe (le milieu étant supposé homogène et isotrope : 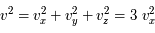 . On retrouve bien le flux de quantité de mouvement
. On retrouve bien le flux de quantité de mouvement 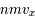 .
.


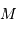 et rayon
et rayon 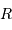 . Elle vaut :
. Elle vaut :
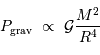
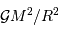 étant homogène à une force.
étant homogène à une force.
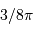 ; comme vérifié en
; comme vérifié en 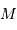 (kg)
(kg)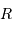 (km)
(km) 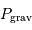 (Pa)
(Pa)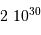
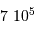
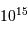
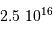
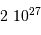
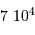
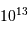
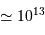
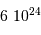
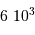
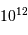
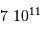
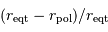 .
.
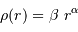 .
.
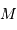 et le rayon extérieur
et le rayon extérieur 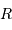 . En déduire l'expression du coefficient
. En déduire l'expression du coefficient 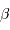 en fonction de ces grandeurs.
en fonction de ces grandeurs.
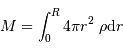
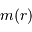 et le champ gravitationnel en un point de rayon
et le champ gravitationnel en un point de rayon 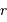 . Quelle condition sur l'exposant
. Quelle condition sur l'exposant 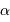 garantit que le champ ne diverge pas ?
garantit que le champ ne diverge pas ?
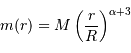
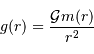
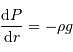
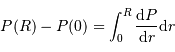
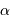 .
.
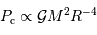 ?
?

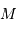 et rayon
et rayon 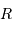 , pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
, pour en déduire la transition entre un objet sphérique et un autre ressemblant plutôt, comme les noyaux cométaires, à une grosse cacahuète.
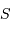 et hauteur
et hauteur 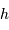 , dans le champ gravitationnel uniforme de la planète.
, dans le champ gravitationnel uniforme de la planète.
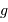 . Déterminer l'énergie supplémentaire pour rajouter au sommet une masse
. Déterminer l'énergie supplémentaire pour rajouter au sommet une masse 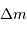 , en fonction de
, en fonction de 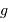 et
et 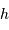 .
.
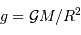 .
.
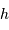 , pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches
, pour laquelle la couche rajoutée au sommet va conduire à faire fondre une couche équivalente à la base de la montagne. L'exprimer en fonction de la chaleur latente de fusion des roches 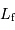 . Faire l'application numérique pour la Terre, avec
. Faire l'application numérique pour la Terre, avec 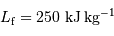 .
.
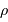 la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de
la masse volumique uniforme de la planète, en déduire le rayon minimum d'une planète sphérique, défini pour des montagnes de hauteur égale au rayon de la planète. Faire l'application numérique avec une masse volumique crustale (de la croûte terrestre) de 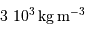 .
.
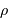 à la température
à la température 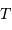 , composé de particules de masse
, composé de particules de masse 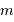 :
:
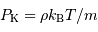
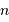 , la définition devient :
, la définition devient :
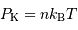
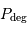 des électrons (s'il y a des électrons).
Ce terme de pression révèle la nature quantique de la matière : les électrons sont des fermions. Quand ces effets quantiques apparaissent, c'est que la densité de matière devient suffisamment importante pour négliger dans un premier temps l'agitation cinétique.
des électrons (s'il y a des électrons).
Ce terme de pression révèle la nature quantique de la matière : les électrons sont des fermions. Quand ces effets quantiques apparaissent, c'est que la densité de matière devient suffisamment importante pour négliger dans un premier temps l'agitation cinétique.
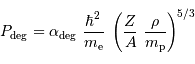
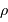 la masse volumique, et
la masse volumique, et 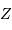 et
et 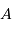 respectivement la charge et le nombre de masse des atomes en présence. La constante
respectivement la charge et le nombre de masse des atomes en présence. La constante 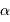 est un nombre : le calcul précis donne
est un nombre : le calcul précis donne 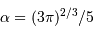 .
.
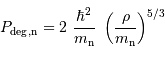
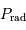 du gaz de photons à la température
du gaz de photons à la température 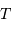 s'exprime par :
s'exprime par :
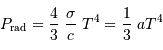
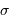 est la constante de Stefan-Boltzmann :
est la constante de Stefan-Boltzmann :
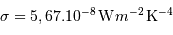 .
La grandeur
.
La grandeur 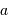 s'écrit :
s'écrit :
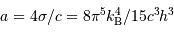 . En unité SI,
. En unité SI, 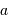 vaut
vaut
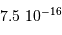 . La dépendance de cette pression avec la puissance quatrième de la température est bien sûr reliée au spectre du
. La dépendance de cette pression avec la puissance quatrième de la température est bien sûr reliée au spectre du 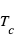 centrale (en million de Kelvin) et de la masse volumique
centrale (en million de Kelvin) et de la masse volumique 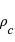 centrale (en unité
centrale (en unité 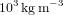 ). Le but de la simulation est d'estimer le terme de pression dominant au centre de l'étoile, en fonction de sa masse. On mènera les calculs avec des pressions exprimées en unité 1 Gbar (1 milliard de fois la pression atmosphérique, soit
). Le but de la simulation est d'estimer le terme de pression dominant au centre de l'étoile, en fonction de sa masse. On mènera les calculs avec des pressions exprimées en unité 1 Gbar (1 milliard de fois la pression atmosphérique, soit 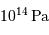 ).
).
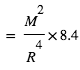 ] pour avoir la bonne unité
] pour avoir la bonne unité
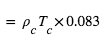 ]
]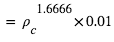 ]
]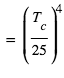 ]
]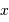 d'une particule sur un axe et sa quantité de mouvement
d'une particule sur un axe et sa quantité de mouvement 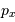 .
.
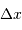 à la densité particulaire
à la densité particulaire 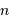 .
.
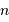 et le volume moyen par particule.
et le volume moyen par particule.
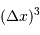 .
.
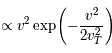 avec
avec 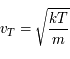
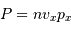
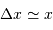 ), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
), montrer que pour un gaz classique la pression de dégénérescence s'écrit :
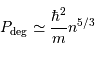
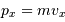 .
.

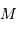 et rayon
et rayon 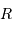 . Quelle énergie peut-on lui associer de par sa gravitation ?
. Quelle énergie peut-on lui associer de par sa gravitation ?
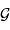 :
:
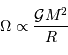
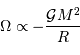
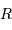 et masse
et masse 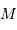 . Dans cette modélisation, on suppose qu'à tout moment la masse volumique
. Dans cette modélisation, on suppose qu'à tout moment la masse volumique 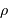 est uniforme.
est uniforme.
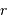 et une masse
et une masse 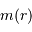 . Déterminer cette masse, ainsi que son champ gravitationnel.
. Déterminer cette masse, ainsi que son champ gravitationnel.
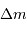 depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
depuis l'infini jusqu'à la surface de cet objet.
On définit ce travail par une étape élémentaire (déplacement
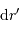 ):
):
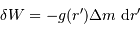
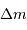 sert à construire l'objet. L'exprimer en fonction de l'accroissement de rayon
sert à construire l'objet. L'exprimer en fonction de l'accroissement de rayon 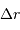 . Pour simplifier, on suppose ces 2 grandeurs petites, et l'on utilise en conséquence la notation différentielle
. Pour simplifier, on suppose ces 2 grandeurs petites, et l'on utilise en conséquence la notation différentielle 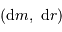 . Exprimer alors
. Exprimer alors 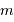 et
et 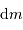 en fonction de la masse totale finale
en fonction de la masse totale finale 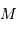 , des rayons
, des rayons 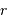 et
et 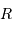 , et l'accroissement
, et l'accroissement 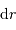 .
.
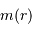 à
à 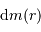 .
.


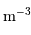 ), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement
), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement 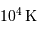 en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement
en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement 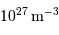 ).
).
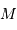 de gaz conduisant à un corps condensé de rayon
de gaz conduisant à un corps condensé de rayon 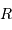 donne une température centrale variant comme
donne une température centrale variant comme 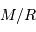 , d'autant plus élevée que le corps est massif et dense.
, d'autant plus élevée que le corps est massif et dense.
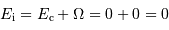
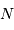 atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de
atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de 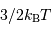 par nucléon :
par nucléon :
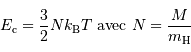
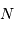 atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours
atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours 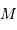 la masse concernée, et
la masse concernée, et 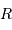 le rayon final de l'objet condensé.
le rayon final de l'objet condensé.
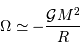
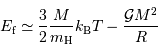

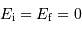
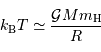
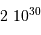
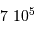
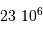
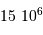
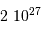
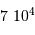
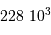
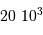
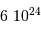
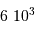
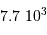
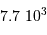

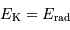 .
.
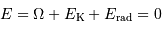
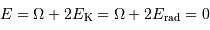
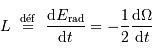
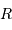 , obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
, obéit à l'équation d'état du gaz parfait classique. On suppose également qu'il possède la symétrie sphérique. La pression est à l'équilibre hydrostatique.
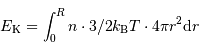 .
Réécrire cette intégrale en fonction de la pression.
.
Réécrire cette intégrale en fonction de la pression.
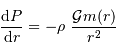
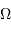 peut s'écrire sous la forme d'une intégrale du gradient de la pression.
peut s'écrire sous la forme d'une intégrale du gradient de la pression.
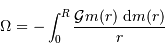
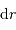 au rayon
au rayon 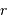 :
:
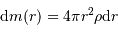
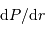 et
et 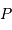 en procédant à l'intégration par parties du terme :
en procédant à l'intégration par parties du terme :
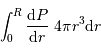
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation22.png)
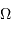 et
et 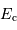 .
.
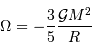
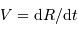 .
.
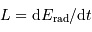 .
.
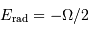 .
.
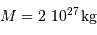 et
et 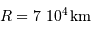 . Comparer le résultat à la puissance lumineuse reçue du Soleil par Jupiter, de l'ordre de
. Comparer le résultat à la puissance lumineuse reçue du Soleil par Jupiter, de l'ordre de 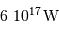 .
.






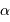 de l'hydrogène
de l'hydrogène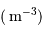
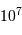
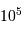
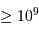
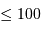
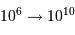
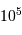
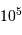

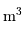 présente une masse de l'ordre de (en unité de masse solaire)
présente une masse de l'ordre de (en unité de masse solaire)
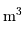 )
)


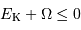
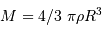 . On en déduit, quand il y a effondrement, l'inégalité sur les énergies cinétique et potentielle :
. On en déduit, quand il y a effondrement, l'inégalité sur les énergies cinétique et potentielle :
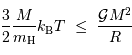
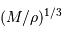 à
à 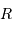 , le cas limite de l'égalité précédente donne une dépendance :
, le cas limite de l'égalité précédente donne une dépendance :
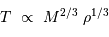

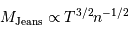
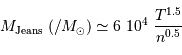

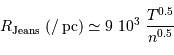


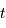 vérifiant :
vérifiant :
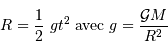
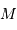 et rayon
et rayon 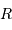 , l'analyse dimensionnelle impose :
, l'analyse dimensionnelle impose :
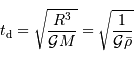
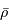 est la masse volumique moyenne du corps.
Comme l'on considère seulement l'interaction gravitationnelle, en négligeant toute résistance, la température du nuage ne joue aucun rôle. En fonction de la densité particulaire, le temps de chute libre s'exprime :
est la masse volumique moyenne du corps.
Comme l'on considère seulement l'interaction gravitationnelle, en négligeant toute résistance, la température du nuage ne joue aucun rôle. En fonction de la densité particulaire, le temps de chute libre s'exprime :
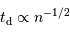
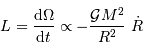
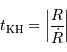
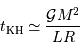
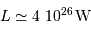 et les masse et rayon actuels) la constante de temps est de l'ordre de 30 millions d'années. Ceci signifie que, par simple contraction gravitationnelle, le Soleil peut rayonner pendant cette durée, sans autre source d'énergie.
et les masse et rayon actuels) la constante de temps est de l'ordre de 30 millions d'années. Ceci signifie que, par simple contraction gravitationnelle, le Soleil peut rayonner pendant cette durée, sans autre source d'énergie.




 .
.








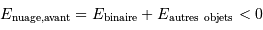
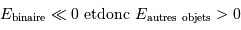




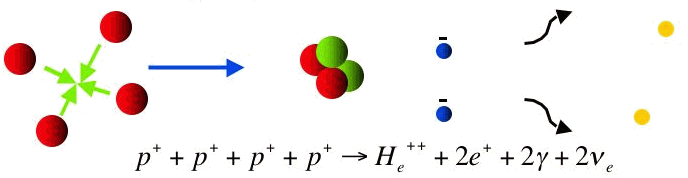
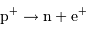 . L'interaction faible mise en jeu induit un très faible taux de réaction.
. L'interaction faible mise en jeu induit un très faible taux de réaction.

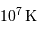 .
.

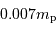 par proton. L'énergie nucléaire disponible, par fusion de l'hydrogène, est donc de
par proton. L'énergie nucléaire disponible, par fusion de l'hydrogène, est donc de 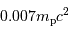 , soit 7 MeV, par nucléon, et a priori de
, soit 7 MeV, par nucléon, et a priori de 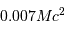 pour toute l'étoile.
pour toute l'étoile.
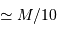 est concernée.
est concernée.
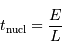
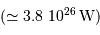 , le taux de conversion par nucléon et la masse concernée donne :
, le taux de conversion par nucléon et la masse concernée donne :
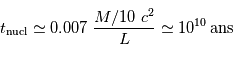
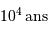 seulement.
seulement.


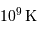 . Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
. Traduite en masse stellaire, ceci nécessiterait un minimum de 30 fois la masse du Soleil.
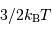 , une proportion non négligeable de protons est sensiblement plus rapide.
, une proportion non négligeable de protons est sensiblement plus rapide.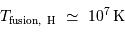
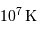 . Au delà de
. Au delà de 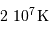 , le cycle CNO est prépondérant.
, le cycle CNO est prépondérant.
 de l'élément considéré :
de l'élément considéré :
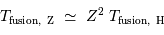

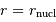
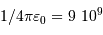 en unité SI, et
en unité SI, et 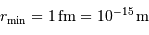 . Qu'en pensez-vous ?
. Qu'en pensez-vous ?
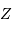 .
.
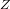 .
.
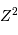
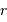 la position d'un proton par rapport à un autre et
la position d'un proton par rapport à un autre et 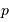 la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
la quantité de mouvement du proton incident.
L'effet tunnel relie les incertitudes sur la position et la quantité de mouvement d'une particule par la relation :
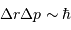
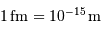
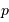 et
et 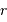 avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
avec leurs incertitudes. On se place dans ce cadre là pour traiter cette question.
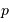 ).
).
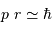
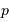 et l'énergie potentielle à distance minimale
et l'énergie potentielle à distance minimale 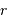 donne une autre relation entre ces 2 variables.
donne une autre relation entre ces 2 variables.
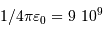 en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
en unité SI). En déduire que la température du milieu peut être plus basse pour aboutir à la fusion.
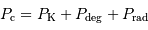
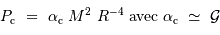
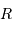 comme :
comme :
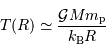
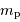 la masse du proton).
Lorsque
la masse du proton).
Lorsque 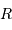 décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
décroît, la température augmente, et la pression aussi.
La température limite d'enclenchement des réactions nucléaires peut-elle être atteinte ?
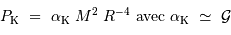
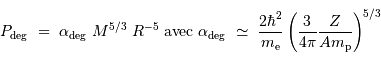
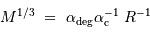
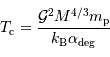
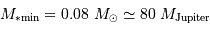
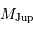 , l'objet ne peut brûler que son
, l'objet ne peut brûler que son 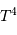 , donc :
, donc :
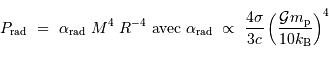
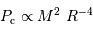 .
.
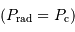 est atteinte lorsque :
est atteinte lorsque :
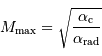
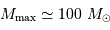

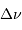 et
et 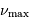 d'un
spectre d'oscillation stellaire.
d'un
spectre d'oscillation stellaire.
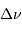 et
et 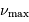 ,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse
,
respectivement appelées grande séparation et fréquence du maximum
de signal sismique. Elles dépendent de la masse 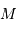 , du rayon
, du rayon 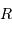 et de la température effective
et de la température effective 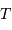 de l'étoile via les définitions :
de l'étoile via les définitions :
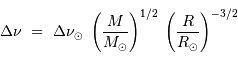
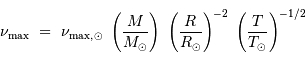
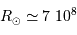 m,
m, 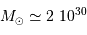 kg,
kg, 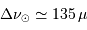 Hz,
Hz, 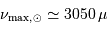 Hz, et
Hz, et 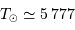 K.
K.
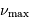 pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
pour deux étoiles de même type
spectral mais présentant un champ gravitationnel très différent.
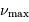 ce qui peut ressemble au
champ gravitationnel d'une étoile.
ce qui peut ressemble au
champ gravitationnel d'une étoile.
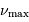 , grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
, grandeur mesurée à
une précision de l'ordre de quelques pourcents ?
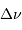 pour deux
étoiles présentant une masse volumique moyenne très différente.
pour deux
étoiles présentant une masse volumique moyenne très différente.
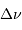 et la masse volumique moyenne ?
et la masse volumique moyenne ?
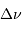 et
et 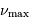 pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à
pour une géante rouge, de masse égale
à la masse du Soleil, de rayon égal à 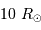 et de température
effective 4 800 K.
et de température
effective 4 800 K.
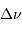 ,
, 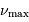 et
et
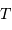 une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
une estimation des masse et rayon stellaires. Donner ces
expressions ; les exprimer en fonction des valeurs solaires.
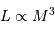 ).
).

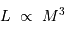
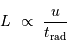
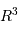 , ainsi qu'à
, ainsi qu'à 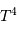 selon la loi de rayonnement du
selon la loi de rayonnement du 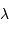 d'un photon est uniforme dans tout l'intérieur stellaire. Le processus de marche au hasard demande alors, pour parcourir une distance
d'un photon est uniforme dans tout l'intérieur stellaire. Le processus de marche au hasard demande alors, pour parcourir une distance 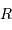 par étapes de longueur élémentaire
par étapes de longueur élémentaire 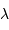 , un nombre d'étapes variant comme
, un nombre d'étapes variant comme 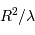 . On en déduit la constante de temps radiative :
. On en déduit la constante de temps radiative :
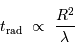
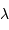 est en fait inversement proportionnel à l'encombrement, donc à la masse volumique, on a :
est en fait inversement proportionnel à l'encombrement, donc à la masse volumique, on a :
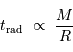
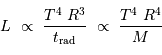
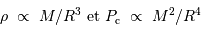
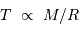
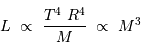
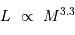
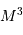 , la durée de vie stellaire varie comme :
, la durée de vie stellaire varie comme :
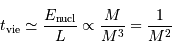
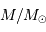
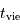 (ans)
(ans)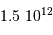
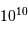
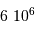
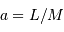 , la luminosité
, la luminosité 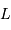 donnant la mesure de l'énergie transportée par convection, et la masse
donnant la mesure de l'énergie transportée par convection, et la masse 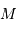 mesurant l'inertie de la réponse. Ces deux grandeurs ne peuvent être mesurées qu'indirectement : la mesure de la luminosité dépend de la distance, et la mesure de la masse nécessite un modèle de structure interne.
mesurant l'inertie de la réponse. Ces deux grandeurs ne peuvent être mesurées qu'indirectement : la mesure de la luminosité dépend de la distance, et la mesure de la masse nécessite un modèle de structure interne.
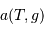 , avec
, avec 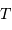 la température effective (déduit du spectre) et
la température effective (déduit du spectre) et 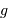 le champ gravitationnel (déduit des profils de raies).
le champ gravitationnel (déduit des profils de raies).

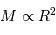





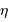 Carinae, de masse de l'ordre de 100 fois la masse du Soleil.
Carinae, de masse de l'ordre de 100 fois la masse du Soleil.
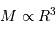
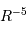 l'emporte. L'équilibre de la compression gravitationnelle
l'emporte. L'équilibre de la compression gravitationnelle 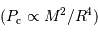 par la pression de dégénérescence
par la pression de dégénérescence 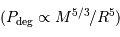 conduit à la relation masse-rayon :
conduit à la relation masse-rayon :
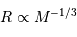
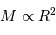
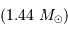 évolue vers le stade de naine blanche.
évolue vers le stade de naine blanche.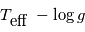 (les logarithmes sont calculés pour des gravités exprimées en cm.s-2). Le graphe montre deux populations, que l'on souhaite caractériser.
(les logarithmes sont calculés pour des gravités exprimées en cm.s-2). Le graphe montre deux populations, que l'on souhaite caractériser.

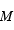 et rayon
et rayon 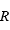 .
.
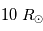 . Exprimer les résultats par la valeur
. Exprimer les résultats par la valeur 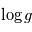 .
.
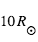



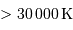 ).
).


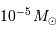 par an avec des vitesses d'éjection de l'ordre
de 5 à
par an avec des vitesses d'éjection de l'ordre
de 5 à 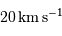 . Cette perte de masse apparaît quand la gravité de surface de l'étoile est devenue très faible : les couches périphériques de l'enveloppe stellaire ne sont plus que très (trop) faiblement liées à l'étoile. L'étoile résiduelle a
d'autant plus maigri qu'elle était peu massive au départ, ce qui
conduit à des géantes rouges aussi peu massive 0.6 masse solaire après la
perte de masse.
. Cette perte de masse apparaît quand la gravité de surface de l'étoile est devenue très faible : les couches périphériques de l'enveloppe stellaire ne sont plus que très (trop) faiblement liées à l'étoile. L'étoile résiduelle a
d'autant plus maigri qu'elle était peu massive au départ, ce qui
conduit à des géantes rouges aussi peu massive 0.6 masse solaire après la
perte de masse.

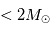 ) . Les étoiles plus massives la rejoignent à plus grand luminosité.
) . Les étoiles plus massives la rejoignent à plus grand luminosité.
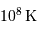 , la fusion de l'hélium peut conduire au carbone, par la réaction bilan :
, la fusion de l'hélium peut conduire au carbone, par la réaction bilan : 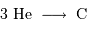 . L'étoile, retrouvant une source d'énergie, retrouve donc une situation d'équilibre. L'apport d'énergie de fusion de l'hélium provoque la dilatation du cœur et l'effondrement de l'enveloppe.
. L'étoile, retrouvant une source d'énergie, retrouve donc une situation d'équilibre. L'apport d'énergie de fusion de l'hélium provoque la dilatation du cœur et l'effondrement de l'enveloppe.
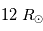 .
.





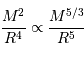
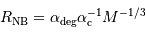
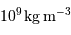 , ce qui représente environ 1 million de fois la masse volumique initiale.
, ce qui représente environ 1 million de fois la masse volumique initiale.
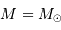 et de rayon
et de rayon 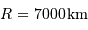 .
.
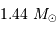 , il arrive un stade de l'évolution où la pression de Fermi des électrons ne parvient plus à soutenir l'étoile.
, il arrive un stade de l'évolution où la pression de Fermi des électrons ne parvient plus à soutenir l'étoile.
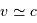 ) :
) :
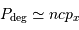
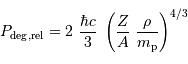
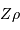 représente la charge volumique, et
représente la charge volumique, et 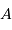 le nombre de masse des atomes en présence.
le nombre de masse des atomes en présence.
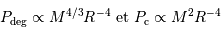
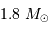 , l'étoile n'est plus soutenue. Un calcul plus précise donne pour cette masse limite, dite masse de Chandrasekhar, au-delà de laquelle l'étoile va s'effondrer faute du soutien de la pression de dégénérescence des électrons, la valeur :
, l'étoile n'est plus soutenue. Un calcul plus précise donne pour cette masse limite, dite masse de Chandrasekhar, au-delà de laquelle l'étoile va s'effondrer faute du soutien de la pression de dégénérescence des électrons, la valeur :
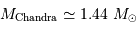


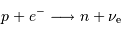

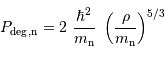
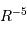 . On assiste alors à un nouvel équilibre, atteint pour un rayon bien plus petit que pour une naine blanche, en raison du facteur
. On assiste alors à un nouvel équilibre, atteint pour un rayon bien plus petit que pour une naine blanche, en raison du facteur 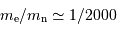 .
.
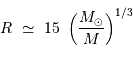
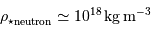
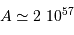 .
.


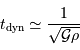
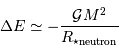
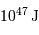 :
:
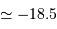 )
)

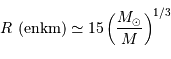
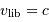 correspond au rayon dit de Schwarzschild
correspond au rayon dit de Schwarzschild
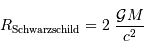 .
.
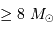 ), mais diminuée des pertes par vent stellaire.
), mais diminuée des pertes par vent stellaire.

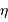 de la Carène, est tellement massive (de l'ordre de 100 fois la masse du Soleil) et lumineuse (5 millions de fois le Soleil), qu'elle sera bientôt en fin de vie, quand bien même elle réside encore dans la nébuleuse qui l'a formée.
de la Carène, est tellement massive (de l'ordre de 100 fois la masse du Soleil) et lumineuse (5 millions de fois le Soleil), qu'elle sera bientôt en fin de vie, quand bien même elle réside encore dans la nébuleuse qui l'a formée.






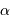
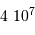
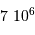 ans
ans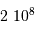
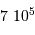
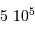 ans
ans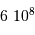
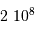
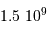
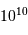
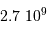
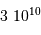
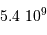
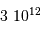



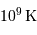 , non atteinte pour ces masses intermédiaires.
, non atteinte pour ces masses intermédiaires.
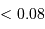
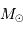 .
.







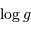 (avec
(avec 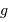 en g cm
en g cm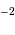 ) d'étoiles observées par CoRoT.
) d'étoiles observées par CoRoT.
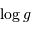 (avec
(avec 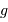 en cm s
en cm s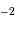 ).
).
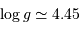 .
.




![M = \int_0^R 4\pi r^2\ \rho {\mathrm{d}} r = 4\pi \beta \ \int_0^R r^{\alpha+2} {\mathrm{d}} r = 4\pi \beta \ \left[ {r^{\alpha+3}\over \alpha+3} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation27.png)
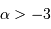 , alors :
, alors :
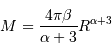
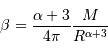
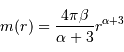
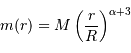
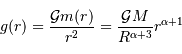
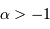 , afin d'éviter que le champ ne diverge au centre.
, afin d'éviter que le champ ne diverge au centre.
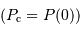 vers la surface
vers la surface 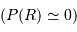 :
:
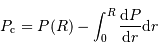
![P _{\mathrm{c}} = \int_0^R \rho g\ {\mathrm{d}} r = \int_0^R \beta r^\alpha \ { {\cal G} M \over R^{\alpha+3}} r^{\alpha+1} {\mathrm{d}} r = \beta { {\cal G} M \over R^{\alpha+3}} \int_0^R r^{2\alpha+1} {\mathrm{d}} r = {\alpha+3 \over 4\pi}\ { {\cal G} M^2 \over R^{2\alpha+6}} \left[ {r^{2\alpha+2}\over 2\alpha+2} \right]_0^R](../pages_physique-evolution/equations_pression-centrale/equation45.png)
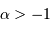 ; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
; dans ce cas, la contribution en 0 ne diverge pas, et l'on trouve :
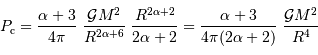
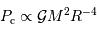 est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel
est logique : l'analyse dimensionnelle permet cette seule écriture de la pression en fonction des 3 grandeurs reliées au problème gravitationnel 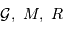 .
.
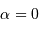 , on trouve :
, on trouve :
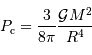
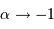 , on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la
, on voit que la constante de proportionnalité devient de plus en plus grande. C'est ce que l'on a vu dans la 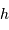 la masse considérée coûte en énergie, dans le champ
la masse considérée coûte en énergie, dans le champ 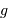 supposé uniforme :
supposé uniforme :
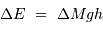
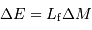 , et donc si :
, et donc si :
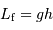
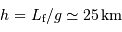
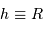 , et la définition de la masse pour une masse volumique uniforme
, et la définition de la masse pour une masse volumique uniforme
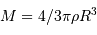 conduisent à :
conduisent à :
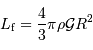
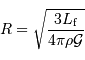
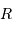 de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.
de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.
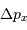 et
et 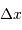 les incertitudes respectives.
les incertitudes respectives.
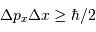
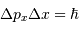
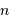 correspond à un volume par particule
correspond à un volume par particule 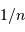 .
Ce volume par particule est lui-même de l'ordre de
.
Ce volume par particule est lui-même de l'ordre de 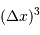 . On en déduit :
. On en déduit :
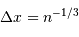

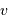 et
et 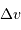 .
.
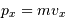 .
.
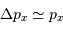 et
et 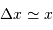 on tire :
on tire :
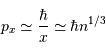
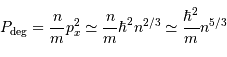
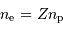 .
.
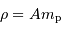 .
.
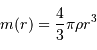
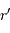 vaut :
vaut :
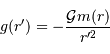
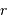 , rayon actuel de l'objet en cours de formation, et
, rayon actuel de l'objet en cours de formation, et 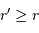 , distance à cet objet.
, distance à cet objet.
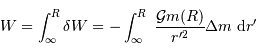
![W = + \left[ { {\cal G} m(M) \over r'}\ \Delta m \right]_\infty^R](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation20.png)
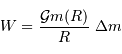
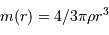 s'écrit par différentiation :
s'écrit par différentiation :
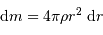
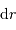 et de surface
et de surface 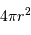 .
.
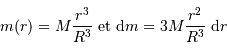
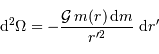
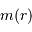 la masse accrétée au rayon
la masse accrétée au rayon 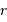 et
et 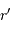 une position entre
une position entre 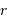 et
et 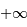 . Une première étape d'intégration conduit à apporter la masse
. Une première étape d'intégration conduit à apporter la masse 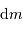 de l'infini à la surface :
de l'infini à la surface :
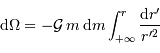
![\left[ - \displaystyle{1\over r'}\right]_\infty^r = - \displaystyle{1\over r}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation46.png) . D'où la variation de potentiel :
. D'où la variation de potentiel :
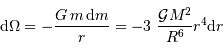
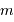 et
et 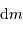 par leur valeurs.
Et donc finalement :
par leur valeurs.
Et donc finalement :
![\Omega = \int_0^R {\mathrm{d}} \Omega = \left[ - 3 { {\cal G} M^2\over R^6} {r^5\over 5} \right]_0^R = -{3\over 5} { {\cal G} M^2\over R}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation50.png)
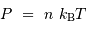 , on introduit simplement la pression, pour obtenir :
, on introduit simplement la pression, pour obtenir :
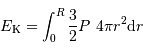
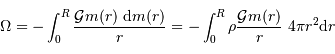
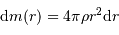 :
:
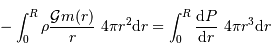
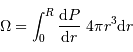
![\int_0^R { {\mathrm{d}} P\over {\mathrm{d}} r} \ 4\pi r^{3} {\mathrm{d}} r = \Bigl[P.4\pi r^{3}\Bigr]_0^R - 3 \int_0^R P\ 4\pi r^{2} {\mathrm{d}} r](../pages_physique-evolution/equations_theoreme-viriel/equation23.png)
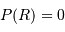 ).
).
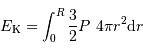
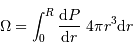
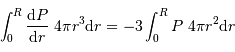
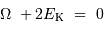
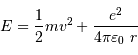
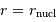 , le proton doit avoir une énergie vérifiant :
, le proton doit avoir une énergie vérifiant :
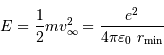
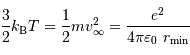
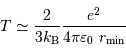
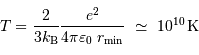
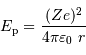
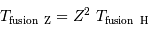
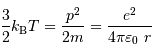
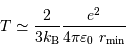
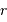 la distance minimale d'approche, et
la distance minimale d'approche, et 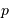 la quantité de mouvement incidente, l'équation énergétique dit :
la quantité de mouvement incidente, l'équation énergétique dit :
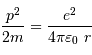
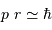 On en déduite la valeur de
On en déduite la valeur de 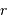 , en éliminant
, en éliminant 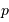 :
:
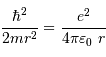
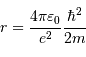
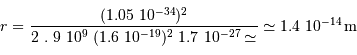
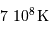 .
.
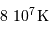 .
.
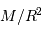 , comme
, comme
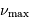 , dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et
, dont l'expression comporte juste une dépendance
supplémentaire en fonction de la température. Comme le type
spectral est supposé fixé, cette dépendance est donc transparente,
et 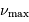 porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
porte la même information que le champ gravitationnel,
et réciproquement. On en déduit qu'une étoile de champ
gravitationnel plus intense présente un spectre avec une fréquence
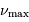 plus élevée, et réciproquement.
plus élevée, et réciproquement.
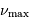 , identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
, identifiée à partir du spectre
d'oscillation, permet une estimation précise du champ
gravitationnel à la surface de l'étoile.
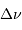 montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
montre que cette fréquence
varie comme la racine carrée de la masse volumique de l'étoile.
Une étoile peu dense présentera donc une plus petite valeur de
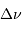 qu'une étoile plus dense.
qu'une étoile plus dense.
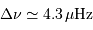 . Pour
. Pour 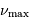 , l'application
numérique donne
, l'application
numérique donne 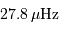 .
.
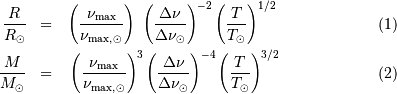
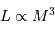 , on trouve :
, on trouve :
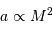 . L'amplitude des oscillations augmente vers les types spectraux plus massifs.
. L'amplitude des oscillations augmente vers les types spectraux plus massifs.