Le milieu interstellaire
Auteurs: Cecilia Pinto, Sylvie Cabrit
- Introduction au Milieu Interstellaire
- Présentation Générale
- Rappel : structure de notre galaxie
- Composition du MIS
- Phases du MIS
- Le cycle du milieu interstellaire
- Le cycle de transformation du milieu interstellaire
- Régulation de la formation stellaire
- L'instabilité thermique du MIS
- Sources et réservoirs
- Sources et réservoirs d'énergie
- Réservoirs d'énergie : champ de rayonnement
- Réservoirs d'énergie : champ magnétique
- Réservoirs d'énergie : rayons cosmiques
- Images
- Détection du milieu interstellaire à différentes longueurs d'onde
- Images de la Galaxie à differentes longueurs d'onde
- Détection du gaz atomique: L'atome d'hydrogène
- Détection du gaz neutre atomique : raies spectrales
- Détection du gaz neutre moléculaire
- Détection du gaz ionisé
- Travaux pratiques : logiciel Aladin
- Introduction
- Mesure de la taille des structures
- Comparaison d'images : infrarouge proche et visible
- Comparaison d'images à plusieurs longueurs d'onde : structuration en phases
- Spectres
- Transfert de rayonnement
- Notions de transfert de rayonnement
- Interaction rayonnement-matière
- L'équation de transfert de rayonnement
- Coefficients d'Einstein
- Conditions d'excitation et intensité émergente
- Application : la raie à 21 cm de l'hydrogène neutre
- Profils de raie pour les atomes et les molécules en l'absence de mouvements d'ensemble
- Profils de raie associés aux mouvements d'ensemble d'atomes et de molécules
- Raies en absorption
- Absorption par les poussières interstellaires
- Travaux pratiques : logiciel VOSpec
- Introduction
- Spectre en émission : profils de raie et élargissement
- Spectre en absorption : mesure de la densité de colonne
Introduction au Milieu Interstellaire
Auteurs: Cecilia Pinto, Sylvie Cabrit
Présentation Générale
Le vaste espace qui s'étend entre les étoiles n'est pas vide, mais rempli d'un gaz poussiéreux que l'on appelle le milieu interstellaire (ou MIS). Essentiellement invisible à l'oeil nu, sauf sous la forme de bandes sombres à travers la Voie Lactée, le MIS lorsqu'il est éclairé ou choqué par les étoiles produit les images parmi les plus belles et spectaculaires que nous connaissions, comme par exemple cette image du Hubble Space Telecope (HST) de la nébuleuse de la Carène.
La "Montagne Mystique" dans la Nébuleuse de la Carène

Image optique de la 'Montagne Mystique', un nuage dense de matière interstellaire situé dans la Nébuleuse de la Carène, irradié et érodé de l'extérieur par un amas d'étoiles massives très chaudes ; cette image obtenue par le HST combine le rayonnement de plusieurs atomes (oxygène ionisé en bleu, hydrogène et azote ionisé en vert, soufre ionisé en rouge) qui soulignent le gaz ionisé à la surface du nuage et dans la nébuleuse diffuse qui l'entoure. Les zones sombres, trop denses pour laisser pénétrer le rayonnement, apparaissent en silhouette sur ce fond lumineux. Aux pointes de ces "piliers", deux nouvelles étoiles viennent de se former qui éjectent des jets bipolaires de matière.
Crédit :
NASA/ESA/M. Livio & Hubble 20th Anniversary Team (STScI)
En plus de sa beauté intrinsèque, le MIS est une composante essentielle des galaxies puisque c'est la "matrice" à partir de laquelle se forment les nouvelles étoiles, et leurs cortèges de planètes. Comprendre la structure et l'évolution du MIS est donc un enjeu majeur pour comprendre l'évolution globale de la matière dans notre Univers et répondre à plusieurs questions fondamentales telles que :
- comment le gaz primordial hérité du Big-Bang se transforme-t'il petit à petit en étoiles ?
- pourquoi cette transformation est-elle plus ou moins rapide et efficace selon les galaxies, et même selon les régions à l'intérieur d'une même galaxie ?
- quels paramètres et processus gouvernent la distribution statistique en masse des étoiles formées (la fameuse "Fonction de Masse Initiale", ou IMF d'après l'acronyme anglais) ?
Comprendre le MIS est également essentiel pour comprendre l'origine de la vie : la vie repose sur l'existence d'éléments "lourds" (carbone, calcium, phosphore, etc...) produits par nucléosynthèse au coeur des étoiles et libérés par les vents stellaires, les nébuleuses planétaires et les explosions de supernova. Au fur et à mesure que les générations stellaires se succèdent, le milieu interstellaire s'enrichit en ces éléments lourds contenus sous forme de gaz, de grains de poussière, et de manteaux de glaces moléculaires à la surface de ces grains. Ils sont incorporés à la prochaine génération d'étoiles et, par sédimentation et agglomération des grains dans le disque circumstellaire, ils permettent la formation de planète rocheuses comme la nôtre. De plus, malgré les conditions interstellaires très hostiles (températures et densités très faibles, flux ultraviolet destructeur) une chimie étonnament riche est observée dans le MIS, avec la formation d'eau (avec une abondance qui atteint 10-4 de l'hydrogène) et de molécules organiques ou azotées parfois "complexes" et dont certaines constituent des briques de base du vivant. Ces molécules sont préservées à l'état de glaces dans les comètes ; lors de la phase de bombardement intensif qui a suivi la formation de notre Système Solaire, elles pourraient peut-être avoir contribué à alimenter nos océans, voire favoriser l'apparition de la vie sur Terre. Ce scenario est illustré dans la figure ci-dessous.
Cycle chimique du MIS et apparition de la vie
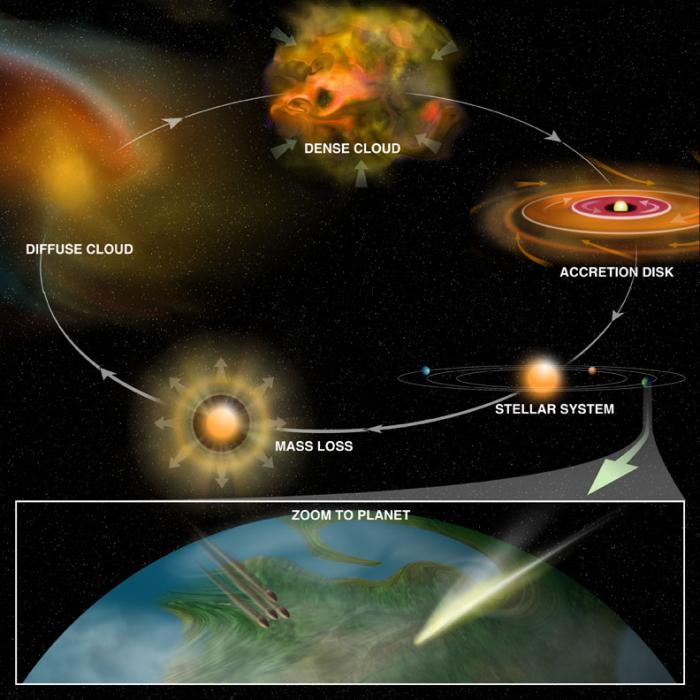
Le cycle d'enrichissement chimique de la matière cosmique, depuis le MIS jusqu'aux planètes (via les impacts cométaires).
Crédit :
Bill Saxton, NRAO/AUI/NSF
Dans notre Galaxie, la masse du MIS représente aujourd'hui environ 15% de la masse sous forme d'étoiles. Cette fraction est plus élevée dans les galaxies jeunes où la formation stellaire commence tout juste. Dans ce cours nous étudierons le MIS galactique, qui est le mieux connu. La physique fondamentale du MIS dans les autres galaxies est similaire, même si les conditions d'irradiation et les abondances chimiques y diffèrent. Après un rappel sur la structure de notre Galaxie, nous verrons les différentes Phases en température et densité sous lesquelles le MIS se rencontre, le "cycle évolutif du MIS" qui permet au gaz de passer d'une phase à l'autre en formant des étoiles, et enfin les différentes sources et réservoirs d'énergie du MIS qui contrôlent ce cycle.
Rappel : structure de notre galaxie
Notre Galaxie, la Voie Lactée, est un ensemble auto-gravitant constitué d'un disque tournant autour d'un bulbe central, bien visibles par exemple sur l'image ci-contre, et entouré d'un halo sphérique. Le bulbe est très lumineux, avec un rayon de l'ordre de 2 kpc, et abrite en son coeur un trou noir géant dont la masse serait environ 4x106 masses solaires. Le disque s'étend sur 15 kpc de rayon, pour une épaisseur de quelques centaines de parsecs. Il est parcouru d'ondes de densité qui sont responsables de sa structure en bras spiraux (une vue de face synthétique est présentée ci-dessous. Le Soleil s'y trouve à 8.5 kpc du Centre galactique et tourne autour de lui à une vitesse de l'ordre de 200 km.s-1.
Le halo s'étend bien au delà des limites du disque Galactique et il est peu brillant. Il contient très peu d'étoiles, dont les amas globulaires, très âgés. En revanche, l'observation de la courbe de rotation montre qu'il abrite la plus grande partie de la matière gravitante non lumineuse (la matière noire) de la Galaxie.
Les constituants du disque et du halo présentent des propriétés très différentes. Les étoiles du halo sont vieilles, peu lumineuses et dépourvues d'éléments autres que l'hydrogène ou l'hélium (ce sont les étoiles de population II). De plus, le halo est pratiquement dépourvu de gaz et de poussières. Au contraire, les étoiles du disque ont une gamme d'âge et de luminosité bien plus étendue, et les étoiles y sont riches en éléments plus lourds que l'hydrogène et l'hélium (étoiles de population I). On y trouve en particulier des associations OB, formées d'astres jeunes, massifs et lumineux. En effet, le disque contient un milieu interstellaire très riche, grâce auquel la formation stellaire continue d'être active.
La masse totale de la Galaxie est estimée à 1011 masses solaires à l'intérieur d'un rayon de 15 kpc. Cette masse est répartie entre la masse des étoiles : environ 5x1010 masses solaires, la masse de la matière noire : environ 5x1010 masses solaires, et la masse du milieu interstellaire, environ 7x109 masses solaires. La masse du MIS dans notre Galaxie représente donc environ 15% de la masse sous forme d'étoiles. Cette fraction est plus élevée dans les galaxies jeunes où la formation stellaire commence tout juste.

La Galaxie vue par le satellite COBE : bulbe en blanc, disque en jaune, poussières en orange.
Crédit :
NASA

Reconstruction synthétique de la structure spirale de notre Galaxie vue de face
Crédit :
NASA JPL-Caltech
Composition du MIS
Phase Gazeuse
Le gaz interstellaire est composé principalement d'hydrogène (70% en masse, 90% en nombre d'atomes) et d'hélium (28% en masse, 9% en nombre d'atomes). Ces éléments persistent depuis le Big Bang, avec une petite réduction de l'Hydrogène (de 75 % à 70% ) et une augmentation de l'Hélium (de 24 % à 28% ) dues à la transformation d'un élément en l'autre par la nucléosynthèse stellaire. Ce processus de nucléosynthèse stellaire produit également les atomes plus lourds (C, N, O, S, ....) qui représentent environ 2% en masse et 1% en nombre d'atomes du milieu interstellaire. Les abondances des élément lourds diminuent avec la distance au Centre Galactique, les abondances au voisinage du Soleil étant environ la moitié de celles atteintes dans la région du Centre Galactique.
Dans les zones protégées du rayonnement ultraviolet des étoiles, les atomes s'assemblent en molécules de tailles variées, depuis les molécules simples diatomiques et triatomiques (principalement H2, CO, et H2O) jusqu'à des espèces organiques complexes, dont certaines se retrouvent dans les comètes. On a identifié actuellement plus de 200 molécules interstellaires dans le MIS. On a en en particulier détecté du glycolaldéhyde, un sucre nécessaire à la synthèse de l'ARN (Acide RiboNucléique). Cela suggère qu’une partie de la composition de notre système solaire, des océans terrestres, et peut-être des briques de base de la vie, pourrait être directement héritée de la chimie interstellaire. Cette question constitue un domaine nouveau et très actif de recherche, l'astrochimie du MIS, à la frontière avec l'astrobiologie.
La composition du gaz interstellaire, ainsi que ses conditions physiques, sont déterminées grâce à des observations spectroscopiques de raies d'absorption et d'émission, atomiques ou moléculaires, dont les principales seront présentées en détail dans la suite du cours.
Les grains interstellaires
Le MIS contient aussi une phase solide : les grains interstellaires, qui contiennent environ 1% de la masse du gaz. Leur présence est décelable par leur effet d'extinction (bandes sombres) et diffusion (nébuleuses par réflexion) de la lumière stellaire, ainsi que par leur rayonnement thermique dans le domaine infrarouge. L’analyse de ces phénomènes en fonction de la longueur d'onde permet de contraindre leur distribution en taille et leur type de matériau (cristallin ou amorphe, aromatique..). On en déduit que les grains présentent un vaste continuum de tailles, allant de quelques dizaines d'Angstrom pour les petits agrégats jusqu'à une fraction de μm, voire plusieurs μm dans les régions très denses. Les matériaux principaux qui composent la poussière interstellaire sont les éléments réfractaires comme les silicates et le carbone. Les grains jouent un rôle fondamental dans le MIS à plusieurs points de vue :
- L' absorption de photons UV arrache aux grains un électron (effet photo-électrique) qui communique ensuite son énergie au gaz par collisions; c'est le terme de "chauffage photoélectrique", dominant dans le milieu atomique et moléculaire diffus (AV < 1 mag), qui le maintient autour de 100 K, ainsi que dans les régions denses irradiées par un champ UV plus intense (régions de photodissociation).
- Les grains sont le site de formation des molécules H2 (la réaction H+H en phase gazeuse menant à un état répulsif non lié), qui initie toute la chimie interstellaire et la formation des nuages moléculaires.
- Au sein de ces nuages, ils absorbent la lumière visible et ultraviolette des étoiles, protégeant ainsi les autres molécules de la photodissociation et permettant au gaz de s'y refroidir suffisamment (10 K) pour que la gravité l'emporte et que des étoiles s'y forment.
- Dans les régions les plus froides et denses des nuages, les grains réfractaires se couvrent de manteaux de glaces (par ex. H2O, NH3, CO, CO2...), et sont un site de catalyse favorable pour la formation d'espèces plus complexes dont la synthèse ne semble pas énergétiquement possible en phase gazeuse.
Dans l'histogramme ci-dessous on compare les abondances mesurées dans le soleil (utilisées couramment comme abondances standard de référence) avec les abondances du gaz ionisé dans la nébuleuse d'Orion. Cela permet d’en déduire, par différence, la composition de la poussière sur la ligne de visée:
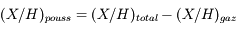 où
où 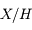 est l'abondance de l'élément par rapport à l'hydrogène (en nombre d'atomes).
est l'abondance de l'élément par rapport à l'hydrogène (en nombre d'atomes).
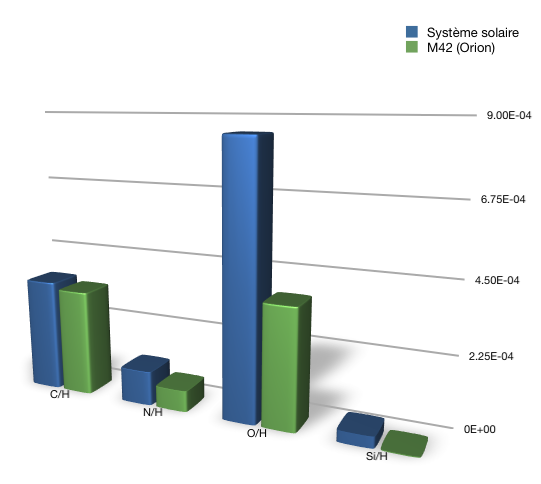
Crédit :
Franck Le Petit
Dans la figure ci-dessous, une analyse similaire est présentée à partir de spectres en absorption sur la ligne de visée vers l'étoile Zeta Oph. On voit que plus la température de condensation (solidification) d'un élément est élevée, c'est-à-dire plus l'élément est "réfractaire", et plus son abondance dans la phase gazeuse est faible par rapport au standard des abondances solaires. Cela indique que lorsque les élements lourds synthétisés par les étoiles sont expulsés lors de la phase géante rouge, les atomes les plus réfractaires se condensent rapidement sous forme de grains lorsque la température passe sous 1500 K. Ils restent ensuite piégés sous cette forme dans le MIS diffus. Par exemple, seulement 1% du fer est sous forme gazeuse dans le MIS.
Déplétion des éléments dans le MIS diffus
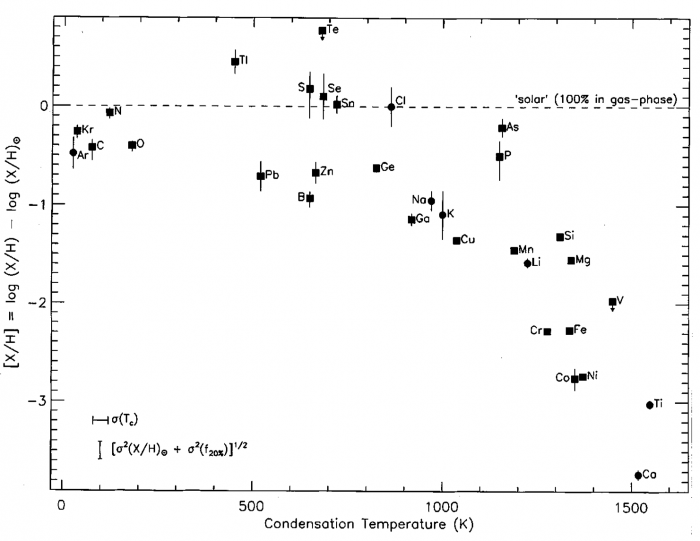
Rapports (en échelle log10) entre les abondances en phase gazeuse sur la ligne de visée vers Zeta Oph et les abondances "standard" dans le soleil, en fonction de la température de condensation de chaque atome (celle au dessous de laquelle il se condense sous forme d'aggrégat solide). L'anticorrélation observée indique que les éléments déplétés sont piégés dans des grains condensés dans les enveloppes d'étoiles AGB.
Crédit :
Savage & Sembach (1996, ARAA)
Phases du MIS
Une caractéristique fondamentale du MIS est sa forte inhomogénéité. En effet, on y rencontre des valeurs très variées de densité et de température, de moins de 1 à plus de 108 particules par cm3 et de 10 K à plusieurs millions de degrés. Cependant, on peut schématiquement considérer que le gaz s'y structure sous la forme d'un petit nombre de composantes ou « phases » correspondant aux divers états stables possibles de la matière interstellaire, et distinguées par l'état d'ionisation qu'y prend l'hydrogène (ionisé, atomique = neutre, moléculaire), et par la température typique d'équilibre (chaud > 105 K, tiède, froid < 100 K). Ces phases coexistent entre elles, donnant au MIS son aspect sculpté, chamarré et structuré à toutes les échelles (voir Figure ci-contre).
La structure multi-phase du MIS dans Cygnus X

Image du satellite Herschel de Cygnus X, une région d'intense activité de formation d'étoiles massives où plusieurs phases du MIS co-existent. L'image superpose l'émission de la poussière à 70 μm (bleu), 160 μm (vert) et 250 μm (rouge). Les régions chaudes apparaissent donc plus bleues et les froides, plus rouges. Les régions HII ionisées par les jeunes étoiles massives apparaissent comme des bulles blanc-bleuté. Les filaments rouges et jaunes tracent de la matière moléculaire dense et froide, dont certains abritent des étoiles en formation (globules rouges très compacts). La région sombre au centre de l'image a été chauffée et balayée par les vents et le rayonnement d'un amas d'étoiles OB (non visible ici) de sorte qu'elle est dans une phase diffuse et tiède du MIS qui émet peu dans les bandes spectrales utilisées ici.
Crédit :
ESA/PACS/SPIRE/ Martin Hennemann & Frédérique Motte.
 Remarque
Remarque
Afin de détecter les différentes phases du milieu interstellaire, il faut combiner des observations à différentes longueurs d'onde qui permettent de sonder du gaz sur un vaste domaine de température et de densité. Ces observations et leurs résultats seront présentés plus en détail dans le chapitre Détection du milieu interstellaire à différentes longueurs d'onde. Le tableau ci-dessous résume les propriétés typiques déduites pour chaque phase, ainsi que les principaux traceurs.
Phases du milieu interstellaire
| Phase | Densité | Température | Masse | Traceur principal |
|---|
| cm-3 | K | 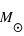 | |
| Milieu ionisé (HII) chaud = HIM (Hot Ionized Medium) | ∼0.005 | ≥ 3 105 | 108 | Rayons X, OVI |
| Milieu ionisé (HII) tiède = WIM (Warm Ionized Medium) | 0.6 | 8000 | 109 | Hα, NII, SII, radio |
| Milieu atomique (HI) tiède = WNM (Warm Neutral Medium) | 0.5 | 5000 | 2X109 | HI 21 cm, C+, O |
| Milieu atomique (HI) froid = CNM (Cold Neutral Medium) | 30 | 100 | 2X109 | HI 21 cm (abs) |
| Nuage moléculaire (H2) = GMC (Giant Molecular Cloud) | 100-108 | 10-100 | 109 | CO, H2, etc. (em et abs) |
| Régions HII | 0.3-104 | 104 | 5x107 | Hα, NII, SII, radio |
On note que le gaz neutre atomique représente la composante la plus importante en masse (NB : Ici les masses totales sont incertaines, et reflètent plutôt les proportions entre les différentes composantes dans quelques kpc autour du Soleil). Dans le milieu interstellaire "diffus" (n < 100 cm-3) l'auto-gravité est négligeable et comme le montre le tableau, les phases sont en approximatif équilibre de pression entre elles (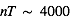 K cm-3) malgré leurs forts contrastes de densité et de température. Par contre la phase moléculaire froide et dense, qui se condense sur des échelles < 50 pc, est autogravitante et sous cet effet se comprime pour atteindre une pression plus élevée. Enfin, au sein des nuages moléculaires, on trouve les régions HII, bulles de gaz ionisées par le rayonnement UV d’une ou plusieurs jeunes étoiles OB, où le gaz tiède est localement en surpression par rapport au nuage environnant.
K cm-3) malgré leurs forts contrastes de densité et de température. Par contre la phase moléculaire froide et dense, qui se condense sur des échelles < 50 pc, est autogravitante et sous cet effet se comprime pour atteindre une pression plus élevée. Enfin, au sein des nuages moléculaires, on trouve les régions HII, bulles de gaz ionisées par le rayonnement UV d’une ou plusieurs jeunes étoiles OB, où le gaz tiède est localement en surpression par rapport au nuage environnant.
Le cycle du milieu interstellaire
Auteur: Sylvie Cabrit
Le cycle de transformation du milieu interstellaire
Le milieu interstellaire est un milieu dynamique en perpétuelle transformation, où le gaz circule rapidement (< 107 ans) d’une phase thermique à une autre, via un « cycle » évolutif illustré dans la figure ci-dessous.
La première moitié du cycle (du haut en bas de la figure dans le sens inverse des aiguilles d'une montre) est une séquence de condensation depuis la phase diffuse et tiède vers le gaz moléculaire froid et dense où vont se former les étoiles.
la deuxième moitié du cycle (de bas en haut dans le sens inverse des aiguilles d'une montre) est une séquence de ré-expansion où les effets de rétroaction radiative et mécanique des étoiles ramènent le gaz dans la phase diffuse.
 Le rôle central du MIS dans la formation stellaire
Le rôle central du MIS dans la formation stellaire
Les mécanismes qui induisent ou influencent le cycle du MIS déterminent le taux de conversion du gaz en étoiles, qui est un paramètre fondamental pour l’évolution des galaxies. Cela en fait un sujet de recherche très important en astrophysique. Plusieurs mécanismes de base qui entretiennent le cycle du MIS ont été identifiés (indiqués en rouge sur la Figure ci-dessous) et bien que plusieurs aspects posent encore question, ils permettent d'en comprendre les grandes étapes, que nous décrivons brièvement ci-dessous :
Le Cycle du MIS
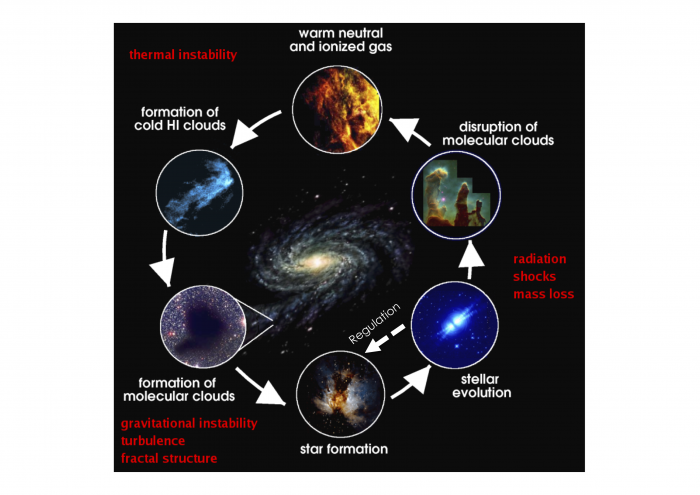
Crédit :
Copyleft © 2013 Steward Observatory Radio Astronomy Laboratory
Cycle de condensation du MIS
- La majorité de la masse du MIS se trouve dans la phase tiède diffuse, neutre ou ionisée (WIM ou WNM)
- Sous l'effet d'une compression, par exemple passage d'une onde de choc, le gaz subit une instabilité thermique (voir ci-dessous) qui le fait passer dans la phase atomique froide (100 K, CNM), pour former un nuage HI plus dense.
- Dans les zones abritées du flux UV interstellaire, l'hydrogène devient majoritairement moléculaire et il se forme un nuage moléculaire géant (GMC). Le rayonnement très efficace des molécules de CO refroidit le gaz, qui se condense sous l'effet de la pression ambiante et de l'auto-gravité.
- Sous l'effet combiné de la turbulence et du champ magnétique, une structure filamentaire / fractale s'établit et des petits globules (appelés "coeurs denses") se forment dont certains deviennent instables par leur propre gravité et s’effondrent pour former des étoiles.
Cycle de ré-expansion du MIS
Une fois formées, les étoiles ont une forte rétroaction sur le MIS via plusieurs agents qui agissent en parallèle, et ont tendance à faire retourner le gaz de la phase dense à la phase diffuse tiède :
- Le rayonnement UV ionisant ou UV "extreme" (EUV > 13.6 eV) émis par les jeunes étoiles massives (type OB) forme autour d’elles des bulles d’hydrogène ionisé dénommées régions HII qui progressent dans le nuage moléculaire jusqu’à en ioniser un vaste volume.
- Le rayonnement UV non ionisant, ou UV "lointain" (Far-UV : 6-13.6 eV) crée des « régions de photodissociation » ou PDR (d'après l'acronyme anglais pour "Photo-Dissociation Regions") à l’interface avec le nuage moléculaire environnant, où le gaz est chauffé par effet photo-électrique sur les grains et s’évapore pour retourner dans la phase diffuse tiède.
- La perte de masse : les étoiles jeunes, les étoiles chaudes de type OB, et les étoiles en fin de vie (géantes rouges) ont une perte de masse intense qui balaye et sculpte le MIS ambiant via des ondes de choc, sur des échelles atteignant plusieurs pc. Il se creuse ainsi dans le milieu ambiant des cavités en expansion remplies par les éjecta stellaires plus diffus, qui peuvent finir par occuper une large fraction de volume du nuage. Sous l'effet de cette expansion, une partie du nuage parent peut atteindre la vitesse de libération et se trouver expulsé dans la phase diffuse.
- Les explosions de supernovae : ces événements très violents génèrent des ondes de choc gigantesques et d'immenses bulles de gaz très chaud appelées restes de supernovae (ou SNR pour SuperNova Remnant) qui se répandent ensuite dans la Galaxie pour alimenter la phase ionisée chaude (HIM), aux alentours de 106 K.
Par l'effet cumulatif du rayonnement UV et des ondes de chocs, les étoiles massives finissent par détruire leur nuage moléculaire parent en quelques millions d'années ; le cycle du MIS est alors bouclé et un nouveau cycle peut commencer.
Régulation de la formation stellaire
Auto-régulation de la formation stellaire
La rétroaction des étoiles a globalement un effet auto-régulateur sur la formation stellaire : l’injection d’énergie à toutes les échelles, par le rayonnement et les ondes de choc produites par les vents stellaires, contribue à alimenter les mouvements turbulents du gaz qui s’opposent à la gravité : cela pourrait expliquer pourquoi seulement quelques % de la masse d’un GMC sont convertis en étoiles avant que le nuage ne soit détruit par les étoiles massives. Un autre facteur régulateur possible est le champ magnétique, qui semble être suffisamment fort pour réguler la formation des filaments denses où se forment préférentiellement les étoiles (voir la partie sur les mesures de Champ magnétique).
Formation stellaire induite
En parallèle à cet effet global régulateur, on a récemment observé (en particulier grâce au satellite Herschel) que la compression induite par les ondes de choc autour des régions HII et des restes de supernovae peut localement avoir une rétroaction positive et au contraire favoriser la formation de nouvelles étoiles massives. C'est le phénomène de « formation stellaire induite ». Un exemple est présenté dans la figure ci-contre. L'efficacité globale de ce phénomène, et la distribution en masse des étoiles qui en résulte, sont encore un sujet de recherche très ouvert.
Formation stellaire induite

Images de la jeune région HII RCW120 obtenues par le satellite Herschel (bleu : 100 μm, vert : 160 μm, rouge : 250 μm) ; à l'interface entre la bulle de gaz ionisé (en bleu) et le nuage ambiant (jaune-orangé), une protoétoile massive s'est formée, qui apparaît ici comme un point lumineux blanc sur la droite de la bulle.
Crédit :
ESA, PACS & SPIRE Consortia, A. Zavagno pour les programmes clefs Herschel HOBYS et Evolution of Interstellar Dust
L'instabilité thermique du MIS
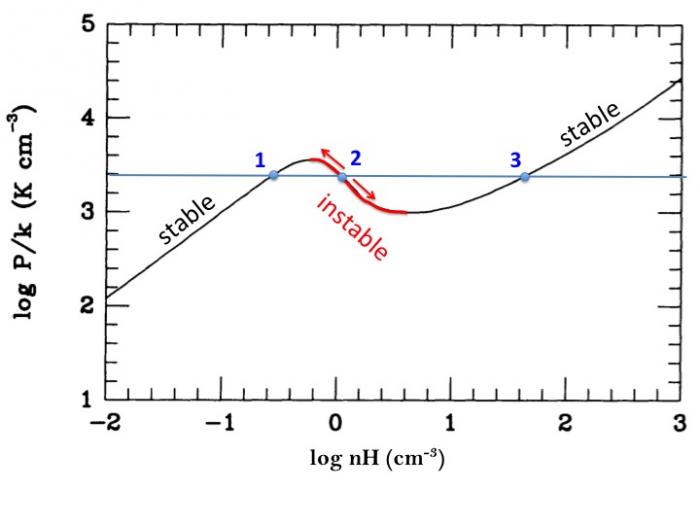
La plupart du milieu interstellaire de notre Galaxie se trouve dans la phase diffuse tiède, atomique ou ionisée, à 5000-10000 K (WNM et WIM) ; sous l'effet d'une compression extérieure le gaz va directement passer dans la phase atomique froide à 100 K (CNM) sans passer par des stades de température intermédiaire, car ces derniers sont instables. L'origine de cette instabilitié thermique est la forme de la courbe qui donne la pression d'équilibre du gaz 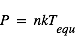 en fonction de sa densité
en fonction de sa densité 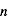 . Ici
. Ici 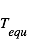 est la température d'équilibre où le taux de refroidissement radiatif compense le taux de chauffage du gaz (dû principalement à l'effet photoélectrique des photons UV interstellaires sur les grains). La figure ci-contre illustre la courbe d'équilibre de
est la température d'équilibre où le taux de refroidissement radiatif compense le taux de chauffage du gaz (dû principalement à l'effet photoélectrique des photons UV interstellaires sur les grains). La figure ci-contre illustre la courbe d'équilibre de 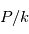 en fonction de
en fonction de 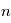 pour des conditions d'irradiation typiques de l'environnement solaire. On voit qu'elle est composée de deux "branches" stables de dérivée
pour des conditions d'irradiation typiques de l'environnement solaire. On voit qu'elle est composée de deux "branches" stables de dérivée 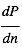 positive : celle à basse densité est le WIM (température d'environ 10 000 K, refroidissement principalement par la raie Lyman α et les raies de recombinaison) ; celle à haute densité est le CNM (température ≤ 100 K, refroidissement dominé par les raies hyperfines de O et C+). Entre les deux il y a une portion de courbe (en rouge) autour de
positive : celle à basse densité est le WIM (température d'environ 10 000 K, refroidissement principalement par la raie Lyman α et les raies de recombinaison) ; celle à haute densité est le CNM (température ≤ 100 K, refroidissement dominé par les raies hyperfines de O et C+). Entre les deux il y a une portion de courbe (en rouge) autour de 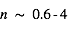 cm-3 où la dérivée
cm-3 où la dérivée 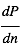 est négative. Elle correspond à un équilibre instable qui ne peut être rencontré durablement : si un élément de gaz situé au point 2 est perturbé pour se trouver en très légère sous-pression par rapport à son environnement (P < Pext), il va être comprimé par le milieu extérieur et augmenter sa densité, mais en raison de la pente négative de la courbe
est négative. Elle correspond à un équilibre instable qui ne peut être rencontré durablement : si un élément de gaz situé au point 2 est perturbé pour se trouver en très légère sous-pression par rapport à son environnement (P < Pext), il va être comprimé par le milieu extérieur et augmenter sa densité, mais en raison de la pente négative de la courbe 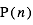 , sa pression interne va encore diminuer : il continuera donc d'être comprimé et à se densifier jusqu'à atteindre un nouvel équilibre (stable) au point 3 où P = Pext. De même s'il est en légère surpression par rapport à l'environnement (P > Pext), il subira une expansion qui diminuera sa densité ; sa pression d'équilibre (donnée par la courbe rouge) augmentera alors, et l'expansion se poursuivra jusqu'à ce qu'il passe sur la branche gauche de la courbe et atteigne un équilibre stable, de plus faible densité et de plus haute température, au point 1. On voit que dès que la pression ambiante dépasse environ 3000 K cm-3, le gaz passera rapidement du Milieu tiède (branche stable de gauche) au Milieu atomique HI plus dense à 100 K (branche stable de droite) via cette instabilité thermique. Ce changement de phase initie le début du cycle de condensation du MIS (voir ci-dessus) qui mène à la formation stellaire.
, sa pression interne va encore diminuer : il continuera donc d'être comprimé et à se densifier jusqu'à atteindre un nouvel équilibre (stable) au point 3 où P = Pext. De même s'il est en légère surpression par rapport à l'environnement (P > Pext), il subira une expansion qui diminuera sa densité ; sa pression d'équilibre (donnée par la courbe rouge) augmentera alors, et l'expansion se poursuivra jusqu'à ce qu'il passe sur la branche gauche de la courbe et atteigne un équilibre stable, de plus faible densité et de plus haute température, au point 1. On voit que dès que la pression ambiante dépasse environ 3000 K cm-3, le gaz passera rapidement du Milieu tiède (branche stable de gauche) au Milieu atomique HI plus dense à 100 K (branche stable de droite) via cette instabilité thermique. Ce changement de phase initie le début du cycle de condensation du MIS (voir ci-dessus) qui mène à la formation stellaire.
origine de l'instabilité thermique dans le milieu atomique
Pression thermique P/k à l'équilibre en fonction de la densité dans le milieu atomique, pour des conditions d'irradiation typiques de l'environnement solaire. Les parties stables et instables de la courbe sont indiquées (voir texte).
Crédit :
Adapté d'après Wolfire et al. 1995, ApJ
Sources et réservoirs
Auteurs: Sylvie Cabrit, Cecilia Pinto
Sources et réservoirs d'énergie
Le MIS est un milieu dissipatif semi-ouvert ; en même temps qu'il perd de l'énergie par émission de rayonnement à diverses longueurs d'onde qui s’échappent dans l'environnement extragalactique (voir le chapitre correspondant), il reçoit aussi de l'énergie par plusieurs sources « externes » qui le maintiennent en état de semi-équilibre et régulent son cycle de condensation et de transformation :
- la rotation différentielle de la Galaxie autour de son centre, qui induit ondes spirales et cisaillement dans le gaz
- les étoiles
- les rayons cosmiques (particules relativistes)
- le rayonnement fossile du fond cosmologique
Une partie de cette énergie externe est transférée dans d'autres réservoirs d'énergie interne et de pression, qui communiquent et échangent entre eux :
- rayonnement diffus de la poussière (dans l'infrarouge) et du gaz ionisé chaud (dans le domaine X ou radio)
- énergie magnétique (amplifiée par l'effet dynamo de la rotation galactique et par la compression du gaz)
- énergie cinétique (turbulence, rotation, ondes de choc générées par les ejecta stellaires, collisions entre nuages…)
- énergie thermique (du gaz et des grains)
Une description et compréhension exhaustive du milieu interstellaire nécessite donc de prendre en compte les interactions et transferts entre tous ces différents sources et réservoirs d'énergie, qui détermineront sa structuration en densité et son évolution thermique et chimique.
Dans le voisinage solaire, les densités d'énergie sous forme de photons, de rayonnement cosmique, de champ magnétique et des mouvements du milieu interstellaire sont comparables, de l'ordre de 0.5-1 eV cm-3.
Densités d'énergie dans le voisinage solaire
| Forme d'énergie | Densité d'énergie (eV cm-3) |
|---|
| rayonnement cosmologique (CMB : T=2.7 K) | 0.265 |
| rayonnement de la poussière | 0.31 |
| rayonnement stellaire | 0.54 |
| énergie cinétique thermique | 0.49 |
| énergie cinétique turbulente | 0.22 |
| énergie magnétique | 0.89 |
| énergie des rayons cosmiques | 0.8 |
 Remarque
Remarque
La coïncidence entre ces différentes formes d'énergie, appelée « équipartition », n'est pas fortuite, mais résulte des transferts et des interactions efficaces entre ces composantes.
Par exemple, si la densité d'énergie des rayons cosmiques était beaucoup plus élevée, le milieu interstellaire magnétisé ne serait pas capable de les confiner et ils pourraient s'échapper librement de la Galaxie. La densité d'énergie des rayons cosmiques piégés dans la Galaxie tend donc vers l'équipartition avec l’énergie magnétique.
De la même façon, les densités d'énergie magnétique et cinétique sont comparables très probablement à cause du couplage entre le champ magnétique et les mouvements du fluide (le champ magnétique est amplifié par effet dynamo et par compression dans les ondes de choc).
Enfin, si la densité d'énergie du rayonnement interstellaire n'était pas du même ordre que celle du gaz, la pression de rayonnement qui agit sur la poussière comprimerait le gaz jusqu’à ce que leurs pressions deviennent comparables.
Notons cependant que dans les nuages denses où le rayonnement stellaire pénètre peu, l’énergie sous forme de rayonnement devient négligeable par rapport aux autres réservoirs.
Notons aussi que si l’énergie thermique est du même ordre que l’énergie turbulente dans la « bulle locale » chaude où se situe le soleil, la grande majorité du gaz interstellaire est dans la situation inverse où la turbulence l’emporte sur l’agitation thermique : les mouvements turbulents y sont supersoniques, et contribuent de façon majeure à la pression.
Réservoirs d'énergie : champ de rayonnement
Des photons de toutes énergies baignent le milieu interstellaire. Ils ont pour principale origine les étoiles, les grains, et le fond cosmologique. Ce champ de rayonnement est une forme d'énergie importante. Mais son intensité et sa distribution spectrale dépendent fortement de l'endroit où l'on se trouve : distance aux étoiles chaudes, et quantité de poussière sur la ligne de visée vers la source (mesurée par l'extinction AV en magnitudes).
Rayonnement stellaire (UV, VIS, IR)
Les étoiles créent un rayonnement interstellaire diffus dans la Galaxie. Le rayonnement ultraviolet (UV) est dominé par la contribution des étoiles massives, très chaudes (de type O-B), la lumière visible est associée à des étoiles de type A, tandis que les étoiles de type K-M fournissent une contribution infrarouge. Le champ ultraviolet interstellaire est celui qui a l'impact le plus important sur le MIS : Au dessus de 13.6 eV il possède l'énergie suffisante pour photoioniser l'hydrogène (voire l'Helium) et créer des régions de gaz ionisé (régions HII); cependant, du fait de la forte abondance de H et He, ce rayonnement est entièrement absorbé dans une région limitée(appelée Sphère de Stromgren) autour des étoiles massives, de taille inférieure à quelques pc. Par contre, le rayonnement UV non ionisant, d'énergie inférieure à 13.6 eV, est moins absorbé et peut pénétrer plus loin dans le milieu jusqu'à rejoindre les régions d'interface appellée régions de photodissociation (PDR) entre régions HII et nuage moléculaire parent. Là, il y photoexcite et photodissocie les molécules, photoionise les nombreux éléments lourds, et chauffe le milieu par effet photoélectrique sur les grains de poussière.
L'intensité du champ de rayonnement ultraviolet dans le voisinage solaire à été estimée par Habing et vaut 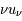 ≈4x10-14 erg cm-3 à
≈4x10-14 erg cm-3 à 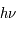 =12.4 eV. L'intégration du spectre UV de Habing de 6 à 13 eV donne une densité d'énergie
=12.4 eV. L'intégration du spectre UV de Habing de 6 à 13 eV donne une densité d'énergie 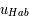 (6-13eV)≈5.29x10-14 erg cm-3. Pour décrire l'intensité du champ FUV incident sur une PDR on utilise souvent un facteur d'échelle
(6-13eV)≈5.29x10-14 erg cm-3. Pour décrire l'intensité du champ FUV incident sur une PDR on utilise souvent un facteur d'échelle 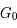 qui est défini comme le rapport de la densité de rayonnement de 6 à 13 eV à celle de Habing :
qui est défini comme le rapport de la densité de rayonnement de 6 à 13 eV à celle de Habing : 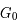 =
=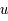 (6-13eV)/
(6-13eV)/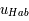 (6-13eV). Des estimations récentes donnent pour le champ de rayonnement interstellaire moyen la valeur
(6-13eV). Des estimations récentes donnent pour le champ de rayonnement interstellaire moyen la valeur 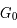 =1.7. Dans des régions de photodissociation typiques comme la nébuleuse de la Tête de Cheval on trouve
=1.7. Dans des régions de photodissociation typiques comme la nébuleuse de la Tête de Cheval on trouve 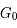 =100, alors que des valeurs de
=100, alors que des valeurs de 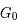 =104-105 sont atteintes au sein des régions de formation stellaire.
=104-105 sont atteintes au sein des régions de formation stellaire.
L'interface entre la région HII M17 et le nuage moléculaire adjacent

Image infrarouge obtenue avec le télescope NTT de l'Observatoire Européen Austral. La région HII M17, dans la partie gauche de l'image, est ionisée par un amas d'étoiles chaudes. L'émission diffuse est associée au continuum du gas ionisé. Le nuage moléculaire adjacent, à droite de l'image, apparaît ici comme une masse sombre qui absorbe la lumière de la plupart des étoiles situées derrière. A l'interface entre les deux, le nuage moléculaire est photodissocié par le rayonnement FUV et s'evapore vers la gauche en formant une région de photodissociation très fragmentée.
Crédit :
SOFI,NTT,ESO
Conversions du système CGS au système SI
| Grandeur | Unité CGS | Définition | SI |
|---|
| longueur | centimètre | 1 cm | =10-2 m |
| masse | gramme | 1 g | =10-3 kg |
| temps | seconde | 1 seconde | =1 s |
| force | dyne | 1 dyn =1 g cm s-2 | =10-5 N |
| énergie | erg | 1 erg = 1 g cm2 s-2 | =10-7 J |
| pression | barye | 1 Ba = 1 dyn/cm2 | =10-1 Pa |
Rayonnement de la poussière (IR)
Le champ de rayonnement infrarouge provient essentiellement des grains de poussière. Ils sont très efficaces à absorber les photons ultraviolets, qui les chauffent, et ils se refroidissent en rayonnant dans les régions du spectre de l'infrarouge et du submillimétrique; Les grains de poussière transforment donc une partie de l'énergie stellaire ultraviolette en énergie infrarouge et en énergie thermique des grains; le reste étant transformé en énergie thermique et cinétique du gaz (effet photo-électrique, évaporation). A l'équilibre thermique, les grains atteignent des températures typiques de 5-50 K dans le MIS; ils peuvent atteindre 100-1000 K à proximité immédiate des étoiles jeunes (disques et enveloppes circumstellaires). Le spectre d'émission est alors continu et déterminé par la température et la composition des grains mais il peut être décrit avec une bonne approximation comme un spectre de corps noir (voir le cours " Fenêtres sur l'Univers"). Cette émission thermique représente en moyenne les 2/3 de la puissance irradiée par la poussière dans le MIS. Le 3ème tiers de cette puissance est rayonné dans l'infrarouge moyen dans des bandes d'émission discrètes (3.3, 6.2, 7.7, 8.6, 11.2, 12.7 μm) qui sont attribués à des hydrocarbures aromatiques polycycliques (PAH = Polycyclic Aromatic Hydrocarbons). Il s'agit de macro-molécules constituées d'atomes de carbone et d'hydrogène, avec une structure planaire composée de cellules hexagonales benzéniques. Ces macro-molécules sont trop petites pour être à l'équilibre thermique et rayonnent de façon "impulsionnelle" suite à l'absorption de chaque photon UV.
Rayonnement cosmologique
Le rayonnement cosmologique est essentiellement isotrope et présente un spectre de corps noir à la température de 2.7 K. Ce rayonnement millimétrique et submillimétrique apporte un chauffage et une source d'excitation minimum au MIS, important en particulier pour la population des niveaux rotationnels de basse énergie des molécules.
La figure ci-dessous montre un exemple des différentes contributions au champ de rayonnement, tel que prédit au voisinage d'une étoile B sans atténuation sur la ligne de visée.
Exemple de champ de rayonnement interstellaire (code PDR de Meudon + code DUSTEM IAS)
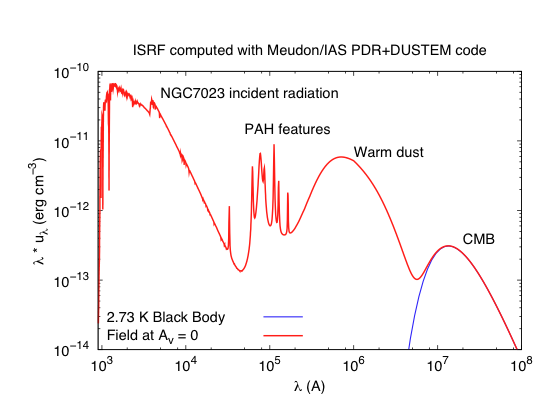
Crédit :
Manuel Gonzalez
Réservoirs d'énergie : champ magnétique
Effet sur le MIS
Le champ magnétique représente une forme d'énergie et de pression très importante pour le milieu interstellaire. Aux grandes échelles, la pression magnétique et la pression des rayons cosmiques s'ajoutent à la pression cinétique turbulente pour contrebalancer l'attraction gravitationnelle de la matière du disque galactique et déterminer la distribution verticale du gaz. Aux plus petites échelles, le champ magnétique joue un rôle majeur dans la structuration, la fragmentation et l'effondrement des nuages interstellaires qui aboutit à la formation des étoiles et des disques protoplanétaires.
Mesures du champ magnétique
Il existe différentes méthodes de mesure de l'intensité et/ou de la direction du champ magnétique interstellaire. Leur domaine d'utilisation varie selon la phase du MIS (ionisée ou neutre) et l'échelle spatiale que l'on souhaite sonder. Les 4 principales sont :
- La rotation Faraday
- L’émission du rayonnement synchrotron diffus galactique
- La polarisation de la lumière par les grains de poussière (en transmission ou en émission)
- L’effet Zeeman dans les raies spectrales
Nous décrivons d’abord brièvement le principe de chaque méthode, puis les résultats obtenus sur le champ magnétique du MIS dans la Galaxie.
Rotation Faraday
Dans le milieu diffus ionisé, le module du champ magnétique le long de la ligne de visée est estimé par la mesure de l'angle de rotation du plan de polarisation d'une onde radio polarisée linéairement émise par une source d’arrière plan, pulsars ou sources extragalactiques. Cette rotation est induite dans un milieu magnétisé par la présence d'électrons libres qui rend le milieu diélectrique.
L’angle de rotation est proportionnel à 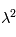 et au produit de la densité électronique et de la composante longitudinale du champ, intégré le long de la ligne de visée vers la source. Par des mesures d’angle à plusieurs longueurs d’onde, on obtient ce produit (appelé « mesure de rotation » ou RM). D’autre part, l’intégrale de la densité électronique seule peut aussi être mesurée grâce à son effet dispersif sur le signal des pulsars : les ondes de différentes fréquences ne se propagent plus exactement à la même vitesse, ce qui produit un décalage du temps d’arrivée de l’impulsion en fonction de la fréquence. De ces 2 mesures on peut alors déduire la valeur du champ longitudinal moyen sur la ligne de visée.
et au produit de la densité électronique et de la composante longitudinale du champ, intégré le long de la ligne de visée vers la source. Par des mesures d’angle à plusieurs longueurs d’onde, on obtient ce produit (appelé « mesure de rotation » ou RM). D’autre part, l’intégrale de la densité électronique seule peut aussi être mesurée grâce à son effet dispersif sur le signal des pulsars : les ondes de différentes fréquences ne se propagent plus exactement à la même vitesse, ce qui produit un décalage du temps d’arrivée de l’impulsion en fonction de la fréquence. De ces 2 mesures on peut alors déduire la valeur du champ longitudinal moyen sur la ligne de visée.
Emission synchrotron des électrons relativistes
Les électrons relativistes qui composent environ 1% des rayons cosmiques émettent dans le champ magnétique galactique un rayonnement synchrotron dans le domaine radio centimétrique. Il est polarisé linéairement dans la direction perpendiculaire au champ. On peut donc connaître l'orientation du champ transverse (voir plus haut). Si on connaît (ou suppose) le flux d'électrons relativistes, on peut aussi déduire le module du champ magnétique transverse ou total, à partir de l’intensité polarisée ou totale du signal synchrotron. Notons que seule l’intensité totale est sensible à la composante aléatoire du champ. Le développement de modèles sophistiqués de la propagation des électrons cosmiques dans la Galaxie a donné une nouvelle assise à cette méthode.
Polarisation de la lumière par les grains de poussière
On observe une faible polarisation linéaire de la lumière des étoiles, corrélée avec leur extinction due aux poussières. Cette anisotropie est attribuée à la présence de grains chargés non sphériques. Sous l’effet de leur rotation, qui induit un moment magnétique, les grains allongés ont tendance à s’orienter avec leur grand axe perpendiculaire au champ magnétique, comme des pinces à linge sur un fil (voir ce schéma). Ils se comportent comme de petites antennes qui absorbent (et émettent) plus efficacement les ondes polarisées le long de leur grand axe, c’est à dire perpendiculairement au champ magnétique. En conséquence, ils transmettent mieux la composante de lumière stellaire polarisée dans la direction parallèle au champ. On peut ainsi construire des cartes de l'orientation du champ magnétique projeté dans le plan du ciel.
On peut également mesurer la direction de polarisation (perpendiculaire au champ magnétique) de l'émission thermique intrinsèque des poussières dans le continu millimétrique et submillimétrique. A cause des limites de sensibilité, cette méthode est surtout employée pour cartographier le champ dans les nuages moléculaires très denses. Mais le satellite Planck a pu tout récemment cartographier la polarisation de l’émission des poussières dans le MIS plus diffus à l’échelle de la Galaxie.
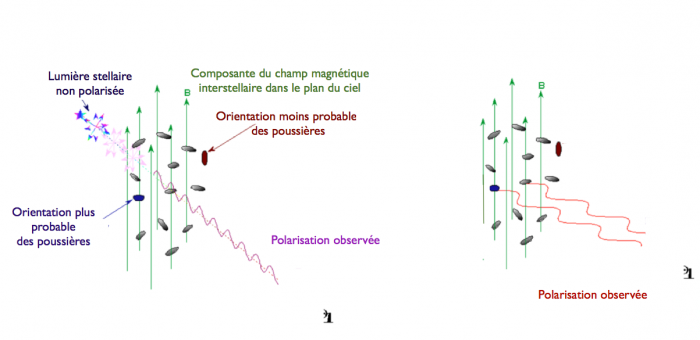
Schéma illustrant la polarisation de la lumière stellaire transmise parallèle à la composante du champ dans le plan du ciel (à gauche) et la polarisation de l'émission des poussières perpendiculaire à ce même champ (à droite).
Crédit :
Présentation de Alyssa Goodman à la conférence Protostar & Planets (1998) traduite en français.
Carte galactique de polarisation de la lumière stellaire par les poussières
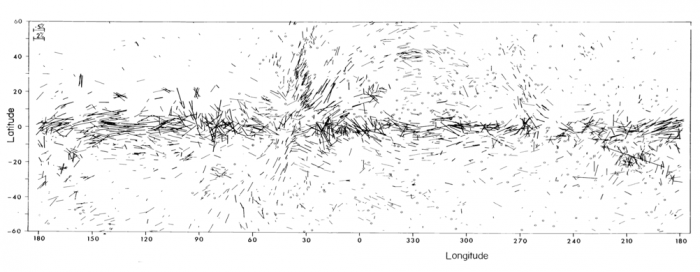
Cette carte de polarisation des étoiles par les poussières interstellaires suggère la présence d'une composante organisée du champ à grande échelle dans le plan Galactique, ainsi qu'une composante plus aléatoire.
Crédit :
D.S. Mathewson & L.V. Ford, Mem. R. astr. Soc. 1970
Effet Zeeman
L'effet Zeeman offre la façon la plus directe de mesurer l'intensité du champ magnétique interstellaire. Il s'agit de la séparation sous l'effet d'un champ magnétique des niveaux d'énergie d'un atome ou d'une molécule (de moment magnétique non nul) en des sous-niveaux équidistants. Cela entraine la division d'une raie spectrale en différentes composantes, dont le déplacement par rapport à la fréquence centrale de la raie est proportionnel à l'intensité du champ magnétique, par un facteur qui dépend de la transition. Dans le cas de l'atome d'hydrogène et de molécules comme OH et CN ce déplacement est d’environ 1,4 Hz par microG. Sauf dans les masers où le champ est intense, on ne peut le mesurer qu’en comparant une paire de composantes (σ) polarisées circulairement en sens inverse l'une de l'autre. L'ajustement de la différence des profils permet d’en déduire la composante du champ le long de la ligne de visée. Notons cependant que le déplacement en fréquence étant sensible au signe de B, il sera considérablement diminué si le champ se renverse dans le lobe d'observation. Il est donc important d’utiliser des lobes d’antenne les plus petits possibles pour éviter cet effet de moyenne.
Cette technique a permis de mesurer le champ magnétique du MIS neutre dans un vaste domaine de densités : avec HI en émission dans les nuages neutres diffus (1-100 cm-3), avec HI en absorption et OH vers les nuages moléculaires (100 à 104 cm-3), et avec CN dans les coeurs denses sites de formation stellaire
(>105 cm-3).
Résultats des mesures de champ magnétique dans la Galaxie
Aux grandes échelles, la combinaison de la rotation de Faraday, de la polarisation optique et de l’émission radio synchrotron a été utilisée pour contraindre la structure du champ magnétique galactique. Elle montre la présence dans le disque d'un champ ordonné orienté sensiblement le long des bras spiraux (comme observé dans les galaxies spirales externes), de valeur environ 1,5 μG au voisinage solaire, et qui change de sens à 5,5 kpc du centre galactique. La polarisation optique des étoiles proches est par contre dominée par une composante désordonnée du champ d'intensité plus élevée d'environ 5 μG. Les modèles les plus récents indiquent aussi la présence d’un champ magnétique toroidal dans le halo, et d’une composante poloidale évasée hors du plan de la Galaxie. La géométrie 3D proposée est illustrée dans la Figure ci-contre.
Modèle du champ magnétique de la Galaxie

Reconstruction synthétique de la structure 3D du champ magnétique Galactique obtenue par ajustement des mesures de rotation Faraday et d'émission synchrotron polarisée.
Crédit :
Farrar G. R. et al. 2015, The 34th International Cosmic Ray Conference.
Aux échelles plus petites des nuages interstellaires et des condensations moléculaires, les méthodes de mesure employées sont l'effet Zeeman (pour le module du champ longitudinal) et la polarisation de l'émission des poussières (pour la direction du champ)
Une compilation récente des mesures Zeeman est présentée dans la Figure ci-contre. Une analyse Bayesienne prenant en compte les limites supérieures indique que le champ maximum dans le gaz neutre reste à peu près constant ~ 10 μG jusqu’à une densité de 300 cm-3. Cela suggère que les nuages HI diffus se condensent préférentiellement le long des tubes de champ magnétique, sans comprimer le champ. Au dessus de 300 cm-3, le champ augmente avec la densité du milieu selon une loi de la forme 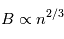 . Cette pente de 2/3 diffère de la pente 1/2 des études précédentes, où la statistique était plus limitée. Elle suggère que la gravité domine la pression magnétique lors de la formation des coeurs denses dans les nuages moléculaires. Cela est cohérent avec les valeurs de B mesurées qui, après correction statistique des effets de projection, restent inférieures en moyenne d’un facteur 2 à la valeur critique nécessaire pour contrecarrer l' autogravité,
. Cette pente de 2/3 diffère de la pente 1/2 des études précédentes, où la statistique était plus limitée. Elle suggère que la gravité domine la pression magnétique lors de la formation des coeurs denses dans les nuages moléculaires. Cela est cohérent avec les valeurs de B mesurées qui, après correction statistique des effets de projection, restent inférieures en moyenne d’un facteur 2 à la valeur critique nécessaire pour contrecarrer l' autogravité, 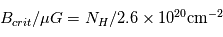 . Cependant une large dispersion est observée d'un nuage à l'autre.
. Cependant une large dispersion est observée d'un nuage à l'autre.
Mesures du champ B dans les nuages denses
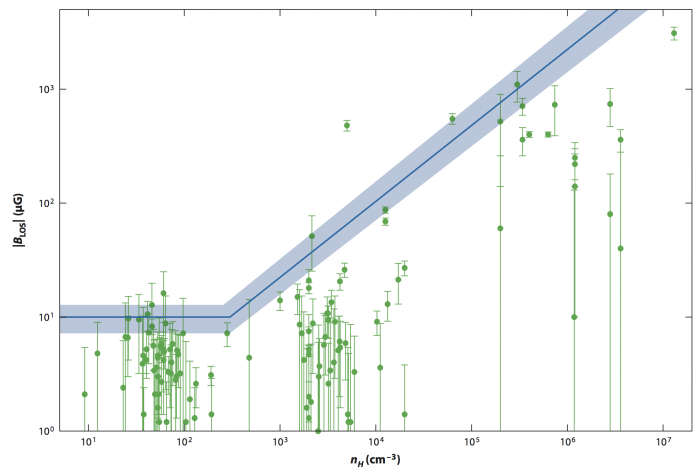
Intensité moyenne du champ magnétique le long de la ligne de visée déduite de mesures de l'effet Zeeman dans les nuages atomiques HI et moléculaires, en fonction de la densité du gaz. La courbe bleue montre la valeur maximum la plus probable, corrigée des effets de projection.
Crédit :
Crutcher, R.M. 2012, Ann. Rev. Astron. Astrophys.
L’étude de la polarisation de l’émission des poussières a fait un grand bond en avant ces dernières années grâce aux progrès des télescopes et interféromètres submillimétriques, et au satellite Planck qui a cartographié la polarisation du continu submillimétrique dans l'ensemble du ciel avec une très grande précision. Les cartes dans les nuages moléculaires (par exemple le Taureau) révèlent une distribution de lignes de champ assez uniforme et cohérente qui suggère la présence d'une composante à grande échelle d’intensité suffisante pour resister à la turbulence. Les filaments denses de matière semblent préférentiellement parallèles ou perpendiculaires au champ, ce qui suggère que ce dernier joue un rôle dans leur formation ou leur confinement.
Champ magnétique dans le Taureau avec Planck
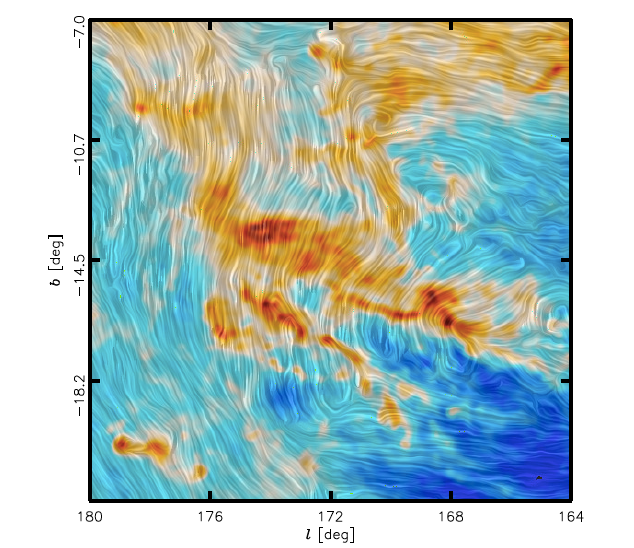
Orientation du champ magnétique (en courbes grises) et densité colonne (en couleurs) dans le nuage moléculaire du Taureau. La direction du champ est déterminée par la polarisation de l'émission des poussières cartographiée par le satellite Planck.
Crédit :
Planck Collaboration XXXV, 2015 Astronomy & Astrophysics, in press.
L’orientation globale du champ est souvent préservée jusque dans les coeurs denses (0.1 pc) où se forment les étoiles. Une composante aléatoire turbulente est également présente, mais généralement plus faible que la composante organisée. A petite échelle une géométrie en « sablier » est parfois observée suggérant que le champ est pincé et comprimé par la contraction gravitationnelle (voir ci-dessous).
Carte du champ magnétique dans un coeur dense
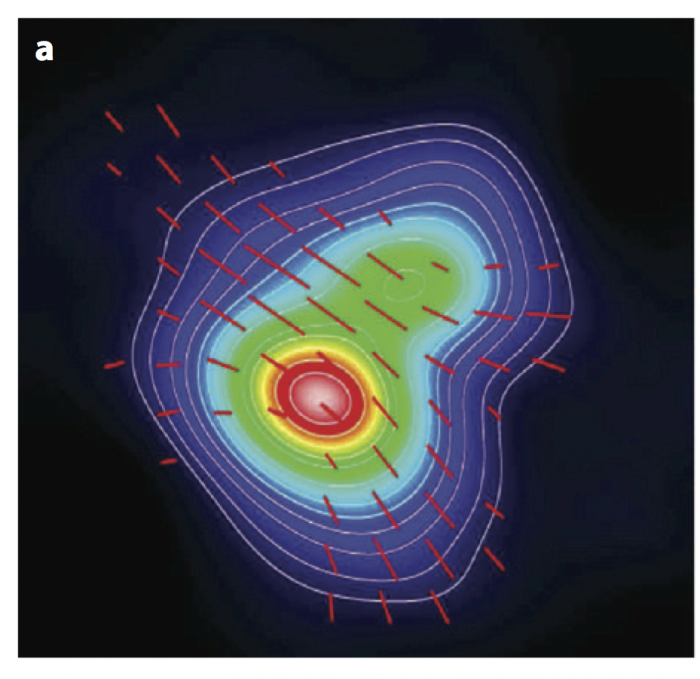
Orientation du champ magnétique dans le plan du ciel (en rouge) déduite de la polarisation de l'émission des poussières (intensité totale en couleurs) dans la condensation NGC1333-IRAS4A qui abrite une protoétoile.
Crédit :
Girart, Rao et Marrone 2006, Science
Réservoirs d'énergie : rayons cosmiques
Les rayons cosmiques ne sont pas réellement un rayonnement : ils sont constitués de particules chargées (environ 99% de noyaux atomiques et 1% d'électrons) qui circulent à très grande vitesse dans la Galaxie de façon à peu près isotrope. Les noyaux sont des protons (90%), des noyaux d'hélium (environ 9%) et des atomes plus lourds (1%).
Des études détaillées sur la composition des rayons cosmiques montrent une forte surabondance des éléments légers (Li, Be, B) par rapport aux abondances standards solaires. Elles révèlent également une abondance relativement élevée de noyaux provenant d'atomes lourds habituellement inclus dans les grains de poussière (par exemple le fer, voir cette figure). Les grains étant chargés électriquement, ils peuvent être accélérés comme des ions très lourds. Suite à cette accélération ils subissent une érosion sous l'impact des atomes du gaz, et libèrent les éléments qui les composent.
Les rayons cosmiques présentent une gamme d’énergie très vaste qui s’étend sur au moins 14 décades, de qques 107 eV (= 10 Mev) à plus de 1020 eV (=1011 GeV). Le spectre en énergie au voisinage de la Terre est présenté dans la figure ci-dessous. Il peut se décomposer en trois parties. De quelques GeV jusqu'à 106 GeV, le spectre suit une première loi de puissance avec l'énergie de la forme 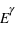 , avec l'indice γ proche de -2.7. Pour cet intervalle d'énergie, des mesures directes menées à l'aide de ballons ou satellites sont disponibles. C’est le domaine des rayons cosmiques dits « galactiques ». Les explosions de supernovae constituent une source d'énergie suffisante pour les expliquer. En effet, les particules chargées peuvent être accélérées de façon très efficace par le champ magnétique dans les ondes de choc générées par l'explosion. De 106 GeV à 109 GeV le spectre s’infléchit (« genou ») pour suivre une loi de puissance plus raide, avec un indice γ d'environ -3. Cette composante pourrait avoir en partie une origine extragalactique (par exemple noyaux actifs de galaxie). Au delà de 109 GeV on observe une nouvelle rupture de pente qu'on appelle la cheville et le nombre d'événements enregistrés est très faible. C'est le domaine des rayons cosmiques ultra-énergétiques, dont l'origine est encore mal contrainte.
, avec l'indice γ proche de -2.7. Pour cet intervalle d'énergie, des mesures directes menées à l'aide de ballons ou satellites sont disponibles. C’est le domaine des rayons cosmiques dits « galactiques ». Les explosions de supernovae constituent une source d'énergie suffisante pour les expliquer. En effet, les particules chargées peuvent être accélérées de façon très efficace par le champ magnétique dans les ondes de choc générées par l'explosion. De 106 GeV à 109 GeV le spectre s’infléchit (« genou ») pour suivre une loi de puissance plus raide, avec un indice γ d'environ -3. Cette composante pourrait avoir en partie une origine extragalactique (par exemple noyaux actifs de galaxie). Au delà de 109 GeV on observe une nouvelle rupture de pente qu'on appelle la cheville et le nombre d'événements enregistrés est très faible. C'est le domaine des rayons cosmiques ultra-énergétiques, dont l'origine est encore mal contrainte.
Bien que les particules de haute énergie subissent des collisions avec les atomes, les molécules et les grains de poussière du milieu interstellaire, leurs trajectoires sont dominées par le champ magnétique. Les particules chargées effectuent un mouvement de giration (dans le plan perpendiculaire aux lignes de champ magnétique) dont le rayon dépend de leur énergie et de l'intensité du champ magnétique. Des protons d'énergie de l'ordre de 106 GeV dans un champ de 5 μG ont un rayon de giration d'environ 1016 m = 0.3 pc, soit beaucoup moins que l'échelle de hauteur de la Galaxie. Ces particules sont donc bien confinées par le champ magnétique. La présence d'irrégularités magnétiques peut néanmoins produire une diffusion transversale des particules en changeant l'orientation des orbites de giration. La diffusion à travers les lignes de champ magnétique est à l'origine de l'isotropie observée dans le flux des rayons cosmiques. Il s'établit une équipartition de l'énergie entre les rayons cosmiques et le milieu interstellaire. Les particules diffusent le long des structures magnétiques à grande échelle et traversent de nombreuses fois la Galaxie. La diffusion transversale peut les amener dans le halo ou leur permettre de s'échapper définitivement vers l'espace extragalactique.
Spectre en énergie des rayons cosmiques
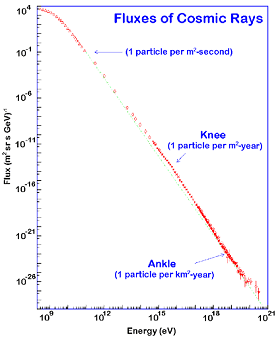
Flux de rayons cosmiques au sol en fonction de leur énergie par nucléon (knee=genou, ankle=cheville).
Crédit :
NASA
Effet des rayons cosmiques sur le MIS
Ce sont les rayons cosmiques de basse énergie (de l'ordre du MeV) qui jouent un rôle important dans l'ionisation et le chauffage du milieu interstellaire moléculaire. Leur flux au bord des nuages est moins intense que celui des photons ultraviolets mais leur degré de pénétration est beaucoup plus élevé, ce qui fournit une source d'ionisation s'étendant jusqu'au plus profond de ces objets. Les rayons cosmiques influencent donc la chimie du milieu, en particulier en favorisant la formation de molécules grâce à des réactions ions-neutres (qui n'ont pas de barrière énergétique). L’ionisation par les rayons cosmiques produit aussi des électrons énergétiques qui chauffent le gaz via interaction colombienne. Ce processus est la source principale de chauffage dans les nuages moléculaires où le flux UV est faible et la densité < 104 cm-3 (au dessus, le chauffage par collisions avec les grains entre en jeu). La compétition avec le refroidissement radiatif par CO y maintient une température d’équilibre autour de 10 K.
Le flux de rayons cosmiques de basse énergie dans la Galaxie n'est pas mesurable directement. En dessous de 10 GeV, les particules détectées proviennent essentiellement du Soleil, car les rayons cosmiques de même énergie qui proviendraient de l'extérieur sont repoussés par le vent solaire (effet de modulation solaire). Leur flux incident dans l’espace interstellaire doit donc être estimé de manière indirecte. Une première méthode a consisté à modéliser la surabondance de noyaux légers (Li, Be, B) qui résulte de la fragmentation des noyaux de C,N ou O du milieu interstellaire par l’impact des protons rapides (réactions de spallation). Le seuil de cette réaction se situant vers 30-50 MeV, elle est très sensible aux protons de faible énergie. Une approche plus directe consiste à mesurer l'abondance de certains ions moléculaires, comme H3+ qui résulte de l'ionisation de H2 par les rayons cosmiques de basse énergie (les photons UV capables d'ioniser H2 sont absorbés par l’hydrogène atomique). Les résultats récents illustrés ci-dessous révèlent un taux moyen d'ionisation par les cosmiques dans le MIS diffus d'environ 3x10-16 s-1, qui chute d'un facteur 10 dans les nuages denses (NH > 5x1022 cm-2). Des variations importantes sont observées entre nuages diffus, qui pourraient refléter leur distance aux sites locaux d’accélération des RCs ou bien des effets de propagation.
Taux d'ionisation par les rayons cosmiques
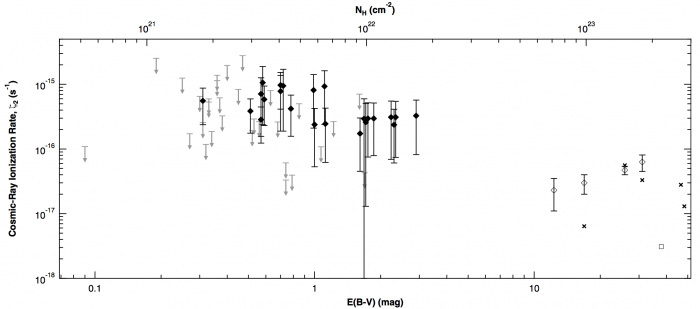
Taux d'ionisation par les rayons cosmiques (normalisé par noyau d'hydrogène) sur plusieurs lignes de visées, tracé en fonction de la densité colonne NH du nuage. Les valeurs sont principalement déduites de l'abondance de H3+ (losanges pleins et ouverts pour les détections, flèches grises pour les limites supérieures); et complétées par des mesures de HCO+ (croix) et HCNH+ (carré).
Crédit :
Indriolo & McCall (2012, ApJ)
Images
Auteurs: Cecilia Pinto, Sylvie Cabrit
Détection du milieu interstellaire à différentes longueurs d'onde
Auteur: Cecilia Pinto et Sylvie Cabrit
Images de la Galaxie à differentes longueurs d'onde
 Introduction
Introduction
Nous ne pouvons étudier le milieu interstellaire que par le moyen de l'analyse de son rayonnement, sous forme d'émission continue et de raies spectrales. Les caractéristiques de cette émission dépendent des conditions physiques (densité, température, composition chimique) du gaz et des poussières, qui sont très variées. Certaines composantes du MIS sont bien visibles dans des régions particulières du spectre mais ne sont pas relevées dans d' autres. Il nous faut donc combiner des observations dans un vaste intervalle d'énergies pour avoir accès aux différentes phases du milieu, ainsi qu'aux différents diagnostics radiatifs des conditions qui y règnent.
L'image La Voie Lactée à diverses longueurs d'onde
montre une image complète du plan de la Galaxie (± 10 degrés de part et d'autre) à des fréquences croissantes de haut en bas, s'étendant sur un intervalle de fréquence de 14 ordres de grandeur. Chaque planche correspond à un différent mécanisme d'émission, qui apporte donc des informations différentes: de haut en bas:
- Le continu radio à 408 MHz est dû au rayonnement synchrotron émis par les électrons relativistes circulant dans le champ magnétique interstellaire et accélérés par les ondes de choc engendrées par les explosions de supernovae (voir la page Réservoirs d'énergie : rayons cosmiques)
- La deuxième planche représente l'émission de la raie à 21 cm de l'hydrogène qui trace le gaz atomique, tiède ou froid du WNM et du CNM (voir la section Détection du gaz atomique : raies spectrales).
- Le continuum radio à haute fréquence (2.5 GHz) est dominé par le rayonnement de freînage (émission libre-libre) des électrons du gaz ionisé dans le WIM (voir la page Détection du gaz ionisé).
- L'image de la densité de colonne de l'hydrogène moléculaire est obtenue via la raie rotationnelle de la molécule de CO(J=1-0) à 115 GHz émise par les nuages moléculaires denses (voir la page Détection du gaz neutre moléculaire
- L'image intitulée "infrarouge" montre l'émission thermique des poussières chauffées par le rayonnement stellaire (voir la section Rayonnement de la poussière), observée par le satellite IRAS. Elle montre en rouge l'émission dans l'infrarouge lointain à 100 μm dominée par les gros grains, en bleu celle à 12 μm dominée par les petits grains, et en vert celle à 60 μm qui a une contribution des deux.
- L'image dans l'infrarouge moyen, obtenue par le satellite MSX, contient une forte contribution de l'émission de petits hydrocarbures aromatiques polycycliques (voir la section Rayonnement de la poussière).
- Dans l'infrarouge proche, l'émission est dominée par les étoiles de type K du disque et du bulbe, avec une contribution du gaz ionisé.
- Dans le domaine optique (visible par nos yeux), l'émission est essentiellement due aux étoiles. Les régions sombres tracent la présence de nuages de poussière qui absorbent la lumière visible. On peut noter que ces nuages sombres apparaissent au contraire brillants dans la raie de CO (planche intitulée "hydrogène moléculaire").
- L'image dans les rayons X, obtenue par le satellite ROSAT, est associée au gaz très chaud et dilué de la phase HIM situé dans les restes de supernova et qui diffuse sur une grande échelle de hauteur au dessus du plan Galactique (voir la page Détection du gaz ionisé).
- La dernière image, en rayons γ, inclut des photons d'énergie supérieure à 300 MeV qui sont produits lors des collisions des rayons cosmiques avec la matière interstellaire.
La Voie Lactée à diverses longueurs d'onde

Crédit :
NASA Goddard Space Flight Center
Dans ce qui suit, nous allons décrire plus en détail les principales méthodes d'observation de chaque phase du MIS, et leurs principaux résultats.
Détection du gaz atomique: L'atome d'hydrogène
Le noyau de l'atome d'hydrogène est constitué d'un seul proton autour duquel ne tourne qu'un seul électron sur des orbites bien définies appelées niveaux d'énergie. L'énergie de l'électron sur une orbite donnée dépend du nombre quantique principal 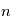 (il prend des valeurs entières) du niveau selon la relation:
(il prend des valeurs entières) du niveau selon la relation: 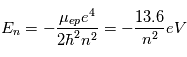 , où
, où 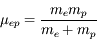 est la masse réduite du système électron-proton. Le niveau fondamental d'énergie minimale,
est la masse réduite du système électron-proton. Le niveau fondamental d'énergie minimale, 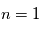 , est situé à une énergie de -13.6 eV sous la limite d'ionisation
, est situé à une énergie de -13.6 eV sous la limite d'ionisation 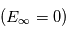 . Lorsque
. Lorsque 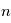 augmente, l'énergie du niveau est de moins en moins négative : elle augmente. Le niveau
augmente, l'énergie du niveau est de moins en moins négative : elle augmente. Le niveau 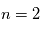 est ainsi situé à -3.4 eV sous la limite d'ionisation
est ainsi situé à -3.4 eV sous la limite d'ionisation 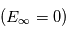 , c'est-à-dire à +10.2 eV au dessus du fondamental. Afin de minimiser l'énergie du système, les électrons sur des orbites excitées vont se désexciter radiativement spontanément vers des niveaux de valeur de
, c'est-à-dire à +10.2 eV au dessus du fondamental. Afin de minimiser l'énergie du système, les électrons sur des orbites excitées vont se désexciter radiativement spontanément vers des niveaux de valeur de 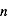 plus faible. Les cascades radiatives des niveaux supérieurs vers le niveau
plus faible. Les cascades radiatives des niveaux supérieurs vers le niveau 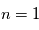 produisent un ensemble de raies spectrales dans l'ultraviolet dénommé Série de Lyman, celles vers le niveau
produisent un ensemble de raies spectrales dans l'ultraviolet dénommé Série de Lyman, celles vers le niveau 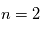 créent des raies dans le visible correspondant à la Série de Balmer. Enfin, les cascades vers les niveaus
créent des raies dans le visible correspondant à la Série de Balmer. Enfin, les cascades vers les niveaus 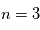 , 4 et 5 donnent les Séries de Paschen, Bracket et Pfund dans l'infrarouge (voir Figure ci-dessous). Ces cascades se produisent lorsqu'un proton et un électron se recombinent pour reformer un atome neutre, car la recombinaison se fait en général sur un état excité. Ces raies dites "de recombinaison" sont donc une signature de régions où l'hydrogène subit une certaine ionisation (par rayonnement ou par collisions).
, 4 et 5 donnent les Séries de Paschen, Bracket et Pfund dans l'infrarouge (voir Figure ci-dessous). Ces cascades se produisent lorsqu'un proton et un électron se recombinent pour reformer un atome neutre, car la recombinaison se fait en général sur un état excité. Ces raies dites "de recombinaison" sont donc une signature de régions où l'hydrogène subit une certaine ionisation (par rayonnement ou par collisions).
Spectre de l'atome d'hydrogène
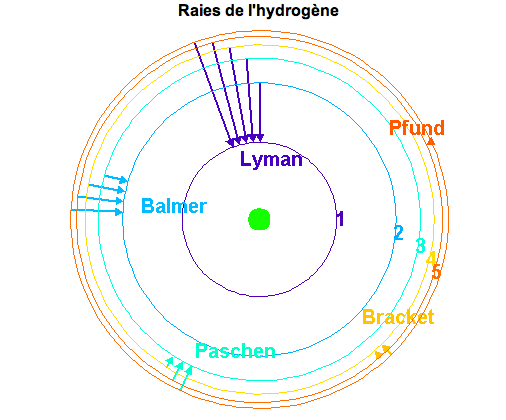
Schéma des 6 premiers niveaux d'énergie de l'Hydrogène, et noms des cascades radiatives qui mènent à chacun d'eux.
Crédit :
Astrophysique sur Mesure
Dans le cas non relativiste, un état de nombre quantique 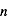 est constitué de
est constitué de 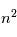 sous-niveaux d'énergie identique. Chaque sous-niveau est caractérisé par un nombre quantique
sous-niveaux d'énergie identique. Chaque sous-niveau est caractérisé par un nombre quantique 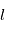 , qui correspond dans le cas classique à l'amplitude du moment orbital angulaire de l'électron, et par un nombre quantique
, qui correspond dans le cas classique à l'amplitude du moment orbital angulaire de l'électron, et par un nombre quantique 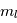 qui équivaut à la projection du moment angulaire orbital sur l'axe de rotation.
qui équivaut à la projection du moment angulaire orbital sur l'axe de rotation. 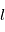 ne peut prendre que les valeurs entières entre 0 et
ne peut prendre que les valeurs entières entre 0 et 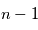 , et
, et 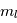 celles entre
celles entre 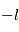 et
et 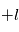 (on dit que le moment orbital est quantifié). L'électron possède aussi un moment cinétique intrinsèque qui n'a pas d'équivalent classique, le spin, lui aussi quantifié comme le moment angulaire orbital. L'interaction dite de structure fine entre le moment orbital
(on dit que le moment orbital est quantifié). L'électron possède aussi un moment cinétique intrinsèque qui n'a pas d'équivalent classique, le spin, lui aussi quantifié comme le moment angulaire orbital. L'interaction dite de structure fine entre le moment orbital 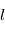 de l'électron et son spin induit la levée de dégénérescence des
de l'électron et son spin induit la levée de dégénérescence des 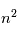 niveaux qui prennent alors des énergies faiblement différentes. Cette décomposition disparaît quand
niveaux qui prennent alors des énergies faiblement différentes. Cette décomposition disparaît quand 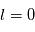 . Le proton possède également un moment cinétique de spin qui se combine avec le spin de l'électron en produisant une sous-structure encore plus fine des niveaux, dite hyperfine. En équivalent classique, l'énergie de l'atome dépend de si le spin de l'électron et du proton sont parallèles (configuration ortho) ou antiparallèles (configuration para).
. Le proton possède également un moment cinétique de spin qui se combine avec le spin de l'électron en produisant une sous-structure encore plus fine des niveaux, dite hyperfine. En équivalent classique, l'énergie de l'atome dépend de si le spin de l'électron et du proton sont parallèles (configuration ortho) ou antiparallèles (configuration para).
Dans le MIS froid, seul le niveau fondamental 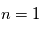 de l'hydrogène est peuplé, où
de l'hydrogène est peuplé, où 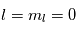 . Il n'y a donc pas de raie de structure fine, seulement une raie de structure hyperfine : la raie à 21 cm dont nous parlons plus en détail ci-dessous.
. Il n'y a donc pas de raie de structure fine, seulement une raie de structure hyperfine : la raie à 21 cm dont nous parlons plus en détail ci-dessous.
Détection du gaz neutre atomique : raies spectrales
Raie de l'hydrogène à 21cm
La raie à 21 cm de longueur d'onde (1.4 GHz de fréquence radio) correspond à la très faible différence d'énergie (5.9x10-5 eV = 0.07 K) entre les deux sous-niveaux hyperfins du niveau fondamental 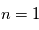 de l'hydrogène atomique, où se trouve la plupart de l'hydrogène dans le MIS atomique froid. La transition se produit lorsque l'électron renverse son spin : le sous-niveau supérieur correspond à la configuration où le spin de l'électron est parallèle à celui du noyau (spin total S =1), et le sous-niveau inférieur à celle où le spin est antiparallèle (S=0). Le taux de désexcitation radiative spontanée (voir la page Coefficients d'Einstein) est très faible : la durée de vie du sous-niveau supérieur est de 107 ans. Aussi, dès que la densité excède 1 cm-3, les collisions maintiennent la population du niveau supérieur à son niveau d'équilibre thermodynamique local
de l'hydrogène atomique, où se trouve la plupart de l'hydrogène dans le MIS atomique froid. La transition se produit lorsque l'électron renverse son spin : le sous-niveau supérieur correspond à la configuration où le spin de l'électron est parallèle à celui du noyau (spin total S =1), et le sous-niveau inférieur à celle où le spin est antiparallèle (S=0). Le taux de désexcitation radiative spontanée (voir la page Coefficients d'Einstein) est très faible : la durée de vie du sous-niveau supérieur est de 107 ans. Aussi, dès que la densité excède 1 cm-3, les collisions maintiennent la population du niveau supérieur à son niveau d'équilibre thermodynamique local 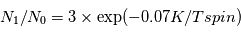 . Chaque dépeuplement par émission spontanée produit un photon à 21 cm. L'intensité du signal radio observé est proportionnelle à la densité de colonne du gaz (nombre d'atomes par unité de surface le long de la ligne de visée). L'étude de l'émission de la raie à 21 cm et des variations spatiales de son intensité a donc permis la détermination de la masse et de la distribution du gaz atomique froid dans notre Galaxie et des galaxies extérieures. La raie à 21 cm peut être observée également en absorption lorsque un nuage d'hydrogène froid est situé sur la même ligne de visée qu'une source puissante de rayonnement radio continu (un pulsar ou une galaxie radio). Une combinaison de mesures en émission et absorption permet de déterminer à la fois la température et la densité de colonne du gaz atomique (voir les détails dans la page Application : la raie à 21 cm de l'hydrogène neutre).
. Chaque dépeuplement par émission spontanée produit un photon à 21 cm. L'intensité du signal radio observé est proportionnelle à la densité de colonne du gaz (nombre d'atomes par unité de surface le long de la ligne de visée). L'étude de l'émission de la raie à 21 cm et des variations spatiales de son intensité a donc permis la détermination de la masse et de la distribution du gaz atomique froid dans notre Galaxie et des galaxies extérieures. La raie à 21 cm peut être observée également en absorption lorsque un nuage d'hydrogène froid est situé sur la même ligne de visée qu'une source puissante de rayonnement radio continu (un pulsar ou une galaxie radio). Une combinaison de mesures en émission et absorption permet de déterminer à la fois la température et la densité de colonne du gaz atomique (voir les détails dans la page Application : la raie à 21 cm de l'hydrogène neutre).
Raies atomiques de structure fine
Contrairement à l'atome d'hydrogène, la plupart des atomes et des ions importants dans le milieu interstellaire ont un moment orbital total L non nul dans leur configuration electronique fondamentale (la seule qui soit peuplée en pratique). Ce niveau est donc décomposé par l'interaction de structure fine entre le moment orbital total 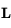 de tous les électrons de l'atome et leur spin total
de tous les électrons de l'atome et leur spin total 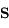 . Le moment angulaire total du système atomique est la somme vectorielle de ces deux moments cinétiques :
. Le moment angulaire total du système atomique est la somme vectorielle de ces deux moments cinétiques : 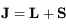 et les transitions dipolaires électriques sont soumises aux règles de sélection :
et les transitions dipolaires électriques sont soumises aux règles de sélection : 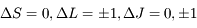 . Les transitions entre les sous-niveaux de structure fine sont dites "interdites" car elles transgressent ces règles de sélection. Elles ont en conséquence un coefficient d'Einstein faible, mais non nul car la transition dipolaire magnétique reste autorisée. Le niveau supérieur est souvent proche du fondamental, ce qui leur donne une grande importance pour la physique du milieu interstellaire : La raie de [CII]λ157.7μm, dont le niveau supérieur n'est qu'à 91,2 K, est très facilement excitée dans le milieu neutre froid et elle en est le principal facteur de refroidissement. En effet, dans cette phase diffuse, le carbone est essentiellement sous forme de C+ à cause du flux UV interstellaire. La raie de [OI]λ63μm, dont le niveau supérieur est à 228 K, participe également au refroidissement à température plus élevée. Ces raies appartiennent à l'infrarouge lointain et ont été observées par de nombreux satellites comme COBE, ISO, SWAS) et récemment Herschel, avec une résolution angulaire atteignant 10 secondes d'arc.
. Les transitions entre les sous-niveaux de structure fine sont dites "interdites" car elles transgressent ces règles de sélection. Elles ont en conséquence un coefficient d'Einstein faible, mais non nul car la transition dipolaire magnétique reste autorisée. Le niveau supérieur est souvent proche du fondamental, ce qui leur donne une grande importance pour la physique du milieu interstellaire : La raie de [CII]λ157.7μm, dont le niveau supérieur n'est qu'à 91,2 K, est très facilement excitée dans le milieu neutre froid et elle en est le principal facteur de refroidissement. En effet, dans cette phase diffuse, le carbone est essentiellement sous forme de C+ à cause du flux UV interstellaire. La raie de [OI]λ63μm, dont le niveau supérieur est à 228 K, participe également au refroidissement à température plus élevée. Ces raies appartiennent à l'infrarouge lointain et ont été observées par de nombreux satellites comme COBE, ISO, SWAS) et récemment Herschel, avec une résolution angulaire atteignant 10 secondes d'arc.
Raies d'absorption interstellaires
De nombreuses raies d'absorption interstellaires ont été observées dans les spectres des étoiles. Dans le visible et le proche ultraviolet on observe les raies d'atomes (Na, Ca, K), d'ions (Ca+) et de molécules (CN, CH+, OH...). Grâce à des satellites comme COPERNICUS, Hubble, et FUSE on a pu observer dans l'ultraviolet lointain un grand nombre de raies atomiques (notamment les raies de la série Lyman de l'hydrogène), ioniques et moléculaires (par exemple H2, qui sera discuté plus bas). L'ensemble de ces raies donne des informations très riches sur les conditions physiques et la composition chimique dans le milieu interstellaire atomique. En particulier il est possible de déduire la colonne de densité de l'élément observé (voir la page Raies en absorption) et ainsi son abondance en phase gazeuse relativement à l'hydrogène.
Résultats des observations spectrales
- Il existe deux phases du milieu interstellaire atomique : l'une tiède (WNM), à plusieurs milliers de degrés, et peu dense (0.1-0.5 cm-3) que l'on voit en émission, l'autre froide (CNM, 60-100 K) et plus dense (10-50 cm-3), qui domine l'absorption. Les densités de colonne sont toutes deux d'environ 1.5x1020 atomes cm-2. Le contenu en matière est comparable pour les deux composantes mais la composante tiède forme un disque plus épais, sa demi-épaisseur étant de l'ordre de 200 kpc, par rapport à celui du gaz froid d'environ 100 kpc. La composante froide forme principalement les structures complexes mentionnées ci-dessus, et se trouve également dans les enveloppes des nuages moléculaires. La composante tiède est distribuée plus uniformément.
- La composante froide est fortement inhomogène. Elle est dominée par des nappes, des coquilles et des filaments à toutes les échelles avec une apparence fractale qui pourrait être créée par la turbulence. Elle se trouve également dans les enveloppes des nuages moléculaires. La composante tiède est distribuée plus uniformément.
- Les abondances des éléments déduites des raies d'absorption ultraviolettes révèlent que la plupart des élément sont sous-abondants dans le gaz atomique froid par rapport aux abondances solaires, stellaires où dans les régions HII à l'exception de S, Zn et P. Les élément manquants sont supposés se trouver dans les grains de poussière. La sous-abondance est moins grande dans le gaz neutre tiède, ce qui indique une destruction partielle des grains, peut-être sous l'effet d'ondes de chocs violentes (restes de supernovae).
Carte du plan galactique dans la raie à 21cm dans une région du bras de Persée

Grumeaux et filaments (en pourpre) d'hydrogène froid superposés sur un fond diffus d'hydrogène plus chaud (en jaune).
Crédit :
J. English : données obtenues par le Relevé Canadian du Plan Galactique.
Carte du gaz neutre atomique dans la Galaxie
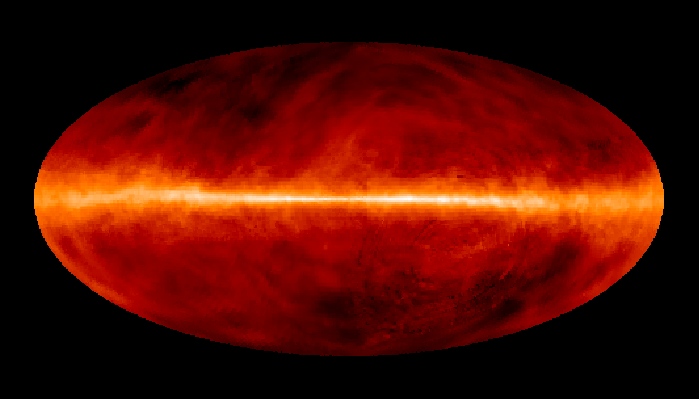
Crédit :
J.Dickey (Université du Minnesota), F.Lockman (National Radio Astronomy Observatory)
Détection du gaz neutre moléculaire
Transitions moléculaires
Aujourd'hui on a identifié plus de 200 molécules différentes dans le milieu interstellaire. Les molécules sont fragiles et peuvent être dissociées par le rayonnement visible et ultraviolet. Elles sont donc principalement localisées dans des nuages moléculaires denses où elles sont protégés du flux de photons de haute énergie par la poussière et l'hydrogène moléculaire diffus situé aux bords des nuages. Leurs raies spectrales fournissent donc des informations précieuses sur les régions les plus denses du milieu interstellaire.
Tandis que les transitions dans les atomes proviennent uniquement des changements d’orbite des électrons, les molécules émettent selon trois type de transitions : électroniques, vibrationnelles et rotationnelles, qui tracent des gammes d'énergie décroissantes.
-
Les transitions électroniques des molécules sont l'équivalent des transitions atomiques. Pour H2, la molécule interstellaire la plus importante, ces transitions sont à des longueurs d'onde λ < 115 nm. Les autres molécules détectées par leurs transitions électroniques sont CO et OH dans l'ultraviolet lointain, CH, CH+ et CN dans l'ultraviolet proche et le bleu, et C2 et CN dans le proche infrarouge à 800-900 nm. Cependant, les niveaux électroniques des molécules sont situés à des énergies trop élevées pour être peuplés par collisions thermiques car cela nécessiterait des températures où le gaz ne serait plus moléculaire. Ils peuvent par contre être peuplés par l’absorption d’un photon ultraviolet, ou par l’impact d’un électron énergétique issu de l’ionisation du gaz par des rayons X ou des rayons cosmiques. La molécule ainsi excitée cascade vers les niveaux inférieurs en émettant des photons dans ses transitions électroniques : c’est le phénomène de fluorescence. Celui-ci n’a lieu qu’à proximité d’une source intense d’UV ou d’ionisation (par ex. étoiles jeunes, Noyau actif de galaxie...). Dans les conditions interstellaires typiques, les transitions électroniques des molécules sont seulement observables en absorption à partir du niveau électronique fondamental, en direction d'étoiles ou de sources extragalactiques. En particulier, les observations dans l'UV lointain menées avec les satellites COPERNICUS et FUSE ont fourni le rapport d'abondance H2/H sur de nombreuses lignes de visée du milieu moléculaire diffus (où l'extinction par les poussières n'est pas trop élevée), par l'observation de raies d'absorption électroniques de H2 et de H (raie Lyman α).
-
Selon leur géométrie, les molécules possèdent un certain nombre de modes de vibration possibles qui sont quantifiés et associés à des niveaux d'énergie approximativement équidistants, de séparation typique ~ 3000 K. Les transitions entre ces niveaux, dites vibrationnelles, sont caractérisées par des longueurs d'onde typiques de l'infrarouge proche. Ces transitions sont vues soit en absorption devant une source intense de continuum infrarouge, soit en émission si la température du milieu est suffisamment élevée, par exemple dans les chocs, ou les régions de photodissociation (PDRs) exposées à un fort flux UV. Les transitions vibrationnelles de H2, ainsi que celles de CO et H2O, sont observées à la fois du sol et de l'espace (par ex. par le satellite Spitzer). Chaque transition vibrationnelle est composée d’une série de raies distinctes de longueurs d’onde très proches, provenant des différents sous-niveaux de rotation (voir ci-dessous). Les meilleurs spectromètres infrarouges au sol sont capables de résoudre ces sous-composantes individuelles dites ''ro-vibrationnelles" pour en déduire la température du gaz via la loi de Boltzman.
-
Les transitions rotationnelles correspondent à la quantification des modes de rotation des molécules. Pour H2 ces raies sont dans l’infrarouge moyen (λ ≤ 28 μm) et issues de niveaux > 500 K, qui ne sont excités en émission que dans des zones localement chauffées (chocs ou PDRs). Les molécules plus lourdes, par contre, ont des niveaux rotationnels faiblement espacés (10-100 K) bien adaptés pour sonder les nuages moléculaires froids et denses. Leurs raies rotationnelles sont caractérisées par des longueurs d'onde submillimétriques, millimétriques ou centimétriques. Les avantages d'observer dans ce domaine radio sont (1) l'absence d'extinction par les poussières à ces longueurs d'onde, (2) la très haute résolution spectrale (<1 km/s) obtenue par les techniques de détection hétérodynes, qui permet de mesurer l’élargissement thermique et/ou turbulent de la raie et les gradients de vitesse entre différentes parties du nuage. La molécule la plus intense est CO : c’est la plus abondante après H2 et elle possède un premier niveau rotationnel à 5 K, facilement excité collisionnellement dans le gaz froid dès que la densité dépasse quelques 100 cm-3. La raie correspondante à 2.6 mm est utilisée pour cartographier à grande échelle les nuages moléculaires. L'application la plus importante de ces observations est l'estimation de la structure, de la masse et de la cinématique des nuages moléculaires. D’autres molécules souvent utilisées comme traceurs plus spécifiques de température et/ou de régions denses sont NH3, CS, N2H+. Enfin, l'étude des raies rotationnelles moléculaires en absorption en direction de sources radio extragalactiques (quasars) a permis de sonder en détail la chimie de la composante moléculaire diffuse, notamment les hydrides dans le submillimétrique avec le satellite Herschel et l'avion stratosphérique SOFIA.
Résultats des observations :
L'étude de la distribution de la raie J=1-0 de CO à 2.6 mm montre que la plupart du gaz moléculaire dans la Galaxie est localisé dans des nuages moléculaires géants de taille typique 40 pc, masse d'environ 4x105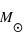 , densité ≥ 200 cm-3 et température 10-30 K. L'abondance de CO y est d'environ 10-4 celle de H2. Ces nuages sont des objets auto-gravitants, plutôt qu'à l'équilibre de pression avec les autres phases du milieu interstellaire. Leur pression turbulente (mesurée par l'élargissement Doppler des raies CO) et magnétique (mesurée comme expliqué dans la Section "Energie magnétique") est globalement suffisante pour contrebalancer la gravité, ce qui les maintient globalement stables sur des échelles de l'ordre de 106-107 ans. Les observations des transitions rotationnelles de nombreuses molécules ont permis de mener une étude détaillée de leurs propriétés physiques et chimiques. En particulier cela a montré qu'ils sont fortement structurés à toutes les échelles, dans une structure hierarchique de type "fractale". Ils contiennent des condensations sombres de taille environ 1 pc, densité 103 cm-3 et masse d'environ 103
, densité ≥ 200 cm-3 et température 10-30 K. L'abondance de CO y est d'environ 10-4 celle de H2. Ces nuages sont des objets auto-gravitants, plutôt qu'à l'équilibre de pression avec les autres phases du milieu interstellaire. Leur pression turbulente (mesurée par l'élargissement Doppler des raies CO) et magnétique (mesurée comme expliqué dans la Section "Energie magnétique") est globalement suffisante pour contrebalancer la gravité, ce qui les maintient globalement stables sur des échelles de l'ordre de 106-107 ans. Les observations des transitions rotationnelles de nombreuses molécules ont permis de mener une étude détaillée de leurs propriétés physiques et chimiques. En particulier cela a montré qu'ils sont fortement structurés à toutes les échelles, dans une structure hierarchique de type "fractale". Ils contiennent des condensations sombres de taille environ 1 pc, densité 103 cm-3 et masse d'environ 103 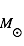 , des filaments, ainsi que des coeurs denses de taille ~ 0.1 pc, densité > 104 cm-3, et masse ~ 0.1-10
, des filaments, ainsi que des coeurs denses de taille ~ 0.1 pc, densité > 104 cm-3, et masse ~ 0.1-10 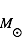 qui approchent de l'instabilité gravitationnelle (leur turbulence est subsonique) et sont le site de formation des étoiles. La structure spatiale filamentaire et la cinématique complexe de ces nuages sont illustrées ci-dessous dans le cas du nuage du Taureau.
qui approchent de l'instabilité gravitationnelle (leur turbulence est subsonique) et sont le site de formation des étoiles. La structure spatiale filamentaire et la cinématique complexe de ces nuages sont illustrées ci-dessous dans le cas du nuage du Taureau.
Gaz moléculaire translucent : les observations en absorption dans l'UV menées avec les satellites COPERNICUS, Hubble et FUSE montrent que la proportion d'hydrogène sous forme de H2, moyennée sur la ligne de visée, augmente brutalement pour atteindre 10%-60% lorsque la densité de colonne totale dépasse ~ 3x1020 atomes cm-2 (Av ~ 0.2 mag). Ce gaz moléculaire diffus a une densité d'environ 100 cm-3 et une température d'environ 80 K, similaire à celle du HI froid. Une deuxième composante de H2 plus chaud à environ 200-300 K est également présente, ainsi que du CO en faible abondance (quelques 10-6). Pourtant, l'étude des raies radio rotationnelles en absorption a révélé une chimie étonnamment riche avec près de 30 espèces détectées. Leur survie dans le champ UV ambiant, et la formation fortement endothermique de certaines d'entre elles (ex. CH+), posent question. Le modèle actuellement favorisé est que ces molécules se reformeraient en permanence dans des vortex turbulents ou des chocs magnétisés qui chauffent le gaz par friction ion-neutre et y accélèrent la chimie.
Carte du complexe moléculaire du Taureau dans la raie de CO à 2.6 mm
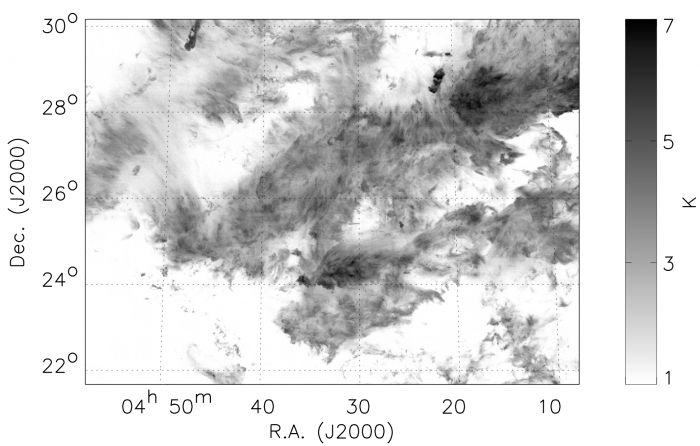
Exemple de structure filamentaire "fractale" du milieu moléculaire observée dans la raie rotationnelle de CO (J=1-0) : l'extension de l'image correspond à environ 25 pc.
Crédit :
Goldsmith, P. et al., ApJ, 2008
Champ de vitesse du complexe moléculaire du Taureau
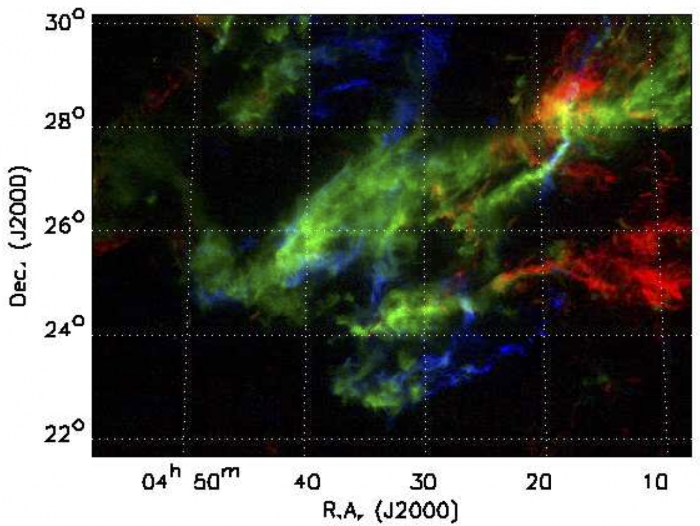
La cinématique du nuage moléculaire du Taureau mesurée par la raie J=1-0 de l'isotope 13CO ; L'émission est sommée sur différents intervalles de vitesse codés en couleur : 3-5 km/s en bleu, 5-7 km/s en vert, et 7-9 km/s en rouge.
Crédit :
Goldsmith P. et al. ApJ, 2008.
Détection du gaz ionisé
Le milieu ionisé dans la Galaxie comprend une composante tiède à environ 10 000 K (WIM) et une composante beaucoup plus chaude autour de 106 K (HIM). Nous résumons séparément pour chacune leurs principales méthodes d'observation et les caractéristiques qui en sont déduites.
Le milieu ionisé tiède (WIM)
Ce milieu est réparti en une composante organisée en structures bien définies, les régions HII ou nébuleuses gazeuses, et une composante plus diffuse. Les régions HII peuvent être décrites schématiquement comme des sphères ionisées (sphères de Strömgren) entourant une ou plusieurs étoiles chaudes de type O ou B qui sont responsables des photons UV ionisants > 13.6 eV (voir la page Réservoirs d'énergie : champ de rayonnement). Le gaz y possède de nombreux mécanismes d'émission de l'ultraviolet jusqu'au domaine radio. Les principales méthodes utilisées pour le cartographier et obtenir ses conditions physiques sont les suivantes :
- l'émission continue dite "libre-libre" ou brehmstrahlung produite par le freinage des électrons libres passant à proximité des ions. Il se trouve dans le domaine radio centimétrique pour ces températures. L'interféromètre du VLA est un instrument de choix pour ce type d'observations. La cartographie révèle la distribution spatiale et la brillance donne accès à la mesure d'émission du gaz, c'est-à-dire l'intégrale de
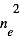 sur la ligne de visée.
sur la ligne de visée. - Les raies de recombinaison : lorsqu'un électron se recombine avec un ion sur un niveau excité, l'atome se désexcite vers les niveaux plus bas par une cascade radiative entraînant l'émission d'un ou plusieurs photons. Cette cascade produit un spectre de recombinaison avec des rapports de raies caractéristiques, qui dépendent peu de
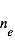 et
et 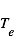 . L'atome est ensuite ionisé à nouveau par un photon UV, et le phénomène se reproduit. On peut donc déduire du flux de ces raies le flux de photons UV ionisants (si on connaît la température, qui affecte le taux de recombinaison). Les raies de recombinaison les plus importantes sont celles de l'hydrogène, en particulier la raie Hα de la série de Balmer dans l'optique (voir la page Détection du gaz atomique : l'atome d'hydrogène). Une carte de la Galaxie dans la raie Hα est présentée dans la figure ci-dessous. On utilise aussi les raies de recombinaison radio associées aux transitions entre niveaux de nombre quantique élevé (
. L'atome est ensuite ionisé à nouveau par un photon UV, et le phénomène se reproduit. On peut donc déduire du flux de ces raies le flux de photons UV ionisants (si on connaît la température, qui affecte le taux de recombinaison). Les raies de recombinaison les plus importantes sont celles de l'hydrogène, en particulier la raie Hα de la série de Balmer dans l'optique (voir la page Détection du gaz atomique : l'atome d'hydrogène). Une carte de la Galaxie dans la raie Hα est présentée dans la figure ci-dessous. On utilise aussi les raies de recombinaison radio associées aux transitions entre niveaux de nombre quantique élevé (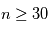 environ). Elles permettent de déduire la température du gaz à partir du rapport raie/continuum, de mesurer précisément la vitesse de la source (ce qui aide a déterminer sa distance), et de sonder les régions HII trop jeunes et enfouies pour être détectables en Hα.
environ). Elles permettent de déduire la température du gaz à partir du rapport raie/continuum, de mesurer précisément la vitesse de la source (ce qui aide a déterminer sa distance), et de sonder les régions HII trop jeunes et enfouies pour être détectables en Hα. - Les raies interdites : beaucoup de raies très intenses émises dans les régions HII sont dues à des raies "interdites" du point de vue dipolaire électrique. Les raies métastables dans l'optique sont des traceurs très usités, très sensibles à la densité et/ou à la température du gaz, en particulier [SII]6716,6731, [NII]5755,6584, [OIII]4363,4959,5007. Les raies ioniques de structure fine dans l'infrarouge lointain (eg. [NII], [NIII], [OIII]52,88mic, [NeII], [NeIII], [SIII], [SIV]) sont moins sensibles à la température et peu affectées par l'extinction, ce qui en fait de bons traceurs de densité et d'abondance. Mais elles ne sont accessibles que de l'espace (ISO, puis Herschel) ou par l'avion SOFIA.
Résultats des observations : l'étude de ces différents diagnostics a permis la détermination de la température et de la densité des électrons ainsi que des abondances de nombreuses espèces dans les régions photo-ionisées. Dans l'histogramme de la page Composition du MIS les abondances solaires sont comparées aux abondances de la nébuleuse gazeuse d'Orion, la région HII la plus proche de nous. On trouve que les régions HII ont des tailles typiques de 0.1-3 parsecs, une température d'environ T=104 K, une densité d'environ 1-104 cm-3 et qu'elles émettent la plupart de la luminosité totale du gaz ionisé tiède. Le milieu ionisé diffus est moins dense et chaud (n≈0.5 cm-3, T≈8000 K) mais contient la presque totalité de la masse du gaz ionisé (109 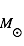 ). On pense que cette composante diffuse provient des fuites de gaz ionisé hors des régions HII par effet "champagne" (surpression) et de l'ionisation du milieu atomique diffus par des étoiles OB isolées. Au dessus du plan Galactique, la dissipation de la turbulence du plasma pourrait contribuer à son chauffage.
). On pense que cette composante diffuse provient des fuites de gaz ionisé hors des régions HII par effet "champagne" (surpression) et de l'ionisation du milieu atomique diffus par des étoiles OB isolées. Au dessus du plan Galactique, la dissipation de la turbulence du plasma pourrait contribuer à son chauffage.
Carte en Halpha du gaz ionisé à 10 000K dans la Galaxie
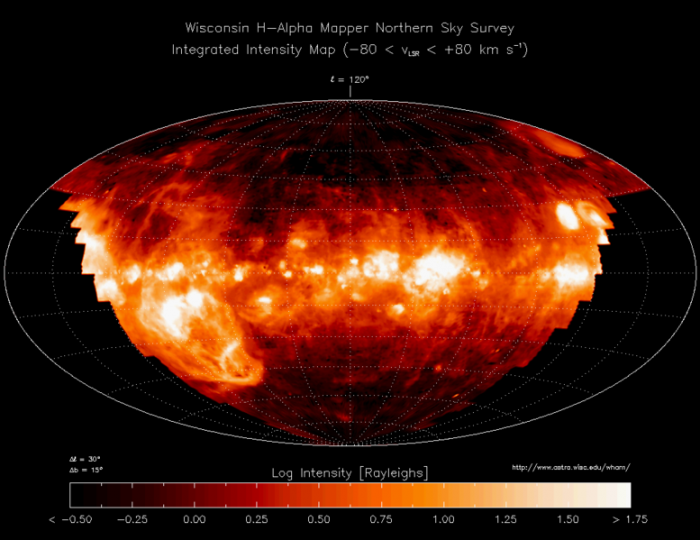
Carte de la Voie Lactée dans la raie Hα de l'hydrogène, montrant le gaz ionisé tiède (WIM) situé dans les régions HII (zones brillantes en blanc) ainsi qu'une composante plus diffuse.
Crédit :
WHAM, Haffner 2003
Le milieu ionisé chaud (HIM)
La composante de gaz ionisé très chaud dans le MIS, de température 105 K à 107 K, est principalement détectée par l'émission diffuse de rayons X mous (énergie inférieure à 1 keV) due à son rayonnement libre-libre, par les raies d'absorption dans l'ultraviolet d'atomes très ionisés (OVI, NV, CIV), et par des raies en émission de OVII, OVIII dans le domaine X. Ce gaz très ténu et chaud provient des restes de supernovae (voir le cours Astronomie et Mécanique Céleste). Comme il se refroidit lentement du fait de sa faible densité, il se répand dans le milieu interstellaire et remplit un large volume du disque et du halo galactique, où sa pression contribue à confiner les nuages HI à grande vitesse.
Travaux pratiques : logiciel Aladin
Auteur: Cecilia Pinto et Sylvie Cabrit
Introduction
 Objectifs
Objectifs
L'objectif de ce TP est d'exploiter l'atlas interactif Aladin afin de se familiariser avec la visualisation, la manipulation et l'exploration d'images et de catalogues astronomiques. Le traitement et l'analyse des images permettra de mesurer la taille des structures dans un nuage de gaz et de poussière. De plus, la comparaison d'images obtenues à différentes longueurs d'onde permettra de distinguer les différentes zones émettrices, et ainsi de mieux comprendre la structuration en phases du milieu interstellaire.
Le logiciel Aladin
Aladin est un logiciel développé au Centre de Données astronomiques de Strasbourg (CDS) dans le cadre de l'Observatoire Virtuel (OV). Il permet de visualiser des images digitalisées du ciel et d'y superposer de façon interactive des informations issues de catalogues ou de bases de données astronomiques. Aladin offre une série d'outils pour interroger les différentes bases de données et manipuler les images et les catalogues. Au cours de ce TP nous exploiterons une partie de ces outils afin d'apprendre à chercher, choisir et extraire des images d'un objet astronomique dans les différentes bandes du spectre électromagnétique ; et à obtenir des informations complémentaires sur l'objet (par exemple distance, position et origine des cibles) en utilisant les catalogues disponibles. Nous effectuerons les opérations suivantes :
- ajustement de la dynamique d'affichage des pixels (c'est-à-dire du contraste de l'image)
- mesure de distance angulaire dans le champ de vue
- traçage de courbes isophotes (courbes d'égale brillance lumineuse) sur une image
- création de vues simultanées afin de comparer facilement des images à différentes longueurs d'onde de la même région du ciel.
La nébuleuse de l'Aigle
L'objet d'étude de ce TP est la nébuleuse de l'Aigle (M16), une région de formation d'étoiles massives située à l'intérieur du bras galactique du Sagittaire. Un grand nuage de gaz et de poussière interstellaire, d'extension environ 50 années-lumière, est illuminé et ionisé par les nombreuses étoiles massives (type OB) du jeune amas stellaire ouvert NGC6611. La façon dont le rayonnement ionisant stellaire sculpte le nuage a été étudiée à haute résolution dans l'optique par le télescope Hubble. Ces observations ont révélé la présence de structures denses et sombres de gaz et de poussière en forme de doigts, appelés ici les Piliers de la Création.
La formation des piliers s'interprète comme le résultat de l'ionisation d'un nuage moléculaire fortement inhomogène. La photo-ionisation du gaz à la surface du nuage chauffe cette interface à environ 104 K, et sous l'effet de la pression thermique ce gaz chaud s'échappe du nuage vers la région HII : c'est le phénomène de photo-evaporation. Ce phénomène est particulièrement visible dans les images Hubble sous la forme d'un halo luminescent entourant le sommet de chacun des piliers. La photo-évaporation "érode" graduellement le nuage moléculaire, dont la matière est progressivement incorporée dans la région HII, qui croît en taille. Dans un nuage inhomogène, les régions initialement plus denses sont plus opaques au rayonnement ultraviolet et résistent plus longtemps à la photo-évaporation. Leur cone d'ombre, bien protégé du rayonnement, s'érode beaucoup plus lentement que le reste du nuage et subsiste ainsi sous forme de piliers. C'est le même processus qui mène sur terre à la format ion des cheminées de fées, qu'une pierre plus dure protège de l'érosion du vent et de l'eau.
Les observations du télescope VLT dans l'infrarouge proche, et des satellites Spitzer et Herschel dans l'infrarouge moyen et lointain, ont permis de sonder l'intérieur des piliers de la Création (grâce à la plus faible opacité de la poussière aux grandes longueurs d'onde), et de révéler la présence d'étoiles naissantes en leur sein. Au cours de ce TP nous analyserons des images de la nébuleuse de l'Aigle à différentes longueurs d'onde en identifiant les diverses composantes responsables de son émission.
Mesure de la taille des structures
Procédure
- Lancement d'Aladin : Aladin peut être utilisé sans aucune installation, simplement en utilisant un navigateur Web. Il faut charger la page : http://aladin.u-strasbg.fr/java/nph-aladin.pl et accepter l'exécution de l'applet.
- Recherche d'une image : pour charger une image astronomique utiliser le menu Ouvrir ⇒ All VO, puis indiquer le nom ou la position de l'objet dans le formulaire qui apparaît. Dans notre exemple il s'agit de M16 avec un rayon de recherche de 14' (décocher les cases Catalogues et Spectres pour effectuer une recherche plus rapide). Sélectionner l'image "Pillars of Creation in a Star-Forming Region" avec un champ de 2.6' X 2.5' en dépliant le menu "Hubble press release images" et appuyer sur le bouton Chercher. L'image visualisée est en "vraies couleurs" et résulte de la combinaison de trois images correspondant à l'émission dans le visible de trois traceurs typiques du gaz ionisé : Hα (vert) , SII (rouge) et OIII (bleu) (voir la Section Détection du gaz ionisé). La fenêtre de contrôle de la dynamique des pixels, activée en cliquant sur l'icône pixel du menu à droite de l'image, fait apparaître trois histogrammes correspondant à la répartition des valeurs des pixels dans les composantes Rouge, Vert, Bleu. Il est possible d'ajuster le contraste des différentes couleurs en déplaçant les curseurs.
- Manipulation des images d'archives : pour accéder aux archives du télescope Hubble sélectionner Ouvrir ⇒ Missions et choisir logHST dans la liste d'observations disponibles. Les objets issus du catalogue sont superposés à l'image et chaque objet peut être sélectionné au moyen de la souris en y cliquant dessus. En sélectionnant les différentes cibles repérer les objets qui appartiennent à M16, dont les cordonnées s'affichent sous forme d'une table en dessous de l'image, en les différenciant des objets de l'amas ouvert NGC6611. Pour charger les images d'archives correspondant il faut cliquer sur Image dans la table. Choisir l'image et la position du champ (par la fenêtre de zoom à droite de l'image) les plus appropriées pour effectuer des mesures de la taille des piliers. Ces mesures se font en activant l'outil graphique dist dans le menu de droite et en déplaçant le curseur associé avec la souris sur la région d'intérêt de l'image. La distance angulaire mesurée s'affiche en bas de l'image et peut être relue en passant la souris sur la flèche. Elle est donnée en minutes d'arc et non en degrés. Aladin ne manipule pas la notion de distance à l'observateur, uniquement la représentation sur la sphère céleste en fournissant donc des mesures de taille angulaire des objets analysés. L'information sur la distance à l'observateur peut être dérivée en interrogeant le catalogue Simbad à l'adresse http://simbad.u-strasbg.fr/simbad/sim-fid. Il faut sélectionner le nom de l'objet recherché ainsi que le champ de vue et cocher la case distance dans la liste des mesures disponibles.
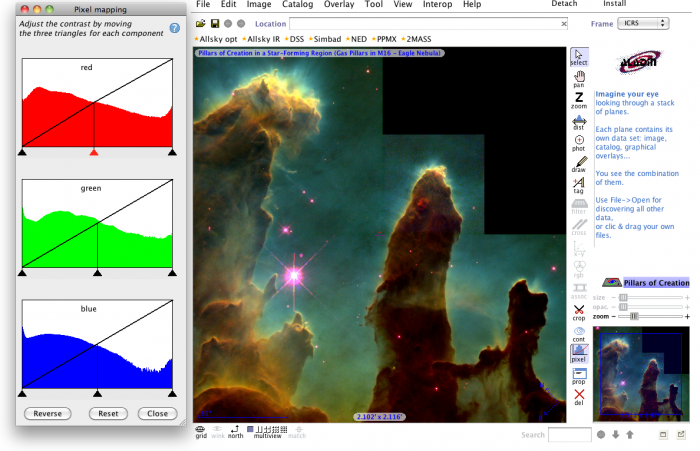
 Mesure de la taille des piliers de la création
Mesure de la taille des piliers de la création
Question 1)
Vérifier que la taille linéaire caractéristique des piliers de gaz et de poussière observés par le télescope Hubble dans la nébuleuse de l'Aigle est de l'ordre du parsec.
Comparaison d'images : infrarouge proche et visible
Procédure
- Chargement des images : lister les images disponible de M16 avec un rayon de recherche de 14' dans le serveur d'images Aladin en utilisant le menu : Fichier ⇒Charger une image astronomique⇒serveur d'images Aladin. Charger l'image dans le visible POSSI O-DSS2 750 avec un champ de vue de 13' X 13' et l'image dans l'infrarouge proche 2MASS K(IR K) 99052S_KI1320103 dont le champ de vue est 8.6' X 17.1'.
- Gestion du contraste des images : La dynamique des valeurs d'intensité des images astronomiques, c'est-à-dire leur contraste, est représentée dans le logiciel par le moyen d'une table de gris qui établit une correspondance entre l'intensité mesurée en chaque pixel de l'image et un niveau de gris. Aladin effectue un échantillonnage des pixels de l'image afin d'appliquer un seuillage : toutes les valeurs de pixels inférieures au seuil bas sont affichées en blanc, celles au-dessus du seuil haut en noir et les valeurs intermédiaires sont converties entre 0 et 255 linéairement (sur les matériels informatiques actuels le rendu visuel monochromatique est codé sur 1 octet) et affichées en niveaux de gris. L'utilisateur peut modifier le contraste des images en appuyant sur le bouton pixel accessible dans la barre d'outils à droite de l'image. Un exemple de la fenêtre qui s'affiche est montré sur la figure Fenêtre de contrôle de la dynamique des pixels. Il s'agit d'un histogramme de la répartition des pixels entre la plus petite et la plus grande valeur retenues par Aladin, qui peut être plus simplement interprété comme le nombre des pixels en fonction de l'intensité mesurée et donc émise par les objets (gaz, étoiles, poussières) contenus dans la région observée. Pour augmenter ou diminuer le contraste de l'image il suffit de modifier la fonction de transfert qui établit la correspondance entre les valeurs d'intensité des pixels et le tableau de gris. Le maximum du contraste est obtenu en activant la fonction Log dans la fenêtre de la dynamique des pixels. On peut également déplacer les curseurs en bas de l'histogramme pour modifier les seuils de l'image afin de rendre plus ou moins visible l'émission des différents objets ou zones de l'image.
- Extraction des contours : Aladin fournit un outil graphique permettant de générer des isophotes (courbe d'égale intensité lumineuse) d'une image. En appuyant sur le bouton cont de la barre des outils à droite de l'image on active une fenêtre (un exemple est montré sur la figure Fenêtre de contrôle des isophotes) qui permet d'ajuster le nombre de contours souhaités (à chaque contour est associé un curseur) ainsi que le niveau d'intensité correspondant. La fenêtre affiche en effet l'histogramme de la distribution des pixels présents dans l'image et les curseurs donnent les valeurs des pixels en correspondance avec les niveaux de gris. Leur déplacement se fait selon les même critères utilisés pour la gestion du contraste de l'image. L'extension des contours croît avec le nombre de pixels décomptés à la position du curseur qui correspond à une valeur d'intensité de pixel.
Fenêtre de contrôle de la dynamique des pixels
Crédit :
http://aladin.u-strasbg.fr/java/AladinManuel6.pdf
Fenêtre de contrôle des isophotes
Crédit :
http://aladin.u-strasbg.fr/java/AladinManuel6.pdf
 Génération et comparaison de contours dans l'infrarouge et le visible
Génération et comparaison de contours dans l'infrarouge et le visible
Ce TP consiste à appliquer les opérations décrites en détail dans la section précédente sur deux images de la nébuleuse de l'Aigle dans le visible (POSSI O-DSS2 750) et dans l'infrarouge proche (2MASS K(IR K) 99052S_KI1320103) et à analyser les informations complémentaires dérivant des observations dans ces deux bandes du spectre électromagnétique.
Question 1)
Modifier le contraste de l'image 2MASS K(IR K) 99052S_KI1320103 de façon à mieux visualiser les régions de l'image caractérisées par des valeurs d'intensité faibles par rapport aux étoiles brillantes qui dominent l'image d'archive. Utiliser à la fois la fonction de transfert et le déplacement des curseurs dans la fenêtre de la dynamique des pixels.
Question 2)
Cocher l'icône correspondant à l'image contrastée dans l'infrarouge proche et tracer quatre isophotes représentatives des étoiles faibles dans le champ de vue. Puis sélectionner l'image dans le visible POSSI O-DSS2 750 (cliquer sur l'icône des contours de l'image dans l'infrarouge pour la désactiver) et générer les contours correspondant aux étoiles brillantes ainsi qu'à l'intense émission diffuse environnant les piliers, et à deux niveaux de l'émission du fond de l'image. Dans la représentation des intensités au moyen de la table de gris, ce fond plus clair correspond à l'absorption dans le visible due à la poussière. Noter que les échelles de gris pour les deux images sont différentes, le niveau de gris du fond de l'image dans le visible étant plus foncé que celui de l'image dans l'infrarouge.
Question 3)
Superposer les contours des deux images (en cliquant sur les deux icônes contours) et commenter les différences : 1) quelle émission est dévoilée par les contours de l'image dans l'infrarouge ? 2) et quelle émission est tracée par les isophotes de l'image dans le visible ?
Charger et superposer (en passant sur l'icône correspondante sans la cocher) l'image en vraies couleurs utilisée dans la première partie du TP ("Pillars of Creation in a Star-Forming Region" avec un champ de 2.6' X 2.5' , logHST) pour mieux comprendre les différentes contributions à l'émission dans le visible.
Comparaison d'images à plusieurs longueurs d'onde : structuration en phases
Pour mieux comprendre la contribution à l'émission de chaque "phase" qui compose la nébuleuse de l'Aigle il faut comparer des images à différentes longueurs d'onde sur un intervalle plus large du spectre, allant du visible au rayons X. Les images issues d' observations récentes non disponibles dans les archives du logiciel Aladin peuvent être aisément chargées en saisissant l'adresse Web des sites des observatoires ou des agences spatiales concernées (ESO, NASA) dans le bandeau de localisation Commande en haut de la fenêtre de visualisation. On utilisera pour ce TP des images à grand champ de la nébuleuse de l'Aigle, qui permettent de voir de manière détaillée l'ensemble de la région environnant les piliers.
Procédure
- Chargement des images à différentes longueurs d'onde :
- Visible : combinaison en fausses couleurs pour une image composée de trois filtres optiques : 451 nm bande B ( en bleu), 539 nm bande V( en vert), 651 nm bande R(en rouge) obtenue avec le télescope MGP/ESO à l'Observatoire de La Silla, au Chili. Le champ de vue est de 32 X 32 minutes d'arc. L'image peut être téléchargée à l'adresse : http://www.eso.org/public/archives/images/screen/eso0926a.jpg.
- Infrarouge moyen : combinaison en fausses couleurs de quatre canaux infrarouges : 3.6 μm (en bleu), 4.5 μm (en vert), 5.8 μm (en orange), 8 μm (en rouge) obtenue avec le télescope spatial Spitzer. Le champ de vue est de 28 X 32 minutes d'arc. L'image peut être téléchargée à l'adresse : http://www.spitzer.caltech.edu/uploaded_files/images/0008/0952/ssc2007-01c1_Ti.jpg.
- Infrarouge moyen-lointain : combinaison en fausses couleurs de trois canaux infrarouges : de 4.5 μm à 8 μm (en bleu), 24 μm (en vert), 70 μm (en rouge) obtenue avec le télescope spatial Spitzer. Le champ de vue est de 28 X 32 minutes d'arc. L'image peut être téléchargée à l'adresse : http://www.spitzer.caltech.edu/uploaded_files/images/0008/1741/ssc2007-01a1_Ti.jpg.
- Infrarouge lointain-submillimetrique et rayons X : combinaison en fausses couleurs de trois canaux infrarouges/submillimétriques à 70 μm (bleu), 160 μm (vert), 250 μm (rouge) obtenue avec le télescope spatial Herschel et d'une image en rayons X prise par le télescope spatial XMM-Newton. L'image peut être téléchargée à l'adresse : http://www.nasa.gov/images/content/616643main_pia15260b-full_full.jpg.
- Activation des vues multiples : en cliquant sur l'icône multivues en bas à gauche de l'image créer simultanément plusieurs vues afin de comparer facilement les images chargées. L'activation de l'icône north en bas à gauche de l'image permet de changer l'orientation des différentes images afin de les comparer plus aisément.
 Images à différentes longueurs d'onde : structuration de l'émission
Images à différentes longueurs d'onde : structuration de l'émission
Question 1)
Comparer les images et identifier les différentes composantes (gaz, poussières de différentes tailles et températures, étoiles) responsables de l'émission observée aux différentes longueurs d'onde. Utiliser les notions apprises dans le cours et en particulier à la page Images à différentes longueurs d'onde.
Spectres
Auteur: Cecilia Pinto
Transfert de rayonnement
Auteur: Cecilia Pinto & Sylvie Cabrit
Notions de transfert de rayonnement
L'analyse des spectres interstellaires requiert l'introduction d'un certain nombre de notions théoriques de transfert de rayonnement. Cette théorie consiste en une description macroscopique de la propagation du rayonnement et de son interaction avec la matière qui compose le milieu traversé. Dans cette description le rayonnement est supposé se propager, dans le vide ou dans un milieu homogène, rectilignement (les lignes de propagation sont appelées rayons) si l'échelle du système considéré est très supérieure à la longueur d'onde du rayonnement.
 Intensité spécifique
Intensité spécifique
On considère en un point de l'espace un faisceau de rayonnement contenu dans un angle solide 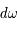 , dans un intervalle de fréquence de
, dans un intervalle de fréquence de 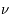 à
à 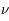 +
+ 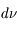 et traversant une surface
et traversant une surface 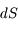 perpendiculaire à sa direction de propagation. L'énergie de ce rayonnement qui passe à travers la surface pendant le temps
perpendiculaire à sa direction de propagation. L'énergie de ce rayonnement qui passe à travers la surface pendant le temps 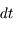 est :
est :
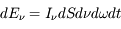 .
Le coefficient de proportionnalité
.
Le coefficient de proportionnalité 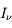 dans cette expression est appelé intensité spécifique et représente donc l'énergie par unité de surface, par unité de fréquence, par unité d'angle solide et par unité de temps, qui traverse une surface perpendiculaire au faisceau de rayonnement. L'intensité spécifique s'exprime en erg cm-2 Hz-1 sr-1 s-1 dans le système CGS.
Si la direction du rayonnement, centrée sur l'angle solide
dans cette expression est appelé intensité spécifique et représente donc l'énergie par unité de surface, par unité de fréquence, par unité d'angle solide et par unité de temps, qui traverse une surface perpendiculaire au faisceau de rayonnement. L'intensité spécifique s'exprime en erg cm-2 Hz-1 sr-1 s-1 dans le système CGS.
Si la direction du rayonnement, centrée sur l'angle solide 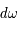 , fait un angle
, fait un angle 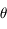 avec la normale à
avec la normale à 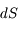 (voir la figure), la surface efficace perpendiculaire au faisceau vaut
(voir la figure), la surface efficace perpendiculaire au faisceau vaut 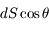 et l'énergie s'écrit alors :
et l'énergie s'écrit alors : 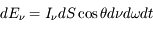 .
.
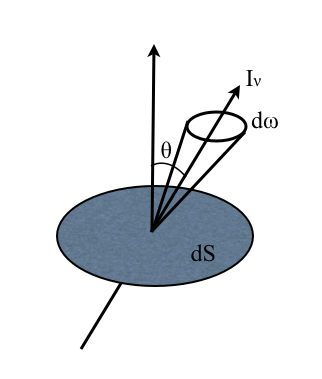
Crédit :
Cecilia Pinto
L'intensité spécifique est fonction du point de l'espace considéré, de la direction du rayonnement, de la fréquence et du temps. Elle peut être exprimée en termes de longueur d'onde plutôt que de fréquence avec l'égalité : 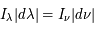 . Puisque
. Puisque 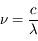 , on en déduit que
, on en déduit que 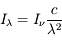 avec
avec 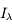 en erg cm-2
en erg cm-2 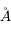 -1 sr-1 s-1. L'intensité spécifique est une quantité fondamentale dont dérivent les autres grandeurs physiques qui caractérisent le rayonnement, comme la densité d'énergie monochromatique
-1 sr-1 s-1. L'intensité spécifique est une quantité fondamentale dont dérivent les autres grandeurs physiques qui caractérisent le rayonnement, comme la densité d'énergie monochromatique 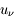 par unité de volume et par unité d'intervalle de fréquence,
par unité de volume et par unité d'intervalle de fréquence, 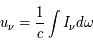 , ou le flux net
, ou le flux net 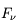 , c'est-à-dire le flux d'énergie par unité de surface, de fréquence et de temps,
, c'est-à-dire le flux d'énergie par unité de surface, de fréquence et de temps, 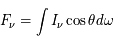 .
.
Interaction rayonnement-matière
La conservation de l'énergie implique que l'intensité spécifique du rayonnement reste constante le long d'un rayon uniquement si la propagation se produit dans l'espace vide. Autrement dit, l'intensité spécifique est indépendante de la distance entre la source de rayonnement et l'observateur en l'absence de gains ou pertes d'énergie le long de la ligne de visée. Lorsqu'un rayonnement traverse un milieu, l'interaction avec la matière qui le compose ajoute ou soustrait de l'énergie du faisceau. Cette modification de l'intensité spécifique se réalise par des processus d'émission, d'absorption et de diffusion.
L'équation de transfert de rayonnement
L'équation de transfert de rayonnement décrit la variation de l'intensité spécifique le long de la direction de propagation d'un faisceau de rayonnement traversant un milieu qui absorbe et émet. En se limitant au cas stationnaire (intensité spécifique indépendante du temps) et en négligeant la diffusion du rayonnement, cette équation se réduit à une équation différentielle ordinaire qui peut être résolue à chaque fréquence donnée, les coefficients d'absorption et d'émission étant connus. Lorsque les effets de diffusion sont inclus, l'équation devient une équation intégro-différentielle, car l'émission entraîne une intégrale de l'intensité spécifique sur l'angle solide de diffusion (voir la page Interaction rayonnement-matière), et il faut employer des méthodes numériques pour sa résolution.
Equation de transfert et profondeur optique
Dans le cas stationnaire et en absence de diffusion, l'équation de transfert est obtenue par le bilan d'énergie absorbée et émise dans le passage d'un faisceau de rayonnement à travers un volume élémentaire d'épaisseur 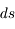 et surface
et surface  = 1 perpendiculaire à la direction de propagation
= 1 perpendiculaire à la direction de propagation 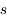 . En utilisant les définitions des coefficients d'absorption et d'émission données à la page Interaction rayonnement-matière on obtient :
. En utilisant les définitions des coefficients d'absorption et d'émission données à la page Interaction rayonnement-matière on obtient :
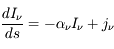 .
.
Considérons d'abord le cas limite où le milieu émet, mais n'absorbe pas le rayonnement. Dans ce cas 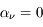 et l'équation de transfert devient :
et l'équation de transfert devient : 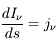 qui admet la solution
qui admet la solution 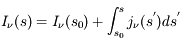 . Cela signifie que l'augmentation de l'intensité spécifique entre la position initiale
. Cela signifie que l'augmentation de l'intensité spécifique entre la position initiale 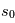 et le point final
et le point final 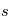 est égale au coefficient d'émission intégré le long de cette "ligne de visée" à travers la couche de matière.
est égale au coefficient d'émission intégré le long de cette "ligne de visée" à travers la couche de matière.
Dans le cas inverse où le milieu absorbe, mais n'émet pas de rayonnement (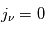 ) on obtient :
) on obtient : 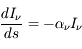 , dont la solution est
, dont la solution est 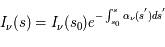 . L'intensité spécifique au point final
. L'intensité spécifique au point final 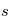 est égale à l'intensité spécifique au point initial
est égale à l'intensité spécifique au point initial 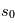 , atténuée par un facteur exponentiel dont l'argument est l'intégrale du coefficient d'absorption le long de la ligne de visée entre
, atténuée par un facteur exponentiel dont l'argument est l'intégrale du coefficient d'absorption le long de la ligne de visée entre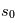 et
et 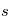 . Cette intégrale est un nombre sans dimension appelé la profondeur optique du milieu:
. Cette intégrale est un nombre sans dimension appelé la profondeur optique du milieu:
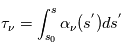 .
.
La solution de l'équation de transfert dans un milieu purement absorbant s'écrit alors 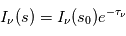 . On voit ainsi que la profondeur optique détermine la fraction de l'intensité incidente qui peut s'échapper du milieu. Afin de mieux comprendre le concept de profondeur optique, on introduit le libre parcours moyen du rayonnement qui représente la distance moyenne qu'un photon parcourt à travers un milieu sans être absorbé. Le coefficient
. On voit ainsi que la profondeur optique détermine la fraction de l'intensité incidente qui peut s'échapper du milieu. Afin de mieux comprendre le concept de profondeur optique, on introduit le libre parcours moyen du rayonnement qui représente la distance moyenne qu'un photon parcourt à travers un milieu sans être absorbé. Le coefficient 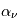 est l'inverse de ce libre parcours moyen, pour un photon de fréquence
est l'inverse de ce libre parcours moyen, pour un photon de fréquence 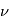 . La profondeur optique
. La profondeur optique 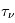 est donc égale au nombre total de libres parcours moyens traversés entre
est donc égale au nombre total de libres parcours moyens traversés entre 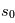 et
et 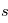 . Si la distance à travers le nuage est égale au libre parcours moyen (
. Si la distance à travers le nuage est égale au libre parcours moyen (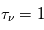 ), l'intensité subit une atténuation d'un facteur e-1 =0.368, ie. en moyenne seulement 36.8% des photons incidents sortiront du nuage. Si la distance parcourue équivaut à deux fois le libre parcours moyen (
), l'intensité subit une atténuation d'un facteur e-1 =0.368, ie. en moyenne seulement 36.8% des photons incidents sortiront du nuage. Si la distance parcourue équivaut à deux fois le libre parcours moyen (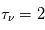 ), seulement 13.5% (e-2 =0.135) des photons incidents survivront en traversant le nuage. Pour cette raison, un milieu caractérisé par une profondeur optique
), seulement 13.5% (e-2 =0.135) des photons incidents survivront en traversant le nuage. Pour cette raison, un milieu caractérisé par une profondeur optique 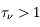 est dit optiquement épais ou opaque, alors qu'un milieu avec
est dit optiquement épais ou opaque, alors qu'un milieu avec 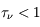 est dit optiquement mince ou transparent.
est dit optiquement mince ou transparent.
Coefficients d'Einstein
L'équation de transfert décrit la variation macroscopique de l'intensité spécifique du rayonnement lorsqu'il traverse de la matière. De leur coté, les coefficients d'absorption et d'émission qui apparaissent dans cette équation contiennent l'information concernant les processus microscopiques qui interviennent. En étudiant l'interaction entre le rayonnement et un système (atome ou molécule) avec des niveaux d'énergie quantifiés, Einstein a identifié 3 processus d'émission et d'absorption de photons, caractérisés chacun par un coefficient. Il est donc possible d'exprimer l'équation de transfert en fonction de ces coefficients et d'en dériver des solutions en fonction des propriétés microscopiques locales de l'atome considéré.
 Définition des coefficients d'Einstein
Définition des coefficients d'Einstein
Considérons pour simplifier un milieu formé d'atomes (ou de molécules) identiques avec seulement deux niveaux d'énergie : le niveau fondamental l et le niveau excité u, séparés par une énergie 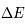 . Nous nous intéressons aux transitions radiatives entres ces deux états. Comme nous verrons en détail dans la suite du cours ces transitions ne se produisent pas uniquement à la fréquence
. Nous nous intéressons aux transitions radiatives entres ces deux états. Comme nous verrons en détail dans la suite du cours ces transitions ne se produisent pas uniquement à la fréquence 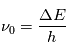 mais également aux fréquences voisines de
mais également aux fréquences voisines de 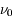 . Par conséquent les raies spectrales associées à ces transitions sont caractérisées par un profil de raie
. Par conséquent les raies spectrales associées à ces transitions sont caractérisées par un profil de raie 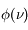 , piqué à la fréquence
, piqué à la fréquence 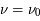 , qui décrit l'efficacité des fréquences voisines de
, qui décrit l'efficacité des fréquences voisines de 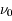 à induire ces transitions. L'agitation thermique du gaz (mouvement brownien) produit par exemple un élargissement du profil par effet Doppler, car un atome en mouvement peut absorber un photon de fréquence légèrement différente de
à induire ces transitions. L'agitation thermique du gaz (mouvement brownien) produit par exemple un élargissement du profil par effet Doppler, car un atome en mouvement peut absorber un photon de fréquence légèrement différente de 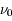 . La largeur du profil est alors de l'ordre de
. La largeur du profil est alors de l'ordre de 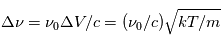 . Dans la suite on fera l'hypothèse que la forme de la raie est la même en absorption et en émission. Les 3 processus de transitions radiatives quantifiés par Einstein sont les suivants :
. Dans la suite on fera l'hypothèse que la forme de la raie est la même en absorption et en émission. Les 3 processus de transitions radiatives quantifiés par Einstein sont les suivants :
- L'émission spontanée qui est la désexcitation spontanée du niveau u vers le niveau l par l'émission d'un photon d'énergie
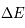 . Cette transition se produit même en l'absence d'un champ de rayonnement. Elle est caractérisée par le coefficient d'Einstein
. Cette transition se produit même en l'absence d'un champ de rayonnement. Elle est caractérisée par le coefficient d'Einstein 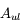 , qui représente une probabilité de transition par unité de temps et est exprimé en s-1. Ce coefficient ne dépend que des termes de couplages électro-magnétique entre les 2 niveaux quantiques u et l.
, qui représente une probabilité de transition par unité de temps et est exprimé en s-1. Ce coefficient ne dépend que des termes de couplages électro-magnétique entre les 2 niveaux quantiques u et l. - L'absorption stimulée (ou excitation radiative) qui est l'absorption d'un photon d'énergie
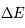 , faisant passer les atomes du niveaux l au niveau u. Elle est caractérisée par une probabilité de transition par unité de temps
, faisant passer les atomes du niveaux l au niveau u. Elle est caractérisée par une probabilité de transition par unité de temps 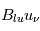 , où
, où 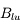 est le coefficient d'absorption d'Einstein et
est le coefficient d'absorption d'Einstein et 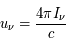 est la densité d'énergie monochromatique à la fréquence
est la densité d'énergie monochromatique à la fréquence 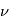 pour un champ de rayonnement isotrope.
pour un champ de rayonnement isotrope. - L'émission stimulée qui est le processus inverse de l'absorption stimulée : Lors de cette transition, l'atome absorbe un photon d'énergie
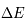 et passe de l'état u à l'état l en emettant un deuxième photon identique à celui qu'il a absorbé. Ce processus est caractérisé par une probabilité par unité de temps
et passe de l'état u à l'état l en emettant un deuxième photon identique à celui qu'il a absorbé. Ce processus est caractérisé par une probabilité par unité de temps 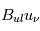 .
.
Les 3 coefficients d'Einstein décrivant les probabilités de ces 3 processus sont reliés par les relations d'Einstein :
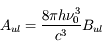 et
et
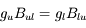 .
.
Il est important de noter que ces relations ne dépendent ni de la température du gaz, ni du profil de la raie. Elles représentent des relations de bilan détaillé, c'est-à-dire des relations entre un processus microscopique quantique et son processus inverse, dans ce cas l'absorption et l'émission de rayonnement. La connaissance d'un seul des coefficients d'Einstein (à partir de calculs quantiques) permet ainsi de déterminer les 2 autres. Notons aussi que ces coefficients donnent la probabilité de transition par atome dans le niveau de départ (u ou l) considéré. Le bilan net de ces 3 types de transitions va donc dépendre des densités de populations moyennes respectives dans les niveaux u et l.
L'équation de transfert en termes de coefficients d'Einstein
Considérons un rayonnement à la fréquence 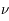 (contenue dans le profil de la raie) qui arrive sur une tranche du milieu avec une intensité spécifique
(contenue dans le profil de la raie) qui arrive sur une tranche du milieu avec une intensité spécifique 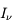 par unité de surface, de fréquence, et d'angle solide. Le long de la distance
par unité de surface, de fréquence, et d'angle solide. Le long de la distance 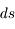 dans sa direction de propagation, l'intensité sera augmentée à la fois par l'émission spontanée et par l'émission stimulée des atomes dans l'état u ; simultanément elle sera diminuée par l'absorption de photons par les atomes dans l'état l. Considérons d'abord le cas de l'émission spontanée : le nombre total d'atomes dans l'état u rencontré par unité de surface est
dans sa direction de propagation, l'intensité sera augmentée à la fois par l'émission spontanée et par l'émission stimulée des atomes dans l'état u ; simultanément elle sera diminuée par l'absorption de photons par les atomes dans l'état l. Considérons d'abord le cas de l'émission spontanée : le nombre total d'atomes dans l'état u rencontré par unité de surface est 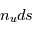 . L'augmentation d'intensité à la fréquence
. L'augmentation d'intensité à la fréquence 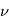 causée par ce processus est obtenue en multipliant
causée par ce processus est obtenue en multipliant 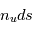 par le coefficient d'Einstein correspondant
par le coefficient d'Einstein correspondant 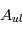 divisé par
divisé par 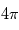 (car chaque photon est supposé émis ou absorbé de façon isotrope et nous regardons la variation par unité d'angle solide), par le profil de la raie
(car chaque photon est supposé émis ou absorbé de façon isotrope et nous regardons la variation par unité d'angle solide), par le profil de la raie 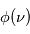 , et enfin par l'énergie de chaque photon (
, et enfin par l'énergie de chaque photon (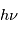 ) ; en appliquant le même raisonnement à l'émission et absorption stimulées, le bilan de ces transition radiatives donne l'équation de transfert :
) ; en appliquant le même raisonnement à l'émission et absorption stimulées, le bilan de ces transition radiatives donne l'équation de transfert :
![\frac{dI_\nu}{ds} = \frac{h\nu }{4\pi} \phi(\nu) [n_u A_{ul} +(n_u B_{ul} - n_l B_{lu})\frac{4\pi I_\nu}{c}]](../pages_transfert-rayon/equations_transfert-rayon/equation110.png) .
.
En comparant avec l'expression générale de l'équation de transfert 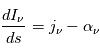 , présentée dans la section précédente on obtient en fonction des coefficients d'Einstein :
, présentée dans la section précédente on obtient en fonction des coefficients d'Einstein :
le coefficient d'émissivité 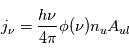
le coefficient d'absorption 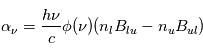
et la fonction source, 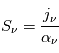
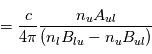 .
.
On remarque que la fonction source 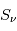 ne dépend pas de
ne dépend pas de 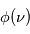 , mais uniquement des coefficients d'Einstein et des populations des niveaux impliqués. Plus précisément elle ne dépend que du rapport entre ces populations . En effet, en utilisant les relations entre coefficients d'Einstein données ci-dessus, on obtient :
, mais uniquement des coefficients d'Einstein et des populations des niveaux impliqués. Plus précisément elle ne dépend que du rapport entre ces populations . En effet, en utilisant les relations entre coefficients d'Einstein données ci-dessus, on obtient :
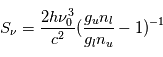 , où
, où 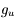 et
et 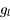 sont les poids statistiques (dégénérescences) de chaque niveau.
sont les poids statistiques (dégénérescences) de chaque niveau.
En utilisant les relations d'Einstein on voit aussi que le coefficient d'absorption peut se réécrire sous la forme :
![\alpha_\nu=\frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-\frac{n_ug_l}{n_lg_u}]](../pages_transfert-rayon/equations_transfert-rayon/equation121.png) .
.
Si l'on dénote par 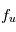 et
et 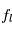 les fractions
les fractions 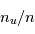 et
et  d'atomes qui sont dans les niveaux u et l, on remarque qu'
d'atomes qui sont dans les niveaux u et l, on remarque qu'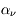 est proportionnel à la densité volumique totale des atomes,
est proportionnel à la densité volumique totale des atomes, 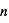 , et à une fonction qui ne dépend que de
, et à une fonction qui ne dépend que de 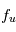 et
et 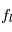 , c'est-à-dire à la répartition statistique des atomes entre leurs différents niveaux d'énergie. Il en découle que la profondeur optique, obtenue en intégrant cette quantité le long de la ligne de visée, sera proportionnelle à
, c'est-à-dire à la répartition statistique des atomes entre leurs différents niveaux d'énergie. Il en découle que la profondeur optique, obtenue en intégrant cette quantité le long de la ligne de visée, sera proportionnelle à 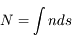 que l'on appelle la densité de colonne des atomes (en unité d'atomes par cm-2), c'est-à-dire le nombre d'atomes dans un cylindre de section unité le long de la ligne de visée. C'est par ce biais que l'observation des raies spectrales pourra nous donner accès à la masse de gaz émetteur --- à condition que l'on puisse connaître (ou estimer) les fractions
que l'on appelle la densité de colonne des atomes (en unité d'atomes par cm-2), c'est-à-dire le nombre d'atomes dans un cylindre de section unité le long de la ligne de visée. C'est par ce biais que l'observation des raies spectrales pourra nous donner accès à la masse de gaz émetteur --- à condition que l'on puisse connaître (ou estimer) les fractions 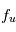 et
et 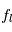 d'atomes peuplant les niveaux u et l, ou en d'autres termes les "conditions d'excitation" de la transition.
d'atomes peuplant les niveaux u et l, ou en d'autres termes les "conditions d'excitation" de la transition.
Conditions d'excitation et intensité émergente
Puisque les coefficients d'absorption et d'émission dépendent des populations des niveaux, la résolution de l'équation de transfert de rayonnement requiert la connaissance de l'état d'excitation de l'atome (ou de la molécule). De façon générale, ces conditions d'excitation dépendent à la fois de la température, de la densité, et du champ de rayonnement dans lequel baigne le gaz. Nous introduisons ici les quantités importantes (densité critique, équilibre thermodynamique local, et température d'excitation) qui permettent de caractériser ces conditions d'excitation et de comprendre les observations spectrales du milieu interstellaire.
Densité critique et Equilibre thermodynamique local
En régime stationnaire, la fraction d'atomes (ou "population") dans chaque niveau est fixée par l'équilibre statistique entre les taux de transitions qui peuplent ce niveau et celles qui le dépeuplent. Ces transitions sont produites non seulement par les 3 processus radiatifs d'absorption et émission discutés plus haut, étudiés par Einstein, mais aussi par des processus collisionnels d'excitation et désexcitation, lors de collisions inélastiques de l'atome considéré avec les particules les plus abondantes et rapides du milieu (H2, He, H, et les électrons si les gaz est significativement ionisé). Pour chaque transition, on peut calculer une densité critique au-dessus de laquelle les transitions collisionnelles deviennent plus importantes que les transitions radiatives. Pour les systèmes à deux niveaux, et avec un seul collisionneur dominant, elle s'écrit simplement :
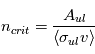
où 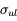 est la section efficace de désexcitation collisionnelle, qui dépend en général de la vitesse
est la section efficace de désexcitation collisionnelle, qui dépend en général de la vitesse 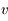 du collisionneur. Les crochets signifient qu'on prend la moyenne sur toute la distribution statistique des vitesses
du collisionneur. Les crochets signifient qu'on prend la moyenne sur toute la distribution statistique des vitesses 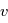 (distribution Boltzmanienne) ce qui donne une valeur dépendant de la température du gaz.
(distribution Boltzmanienne) ce qui donne une valeur dépendant de la température du gaz.
Lorsque la densité des collisionneurs 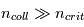 , les transitions radiatives sont négligeables devant les transitions collisionnelles et on atteint l'équilibre thermodynamique local (ou ETL),
où les populations relatives des niveaux des atomes (ou molécules) ne dépendent ni de
, les transitions radiatives sont négligeables devant les transitions collisionnelles et on atteint l'équilibre thermodynamique local (ou ETL),
où les populations relatives des niveaux des atomes (ou molécules) ne dépendent ni de 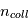 ni du champ de rayonnement et obéissent simplement à la loi de Boltzmann :
ni du champ de rayonnement et obéissent simplement à la loi de Boltzmann :
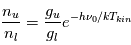
ici 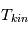 est la température cinétique des collisionneurs, qui caractérise la distribution de vitesse des particules,
est la température cinétique des collisionneurs, qui caractérise la distribution de vitesse des particules, 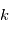 la constante de Boltzmann,
la constante de Boltzmann, 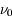 est la fréquence de la transition entre les états u et l,
est la fréquence de la transition entre les états u et l, 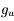 et
et 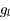 sont les poids statistiques. Plus le coefficient d'Einstein est fort, et plus la densité critique nécessaire pour atteindre l'ETL sera élevée. Cette densité critique est très variable selon les espèces et les transitions considérées : elle est très faible pour la raie hyperfine de l'hydrogène atomique (voir ci-dessous), de l'ordre de 1000 cm-3 pour les premières raies rotationnelles de CO, mais atteint 108 cm-3 pour H2O.
sont les poids statistiques. Plus le coefficient d'Einstein est fort, et plus la densité critique nécessaire pour atteindre l'ETL sera élevée. Cette densité critique est très variable selon les espèces et les transitions considérées : elle est très faible pour la raie hyperfine de l'hydrogène atomique (voir ci-dessous), de l'ordre de 1000 cm-3 pour les premières raies rotationnelles de CO, mais atteint 108 cm-3 pour H2O.
Température d'excitation de la transition
Par analogie avec la loi de Boltzmann, on peut toujours définir une température d'excitation de la transition 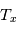 , telle que
, telle que
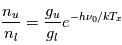 .
.
A l'équilibre thermodynamique local (ETL), on a 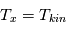 . Dans le cas contraire,
. Dans le cas contraire, 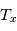 dépend aussi du rapport
dépend aussi du rapport 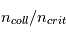 et de l'intensité du champ de rayonnement local, qui peuvent varier fortement d'un point à l'autre. Elle peut être inférieure à
et de l'intensité du champ de rayonnement local, qui peuvent varier fortement d'un point à l'autre. Elle peut être inférieure à 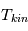 (cas le plus courant dans le MIS) ou bien supérieure si le pompage radiatif est important (par exemple à proximité d'une source de rayonnement intense), voire négative en présence d'un effet maser (inversion de population). En outre, il peut y avoir des températures d'excitation différentes pour différentes transitions d'un même atome.
(cas le plus courant dans le MIS) ou bien supérieure si le pompage radiatif est important (par exemple à proximité d'une source de rayonnement intense), voire négative en présence d'un effet maser (inversion de population). En outre, il peut y avoir des températures d'excitation différentes pour différentes transitions d'un même atome.
En insérant cette définition de la température d'excitation dans la définition de la fonction source dérivée dans la page Coefficients d'Einstein, on peut exprimer la fonction source comme une fonction de Planck :
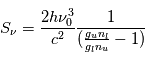
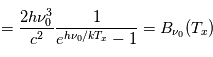 .
.
Notons aussi que le coefficient d'absorption peut s'écrire :
![\alpha_\nu=\frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-\frac{n_ug_l}{n_lg_u}]](../pages_transfert-rayon/equations_transfert-rayon/equation153.png)
![= \frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-e^{-h\nu_0/kT_x}]](../pages_transfert-rayon/equations_transfert-rayon/equation154.png) .
.
Si la température d'excitation est uniforme le long de ligne de visée, la solution formelle de l'équation du transfert radiatif devient :
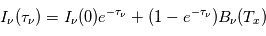 .
.
Notons qu'aux fréquences situées en dehors du profil spectral de la raie, on aura 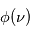 = 0, donc
= 0, donc 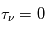 , et
, et 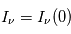 . Ceci définit le niveau du "continuum" que l'on mesure autour de la raie spectrale. Dans ce qui suit nous allons examiner sous quelles conditions la raie apparaîtra en émission ou en absorption par rapport à ce niveau de continu de référence.
. Ceci définit le niveau du "continuum" que l'on mesure autour de la raie spectrale. Dans ce qui suit nous allons examiner sous quelles conditions la raie apparaîtra en émission ou en absorption par rapport à ce niveau de continu de référence.
Limites optiquement épaisse et optiquement mince
Dans un milieu optiquement épais (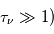 , on obtient
, on obtient 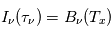 : le rayonnement d'un nuage optiquement épais s'apparente au rayonnement d'un corps noir à la température d'excitation
: le rayonnement d'un nuage optiquement épais s'apparente au rayonnement d'un corps noir à la température d'excitation 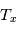 de la transition considérée. Si de plus on est à l'ETL, alors
de la transition considérée. Si de plus on est à l'ETL, alors 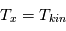 et on peut déduire la température cinétique du gaz à partir de
et on peut déduire la température cinétique du gaz à partir de 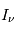 . Cette technique s'applique par exemple à la raie rotationnelle fondamentale de CO à une longueur d'onde de 2.6mm ; elle donne des valeurs typiques de température de 10-20 K dans les nuages moléculaires. Par contre, on voit que dans le cas optiquement épais l'intensité ne dépend plus de
. Cette technique s'applique par exemple à la raie rotationnelle fondamentale de CO à une longueur d'onde de 2.6mm ; elle donne des valeurs typiques de température de 10-20 K dans les nuages moléculaires. Par contre, on voit que dans le cas optiquement épais l'intensité ne dépend plus de  , c'est-à-dire de la quantité de matière traversée ; on dit que la raie est "saturée". Il n'est donc pas possible de déduire la masse de gaz.
, c'est-à-dire de la quantité de matière traversée ; on dit que la raie est "saturée". Il n'est donc pas possible de déduire la masse de gaz.
Pour un milieu optiquement mince (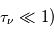 , on obtient
, on obtient ![I_\nu(\tau_\nu) - I_\nu(0) = \tau_\nu [B_\nu(T_x) - B_\nu(T_{bg})]](../pages_transfert-rayon/equations_transfert-rayon/equation173.png) : l'excès d'intensité au-dessus du continu est proportionnel à l'opacité, dont nous avons vu qu'est elle-même proportionnelle à la densité colonne
: l'excès d'intensité au-dessus du continu est proportionnel à l'opacité, dont nous avons vu qu'est elle-même proportionnelle à la densité colonne 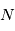 de l'atome considéré, et à une fonction de
de l'atome considéré, et à une fonction de 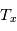 (qui fixe les populations relatives des niveaux). Avec une estimation indépendante de
(qui fixe les populations relatives des niveaux). Avec une estimation indépendante de 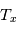 (par ex.
(par ex. 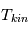 si la raie est à l'ETL), il est donc possible de déduire de ces observations la valeur de
si la raie est à l'ETL), il est donc possible de déduire de ces observations la valeur de 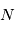 , et ensuite de la masse de gaz si la taille de la région d'émission et l'abondance de l'atome ou molécule sont connues. Cette technique est utilisée par exemple pour mesurer les masses des nuages moléculaires, grâce à des isotopes peu abondants comme 13CO et C18O qui sont (généralement) optiquement minces.
, et ensuite de la masse de gaz si la taille de la région d'émission et l'abondance de l'atome ou molécule sont connues. Cette technique est utilisée par exemple pour mesurer les masses des nuages moléculaires, grâce à des isotopes peu abondants comme 13CO et C18O qui sont (généralement) optiquement minces.
Enfin, une façon d'obtenir à la fois la température et la densité colonne de gaz est la combinaison d'observations en absorption et en émission. Nous en verrons un exemple détaillé plus loin avec la raie hyperfine de HI à 21 cm.
Application : la raie à 21 cm de l'hydrogène neutre
Les notions de transfert de rayonnement apprises au cours de ce chapitre nous donnent tous les éléments pour mieux comprendre les observations de la raie à 21 cm de HI que nous avons vu être le traceur principal de la composante de gaz atomique neutre du milieu interstellaire (voir la page Détection du gaz neutre atomique : raies spectrales).
Mesure en émission: approximation optiquement mince
Nous allons maintenant calculer l'opacité de la raie à 21 cm en utilisant l'expression du coefficient d'absorption en fonction de la température d'excitation, obtenue dans la page Conditions d'excitation de la transition.
![\alpha_\nu = \frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-e^{-h\nu_0/kT_x}]](../pages_transfert-rayon/equations_transfert-rayon/equation201.png) .
.
Pour cette transition, on a 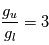 . De plus, à la basse fréquence de cette raie, 1420 MHz, nous sommes toujours dans le domaine
. De plus, à la basse fréquence de cette raie, 1420 MHz, nous sommes toujours dans le domaine 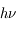 <<
<<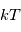 (approximation de Rayleigh-Jeans). Le facteur de Boltzmann
(approximation de Rayleigh-Jeans). Le facteur de Boltzmann 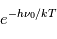 est donc proche de 1 et le rapport entre les populations des 2 sous-niveaux hyperfins à l'ETL vaut
est donc proche de 1 et le rapport entre les populations des 2 sous-niveaux hyperfins à l'ETL vaut 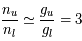 . Le gaz étant beaucoup trop froid pour peupler le premier niveau électronique excité
. Le gaz étant beaucoup trop froid pour peupler le premier niveau électronique excité 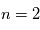 de l'hydrogène, l'essentiel des atomes se trouvent dans l'un de ces deux sous-niveaux hyperfins du niveau fondamental. La densité totale de HI est donc reliée à
de l'hydrogène, l'essentiel des atomes se trouvent dans l'un de ces deux sous-niveaux hyperfins du niveau fondamental. La densité totale de HI est donc reliée à 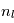 par :
par :
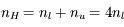 .
.
Enfin, dans le régime Rayleigh-Jeans, le facteur ![[1- e^{-h\nu_0/kT_s}] \simeq h\nu_0 / kT_s](../pages_transfert-rayon/equations_transfert-rayon/equation210.png) au premier ordre. En insérant ces expressions dans l'équation de
au premier ordre. En insérant ces expressions dans l'équation de 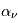 on en déduit :
on en déduit :
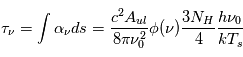 ,
,
où 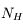 est la densité de colonne de l'hydrogène atomique neutre. On a fait ici l'hypothèse d'un milieu homogène, de sorte que
est la densité de colonne de l'hydrogène atomique neutre. On a fait ici l'hypothèse d'un milieu homogène, de sorte que 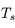 et
et 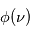 ne dépendent pas de la position
ne dépendent pas de la position  le long de la ligne de visée. On note ainsi que la profondeur optique de la raie à 21 cm est inversement proportionnelle à la température de spin,
le long de la ligne de visée. On note ainsi que la profondeur optique de la raie à 21 cm est inversement proportionnelle à la température de spin,
En supposant le rayonnement de fond négligeable et la raie optiquement mince, la température de brillance vaut : 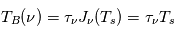 (approximation de Rayleigh-Jeans). Puisque
(approximation de Rayleigh-Jeans). Puisque 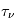 est inversement proportionnel à la température de spin, on voit que
est inversement proportionnel à la température de spin, on voit que 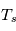 se simplifie dans cette expression et que l'intensité de la raie ne dépend plus de la température mais uniquement de la densité de colonne totale d'hydrogène,
se simplifie dans cette expression et que l'intensité de la raie ne dépend plus de la température mais uniquement de la densité de colonne totale d'hydrogène, 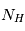 , dont on obtient ainsi une détermination directe. Cette approche est souvent appliquée même dans des cas où l'approximation de raie optiquement mince ne peut pas être vérifiée, et il faut garder à l'esprit que les estimations de la densité de colonne ainsi obtenues sont alors des limites inférieures.
, dont on obtient ainsi une détermination directe. Cette approche est souvent appliquée même dans des cas où l'approximation de raie optiquement mince ne peut pas être vérifiée, et il faut garder à l'esprit que les estimations de la densité de colonne ainsi obtenues sont alors des limites inférieures.
Mesure en absorption et émission: masse et température
Considérons l'absorption de la raie à 21 cm par une source de continuum radio variant lentement avec la fréquence dans un nuage de HI uniforme et écrivons la solution de l'équation de transfert en fonction de la température de brillance du continuum 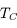 et de la température cinétique du nuage de HI interposé
et de la température cinétique du nuage de HI interposé 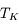 , telle que :
, telle que : 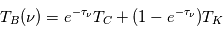 .
.
Les observations en absorption sont effectuées avec des interféromètres à haute résolution angulaire qui sont insensibles à l'émission étendue du nuage. Le deuxième terme dans l'équation pour la température de brillance est donc nul, et la solution devient 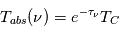 . Le rapport entre la température de brillance dans la raie d'absorption et la température de brillance dans le continu hors de la raie (où
. Le rapport entre la température de brillance dans la raie d'absorption et la température de brillance dans le continu hors de la raie (où 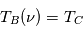 ) permet d'obtenir la valeur de
) permet d'obtenir la valeur de 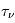 . Mais comme la profondeur optique est proportionnelle à
. Mais comme la profondeur optique est proportionnelle à 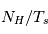 (voir section précédente), il n'est pas possible de dériver la densité de colonne
(voir section précédente), il n'est pas possible de dériver la densité de colonne 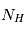 à partir de ces mesures en absorption seules. Il faut une information supplémentaire sur la température du gaz.
à partir de ces mesures en absorption seules. Il faut une information supplémentaire sur la température du gaz.
La technique généralement adoptée est la combinaison de ces résultats avec des observations en émission effectuées à l'aide d'un radiotélescope à plus basse résolution angulaire pointé sur des régions immédiatement adjacentes, où l'intensité moyenne du fond est négligeable. Cela donne la quantité : 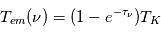 .
.
En combinant ces observations en absorption et en émission on voit qu'on peut déterminer à la fois la température cinétique 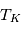 et la profondeur optique
et la profondeur optique 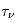 (qu'on suppose identiques entre les 2 régions observées), et d'en déduire ainsi la densité de colonne
(qu'on suppose identiques entre les 2 régions observées), et d'en déduire ainsi la densité de colonne 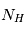 du nuage. Cette méthode est pratiquement la seule qui permet d'obtenir directement la température des nuages interstellaires atomiques.
du nuage. Cette méthode est pratiquement la seule qui permet d'obtenir directement la température des nuages interstellaires atomiques.
Ces observations sont compliquées en présence d'un mélange des composantes tièdes et froides le long de la ligne de visée, qui sont difficiles à séparer. On montre ci-dessous le spectre d'un nuage de HI interposé entre l'observateur et le quasar 3C 161. En ordonnée est présentée la température d'antenne 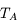 , généralement utilisée par les radioastronomes comme mesure de l'énergie reçue par une antenne radio. Il s'agit de la température du corps noir qui entourerait totalement l'antenne pour donner le signal observé. La puissance captée par l'antenne est alors
, généralement utilisée par les radioastronomes comme mesure de l'énergie reçue par une antenne radio. Il s'agit de la température du corps noir qui entourerait totalement l'antenne pour donner le signal observé. La puissance captée par l'antenne est alors 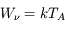 . Si l'antenne était parfaite, une région étendue de brillance uniforme
. Si l'antenne était parfaite, une région étendue de brillance uniforme 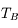 donnerait
donnerait 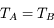 (en général il faut introduire un facteur de rendement). La quantité en abscisse de la figure est la vitesse radiale donnée par la formule de l'effet Doppler
(en général il faut introduire un facteur de rendement). La quantité en abscisse de la figure est la vitesse radiale donnée par la formule de l'effet Doppler 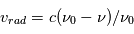 , utilisée d'habitude par les radioastronomes plutôt que la fréquence. La courbe en émission est associée au signal des régions immédiatement adjacentes. En soustrayant cette émission du signal obtenu avec l'antenne pointée sur le quasar on obtient la courbe en absorption. Enfin, la ligne en pointillé est due à une composante tiède pour laquelle l'absorption est plus faible.
, utilisée d'habitude par les radioastronomes plutôt que la fréquence. La courbe en émission est associée au signal des régions immédiatement adjacentes. En soustrayant cette émission du signal obtenu avec l'antenne pointée sur le quasar on obtient la courbe en absorption. Enfin, la ligne en pointillé est due à une composante tiède pour laquelle l'absorption est plus faible.
Observations de la raie à 21 cm devant le quasar 3C 161
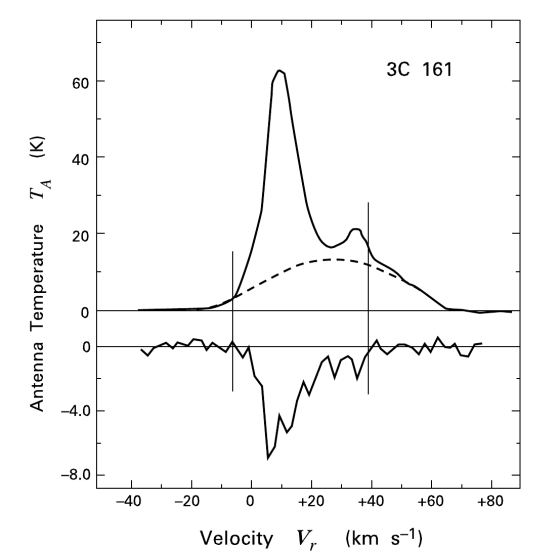
Crédit :
Stahler & Palla, "The Formation of Stars"
Profils de raie pour les atomes et les molécules en l'absence de mouvements d'ensemble
On observe des raies spectrales en émission ou en absorption lors des transitions entre deux niveaux discrets dans un atome ou une molécule. Ces niveaux ne sont pas infiniment fins, de sorte que la raie est élargie. Afin de prendre en compte cet élargissement, nous avons introduit (voir la page Coefficients d'Einstein) un profil de raie 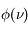 , normalisé et centré sur
, normalisé et centré sur 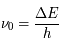 , avec
, avec 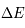 >0 l'écart en énergie entre les niveaux. Dans cette page nous présenterons les différents processus qui causent l'élargissement et analyserons les caractéristiques des profils de raie associés à chacun de ces processus. Nous ne considérons pas les effets associés à la présence de champs électromagnétiques externes (par exemple l'effet Zeeman).
>0 l'écart en énergie entre les niveaux. Dans cette page nous présenterons les différents processus qui causent l'élargissement et analyserons les caractéristiques des profils de raie associés à chacun de ces processus. Nous ne considérons pas les effets associés à la présence de champs électromagnétiques externes (par exemple l'effet Zeeman).
Largeur naturelle et collisionnelle : profil de raie Lorentzien
La largeur naturelle d'une raie spectrale est la largeur minimale que la raie, en émission ou en absorption, puisse présenter. Elle est reliée à l'inégalité de Heisenberg. Soit une transition entre les niveaux u et l d'un atome. Les relations d'incertitude nous donnent : 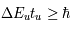 , où
, où 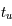 représente la durée de vie du niveau u, telle que
représente la durée de vie du niveau u, telle que 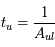 . La largeur de raie naturelle en énergie
. La largeur de raie naturelle en énergie 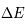 correspond au cas de l'égalité. Elle est proportionnelle au coefficient d'Einstein d'émission spontanée en absence de rayonnement (en présence de rayonnement il faudra considérer ainsi la désexcitation stimulée qui contribue à réduire la durée de vie du niveau u et donc à augmenter la largeur de raie). Du fait de l'élargissement des niveaux il faut prendre en compte toutes les transitions possibles avec une énergie
correspond au cas de l'égalité. Elle est proportionnelle au coefficient d'Einstein d'émission spontanée en absence de rayonnement (en présence de rayonnement il faudra considérer ainsi la désexcitation stimulée qui contribue à réduire la durée de vie du niveau u et donc à augmenter la largeur de raie). Du fait de l'élargissement des niveaux il faut prendre en compte toutes les transitions possibles avec une énergie 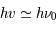 . On définit généralement une largeur naturelle de la raie en fréquence
. On définit généralement une largeur naturelle de la raie en fréquence 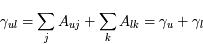 , où les indices
, où les indices 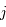 et
et 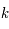 correspondent à des états d'énergie inférieure respectivement à l'énergie du niveau supérieur et à l'énergie du niveau inférieur et les deux sommes donnent la largeur du niveau supérieur et du niveau inférieur. Par exemple, on observera une raie faible mais large si le niveau inférieur est fortement élargi.
correspondent à des états d'énergie inférieure respectivement à l'énergie du niveau supérieur et à l'énergie du niveau inférieur et les deux sommes donnent la largeur du niveau supérieur et du niveau inférieur. Par exemple, on observera une raie faible mais large si le niveau inférieur est fortement élargi.
Une autre cause d'élargissement de raie est représentée par les collisions qui perturbent l'atome pendant le processus d'émission. Les collisions modifient soudainement la phase du rayonnement émis par l'atome. Les sauts de phase se produisent à une fréquence moyenne 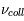 (chaque atome subit en moyenne
(chaque atome subit en moyenne 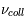 collisions par unité de temps) et contribuent à l'élargissement de la raie en fréquence qu'on écrit :
collisions par unité de temps) et contribuent à l'élargissement de la raie en fréquence qu'on écrit : 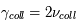 . Il faut remarquer que la fréquence des collisions augmente avec la densité du milieu. On s'attend donc à observer des élargissements collisionnels plus importants dans des environnement denses, comme les atmosphères planétaires et stellaires. Dans les nuages d'hydrogène atomique et les nuages moléculaires les effets collisionnels sont dominés par d'autres sources d'élargissement que nous allons voir dans la suite du cours (effet Doppler, turbulence). Puisque à la fois l'élargissement naturel et l'élargissement associé aux collisions sont caractérisés par des profils de la même forme, on peut définir une constante
. Il faut remarquer que la fréquence des collisions augmente avec la densité du milieu. On s'attend donc à observer des élargissements collisionnels plus importants dans des environnement denses, comme les atmosphères planétaires et stellaires. Dans les nuages d'hydrogène atomique et les nuages moléculaires les effets collisionnels sont dominés par d'autres sources d'élargissement que nous allons voir dans la suite du cours (effet Doppler, turbulence). Puisque à la fois l'élargissement naturel et l'élargissement associé aux collisions sont caractérisés par des profils de la même forme, on peut définir une constante 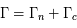 qui contient une contribution naturelle
qui contient une contribution naturelle 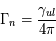 et une contribution collisionnelle
et une contribution collisionnelle 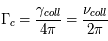 et décrire le profil de la raie tel que :
et décrire le profil de la raie tel que :
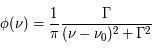 .
.
Il s'agit d'une fonction lorentzienne caractérisée par son aire, calculée comme l'intégrale sur la fréquence et égal à 1, sa valeur maximale atteinte à 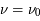 , qui vaut
, qui vaut 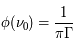 et sa largeur totale à mi-hauteur en unité de fréquence
et sa largeur totale à mi-hauteur en unité de fréquence 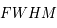 (de l'anglais Full Width at Half Maximum). Cette largeur est déterminée en remplaçant la valeur de la fonction à mi-hauteur (
(de l'anglais Full Width at Half Maximum). Cette largeur est déterminée en remplaçant la valeur de la fonction à mi-hauteur (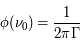 ) dans l'équation qui décrit
) dans l'équation qui décrit 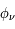 , dont on obtient
, dont on obtient 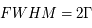 . Un profil Lorentzien centré (
. Un profil Lorentzien centré (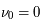 ) est montré sur la figure pour différentes valeurs de la constante
) est montré sur la figure pour différentes valeurs de la constante 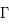 .
.
Profil de Lorentz
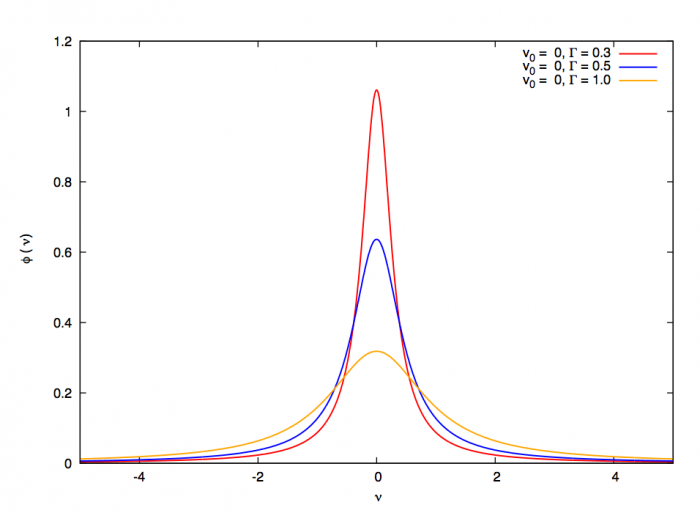
Crédit :
Cecilia Pinto
Profils de raie associés aux mouvements d'ensemble d'atomes et de molécules
Agitation thermique : profil Doppler
Jusqu'à présent, nous avons considéré que les atomes et les molécules étaient à repos. Dans cette page nous allons analyser l'effet d'élargissement de raie par les mouvements des particules. Du fait de l'effet Doppler, les photons émis à une fréquence 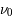 dans le référentiel d'un atome en mouvement seront détectés à une fréquence
dans le référentiel d'un atome en mouvement seront détectés à une fréquence 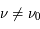 par l'observateur. Le décalage en fréquence d'un atome qui possède une vitesse relative le long de la ligne de visée
par l'observateur. Le décalage en fréquence d'un atome qui possède une vitesse relative le long de la ligne de visée 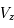 , pour des vitesses non relativistes, vaut :
, pour des vitesses non relativistes, vaut : 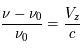 .
.
Puisque chaque atome subit son propre décalage Doppler, l'effet net est un élargissement de la raie, tandis que son intensité totale ne change pas. Les atomes et les molécules d'un gaz effectuent des mouvement aléatoires dépendant de la température. La théorie cinétique des gaz prévoit que cette agitation thermique induit une distribution maxwellienne de vitesse. Le nombre d'atomes à la température 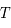 dont la projection de la vitesse sur l'axe de visée
dont la projection de la vitesse sur l'axe de visée 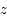 est comprise entre
est comprise entre 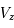 et
et 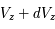 est donc proportionnel à la fonction
est donc proportionnel à la fonction 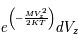 , où M est la masse d'un atome. En utilisant la formule pour le décalage Doppler on déduit
, où M est la masse d'un atome. En utilisant la formule pour le décalage Doppler on déduit 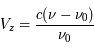 ,
, 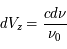 et on peut exprimer la distribution des atomes en fonction de la fréquence. Par conséquent, l'intensité de l'émission dans l'intervalle de fréquence de
et on peut exprimer la distribution des atomes en fonction de la fréquence. Par conséquent, l'intensité de l'émission dans l'intervalle de fréquence de 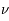 à
à 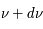 est proportionnelle à
est proportionnelle à 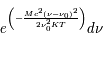 . Si l'effet Doppler est la source dominant d'élargissement de la raie, son profil est la somme des contributions de chaque atome, ce qui donne un profil de forme gaussienne :
. Si l'effet Doppler est la source dominant d'élargissement de la raie, son profil est la somme des contributions de chaque atome, ce qui donne un profil de forme gaussienne :
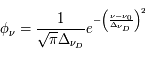 .
.
La quantité 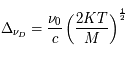 , appelée largeur Doppler de la raie, est reliée à la largeur à mi-hauteur de la gaussienne par
, appelée largeur Doppler de la raie, est reliée à la largeur à mi-hauteur de la gaussienne par 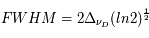 . L'aire du profil, obtenue intégrant sur la fréquence, vaut 1 et sa valeur maximale, atteinte à
. L'aire du profil, obtenue intégrant sur la fréquence, vaut 1 et sa valeur maximale, atteinte à 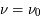 , est
, est 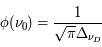 . Dans le milieu interstellaire, l'élargissement associé à l'effet Doppler est généralement plus important que la largeur naturelle et l'élargissement dû aux collisions. Un exemple est représenté par la raie à 21 cm de l'hydrogène atomique, l'élargissement lorentzien étant extrêmement faible puisque la durée de vie du niveau supérieur n'est limitée que par les collisions, rares dans le milieu interstellaire diffus.
. Dans le milieu interstellaire, l'élargissement associé à l'effet Doppler est généralement plus important que la largeur naturelle et l'élargissement dû aux collisions. Un exemple est représenté par la raie à 21 cm de l'hydrogène atomique, l'élargissement lorentzien étant extrêmement faible puisque la durée de vie du niveau supérieur n'est limitée que par les collisions, rares dans le milieu interstellaire diffus.
D'autres mouvements peuvent se superposer à la distribution de vitesse due à l'excitation thermique. S'il s'agit d'un mouvement d'ensemble, le centre de la raie est globalement déplacé par effet Doppler. Si, par contre, il s'agit d'une distribution de vitesse supplémentaire, la raie subit un élargissement gaussien. Par exemple, en présence de mouvements aléatoires de turbulence au sein du milieu, la largeur Doppler devient, par composition de profils gaussiens : 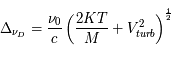 , où
, où 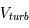 est la vitesse caractéristique de la turbulence. Dans les nuages interstellaires, la vitesse turbulente est de l'ordre de quelques kilomètres par seconde. Puisque la température des nuages n'est pas élevée, l'effet Doppler est dominé par la turbulence. Des mouvements turbulents plus importants ont été observés dans la nébuleuse d'Orion (voir le TP Spectre en émission).
est la vitesse caractéristique de la turbulence. Dans les nuages interstellaires, la vitesse turbulente est de l'ordre de quelques kilomètres par seconde. Puisque la température des nuages n'est pas élevée, l'effet Doppler est dominé par la turbulence. Des mouvements turbulents plus importants ont été observés dans la nébuleuse d'Orion (voir le TP Spectre en émission).
Convolution de profils : profil de Voigt
En général, le profil d'une raie résulte de la composition des profils induits par tous les différents effets décrits précédemment : élargissement naturel, collisions, effet Doppler thermique et turbulent. On obtient un profil qui dérive de la convolution d'une courbe Lorentzienne et d'une courbe gaussienne appelé profil de Voigt. Ce profil est exprimé en termes d'une fonction mathématiquement connue, la fonction de Voigt 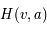 , dont les valeurs sont données dans la littérature :
, dont les valeurs sont données dans la littérature : 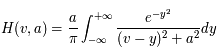 . Cette forme est obtenue par un changement de variable dans les fonctions lorentzienne et gaussienne tel que :
. Cette forme est obtenue par un changement de variable dans les fonctions lorentzienne et gaussienne tel que : 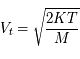 ,
, 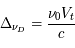 ,
, 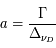 ,
, 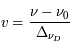 et donne le profil de raie normalisé :
et donne le profil de raie normalisé :
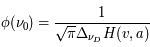 .
.
La fonction de Voigt est montrée sur la figure pour différentes valeurs du paramètre 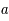 qui quantifie l'importance relative des différents processus qui contribuent à l'élargissement de raie. On remarque que dans le cas limite d'élargissement naturel et collisionnel négligeable (a=0) la fonction a une forme gaussienne, tandis que c'est une lorentzienne pour un élargissement Doppler négligeable (voir par exemple la courbe a=20). En général la fonction présente une allure gaussienne au coeur (
qui quantifie l'importance relative des différents processus qui contribuent à l'élargissement de raie. On remarque que dans le cas limite d'élargissement naturel et collisionnel négligeable (a=0) la fonction a une forme gaussienne, tandis que c'est une lorentzienne pour un élargissement Doppler négligeable (voir par exemple la courbe a=20). En général la fonction présente une allure gaussienne au coeur (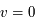 ) et lorentzienne dans les ailes.
) et lorentzienne dans les ailes.
Fonction de Voigt
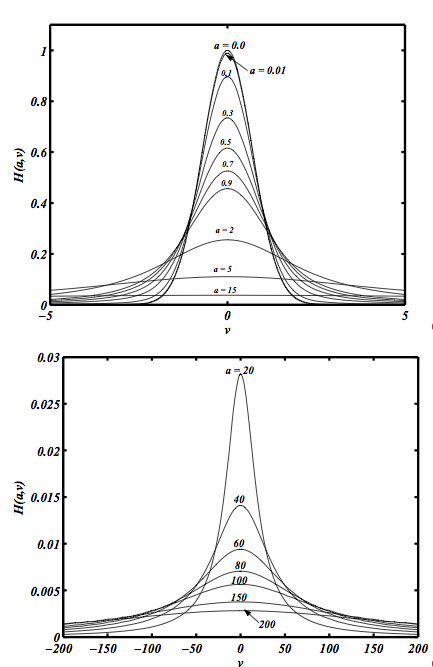
Crédit :
M.R. Zaghloul, MNRAS, 375,1043,2007
Raies en absorption
Dans le premier chapitre du cours (Détection du gaz neutre atomique : raies spectrales) nous avons mentionné que les raies d'absorption interstellaires observées dans le visible et l'ultraviolet fournissent des informations précieuses sur les conditions physiques au sein du milieu interstellaire. Nous allons analyser en détail ce sujet en montrant comment on peut en déduire la densité de colonne des éléments observés.
Courbe de croissance
On peut exprimer la profondeur optique de la raie en terme de la fonction de Voigt 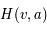 , qui contient l'information sur le profil de la raie dans le cas général où la largeur naturelle, les effets collisionnels et l'effet Doppler sont pris en compte, et un paramètre
, qui contient l'information sur le profil de la raie dans le cas général où la largeur naturelle, les effets collisionnels et l'effet Doppler sont pris en compte, et un paramètre 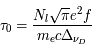 qui représente la profondeur optique au centre de la raie et dépend de la densité de colonne, de la largeur Doppler de la raie et des caractéristiques de la transition atomique par la quantité
qui représente la profondeur optique au centre de la raie et dépend de la densité de colonne, de la largeur Doppler de la raie et des caractéristiques de la transition atomique par la quantité 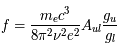 . Il s'agit d'un coefficient sans dimension souvent utilisé pour exprimer la probabilité d'émission spontanée qu'on appelle force de l'oscillateur. Il est possible de trouver dans la littérature des tables de
. Il s'agit d'un coefficient sans dimension souvent utilisé pour exprimer la probabilité d'émission spontanée qu'on appelle force de l'oscillateur. Il est possible de trouver dans la littérature des tables de 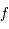 pour chaque raie. Nous pouvons donc écrire
pour chaque raie. Nous pouvons donc écrire 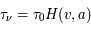 .
.
On identifie trois régimes concernant le profil de raie dépendant de la valeur du paramètre 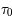 et donc du nombre d'atomes absorbants le long de la ligne de visée.
et donc du nombre d'atomes absorbants le long de la ligne de visée.
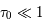 : la raie est optiquement mince. On en déduit que
: la raie est optiquement mince. On en déduit que 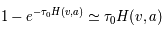 et le calcul de la largeur équivalente se réduit à :
et le calcul de la largeur équivalente se réduit à : 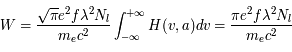 car l'intégrale de la fonction de Voigt vaut
car l'intégrale de la fonction de Voigt vaut 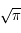 . Il s'agit en effet de raies faibles où la partie centrale domine le profil. On a vu que dans cette région la fonction de Voigt a une allure gaussienne. Le coeur dû à l'effet Doppler domine. Pour les raies optiquement minces la largeur équivalente est proportionnelle à la densité de colonne et on parle de régime linéaire. Dans ce régime les mesures de la largeur équivalente permettent une détermination précise de la densité de colonne, les paramètres atomiques étant connus.
. Il s'agit en effet de raies faibles où la partie centrale domine le profil. On a vu que dans cette région la fonction de Voigt a une allure gaussienne. Le coeur dû à l'effet Doppler domine. Pour les raies optiquement minces la largeur équivalente est proportionnelle à la densité de colonne et on parle de régime linéaire. Dans ce régime les mesures de la largeur équivalente permettent une détermination précise de la densité de colonne, les paramètres atomiques étant connus. 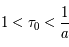 : lorsque le nombre d'atomes absorbants augmente, le centre de la raie devient de plus en plus optiquement épais. La contribution des ailes du profil reste toutefois négligeable. L'absorption principale est toujours due à l'effet Doppler, mais il y a une saturation de la raie qui prend une forme rectangulaire au centre. En s'éloignant du centre une absorption partielle persiste et la largeur équivalente croît lentement en fonction de la densité de colonne. On peut montrer que dans ce domaine
: lorsque le nombre d'atomes absorbants augmente, le centre de la raie devient de plus en plus optiquement épais. La contribution des ailes du profil reste toutefois négligeable. L'absorption principale est toujours due à l'effet Doppler, mais il y a une saturation de la raie qui prend une forme rectangulaire au centre. En s'éloignant du centre une absorption partielle persiste et la largeur équivalente croît lentement en fonction de la densité de colonne. On peut montrer que dans ce domaine 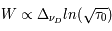 . Malheureusement des nombreuses raies d'absorption interstellaire se trouvent dans ce régime où la largeur équivalente est très peu sensible à la densité de colonne, ce qui en rend difficile l'estimation. De plus les mesures sont compliquées par la dépendance de la largeur Doppler.
. Malheureusement des nombreuses raies d'absorption interstellaire se trouvent dans ce régime où la largeur équivalente est très peu sensible à la densité de colonne, ce qui en rend difficile l'estimation. De plus les mesures sont compliquées par la dépendance de la largeur Doppler.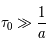 : la raie est saturée jusqu'aux ailes lorentziennes et la largeur équivalente varie proportionnellement à la racine de la densité de colonne et de la largeur naturelle (
: la raie est saturée jusqu'aux ailes lorentziennes et la largeur équivalente varie proportionnellement à la racine de la densité de colonne et de la largeur naturelle (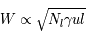 ).
).
Pour chaque raie spectrale il est donc possible de construire une courbe de croissance théorique où l'on porte 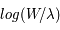 en fonction de
en fonction de 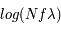 . Elle est composée d'une partie linéaire, d'une portion plate dont la position sur l'axe vertical dépend de la valeur de la largeur Doppler et d'une région dont la pente est fonction de la largeur naturelle (et éventuellement de la densité du gaz s'il existe une contribution des collisions à l'élargissement). Pour construire cette courbe il faut donc connaître
. Elle est composée d'une partie linéaire, d'une portion plate dont la position sur l'axe vertical dépend de la valeur de la largeur Doppler et d'une région dont la pente est fonction de la largeur naturelle (et éventuellement de la densité du gaz s'il existe une contribution des collisions à l'élargissement). Pour construire cette courbe il faut donc connaître 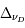 et
et 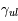 . Dans ce cas, on peut placer la raie sur la courbe, en déterminant la largeur équivalente et en déduire la densité de colonne. Dans la figure on montre les courbes de croissance obtenues d'observations de l'étoile ζ Ophiuchi. Les valeurs mesurées, pour différents éléments à différentes longueurs d'onde provenant du même nuage, sont superposées à une courbe de croissance théorique obtenue avec une distribution fixée des vitesses, ce qui donne ainsi des renseignements sur la dispersion de vitesse ou les mouvement aléatoires d'ensemble au sein du nuage.
. Dans ce cas, on peut placer la raie sur la courbe, en déterminant la largeur équivalente et en déduire la densité de colonne. Dans la figure on montre les courbes de croissance obtenues d'observations de l'étoile ζ Ophiuchi. Les valeurs mesurées, pour différents éléments à différentes longueurs d'onde provenant du même nuage, sont superposées à une courbe de croissance théorique obtenue avec une distribution fixée des vitesses, ce qui donne ainsi des renseignements sur la dispersion de vitesse ou les mouvement aléatoires d'ensemble au sein du nuage.
Courbe de croissance
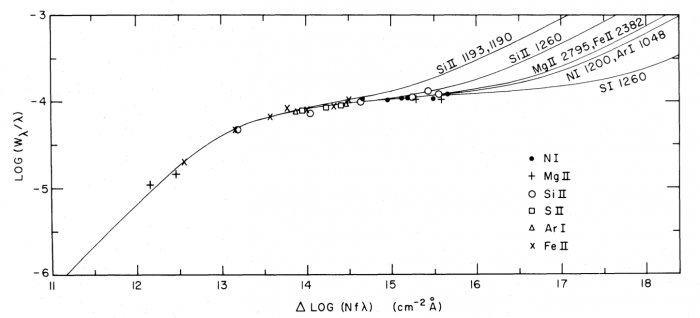
Crédit :
D. Morton, Apj, 197, 85, 1975
Absorption par les poussières interstellaires
Au cours du premier chapitre nous avons souligné l'importance des poussières pour le bilan énergétique (émission thermique et chauffage photoélectrique) et la chimie (déplétion des éléments) du milieu interstellaire. Pendant les travaux pratiques nous avons également constaté l'absorption de la lumière stellaire en comparant des images à différentes longueurs d'onde. Dans cette page nous allons détailler ce processus grâce aux notions de transfert de rayonnement acquises. Il faut remarquer que, différemment de l'absorption des atomes et des molécules que nous avons vu se produire dans des raies spectrales étroites, l'absorption par les poussières a lieu dans le continu, et dans quelques bandes larges produites par les modes de vibration ou pliage des molécules du matériau solide (silicates, glaces, PAHs...).
Extinction et rougissement interstellaires
La diminution de la luminosité d'une étoile vue à travers un nuage de poussières est due à deux phénomènes physiques : l'absorption des photons par le matériau du grain, et la diffusion des photons dans d'autres directions que la direction incidente. La somme de ces 2 processus est appelée extinction. Cette quantité dépend de la composition des poussières, de leur forme, de la distribution de leurs tailles et de la longueur d'onde. En particulier, la diffusion étant sélective en longueur d'onde, la lumière diffusée est plus bleue que celle de l'étoile, tandis que la lumière transmise à travers un nuage de poussières est plus rouge. La lumière diffusée forme des objets étendus, appelés nébuleuses par réflexion, qui réfléchissent la lumière de l'étoile illuminatrice et sont habituellement bleues. En expliquant les méthodes de mesure du champ magnétique (voir la page Source d'énergie : champ magnétique ) nous avons également mentionné que la lumière diffusée ou transmise est partiellement polarisée.
L'extinction d'un nuage de poussières à une longueur d'onde 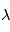 est décrite par la quantité
est décrite par la quantité 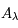 (mesurée en magnitude), définie comme la différence entre la magnitude observée
(mesurée en magnitude), définie comme la différence entre la magnitude observée 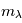 d'une étoile dont la lumière a traversé le nuage de poussières (de profondeur optique
d'une étoile dont la lumière a traversé le nuage de poussières (de profondeur optique 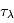 ) et celle qu'on observerait en l'absence d'extinction,
) et celle qu'on observerait en l'absence d'extinction, 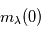 . Comme l'émission des poussières est en général négligeable à la longueur d'onde considérée, le flux spécifique
. Comme l'émission des poussières est en général négligeable à la longueur d'onde considérée, le flux spécifique 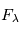 est atténué par un facteur
est atténué par un facteur 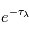 . Avec la relation entre magnitude et flux, on obtient :
. Avec la relation entre magnitude et flux, on obtient : ![A_\lambda(mag)=m_\lambda - m_\lambda(0) = -2.5log_{10}\left[\frac{F_\lambda(\tau_\lambda)}{F_\lambda(0)}\right]=-2.5log_{10}[e^{-\tau_\lambda}]=1.086\tau_\lambda](../pages_transfert-rayon/equations_transfert-rayon/equation328.png) . On voit que la valeur de
. On voit que la valeur de 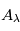 en magnitude est essentiellement égale à l'opacité des poussières à cette longueur d'onde ; elle est donc proportionnelle à la densité colonne de poussières sur la ligne de visée.
en magnitude est essentiellement égale à l'opacité des poussières à cette longueur d'onde ; elle est donc proportionnelle à la densité colonne de poussières sur la ligne de visée.
Courbe d'extinction
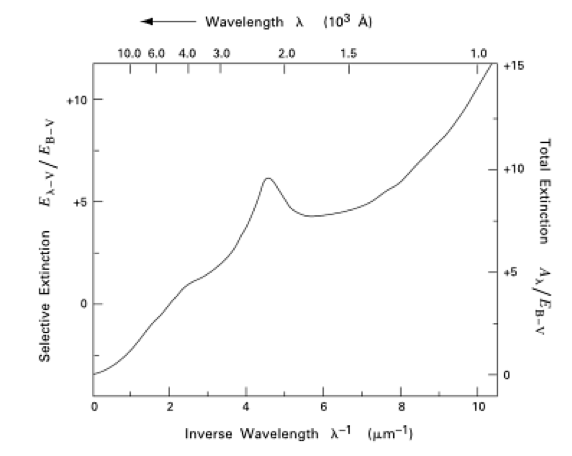
Crédit :
Stahler & Palla, "The Formation of Stars"
Travaux pratiques : logiciel VOSpec
Auteur: Cecilia Pinto
Introduction
Le logiciel VOSpec
Il s'agit d'un logiciel développé au Centre Européen d'Astronomie Spatiale (European Space Astronomy Centre ESAC) de Villafranca du Castillo, en Espagne, dans le cadre des activités de l'Observatoire Virtuel liées à la recherche spatiale. VOSpec est un outil de visualisation et d'analyse multi-longueur d'onde de spectres astronomiques. Il permet d'accéder à des spectres observés ainsi qu'à des modèles théoriques et des bases de données de raies atomiques et moléculaires disponibles dans le contexte de l'Observatoire Virtuel. Le logiciel se caractérise par une grande flexibilité : il peut traiter différents intervalles de longueur d'onde et manipuler différentes unités de mesure du flux d'énergie, ce qui est essentiel pour superposer les données spectrales fortement hétérogènes dérivant des différents projets de l'Observatoire Virtuel. VOSpec fournit également des outils d'ajustement des raies spectrales, de correction du décalage vers le rouge, d'opérations d'arithmétique (par exemple addition) sur les spectres et de calcul de la largeur équivalente de raies d'absorption.
Spectres ISO et FUSE
Au cours de ce TP nous exploiterons la flexibilité du logiciel VOSpec pour analyser des spectres observés par les satellites ISO et FUSE qui ont été lancés afin de sonder des intervalles de longueur d'onde différents. ISO a été envoyé en 1995 pour des observations dans les domaines infrarouge moyen et lointain, entre 2 et 200 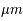 . Les nuages moléculaires représentent une classe privilégiée d'objets détectés avec cet instrument. Nous analyserons notamment un spectre en émission de la nébuleuse d'Orion. FUSE a été lancé en 1999 afin d'obtenir des spectres stellaires dans le domaine de l'ultraviolet lointain (de 90 à 120 nm). La deuxième partie du TP sera consacrée à l'étude des raies d'absorption interstellaires observées dans le spectre de l'étoile HD34078. Nous profiterons notamment des outils qui permettent de visualiser les spectres en utilisant différentes unités de mesure afin d'identifier les spectres et les raies d'intérêt dans les nombreuses données spectrales d'archives disponibles. En étudiant une raie en émission du carbone excité observée par ISO nous exploiterons les outils d'ajustement afin de déterminer l'effet d'élargissement dominant. Enfin, l'outil de calcul de la largeur équivalente nous permettra de dériver la densité de colonne d'une raie excitée en absorption de l'hydrogène moléculaire observée par FUSE.
. Les nuages moléculaires représentent une classe privilégiée d'objets détectés avec cet instrument. Nous analyserons notamment un spectre en émission de la nébuleuse d'Orion. FUSE a été lancé en 1999 afin d'obtenir des spectres stellaires dans le domaine de l'ultraviolet lointain (de 90 à 120 nm). La deuxième partie du TP sera consacrée à l'étude des raies d'absorption interstellaires observées dans le spectre de l'étoile HD34078. Nous profiterons notamment des outils qui permettent de visualiser les spectres en utilisant différentes unités de mesure afin d'identifier les spectres et les raies d'intérêt dans les nombreuses données spectrales d'archives disponibles. En étudiant une raie en émission du carbone excité observée par ISO nous exploiterons les outils d'ajustement afin de déterminer l'effet d'élargissement dominant. Enfin, l'outil de calcul de la largeur équivalente nous permettra de dériver la densité de colonne d'une raie excitée en absorption de l'hydrogène moléculaire observée par FUSE.
Spectre en émission : profils de raie et élargissement
Procédure : observations ISO
- Lancement de VOSpec : VOSpec peut être lancé à partir de la page Web http://www.sciops.esa.int/index.php?project=SAT&page=vospec en cliquant sur WebStart et en acceptant l'exécution de l'applet.
-
Recherche du spectre et identification d'une raie : On s'intéresse au spectre montré sur la figure Spectre en émission et observé par le satellite ISO dans la nébuleuse d'Orion. Interroger les bases de données spectrales en indiquant le nom de l'objet (ORION) dans la case Target de la fenêtre de contrôle du logiciel et en validant la requête avec la commande Query. Une nouvelle fenêtre contenant la liste des données disponibles s'affiche. Accéder aux spectres en dépliant le menu Observational Spectra Services et sélectionner les données du satellite ISO (The ISO Data Archive Interoperability System). En confirmant la requête avec Query (dans cette fenêtre de recherche) la liste des spectres ISO disponibles s'affiche dans la partie inférieure de la fenêtre de contrôle. Une fois la liste dépliée, il faut cocher les spectres d'intérêt et les extraire en cliquant sur RETRIEVE en bas à droite de la fenêtre de contrôle.
Le spectre montré sur la figure concerne des observations de la source très lumineuse IRC2 dans Orion, menées en utilisant le spectromètre LWS à bord du satellite ISO. Il faut donc extraire les spectres catalogués avec la légende de type ISO LWS01 Spectrum Target : ORIAIRC2 afin de procéder à l'identification du spectre. La gestion de la visualisation se fait par la fenêtre de Graphic mode où la couleur correspondant à chaque spectre s'affiche sous forme de case et le type de caractères (points, lignes, ...) peut être changé en le saisissant dans la liste à droite de cette case. Par défaut, tous les spectres extraits sont visualisés simultanément et il est nécessaire de décocher les cases correspondantes si on veut exclure certains spectres de l'affichage. Chaque changement au niveau de la visualisation doit être mis à jour en cliquant sur la commande View en bas de la fenêtre de Graphic mode.
Afin d'identifier le spectre d'intérêt entre les spectres extraits (ou isoler une seule raie dans un spectre) on peut utiliser deux fonctionnalités fournies par le logiciel : le convertisseur des unités de mesure et la fonction de zoom. La conversion des unités est obtenue en choisissant les unités désirées pour les axes dans les deux listes Wave Unit et Flux Unit situées à gauche de la fenêtre de contrôle. On peut ainsi choisir d'utiliser des échelles linéaires ou logarithmiques pour les axes. Pour zoomer, il faut sélectionner (en gardant la souris appuyée) la région d'étude sur le spectre affiché dans la fenêtre de contrôle (pour annuler l'opération de zoom choisir dans le menu principal : View ⇒ Unzoom).
- Outils d'ajustement des profils de raie (ajustement gaussien et lorentzien) : Le logiciel VOSpec fournit des outils d'ajustement des raies spectrales. Une fois la raie d'intérêt sélectionnée par la fonction de zoom, on peut les activer en cliquant sur la deuxième icône dans la barre des outils en dessous de la fenêtre de contrôle (en parcourant la barre avec le curseur de la souris, les fonctions correspondantes à chaque icône s'affichent). Une fenêtre d'ajustement s'ouvre et une flèche dans la barre en haut de la fenêtre permet de faire défiler les fonctions d'ajustement disponibles. On s'intéresse à une fonction gaussienne et une fonction lorentzienne. En cliquant sur le type de fonction choisi (Gaussian ou Lorentzian) et sur la touche Generate les paramètres d'ajustement s'affichent et le profil correspondant apparaît sous forme de case dans la fenêtre de Graphic Mode. Pour visualiser le résultat dans la fenêtre de contrôle et le comparer aux donnés spectrales cocher uniquement les cases du spectre observé d'intérêt et du profil calculé et valider en cliquant sur View. En zoomant en longueur d'onde autour de la raie visualiser le résultat de l'ajustement superposé au profil de la raie observée. Répéter la procédure avec une fonction lorentzienne et visualiser simultanément les deux ajustements et la raie observée.
Spectre en émission observé par le satellite ISO
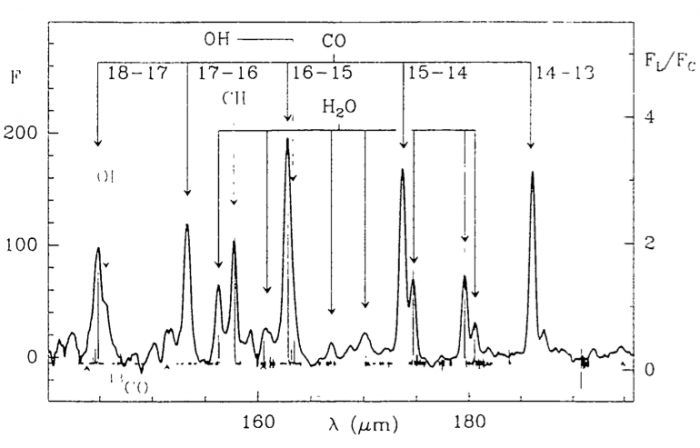
Le flux F en ordonnée est exprimé en unités de 10-18 W cm-2 μm-1.
Crédit :
Cernicharo, J. et al. ESASR.427..565C 1999
 Profil d'une raie du carbone dans la nébueluse d'Orion
Profil d'une raie du carbone dans la nébueluse d'Orion
Question 1)
Parmi les données spectrales acquises avec le satellite ISO en direction de la source IRC2 dans la nébuleuse d'Orion identifier le spectre montré dans l'image Spectre en émission et en particulier les raies en émission du carbone correspondant aux transitions entre les niveaux d'énergie caractérisés par les nombres quantiques J=15-14 et J=14-13.
Les spectres extraits à l'aide de VOSpec ont été seulement prétraités. Noter par exemple l'absence de soustraction du continu par rapport à l'image.
Question 2)
Se concentrer sur la raie du carbone J=14-13 et utiliser les outils d'ajustement des raies spectrales pour établir la cause principale d'élargissement de la raie observée.
Se rappeler que le profil lorentzien associé à la largeur naturelle de la raie et dû aux processus de collision domine les ailes des raies spectrales. Il faudra donc sélectionner un intervalle de longueur d'onde suffisamment étendu autour de la raie afin de visualiser cette contribution à l'élargissement de raie.
Question 3)
En utilisant le profil gaussien d'ajustement issu de la question précédente mesurer la largeur de la raie du carbone J=14-13. Négliger le décalage vers le rouge de la fréquence du centre de la raie. En déduire une estimation de la dispersion de vitesse  de la source IRC2 dans la nébuleuse d'Orion et comparer le résultat avec les valeurs suggérées dans l'article de la littérature dont la figure est extraite et qui sont supérieures à 100 km.s-1.
de la source IRC2 dans la nébuleuse d'Orion et comparer le résultat avec les valeurs suggérées dans l'article de la littérature dont la figure est extraite et qui sont supérieures à 100 km.s-1.
Afin d'avoir une mesure plus précise noter que la valeur de la longueur d'onde à différentes positions du spectre visualisé s'affiche en dessous de la commande View lorsque on déplace le curseur de la souris sur la fenêtre de visualisation.
Spectre en absorption : mesure de la densité de colonne
Procédure : observations FUSE
- Recherche du spectre et identification d'une raie optiquement mince : On s'intéresse au spectre montré dans l'image Spectre en absorption. Il s'agit d'un spectre de l'étoile HD 34078 obtenu par le satellite FUSE. Cette ligne de visée a permis la détection en absorption de nombreuses espèces moléculaires, ce qui atteste de la présence d'un nuage interstellaire en cette direction. À l'exception des raies de H2 et de l'Ar explicitement notées, l'image montre des raies de l'hydrogène moléculaire qui correspondent à des transitions Lyman. Les nombres quantiques
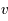 et J du niveau d'énergie inférieur de ces transitions sont également affichés en haut de la figure. En suivant la procédure décrite dans la page précédente, charger les données spectrales FUSE (Far Ultraviolet Spectroscopic Explorer) disponibles pour la cible HD 34078. Ajuster les unités de mesure des axes et visualiser les spectres dans le même intervalle de longueur d'onde du spectre montré sur la figure . La richesse de ces spectres les rend difficiles à analyser, en particulier en ce qui concerne l'identification des raies. Le logiciel VoSpec fournit un outil d'exécution d'opérations arithmétiques sur les spectres. On peut notamment sommer des spectres afin de maximiser le rapport entre le signal observé et le bruit instrumental. Cet outil s'active en cliquant sur la première icône qui apparaît dans la barre des outils de la fenêtre de contrôle. Une fenêtre de calcul s'affiche et il faut y déplacer les spectres à sommer, en interposant le symbole +, et enfin appuyer sur le symbole =. Une nouvelle liste, appelée ADD, apparaît en bas de celle des spectres extraits. Il faut la déplier, cocher la case du nouveau spectre calculé et valider avec View pour visualiser le résultat.
et J du niveau d'énergie inférieur de ces transitions sont également affichés en haut de la figure. En suivant la procédure décrite dans la page précédente, charger les données spectrales FUSE (Far Ultraviolet Spectroscopic Explorer) disponibles pour la cible HD 34078. Ajuster les unités de mesure des axes et visualiser les spectres dans le même intervalle de longueur d'onde du spectre montré sur la figure . La richesse de ces spectres les rend difficiles à analyser, en particulier en ce qui concerne l'identification des raies. Le logiciel VoSpec fournit un outil d'exécution d'opérations arithmétiques sur les spectres. On peut notamment sommer des spectres afin de maximiser le rapport entre le signal observé et le bruit instrumental. Cet outil s'active en cliquant sur la première icône qui apparaît dans la barre des outils de la fenêtre de contrôle. Une fenêtre de calcul s'affiche et il faut y déplacer les spectres à sommer, en interposant le symbole +, et enfin appuyer sur le symbole =. Une nouvelle liste, appelée ADD, apparaît en bas de celle des spectres extraits. Il faut la déplier, cocher la case du nouveau spectre calculé et valider avec View pour visualiser le résultat. - Outil de correction du décalage vers le rouge : Nous avons mentionné (voir la page Profils de raie associés aux mouvements d'ensemble d'atomes et de molécules) que la présence de mouvements d'ensemble au sein des objets observés induit, par effet Doppler, un décalage vers le rouge du centre des raies observées. VoSpec permet de corriger cet effet par l'insertion de la valeur du décalage dans la case RedShift à gauche de la fenêtre de contrôle. Une fois la longueur d'onde au repos de la transition (
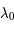 ) connue, on peut évaluer le décalage par différence entre la valeur de la longueur d'onde du centre de la raie
) connue, on peut évaluer le décalage par différence entre la valeur de la longueur d'onde du centre de la raie 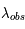 et la valeur à repos :
et la valeur à repos : 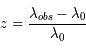 (se rappeler que la valeur de la longueur d'onde à différentes positions du spectre s'affiche en bas à gauche en suivant le déplacement du curseur dans la fenêtre de visualisation). La correction s'applique en cochant la petite case à côté de la case Redshift et en visualisant à nouveau le spectre.
(se rappeler que la valeur de la longueur d'onde à différentes positions du spectre s'affiche en bas à gauche en suivant le déplacement du curseur dans la fenêtre de visualisation). La correction s'applique en cochant la petite case à côté de la case Redshift et en visualisant à nouveau le spectre. - Outil de calcul de la largeur équivalente : VoSpec permet le calcul interactif de la largeur équivalente d'une raie spectrale. La raie d'intérêt étant sélectionnée par la fonction de zoom, on active la fenêtre Analysis Tools en cliquant sur la sixième icône de la barre des outils de la fenêtre de contrôle. On choisit la fonction Equivalent Width et on appuie sur la commande Calculate afin d'obtenir la valeur de la largeur équivalente.
Spectre en absorption observé par le satellite FUSE
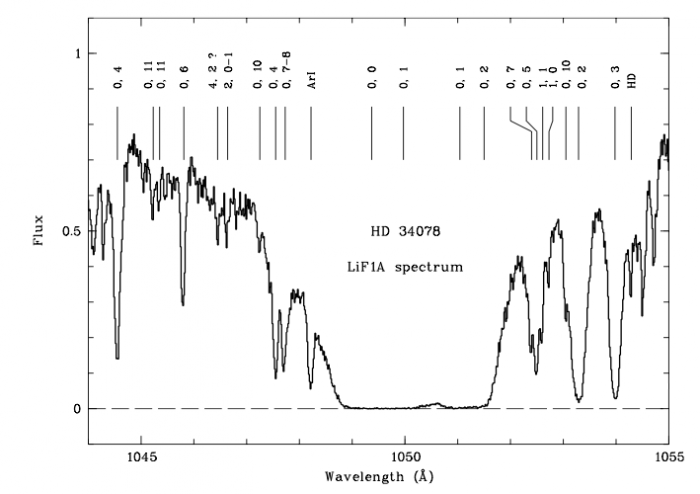
Le flux F en ordonnées est exprimé en unités de 10
-11 erg cm
-2 s
-1 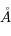 -1
-1.
Crédit :
Boissé, P. et al. A&A 429, 509, 2005
 Densité de colonne d'une raie d'hydrogène moléculaire dans le spectre de HD 34078
Densité de colonne d'une raie d'hydrogène moléculaire dans le spectre de HD 34078
Les raies spectrales montrées sur la figure occupent des positions différentes sur la courbe de croissance décrite en détail dans la page Raies en absorption. . Les raies de basse énergie sont lorentziennes et, bien que saturées, leur profil est indépendant de la largeur Doppler 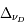 . Elles fournissent donc une mesure de la densité de colonne, la largeur naturelle de la raie (
. Elles fournissent donc une mesure de la densité de colonne, la largeur naturelle de la raie (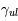 ) étant connue. Par contre, les raies issues des niveaux compris entre
) étant connue. Par contre, les raies issues des niveaux compris entre 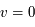 , J = 4 et
, J = 4 et 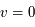 , J = 9 sont saturées et non lorentziennes, elles se situent donc sur la partie plate de la courbe de croissance. La connaissance de la largeur Doppler est alors un élément indispensable à la détermination des densités de colonne. Pour les niveaux d'énergie supérieure à
, J = 9 sont saturées et non lorentziennes, elles se situent donc sur la partie plate de la courbe de croissance. La connaissance de la largeur Doppler est alors un élément indispensable à la détermination des densités de colonne. Pour les niveaux d'énergie supérieure à 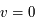 , J = 9, il est possible de trouver dans le spectre des raies optiquement minces et d'en déduire la densité de colonne directement à partir des largeurs équivalentes.
On s'intéresse donc à la raie spectrale optiquement mince correspondante à la transition
, J = 9, il est possible de trouver dans le spectre des raies optiquement minces et d'en déduire la densité de colonne directement à partir des largeurs équivalentes.
On s'intéresse donc à la raie spectrale optiquement mince correspondante à la transition 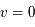 , J = 10, dont la longueur d'onde à repos vaut
, J = 10, dont la longueur d'onde à repos vaut 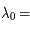 1045.051
1045.051 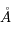 et la force de l'oscillateur
et la force de l'oscillateur 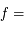 1.47x10-2. Noter que le centre de la raie peut être décalé dans le spectre observé à cause du mouvement du nuage interstellaire interposé entre la source HD 34078 et l'observateur. Pour les applications numériques, on rappelle également les valeurs de la charge de l'électron (e=4.0832x10-10 esu), de sa masse (
1.47x10-2. Noter que le centre de la raie peut être décalé dans le spectre observé à cause du mouvement du nuage interstellaire interposé entre la source HD 34078 et l'observateur. Pour les applications numériques, on rappelle également les valeurs de la charge de l'électron (e=4.0832x10-10 esu), de sa masse (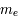 =9.1094x10-28 g) et de la vitesse de la lumière (c=2.9979x1010 cm.s-1) dans le système CGS.
=9.1094x10-28 g) et de la vitesse de la lumière (c=2.9979x1010 cm.s-1) dans le système CGS.
Question 1)
Parmi les données spectrales du satellite FUSE extraites par VOSpec identifier la raie 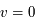 , J = 10 et choisir le spectre où la raie est plus visible. Vérifier en particulier que la somme de plusieurs spectres caractérisés par des temps de pose différents maximise le rapport signal sur bruit, ce qui rend les raies plus visibles.
, J = 10 et choisir le spectre où la raie est plus visible. Vérifier en particulier que la somme de plusieurs spectres caractérisés par des temps de pose différents maximise le rapport signal sur bruit, ce qui rend les raies plus visibles.
Question 2)
Se concentrer sur le spectre simple (sans opération de somme de spectres différents) où la raie est mieux visible. Calculer le décalage Doppler de la raie 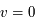 , J = 10 et appliquer la correction par l'outil de calcul du décalage vers le rouge. Vérifier sur le spectre corrigé que la longueur d'onde du centre de la raie se trouve bien à la valeur au repos donnée dans l'énoncé du TP.
, J = 10 et appliquer la correction par l'outil de calcul du décalage vers le rouge. Vérifier sur le spectre corrigé que la longueur d'onde du centre de la raie se trouve bien à la valeur au repos donnée dans l'énoncé du TP.
Question 3)
Calculer la largeur équivalente de la raie 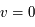 , J = 10 et en déduire une estimation de la densité de colonne de l'hydrogène moléculaire. Comparer le résultat avec les valeurs suggérées dans l'article de la littérature dont la figure est extraite, tels que 2.5 1013<
, J = 10 et en déduire une estimation de la densité de colonne de l'hydrogène moléculaire. Comparer le résultat avec les valeurs suggérées dans l'article de la littérature dont la figure est extraite, tels que 2.5 1013<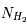 < 6 1013.
< 6 1013.
Réponses aux exercices
pages_tp-aladin/aladin-structures.html
Exercice
'Mesure de la taille des piliers de la création'
- Question 1
Solution :
En application directe de la définition de parsec un objet de taille angulaire β exprimée en secondes d'arc vu à une distance D en parsec possède une taille linéaire L en unité astronomique (dans l'approximation de petits angles) : 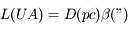 .
La mesure de la taille angulaire β est obtenue par l'outil graphique dist de Aladin en suivant la procédure décrite en détail dans la section précédente. Elle donne la valeur d'environ 1.65 minutes d'arc. La distance de la nébuleuse issue par le catalogue Simbad est 1700 pc. On en déduit : L(UA) = 1.65 X 60 X 1700 pc = 168200 UA, c'est-à-dire environ 0.81 pc. Comme les images disponibles ne permettent pas de mesurer le pilier principal jusqu'à la base on estime une taille linéaire comparable mais inférieure à l'estimation plus précise de 1.2 pc. Résultat
.
La mesure de la taille angulaire β est obtenue par l'outil graphique dist de Aladin en suivant la procédure décrite en détail dans la section précédente. Elle donne la valeur d'environ 1.65 minutes d'arc. La distance de la nébuleuse issue par le catalogue Simbad est 1700 pc. On en déduit : L(UA) = 1.65 X 60 X 1700 pc = 168200 UA, c'est-à-dire environ 0.81 pc. Comme les images disponibles ne permettent pas de mesurer le pilier principal jusqu'à la base on estime une taille linéaire comparable mais inférieure à l'estimation plus précise de 1.2 pc. Résultat
pages_tp-aladin/image-vis-if.html
Exercice
'Génération et comparaison de contours dans l'infrarouge et le visible'
- Question 1
Solution :
La première opération pour augmenter le contraste consiste à modifier le choix de la fonction de transfert qui est par défaut linéaire. En choisissant une échelle logarithmique on obtient une image très contrastée. Pour distinguer les régions de faible émission il faut modifier le seuillage et le tableau de gris de l'image en déplaçant les curseurs de seuil haut et intermédiaire à gauche de la fenêtre de contrôle. Résultats avant et après modification
- Question 2
Solution :
Pour générer des contours correspondants à des faibles intensités sur l'image dans l'infrarouge il faut déplacer les curseurs à gauche vers les valeurs de pixel moins élevées. Sur l'image dans le visible le déplacement des deux curseurs bien à droite de l'histogramme de la distribution des pixels permettra d'associer des isophotes aux étoiles brillantes et à l'émission autour des piliers. Enfin, en positionnant deux curseurs environ au centre on rendra compte d'un premier niveau d'absorption correspondant au profil externe des piliers et un deuxième plus prononcé à leur intérieur. Résultats

- Question 3
Aide :
Charger et superposer (en passant sur l'icône correspondante sans la cocher) l'image en vraies couleurs utilisée dans la première partie du TP ("Pillars of Creation in a Star-Forming Region" avec un champ de 2.6' X 2.5' , logHST) pour mieux comprendre les différentes contributions à l'émission dans le visible.
Solution :
L'image dans l'infrarouge proche révèle la présence d'un grand nombre d'étoiles invisibles en optique. En particulier, les observations dans cette bande du spectre permettent de pénétrer plus en profondeur dans la poussière dense et de dévoiler des étoiles très jeunes à l'intérieur des piliers. Les deux premiers contours dans le visible correspondent aux piliers obscurcis de gaz sous forme moléculaire mêlés aux poussières, le troisième au flot de photo-évaporation (particulièrement visible aux sommets des piliers dans l'image HST) qui trace la matière photo-ionisée chaude s'échappant du nuage moléculaire vers la région HII ionisée. Cette photo-évaporation est induite par le rayonnement ultraviolet des étoiles brillantes, qui sont représentées par le quatrième contour. Résultats

pages_tp-aladin/images-vi-if-x.html
Exercice
'Images à différentes longueurs d'onde : structuration de l'émission'
- Question 1
Solution :
Résultat
Image dans le visible : les piliers sont visibles au centre de l'image et émergent du vaste mur sombre de gaz froid et de poussière. Ces colonnes de gaz moléculaire et de poussière sont sculptées, illuminées et détruites par l'intense radiation provenant des étoiles massives (visible en blanc au centre de l'image) de NGC661, le jeune amas d'étoiles adjacent. La composante d'émission en rouge autour des piliers est associée au processus de photo-évaporation qui résulte de la transition du gaz de l'état moléculaire à l'état ionisé.
Image dans l'infrarouge moyen : dans cette bande du spectre un grand nombre d'étoiles devient visible ainsi que des structures de poussière. La composante en rouge de l'image est associée à l'émission d'hydrocarbures polycycliques aromatiques ; la composante en vert représente l'émission du gaz ; les étoiles sont en bleu.
Image dans l'infrarouge moyen-lointain : cette image met en évidence le contraste entre l'émission d'une composante de poussière chaude (en rouge) et d'une composante de poussière plus froide (en vert) contenue dans le nuage et les piliers. La poussière chaude en forme de coquille a été associée au chauffage induit par une explosion récente de supernova.
Images dans l'infrarouge lointain/submillimétrique et rayons X : l'observation à ces longueurs d'onde permet de percer les piliers et les structures environnantes en éclairant l'anatomie des zones opaques dans le visible. L'image Herschel montre l'émission du gaz froid de la nébuleuse et de la poussière dans l'infrarouge lointain. Chaque couleur correspond à différentes températures de la poussière, d'environ 10 K (rouge) à 40 K (bleu). Le gaz et les poussières fournissent le matériau nécessaire à la formation d'étoiles. En allant jusqu'au domaine submillimétrique qui caractérise la phase de formation, les observations Herschel permettent la recherche d'étoiles en formation dans l'intérieur du nuage. Les données X superposées à l'image Herschel révèlent les étoiles chaudes au centre du nuage.

pages_tp-vospectre/vo-spec-emiss.html
Exercice
'Profil d'une raie du carbone dans la nébueluse d'Orion'
pages_tp-vospectre/vo-spec-abs.html
Exercice
'Densité de colonne d'une raie d'hydrogène moléculaire dans le spectre de HD 34078'




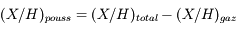 où
où 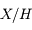 est l'abondance de l'élément par rapport à l'hydrogène (en nombre d'atomes).
est l'abondance de l'élément par rapport à l'hydrogène (en nombre d'atomes).



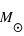
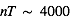 K cm-3) malgré leurs forts contrastes de densité et de température. Par contre la phase moléculaire froide et dense, qui se condense sur des échelles < 50 pc, est autogravitante et sous cet effet se comprime pour atteindre une pression plus élevée. Enfin, au sein des nuages moléculaires, on trouve les régions HII, bulles de gaz ionisées par le rayonnement UV d’une ou plusieurs jeunes étoiles OB, où le gaz tiède est localement en surpression par rapport au nuage environnant.
K cm-3) malgré leurs forts contrastes de densité et de température. Par contre la phase moléculaire froide et dense, qui se condense sur des échelles < 50 pc, est autogravitante et sous cet effet se comprime pour atteindre une pression plus élevée. Enfin, au sein des nuages moléculaires, on trouve les régions HII, bulles de gaz ionisées par le rayonnement UV d’une ou plusieurs jeunes étoiles OB, où le gaz tiède est localement en surpression par rapport au nuage environnant.


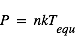 en fonction de sa densité
en fonction de sa densité 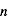 . Ici
. Ici 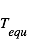 est la température d'équilibre où le taux de refroidissement radiatif compense le taux de chauffage du gaz (dû principalement à l'effet photoélectrique des photons UV interstellaires sur les grains). La figure ci-contre illustre la
est la température d'équilibre où le taux de refroidissement radiatif compense le taux de chauffage du gaz (dû principalement à l'effet photoélectrique des photons UV interstellaires sur les grains). La figure ci-contre illustre la 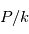 en fonction de
en fonction de 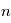
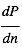 positive : celle à basse densité est le WIM (température d'environ 10 000 K, refroidissement principalement par la raie Lyman
positive : celle à basse densité est le WIM (température d'environ 10 000 K, refroidissement principalement par la raie Lyman 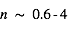 cm-3 où la dérivée
cm-3 où la dérivée 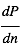 est négative. Elle correspond à un équilibre instable qui ne peut être rencontré durablement : si un élément de gaz situé au point 2 est perturbé pour se trouver en très légère sous-pression par rapport à son environnement (P < Pext), il va être comprimé par le milieu extérieur et augmenter sa densité, mais en raison de la pente négative de la courbe
est négative. Elle correspond à un équilibre instable qui ne peut être rencontré durablement : si un élément de gaz situé au point 2 est perturbé pour se trouver en très légère sous-pression par rapport à son environnement (P < Pext), il va être comprimé par le milieu extérieur et augmenter sa densité, mais en raison de la pente négative de la courbe 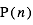 , sa pression interne va encore diminuer : il continuera donc d'être comprimé et à se densifier jusqu'à atteindre un nouvel équilibre (stable) au point 3 où P = Pext. De même s'il est en légère surpression par rapport à l'environnement (P > Pext), il subira une expansion qui diminuera sa densité ; sa pression d'équilibre (donnée par la courbe rouge) augmentera alors, et l'expansion se poursuivra jusqu'à ce qu'il passe sur la branche gauche de la courbe et atteigne un équilibre stable, de plus faible densité et de plus haute température, au point 1. On voit que dès que la pression ambiante dépasse environ 3000 K cm-3, le gaz passera rapidement du Milieu tiède (branche stable de gauche) au Milieu atomique HI plus dense à 100 K (branche stable de droite) via cette instabilité thermique. Ce changement de phase initie le début du cycle de condensation du MIS (voir
, sa pression interne va encore diminuer : il continuera donc d'être comprimé et à se densifier jusqu'à atteindre un nouvel équilibre (stable) au point 3 où P = Pext. De même s'il est en légère surpression par rapport à l'environnement (P > Pext), il subira une expansion qui diminuera sa densité ; sa pression d'équilibre (donnée par la courbe rouge) augmentera alors, et l'expansion se poursuivra jusqu'à ce qu'il passe sur la branche gauche de la courbe et atteigne un équilibre stable, de plus faible densité et de plus haute température, au point 1. On voit que dès que la pression ambiante dépasse environ 3000 K cm-3, le gaz passera rapidement du Milieu tiède (branche stable de gauche) au Milieu atomique HI plus dense à 100 K (branche stable de droite) via cette instabilité thermique. Ce changement de phase initie le début du cycle de condensation du MIS (voir 
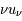
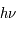 =12.4 eV. L'intégration du spectre UV de Habing de 6 à 13 eV donne une densité d'énergie
=12.4 eV. L'intégration du spectre UV de Habing de 6 à 13 eV donne une densité d'énergie 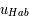 (6-13eV)
(6-13eV)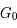 qui est défini comme le rapport de la densité de rayonnement de 6 à 13 eV à celle de Habing :
qui est défini comme le rapport de la densité de rayonnement de 6 à 13 eV à celle de Habing : 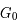 =
=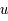 (6-13eV)/
(6-13eV)/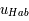 (6-13eV). Des estimations récentes donnent pour le champ de rayonnement interstellaire moyen la valeur
(6-13eV). Des estimations récentes donnent pour le champ de rayonnement interstellaire moyen la valeur 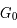 =1.7. Dans des régions de photodissociation typiques comme la nébuleuse de la Tête de Cheval on trouve
=1.7. Dans des régions de photodissociation typiques comme la nébuleuse de la Tête de Cheval on trouve 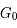 =100, alors que des valeurs de
=100, alors que des valeurs de 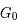 =104-105 sont atteintes au sein des régions de formation stellaire.
=104-105 sont atteintes au sein des régions de formation stellaire.


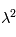 et au produit de la densité électronique et de la composante longitudinale du champ, intégré le long de la ligne de visée vers la source. Par des mesures d’angle à plusieurs longueurs d’onde, on obtient ce produit (appelé « mesure de rotation » ou RM). D’autre part, l’intégrale de la densité électronique seule peut aussi être mesurée grâce à son effet dispersif sur le signal des pulsars : les ondes de différentes fréquences ne se propagent plus exactement à la même vitesse, ce qui produit un décalage du temps d’arrivée de l’impulsion en fonction de la fréquence. De ces 2 mesures on peut alors déduire la valeur du champ longitudinal moyen sur la ligne de visée.
et au produit de la densité électronique et de la composante longitudinale du champ, intégré le long de la ligne de visée vers la source. Par des mesures d’angle à plusieurs longueurs d’onde, on obtient ce produit (appelé « mesure de rotation » ou RM). D’autre part, l’intégrale de la densité électronique seule peut aussi être mesurée grâce à son effet dispersif sur le signal des pulsars : les ondes de différentes fréquences ne se propagent plus exactement à la même vitesse, ce qui produit un décalage du temps d’arrivée de l’impulsion en fonction de la fréquence. De ces 2 mesures on peut alors déduire la valeur du champ longitudinal moyen sur la ligne de visée.



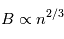 . Cette pente de 2/3 diffère de la pente 1/2 des études précédentes, où la statistique était plus limitée. Elle suggère que la gravité domine la pression magnétique lors de la formation des coeurs denses dans les nuages moléculaires. Cela est cohérent avec les valeurs de B mesurées qui, après correction statistique des effets de projection, restent inférieures en moyenne d’un facteur 2 à la valeur critique nécessaire pour contrecarrer l' autogravité,
. Cette pente de 2/3 diffère de la pente 1/2 des études précédentes, où la statistique était plus limitée. Elle suggère que la gravité domine la pression magnétique lors de la formation des coeurs denses dans les nuages moléculaires. Cela est cohérent avec les valeurs de B mesurées qui, après correction statistique des effets de projection, restent inférieures en moyenne d’un facteur 2 à la valeur critique nécessaire pour contrecarrer l' autogravité, 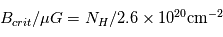 . Cependant une large dispersion est observée d'un nuage à l'autre.
. Cependant une large dispersion est observée d'un nuage à l'autre.



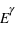 , avec l'indice
, avec l'indice 


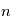 (il prend des valeurs entières) du niveau selon la relation:
(il prend des valeurs entières) du niveau selon la relation: 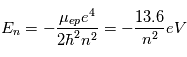 , où
, où 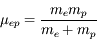 est la masse réduite du système électron-proton. Le niveau fondamental d'énergie minimale,
est la masse réduite du système électron-proton. Le niveau fondamental d'énergie minimale, 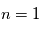 , est situé à une énergie de -13.6 eV sous la limite d'ionisation
, est situé à une énergie de -13.6 eV sous la limite d'ionisation 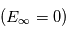 . Lorsque
. Lorsque 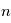 augmente, l'énergie du niveau est de moins en moins négative : elle augmente. Le niveau
augmente, l'énergie du niveau est de moins en moins négative : elle augmente. Le niveau 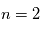 est ainsi situé à -3.4 eV sous la limite d'ionisation
est ainsi situé à -3.4 eV sous la limite d'ionisation 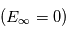 , c'est-à-dire à +10.2 eV au dessus du fondamental. Afin de minimiser l'énergie du système, les électrons sur des orbites excitées vont se désexciter radiativement spontanément vers des niveaux de valeur de
, c'est-à-dire à +10.2 eV au dessus du fondamental. Afin de minimiser l'énergie du système, les électrons sur des orbites excitées vont se désexciter radiativement spontanément vers des niveaux de valeur de 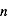 plus faible. Les cascades radiatives des niveaux supérieurs vers le niveau
plus faible. Les cascades radiatives des niveaux supérieurs vers le niveau 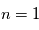 produisent un ensemble de raies spectrales dans l'ultraviolet dénommé Série de Lyman, celles vers le niveau
produisent un ensemble de raies spectrales dans l'ultraviolet dénommé Série de Lyman, celles vers le niveau 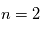 créent des raies dans le visible correspondant à la Série de Balmer. Enfin, les cascades vers les niveaus
créent des raies dans le visible correspondant à la Série de Balmer. Enfin, les cascades vers les niveaus 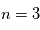 , 4 et 5 donnent les Séries de Paschen, Bracket et Pfund dans l'infrarouge (voir Figure ci-dessous). Ces cascades se produisent lorsqu'un proton et un électron se recombinent pour reformer un atome neutre, car la recombinaison se fait en général sur un état excité. Ces raies dites "de recombinaison" sont donc une signature de régions où l'hydrogène subit une certaine ionisation (par rayonnement ou par collisions).
, 4 et 5 donnent les Séries de Paschen, Bracket et Pfund dans l'infrarouge (voir Figure ci-dessous). Ces cascades se produisent lorsqu'un proton et un électron se recombinent pour reformer un atome neutre, car la recombinaison se fait en général sur un état excité. Ces raies dites "de recombinaison" sont donc une signature de régions où l'hydrogène subit une certaine ionisation (par rayonnement ou par collisions).

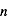 est constitué de
est constitué de 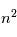 sous-niveaux d'énergie identique. Chaque sous-niveau est caractérisé par un nombre quantique
sous-niveaux d'énergie identique. Chaque sous-niveau est caractérisé par un nombre quantique 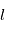 , qui correspond dans le cas classique à l'amplitude du moment orbital angulaire de l'électron, et par un nombre quantique
, qui correspond dans le cas classique à l'amplitude du moment orbital angulaire de l'électron, et par un nombre quantique 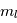 qui équivaut à la projection du moment angulaire orbital sur l'axe de rotation.
qui équivaut à la projection du moment angulaire orbital sur l'axe de rotation. 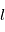 ne peut prendre que les valeurs entières entre 0 et
ne peut prendre que les valeurs entières entre 0 et 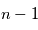 , et
, et 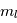 celles entre
celles entre 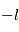 et
et 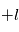 (on dit que le moment orbital est quantifié). L'électron possède aussi un moment cinétique intrinsèque qui n'a pas d'équivalent classique, le spin, lui aussi quantifié comme le moment angulaire orbital. L'interaction dite de structure fine entre le moment orbital
(on dit que le moment orbital est quantifié). L'électron possède aussi un moment cinétique intrinsèque qui n'a pas d'équivalent classique, le spin, lui aussi quantifié comme le moment angulaire orbital. L'interaction dite de structure fine entre le moment orbital 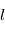 de l'électron et son spin induit la levée de dégénérescence des
de l'électron et son spin induit la levée de dégénérescence des 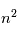 niveaux qui prennent alors des énergies faiblement différentes. Cette décomposition disparaît quand
niveaux qui prennent alors des énergies faiblement différentes. Cette décomposition disparaît quand 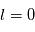 . Le proton possède également un moment cinétique de spin qui se combine avec le spin de l'électron en produisant une sous-structure encore plus fine des niveaux, dite hyperfine. En équivalent classique, l'énergie de l'atome dépend de si le spin de l'électron et du proton sont parallèles (configuration ortho) ou antiparallèles (configuration para).
. Le proton possède également un moment cinétique de spin qui se combine avec le spin de l'électron en produisant une sous-structure encore plus fine des niveaux, dite hyperfine. En équivalent classique, l'énergie de l'atome dépend de si le spin de l'électron et du proton sont parallèles (configuration ortho) ou antiparallèles (configuration para).
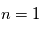 de l'hydrogène est peuplé, où
de l'hydrogène est peuplé, où 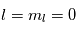 . Il n'y a donc pas de raie de structure fine, seulement une raie de structure hyperfine : la raie à 21 cm dont nous parlons plus en détail ci-dessous.
. Il n'y a donc pas de raie de structure fine, seulement une raie de structure hyperfine : la raie à 21 cm dont nous parlons plus en détail ci-dessous.
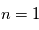 de l'hydrogène atomique, où se trouve la plupart de l'hydrogène dans le MIS atomique froid. La transition se produit lorsque l'électron renverse son spin : le sous-niveau supérieur correspond à la configuration où le spin de l'électron est parallèle à celui du noyau (spin total S =1), et le sous-niveau inférieur à celle où le spin est antiparallèle (S=0). Le taux de désexcitation radiative spontanée (voir la page
de l'hydrogène atomique, où se trouve la plupart de l'hydrogène dans le MIS atomique froid. La transition se produit lorsque l'électron renverse son spin : le sous-niveau supérieur correspond à la configuration où le spin de l'électron est parallèle à celui du noyau (spin total S =1), et le sous-niveau inférieur à celle où le spin est antiparallèle (S=0). Le taux de désexcitation radiative spontanée (voir la page 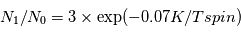 . Chaque dépeuplement par émission spontanée produit un photon à 21 cm. L'intensité du signal radio observé est proportionnelle à la densité de colonne du gaz (nombre d'atomes par unité de surface le long de la ligne de visée). L'étude de l'émission de la raie à 21 cm et des variations spatiales de son intensité a donc permis la détermination de la masse et de la distribution du gaz atomique froid dans notre Galaxie et des galaxies extérieures. La raie à 21 cm peut être observée également en absorption lorsque un nuage d'hydrogène froid est situé sur la même ligne de visée qu'une source puissante de rayonnement radio continu (un pulsar ou une galaxie radio). Une combinaison de mesures en émission et absorption permet de déterminer à la fois la température et la densité de colonne du gaz atomique (voir les détails dans la page
. Chaque dépeuplement par émission spontanée produit un photon à 21 cm. L'intensité du signal radio observé est proportionnelle à la densité de colonne du gaz (nombre d'atomes par unité de surface le long de la ligne de visée). L'étude de l'émission de la raie à 21 cm et des variations spatiales de son intensité a donc permis la détermination de la masse et de la distribution du gaz atomique froid dans notre Galaxie et des galaxies extérieures. La raie à 21 cm peut être observée également en absorption lorsque un nuage d'hydrogène froid est situé sur la même ligne de visée qu'une source puissante de rayonnement radio continu (un pulsar ou une galaxie radio). Une combinaison de mesures en émission et absorption permet de déterminer à la fois la température et la densité de colonne du gaz atomique (voir les détails dans la page 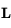 de tous les électrons de l'atome et leur spin total
de tous les électrons de l'atome et leur spin total 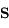 . Le moment angulaire total du système atomique est la somme vectorielle de ces deux moments cinétiques :
. Le moment angulaire total du système atomique est la somme vectorielle de ces deux moments cinétiques : 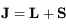 et les transitions dipolaires électriques sont soumises aux règles de sélection :
et les transitions dipolaires électriques sont soumises aux règles de sélection : 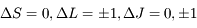 . Les transitions entre les sous-niveaux de structure fine sont dites "interdites" car elles transgressent ces règles de sélection. Elles ont en conséquence un coefficient d'Einstein faible, mais non nul car la transition dipolaire magnétique reste autorisée. Le niveau supérieur est souvent proche du fondamental, ce qui leur donne une grande importance pour la physique du milieu interstellaire : La raie de [CII]
. Les transitions entre les sous-niveaux de structure fine sont dites "interdites" car elles transgressent ces règles de sélection. Elles ont en conséquence un coefficient d'Einstein faible, mais non nul car la transition dipolaire magnétique reste autorisée. Le niveau supérieur est souvent proche du fondamental, ce qui leur donne une grande importance pour la physique du milieu interstellaire : La raie de [CII]

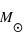 , densité
, densité 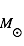 , des filaments, ainsi que des coeurs denses de taille ~ 0.1 pc, densité > 104 cm-3, et masse ~ 0.1-10
, des filaments, ainsi que des coeurs denses de taille ~ 0.1 pc, densité > 104 cm-3, et masse ~ 0.1-10 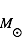 qui approchent de l'instabilité gravitationnelle (leur turbulence est subsonique) et sont le site de formation des étoiles. La structure spatiale filamentaire et la cinématique complexe de ces nuages sont illustrées ci-dessous dans le cas du nuage du Taureau.
qui approchent de l'instabilité gravitationnelle (leur turbulence est subsonique) et sont le site de formation des étoiles. La structure spatiale filamentaire et la cinématique complexe de ces nuages sont illustrées ci-dessous dans le cas du nuage du Taureau.


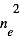 sur la ligne de visée.
sur la ligne de visée. 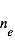 et
et 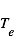 . L'atome est ensuite ionisé à nouveau par un photon UV, et le phénomène se reproduit. On peut donc déduire du flux de ces raies le flux de photons UV ionisants (si on connaît la température, qui affecte le taux de recombinaison). Les raies de recombinaison les plus importantes sont celles de l'hydrogène, en particulier la raie Hα de la série de Balmer dans l'optique (voir la page
. L'atome est ensuite ionisé à nouveau par un photon UV, et le phénomène se reproduit. On peut donc déduire du flux de ces raies le flux de photons UV ionisants (si on connaît la température, qui affecte le taux de recombinaison). Les raies de recombinaison les plus importantes sont celles de l'hydrogène, en particulier la raie Hα de la série de Balmer dans l'optique (voir la page  environ). Elles permettent de déduire la température du gaz à partir du rapport raie/continuum, de mesurer précisément la vitesse de la source (ce qui aide a déterminer sa distance), et de sonder les régions HII trop jeunes et enfouies pour être détectables en H
environ). Elles permettent de déduire la température du gaz à partir du rapport raie/continuum, de mesurer précisément la vitesse de la source (ce qui aide a déterminer sa distance), et de sonder les régions HII trop jeunes et enfouies pour être détectables en H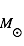 ). On pense que cette composante diffuse provient des fuites de gaz ionisé hors des régions HII par effet "champagne" (surpression) et de l'ionisation du milieu atomique diffus par des étoiles OB isolées. Au dessus du plan Galactique, la dissipation de la turbulence du plasma pourrait contribuer à son chauffage.
). On pense que cette composante diffuse provient des fuites de gaz ionisé hors des régions HII par effet "champagne" (surpression) et de l'ionisation du milieu atomique diffus par des étoiles OB isolées. Au dessus du plan Galactique, la dissipation de la turbulence du plasma pourrait contribuer à son chauffage.



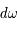 , dans un intervalle de fréquence de
, dans un intervalle de fréquence de 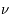 à
à 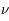 +
+ 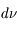 et traversant une surface
et traversant une surface 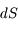 perpendiculaire à sa direction de propagation. L'énergie de ce rayonnement qui passe à travers la surface pendant le temps
perpendiculaire à sa direction de propagation. L'énergie de ce rayonnement qui passe à travers la surface pendant le temps 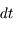 est :
est :
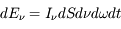 .
Le coefficient de proportionnalité
.
Le coefficient de proportionnalité 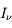 dans cette expression est appelé intensité spécifique et représente donc l'énergie par unité de surface, par unité de fréquence, par unité d'angle solide et par unité de temps, qui traverse une surface perpendiculaire au faisceau de rayonnement. L'intensité spécifique s'exprime en erg cm-2 Hz-1 sr-1 s-1 dans le système CGS.
Si la direction du rayonnement, centrée sur l'angle solide
dans cette expression est appelé intensité spécifique et représente donc l'énergie par unité de surface, par unité de fréquence, par unité d'angle solide et par unité de temps, qui traverse une surface perpendiculaire au faisceau de rayonnement. L'intensité spécifique s'exprime en erg cm-2 Hz-1 sr-1 s-1 dans le système CGS.
Si la direction du rayonnement, centrée sur l'angle solide 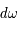 , fait un angle
, fait un angle 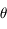 avec la normale à
avec la normale à 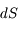 (voir la figure), la surface efficace perpendiculaire au faisceau vaut
(voir la figure), la surface efficace perpendiculaire au faisceau vaut 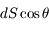 et l'énergie s'écrit alors :
et l'énergie s'écrit alors : 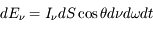 .
.

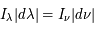 . Puisque
. Puisque 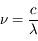 , on en déduit que
, on en déduit que 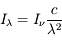 avec
avec 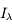 en erg cm-2
en erg cm-2 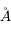 -1 sr-1 s-1. L'intensité spécifique est une quantité fondamentale dont dérivent les autres grandeurs physiques qui caractérisent le rayonnement, comme la densité d'énergie monochromatique
-1 sr-1 s-1. L'intensité spécifique est une quantité fondamentale dont dérivent les autres grandeurs physiques qui caractérisent le rayonnement, comme la densité d'énergie monochromatique 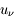 par unité de volume et par unité d'intervalle de fréquence,
par unité de volume et par unité d'intervalle de fréquence, 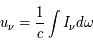 , ou le flux net
, ou le flux net 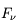 , c'est-à-dire le flux d'énergie par unité de surface, de fréquence et de temps,
, c'est-à-dire le flux d'énergie par unité de surface, de fréquence et de temps, 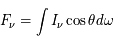 .
.
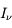 traverse une épaisseur
traverse une épaisseur 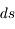 de matière, il subit une atténuation
de matière, il subit une atténuation 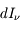 proportionnelle à
proportionnelle à 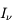 telle que :
telle que :
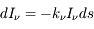 . La quantité
. La quantité 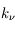 est appelée coefficient d'extinction et inclut à la fois les processus d'absorption et de diffusion. On peut donc l'exprimer comme la somme d'un coefficient d'absorption
est appelée coefficient d'extinction et inclut à la fois les processus d'absorption et de diffusion. On peut donc l'exprimer comme la somme d'un coefficient d'absorption 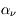 et d'un coefficient de diffusion
et d'un coefficient de diffusion 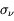 :
: 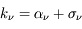 . L'absorption résulte de divers processus physiques intervenant dans le milieu qui impliquent des changements des degrés de liberté internes d'un atome ou d'une molécule. Des exemples de ces processus sont :
. L'absorption résulte de divers processus physiques intervenant dans le milieu qui impliquent des changements des degrés de liberté internes d'un atome ou d'une molécule. Des exemples de ces processus sont :
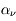 dépend de l'état thermodynamique de la matière traversée (pression, température, abondances chimiques) en un point donné du milieu. Le faisceau peut perdre de l'énergie également à cause du processus de diffusion, qui change à la fois la direction et l'énergie des photons. Cette énergie, contrairement au processus d'absorption, n'est pas transformée en énergie cinétique du milieu. Les variations locales d'énergie associées au processus de diffusion dépendent donc principalement du champ de rayonnement et faiblement des propriétés thermodynamiques locales du milieu.
dépend de l'état thermodynamique de la matière traversée (pression, température, abondances chimiques) en un point donné du milieu. Le faisceau peut perdre de l'énergie également à cause du processus de diffusion, qui change à la fois la direction et l'énergie des photons. Cette énergie, contrairement au processus d'absorption, n'est pas transformée en énergie cinétique du milieu. Les variations locales d'énergie associées au processus de diffusion dépendent donc principalement du champ de rayonnement et faiblement des propriétés thermodynamiques locales du milieu.
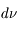 à
à 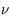 +
+ 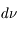 :
: 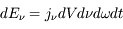 . Il s'exprime en erg cm-3 Hz-1 sr-1 s-1. En parcourant une distance
. Il s'exprime en erg cm-3 Hz-1 sr-1 s-1. En parcourant une distance 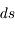 , un faisceau de rayonnement de section efficace
, un faisceau de rayonnement de section efficace 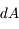 traverse un volume
traverse un volume 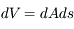 . On en déduit que l'intensité ajoutée au faisceau par l'émission est
. On en déduit que l'intensité ajoutée au faisceau par l'émission est 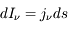 . L'émission résulte de la combinaison des processus physiques inverses à ceux qui provoquent l'absorption. Ces processus sont :
. L'émission résulte de la combinaison des processus physiques inverses à ceux qui provoquent l'absorption. Ces processus sont :
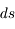 et surface
et surface 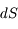 = 1 perpendiculaire à la direction de propagation
= 1 perpendiculaire à la direction de propagation 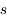 . En utilisant les définitions des coefficients d'absorption et d'émission données à la page
. En utilisant les définitions des coefficients d'absorption et d'émission données à la page 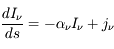 .
.
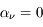 et l'équation de transfert devient :
et l'équation de transfert devient : 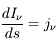 qui admet la solution
qui admet la solution 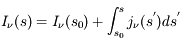 . Cela signifie que l'augmentation de l'intensité spécifique entre la position initiale
. Cela signifie que l'augmentation de l'intensité spécifique entre la position initiale 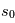 et le point final
et le point final 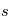 est égale au coefficient d'émission intégré le long de cette "ligne de visée" à travers la couche de matière.
est égale au coefficient d'émission intégré le long de cette "ligne de visée" à travers la couche de matière.
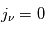 ) on obtient :
) on obtient : 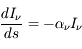 , dont la solution est
, dont la solution est 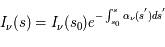 . L'intensité spécifique au point final
. L'intensité spécifique au point final 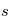 est égale à l'intensité spécifique au point initial
est égale à l'intensité spécifique au point initial 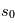 , atténuée par un facteur exponentiel dont l'argument est l'intégrale du coefficient d'absorption le long de la ligne de visée entre
, atténuée par un facteur exponentiel dont l'argument est l'intégrale du coefficient d'absorption le long de la ligne de visée entre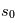 et
et 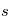 . Cette intégrale est un nombre sans dimension appelé la profondeur optique du milieu:
. Cette intégrale est un nombre sans dimension appelé la profondeur optique du milieu:
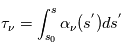 .
.
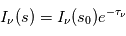 . On voit ainsi que la profondeur optique détermine la fraction de l'intensité incidente qui peut s'échapper du milieu. Afin de mieux comprendre le concept de profondeur optique, on introduit le libre parcours moyen du rayonnement qui représente la distance moyenne qu'un photon parcourt à travers un milieu sans être absorbé. Le coefficient
. On voit ainsi que la profondeur optique détermine la fraction de l'intensité incidente qui peut s'échapper du milieu. Afin de mieux comprendre le concept de profondeur optique, on introduit le libre parcours moyen du rayonnement qui représente la distance moyenne qu'un photon parcourt à travers un milieu sans être absorbé. Le coefficient  est l'inverse de ce libre parcours moyen, pour un photon de fréquence
est l'inverse de ce libre parcours moyen, pour un photon de fréquence  . La profondeur optique
. La profondeur optique 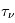 est donc égale au nombre total de libres parcours moyens traversés entre
est donc égale au nombre total de libres parcours moyens traversés entre  et
et 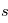 . Si la distance à travers le nuage est égale au libre parcours moyen (
. Si la distance à travers le nuage est égale au libre parcours moyen (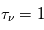 ), l'intensité subit une atténuation d'un facteur e-1 =0.368, ie. en moyenne seulement 36.8% des photons incidents sortiront du nuage. Si la distance parcourue équivaut à deux fois le libre parcours moyen (
), l'intensité subit une atténuation d'un facteur e-1 =0.368, ie. en moyenne seulement 36.8% des photons incidents sortiront du nuage. Si la distance parcourue équivaut à deux fois le libre parcours moyen (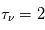 ), seulement 13.5% (e-2 =0.135) des photons incidents survivront en traversant le nuage. Pour cette raison, un milieu caractérisé par une profondeur optique
), seulement 13.5% (e-2 =0.135) des photons incidents survivront en traversant le nuage. Pour cette raison, un milieu caractérisé par une profondeur optique 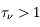 est dit optiquement épais ou opaque, alors qu'un milieu avec
est dit optiquement épais ou opaque, alors qu'un milieu avec 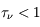 est dit optiquement mince ou transparent.
est dit optiquement mince ou transparent.
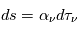 et en définissant la quantité
et en définissant la quantité 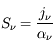 (appelée fonction source) ; l'équation prend la forme :
(appelée fonction source) ; l'équation prend la forme :
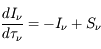 .
.
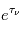 et posé
et posé 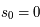 ) on obtient la solution formelle :
) on obtient la solution formelle :
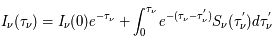 .
.
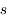 . Le second terme décrit l'émission dérivant de toutes les couches
. Le second terme décrit l'émission dérivant de toutes les couches 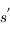 (car
(car 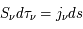 ) dont la contribution est atténuée par la profondeur optique
) dont la contribution est atténuée par la profondeur optique 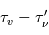 entre le point d'émission
entre le point d'émission 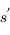 et le points
et le points 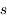 où l'on calcule l'intensité.
où l'on calcule l'intensité.
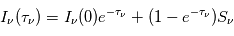 .
.
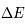 . Nous nous intéressons aux transitions radiatives entres ces deux états. Comme nous verrons en détail dans la suite du cours ces transitions ne se produisent pas uniquement à la fréquence
. Nous nous intéressons aux transitions radiatives entres ces deux états. Comme nous verrons en détail dans la suite du cours ces transitions ne se produisent pas uniquement à la fréquence 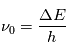 mais également aux fréquences voisines de
mais également aux fréquences voisines de 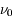 . Par conséquent les raies spectrales associées à ces transitions sont caractérisées par un profil de raie
. Par conséquent les raies spectrales associées à ces transitions sont caractérisées par un profil de raie 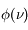 , piqué à la fréquence
, piqué à la fréquence 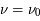 , qui décrit l'efficacité des fréquences voisines de
, qui décrit l'efficacité des fréquences voisines de 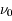 à induire ces transitions. L'agitation thermique du gaz (mouvement brownien) produit par exemple un élargissement du profil par effet Doppler, car un atome en mouvement peut absorber un photon de fréquence légèrement différente de
à induire ces transitions. L'agitation thermique du gaz (mouvement brownien) produit par exemple un élargissement du profil par effet Doppler, car un atome en mouvement peut absorber un photon de fréquence légèrement différente de 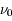 . La largeur du profil est alors de l'ordre de
. La largeur du profil est alors de l'ordre de 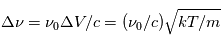 . Dans la suite on fera l'hypothèse que la forme de la raie est la même en absorption et en émission. Les 3 processus de transitions radiatives quantifiés par Einstein sont les suivants :
. Dans la suite on fera l'hypothèse que la forme de la raie est la même en absorption et en émission. Les 3 processus de transitions radiatives quantifiés par Einstein sont les suivants :
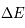 . Cette transition se produit même en l'absence d'un champ de rayonnement. Elle est caractérisée par le coefficient d'Einstein
. Cette transition se produit même en l'absence d'un champ de rayonnement. Elle est caractérisée par le coefficient d'Einstein 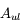 , qui représente une probabilité de transition par unité de temps et est exprimé en s-1. Ce coefficient ne dépend que des termes de couplages électro-magnétique entre les 2 niveaux quantiques u et l.
, qui représente une probabilité de transition par unité de temps et est exprimé en s-1. Ce coefficient ne dépend que des termes de couplages électro-magnétique entre les 2 niveaux quantiques u et l. 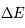 , faisant passer les atomes du niveaux l au niveau u. Elle est caractérisée par une probabilité de transition par unité de temps
, faisant passer les atomes du niveaux l au niveau u. Elle est caractérisée par une probabilité de transition par unité de temps 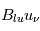 , où
, où 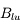 est le coefficient d'absorption d'Einstein et
est le coefficient d'absorption d'Einstein et 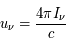 est la densité d'énergie monochromatique à la fréquence
est la densité d'énergie monochromatique à la fréquence 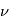 pour un champ de rayonnement isotrope.
pour un champ de rayonnement isotrope. 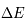 et passe de l'état u à l'état l en emettant un deuxième photon identique à celui qu'il a absorbé. Ce processus est caractérisé par une probabilité par unité de temps
et passe de l'état u à l'état l en emettant un deuxième photon identique à celui qu'il a absorbé. Ce processus est caractérisé par une probabilité par unité de temps 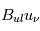 .
. 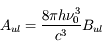 et
et
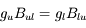 .
.
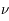 (contenue dans le profil de la raie) qui arrive sur une tranche du milieu avec une intensité spécifique
(contenue dans le profil de la raie) qui arrive sur une tranche du milieu avec une intensité spécifique 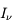 par unité de surface, de fréquence, et d'angle solide. Le long de la distance
par unité de surface, de fréquence, et d'angle solide. Le long de la distance 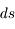 dans sa direction de propagation, l'intensité sera augmentée à la fois par l'émission spontanée et par l'émission stimulée des atomes dans l'état u ; simultanément elle sera diminuée par l'absorption de photons par les atomes dans l'état l. Considérons d'abord le cas de l'émission spontanée : le nombre total d'atomes dans l'état u rencontré par unité de surface est
dans sa direction de propagation, l'intensité sera augmentée à la fois par l'émission spontanée et par l'émission stimulée des atomes dans l'état u ; simultanément elle sera diminuée par l'absorption de photons par les atomes dans l'état l. Considérons d'abord le cas de l'émission spontanée : le nombre total d'atomes dans l'état u rencontré par unité de surface est 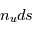 . L'augmentation d'intensité à la fréquence
. L'augmentation d'intensité à la fréquence 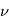 causée par ce processus est obtenue en multipliant
causée par ce processus est obtenue en multipliant 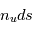 par le coefficient d'Einstein correspondant
par le coefficient d'Einstein correspondant 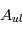 divisé par
divisé par 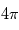 (car chaque photon est supposé émis ou absorbé de façon isotrope et nous regardons la variation par unité d'angle solide), par le profil de la raie
(car chaque photon est supposé émis ou absorbé de façon isotrope et nous regardons la variation par unité d'angle solide), par le profil de la raie 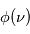 , et enfin par l'énergie de chaque photon (
, et enfin par l'énergie de chaque photon (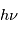 ) ; en appliquant le même raisonnement à l'émission et absorption stimulées, le bilan de ces transition radiatives donne l'équation de transfert :
) ; en appliquant le même raisonnement à l'émission et absorption stimulées, le bilan de ces transition radiatives donne l'équation de transfert :
![\frac{dI_\nu}{ds} = \frac{h\nu }{4\pi} \phi(\nu) [n_u A_{ul} +(n_u B_{ul} - n_l B_{lu})\frac{4\pi I_\nu}{c}]](../pages_transfert-rayon/equations_transfert-rayon/equation110.png) .
.
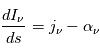 , présentée dans la section
, présentée dans la section 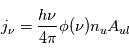
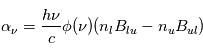
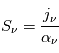
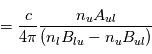 .
.
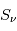 ne dépend pas de
ne dépend pas de 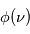 , mais uniquement des coefficients d'Einstein et des populations des niveaux impliqués. Plus précisément elle ne dépend que du rapport entre ces populations . En effet, en utilisant les relations entre coefficients d'Einstein données ci-dessus, on obtient :
, mais uniquement des coefficients d'Einstein et des populations des niveaux impliqués. Plus précisément elle ne dépend que du rapport entre ces populations . En effet, en utilisant les relations entre coefficients d'Einstein données ci-dessus, on obtient :
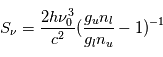 , où
, où 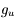 et
et 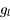 sont les poids statistiques (dégénérescences) de chaque niveau.
sont les poids statistiques (dégénérescences) de chaque niveau.
![\alpha_\nu=\frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-\frac{n_ug_l}{n_lg_u}]](../pages_transfert-rayon/equations_transfert-rayon/equation121.png) .
.
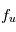 et
et 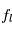 les fractions
les fractions 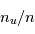 et
et  d'atomes qui sont dans les niveaux u et l, on remarque qu'
d'atomes qui sont dans les niveaux u et l, on remarque qu'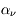 est proportionnel à la densité volumique totale des atomes,
est proportionnel à la densité volumique totale des atomes, 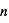 , et à une fonction qui ne dépend que de
, et à une fonction qui ne dépend que de 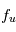 et
et 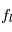 , c'est-à-dire à la répartition statistique des atomes entre leurs différents niveaux d'énergie. Il en découle que la profondeur optique, obtenue en intégrant cette quantité le long de la ligne de visée, sera proportionnelle à
, c'est-à-dire à la répartition statistique des atomes entre leurs différents niveaux d'énergie. Il en découle que la profondeur optique, obtenue en intégrant cette quantité le long de la ligne de visée, sera proportionnelle à 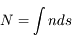 que l'on appelle la densité de colonne des atomes (en unité d'atomes par cm-2), c'est-à-dire le nombre d'atomes dans un cylindre de section unité le long de la ligne de visée. C'est par ce biais que l'observation des raies spectrales pourra nous donner accès à la masse de gaz émetteur --- à condition que l'on puisse connaître (ou estimer) les fractions
que l'on appelle la densité de colonne des atomes (en unité d'atomes par cm-2), c'est-à-dire le nombre d'atomes dans un cylindre de section unité le long de la ligne de visée. C'est par ce biais que l'observation des raies spectrales pourra nous donner accès à la masse de gaz émetteur --- à condition que l'on puisse connaître (ou estimer) les fractions 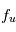 et
et 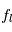 d'atomes peuplant les niveaux u et l, ou en d'autres termes les "conditions d'excitation" de la transition.
d'atomes peuplant les niveaux u et l, ou en d'autres termes les "conditions d'excitation" de la transition.
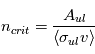
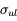 est la section efficace de désexcitation collisionnelle, qui dépend en général de la vitesse
est la section efficace de désexcitation collisionnelle, qui dépend en général de la vitesse 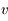 du collisionneur. Les crochets signifient qu'on prend la moyenne sur toute la distribution statistique des vitesses
du collisionneur. Les crochets signifient qu'on prend la moyenne sur toute la distribution statistique des vitesses 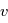 (distribution Boltzmanienne) ce qui donne une valeur dépendant de la température du gaz.
(distribution Boltzmanienne) ce qui donne une valeur dépendant de la température du gaz.
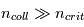 , les transitions radiatives sont négligeables devant les transitions collisionnelles et on atteint l'équilibre thermodynamique local (ou ETL),
où les populations relatives des niveaux des atomes (ou molécules) ne dépendent ni de
, les transitions radiatives sont négligeables devant les transitions collisionnelles et on atteint l'équilibre thermodynamique local (ou ETL),
où les populations relatives des niveaux des atomes (ou molécules) ne dépendent ni de 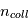 ni du champ de rayonnement et obéissent simplement à la loi de Boltzmann :
ni du champ de rayonnement et obéissent simplement à la loi de Boltzmann :
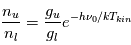
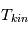 est la température cinétique des collisionneurs, qui caractérise la distribution de vitesse des particules,
est la température cinétique des collisionneurs, qui caractérise la distribution de vitesse des particules, 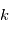 la constante de Boltzmann,
la constante de Boltzmann, 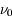 est la fréquence de la transition entre les états u et l,
est la fréquence de la transition entre les états u et l, 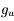 et
et 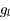 sont les poids statistiques. Plus le coefficient d'Einstein est fort, et plus la densité critique nécessaire pour atteindre l'ETL sera élevée. Cette densité critique est très variable selon les espèces et les transitions considérées : elle est très faible pour la raie hyperfine de l'hydrogène atomique (voir ci-dessous), de l'ordre de 1000 cm-3 pour les premières raies rotationnelles de CO, mais atteint 108 cm-3 pour H2O.
sont les poids statistiques. Plus le coefficient d'Einstein est fort, et plus la densité critique nécessaire pour atteindre l'ETL sera élevée. Cette densité critique est très variable selon les espèces et les transitions considérées : elle est très faible pour la raie hyperfine de l'hydrogène atomique (voir ci-dessous), de l'ordre de 1000 cm-3 pour les premières raies rotationnelles de CO, mais atteint 108 cm-3 pour H2O.
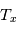 , telle que
, telle que
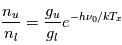 .
.
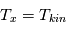 . Dans le cas contraire,
. Dans le cas contraire, 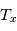 dépend aussi du rapport
dépend aussi du rapport 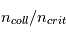 et de l'intensité du champ de rayonnement local, qui peuvent varier fortement d'un point à l'autre. Elle peut être inférieure à
et de l'intensité du champ de rayonnement local, qui peuvent varier fortement d'un point à l'autre. Elle peut être inférieure à 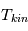 (cas le plus courant dans le MIS) ou bien supérieure si le pompage radiatif est important (par exemple à proximité d'une source de rayonnement intense), voire négative en présence d'un effet maser (inversion de population). En outre, il peut y avoir des températures d'excitation différentes pour différentes transitions d'un même atome.
(cas le plus courant dans le MIS) ou bien supérieure si le pompage radiatif est important (par exemple à proximité d'une source de rayonnement intense), voire négative en présence d'un effet maser (inversion de population). En outre, il peut y avoir des températures d'excitation différentes pour différentes transitions d'un même atome.
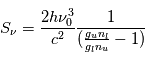
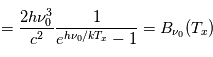 .
.
![\alpha_\nu=\frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-\frac{n_ug_l}{n_lg_u}]](../pages_transfert-rayon/equations_transfert-rayon/equation153.png)
![= \frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-e^{-h\nu_0/kT_x}]](../pages_transfert-rayon/equations_transfert-rayon/equation154.png) .
.
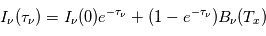 .
.
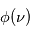 = 0, donc
= 0, donc 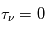 , et
, et 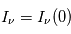 . Ceci définit le niveau du "continuum" que l'on mesure autour de la raie spectrale. Dans ce qui suit nous allons examiner sous quelles conditions la raie apparaîtra en émission ou en absorption par rapport à ce niveau de continu de référence.
. Ceci définit le niveau du "continuum" que l'on mesure autour de la raie spectrale. Dans ce qui suit nous allons examiner sous quelles conditions la raie apparaîtra en émission ou en absorption par rapport à ce niveau de continu de référence.
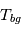 , telle que l'intensité du continu en dehors de la raie s'écrive
, telle que l'intensité du continu en dehors de la raie s'écrive
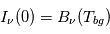 . La solution formelle de l'équation du transfert radiatif devient
. La solution formelle de l'équation du transfert radiatif devient
![I_\nu(\tau_\nu) - I_\nu(0) = (1 - e^{-\tau_\nu} )[B_\nu(T_x) - B_\nu(T_{bg})]](../pages_transfert-rayon/equations_transfert-rayon/equation161.png) .
.
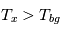 alors le terme de droite est positif et la raie spectrale apparaîtra en émission, avec une intensité supérieure au niveau du continu
alors le terme de droite est positif et la raie spectrale apparaîtra en émission, avec une intensité supérieure au niveau du continu 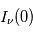 ;
alors que si
;
alors que si 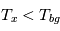 la raie apparaîtra en absorption, avec une intensité qui descend sous le niveau du continu. Enfin dans le cas particulier où
la raie apparaîtra en absorption, avec une intensité qui descend sous le niveau du continu. Enfin dans le cas particulier où 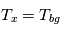 , la raie spectrale se confondra avec le continu et ne sera plus observable en tant que telle. Cette situation ne se rencontre que très rarement dans le MIS.
, la raie spectrale se confondra avec le continu et ne sera plus observable en tant que telle. Cette situation ne se rencontre que très rarement dans le MIS.
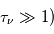 , on obtient
, on obtient 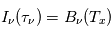 : le rayonnement d'un nuage optiquement épais s'apparente au rayonnement d'un corps noir à la température d'excitation
: le rayonnement d'un nuage optiquement épais s'apparente au rayonnement d'un corps noir à la température d'excitation 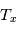 de la transition considérée. Si de plus on est à l'ETL, alors
de la transition considérée. Si de plus on est à l'ETL, alors 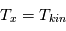 et on peut déduire la température cinétique du gaz à partir de
et on peut déduire la température cinétique du gaz à partir de 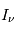 . Cette technique s'applique par exemple à la raie rotationnelle fondamentale de CO à une longueur d'onde de 2.6mm ; elle donne des valeurs typiques de température de 10-20 K dans les nuages moléculaires. Par contre, on voit que dans le cas optiquement épais l'intensité ne dépend plus de
. Cette technique s'applique par exemple à la raie rotationnelle fondamentale de CO à une longueur d'onde de 2.6mm ; elle donne des valeurs typiques de température de 10-20 K dans les nuages moléculaires. Par contre, on voit que dans le cas optiquement épais l'intensité ne dépend plus de  , c'est-à-dire de la quantité de matière traversée ; on dit que la raie est "saturée". Il n'est donc pas possible de déduire la masse de gaz.
, c'est-à-dire de la quantité de matière traversée ; on dit que la raie est "saturée". Il n'est donc pas possible de déduire la masse de gaz.
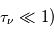 , on obtient
, on obtient ![I_\nu(\tau_\nu) - I_\nu(0) = \tau_\nu [B_\nu(T_x) - B_\nu(T_{bg})]](../pages_transfert-rayon/equations_transfert-rayon/equation173.png) : l'excès d'intensité au-dessus du continu est proportionnel à l'opacité, dont nous avons vu qu'est elle-même proportionnelle à la densité colonne
: l'excès d'intensité au-dessus du continu est proportionnel à l'opacité, dont nous avons vu qu'est elle-même proportionnelle à la densité colonne 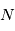 de l'atome considéré, et à une fonction de
de l'atome considéré, et à une fonction de 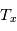 (qui fixe les populations relatives des niveaux). Avec une estimation indépendante de
(qui fixe les populations relatives des niveaux). Avec une estimation indépendante de 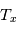 (par ex.
(par ex. 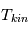 si la raie est à l'ETL), il est donc possible de déduire de ces observations la valeur de
si la raie est à l'ETL), il est donc possible de déduire de ces observations la valeur de 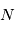 , et ensuite de la masse de gaz si la taille de la région d'émission et l'abondance de l'atome ou molécule sont connues. Cette technique est utilisée par exemple pour mesurer les masses des nuages moléculaires, grâce à des isotopes peu abondants comme 13CO et C18O qui sont (généralement) optiquement minces.
, et ensuite de la masse de gaz si la taille de la région d'émission et l'abondance de l'atome ou molécule sont connues. Cette technique est utilisée par exemple pour mesurer les masses des nuages moléculaires, grâce à des isotopes peu abondants comme 13CO et C18O qui sont (généralement) optiquement minces.
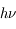 <<
<< 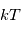 si bien que
si bien que 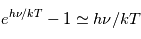 et la fonction de Planck s'écrit :
et la fonction de Planck s'écrit :
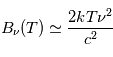 .
.
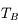 définie par :
définie par :
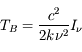 ,
,
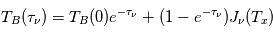 où on a défini la fonction
où on a défini la fonction
 qui tend vers
qui tend vers 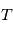 dans la limite de Rayleigh-Jeans.
dans la limite de Rayleigh-Jeans.
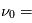 1420 MHz) correspond à une transition hyperfine du niveau fondamental de l'hydrogène atomique, où le photon est émis lorsque le spin de l'électron passe d'un état parallèle (
1420 MHz) correspond à une transition hyperfine du niveau fondamental de l'hydrogène atomique, où le photon est émis lorsque le spin de l'électron passe d'un état parallèle (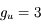 ) à un état antiparallèle (
) à un état antiparallèle (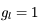 ) au spin du proton. La transition possède un coefficient d'Einstein très faible
) au spin du proton. La transition possède un coefficient d'Einstein très faible 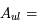 2.85 x 10-15 s-1 (raie "interdite") mais la très grande quantité d'hydrogène le long de la ligne de visée dans la Galaxie la rend cependant parfaitement visible. Du fait de cette très faible valeur d'
2.85 x 10-15 s-1 (raie "interdite") mais la très grande quantité d'hydrogène le long de la ligne de visée dans la Galaxie la rend cependant parfaitement visible. Du fait de cette très faible valeur d'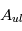 , la densité critique est elle aussi très faible :
, la densité critique est elle aussi très faible : 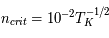 cm-3,
cm-3, 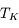 étant la température cinétique du gaz. Dans le milieu atomique neutre du MIS, les températures cinétiques typiques sont de l'ordre de 50-5000 K pour des densités de 30 à 0.1 cm-3 ; On a donc
étant la température cinétique du gaz. Dans le milieu atomique neutre du MIS, les températures cinétiques typiques sont de l'ordre de 50-5000 K pour des densités de 30 à 0.1 cm-3 ; On a donc 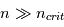 et les niveaux sont à l'équilibre thermodynamique local (ETL), c'est-à-dire
et les niveaux sont à l'équilibre thermodynamique local (ETL), c'est-à-dire 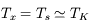 (pour cette raie, la température d'excitation
(pour cette raie, la température d'excitation 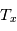 est appelée "température de spin"
est appelée "température de spin" 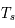 ).
).
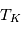 du nuage), la raie à 21 cm peut être observée à la fois en émission et en absorption. La détection est en émission lorsque le nuage est observé sur le fond cosmologique plus froid à 2,7 K, ce qui est la situation la plus courante. La détection est en absorption lorsque le nuage s'interpose sur la la ligne de visée d'une source puissante de rayonnement continu radio synchrotron (quasar lointain) où
du nuage), la raie à 21 cm peut être observée à la fois en émission et en absorption. La détection est en émission lorsque le nuage est observé sur le fond cosmologique plus froid à 2,7 K, ce qui est la situation la plus courante. La détection est en absorption lorsque le nuage s'interpose sur la la ligne de visée d'une source puissante de rayonnement continu radio synchrotron (quasar lointain) où 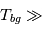 5000 K. Les nuages absorbent alors les photons possédant la bonne énergie pour exciter les électrons du premier niveau hyperfin de l'hydrogène. Ce type d'observation en absorption nécessite un interféromètre pour que le signal vers la source continuum (ponctuelle) ne soit pas complètement "dilué" dans l'émission étendue provenant des lignes de visée adjacentes.
5000 K. Les nuages absorbent alors les photons possédant la bonne énergie pour exciter les électrons du premier niveau hyperfin de l'hydrogène. Ce type d'observation en absorption nécessite un interféromètre pour que le signal vers la source continuum (ponctuelle) ne soit pas complètement "dilué" dans l'émission étendue provenant des lignes de visée adjacentes.
![\alpha_\nu = \frac {c^2 A_{ul}} {8\pi \nu_0^2 } \phi(\nu) n_l\frac{g_u}{g_l}[1-e^{-h\nu_0/kT_x}]](../pages_transfert-rayon/equations_transfert-rayon/equation201.png) .
.
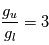 . De plus, à la basse fréquence de cette raie, 1420 MHz, nous sommes toujours dans le domaine
. De plus, à la basse fréquence de cette raie, 1420 MHz, nous sommes toujours dans le domaine 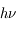 <<
<<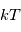 (approximation de Rayleigh-Jeans). Le facteur de Boltzmann
(approximation de Rayleigh-Jeans). Le facteur de Boltzmann 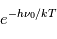 est donc proche de 1 et le rapport entre les populations des 2 sous-niveaux hyperfins à l'ETL vaut
est donc proche de 1 et le rapport entre les populations des 2 sous-niveaux hyperfins à l'ETL vaut 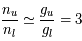 . Le gaz étant beaucoup trop froid pour peupler le premier niveau électronique excité
. Le gaz étant beaucoup trop froid pour peupler le premier niveau électronique excité 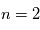 de l'hydrogène, l'essentiel des atomes se trouvent dans l'un de ces deux sous-niveaux hyperfins du niveau fondamental. La densité totale de HI est donc reliée à
de l'hydrogène, l'essentiel des atomes se trouvent dans l'un de ces deux sous-niveaux hyperfins du niveau fondamental. La densité totale de HI est donc reliée à 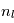 par :
par :
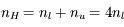 .
.
![[1- e^{-h\nu_0/kT_s}] \simeq h\nu_0 / kT_s](../pages_transfert-rayon/equations_transfert-rayon/equation210.png) au premier ordre. En insérant ces expressions dans l'équation de
au premier ordre. En insérant ces expressions dans l'équation de 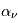 on en déduit :
on en déduit :
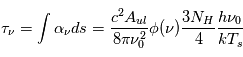 ,
,
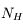 est la densité de colonne de l'hydrogène atomique neutre. On a fait ici l'hypothèse d'un milieu homogène, de sorte que
est la densité de colonne de l'hydrogène atomique neutre. On a fait ici l'hypothèse d'un milieu homogène, de sorte que 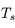 et
et 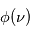 ne dépendent pas de la position
ne dépendent pas de la position  le long de la ligne de visée. On note ainsi que la profondeur optique de la raie à 21 cm est inversement proportionnelle à la température de spin,
le long de la ligne de visée. On note ainsi que la profondeur optique de la raie à 21 cm est inversement proportionnelle à la température de spin,
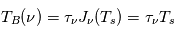 (approximation de Rayleigh-Jeans). Puisque
(approximation de Rayleigh-Jeans). Puisque 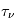 est inversement proportionnel à la température de spin, on voit que
est inversement proportionnel à la température de spin, on voit que 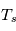 se simplifie dans cette expression et que l'intensité de la raie ne dépend plus de la température mais uniquement de la densité de colonne totale d'hydrogène,
se simplifie dans cette expression et que l'intensité de la raie ne dépend plus de la température mais uniquement de la densité de colonne totale d'hydrogène, 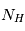 , dont on obtient ainsi une détermination directe. Cette approche est souvent appliquée même dans des cas où l'approximation de raie optiquement mince ne peut pas être vérifiée, et il faut garder à l'esprit que les estimations de la densité de colonne ainsi obtenues sont alors des limites inférieures.
, dont on obtient ainsi une détermination directe. Cette approche est souvent appliquée même dans des cas où l'approximation de raie optiquement mince ne peut pas être vérifiée, et il faut garder à l'esprit que les estimations de la densité de colonne ainsi obtenues sont alors des limites inférieures.
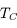 et de la température cinétique du nuage de HI interposé
et de la température cinétique du nuage de HI interposé 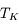 , telle que :
, telle que : 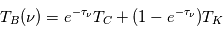 .
.
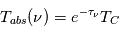 . Le rapport entre la température de brillance dans la raie d'absorption et la température de brillance dans le continu hors de la raie (où
. Le rapport entre la température de brillance dans la raie d'absorption et la température de brillance dans le continu hors de la raie (où 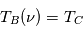 ) permet d'obtenir la valeur de
) permet d'obtenir la valeur de 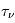 . Mais comme la profondeur optique est proportionnelle à
. Mais comme la profondeur optique est proportionnelle à 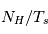 (voir section précédente), il n'est pas possible de dériver la densité de colonne
(voir section précédente), il n'est pas possible de dériver la densité de colonne 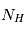 à partir de ces mesures en absorption seules. Il faut une information supplémentaire sur la température du gaz.
à partir de ces mesures en absorption seules. Il faut une information supplémentaire sur la température du gaz.
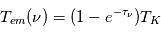 .
.
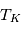 et la profondeur optique
et la profondeur optique 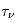 (qu'on suppose identiques entre les 2 régions observées), et d'en déduire ainsi la densité de colonne
(qu'on suppose identiques entre les 2 régions observées), et d'en déduire ainsi la densité de colonne 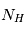 du nuage. Cette méthode est pratiquement la seule qui permet d'obtenir directement la température des nuages interstellaires atomiques.
du nuage. Cette méthode est pratiquement la seule qui permet d'obtenir directement la température des nuages interstellaires atomiques.
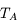 , généralement utilisée par les radioastronomes comme mesure de l'énergie reçue par une antenne radio. Il s'agit de la température du corps noir qui entourerait totalement l'antenne pour donner le signal observé. La puissance captée par l'antenne est alors
, généralement utilisée par les radioastronomes comme mesure de l'énergie reçue par une antenne radio. Il s'agit de la température du corps noir qui entourerait totalement l'antenne pour donner le signal observé. La puissance captée par l'antenne est alors 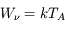 . Si l'antenne était parfaite, une région étendue de brillance uniforme
. Si l'antenne était parfaite, une région étendue de brillance uniforme 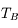 donnerait
donnerait 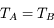 (en général il faut introduire un facteur de rendement). La quantité en abscisse de la figure est la vitesse radiale donnée par la formule de l'effet Doppler
(en général il faut introduire un facteur de rendement). La quantité en abscisse de la figure est la vitesse radiale donnée par la formule de l'effet Doppler 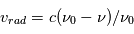 , utilisée d'habitude par les radioastronomes plutôt que la fréquence. La courbe en émission est associée au signal des régions immédiatement adjacentes. En soustrayant cette émission du signal obtenu avec l'antenne pointée sur le quasar on obtient la courbe en absorption. Enfin, la ligne en pointillé est due à une composante tiède pour laquelle l'absorption est plus faible.
, utilisée d'habitude par les radioastronomes plutôt que la fréquence. La courbe en émission est associée au signal des régions immédiatement adjacentes. En soustrayant cette émission du signal obtenu avec l'antenne pointée sur le quasar on obtient la courbe en absorption. Enfin, la ligne en pointillé est due à une composante tiède pour laquelle l'absorption est plus faible.

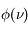 , normalisé et centré sur
, normalisé et centré sur 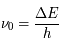 , avec
, avec 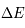 >0 l'écart en énergie entre les niveaux. Dans cette page nous présenterons les différents processus qui causent l'élargissement et analyserons les caractéristiques des profils de raie associés à chacun de ces processus. Nous ne considérons pas les effets associés à la présence de champs électromagnétiques externes (par exemple l'effet Zeeman).
>0 l'écart en énergie entre les niveaux. Dans cette page nous présenterons les différents processus qui causent l'élargissement et analyserons les caractéristiques des profils de raie associés à chacun de ces processus. Nous ne considérons pas les effets associés à la présence de champs électromagnétiques externes (par exemple l'effet Zeeman).
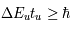 , où
, où 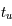 représente la durée de vie du niveau u, telle que
représente la durée de vie du niveau u, telle que 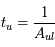 . La largeur de raie naturelle en énergie
. La largeur de raie naturelle en énergie 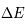 correspond au cas de l'égalité. Elle est proportionnelle au coefficient d'Einstein d'émission spontanée en absence de rayonnement (en présence de rayonnement il faudra considérer ainsi la désexcitation stimulée qui contribue à réduire la durée de vie du niveau u et donc à augmenter la largeur de raie). Du fait de l'élargissement des niveaux il faut prendre en compte toutes les transitions possibles avec une énergie
correspond au cas de l'égalité. Elle est proportionnelle au coefficient d'Einstein d'émission spontanée en absence de rayonnement (en présence de rayonnement il faudra considérer ainsi la désexcitation stimulée qui contribue à réduire la durée de vie du niveau u et donc à augmenter la largeur de raie). Du fait de l'élargissement des niveaux il faut prendre en compte toutes les transitions possibles avec une énergie 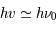 . On définit généralement une largeur naturelle de la raie en fréquence
. On définit généralement une largeur naturelle de la raie en fréquence 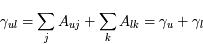 , où les indices
, où les indices 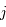 et
et 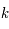 correspondent à des états d'énergie inférieure respectivement à l'énergie du niveau supérieur et à l'énergie du niveau inférieur et les deux sommes donnent la largeur du niveau supérieur et du niveau inférieur. Par exemple, on observera une raie faible mais large si le niveau inférieur est fortement élargi.
correspondent à des états d'énergie inférieure respectivement à l'énergie du niveau supérieur et à l'énergie du niveau inférieur et les deux sommes donnent la largeur du niveau supérieur et du niveau inférieur. Par exemple, on observera une raie faible mais large si le niveau inférieur est fortement élargi.
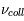 (chaque atome subit en moyenne
(chaque atome subit en moyenne 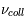 collisions par unité de temps) et contribuent à l'élargissement de la raie en fréquence qu'on écrit :
collisions par unité de temps) et contribuent à l'élargissement de la raie en fréquence qu'on écrit : 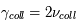 . Il faut remarquer que la fréquence des collisions augmente avec la densité du milieu. On s'attend donc à observer des élargissements collisionnels plus importants dans des environnement denses, comme les atmosphères planétaires et stellaires. Dans les nuages d'hydrogène atomique et les nuages moléculaires les effets collisionnels sont dominés par d'autres sources d'élargissement que nous allons voir dans la suite du cours (effet Doppler, turbulence). Puisque à la fois l'élargissement naturel et l'élargissement associé aux collisions sont caractérisés par des profils de la même forme, on peut définir une constante
. Il faut remarquer que la fréquence des collisions augmente avec la densité du milieu. On s'attend donc à observer des élargissements collisionnels plus importants dans des environnement denses, comme les atmosphères planétaires et stellaires. Dans les nuages d'hydrogène atomique et les nuages moléculaires les effets collisionnels sont dominés par d'autres sources d'élargissement que nous allons voir dans la suite du cours (effet Doppler, turbulence). Puisque à la fois l'élargissement naturel et l'élargissement associé aux collisions sont caractérisés par des profils de la même forme, on peut définir une constante 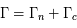 qui contient une contribution naturelle
qui contient une contribution naturelle 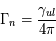 et une contribution collisionnelle
et une contribution collisionnelle 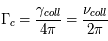 et décrire le profil de la raie tel que :
et décrire le profil de la raie tel que :
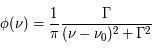 .
.
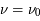 , qui vaut
, qui vaut 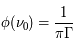 et sa largeur totale à mi-hauteur en unité de fréquence
et sa largeur totale à mi-hauteur en unité de fréquence 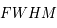 (de l'anglais Full Width at Half Maximum). Cette largeur est déterminée en remplaçant la valeur de la fonction à mi-hauteur (
(de l'anglais Full Width at Half Maximum). Cette largeur est déterminée en remplaçant la valeur de la fonction à mi-hauteur (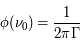 ) dans l'équation qui décrit
) dans l'équation qui décrit 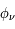 , dont on obtient
, dont on obtient 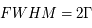 . Un profil Lorentzien centré (
. Un profil Lorentzien centré (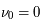 ) est montré sur la figure pour différentes valeurs de la constante
) est montré sur la figure pour différentes valeurs de la constante 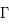 .
.

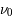 dans le référentiel d'un atome en mouvement seront détectés à une fréquence
dans le référentiel d'un atome en mouvement seront détectés à une fréquence 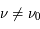 par l'observateur. Le décalage en fréquence d'un atome qui possède une vitesse relative le long de la ligne de visée
par l'observateur. Le décalage en fréquence d'un atome qui possède une vitesse relative le long de la ligne de visée 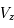 , pour des vitesses non relativistes, vaut :
, pour des vitesses non relativistes, vaut : 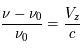 .
.
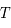 dont la projection de la vitesse sur l'axe de visée
dont la projection de la vitesse sur l'axe de visée 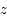 est comprise entre
est comprise entre 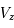 et
et 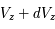 est donc proportionnel à la fonction
est donc proportionnel à la fonction 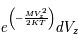 , où M est la masse d'un atome. En utilisant la formule pour le décalage Doppler on déduit
, où M est la masse d'un atome. En utilisant la formule pour le décalage Doppler on déduit 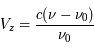 ,
, 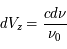 et on peut exprimer la distribution des atomes en fonction de la fréquence. Par conséquent, l'intensité de l'émission dans l'intervalle de fréquence de
et on peut exprimer la distribution des atomes en fonction de la fréquence. Par conséquent, l'intensité de l'émission dans l'intervalle de fréquence de 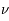 à
à 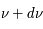 est proportionnelle à
est proportionnelle à 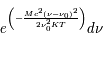 . Si l'effet Doppler est la source dominant d'élargissement de la raie, son profil est la somme des contributions de chaque atome, ce qui donne un profil de forme gaussienne :
. Si l'effet Doppler est la source dominant d'élargissement de la raie, son profil est la somme des contributions de chaque atome, ce qui donne un profil de forme gaussienne :
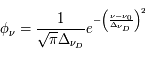 .
.
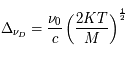 , appelée largeur Doppler de la raie, est reliée à la largeur à mi-hauteur de la gaussienne par
, appelée largeur Doppler de la raie, est reliée à la largeur à mi-hauteur de la gaussienne par 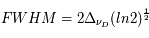 . L'aire du profil, obtenue intégrant sur la fréquence, vaut 1 et sa valeur maximale, atteinte à
. L'aire du profil, obtenue intégrant sur la fréquence, vaut 1 et sa valeur maximale, atteinte à 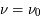 , est
, est 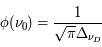 . Dans le milieu interstellaire, l'élargissement associé à l'effet Doppler est généralement plus important que la largeur naturelle et l'élargissement dû aux collisions. Un exemple est représenté par la raie à 21 cm de l'hydrogène atomique, l'élargissement lorentzien étant extrêmement faible puisque la durée de vie du niveau supérieur n'est limitée que par les collisions, rares dans le milieu interstellaire diffus.
. Dans le milieu interstellaire, l'élargissement associé à l'effet Doppler est généralement plus important que la largeur naturelle et l'élargissement dû aux collisions. Un exemple est représenté par la raie à 21 cm de l'hydrogène atomique, l'élargissement lorentzien étant extrêmement faible puisque la durée de vie du niveau supérieur n'est limitée que par les collisions, rares dans le milieu interstellaire diffus.
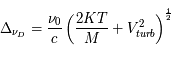 , où
, où 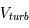 est la vitesse caractéristique de la turbulence. Dans les nuages interstellaires, la vitesse turbulente est de l'ordre de quelques kilomètres par seconde. Puisque la température des nuages n'est pas élevée, l'effet Doppler est dominé par la turbulence. Des mouvements turbulents plus importants ont été observés dans la nébuleuse d'Orion (voir le TP
est la vitesse caractéristique de la turbulence. Dans les nuages interstellaires, la vitesse turbulente est de l'ordre de quelques kilomètres par seconde. Puisque la température des nuages n'est pas élevée, l'effet Doppler est dominé par la turbulence. Des mouvements turbulents plus importants ont été observés dans la nébuleuse d'Orion (voir le TP 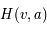 , dont les valeurs sont données dans la littérature :
, dont les valeurs sont données dans la littérature : 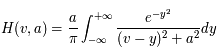 . Cette forme est obtenue par un changement de variable dans les fonctions lorentzienne et gaussienne tel que :
. Cette forme est obtenue par un changement de variable dans les fonctions lorentzienne et gaussienne tel que : 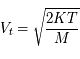 ,
, 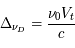 ,
, 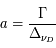 ,
, 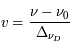 et donne le profil de raie normalisé :
et donne le profil de raie normalisé :
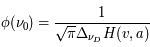 .
.
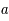 qui quantifie l'importance relative des différents processus qui contribuent à l'élargissement de raie. On remarque que dans le cas limite d'élargissement naturel et collisionnel négligeable (a=0) la fonction a une forme gaussienne, tandis que c'est une lorentzienne pour un élargissement Doppler négligeable (voir par exemple la courbe a=20). En général la fonction présente une allure gaussienne au coeur (
qui quantifie l'importance relative des différents processus qui contribuent à l'élargissement de raie. On remarque que dans le cas limite d'élargissement naturel et collisionnel négligeable (a=0) la fonction a une forme gaussienne, tandis que c'est une lorentzienne pour un élargissement Doppler négligeable (voir par exemple la courbe a=20). En général la fonction présente une allure gaussienne au coeur (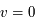 ) et lorentzienne dans les ailes.
) et lorentzienne dans les ailes.

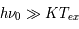 . Le niveau supérieur de la transition a une énergie très élevée et il est donc très peu peuplé, ce qui nous autorise à négliger l'émission spontanée et induite à partir du niveau supérieur. Sous ces hypothèses, la solution de l'équation de transfert et la profondeur optique se réduisent à
. Le niveau supérieur de la transition a une énergie très élevée et il est donc très peu peuplé, ce qui nous autorise à négliger l'émission spontanée et induite à partir du niveau supérieur. Sous ces hypothèses, la solution de l'équation de transfert et la profondeur optique se réduisent à 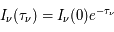 et
et 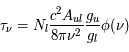 (voir les pages
(voir les pages 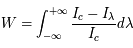 , où
, où 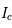 est l'intensité du continuum stellaire du spectre considéré et
est l'intensité du continuum stellaire du spectre considéré et 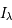 l'intensité de la raie à la longueur d'onde
l'intensité de la raie à la longueur d'onde 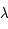 . On l'appelle largeur équivalente car cette quantité est équivalente à la largeur d'une raie absorbante rectangulaire allant du continu jusqu'à 0 et ayant la même aire que la raie observée. En remplaçant l'expression pour l'intensité de raie dans le cas de pure absorption et en posant
. On l'appelle largeur équivalente car cette quantité est équivalente à la largeur d'une raie absorbante rectangulaire allant du continu jusqu'à 0 et ayant la même aire que la raie observée. En remplaçant l'expression pour l'intensité de raie dans le cas de pure absorption et en posant 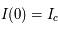 on obtient que
on obtient que 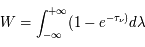 .
.
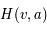 , qui contient l'information sur le profil de la raie dans le cas général où la largeur naturelle, les effets collisionnels et l'effet Doppler sont pris en compte, et un paramètre
, qui contient l'information sur le profil de la raie dans le cas général où la largeur naturelle, les effets collisionnels et l'effet Doppler sont pris en compte, et un paramètre 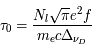 qui représente la profondeur optique au centre de la raie et dépend de la densité de colonne, de la largeur Doppler de la raie et des caractéristiques de la transition atomique par la quantité
qui représente la profondeur optique au centre de la raie et dépend de la densité de colonne, de la largeur Doppler de la raie et des caractéristiques de la transition atomique par la quantité 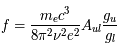 . Il s'agit d'un coefficient sans dimension souvent utilisé pour exprimer la probabilité d'émission spontanée qu'on appelle force de l'oscillateur. Il est possible de trouver dans la littérature des tables de
. Il s'agit d'un coefficient sans dimension souvent utilisé pour exprimer la probabilité d'émission spontanée qu'on appelle force de l'oscillateur. Il est possible de trouver dans la littérature des tables de 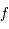 pour chaque raie. Nous pouvons donc écrire
pour chaque raie. Nous pouvons donc écrire 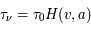 .
.
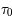 et donc du nombre d'atomes absorbants le long de la ligne de visée.
et donc du nombre d'atomes absorbants le long de la ligne de visée.
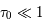 : la raie est optiquement mince. On en déduit que
: la raie est optiquement mince. On en déduit que 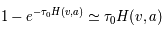 et le calcul de la largeur équivalente se réduit à :
et le calcul de la largeur équivalente se réduit à : 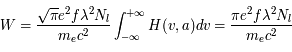 car l'intégrale de la fonction de Voigt vaut
car l'intégrale de la fonction de Voigt vaut 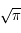 . Il s'agit en effet de raies faibles où la partie centrale domine le profil. On a vu que dans cette région la fonction de Voigt a une allure gaussienne. Le coeur dû à l'effet Doppler domine. Pour les raies optiquement minces la largeur équivalente est proportionnelle à la densité de colonne et on parle de régime linéaire. Dans ce régime les mesures de la largeur équivalente permettent une détermination précise de la densité de colonne, les paramètres atomiques étant connus.
. Il s'agit en effet de raies faibles où la partie centrale domine le profil. On a vu que dans cette région la fonction de Voigt a une allure gaussienne. Le coeur dû à l'effet Doppler domine. Pour les raies optiquement minces la largeur équivalente est proportionnelle à la densité de colonne et on parle de régime linéaire. Dans ce régime les mesures de la largeur équivalente permettent une détermination précise de la densité de colonne, les paramètres atomiques étant connus. 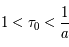 : lorsque le nombre d'atomes absorbants augmente, le centre de la raie devient de plus en plus optiquement épais. La contribution des ailes du profil reste toutefois négligeable. L'absorption principale est toujours due à l'effet Doppler, mais il y a une saturation de la raie qui prend une forme rectangulaire au centre. En s'éloignant du centre une absorption partielle persiste et la largeur équivalente croît lentement en fonction de la densité de colonne. On peut montrer que dans ce domaine
: lorsque le nombre d'atomes absorbants augmente, le centre de la raie devient de plus en plus optiquement épais. La contribution des ailes du profil reste toutefois négligeable. L'absorption principale est toujours due à l'effet Doppler, mais il y a une saturation de la raie qui prend une forme rectangulaire au centre. En s'éloignant du centre une absorption partielle persiste et la largeur équivalente croît lentement en fonction de la densité de colonne. On peut montrer que dans ce domaine 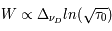 . Malheureusement des nombreuses raies d'absorption interstellaire se trouvent dans ce régime où la largeur équivalente est très peu sensible à la densité de colonne, ce qui en rend difficile l'estimation. De plus les mesures sont compliquées par la dépendance de la largeur Doppler.
. Malheureusement des nombreuses raies d'absorption interstellaire se trouvent dans ce régime où la largeur équivalente est très peu sensible à la densité de colonne, ce qui en rend difficile l'estimation. De plus les mesures sont compliquées par la dépendance de la largeur Doppler.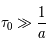 : la raie est saturée jusqu'aux ailes lorentziennes et la largeur équivalente varie proportionnellement à la racine de la densité de colonne et de la largeur naturelle (
: la raie est saturée jusqu'aux ailes lorentziennes et la largeur équivalente varie proportionnellement à la racine de la densité de colonne et de la largeur naturelle (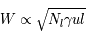 ).
).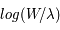 en fonction de
en fonction de 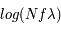 . Elle est composée d'une partie linéaire, d'une portion plate dont la position sur l'axe vertical dépend de la valeur de la largeur Doppler et d'une région dont la pente est fonction de la largeur naturelle (et éventuellement de la densité du gaz s'il existe une contribution des collisions à l'élargissement). Pour construire cette courbe il faut donc connaître
. Elle est composée d'une partie linéaire, d'une portion plate dont la position sur l'axe vertical dépend de la valeur de la largeur Doppler et d'une région dont la pente est fonction de la largeur naturelle (et éventuellement de la densité du gaz s'il existe une contribution des collisions à l'élargissement). Pour construire cette courbe il faut donc connaître 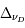 et
et 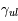 . Dans ce cas, on peut placer la raie sur la courbe, en déterminant la largeur équivalente et en déduire la densité de colonne. Dans la figure on montre les courbes de croissance obtenues d'observations de l'étoile
. Dans ce cas, on peut placer la raie sur la courbe, en déterminant la largeur équivalente et en déduire la densité de colonne. Dans la figure on montre les courbes de croissance obtenues d'observations de l'étoile 
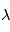 est décrite par la quantité
est décrite par la quantité 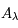 (mesurée en magnitude), définie comme la différence entre la magnitude observée
(mesurée en magnitude), définie comme la différence entre la magnitude observée 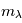 d'une étoile dont la lumière a traversé le nuage de poussières (de profondeur optique
d'une étoile dont la lumière a traversé le nuage de poussières (de profondeur optique 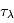 ) et celle qu'on observerait en l'absence d'extinction,
) et celle qu'on observerait en l'absence d'extinction, 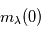 . Comme l'émission des poussières est en général négligeable à la longueur d'onde considérée, le flux spécifique
. Comme l'émission des poussières est en général négligeable à la longueur d'onde considérée, le flux spécifique 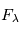 est atténué par un facteur
est atténué par un facteur 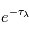 . Avec la relation entre magnitude et flux, on obtient :
. Avec la relation entre magnitude et flux, on obtient : ![A_\lambda(mag)=m_\lambda - m_\lambda(0) = -2.5log_{10}\left[\frac{F_\lambda(\tau_\lambda)}{F_\lambda(0)}\right]=-2.5log_{10}[e^{-\tau_\lambda}]=1.086\tau_\lambda](../pages_transfert-rayon/equations_transfert-rayon/equation328.png) . On voit que la valeur de
. On voit que la valeur de 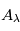 en magnitude est essentiellement égale à l'opacité des poussières à cette longueur d'onde ; elle est donc proportionnelle à la densité colonne de poussières sur la ligne de visée.
en magnitude est essentiellement égale à l'opacité des poussières à cette longueur d'onde ; elle est donc proportionnelle à la densité colonne de poussières sur la ligne de visée.
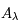 est portée en fonction de l'inverse de la longueur d'onde. Elle est obtenue en comparant à différentes longueurs d'onde la distribution spectrale d'énergie de deux étoiles supposées identiques, puisque de même type spectral et classe de luminosité, l'une de deux étoiles est fortement affectée par l'extinction et donc par la présence d'une grande quantité de poussières le long de la ligne de visée, l'autre se trouve en l'absence d'extinction. Afin d'obtenir un résultat indépendant de la quantité totale de poussières sur la ligne de visée, il est d'usage de normaliser la courbe ainsi obtenue à la différence d'extinction dans les bandes spectrales B (bleue, centrée à 4400
est portée en fonction de l'inverse de la longueur d'onde. Elle est obtenue en comparant à différentes longueurs d'onde la distribution spectrale d'énergie de deux étoiles supposées identiques, puisque de même type spectral et classe de luminosité, l'une de deux étoiles est fortement affectée par l'extinction et donc par la présence d'une grande quantité de poussières le long de la ligne de visée, l'autre se trouve en l'absence d'extinction. Afin d'obtenir un résultat indépendant de la quantité totale de poussières sur la ligne de visée, il est d'usage de normaliser la courbe ainsi obtenue à la différence d'extinction dans les bandes spectrales B (bleue, centrée à 4400 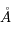 ) et V (visible, centrée à 5500
) et V (visible, centrée à 5500 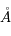 ) dite excès de couleur,
) dite excès de couleur, 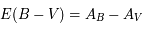 . La courbe d'extinction totaleest alors donnée par
. La courbe d'extinction totaleest alors donnée par 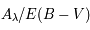 en fonction de
en fonction de 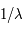 en
en 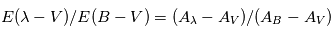 . Un exemple de courbe interstellaire moyenne de l'infrarouge proche à l'ultraviolet est montrée sur la figure ci-dessous. Dans cette courbe on peut distinguer trois régimes selon le domaine de longueur d'onde considéré : une croissance de l'extinction approximativement linéaire en
. Un exemple de courbe interstellaire moyenne de l'infrarouge proche à l'ultraviolet est montrée sur la figure ci-dessous. Dans cette courbe on peut distinguer trois régimes selon le domaine de longueur d'onde considéré : une croissance de l'extinction approximativement linéaire en 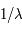 dans la partie proche infrarouge et visible, un pic ultraviolet centré à 2175
dans la partie proche infrarouge et visible, un pic ultraviolet centré à 2175 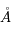 associé à des particules carbonées, une forte augmentation dans l'ultraviolet lointain. La lumière reçue sera donc soumise à un rougissement à cause de la présence d'une extinction plus forte de la lumière bleue que de la lumière rouge.
associé à des particules carbonées, une forte augmentation dans l'ultraviolet lointain. La lumière reçue sera donc soumise à un rougissement à cause de la présence d'une extinction plus forte de la lumière bleue que de la lumière rouge.

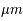 . Les nuages moléculaires représentent une classe privilégiée d'objets détectés avec cet instrument. Nous analyserons notamment un spectre en émission de la nébuleuse d'Orion. FUSE a été lancé en 1999 afin d'obtenir des spectres stellaires dans le domaine de l'ultraviolet lointain (de 90 à 120 nm). La deuxième partie du TP sera consacrée à l'étude des raies d'absorption interstellaires observées dans le spectre de l'étoile HD34078. Nous profiterons notamment des outils qui permettent de visualiser les spectres en utilisant différentes unités de mesure afin d'identifier les spectres et les raies d'intérêt dans les nombreuses données spectrales d'archives disponibles. En étudiant une raie en émission du carbone excité observée par ISO nous exploiterons les outils d'ajustement afin de déterminer l'effet d'élargissement dominant. Enfin, l'outil de calcul de la largeur équivalente nous permettra de dériver la densité de colonne d'une raie excitée en absorption de l'hydrogène moléculaire observée par FUSE.
. Les nuages moléculaires représentent une classe privilégiée d'objets détectés avec cet instrument. Nous analyserons notamment un spectre en émission de la nébuleuse d'Orion. FUSE a été lancé en 1999 afin d'obtenir des spectres stellaires dans le domaine de l'ultraviolet lointain (de 90 à 120 nm). La deuxième partie du TP sera consacrée à l'étude des raies d'absorption interstellaires observées dans le spectre de l'étoile HD34078. Nous profiterons notamment des outils qui permettent de visualiser les spectres en utilisant différentes unités de mesure afin d'identifier les spectres et les raies d'intérêt dans les nombreuses données spectrales d'archives disponibles. En étudiant une raie en émission du carbone excité observée par ISO nous exploiterons les outils d'ajustement afin de déterminer l'effet d'élargissement dominant. Enfin, l'outil de calcul de la largeur équivalente nous permettra de dériver la densité de colonne d'une raie excitée en absorption de l'hydrogène moléculaire observée par FUSE.

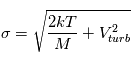 de la source IRC2 dans la nébuleuse d'Orion et comparer le résultat avec les valeurs suggérées dans l'article de la littérature dont la figure est extraite et qui sont supérieures à 100 km.s-1.
de la source IRC2 dans la nébuleuse d'Orion et comparer le résultat avec les valeurs suggérées dans l'article de la littérature dont la figure est extraite et qui sont supérieures à 100 km.s-1.
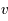 et J du niveau d'énergie inférieur de ces transitions sont également affichés en haut de la figure. En suivant la procédure décrite dans la page précédente, charger les données spectrales FUSE (Far Ultraviolet Spectroscopic Explorer) disponibles pour la cible HD 34078. Ajuster les unités de mesure des axes et visualiser les spectres dans le même intervalle de longueur d'onde du spectre montré sur la figure . La richesse de ces spectres les rend difficiles à analyser, en particulier en ce qui concerne l'identification des raies. Le logiciel VoSpec fournit un outil d'exécution d'opérations arithmétiques sur les spectres. On peut notamment sommer des spectres afin de maximiser le rapport entre le signal observé et le bruit instrumental. Cet outil s'active en cliquant sur la première icône qui apparaît dans la barre des outils de la fenêtre de contrôle. Une fenêtre de calcul s'affiche et il faut y déplacer les spectres à sommer, en interposant le symbole +, et enfin appuyer sur le symbole =. Une nouvelle liste, appelée ADD, apparaît en bas de celle des spectres extraits. Il faut la déplier, cocher la case du nouveau spectre calculé et valider avec View pour visualiser le résultat.
et J du niveau d'énergie inférieur de ces transitions sont également affichés en haut de la figure. En suivant la procédure décrite dans la page précédente, charger les données spectrales FUSE (Far Ultraviolet Spectroscopic Explorer) disponibles pour la cible HD 34078. Ajuster les unités de mesure des axes et visualiser les spectres dans le même intervalle de longueur d'onde du spectre montré sur la figure . La richesse de ces spectres les rend difficiles à analyser, en particulier en ce qui concerne l'identification des raies. Le logiciel VoSpec fournit un outil d'exécution d'opérations arithmétiques sur les spectres. On peut notamment sommer des spectres afin de maximiser le rapport entre le signal observé et le bruit instrumental. Cet outil s'active en cliquant sur la première icône qui apparaît dans la barre des outils de la fenêtre de contrôle. Une fenêtre de calcul s'affiche et il faut y déplacer les spectres à sommer, en interposant le symbole +, et enfin appuyer sur le symbole =. Une nouvelle liste, appelée ADD, apparaît en bas de celle des spectres extraits. Il faut la déplier, cocher la case du nouveau spectre calculé et valider avec View pour visualiser le résultat. 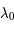 ) connue, on peut évaluer le décalage par différence entre la valeur de la longueur d'onde du centre de la raie
) connue, on peut évaluer le décalage par différence entre la valeur de la longueur d'onde du centre de la raie 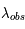 et la valeur à repos :
et la valeur à repos : 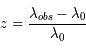 (se rappeler que la valeur de la longueur d'onde à différentes positions du spectre s'affiche en bas à gauche en suivant le déplacement du curseur dans la fenêtre de visualisation). La correction s'applique en cochant la petite case à côté de la case Redshift et en visualisant à nouveau le spectre.
(se rappeler que la valeur de la longueur d'onde à différentes positions du spectre s'affiche en bas à gauche en suivant le déplacement du curseur dans la fenêtre de visualisation). La correction s'applique en cochant la petite case à côté de la case Redshift et en visualisant à nouveau le spectre. 
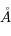 -1.
-1.
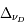 . Elles fournissent donc une mesure de la densité de colonne, la largeur naturelle de la raie (
. Elles fournissent donc une mesure de la densité de colonne, la largeur naturelle de la raie (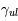 ) étant connue. Par contre, les raies issues des niveaux compris entre
) étant connue. Par contre, les raies issues des niveaux compris entre 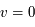 , J = 4 et
, J = 4 et 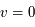 , J = 9 sont saturées et non lorentziennes, elles se situent donc sur la partie plate de la courbe de croissance. La connaissance de la largeur Doppler est alors un élément indispensable à la détermination des densités de colonne. Pour les niveaux d'énergie supérieure à
, J = 9 sont saturées et non lorentziennes, elles se situent donc sur la partie plate de la courbe de croissance. La connaissance de la largeur Doppler est alors un élément indispensable à la détermination des densités de colonne. Pour les niveaux d'énergie supérieure à 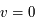 , J = 9, il est possible de trouver dans le spectre des raies optiquement minces et d'en déduire la densité de colonne directement à partir des largeurs équivalentes.
On s'intéresse donc à la raie spectrale optiquement mince correspondante à la transition
, J = 9, il est possible de trouver dans le spectre des raies optiquement minces et d'en déduire la densité de colonne directement à partir des largeurs équivalentes.
On s'intéresse donc à la raie spectrale optiquement mince correspondante à la transition 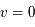 , J = 10, dont la longueur d'onde à repos vaut
, J = 10, dont la longueur d'onde à repos vaut 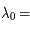 1045.051
1045.051 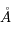 et la force de l'oscillateur
et la force de l'oscillateur 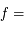 1.47x10-2. Noter que le centre de la raie peut être décalé dans le spectre observé à cause du mouvement du nuage interstellaire interposé entre la source HD 34078 et l'observateur. Pour les applications numériques, on rappelle également les valeurs de la charge de l'électron (e=4.0832x10-10 esu), de sa masse (
1.47x10-2. Noter que le centre de la raie peut être décalé dans le spectre observé à cause du mouvement du nuage interstellaire interposé entre la source HD 34078 et l'observateur. Pour les applications numériques, on rappelle également les valeurs de la charge de l'électron (e=4.0832x10-10 esu), de sa masse (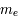 =9.1094x10-28 g) et de la vitesse de la lumière (c=2.9979x1010 cm.s-1) dans le système CGS.
=9.1094x10-28 g) et de la vitesse de la lumière (c=2.9979x1010 cm.s-1) dans le système CGS.
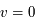 , J = 10 et choisir le spectre où la raie est plus visible. Vérifier en particulier que la somme de plusieurs spectres caractérisés par des temps de pose différents maximise le rapport signal sur bruit, ce qui rend les raies plus visibles.
, J = 10 et choisir le spectre où la raie est plus visible. Vérifier en particulier que la somme de plusieurs spectres caractérisés par des temps de pose différents maximise le rapport signal sur bruit, ce qui rend les raies plus visibles.
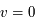 , J = 10 et appliquer la correction par l'outil de calcul du décalage vers le rouge. Vérifier sur le spectre corrigé que la longueur d'onde du centre de la raie se trouve bien à la valeur au repos donnée dans l'énoncé du TP.
, J = 10 et appliquer la correction par l'outil de calcul du décalage vers le rouge. Vérifier sur le spectre corrigé que la longueur d'onde du centre de la raie se trouve bien à la valeur au repos donnée dans l'énoncé du TP.
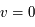 , J = 10 et en déduire une estimation de la densité de colonne de l'hydrogène moléculaire. Comparer le résultat avec les valeurs suggérées dans l'article de la littérature dont la figure est extraite, tels que 2.5 1013<
, J = 10 et en déduire une estimation de la densité de colonne de l'hydrogène moléculaire. Comparer le résultat avec les valeurs suggérées dans l'article de la littérature dont la figure est extraite, tels que 2.5 1013<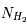 < 6 1013.
< 6 1013.
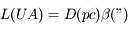 .
La mesure de la taille angulaire
.
La mesure de la taille angulaire 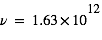 s-1) et une largeur à mi hauteur en unités de fréquence
s-1) et une largeur à mi hauteur en unités de fréquence 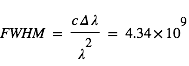 s-1. En utilisant les formules données dans le cours (en négligeant le décalage vers le rouge de la fréquence au centre de la raie
s-1. En utilisant les formules données dans le cours (en négligeant le décalage vers le rouge de la fréquence au centre de la raie 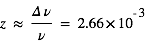 dont
dont 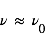 ) on en tire un élargissement Doppler
) on en tire un élargissement Doppler 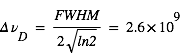 s-1et une dispersion de vitesse
s-1et une dispersion de vitesse 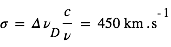 en accord avec les valeurs de l'article de littérature.
en accord avec les valeurs de l'article de littérature.
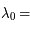 1045.051
1045.051 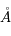 .
.
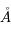 (
(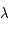 exprimés en
exprimés en 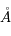 ) :
) : 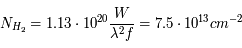 . Cette valeur peut être considérée en accord avec les résultat de l'article de la littérature car le calcul de la largeur équivalente est très sensible au choix du niveau du continu pendant la procédure de sélection de la raie.
. Cette valeur peut être considérée en accord avec les résultat de l'article de la littérature car le calcul de la largeur équivalente est très sensible au choix du niveau du continu pendant la procédure de sélection de la raie.